DOI:10.32604/cmc.2022.024206

| Computers, Materials & Continua DOI:10.32604/cmc.2022.024206 |  |
| Article |
Intelligent Deer Hunting Optimization Based Grid Scheduling Scheme
1Department of Natural and Applied Sciences, College of Community-Aflaj, Prince Sattam bin Abdulaziz University, Al-Kharj, 16278, Saudi Arabia
2Department of Computer Science, College of Science & Art at Mahayil, King Khalid University, Muhayel Aseer, 62529, Saudi Arabia
3Department of Natural and Applied Sciences, Community College, Qassim University, Al-Bukairiyah, 52571, Saudi Arabia
4Faculty of Computer and IT, Sana'a University, Sana'a, Yemen
5Department of Computer and Self Development, Preparatory Year Deanship, Prince Sattam bin Abdulaziz University, Al-Kharj, 16278, Saudi Arabia
*Corresponding Author: Manar Ahmed Hamza. Email: ma.hamza@psau.edu.sa
Received: 08 October 2021; Accepted: 16 November 2021
Abstract: The grid environment is a dynamic, heterogeneous, and changeable computing system that distributes various services amongst different clients. To attain the benefits of collaborative resource sharing in Grid computing, a novel and proficient grid resource management system (RMS) is essential. Therefore, detection of an appropriate resource for the presented task is a difficult task. Several scientists have presented algorithms for mapping tasks to the resource. Few of them focus on fault tolerance, user fulfillment, and load balancing. With this motivation, this study designs an intelligent grid scheduling scheme using deer hunting optimization algorithm (DHOA), called IGSS-DHOA which schedules in such a way that the makespan gets minimized in the grid platform. The IGSS-DHOA technique is mainly based on the hunting nature of humans toward deer. It also derives an objective function with candidate solution (schedule) as input and the outcome is the makespan value denoting the quality of the candidate solution. The simulation results highlighted the supremacy of the IGSS-DHOA technique over the recent state of art techniques with the minimal average processing cost of 31717.9.
Keywords: Grid services; grid scheduling; resources; makespan; np hard problem; metaheuristics
Grid computing is a set of heterogeneous and dynamic resources from various administrative domains and provides access to the resource [1]. The resource in the grid is gathered to create a virtual organization i.e., employed for solving huge business/scientific problems. The primary objective of this technique is to distribute scattered and idle resources like storage capacity and computation power. Mainly, Grid computing is separated into 2 kinds namely data and computation grids. The major purpose of grid computing is problem solving, i.e., time consuming and complex [2]. This aim might be attained by the processing power of the computer present on the grid platform. Computation grid is determined as integration of software and hardware infrastructures which provide inexpensive, consistent, and pervasive accessing to higher end computation resources. Data grid is an integration of huge datasets i.e., primarily utilized for providing data to the application [3]. To exploit the resource effectively and in order to fulfill each requirement of the user, it is necessary to efficient scheduling approach.
Once the Resource Management System (RMS) obtains the service request from the user, it splits the presented service tasks into a subtask that could be performed simultaneously. The RMS assigns 3 subtasks to the accessible resource for concurrent performance [4]. When the resource finishes the allocated subtasks, they return the result back to the RMS. Lastly, the RMS incorporates the obtained result to the whole output of the presented task. In order to attain the aim of computation grids and maximize the consumption of the resource in a grid platform, it is significant how to schedule subtasks amongst the resources, a moderate scheduling approach should be adapted for getting the minimal runtime. Hence, task scheduling need to be tackled is one of NP Complete problem in grid platform. The scheduler could be placed level by level [5]. The local schedulers are positioned within a cluster and are in charge to schedule within the cluster. The scheduler is at the topmost levels in the grid broker. Scheduling could be hierarchical, centralized, and decentralized. In centralized scheduling, the scheduler has higher control over the resource. In decentralized scheduling, there is no central entity for having control over the resource, and the scheduling decisions are created separately. In hierarchical scheduling, various levels of scheduler are positioned and scheduling is made at each level.
Grid schedulers work in 3 stages: job execution, and resource discovery, and allocation [6]. The resource discovery stage consists of detecting the accessible resource from the resource pool, while resource allocation stage includes election of appropriate resources and assigning the elected resource to the tasks. The last stage is implementing the job at resource location. Grid schedulers search the suitable resource for jobs and minimized makespan or runtime, optimal consumption of the resource, and enhanced users fulfillment. Various scheduling approaches were introduced in the previous years. This scheduling algorithm mostly focuses on decreasing fault tolerance and makespan and few algorithms concentrate on user's deadline [7]. The presented method fits for computation grid with computing resource and scheduling is made by focusing on fault tolerance, load balancing, and various QoS needs like user deadline and budget/cost. The residual parts of this study are organized by methods and materials that explain the work made before and the recently presented algorithms nature and architecture. Subsequently, the simulation result shows the conclusion and comparison. The grid computing platform consists of heterogeneous resources i.e., shared geographically. Therefore, detection of an appropriate resource for the presented task is a difficult task [8]. Several scientists have presented algorithms for mapping tasks to the resource. Few of them focus on fault tolerance, user fulfillment, and load balancing.
This study designs an intelligent grid scheduling scheme using deer hunting optimization algorithm (DHOA), called IGSS-DHOA. The goal of the IGSS-DHOA technique aims to determine a solution which produces optimum schedules in such a way that the makespan gets minimized in the grid platform. The IGSS-DHOA algorithm has derived an objective function with the minimization of makespan in the grid environment with the candidate solution as input and makespan value as output. The design of DHOA technique for scheduling process shows the novelty of the work. In order to assess the optimal scheduling performance of the IGSS-DHOA technique, an extensive simulation analysis is carried out.
The rest of the paper is organized as follows. Section 2 offers a literature review and Section 3 proposes the IGSS-DHOA technique. Then, Section 4 offers the experimental validation and Section 5 draws the conclusion.
This section offers a comprehensive review of existing grid scheduling approaches in the literature. Sousa et al. [9] proposed 2 primary solution methods to be utilized by a metaheuristic algorithm (SA). This algorithm is evaluated and tested using another published method which obtains primary solution. The presented algorithm was introduced as a module to be more flexible while using another metaheuristic compared to SA. Liu et al. [10] present a new method on the basis of PSO to schedule tasks on computation grid. The representation of the velocity and position of the particle in traditional PSO is expanded from the real vector to fuzzy matrices. The presented method is to vigorously produce an optimum schedule thus finishing the task within least amount of time and using the resources in an effective manner.
Dan et al. [11] construct the knowledge staff scheduling method with the help of bacterial foraging method and analyze the execution disadvantages, principles, and advantages of the approach. The effect of fundamental parameters in the system performance on the system model is analyzed. For optimizing the untraditional foraging approach, the enhancement measure of bacterial foraging behaviour has been presented. Lastly, the effeminacy of the optimized bacterial foraging approach is compared and tested with the fundamental bacterial foraging, GA, and PSO strategy. Khan et al. [12], proposed a QoS aware architecture for scheduling data traffics in cognitive radio based SG transmission network. The channel accessible to SCN is classified as higher and lower bandwidths. For all bandwidths, each SG application is classified into numerous priority classes includes throughput and latency subclasses. The entire objective functions are the weighted amount of individual utility functions of throughput and latency. New utilization of Adam optimizer is presented for minimizing the latency and maximizing the throughput by attaining optimum system costs, results in optimum decision policy.
In Nazir et al. [13], a COA based LB method is presented for improved management of resources. The COA is utilized for assigning appropriate tasks to VM. The approach identifies over and under used VM and switchoff the under used VM. This procedure ignored several VMs that puts a huge effect on power requirements. Keerthika et al. [14], introduced a novel BSA approach to consider user's fulfillment and fault tolerance. The important role of this study involves attaining user's fulfillment and tolerance and minimize the makespan of tasks. Jayasudha et al. [15] proposed a firefly approach for optimization. It detects a solution to optimization problems in an LB, or method and predicts social behavior in the existence of objectives. The presented method is established to carry out the present systems based on resubmitted moment, quick response, cost time convergence, and complexity completed and finished Grid lets.
Kołodziej et al. [16], proposed a grid resource scheduling approach depending on an optimized hierarchical framework. Initially, using efficiently dividing the hierarchical features of the grid framework, the resource in the intensive grids are classified and scheduled based on the resource characteristics data, thus the grid resource could be hierarchically scheduled, the resource scheduling efficacy could be enhanced by attaining the hierarchical features of the grid, and the grid scheduling approach of the intensive framework could be added by the max and min approach, and lastly, the optimization of the grid resource scheduling approach can be accomplished.
Keerthika et al. [17] designed a RA approach i.e., users fulfillment, fault tolerance, budget limited, and target LB by taking into account the aforementioned conditions. The presented MLFT decreases the task failure rate, schedule cost, and makespan also enhances resource consumption. Eng et al. [18] presented a new hybrid heuristic based approach that synergized the outstanding diversifications ability of GD approach using the strong systematic multi neighbourhood search approach taken in VND approach, for effectively scheduling independent tasks in Grid computing platform with an aim of minimizing the makespan.
The resource in computational grid is needed for performing the function, i.e., the processor utilized to process data. An investigation organization of computational grid has been responsible to study finding and distribution of tasks to certain resources. In general, it can be simple in getting the data on the capability for processing data in accessible resources. During this work, the scheduling issue in which n task works on m calculating resource with objective for minimizing the makespan and employ the resource effectually when the number of tasks is lesser than the number of resources in grid environments, the tasks are assigned on resources based on first-come-first-serve rule. When the number of tasks exceeds the resources, the distribution of tasks is to be developed by utilizing effectual scheduling methods. During this work, it can be assumed that the number of tasks is over the calculating resources, and so the unique task could not be allocated for various resources that represent that the presented techniques avoid job migration [19]. The RMS in grid environments involves evert data on accessible resources.
During these cases, the Expected Time to Compute (ETC) all jobs on all machines are calculated from task set determined as user and CPU time was resultant from grid systems. The resolve of ETC values are distinct investigation issues, and the statement of ETC data was utilized as benchmark for scheduling issues. ETC matrices were utilized for estimating the needed time to applying for all the jobs from all machines. The ETC matrix is
For formulating the issue, determine
An objective is for finding a permutation matrix
subject to
The scheduling constraint guarantee which all the tasks are allocated to exactly one resource.
4 Design of Grid Scheduling Scheme
Fig. 1 illustrates the overall working process of proposed IGSS-DHOA model. The IGSS-DHOA technique determines a solution which produces optimum schedules to minimize makespan in the grid platform. The IGSS-DHOA technique is mainly based on the hunting nature of humans toward deer. It also derives an objective function with candidate solution (schedule) as input and the outcome is the makespan value denoting the quality of the candidate solution.

Figure 1: Overall process of IGSS-DHOA model
4.1 Representation of Solutions
In this case, the vector-based representation was utilized for encoding the schedule or solution to Grid scheduling issue. The size of vector was equivalent to the number of tasks. An index number of the element in vector represents the ID of tasks. Each element is integer in the range of 1 and m, where m implies the entire number of resources. The element in vector represents those resources are selected for processing the equivalent task, and these values are repetitive. For instance, suppose that 5 tasks were scheduled with 3 resources (with ID: 1, 2, 3) and assume schedule be the vector representing the solutions, an initial task was allocated for Resource 3, the second task for Resource 1, the third and fifth task for Resource 2, and the fourth task for Resource 3. By the direct illustration, the solution is signified as schedule = [3, 1, 2, 3, 2].
An essential model of enhancement heuristic was iteratively enhancing incumbent solutions from all searches step by changing the present solution with neighbouring solution interms of quality/fitness value of neighbouring solutions. For describing the quality/fitness of all the solutions and guides the search model on the solution space, an estimation function was utilized for associating a real value for all solutions. The makespan has most general metric utilized to represent the amount of scheduling in Grid computing. Therefore, the estimation function was determined as function that estimates the makespan value of some provided candidate schedules [20]. In the ETC matrix method, the estimation function is written as:
where
where
An objective function in the IGSS-DHOA algorithm has the function which requires that exists optimized for achieving the aim. During this case, it can be regarded as one of the widely studied optimization conditions, for instance, the minimization of makespan, and it can be expressed as determining an objective function as estimation function. The input parameter for an objective function has been candidate solution/schedule. An output of objective function was makespan value demonstrating the estimation/amount of candidate solution or schedule. Assume that
The major goal of the presented DHOA method is to detect an optimum location for an individual to hunt the deer, it is essential to explore the deer's nature. They have special features that make complex hunting for the predator. A separate feature characterizes visual power i.e., 5 times bigger compared to humans. But they had problems seeing red and green colours. This section discusses the mathematical modeling of DHOA.
The major phase of technique is the beginning of hunter population, which is given as follows,
Let n represents entire number of hunters i.e., the solution, in population
After the initiation population, the deer position and wind angles are the important parameters in determining the optimal hunter position are initialized. Since the search spaces are considered as circles, the wind angles following the circumference of a circle.
whereas r denotes arbitrary numbers using a value in the extent of zero and one and i denotes present iteration. In the meantime, the location angle of deer is represented as
In which
Since the location of optimum spaces is initially unidentified, the approach considers the candidate solution near to the optimum i.e., defined according to the FF, as an optimal outcome [21]. Now, it assumes 2 results, i.e., leadership position,
(i) Propagation through leaders’ location: afterward determining the optimum location every individual in the population attempts for attaining an optimum location and therefore, the procedure of upgrading the location starts. Consequently, the encircling nature is demonstrated by,
where
where
where
(ii) Propagation through angle location: for improving the search space, the idea is expanded by assuming the angles location in the upgraded rules. The angle estimation is necessary for defining the hunter's location thus prey isn't attentive to the attacks and henceforth, the hunting procedure would be efficient. The visualization angles of the prey/deer are calculated by,
According to the variance among visual and wind angles of the deer, a variable is calculated which is assist to upgrade the angle location.
where
By considering the angle location, the location is upgraded to implement as,
whereas

Figure 2: Flowchart of DHOA
(iii) Propagation via successor location: In the exploration stage, a similar concept in encircling nature is adjusted by adopting the vector L. As it considers an arbitrary search firstly, the value of vector L is assumed lesser than one. Thus, the upgrade location is depending upon the successor location instead of initial optimum solution attained. This permits a global search which is given by,
where,
From the arbitrary initiation of solution, the method upgrades the search agents’ location at all iterations depending upon attained optimum solution. When
The IGSS-DHOA technique intends to reduce the makespan and scheduling proficiency. Gridsim 5.0 toolkit is employed to evaluate the IGSS-DHOA technique under 16 resources and 512 tasks. The gridlets considered are autonomous and highly computational; it also follows Poisson process. It is considered that every resource can execute an individual gridlet at a time instant. The IGSS-DHOA technique is inspected under 4 cases as listed below.
■ Case 1: High Task Low Machine
■ Case 2: Low Task High Machine
■ Case 3: High Task High Machine
■ Case 4: Low Task Low Machine
Tab. 1 and Fig. 3 offer the makespan analysis of the IGSS-DHOA technique with existing techniques under four cases. The table values exhibited that the IGSS-DHOA technique has accomplished better results with the minimum makespan. For instance, with case 1, the IGSS-DHOA technique has resulted in a lower makespan of 20022.8 m whereas the Min-min, FTMM, BSA, LBFT, and MLFT techniques have obtained a higher makespan of 32734.3, 30695.6, 28177.3, 24819.6, and 22061.4 m respectively.
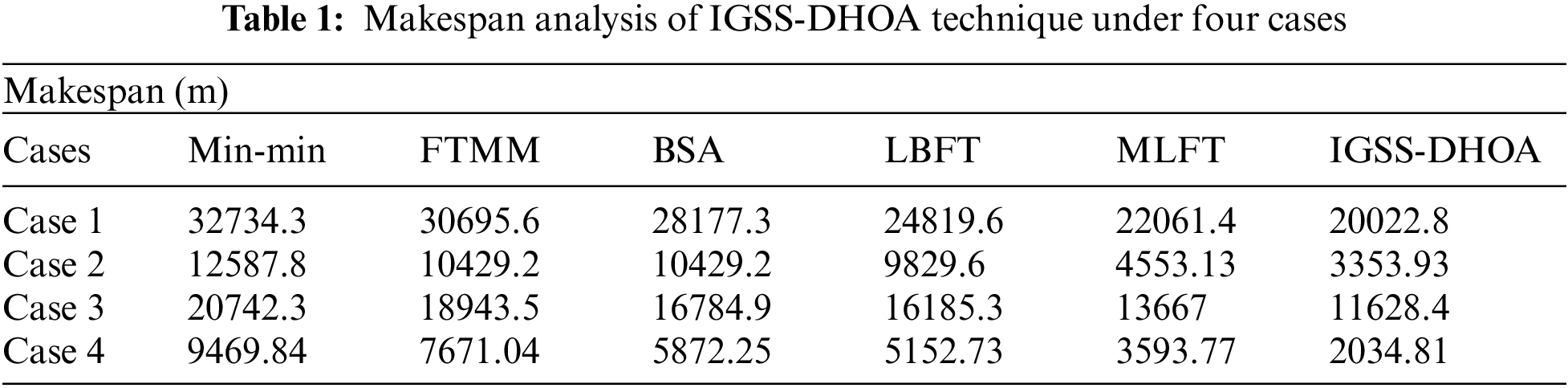

Figure 3: Makespan analysis of IGSS-DHOA model with existing approaches
In line with, with case 4, the IGSS-DHOA approach has resulted in a lesser makespan of 2034.81 m whereas the Min-min, FTMM, BSA, LBFT, and MLFT algorithms have reached a superior makespan of 9469.84, 7671.04, 5872.25, 5152.73, and 3593.77 m correspondingly.
Tab. 2 and Fig. 4 examine the hit count analysis of the IGSS-DHOA technique under four distinct cases. The experimental values highlighted that the IGSS-DHOA technique has showcased improved outcomes with the maximum hit count values. For instance, under case 1, the IGSS-DHOA technique has achieved a higher hit count of 396.29, and Min-min, FTMM, BSA, LBFT, and MLFT techniques have attained a lower hit count of 311.393, 332.801, 380.787, 389.646, and 390.384 respectively. Furthermore, under case 4, the IGSS-DHOA method has reached an increased hit count of 385.216, and Min-min, FTMM, BSA, LBFT, and MLFT manners have gained a minimal hit count of 341.66, 356.425, 361.593, 377.834, and 372.666 correspondingly.
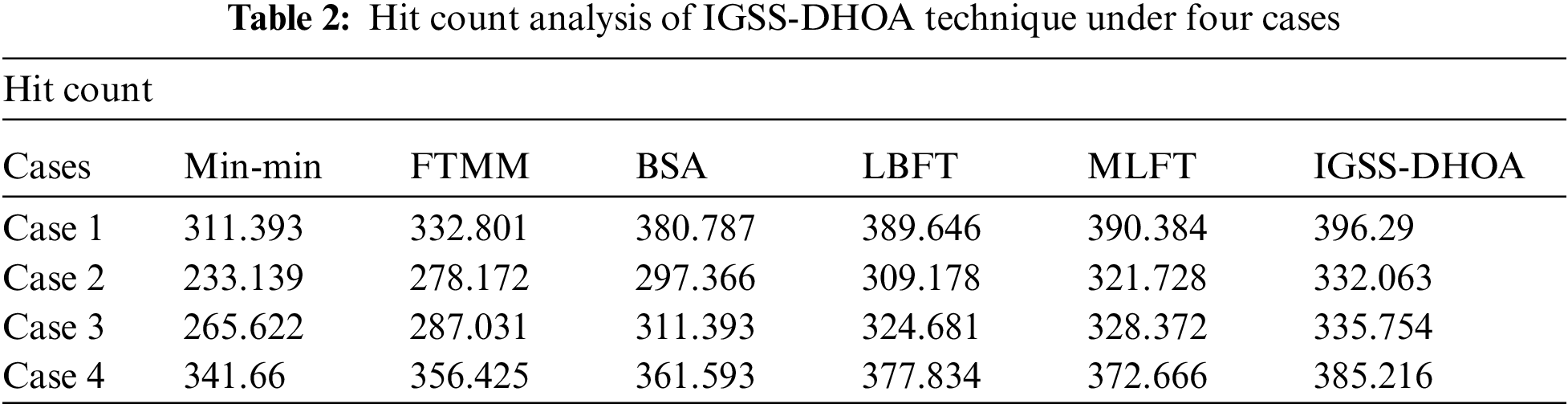
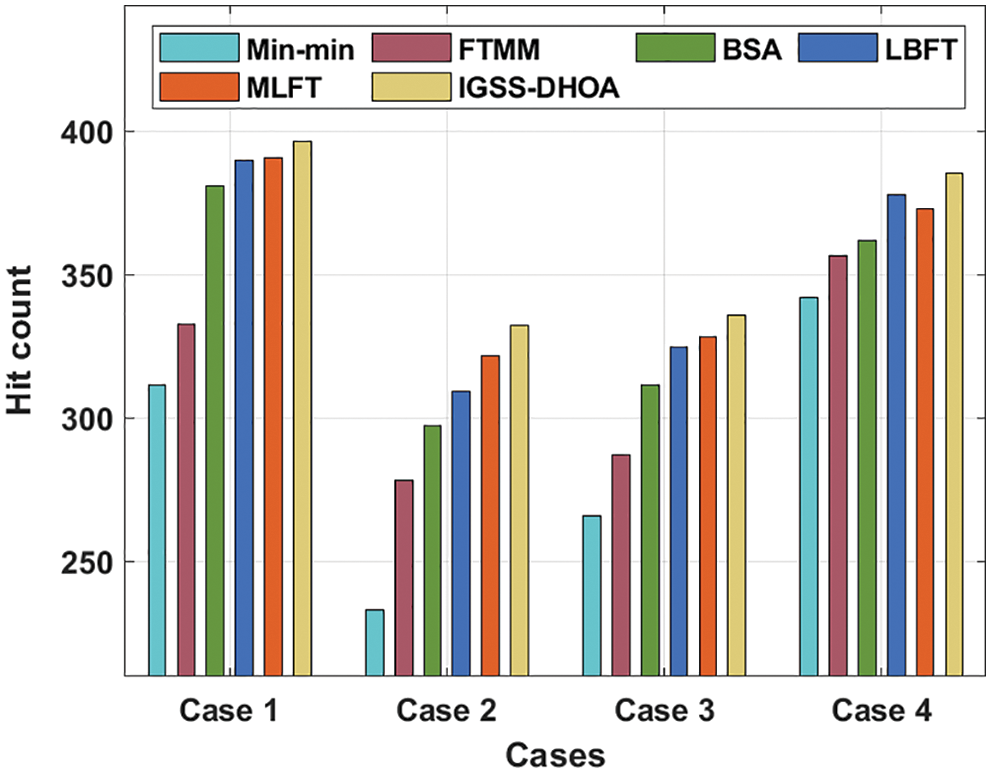
Figure 4: Hit count analysis of IGSS-DHOA model with existing approaches
Tab. 3 and Fig. 5 inspect the deadline hit count analysis of the IGSS-DHOA approach under four varying cases. The experimental values demonstrated that the IGSS-DHOA manner has portrayed increased results with the maximal deadline hit count values. For instance, under case 1, the IGSS-DHOA method has gained an improved deadline hit count of 391.4888, and Min-min, FTMM, BSA, LBFT, and MLFT techniques have obtained the least deadline hit count of 212.2046, 238.4996, 362.8033, 381.927, and 380.7318 correspondingly. Also, under case 4, the IGSS-DHOA approach has attained a superior deadline hit count of 366.389, and Min-min, FTMM, BSA, LBFT, and MLFT methodologies have obtained a minimal deadline hit count of 230.133, 243.2805, 298.261, 312.6037, and 350.8511 respectively.
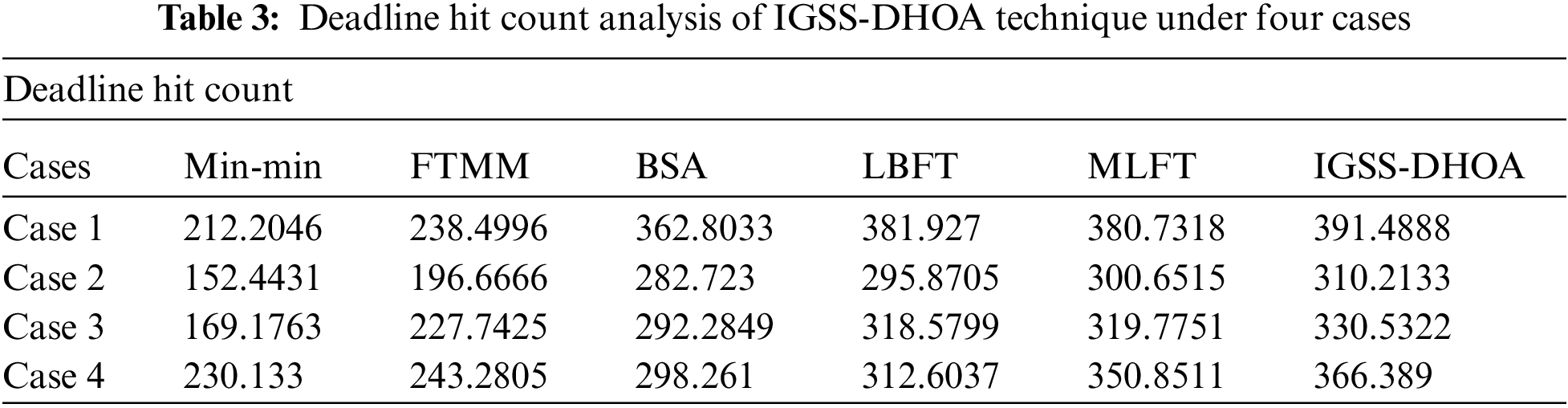
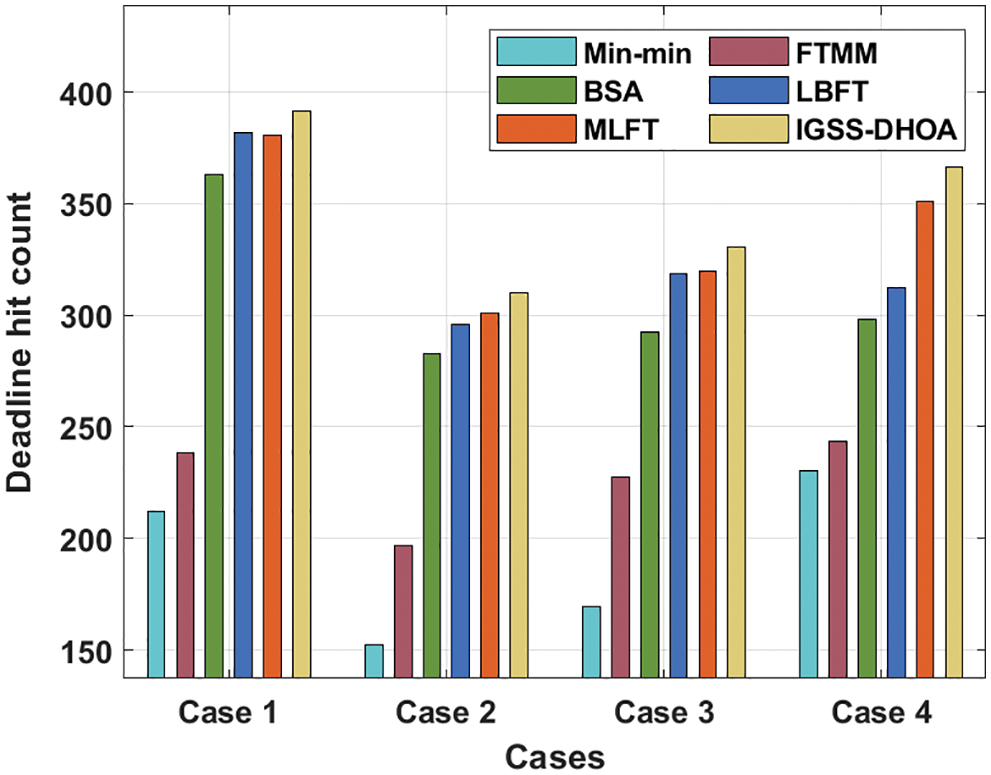
Figure 5: Deadline hit count analysis of IGSS-DHOA model with existing approaches
Tab. 4 and Fig. 6 observe the resource utilization analysis of the IGSS-DHOA manner under four different cases. The experimental values outperformed that the IGSS-DHOA technique has exhibited higher results with the maximal resource utilization values.
For sample, under case 1, the IGSS-DHOA algorithm has achieved an enhanced resource utilization of 93.57213% and Min-min, FTMM, BSA, LBFT, and MLFT techniques have gained a lower resource utilization of 70.393%, 77.00725%, 78.0809%, 90.04442%, and 92.03834% correspondingly. Moreover, under case 4, the IGSS-DHOA approach has reached a maximum resource utilization of 94.10900% and Min-min, FTMM, BSA, LBFT, and MLFT algorithms have achieved a reduced resource utilization of 69.9518%, 76.3170%, 78.54100%, 88.81740%, and 92.07670% correspondingly.
An average resource utilization analysis of the IGSS-DHOA technique with existing techniques take place in Fig. 7. The figure demonstrated that the Min-min technique has depicted poor outcome with the average resource utilization of 69.952% whereas the FTMM and BSA techniques have accomplished moderate perforamcne with the average resource utilization of 76.317% and 78.541% respectively. Moreover, the LBFT and MLFT techniques have demonstrated reasonable average resource utilization of 88.817% and 92.077% respectively. However, the IGSS-DHOA technique has resulted to a higher average resource utilization of 94.109%.
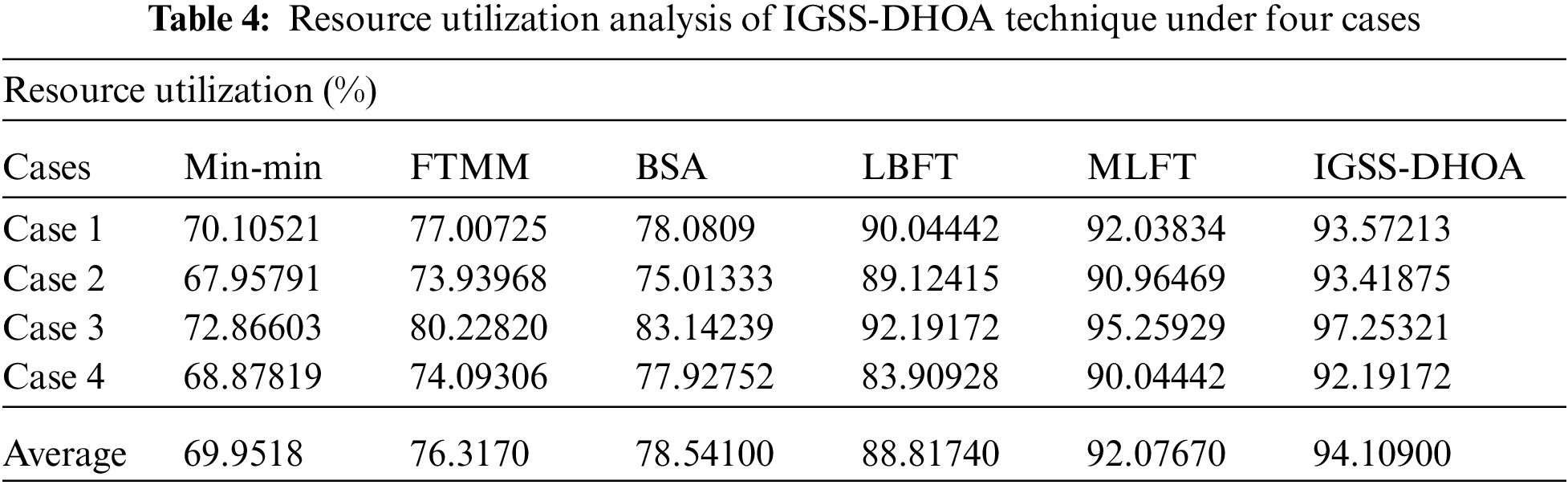
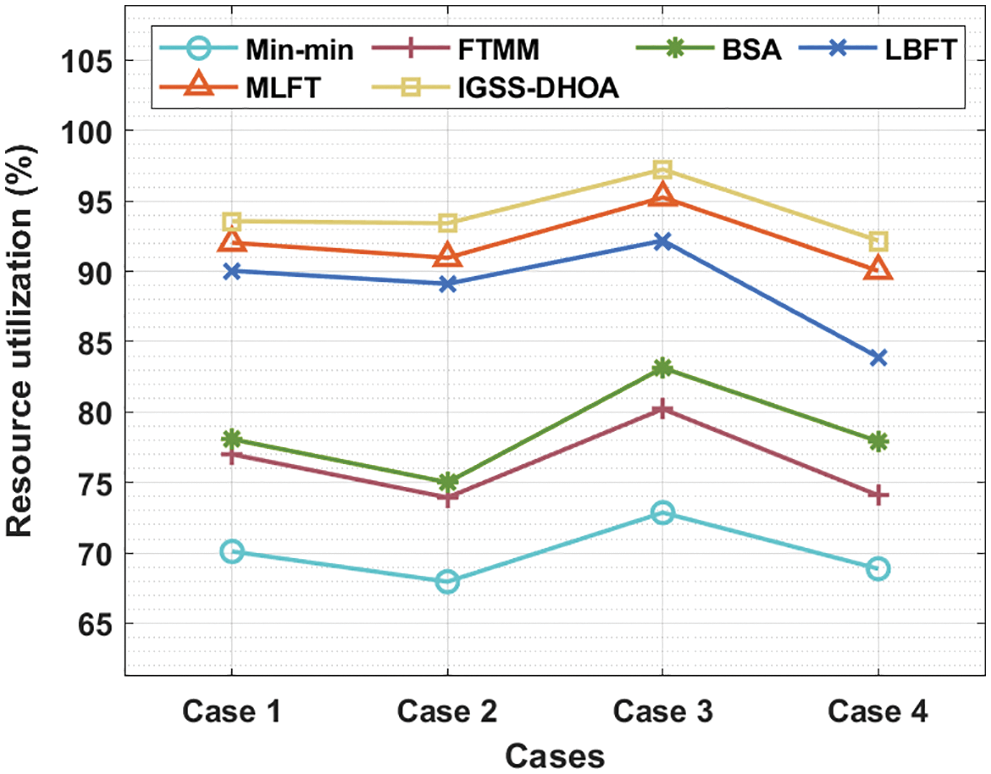
Figure 6: Resource utilization analysis of IGSS-DHOA model with existing approaches
Tab. 5 and Fig. 8 propose the processing time analysis of the IGSS-DHOA method with recent approaches under four cases. The table values demonstrated that the IGSS-DHOA manner has accomplished optimum outcomes with minimal processing time. For sample, with case 1, the IGSS-DHOA method has resulted in a least processing time of 63657.27 whereas the Min-min, FTMM, BSA, LBFT, and MLFT algorithms have reached an increased processing time of 98224.68, 95677.6, 94949.87, 85489.31, and 70206.88 correspondingly. At the same time, with case 4, the IGSS-DHOA approach has resulted in a minimum processing time of 15262.90 whereas the Min-min, FTMM, BSA, LBFT, and MLFT methodologies have attained a superior processing time of 26178.92, 22904.11, 23631.85, 20720.91, and 18901.57 correspondingly.
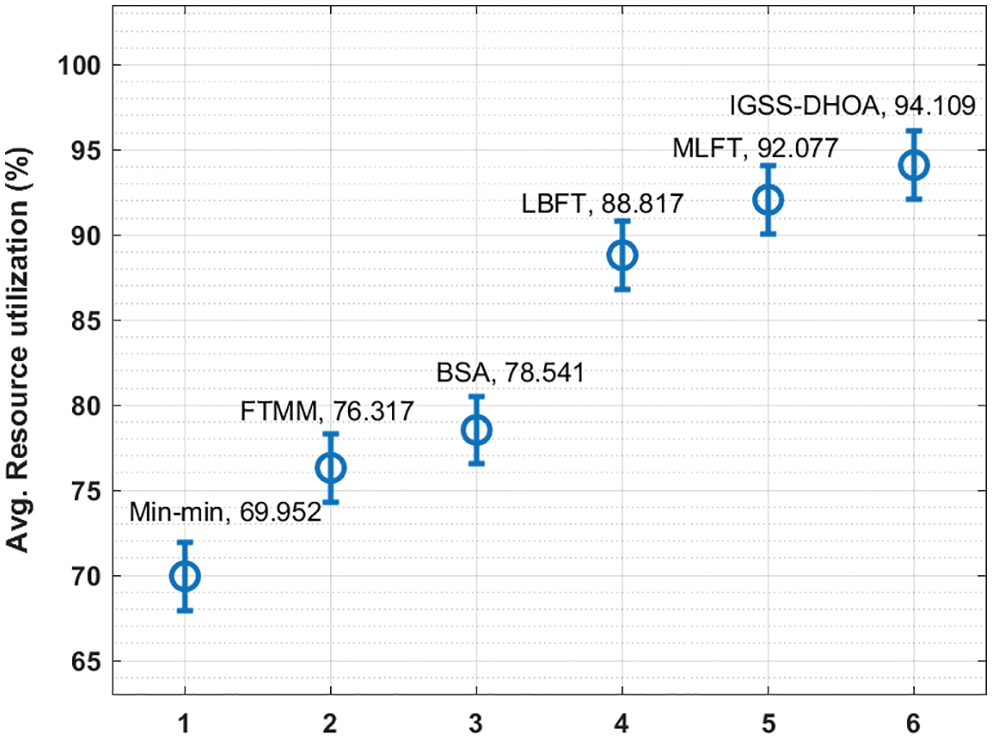
Figure 7: Average resource utilization analysis of IGSS-DHOA model with existing approaches
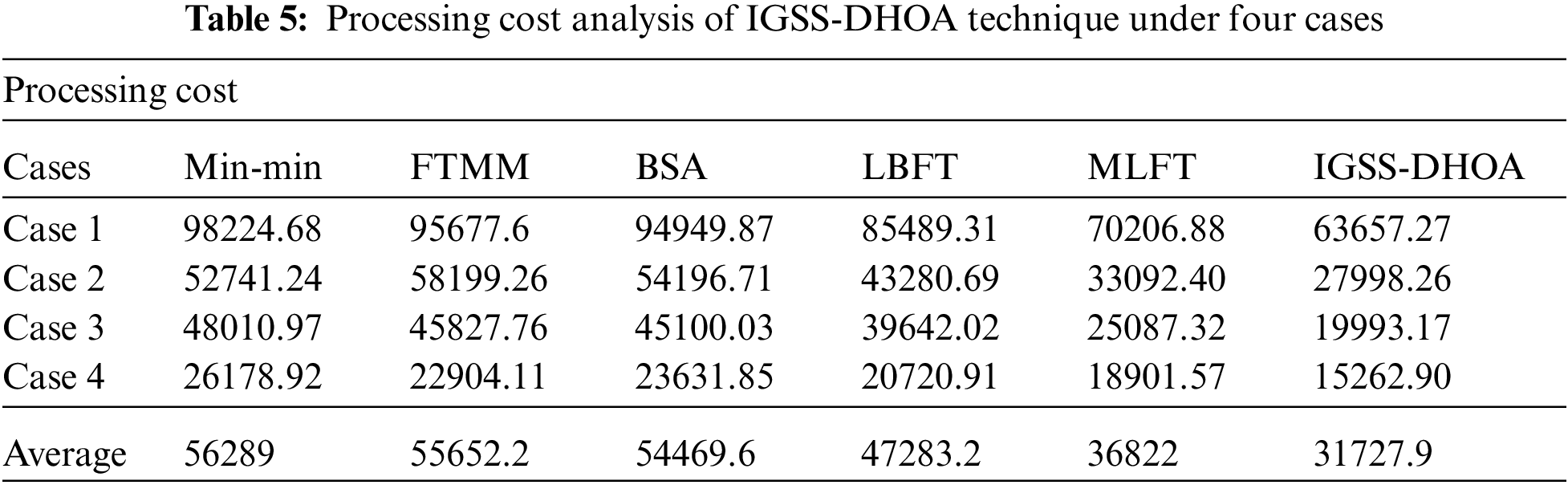

Figure 8: Processing cost analysis of IGSS-DHOA model with existing approaches
Finally, an average processing cost of IGSS-DHOA technique with other techniques is provided in Fig. 9. The simulation results demonstrated that the Min-min, FTMM, and BSA techniques have offered poor outcome with the average processing cost of 56289, 55652.2, and 54469.6 respectively. In addition, the LBFT technique has accomplished moderate average processing time of 47283.2 whereas even improved average process cost of 36822 is offered by the MLFT technique. However, the proposed IGSS-DHOA technique has resulted to superior performance with the minimal average processing cost of 31717.9. From the above-mentioned results analysis, it is demonstrated that the IGSS-DHOA technique is found to be an effective grid scheduler compared to other approaches.
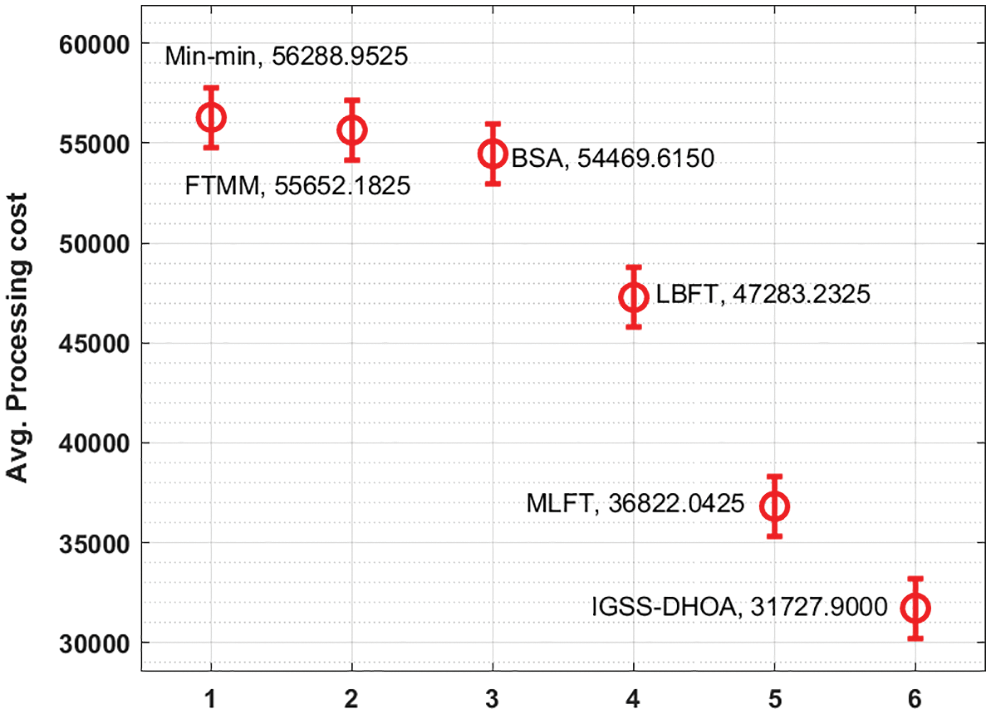
Figure 9: Average processing cost of IGSS-DHOA technique with existing techniques
This study has developed an effective IGSS-DHOA technique to generate optimal schedules in the grid environment. The IGSS-DHOA algorithm is mainly inspired by the hunting characteristics of humans towards deer. The IGSS-DHOA algorithm has derived an objective function with the minimization of makespan in the grid environment with the candidate solution as input and makespan value as output. In order to assess the optimal scheduling performance of the IGSS-DHOA technique, an extensive simulation analysis is carried out. The resultant values ensured the betterment of the IGSS-DHOA technique over the recent state of art techniques interms of different evaluation parameters. As a part of future scope, improved metaheuristic algorithms can be designed to further lessen the makespan in the grid environment.
Funding Statement: The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work under Grant Number (RGP.1/172/42). https://www.kku.edu.sa.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. X. S. He, X. H. Sun and G. von Laszewski, “QoS guided MinMin heuristic for grid task scheduling,” Journal of Computer Science and Technology, vol. 18, no. 4, pp. 442–451, 2003. [Google Scholar]
2. Y. Lyu, L. Chen, C. Zhang, D. Qu, N. M. Allah et al., “An interleaved depth-first search method for the linear optimization problem with disjunctive constraints,” Journal of Global Optimization, vol. 70, no. 4, pp. 737–756, Apr. 2018. [Google Scholar]
3. N. M. Allah, “Effect of ordered set on feasibility analysis of static-priority system,” The Journal of Supercomputing, vol. 75, no. 1, pp. 475–487, Jan. 2019. [Google Scholar]
4. A. P. Sarathchandar, V. Priyesh and D. D. H. Miriam, “Grid scheduling using improved particle swarm optimization with digital pheromones,” International Journal of Scientific & Engineering Research, vol. 3, no. 6, pp. 1–6, 2012. [Google Scholar]
5. T. D. Braun, H. J. Siegel, N. Beck, L. L. Boloni, M. Maheswaran et al., “A comparison of eleven static heuristics for mapping a class of independent tasks onto heterogenous distributed computing systems,” Journal of Parallel and Distributed Computing, vol. 61, pp. 810–837, 2001. [Google Scholar]
6. S. Parsa and R. E. Maleki, “RASA: A new grid task scheduling algorithm,” World Applied Sciences Journal, vol. 7, pp. 152–160, 2009. [Google Scholar]
7. Q. Zhang and Z. Li, “Design of grid resource management system based on information service,” Journal of Computers, vol. 5, no. 5, pp. 687–694, 2010. [Google Scholar]
8. M. Nandagopal and V. R. Uthariaraj, “Fault tolerant scheduling strategy for computational grid environment,” International Journal of Engineering Science and Technology, vol. 2, no. 9, pp. 4361–4372, 2010. [Google Scholar]
9. T. Sousa, H. Morais, R. Castro and Z. Vale, “Evaluation of different initial solution algorithms to be used in the heuristics optimization to solve the energy resource scheduling in smart grids,” Applied Soft Computing, vol. 48, pp. 491–506, 2016. [Google Scholar]
10. H. Liu, A. Abraham and A. E. Hassanien, “Scheduling jobs on computational grids using a fuzzy particle swarm optimization algorithm,” Future Generation Computer Systems, vol. 26, no. 8, pp. 1336–1343, 2010. [Google Scholar]
11. Y. Dan and J. Tao, “Knowledge worker scheduling optimization model based on bacterial foraging algorithm,” Future Generation Computer Systems, vol. 124, pp. 330–337, 2021. [Google Scholar]
12. M. W. Khan, M. Zeeshan, A. Farid and M. Usman, “QoS-Aware traffic scheduling framework in cognitive radio based smart grids using multi-objective optimization of latency and throughput,” Ad Hoc Networks, vol. 97, pp. 102020, 2020. [Google Scholar]
13. S. Nazir, S. Shafiq, Z. Iqbal, M. Zeeshan, S. Tariq et al., “Cuckoo optimization algorithm based job scheduling using cloud and fog computing in smart grid,” in INCoS 2018: Advances in Intelligent Networking and Collaborative Systems, Lecture Notes on Data Engineering and Communications Technologies, Springer, USA, vol. 23, pp. 34–46, 2018. [Google Scholar]
14. P. Keerthika and N. Kasthuri, “An efficient grid scheduling algorithm with fault tolerance and user satisfaction,” Mathematical Problems in Engineering, vol. 2013, pp. 1–9, 2013. [Google Scholar]
15. R. Jayasudha, T. Karthikeyan, N. Karthik, B. Palanisamy and K. Chandrakumar, “Improving optimization technique using firefly algorithm for grid scheduling problem,” Journal of Computational and Theoretical Nanoscience, vol. 16, no. 5, pp. 2389–2392, 2019. [Google Scholar]
16. J. Kołodziej and S. U. Khan, “Multi-level hierarchic genetic-based scheduling of independent jobs in dynamic heterogeneous grid environment,” Information Sciences, vol. 214, pp. 1–19, 2012. [Google Scholar]
17. P. Keerthika and P. Suresh, “A multiconstrained grid scheduling algorithm with load balancing and fault tolerance,” The Scientific World Journal, vol. 2015, pp. 1–10, 2015. [Google Scholar]
18. K. Eng, A. Muhammed, M. A. Mohamed and S. Hasan, “A hybrid heuristic of variable neighbourhood descent and great deluge algorithm for efficient task scheduling in grid computing,” European Journal of Operational Research, vol. 284, no. 1, pp. 75–86, 2020. [Google Scholar]
19. L. J. Ning and W. H. Zhong, “Scheduling in grid computting environment based on genetic algorithm,” Journal of Computer Research and Development, vol. 41, no. 12, pp. 1–12, 2004. [Google Scholar]
20. F. Xhafa and A. Abraham, “Computational models and heuristic methods for grid scheduling problems,” Future Generation Computer Systems, vol. 26, no. 4, pp. 608–621, 2010. [Google Scholar]
21. M. H. Zafar, T. A. Shahrani, N. M. Khan, A. F. Mirza, M. Mansoor et al., “Group teaching optimization algorithm based mppt control of pv systems under partial shading and complex partial shading,” Electronics, vol. 9, no. 11, pp. 1962, 2020. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |