Computers, Materials & Continua DOI:10.32604/cmc.2022.022959
Article

Effective Frameworks Based on Infinite Mixture Model for Real-World Applications

Norah Saleh Alghamdi1, Sami Bourouis2,* and Nizar Bouguila3

1Department of Computer Sciences, College of Computer and Information Sciences, Princess Nourah bint Abdulrahman University, P.O.Box 84428, Riyadh 11671, Saudi Arabia
2College of Computers and Information Technology, Taif University, Taif, 21944, Saudi Arabia
3The Concordia Institute for Information Systems Engineering (CIISE), Concordia University, Montreal, QC H3G 1T7, Canada
*Corresponding Author: Sami Bourouis. Email: s.bourouis@tu.edu.sa
Received: 24 August 2021; Accepted: 01 December 2021

Abstract: Interest in automated data classification and identification systems has increased over the past years in conjunction with the high demand for artificial intelligence and security applications. In particular, recognizing human activities with accurate results have become a topic of high interest. Although the current tools have reached remarkable successes, it is still a challenging problem due to various uncontrolled environments and conditions. In this paper two statistical frameworks based on nonparametric hierarchical Bayesian models and Gamma distribution are proposed to solve some real-world applications. In particular, two nonparametric hierarchical Bayesian models based on Dirichlet process and Pitman-Yor process are developed. These models are then applied to address the problem of modelling grouped data where observations are organized into groups and these groups are statistically linked by sharing mixture components. The choice of the Gamma mixtures is motivated by its flexibility for modelling heavy-tailed distributions. In addition, deploying the Dirichlet process prior is justified by its advantage of automatically finding the right number of components and providing nice properties. Moreover, a learning step via variational Bayesian setting is presented in a flexible way. The priors over the parameters are selected appropriately and the posteriors are approximated effectively in a closed form. Experimental results based on a real-life applications that concerns texture classification and human actions recognition show the capabilities and effectiveness of the proposed framework.

Keywords: Infinite Gamma mixture model; variational Bayes; hierarchical Dirichlet process; Pitman-Yor process; texture classification; human action recognition

1  Introduction and Literature Review

Data clustering has been the subject of wide research to the present days [1–4]. The goal of clustering is to group the observed data into separate subgroups, such as the data in each subgroup shows some similarities to each other. Various clustering approaches have been developed in the past and some of them are based on distance metrics (such as the K-means and SOM algorithms). It is noteworthy that these algorithms are sensitive to noise, are not flexible when dealing with incomplete data, and may not definitely capture heterogeneity inherent in complex datasets. Another important alternative is the model-based clustering approach [5]. It is effective for modelling the structure of clusters since data are supposed to be produced by some distributions. In particular, finite mixture models (such as Gaussian mixture model) have shown to be effective (in terms of discovering complex patterns and grouping them into similar clusters) for many computer vision and pattern recognition applications [6]. Nevertheless, Gaussian model cannot fit well complex non-Gaussian shapes. To cope with the disadvantages related to conventional Gaussian assumption, many contributions have occurred to develop other flexible mixture models and were interested to non-Gaussian behavior of real datasets [7,8]. For instance, Gamma (GaMM) mixtures have demonstrated to offer high flexibility and ease of use than Gaussian [9] for many image processing and pattern recognition problems. This is due their compact analytical form which is able to cover long-tailed distributions and to approximate data with outliers. This mixture has been used with success for a range of interesting problems [7,10–12] especially when dealing with proportional data. An illustration of how mixture models can be applied for data modelling, classification and recognition is given in Fig. 1.

Figure 1: Block diagram of application of mixture model for data classification and recognition

Unfortunately, the inadequacy of finite mixture model has been apparent when selecting the appropriate number of mixture components. In other word, model selection (i.e., model's complexity) is one of the difficult problems within finite mixture models. The crucial problem of “how many groups in the dataset?” still remains of great interest for various data mining fields since determining inappropriate number of clusters may conduct to poor generalization capability. This problem can be solved by considering an infinite number of components via nonparametric Bayesian methods [13,14], principally within “Dirichlet process (DP)” [15]. Indeed, a Dirichlet Process (DP) is a parameterized stochastic process characterized by a base distribution and it can be defined as a probability distribution over discrete distributions. Numerous studies have been devoted to infinite mixture models which are emerged to cope with the challenging problem of model selection.

Two sound hierarchical Bayesian alternatives to the conventional DP named as hierarchical Dirichlet process (HDP) and hierarchical Pitman-Yor process (HPYP) have exposed encouraging results especially when dealing with modeling grouped data [16,17]. Indeed, within hierarchical models, mixture components can be shared through data groups (i.e., parameters are shared among groups). In such cases, it is possible to make a Bayesian hierarchy on the DP and the base distribution of the DP is distributed according to another DP.

Thus, the main contributions of this manuscript are first to extend our previous works about the Gamma mixture by investigating two efficient nonparametric hierarchical Bayesian models based on both Dirichlet and Pitman-Yor processes mixtures of Gamma distributions. Indeed, in order to reach enhanced modeling performance, we consider Gamma distribution which is able to cover long-tailed distributions and to approximate accurately visual vectors. Another critical issue when dealing with mixture models is model parameters estimation. Accordingly, we propose to develop an effective variational Bayes learning algorithm to estimate the parameters of the implemented models. It is noteworthy to indicate that the complexity of variational inference-based algorithm still remains less than Markov Chain Monte Carlo-Based Bayesian inference and leads to faster convergence. Finally, the implemented hierarchical Bayesian models and the variational inference approaches are validated via challenging real-life problems namely human activity recognition and texture categorization.

This manuscript is organized as follows. In Section 2 we introduce the hierarchical DP and PYP mixtures of Gamma distributions which are based on stick-breaking construction. In Section 3, we describe the details of our variational Bayes learning framework. Section 4 reports the obtained results, which are based on two challenging applications, to verify the merits and effectiveness of our framework, and Section 5 is devoted to conclude the manuscript.

2  Model Specification

In this section, we start by briefly presenting finite Gamma mixture model and then we present our nonparametric frameworks based on hierarchical Dirichlet and Pitman-Yor processes mixtures.

2.1 Finite Gamma Mixture Model

If a D-dimensional random vector Y→=(Y1,…,YD) is distributed according to a multidimensional Gamma distribution, then its probability density function (pdf) is defined as:

Ga(Y→∣θ→)=∏d=1D⁡(βd)αdYdαd−1e−βdYdΓ(αd)(1)

where θ→={αd,βd} is the vector of parameters of the Gamma distribution. Here αd denotes the shape and βd is for the location parameters. Γ(.) is the Gamma function which is defined as: Γ(x)=∫0∞⁡sx−1e−sds.

For a random vector Y→ which is produced from a finite Gamma mixture model with M components, we have the following:

p(Y→∣π→,θ→)=p(Y→∣π→,α→,β→)=∑j=1M⁡πjGa(Y→∣θj→)(2)

where θ→j={αj,βj} is the set of parameters of the Gamma distribution Ga(.) corresponding to the jth mixture component. The vector of mixing weights π→=(π1,…,πM) is subject to 0≤πj≤1, and ∑j=1M⁡πj=1.

2.2 Hierarchical Dirichlet Process Mixture Model

The hierarchical Dirichlet process (HDP) is an an effective nonparametric Bayesian method to modelling grouped data, which allows the mixture models to share components. Here, observed data are arranged into groups (i.e., mixture model) that we want to make them statistically linked. HDP It is built on the Dirichlet process (DP) as well described in [17] for each group data. It is noteworthy that the DP has acquired popularity in machine learning to handle nonparametric problems [18]. The DP was presented as a prior on probability distributions and this makes it extremely appropriate for specifying infinite mixture models thanks to the use of the stick-breaking process [19]. In the case of hierarchical Dirichlet process (HDP), the DPs for all groups share a base distribution which is itself distributed according to a Dirichlet process. Let's assume that we have a grouped data set Y separated into M groups, such that each group is associated with a DP Gj, thus the HDP takes part an indexed set of DPs Gj that share a global (or base) distribution G0 which is itself distributed as a DP with base distribution H and concentration parameter γ:

G0∼DP(γ,H)Gj∼DP(λ,G0)foreachj,j∈{1,…,M}(3)

Here, the hierarchical Dirichlet process is represented using the stick-breaking construction [19,20]. The global measure G0 is distributed according to DP(γ,H) and it can be expressed as

G0=∑k=1∞⁡ψkδΩkψk=ψk′∏s=1k−1⁡(1−ψs′)  ψs′∼Beta(1,γ)Ωk∼H(4)

where δΩk represents an atom concentrated at Ωk, and {Ωk} is a set of independent random variables drawn from H. The variable {ψk} are denoted as stick-breaking that verify ∑k=1∞⁡ψk=1. As G0 is defined as the base distribution of the DP Gj and has the stick-breaking representation as shown in Eq. (3), then Gj includes all the atoms Ωk with distinct weights (by following the property of Dirichlet process [18]). On the other side, we carry out another stick-breaking process to construct each group-level DP Gj according to [21] as

Gj=∑t=1∞⁡πjtδωjtπjt=πjt′∏s=1t−1⁡(1−πjs′)πjs′∼Beta(1,λ)ωjt∼G0(5)

where {πjt} is a set of stick-breaking weights which shall be positive and sum to one and δωjt are group-level Dirac delta atoms at ωjt. As ωjt (group-level atom) is distributed according to G0, thus it will take onto Ωk (base-level atoms) with probability ψk.

Next, we introduce a latent indicator Wjtk as an indicator variable, such that Wjtk∈{0,1} (in order to indicate which group-level atom maps to). Wjtk=1 if ωjt (group-level atom) maps to the Ωk (global-level atom) that is indexed by k; otherwise, Wjtk=0. Accordingly, we can have ωjt=ΩkWjtk. By this way, there is no need to keep a representation for ωjt. The indicator variable W→=(Wjt1,Wjt2,…) is distributed as:

p(W→∣ψ→)=∏j=1M⁡∏t=1∞⁡∏k=1∞⁡ψkWjtk(6)

Given that ψ is a function of ψ′ according to Eq. (4), it is possible to rewrite the indicator variable p(W→) as:

p(W→∣ψ′→)=∏j=1M⁡∏t=1∞⁡∏k=1∞⁡[ψk′∏s=1k−1⁡(1−ψs′)]Wjtk(7)

According to Eq. (4) the stick lengths ψ′ are drawn from a specific Beta distribution and their realization is determined as

p(ψ′→)=∏k=1∞⁡Beta(1,γk)=∏k=1∞⁡γk(1−ψk′)γk−1(8)

To complete the description of the HDP mixture model, given a grouped observation (data) Y, we associate each data point Yji→ with a factor θji (here i indexes the data in each group j) such that Yji→ and θj→=(θj1,θj2,…) are distributed according to F(θji) and Gj, respectively. In this case the likelihood function can be written as:

θji∣Gj∼GjYji∣θji∼F(θji)(9)

where F(θji) is the probability distribution of Yji given θji. The base distribution H provides the prior distribution for θji. This setting (i.e., hierarchical Dirichlet process (HDP) mixture model) plays an important role and ensures that each group is associated with a mixture model, and the components of the mixture are shared across different groups.

As each θji is distributed according to Gj (see Eq. (9)), it takes the value ωjt with probability πjt. We then introduce another indicator variable Zjit∈{0,1} for θji as

p(Z→∣π→)=∏j=1M⁡∏i=1N⁡∏t=1∞⁡πjtZjit(10)

That is, the indicator Zjit is used to indicate which component θji belongs to. In particular, Zjit is equal to 1 if θji is associated with component t (also maps to the group-level atom ωjt); else, Zjit=0. Thus, we can write θji=ωjtZjit. As ωjt maps to Ωk, we then can write θji=ωjtZjit=ΩkWjtkZjit.

Based on the stick-breaking construction of the DP (see Eq. (5)), we notice that π→ is a function of π′→, therefore the previous equation becomes

p(Z→∣π→′)=∏j=1M⁡∏i=1N⁡∏t=1∞⁡[πjt′∏s=1t−1⁡(1−πjs′)]Zjit(11)

Finally, according to Eq. (5), the prior distribution of π′ is a Beta and it is given as follows:

p(π′→)=∏j=1M⁡∏t=1∞⁡Beta(1,λjt)=∏j=1M⁡∏k=1∞⁡λjt(1−πjt′)λjt−1(12)

2.3 Hierarchical Pitman-Yor Process Mixture Model

The Pitman-Yor process (PYP) [22] is a two-parameter extension to the DP (i.e., is a generalization of DP) that permits modelling heavier-tailed distributions. It can be applied to build hierarchical models. It offers a sophisticated way to cluster data such that the number of clusters is unknown. It is characterized by an additional discount parameter γa in addition to the concentration parameter γb, that satisfying the 0<γa<1, γb>−γa. Similar to DP, the sample drawn from PYP also associated a probability measure H [23]. Here, a hierarchical Pitman–Yor process (HPYP) is introduced where the base measure for a PYP is itself a draw from a PYP. Specifically, HPYP defines the global-level measure G0 and group-level distribution Gj (that is the indexed Gj shares a same base G0 which itself follows a PYP). This behavior makes the HPYP especially suitable for complex visual data modeling and classification. We can use the HPYP to cluster data by applying the stick-breaking construction that defines the base measure as follows:

G0=∑k=1∞⁡ηkδΛkηk=ηk′∏l=1k−1⁡(1−ηl′)ηk′∼Beta(1−γa,γb+kγa)Λk∼H(13)

where {Λk} is a set of independent random variables drawn from H and δΛk is an atom (probability mass) at Λk. The random variables ηk represent the stick-breaking weights that satisfying ∑k=1∞⁡ηk=1. The stick-breaking representation for the group-level PYP Gj is expressed as:

Gj=∑t=1∞⁡pjtδψjtpjt=pjt′∏s=1t−1⁡(1−pjs′)pjs′∼Beta(1−βa,βb+tβa)ψjt∼G0(14)

where {pjt} are the stick-breaking weights (∑t=1∞⁡pjt=1). ψjt is the atom of second-level PYP that is distributed according to G0. Then, a global-level indicator variables I and a group-level indicator variables C are introduced. Here, C is used to map θji to group-level atom ψjt and the indicator I is used to map the atom θji to base-level atom Λk.

p(I→∣η′→)=∏j=1M⁡∏t=1∞⁡∏k=1∞⁡ηkIjtk=∏j=1M⁡∏t=1T⁡∏k=1K⁡[ηk′∏s=1k−1⁡(1−ηs′)]Ijtk(15)

p(C→∣p′→)=∏j=1M⁡∏i=1N⁡∏t=1∞⁡pjtCjit=∏j=1M⁡∏i=1N⁡∏t=1T⁡[pjt′∏s=1t−1⁡(1−pjs′)]Cjit(16)

2.4 Hierarchical Infinite Gamma Mixture Model

In this subsection, we introduce two hierarchical infinite mixture models with Gamma distributions. In this case, each vector Yji→=(Yji1,…,YjiD), from the grouped data, is drawn from a hierarchical infinite Gamma mixture model. Then, the two likelihood functions of these hierarchical models given the unknown parameters of Gamma and latent variables can be expressed as follows:

p(Y→∣Z→,W→,θ→)=p(Y→∣Z→,W→,α→,β→)=∏j=1M⁡∏i=1N⁡∏t=1∞⁡∏k=1∞⁡Ga(Y→ji∣θ→k)ZjitWjtk

p(Y→∣C→,I→,θ→)=p(Y→∣C→,I→,α→,β→)=∏j=1M⁡∏i=1N⁡∏t=1∞⁡∏k=1∞⁡Ga(Y→ji∣θ→k)CjitIjtk(17)

where θ→k=(αk→,βk→) are the full parameters of the Gamma distribution. The above two functions are HDP Gamma mixture (denoted by HDPGaM) and HPYP Gamma mixture (denoted by HPYPGaM), respectively.

Next, we have to place conjugate distributions over the unknown parameters α and β. As α and β are positive, then it is convenient that they follow Gamma distributions G(.). Thus, we have

p(α→)=G(α→∣u→,v→)=∏k=1∞⁡∏l=1D⁡G(αjd∣ujd,vjd)=∏k=1∞⁡∏l=1D⁡vkluklΓ(ukl)αklukl−1e−vklαkl(18)

p(β→)=G(β→∣g→,h→)=∏k=1∞⁡∏l=1D⁡G(βjd∣gjd,hjd)=∏k=1∞⁡∏l=1D⁡hklgklΓ(gkl)βklgkl−1e−hklβkl(19)

3  Model Learning via Variational Bayes

Variational inference [3,24] is a well-defined method deterministic approximation method that is used in order to approximate posterior probability via an optimization process. In this section, we propose to develop a variational learning framework of our hierarchical infinite Gamma mixture models. Here, Θ={Z→,W,ψ→′,π→′,θ→} represents both unknown and the latent variables. Our objective is to estimate a suitable approximation q(Θ) for the true posterior distribution p(Θ|Y) via a process of maximizing the lower bound of ln p(Y) given as

L(Q)=∫⁡Q(Θ)ln(p(Y,Θ)Q(Θ))dΘ(20)

In particular, we adopt one of the most successfully variational inference techniques namely the factorial approximation (or mean fields approximation) [3], which is able to offer effective updates. Thus, we apply this method to fully factorize q(Θ) of on HDPGaM and HPYPGaM mixtures into disjoint factors. Then, we apply a truncation method as previously applied in [20] to truncate the variational approximations into global truncation level K and group truncation level T as follow:

ψK′=1,∑k=1K⁡ψk=1,ψk=0whenk>K(21)

ηK′=1,∑k=1K⁡ηk=1,ηk=0whenk>K(22)

πjT′=1,∑t=1T⁡πjt=1,πjt=0whent>T(23)

pjT′=1,∑t=1T⁡pjt=1,pjt=0whent>T(24)

where the truncation levels K and T will be optimized over the learning procedure. The approximated posterior distribution is then factorized as

q(Θ)=q(W→,ψ′→,Z→,π′→,α→,β→)=q(W→)q(ψ→′)q(Z→)q(π→′)q(α→)q(β→)

q(Θ)=q(I→,η′→,C→,p′→,α→,β→)=q(I→)q(η→′)q(C→)q(p→′)q(α→)q(β→)(25)

For a specific variational factor qs(Θs), the general equation of the optimal solution is expressed as [3]:

qs(Θs)=exp⟨logp(Y,Θ)⟩i≠s∫⁡exp⟨logp(Y,Θ)⟩i≠sdΘ(26)

where ⟨.⟩i≠s denotes an expectation with respect to all the distributions of qi(Θi) except for i=s. The parametric forms for the variational posteriors (for each factor) are determined on the basis of Eq. (26) as

q(W→)=∏j=1M⁡∏t=1T⁡∏k=1K⁡ϑjtkWjtk(27)

q(Z→)=∏i=1N⁡∏j=1M⁡∏t=1T⁡ρijtZijt(28)

q(ψ→′)=∏k=1K⁡Beta(ψk′∣ck,dk)(29)

q(π→′)=∏j=1M⁡∏t=1T⁡Beta(πjt′∣ajt,bjt)(30)

q(I→)=∏j=1M⁡∏t=1T⁡∏k=1K⁡φjtkIjtk(31)

q(C→)=∏i=1N⁡∏j=1M⁡∏t=1T⁡ϱijtCijt(32)

q(η→′)=∏k=1K⁡Beta(ηk′∣ek,fk)(33)

q(p→′)=∏j=1M⁡∏t=1T⁡Beta(pjt′∣mjt,njt)(34)

q(α→)=∏k=1K⁡∏d=1D⁡G(αkd∣ukd∗,vkd∗)(35)

q(β→)=∏k=1K⁡∏d=1D⁡G(βkd∣skd∗,tkd∗)(36)

where the corresponding hyperparameters in the above equations can be calculated as a similar way in [25,26]. The complete variational Bayes inference algorithms of both HDPGaM and HPYPGaM are summarized in Algorithm 1 and Algorithm 2, respectively.

4  Experimental Results

The principal purpose of the experiment section is to investigate the performance of the developed two frameworks based on HDP mixture and HPYP mixture model with Gamma distributions. Hence, we propose to compare them with other statistical models using two challenging applications: Texture categorization and human action categorization. In all these experiments, the global truncation level K and the group level truncation level T are both initialized to 120 and 60, respectively. For HDP mixture, we set the hyperparameters of the stick lengths γ and λ as (0.25, 0.25). The parameters of HPYP mixture γa, γb, βa and βb are initialized to (0.5, 0.25, 0.5, 0.25). The hyperparameters of Gamma base distribution are initialized by sampling from priors.

4.1 Texture Classification

In this work we are primarily motivated by the problem of modeling and classifying texture images. Contrary to natural images which include certain objects and structures, texture images are very special case of images that do not include a well-defined shape. Texture pattern is one of the most important elements in visual multimedia content analysis. It forms the basis for solving complex machine learning and computer vision tasks. In particular, texture classification supports a wide range of applications, including information retrieval, image categorization [27–30], image segmentation [27,31,32], material classification [33], facial expression recognition [29], and object detection [28,34]. The goal here to classify texture images using the two hierarchical infinite mixtures and also by incorporating three different representations (to extract relevant features from images) from the literature, namely Local Binary Pattern (LBP) [35], Local Binary Pattern (LBP) [35], scale-invariant feature transform (SIFT) [36], and dense micro-block difference (DMD) [37]. A deep review for these methods is outside the scope of current work. Instead, we focus on some powerful feature extraction methods that have shown interesting state-of-the-art results.

4.1.1 Methodology

For this application, we start by extracting features from input images and then we model them using the proposed HDPGaM and HPYPGaM. Each image Ij is considered as a group and is related to a infinite mixture model Gj. Next, every vector Yji of Ij is assumed generated from Gj, where Gj represents visual words. The next step is to generate a global vocabulary to share it among all groups via G0 (global infinite model). It is noteworthy that the the building of the visual vocabulary, here, is part of our hierarchical models and therefore, the size of the vocabulary (i.e., number of components) is inferred automatically from the data thanks to the characteristic of nonparametric Bayesian models. Regarding SIFT features, the bag-of-visual-words model is adopted here to calculate the histogram of visual words from each input image. Regarding the set of DMD descriptors, these are obtained after extracting DMD features and then encoding them though th Fisher vector method as proposed in [37]. The resulting descriptors are able to attain good discrimination thanks to their invariance with respect to scale, resolution, and orientation. Finally, each image is represented by a multidimensional vector of high-order statistics1.

4.1.2 Dataset and Results

We conducted our experiments of texture classification using the proposed hierarchical HDP Gamma mixture (referred to as HDPGaM) and HPYP Gamma mixture (referred to as HPYPGaM) on three publicly available databases. The first one namely UIUCTex [38] contains 25 texture classes and each class has 40 images. The second dataset namely UMD [39] contains 25 textures classes containing each one 40 images. The third dataset namely KTH-TIPS [33] includes 10 classes and each one contains 81 images. Some sample texture images from each class and each dataset are shown in Fig. 2. We use 10-fold cross-validation technique to partition these databases and to study the performance. In addition, the evaluation process and the obtained results are based on 30 runs.

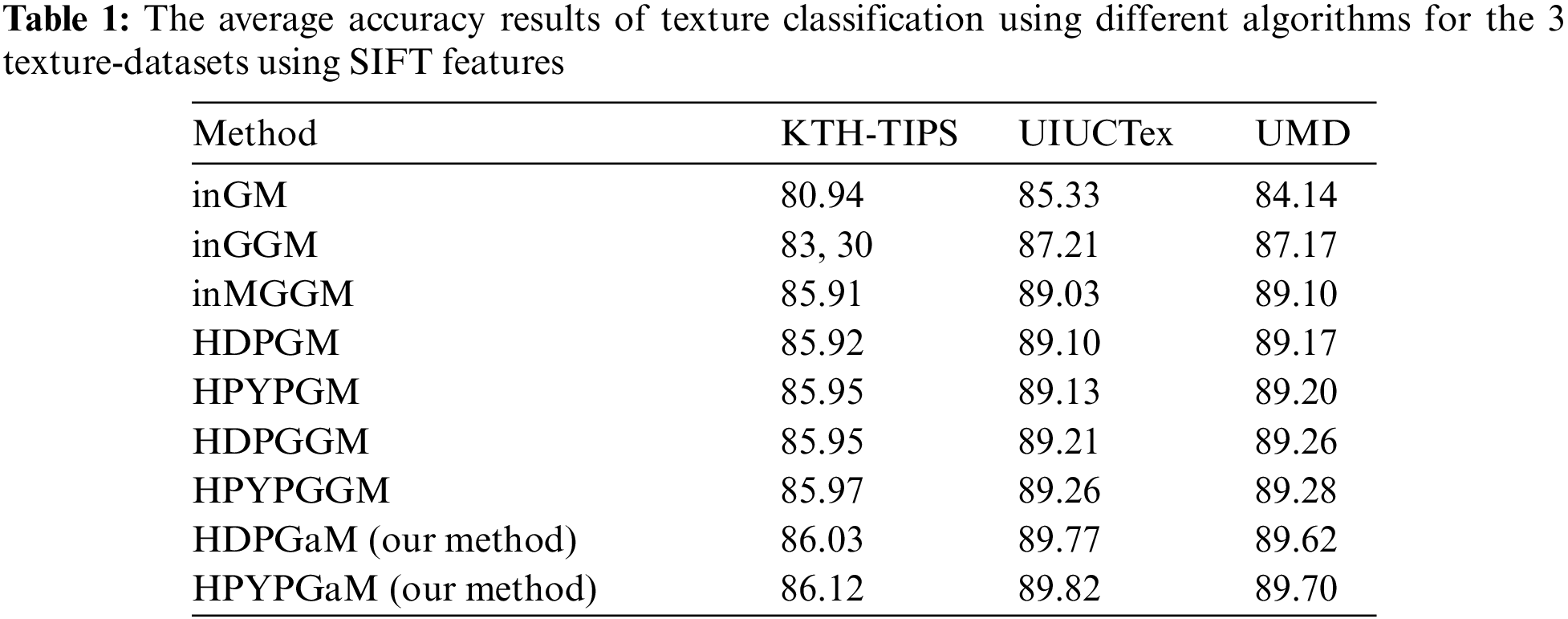
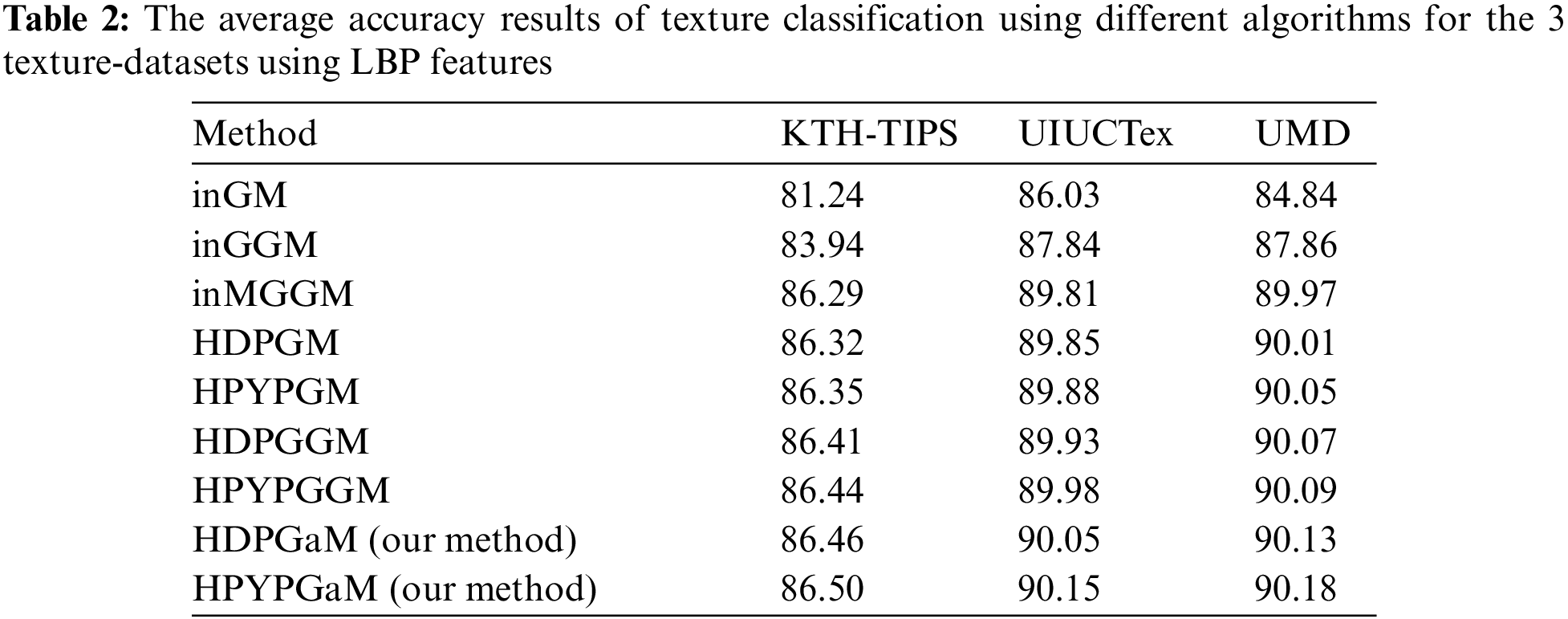
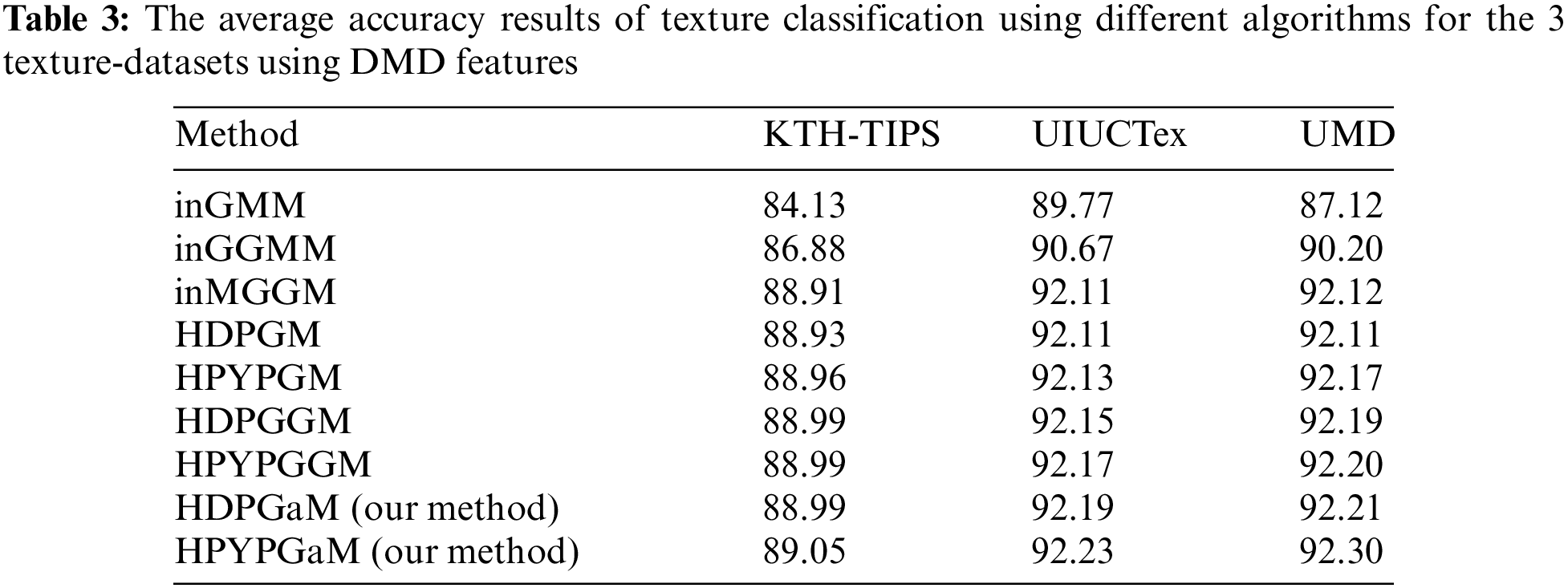
In order to quantify the performance of the proposed frameworks (HDPGaM and HPYPGaM), we proceed by evaluating and comparing the obtained results with seven other methods namely infinite mixture of Gaussian distribution (inGM), infinite mixture of generalized Gaussian distribution (inGGM), infinite mixture of multivariate generalized Gaussian distribution (inMGGM), Hierarchical Dirichlet Process mixture of Gaussian distribution (HDPGM), hierarchical Pitman-Yor process mixture of Gaussian distribution (HPYPGM), Hierarchical Dirichlet Process mixture of generalized Gaussian distribution (HDPGGM), and hierarchical Pitman-Yor process mixture of generalized Gaussian distribution (HPYPGGM).

Figure 2: Texture samples in different categories for different datasets (a) KTH-TIPS, (b) UIUCTex, and (c) UMD dataset

We run all methods 30 times and calculate the average classification accuracy which are depicted in Tabs. 1–3 respectively. According to these results, we can notice that HDPGaM and HPYPGaM have the highest achieved accuracy for the three databases in terms of the texture classification accuracy rate. It is noted that when comparing these results by considering the Student's t-test, the differences in performance are statistically significant between our frameworks and the rest of methods. In particular, results indicate the benefits of our proposed models in terms of texture modeling and classification capabilities which surpass those obtained by HDPGM, HDPGGM, HPYPGM, and HPYPGGM. By contrast, the worst performance is obtained within the infinite Gaussian mixture models. It should be noted that the proposed frameworks outperform the other methods and that the three adopted feature extraction methods (SIFT, LBP and DMD). Thus, these results confirm the merit of the proposed methods. Due to the effectiveness of DMD descriptor for describing and modelling observed texture images, we also find that DMD achieves better accuracy compared with both SIFT and LBP. It shows the merits of DMD which is able to consider all possible fine details images at different resolutions. We also note that with HPYP mixture we can reach better results compared to HDP mixture and this is for all tested distributions. This can be explained by the fact that HPYP mixture model has better generalization capability and better capacity to model heavier-tailed distribution (PYP prior can lead to better modeling ability).

4.2 Human Actions Categorization

Visual multimedia recognition has been a challenging research topic which could attract many applications such as actions recognition [40,41], image categorization [42,43], biomedical image recognition [44], and facial expressions [29,30]. In this work, we are focusing on a particular problem that has received a lot of attention namely Human actions recognition (HAR) through sequence of videos. Indeed, the intention of recognizing activities is to identify and analyze various human actions. At present, HAR is one the hot computer vision topics not only in research but also in industries where automatic identification of any activity can be useful, for instance, for monitoring, healthcare, robotics, and security-based applications [45]. Recognizing manually activities is very challenging and time consuming. This issue has been addressed and so various tools have been implemented such as in [40,45–47]. However, precise recognition of actions is still required using advanced and efficient algorithms in order to deal with complex situations such as noise, occlusions, and lighting.

We perform here the recognition of Human activities using the proposed frameworks HDPGaM and HPYPGaM. Our methodology is outlined as following: First, we extract and normalize SIFT3D descriptor [40] from observed images. These features are then quantized as visual words via bag-of-words (BOW) model and K-means algorithm [48]. Then, these features are quantized as visual words via K-means algorithm [48]. Then, a probabilistic Latent Semantic Analysis (pLSA) [49] is adopted to construct a d-dimensional vector. In particular, each image Ij is considered as a “group” and is associated with an infinite mixture model Gj. Thus, we suppose that Each SIFT3D feature vector is drawn from the infinite mixture model Gj and “visual words” denote mixture components of Gj.

On the other hand, a global vocabulary is generated and shared between all groups via the global-model G0 of the proposed hierarchical models. This setting agrees with the purpose behind the hierarchical process mixture model. It is also noted that the building of the visual vocabulary is part of the hierarchical process mixture models and this step is not carried out separately via the k-means algorithm as many other approaches do. It is also noted that the generation of the visual vocabulary is part of our hierarchical process mixture models and this process is not performed separately via k-means as many other approaches did. In fact, it is due to the property of the nonparametric Bayesian model that the number of components in the global-level mixture model can be deduced from the data. We conducted our experiments of actions recognition using a publicly dataset known as KTH human action dataset [46]. This database contains 2391 sequences of different actions grouped into 6 classes. It also represents four scenarios (outdoors (s1), outdoors with scale variation (s2), outdoors with different clothes (s3) and indoors (s4)). Some scenarios from this dataset are given in Fig. 3. We randomly divided this dataset into 2 subsets to train the developed frameworks and to evaluate its robustness.

Figure 3: Sample frames of the KTH dataset actions with different scenarios

Our purpose through this application is to show the advantages of investigating our proposed hierarchical models HDPGaM and HPYPGaM over other conventional hierarchical mixtures and other methods from the state of the art. Therefore, we focused first on evaluating the performance of HDPGaM and HPYPGaM over Hierarchical Dirichlet Process mixture of Gaussian distribution (HDPGM), hierarchical Pitman-Yor process mixture of Gaussian distribution (HPYPGM), Hierarchical Dirichlet Process mixture of generalized Gaussian distribution (HDPGGM), and hierarchical Pitman-Yor process mixture of generalized Gaussian distribution (HPYPGGM). It is noted that we learned all the implemented models using variational Bayes. The average recognition performances of our frameworks and models based on HDP mixture and HPYP mixture are depicted in Tab. 4.

As we can see in this table, the proposed frameworks were able to offer the highest recognition rates (82.27% for HPYPGaM and 82.13% for HDPGaM) among all tested models. For different runs, we have p-values < 0.05 and therefore, the differences in accuracy between our frameworks and other models are statistically significant according to Student's t-test. Next, we compared our models against other mixture models (here finite Gaussian mixture (GMM) and finite generalized Gaussian mixture (GGMM) and methods from the literature. The obtained results are given in Tab. 5.

Accordingly, we can observe that models again are able to provide higher discrimination rate than the other methods. Clearly, these results confirm the effectiveness of our frameworks for activities modeling and recognition compared to other conventional Dirichlet and Pitman-Yor processes based on Gaussian distribution. Another remark is that our model HPYPGaM outperforms our second model HDPGaM for this specific application and this demonstrates the advantages of using hierarchical Pitman-Yor process over Dirichlet process which is flexible enough to be used for such recognition problem.

5  Conclusions

In this paper two non-parametric Bayesian frameworks based on both hierarchical Dirichlet and Pitman-Yor processes and Gamma distribution are proposed. The Gamma distribution is considered because of its flexibility for semi-bounded data modelling. Both frameworks are learned using variational inference which has certain advantages such as easy assessment of convergence and easy optimization by offering a trade-off between frequentist techniques and MCMC-based ones. An important property of our approach is that it does not need the specification of the number of mixture components in advance. We carried out experiments on texture categorization and human action recognition to demonstrate the performance of our models which can be used further for a variety of other computer vision and pattern recognition applications.

Acknowledgement: The authors would like to thank Taif University Researchers Supporting Project number (TURSP-2020/26), Taif University, Taif, Saudi Arabia. They would like also to thank Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2022R40), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Funding Statement: The authors would like to thank Taif University Researchers Supporting Project number (TURSP-2020/26), Taif University, Taif, Saudi Arabia. They would like also to thank Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2022R40), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.​

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

1The Matlab code for the features is available at http://www.cs.tut.fi/mehta/texturedmd

References

 1.  J. L. Andrews, P. D. McNicholas and S. Subedi, “Model-based classification via mixtures of multivariate t-distributions,” Computational Statistics & Data Analysis, vol. 55, no. 1, pp. 520–529, 2011. [Google Scholar]

 2.  J. W. Lau and P. J. Green, “Bayesian model-based clustering procedures,” Journal of Computational and Graphical Statistics, vol. 16, no. 3, pp. 526–558, 2007. [Google Scholar]

 3.  T. Singh, N. Saxena, M. Khurana, D. Singh, M. Abdalla et al., “Data clustering using moth-flame optimization algorithm,” Sensors, vol. 21, no. 12, pp. 4086, 2021. [Google Scholar]

 4.  W. Fan, N. Bouguila, J. -X. Du and X. Liu, “Axially symmetric data clustering through Dirichlet process mixture models of watson distributions,” IEEE Transactions on Neural Networks and Learning Systems, vol. 30, no. 6, pp. 1683–1694, 2019. [Google Scholar]

 5.  P. D. McNicholas, “Model-based clustering,” Journal of Classification, vol. 33, no. 3, pp. 331–373, 2016. [Google Scholar]

 6.  X. Liu, H. Fu and Y. Jia, “Gaussian mixture modeling and learning of neighboring characters for multilingual text extraction in images,” Pattern Recognition, vol. 41, no. 2, pp. 484–493, 2008. [Google Scholar]

 7.  V. Kumar, D. Kumar, M. Kaur, D. Singh, S. A. Idris et al., “A novel binary seagull optimizer and its application to feature selection problem,” IEEE Access, vol. 9, no. 1, pp. 103481–103496, 2021. [Google Scholar]

 8.  A. Aggarwal, V. Sharma, A. Trivedi, M. Yadav, C. Agrawal et al., “Two-way feature extraction using sequential and multimodal approach for hateful meme classification,” Complexity, vol. 2021, no. 1, pp. 1–7, 2021. [Google Scholar]

 9.  C. Beckmann, M. Woolrich and S. Smith, “Gaussian/gamma mixture modelling of ICA/GLM spatial maps,” Ninth International Conference on Functional Mapping of the Human Brain, New York, pp. 18–22, 2003; NeuroImage, vol. 19, pp. S935, 2003. [Google Scholar]

10. A. Almulihi, F. Alharithi, S. Bourouis, R. Alroobaea, Y. Pawar et al., “Oil spill detection in SAR images using online extended variational learning of Dirichlet process mixtures of gamma distributions,” Remote Sensing, vol. 13, no. 15, pp. 2991, 2021. [Google Scholar]

11. H. -C. Li, V. A. Krylov, P. -Z. Fan, J. Zerubia and W. J. Emery, “Unsupervised learning of generalized gamma mixture model with application in statistical modeling of high-resolution SAR images,” IEEE Transaction on Geoscience Remote Sensing, vol. 54, no. 4, pp. 2153–2170, 2016. [Google Scholar]

12. S. Bourouis, H. Sallay and N. Bouguila, “A competitive generalized gamma mixture model for medical image diagnosis,” IEEE Access, vol. 9, pp. 13727–13736, 2021. [Google Scholar]

13. R. Alroobaea, S. Rubaiee, S. Bourouis, N. Bouguila and A. Alsufyani, “Bayesian inference framework for bounded generalized Gaussian-based mixture model and its application to biomedical images classification,” International Journal of Imaging Systems and Technology, vol. 30, no. 1, pp. 18–30, 2020. [Google Scholar]

14. S. Bourouis, R. Alroobaea, S. Rubaiee, M. Andejany, F. M. Almansour et al., “Markov chain monte carlo-based Bayesian inference for learning finite and infinite inverted beta-liouville mixture models,” IEEE Access, vol. 9, no. 1, pp. 71170–71183, 2021. [Google Scholar]

15. S. N. MacEachern and P. Müller, “Estimating mixture of dirichlet process models,” Journal of Computational and Graphical Statistics, vol. 7, no. 2, pp. 223–238, 1998. [Google Scholar]

16. W. Fan, H. Sallay and N. Bouguila, “Online learning of hierarchical pitman-yor process mixture of generalized dirichlet distributions with feature selection,” IEEE Transactions on Neural Networks and Learning Systems, vol. 28, no. 9, pp. 2048–2061, 2017. [Google Scholar]

17. Y. W. Teh, M. I. Jordan, M. J. Beal and D. M. Blei, “Sharing clusters among related groups: Hierarchical dirichlet processes,” in Advances in Neural Information Processing Systems 17 [Neural Information Processing Systems: NIPS 2004, December 13-18], Vancouver, British Columbia, Canada, pp. 1385–1392, 2004. [Google Scholar]

18. Y. W. Teh, M. I. Jordan, M. J. Beal and D. M. Blei, “Hierarchical dirichlet processes,” Journal of the American Statistical Association, vol. 101, no. 476, pp. 1566–1581, 2006. [Google Scholar]

19. J. Sethuraman, “A constructive definition of dirichlet priors,” Statistica Sinica, vol. 4, pp. 639–650, 1994. [Google Scholar]

20. D. M. Blei and M. I. Jordan, “Variational inference for dirichlet process mixtures,” Bayesian Analysis, vol. 1, no. 1, pp. 121–143, 2006. [Google Scholar]

21. C. Wang, J. W. Paisley, and D. M. Blei, “Online variational inference for the hierarchical dirichlet process,” in Proc. of the Fourteenth Int. Conf. on Artificial Intelligence and Statistics, Fort Lauderdale, USA, vol. 15, pp. 752–760, 2011. [Google Scholar]

22. H. Ishwaran and L. F. James, “Gibbs sampling methods for stick-breaking priors,” Journal of the American Statistical Association, vol. 96, no. 453, pp. 161–173, 2001. [Google Scholar]

23. J. Pitman and M. Yor, “The two-parameter Poisson-Dirichlet distribution derived from a stable subordinator,” The Annals of Probability, vol. 25, no. 2, pp. 855–900, 1997. [Google Scholar]

24. H. Attias, “A variational Bayesian framework for graphical models,” Advances in Neural Information Processing Systems, vol. 12, no. 1–2, pp. 209–215, 2000. [Google Scholar]

25. Z. Song, S. Ali, N. Bouguila and W. Fan, “Nonparametric hierarchical mixture models based on asymmetric Gaussian distribution,” Digit. Signal Process, vol. 106, no. 1, pp. 102829, 2020. [Google Scholar]

26. W. Fan, H. Sallay, N. Bouguila and S. Bourouis, “Variational learning of hierarchical infinite generalized dirichlet mixture models and applications,” Soft Computing, vol. 20, no. 3, pp. 979–990, 2016. [Google Scholar]

27. Y. Huang, F. Zhou and J. Gilles, “Empirical curvelet based fully convolutional network for supervised texture image segmentation,” Neurocomputing, vol. 349, no. 1, pp. 31–43, 2019. [Google Scholar]

28. Q. Zhang, J. Lin, Y. Tao, W. Li and Y. Shi, “Salient object detection via color and texture cues,” Neurocomputing, vol. 243, pp. 35–48, 2017. [Google Scholar]

29. W. Fan and N. Bouguila, “Online facial expression recognition based on finite beta-liouville mixture models,” in 2013 Int. Conf. on Computer and Robot Vision, Regina, Saskatchewan, Canada, 2013, pp. 37–44. [Google Scholar]

30. G. Zhao and M. Pietikainen, “Dynamic texture recognition using local binary patterns with an application to facial expressions,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 29, no. 6, pp. 915–928, 2007. [Google Scholar]

31. A. Badoual, M. Unser and A. Depeursinge, “Texture-driven parametric snakes for semi-automatic image segmentation,” Computer Vision and Image Understanding, vol. 188, no. 3, pp. 102793, 2019. [Google Scholar]

32. Y. Zheng and K. Chen, “A general model for multiphase texture segmentation and its applications to retinal image analysis,” Biomedical Signal Processing and Control, vol. 8, no. 4, pp. 374–381, 2013. [Google Scholar]

33. E. Hayman, B. Caputo, M. Fritz and J. -O. Eklundh, “On the significance of real-world conditions for material classification,” in Computer Vision-ECCV 2004, 8th European Conf. on Computer Vision, Czech Republic, may 11–14, Proc., Part IV, Prague, Czech Republic, 2004, vol. 3024, pp. 253–266. [Google Scholar]

34. J. Zhang, M. Marszalek, S. Lazebnik and C. Schmid, “Local features and kernels for classification of texture and object categories: A comprehensive study,” International Journal of Computer Vision, vol. 73, no. 2, pp. 213–238, 2007. [Google Scholar]

35. Z. Guo, L. Zhang and D. Zhang, “A completed modeling of local binary pattern operator for texture classification,” IEEE Transaction on Image Processing, vol. 19, no. 6, pp. 1657–1663, 2010. [Google Scholar]

36. D. G. Lowe, “Distinctive image features from scale-invariant keypoints,” International Journal of Computer Vision, vol. 60, no. 2, pp. 91–110, 2004. [Google Scholar]

37. R. Mehta and K. O. Egiazarian, “Texture classification using dense micro-block difference,” IEEE Transaction on Image Processing, vol. 25, no. 4, pp. 1604–1616, 2016. [Google Scholar]

38. S. Lazebnik, C. Schmid and J. Ponce, “A sparse texture representation using local affine regions,” IEEE Transaction on Pattern Analysis and Machine Intelligence, vol. 27, no. 8, pp. 1265–1278, 2005. [Google Scholar]

39. Y. Xu, H. Ji and C. Fermüller, “Viewpoint invariant texture description using fractal analysis,” International Journal of Computer Vision, vol. 83, no. 1, pp. 85–100, 2009. [Google Scholar]

40. P. Scovanner, S. Ali and M. Shah, “A 3-dimensional sift descriptor and its application to action recognition,” in Proc. of the 15th ACM Int. Conf. on Multimedia, Augsburg, Germany, 2007, pp. 357–360. [Google Scholar]

41. F. Najar, S. Bourouis, N. Bouguila and S. Belghith, “Unsupervised learning of finite full covariance multivariate generalized Gaussian mixture models for human activity recognition,” Multimedia Tools and Applications, vol. 78, no. 13, pp. 18669–18691, 2019. [Google Scholar]

42. R. Zhu, F. Dornaika and Y. Ruichek, “Learning a discriminant graph-based embedding with feature selection for image categorization,” Neural Networks, vol. 111, pp. 35–46, 2019. [Google Scholar]

43. H. Zhou and S. Zhou, “Scene categorization towards urban tunnel traffic by image quality assessment,” Journal of Visual Communication and Image Representation, vol. 65, pp. 102655, 2019. [Google Scholar]

44. F. S. Alharithi, A. H. Almulihi, S. Bourouis, R. Alroobaea and N. Bouguila, “Discriminative learning approach based on flexible mixture model for medical data categorization and recognition,” Sensors, vol. 21, no. 7, pp. 2450, 2021. [Google Scholar]

45. M. Vrigkas, C. Nikou and I. A. Kakadiaris, “A review of human activity recognition methods,” Frontiers in Robotics and AI, vol. 2, pp. 28, 2015. [Google Scholar]

46. C. Schuldt, I. Laptev and B. Caputo, “Recognizing human actions: A local SVM approach,” in Pattern Recognition, 2004. ICPR 2004. Proc. of the 17th Int. Conf., Cambridge, UK, 2004, vol. 3, pp. 32–36. [Google Scholar]

47. F. Najar, S. Bourouis, N. Bouguila and S. Belghith, “A new hybrid discriminative/generative model using the full-covariance multivariate generalized Gaussian mixture models,” Soft Computing, vol. 24, no. 14, pp. 10611–10628, 2020. [Google Scholar]

48. G. Csurka, C. Dance, L. Fan, J. Willamowski and C. Bray, “Visual categorization with bags of keypoints,” in Workshop on Statistical Learning in Computer Vision, ECCV, Prague, Czech Republic, 2004, vol. 1, pp. 1–2. [Google Scholar]

49. A. Bosch, A. Zisserman and X. Muñoz, “Scene classification via pLSA,” Computer Vision–ECCV, 2006, pp. 517–530, 2006. [Google Scholar]

50. S. -F. Wong and R. Cipolla, “Extracting spatiotemporal interest points using global information,” in IEEE 11th Int. Conf. on Computer Vision, Rio de Janeiro, Brazil, pp. 1–8, 2007. [Google Scholar]

51. W. Fan and N. Bouguila, “Variational learning for dirichlet process mixtures of dirichlet distributions and applications,” Multimedia Tools and Applications, vol. 70, no. 3, pp. 1685–1702, 2014. [Google Scholar]

52. P. Dollár, V. Rabaud, G. Cottrell and S. Belongie, “Behavior recognition via sparse spatio-temporal features,” in 2005 IEEE Int. Workshop on Visual Surveillance and Performance Evaluation of Tracking and Surveillance, Beijing, China, pp. 65–72, 2005. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.