Computers, Materials & Continua DOI:10.32604/cmc.2022.021019
Article

Hyperchaos and MD5 Based Efficient Color Image Cipher

Muhammad Samiullah1, Waqar Aslam1, Saima Sadiq2, Arif Mehmood1 and Gyu Sang Choi3,*

1Department of Computer Science & IT, The Islamia University of Bahawalpur, Bahawalpur, 63100, Pakistan
2Department of Computer Science, Khwaja Fareed University of Engineering and Information Technology, Rahim Yar Khan, 64200, Pakistan
3Department of Information and Communication Engineering, Yeungnam University, Gyeongsan, 38541, Korea
*Corresponding Author: Gyu Sang Choi. Email: castchoi@ynu.ac.kr
Received: 19 June 2021; Accepted: 16 September 2021

Abstract: While designing and developing encryption algorithms for text and images, the main focus has remained on security. This has led to insufficient attention on the improvement of encryption efficiency, enhancement of hyperchaotic sequence randomness, and dynamic DNA-based S-box. In this regard, a new symmetric block cipher scheme has been proposed. It uses dynamic DNA-based S-box connected with MD5 and a hyperchaotic system to produce confusion and diffusion for encrypting color images. Our proposed scheme supports various size color images. It generates three DNA based S-boxes for substitution namely DNA_1_s-box, DNA_2_s-box and DNA_3_s-box, each of size 16×16. Next, the 4D hyperchaotic system followed by MD5 is employed in a novel way to enhance security. The three DNA-based S-boxes are generated from real DNA sequences taken from National Center for Biotechnology Information (NCBI) databases and are dependent on the mean intensity value of an input image, thus effectively introducing content-based confusion. Finally, Conservative Site-Specific Recombination (CSSR) is applied on the output DNA received from DNA based S-boxes. The experimental results indicate that the proposed encryption scheme is more secure, robust, and computationally efficient than some of the recently published similar works. Being computational efficient, our proposed scheme is feasible on many emergent resource-constrained platforms.

Keywords: Block cipher; substitution; permutation; diffusion; confusion

1  Introduction

The official communication based on images in the form of electronic patient records (EPRs), notifications, office orders and scanned documents may suffer from loss and theft if transmitted over an insecure channel. By using existing standard symmetric ciphers such as Data Encryption Standard (DES), 3-DES, Advanced Encryption Standard (AES) for encrypting the digital images, we neglect digital image's intrinsic properties such as pixel correlations, data redundancies, etc., therefore the existing ciphers suffer from low encryption efficiency [1,2]. Thus, the above-mentioned intrinsic properties of an image must be considered while improving or devising the image ciphers. Communication using digital images represents 70 percent of the data transmitted on the internet [3]. To address this issue, the images must be encrypted efficiently with secure key management prior to transmission or storage. Although, some ciphers based on chaotic systems are susceptible to some classical attacks [4], combining the higher dimensional hyperchaotic system or multiple chaotic systems with Deoxyribo Nucleic Acid (DNA) operations in designing the ciphers are proved to be very secure [5–10]. Likewise, a cipher based on chaotic cryptography, DNA cryptography, or a combination of both must contain the confusion and diffusion architecture with any number of rounds. The confusion is normally achieved through S-box (a non-linear function) in which the pixel values are replaced with new values. While in diffusion, the pixel positions are randomly exchanged without changing the actual pixel values. No doubt, S-box obfuscates the relationship between key and encrypted image but is seldom adopted in image ciphers [11]. A good S-box should meet the ideal values of avalanche criterion and completeness. Similarly, the weak randomness produced by chaotic maps can be improved by efficient architectures, jointing it with hyperchaotic systems, DNA operations, and S-boxes to make it eligible for Pseudo-Random Number Generators (PRNGs). In this respect, a sequence produced by the 4D hyperchaotic system is improved in [12]. Likewise, a highly secure and confidential algorithm is proposed that connects the Memetic algorithm with a PRNG to encrypt the sensitive information prior to embedding it into a patient's medical image [13].

Based on the above discussions, a cipher based on MD5, SHA-256, 4D hyperchaotic system jointed with DNA-based S-box is presented. The main contributions of this research work are: (a) Implementation of DNA-based S-box [14] to encrypt RGB images, (b) CSSR is applied after the substitution, (c) initial conditions for the 4D hyperchaotic system are generated from the hash of the plain image and biological DNA which in turn gives encryption key, (d) diffusion using the 4D hyperchaotic system is achieved in an intertwined pattern.

The remaining of this paper is organized as follows: Section 2 deals with background studies. Section 3 describes the related work. The proposed scheme is written in Section 4. Security analysis and performance analysis are carried out in Section 5. Conclusions and future directions are given in Section 6.

2  Background Studies

2.1 Hyperchaos and Lyapunov Exponents

The usual way to identify the hyperchaotic behavior of a non-linear system is to compute Lyapunov Exponents (LEs). The idea behind LEs is as follows: (a) Sensitive dependence on initial conditions is characterized by binary distinctions i.e., either the system has sensitive dependence on initial conditions or it doesn't, (b) how much the particular dynamical system has the sensitivity to changes in initial conditions. The answer is LE, which is a way of quantifying the sensitivity to initial conditions. LE defined in Eq. (1), is the average logarithmic rate of separation or convergence between the two points on the orbits at time series t [15]. In short, LE is the exponential separation rate for two nearby trajectories of a dynamical system.

LE=limn→∞⁡1n∑i=1n⁡ln⁡|ΔDiΔD∘|,(1)

where ΔD∘ is the initial difference between the two initial conditions X∘ and Y∘. If the non-linear system has two or more Positive Lyapunov Exponents (PLEs), it is named hyperchaos and they show much-complicated behavior as compared to chaotic systems. On the other side, chaotic systems have one PLE. Maximum PLEs indicate more chaos and vice versa. And the negative LEs represent no sensitive dependence on initial conditions or no chaos. The first hyperchaotic system with four dimensions was reported in 1979 by Rossler [16]. Hyperchaotic systems have been used practically in encryption, decryption of gray-level and color images and shown excellent results [6]. But the trade-off among the performance and cryptanalysis metrics has always been a challenging subject. For example, a 4D hyperchaotic system Eq. (2) introduced by [17] has four system parameters a,  b,  c,  d and e When a=0.98,  b=9,  c=50,  d=0.06 and e=0.9 with initial conditions x=11.28,  y=11.21,  z=−9,  w=20.49 then the system shows hyperchaotic behavior and has 2 PLEs out of 4 LEs (0.00732,  0.004414,  −0.020359,  −0.898567). The initial conditions can be generated from the hash of the input image or DNA. The hyperchaotic behaviors of the system are shown in Fig. 1

{x˙=a(x−y)−yz+wy˙=−by+xzz˙=−cz+dx+xyw˙=−e(x+y).(2)

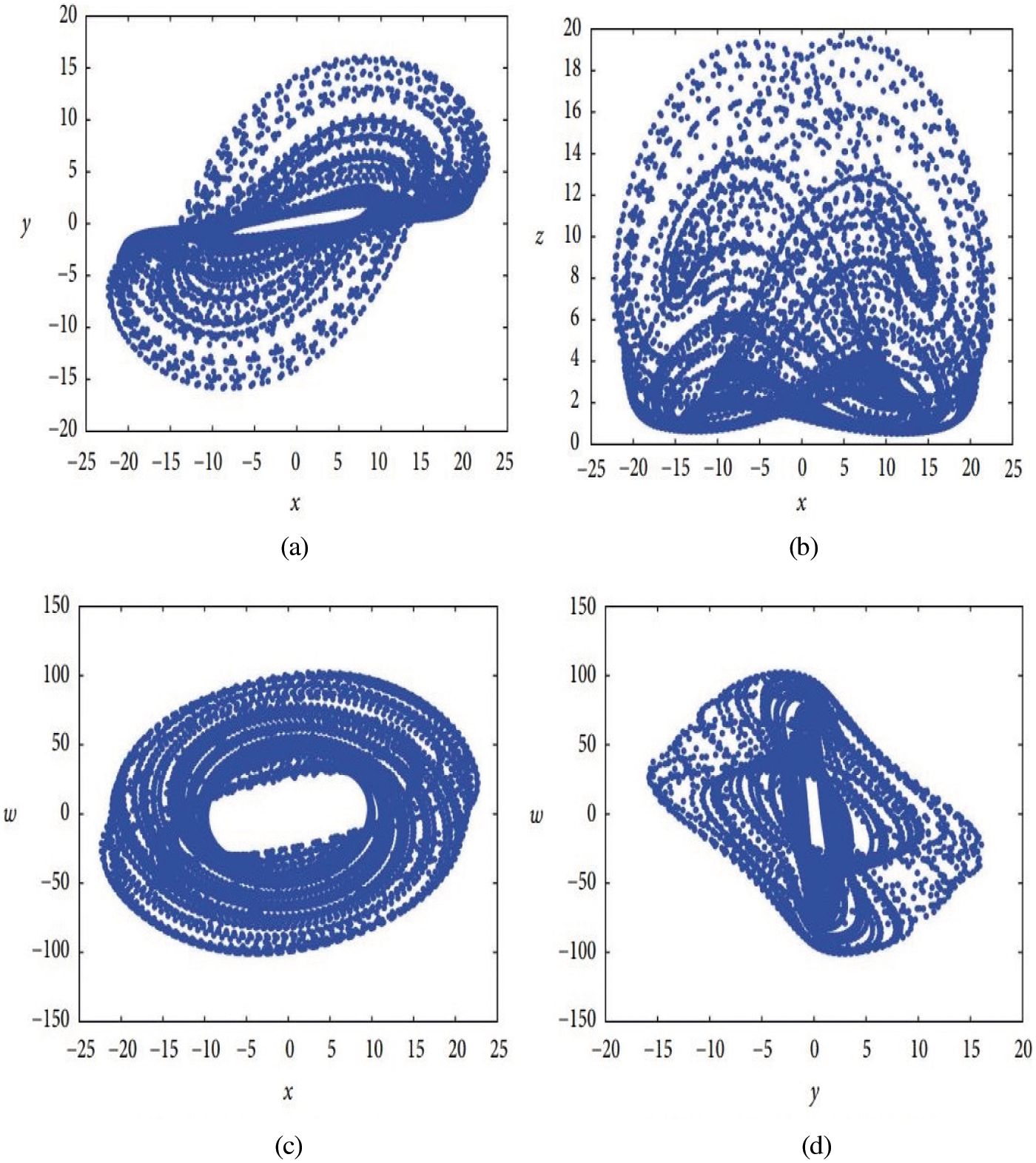
Figure 1: Phase portraits of the dynamic system [17]. (a) Projection onto the x-y plane (b) Projection onto the x-z plane (c) Projection onto the x-w plane (d) Projection onto the y-w plane

This proposed scheme can be considered as an eligible candidate for practical applications as it outperforms some existing cryptosystems concerning encryption efficiency and resistance to statistical and differential attacks.

2.2 DNA Digitization

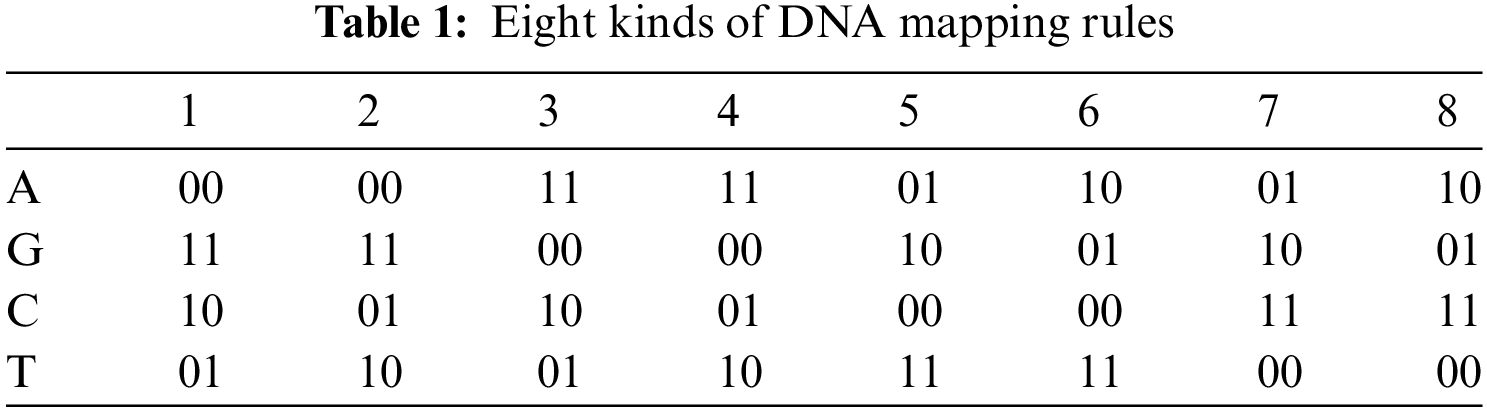
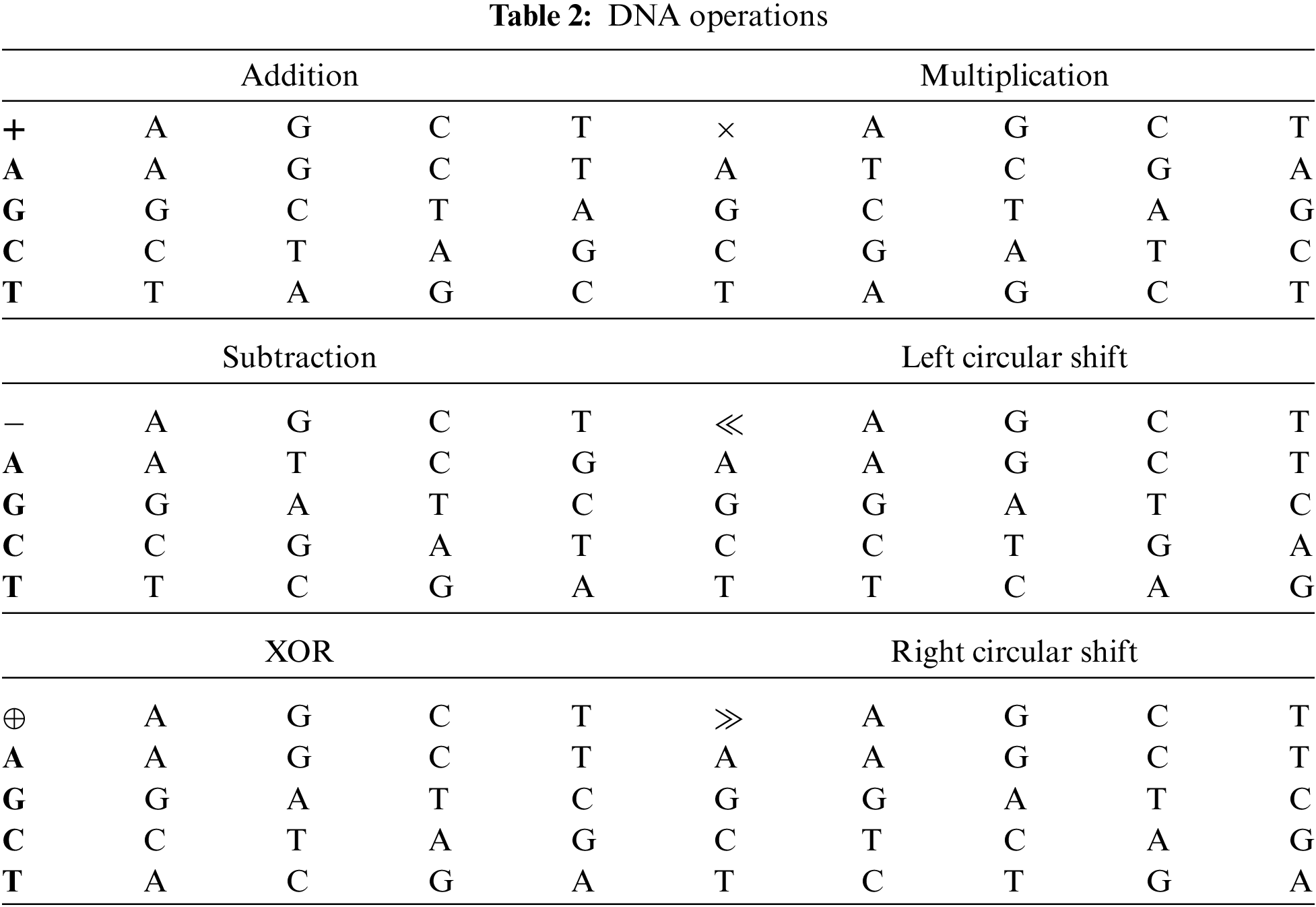
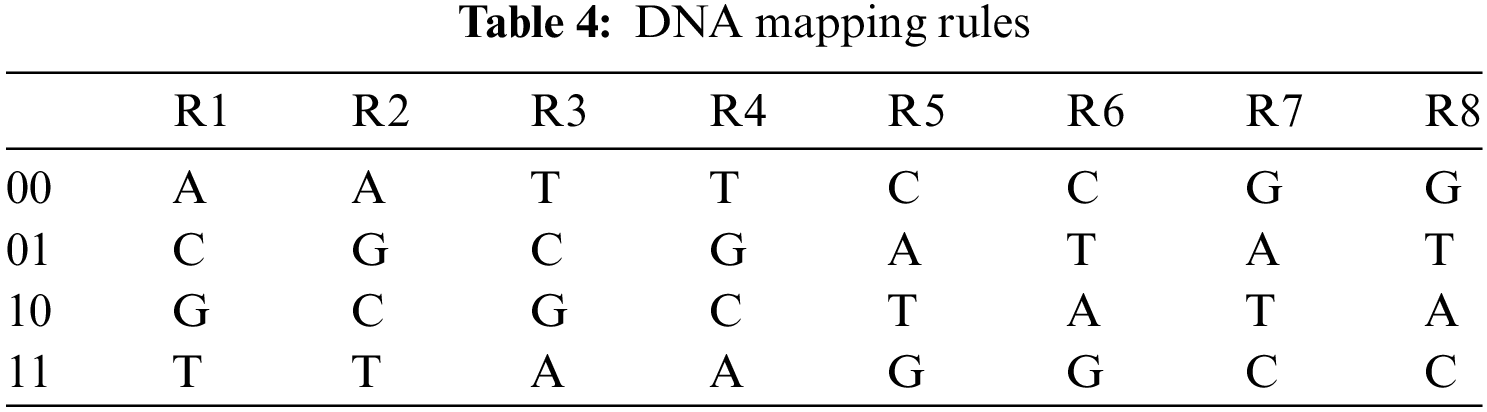
We all are made up of cells. Each cell contains a nucleus and the nucleus has a molecule (called DNA) containing the recipe of an organism's life. Deoxyribo Nucleic Acid (DNA) is composed of two polynucleotide chains coiling around each other. Each polynucleotide is composed of many nucleotides and each nucleotide is composed of pyrimidines (Adenine (A), Guanine (G)), purines (Cytosine (C), Thymine (T)), sugar and phosphate group. Nucleotides on the same strand are interlinked through covalent bonds. And the nucleotides on the opposite strands are interlinked through hydrogen bonds according to base-pairing rules such that A with T and G with C [18]. DNA provides a range of features and new directions for data confidentiality. The research on 7 point Hamiltonian path problem using DNA molecules in test tubes set a new direction towards DNA computing [19]. DNA computing is a premature field but expectations are high due to its efficient molecular structure, massive parallelism, and huge storage capacity. DNA computing can be done in two ways: (a) by using biological DNA molecules in the laboratory, (b) by using digital DNA molecules available on genetic databases. The digital DNA may be divided into real and fake. The real digital DNA represents the real genomes of some organisms. And fake digital DNA is the supposed DNA sequence or it can be derived from some data (text or image) by using the DNA coding rules. The one advantage of digital DNA is that new genes can be designed by using software without chemical processes and accessing the specific physical DNA samples. The use of the current generation of computers by the researchers to analyze, interpret, and store digitized genetic information provided a new direction for computer science researchers towards cryptography. Consequently, many researchers proposed image ciphers based on DNA encoding, decoding, DNA operations, DNA based S-box, and DNA based secret keys. Similarly, jointing DNA operations with hyperchaotic systems improved the security and performance of ciphers [20,21]. The DNA encoding and decoding rules and DNA operations [22,23] are shown in Tabs. 1 and 2 respectively.

2.3 CSSR

Conservative Site-Specific Recombination (CSSR) is a mechanism of site-specific recombination, in which serine or tyrosine recombinase enzymes break the DNA at a specific site called recombination recognition site, and then the process of recombination is started at this site. CSSR is easier than homologous recombination. It is useful in gene conversions and transpositions. CSSR has three forms namely insertion, deletion, and inversion as shown in Fig. 2.

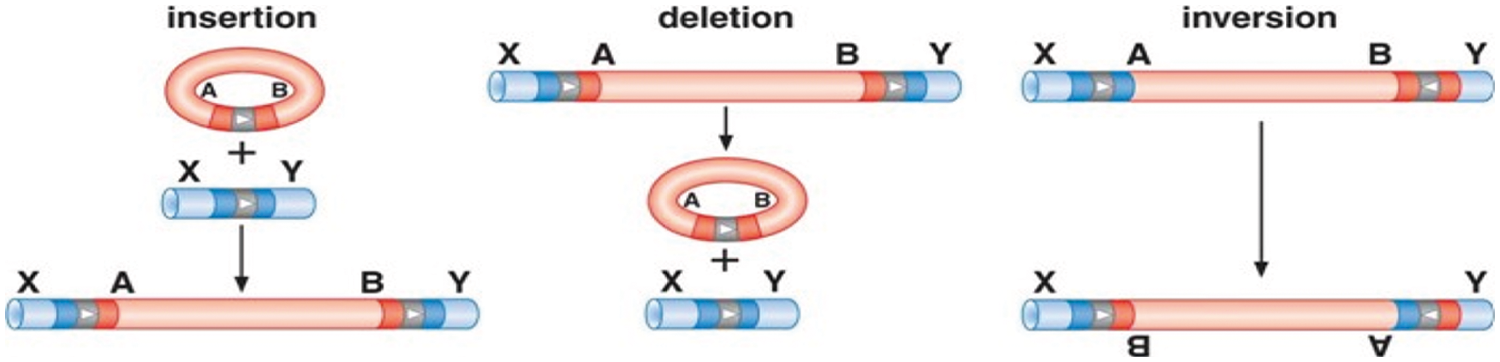
Figure 2: Mechanism of CSSR insertion, deletion, and inversion [24,25]

The above mentioned CSSR mechanism can be applied in cryptography with little modifications while encrypting the images. The image pixels of interest are used as Recombination Recognition Sites/Sequence (RRS) for recombination purposes. The level of confusion can be enhanced by making it a part of encryption algorithms. For example, a plain image can be converted into DNA sequence by using DNA encoding rules, then apply DNA operations, apply the CSSR mechanism, generate hyperchaotic sequence (secret key), permute the resultant DNA sequence according to the hyperchaotic sequence, etc.

2.4 S-Box Module

S-box is a non-linear lookup table and is an essential module in the symmetric block ciphers such as Advanced Encryption Standard (AES), Triple-Data Encryption Standard (3DES), etc. Confusion through substitution in the symmetric ciphers is achieved through S-box. A good S-box abstruses the relationship between secret key and ciphertext and doesn't give the statistical inferences to the cryptanalysts. Moreover, lower delay, higher efficiency, uniqueness of the values, and no correlation between the values in the S-box are also the indicators of a good S-box. S-box must pass the criteria of Bit Independence (BI), Differential Approximation Probability (DAP), Strict Avalanche Criterion (SAC), bijective, nonlinearity, and Linear Approximation Probability (LAP) [26]. A trade-off remains among the S_box criteria metrics and we have to compromise some criteria. For example, maximal non-linearity clashes with balancedness, etc.

S-boxes construction techniques based on Galois Fields (GFs), Galois Rings (GRs), left most semi-groups, linear functional transformation, symmetric groups, coset diagram, the action of the modular group, action of projective general and special linear group are some examples of algebraic structures utilization [27,28]. A large number of S-box construction methods based on chaos and DNA have been proposed by various cryptography researchers in recent years. Chaotic S-boxes based on Fractional Rossler system, time-delay chaotic system, fractional-order chaotic Chen system, and Hénon map are proposed in [29–32]. Hyperchaotic based S-boxes that satisfy the SAC, BI, DAP, and non-linearity are proposed in [33–35]. Similarly, to the best of our literature review, DNA dependent S-boxes have also been proposed but rarely used in symmetric block ciphers. DNA-based S-box is generated in [36], in which the author used DNA operations (addition, subtraction, XOR) and search procedure to remove repeating values. S-box can be generated from different sources as shown in Fig. 3. Some S-box design criteria are discussed as follows:

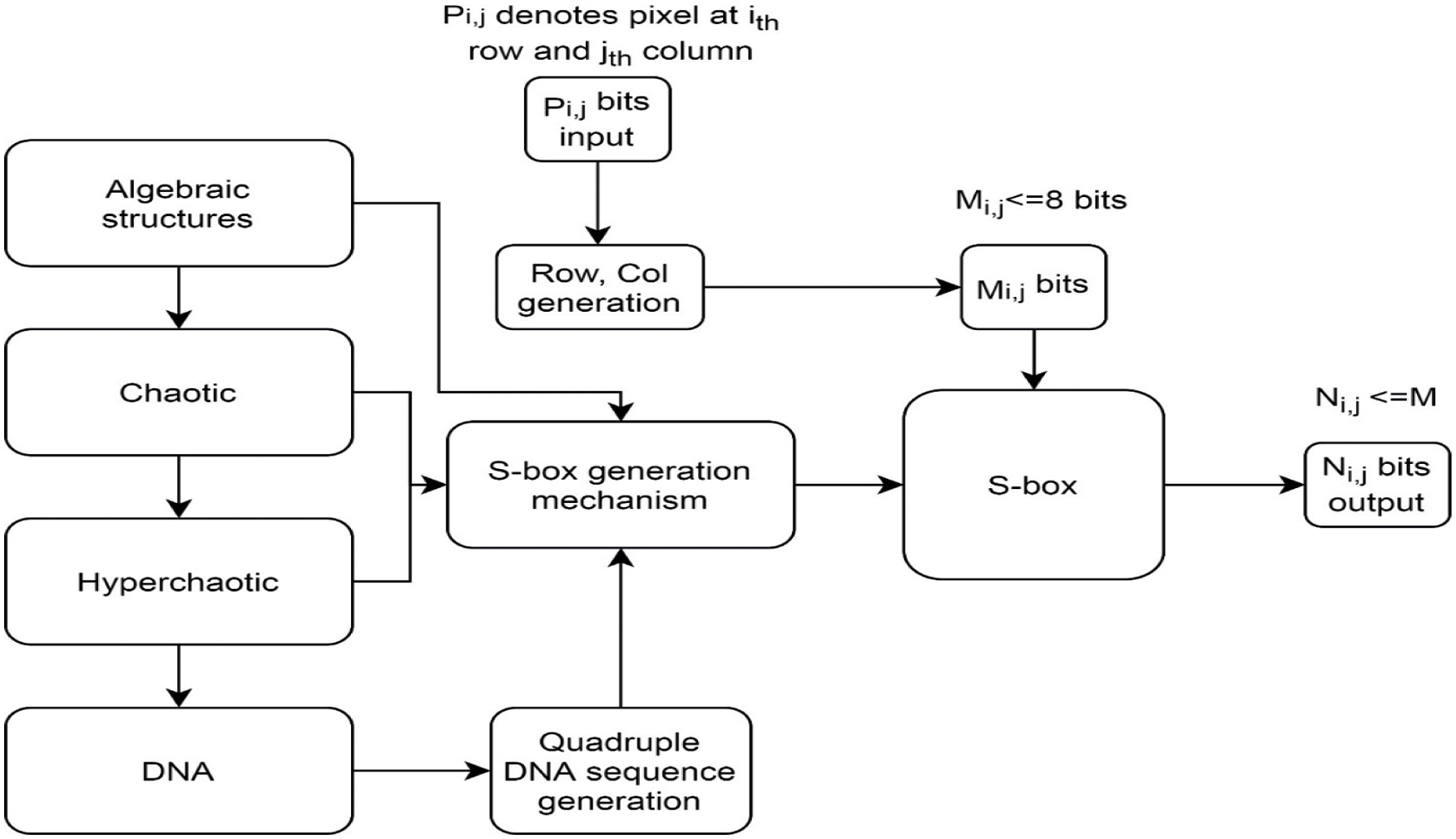
Figure 3: Different sources S-box design

2.4.1 Strict Avalanche Criterion

Avalanche criterion (AC) or propagation criteria is a ratio of the number of flipped bits in the output to the total number of output bits. AC introduced by [37], is a worthwhile property of ciphers and S-boxes, in which a small change in input (a single bit change) creates a significant change in the output bits (e.g., half of the output bits get change). SAC must satisfy the completeness and avalanche criterion. S-box completeness means, each output bit depends on each input bit i.e., a single bit change will create a significant change in the output bits. Higher-order SACs include more than a 1-bit change in the input. S-boxes must satisfy SAC without disturbing the non-linearity. A cipher or S-box that doesn't fulfill the SAC has poor randomization and increases the probability for the cryptanalysts to make predictions about the input. Boolean functions that satisfy the high-order SACs are called bent functions or maximally non-linear functions i.e., they are hard to approximate. But one problem with the bent functions is that they are unbalanced.

2.4.2 Non Linearity Test

The S-boxes’ non-linearity feature controls the vulnerability in cryptography, i.e., it resists linear attacks. The non-linearity of boolean function (as s-box is a boolean function that does mappings from {0,1}m→{0,1}n) is also characterized by the least hamming distance between the boolean function's output and set of all affine functions. The non-linearity of a boolean function Eq. (3), is computed as [38]:

NL(f)=minD(f,∅),(3)

where ∅ belongs to the set of all affine functions and minD is the minimum hamming distance between f and ∅. Walsh spectrum is normally used to quantify this test.

2.4.3 Bijectiveness

Bijective function has the property of both injective and surjective functions, i.e., there is a one to one correspondence and no member in the domain or co-domain is left out. It indicates the uniqueness of values in the S-box. There is no need of Bijectiveness in fiestel ciphers [39].

2.4.4 Balancedness

Balancedness means the balanced distribution of 0 s and 1 s, i.e., equal number of 0 s and 1 s distributed randomly. S-boxes with maximal non-linearity level are called vectorial bent functions but unluckily they lose the property of balancedness to great extent. To this end, [39] designed a better balanced S-box having maximal non-linearity that can resist linear and differential attacks to a large extent.

3  Related Work

For the design of encryption architecture and secret key generation mechanism in block ciphers, encryption efficiency with a reasonable security level has been the major concern of cryptosystem designers. In this regard, cryptographic researchers have proposed various color image encryption schemes. The researchers used chaotic systems, hyperchaotic systems, DNA operations, a variety of S-boxes (chaotic, hyperchaotic, algebraic structures, DNA, etc.) to accomplish the task of confusion and diffusion. In this respect, an encryption algorithm has been presented by [3] that is based on chaos and modified Advanced Encryption Standard (AES). The pros of this approach include the reduced time complexity, efficient row shifting and linear transformation mechanism, larger key space to resist brute force attacks, ideal entropy values, resistance against statistical attacks and shows a significant change in the ciphertext when a small change is made in the input values. The cons include the decrease in encryption efficiency when applied to color images. Digital image encryption that includes, Hill diffusion, modular chaotic maps followed by rows-column diffusion is presented in [40]. The pros of this approach include the need for only two rounds of confusion and diffusion to attain the optimum security analysis parameter values with better encryption efficiency and resistance to statistical and differential attacks. Although, the proposed scheme encrypts only gray-level images but can be expanded to encrypt, decrypt the color images of larger sizes. The selection of prime number modulus is the main constraint of this approach. A real-time digital color image encryption scheme makes use of 3D Orthogonal Latin Squares (OLSs) for performing 3D permutation [41]. The pros of this scheme that make it eligible for real-time use cases include fast encryption time, reasonable security, and resistance to common attacks. Although, certain privacy safeguarding policies exist at the organizational level, still defensible protection of a user's data at various levels, i.e., data gathering, data accessing, reusing and data disclosure etc., have not been implemented to its spirit [42]. The protection image data at these levels can be protected by the efficient cryptographic algorithms.

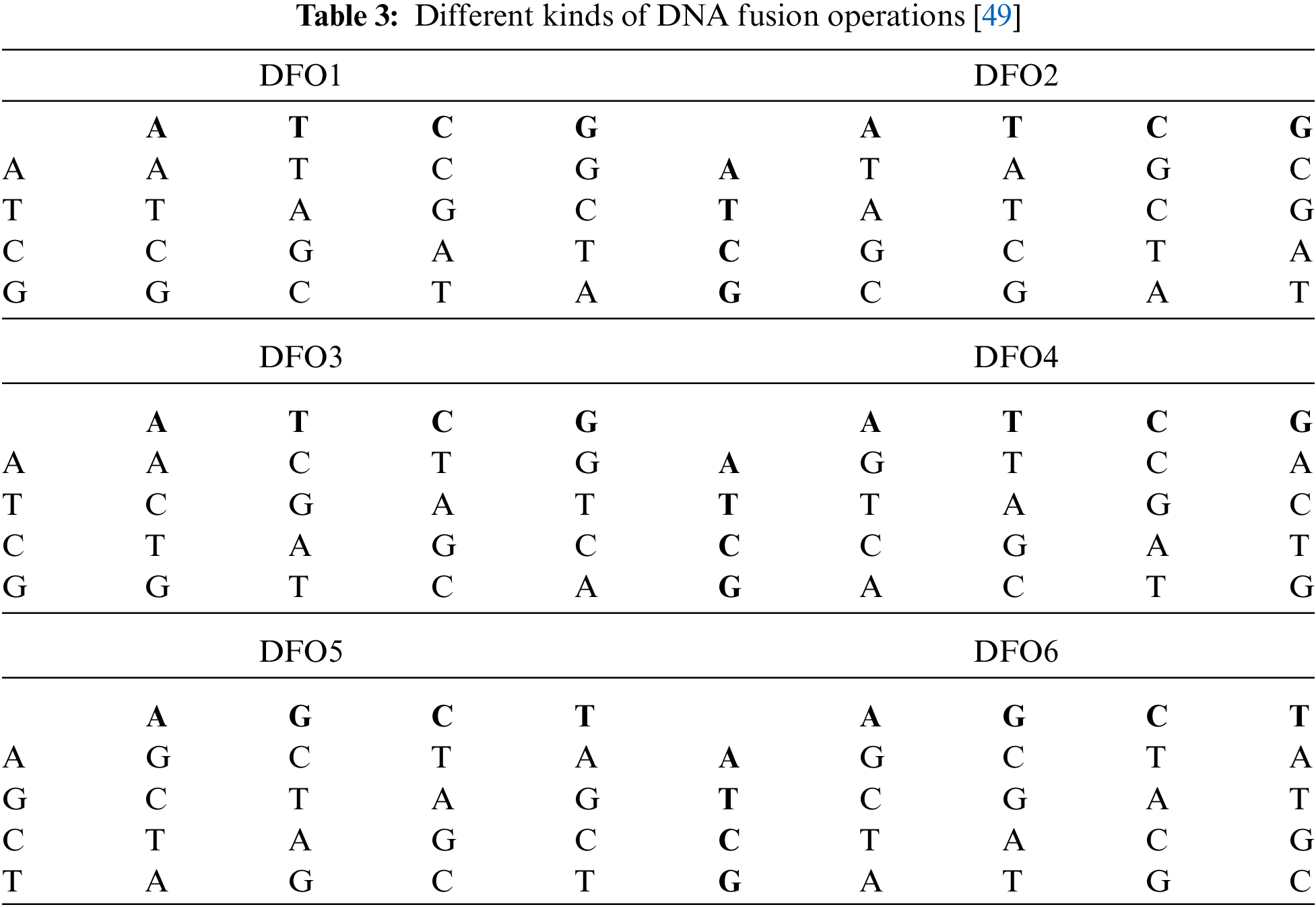
In contrast, double encryption approach based on trigonometric chaotic map and XOR gives better results regarding security and speed. The security of this approach is achieved by means of circular shifts of rows and columns and connecting the XOR operation with modulo function [43]. A novel color image cipher is proposed that exploits 3 S-boxes (each of size 8 × 8) and 3D-Arnold chaotic map for implementing confusion and diffusion respectively [44]. The pros of this approach include the reduced time complexity, efficient substitutions followed by chaos based diffusion, larger key space to resist all types of known brute force attacks, entropy values closer to 8, uniformity in the histograms of encrypted images, resistance against statistical attacks and an average avalanche effect of 50%. The cons include the decrease in encryption efficiency when applied to color images of larger dimensions. A scheme proposed by [45], makes use of Logistic-Sine System (LSS) in creating an S-box and takes two rounds of substitution and one round of permutation. The LSS has a wider chaotic range and better chaotic properties. The cryptosystem has better potential in real-time gray-level image encryption scenarios and can resist the Chosen Plaintext Attack (CPA). Recently, a new gray image encryption scheme is proposed, which is based on Discrete Cosine Transform (DCT), 1D chaotic map for pixel scrambling, and compressive sensing technique based on 3D Lorenz map [46]. It can resist brute force attacks and has the fastest encryption time for gray-level images as it reduces the plain image size and then encrypts the reduced image. A novel encryption scheme based on SHA-512, Elliptic Curve Cryptography (ECC), and the 4D hyperchaotic system is proposed in [47]. In this scheme, multiple images of the same size are converted into the 3D cube, then a hash is generated from the 3D cube, ECC based on the hash is employed to generate a secret key then a 4D hyperchaotic system is applied for scrambling the 3D image to get an encrypted version. This proposed scheme can be considered as an eligible candidate for practical applications as it outperforms with some existing cryptosystems with respect to encryption time and resistance to statistical and differential attacks. Combining high dimensional hyperchaotic system with DNA operations can give strength to the cryptosystems. In this connection, a safe and reliable cryptosystem based on 6D hyperchaotic system coupled with DNA coding and DNA operations (addition, subtraction, XOR and same or) is proposed in [48]. A novel approach consisting of permutation-substitution, complement and multiple DNA Fusion Operations (DFOs) is proposed in [49]. This approach uses three chaotic systems (Lorenz, Henon, Logistic) for performing permutation-substitution. The DFO in this approach refers to the fusion of the DNA image layers with a random DNA sequence to form a third DNA sequence. Some DFOs are listed in Tab. 3.

S-box is an essential component in the cryptosystems such as Advanced Encryption Standard (AES), Triple-Data Encryption Standard (3DES), etc. It is a non-linear lookup table and is a source of creating confusion through substitutions. S-boxes by using algebraic structures, chaos and DNA have designed by various researchers. In this respect, a DNA based S-box is designed in [14], in which two DNA segments (downloaded from gen-bank) are used to construct S-box. This S-box passed the S-box criteria effectively. Another secure S-box based on DNA codons, mathematical operations and XOR operations is designed in [36].

4  Proposed Approach

The method for encrypting image data has five phases (see the general model framework in Fig. 4):

1.    Loading and splitting image data.

2.    Quadruple DNA mapping.

3.    DNA based S-box generation, substitution, and apply Conservative Site Specific Recombination (CSSR).

4.    Computing the secret key using 4D-hyperchaos.

5.    Scrambling.

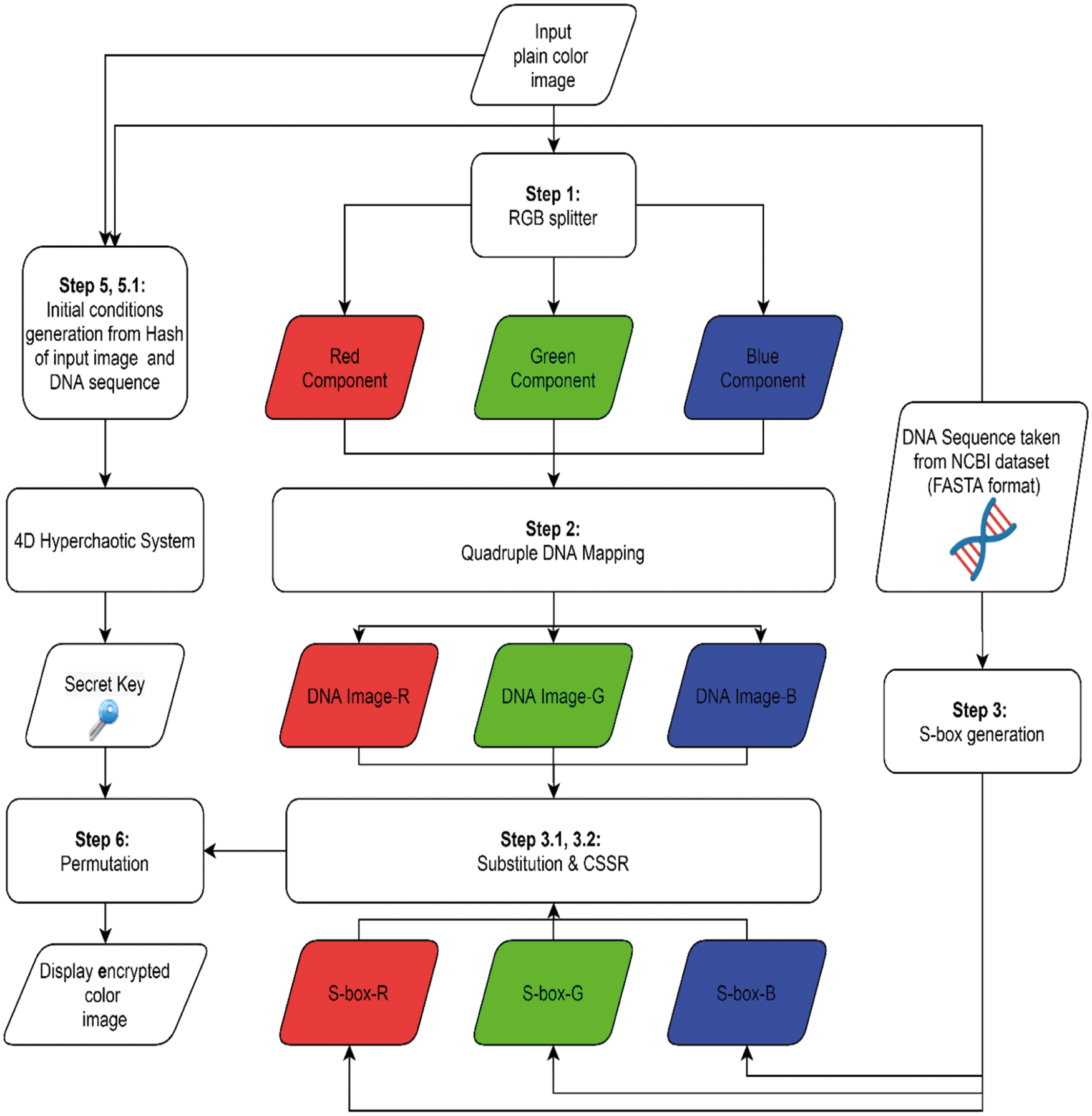
Figure 4: Flowchart of the encryption process

The details of these phases are given in Sections 4.1 to 4.5 and the algorithm steps are given in Algorithms 1–4 respectively.

4.1 DNA Encoding

The input image is decomposed into three components called red, green and blue components. The size of each component is m×n. The pixel value of each component is converted into 8-bit binary equivalent. The 8-bit binary equivalent of each pixel value is mapped to quadruple DNA sequence according to the rules shown in Tab. 4, that meet the Watson-Crick complement rule. The process is repeated for all the pixels of all the components and DNA image DNA_I is obtained.

4.2 Generation of DNA Based S-box

DNA sequence taken from NCBI dataset is large enough to generate three S-boxes each of size 16×16. The mean intensity value of an input image is used for the generation of three DNA based S-boxes. For example, a DNA sequence called ‘sequence_HIV-1 isolate 196JL2007P2B5 from USA defective genome’ having length of 183015 is used for the generation of three S-boxes called DNA_1_s-box, DNA_2_s-box and DNA_3_s-box to substitute the pixel values of red, green and blue component of DNA image DNA_I. An example of DNA_1_s-box is shown in Fig. 5. The algorithm steps to generate DNA based S-box are as follows:

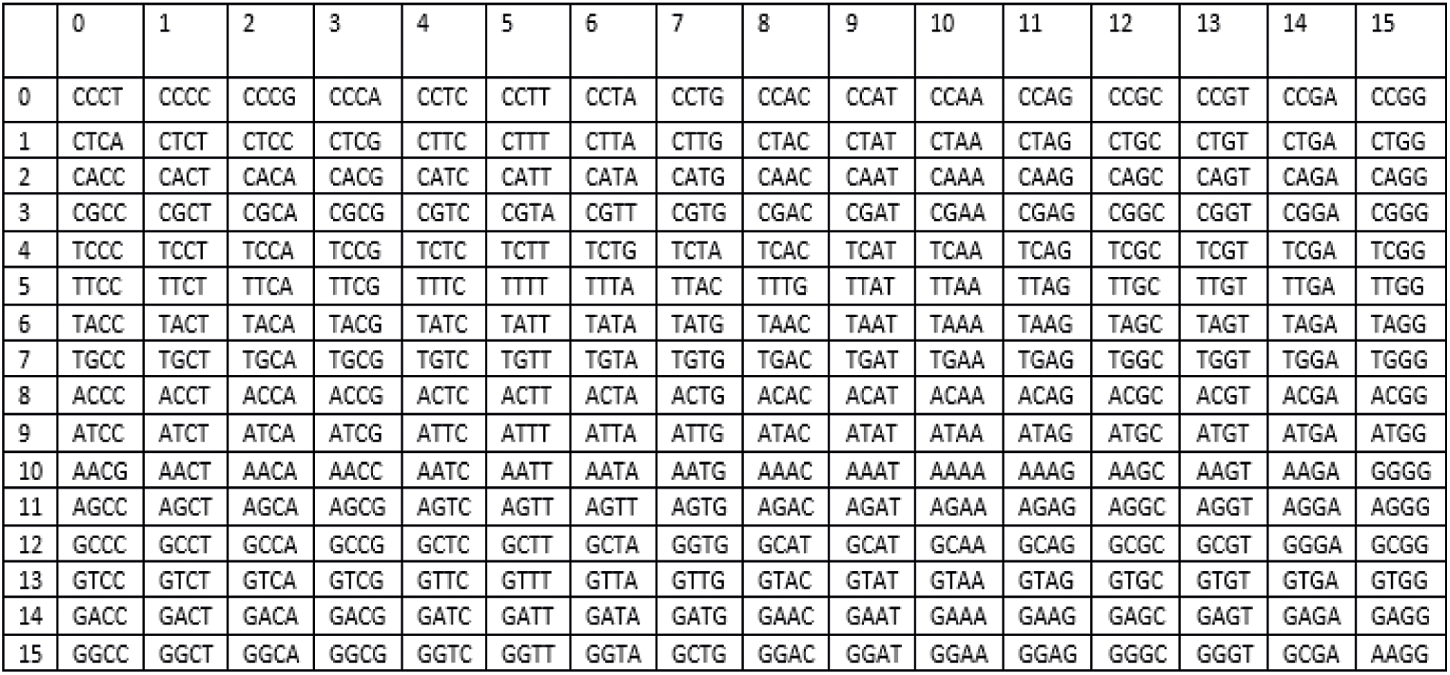
Figure 5: DNA based S-box (DNA_1_s-box) generated from DNA sequence taken from GenBank database

4.3 CSSR Proposal

Conservative Site Specific Recombination (CSSR) is also applied on the substituted DNA (Sub_DNA_I) received from DNA based S-boxes. The Sub_DNA_I contains the encrypted data which is ready for site specific recombination and mutation. The Site Specific Recombination also called Conservative Site Specific Recombination (CSSR) is different from the homologous recombination process. In CSSR the enzyme such as serine recombinase is used to cleave the specific site. The CSSR has of three types called insertion, deletion and inversion. Here we have used the inversion CSSR to be applied on the specific sites of output DNA to produce stage 1 encrypted image in the form of DNA (S1_DNA_eI). In inversion CSSR the specific site of DNA strand can get be cleaved by DNA key enzyme and inverted to 1800 as shown in Fig. 6.

Figure 6: CSSR inversion mechanism

4.4 Computing the Secret Key and Initial Conditions

External key eK of 256 bit is extracted from DNA sequence taken from NCBI dataset. For example, we downloaded a DNA sequence called ‘sequence_HIV-1 isolate 196JL2007P2B5 from USA defective genome’ (DS1) having length of 183015. The mean intensity value of input image is used as a starting index to cut the DNA sequence from this location having length of 128 as shown in Fig. 7. For example, in the Fig. 7, the mean intensity value of an input image is 3 which is used as a starting index in the DS1 vector. DNA sequence from this location having length of 128 is copied and mapped into binary stream equivalent to 256 bit called as eK. The mapping is done by choosing any one of the rule given in the Tab. 4. MD5 of eK and plain image is calculated and is given to SHA-256 thus giving 256-bit hash value hv. The eK is combined with hv using XOR operation thus producing secret key sK=eK⊕hv. In order to create the initial conditions x(0),  y(0),  z(0),  u(0) for the 4D hyperchaotic system, we divide sK into 32 subgroups where each subgroup sg, is comprised of 8 bits and is expressed as follows:

sK={sg1,sg2,…,sg32}

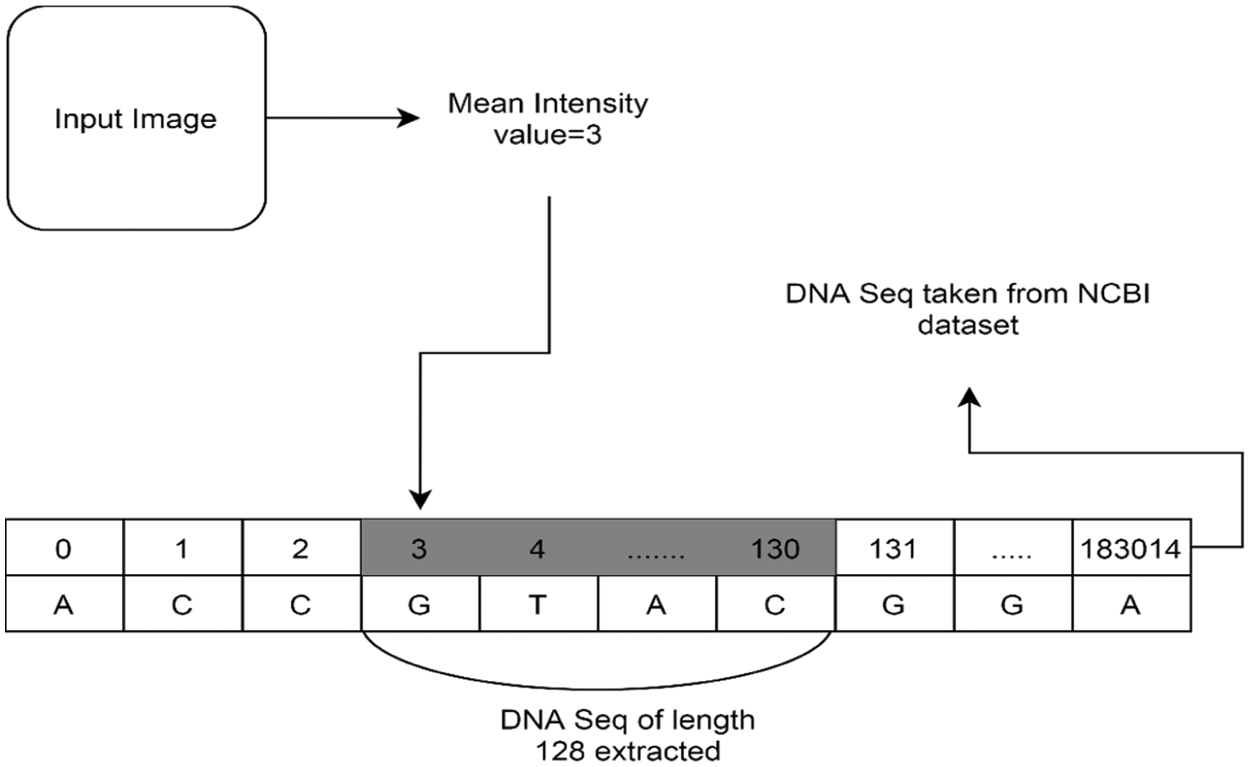
Figure 7: Computing the mean intensity value and DNA sequence length extraction

Now the initial conditions using sK are computed as follows:

{x(0)=(sg1⊕sg2⊕sg3⊕sg4⊕sg5⊕sg6⊕sg7⊕sg8)/256y(0)=(sg9⊕sg10⊕sg11⊕sg12⊕sg13⊕sg14⊕sg15⊕sg16)/256z(0)=(sg17⊕sg18⊕sg19⊕sg20⊕sg21⊕sg22⊕sg23⊕sg24)/256u(0)=(sg25⊕sg26⊕sg27⊕sg28⊕sg29⊕sg30⊕sg31⊕sg32)/256

4.5 Final Encryption

Now, initial conditions generated in Section 4.4 and the control parameters are input to the 4D hyperchaotic system to generate another key called DNA based key DNA−K. Encryption steps based on DNA−K to encrypt the S1_DNA_eI are as follows:

5  Results and Analysis

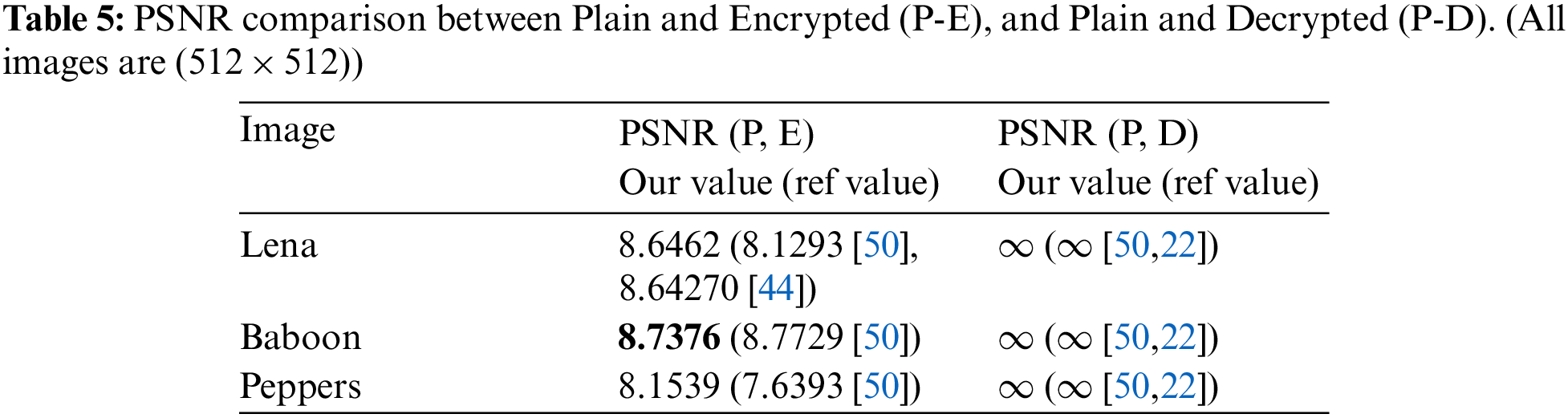
The experiments to test the security, robustness and efficiency of proposed algorithm are reported in this section. All the experiments are conducted in Matlab R2015a installed on windows 7 operating system, 4 GB RAM, Intel (R) Core (TM) i3-4010 CPU @1.70 GHz. The plain color images lena (512 × 512), baboon (512 × 512), peppers (512 × 512) and covid-19-pneumonia (841 × 789) taken from CVG-UGR and radiopaedia.org, are used as test images. The file size of the images lena, baboon, peppers and covid-19-pneumonia are 768 KB, 768 KB, 284 KB, and 200 KB respectively.

5.1 Visual Analysis

Visual analysis of the proposed algorithm is shown in Fig. 8, while the PSNR values are given in Tab. 5. The PSNR value of ∞ between plain and decrypted image indicates that the decrypted image is identical copy of plain image while the lower PSNR values between plain and encrypted image indicates that the difference between the plain and encrypted image is much greater and are not identical and difficult to identify.

Figure 8: Visual results of proposed scheme. (a) Plain lena, (b) Encrypted lena, (c) Decrypted lena, (d) Pain peppers, (e) Encrypted peppers, (f) Decrypted peppers, (g) Plain baboon, (h) Encrypted baboon, (i) Decrypted baboon

5.2 Security Analysis

Security analysis such as key sensitivity, key space, statistical analysis, differential attack analysis, entropy analysis and robustness analysis are reported in this section.

5.2.1 Key Space Analysis

The hyperchaotic system in this scheme uses four state variables as the original symmetric key which is represented by double precision real number upto 15 decimal places. We have also created an external key of 256 bit derived from DNA sequence. Hence, the key space comes out as ((1015)4=1060≅2200)×2256=2456 which is strong enough to resist all kinds of brute force attacks [51,7].

5.2.2 Key Sensitivity Analysis

We tested the sensitivity of secret key of proposed scheme by encrypting the image (Covid-19-pneumonia) with the secret key and decrypting it with slight modifications in the secret key. The visual results shown in Fig. 9 clearly indicate absence of a relation between the plain color image and the decrypted image. We denote the plaintext by P, the key by K1=k01,  k11,  …,  kMN−11, K2=k02,  k12,  …,  kMN−12 and cipher image by C1=c01,  c11,  …,  cMN−11, C2=c02,  c12,  …,  cMN−12. Key sensitivity (kS), computed using the hamming distance [6] is given in Eq. (4):

kS=1MN∑j=0MN−1⁡(cj1⊕cj2),(4)

where C1 and C2 are given by

{C1=encrypt(P,K1),C2=encrypt(P,K2).

Figure 9: Key sensitivity test for the image (Covid-19-pneumonia): (a) The plain image, (b) The encrypted image, (c) The decrypted image with different initial conditions, (d) The decrypted image with same initial conditions

kS=0.5 indicates a good cipher [6]. K1 and K2 have n bit difference. Figs. 9 and 10 show the key sensitivity results for DSHC-v1.0. Under this test, different images (Lena, Baboon, Peppers, Panda) are encrypted by altering n bits in the secret key. The plain image Fig. 9a is encrypted by using the secret key to produce an encrypted image i.e., Fig. 9b. A slight modification (1 or 2-bit change) is done in the secret key. Then Fig. 9b is tried to decrypt with the slightly modified key that results in Fig. 9c which is completely unrecognizable by the Human Visual System. The Fig. 9d is the decrypted image which is decrypted by the unmodified (original secret key) which is the replica of Fig. 9a and is completely recognizable. In the Fig. 10, we can observe that kS approaches to 0.497 when the number of altered is below 3 and it approaches to 0.5 when the number of altered bits becomes greater than 3. As kS=0.5 indicates a good cipher [6], thus DSHC-encryption comes in the umbrella of a good ciphers and is highly sensitive to minor changes in the key.

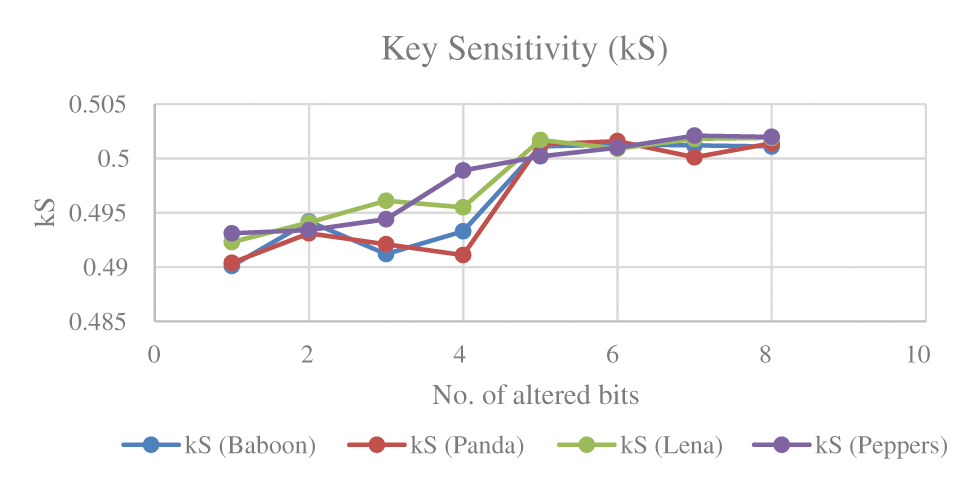
Figure 10: Key sensitivity for the image (Covid-19-pneumonia)

5.2.3 Histogram Analysis

It is a statistical analysis. Histogram variance and histogram have inverse relationship i.e., smaller histogram variance gives high uniformity in the histograms and vice versa and more uniformity in the histograms indicates the more robustness against statistical attacks [52]. Encrypted image's histogram shows uniform distribution as compared to the plain image's histogram. Histograms of the plain color images and encrypted color images Lena and Covid-19-pneumonia are shown in Fig. 11. The Figs. 11a and 11b 3rd row clearly shows the uniform distribution of an encrypted image. Though not enough, but still it provides resistance against statistical attacks based on histogram. Additionally, the Pearson's chi-squared statistic can be computed to identify the histogram's uniformity of an encrypted image. Our average χ2 statistic (258.0026)) derived from hundred encrypted images’ histograms is less than the critical value (χ0.052(255)=293.2478. Therefore, the null hypothesis Ho i.e., (histogram of the encrypted image bears uniform distribution) is accepted.

5.2.4 Correlation Coefficient

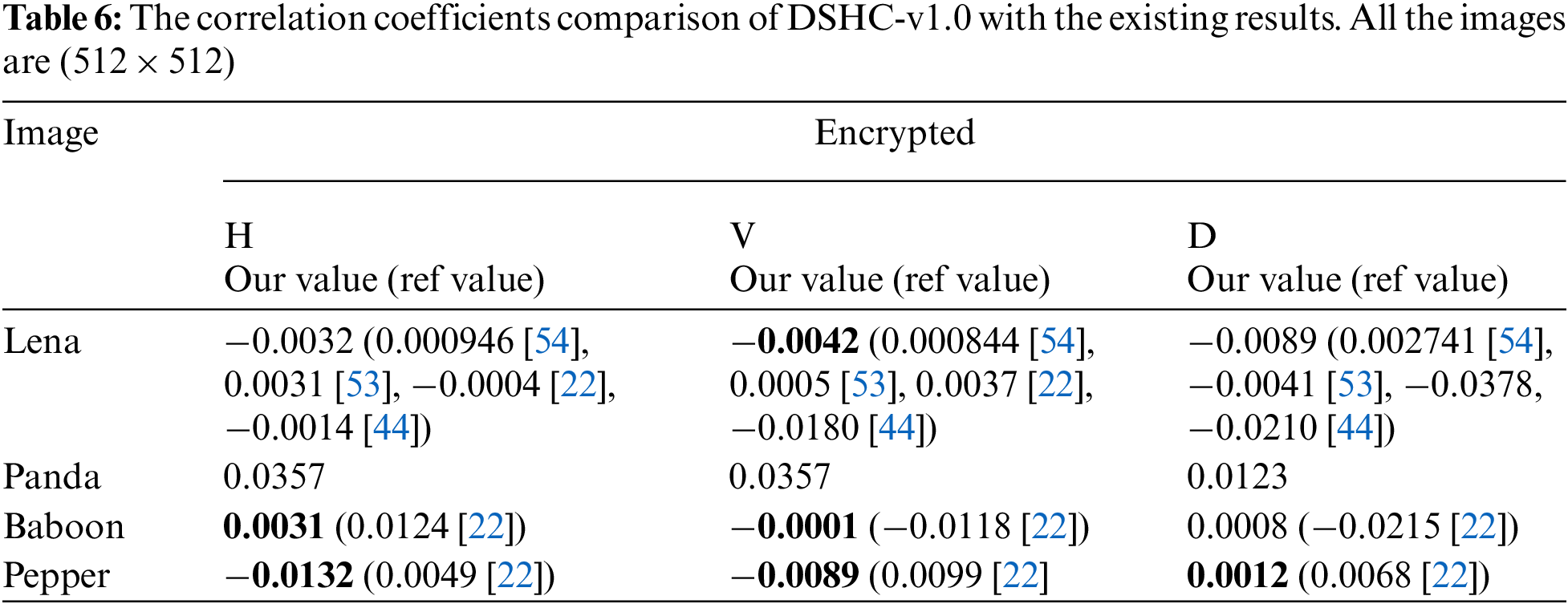
The correlation of digital image whether plain or encrypted, is measured between the pixels in vertical, horizontal and diagonal directions. A high correlation exists among the pixels of plain color images while highly secured ciphers have zero or little correlation among the adjacent pixels [53]. In order to compute the correlation, 10,000 random pairs of adjacent pixels are selected in the horizontal, vertical and diagonal directions. Tab. 6, lists the reduced correlation results of encrypted images (Lena, Panda, Baboon and Peppers) along with three directions, i.e., vertical, horizontal and diagonal while correlations plots for the plain and the encrypted image of Lena are shown in Fig. 12. The Figs. 12a, 12c, 12e represent the positive correlation plots of plain image along vertical, horizontal and diagonal direction whereas Figs. (b, d, f) clearly indicate no correlation among adjacent pixels along vertical, horizontal and diagonal directions.

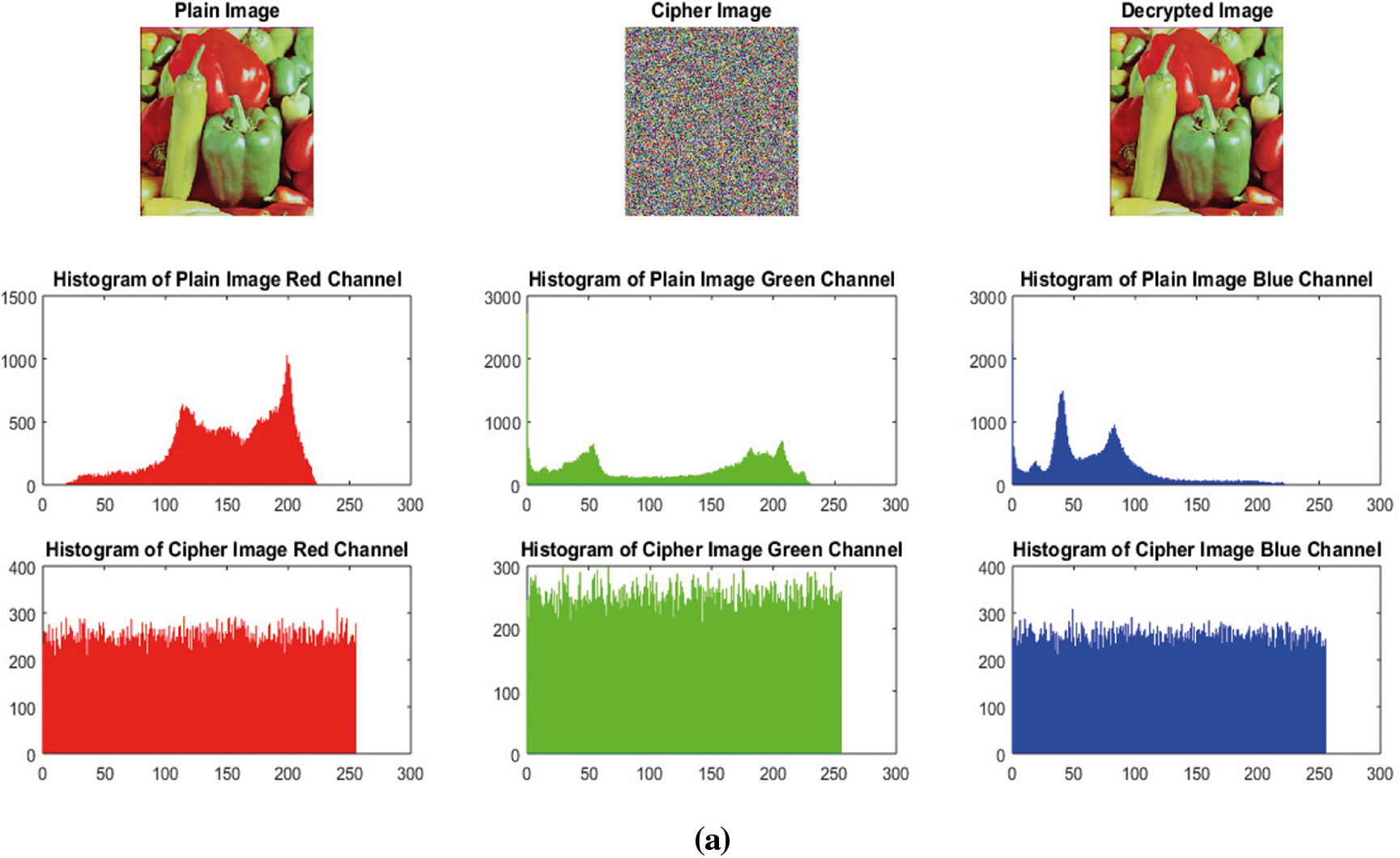
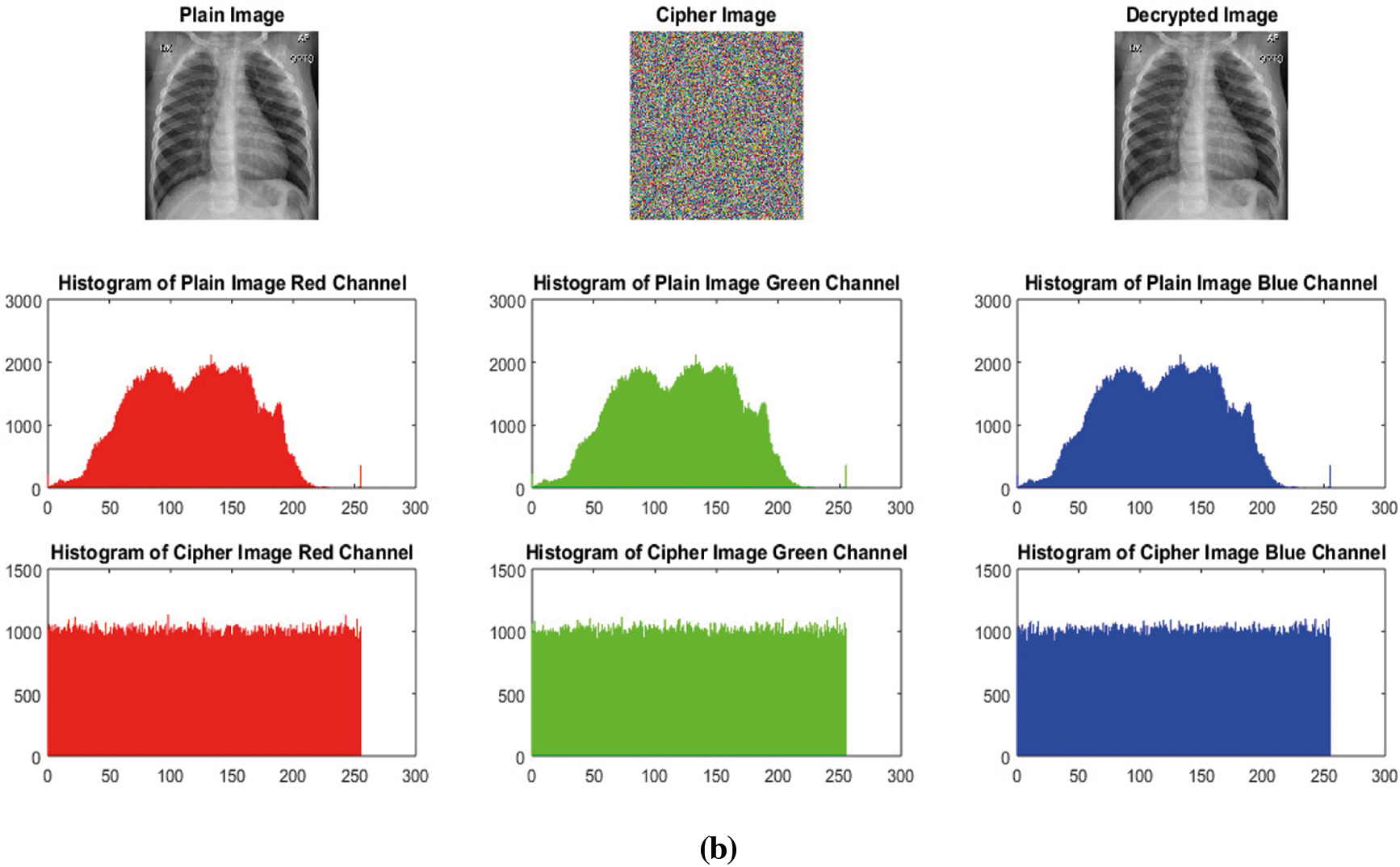
Figure 11: (a) Histograms of Plain-peppers image and Cipher-peppers image (b) Histograms of Plain-covid-19-pneumonia-paediatric image and Cipher-covid-19-pneumonia-paediatric image

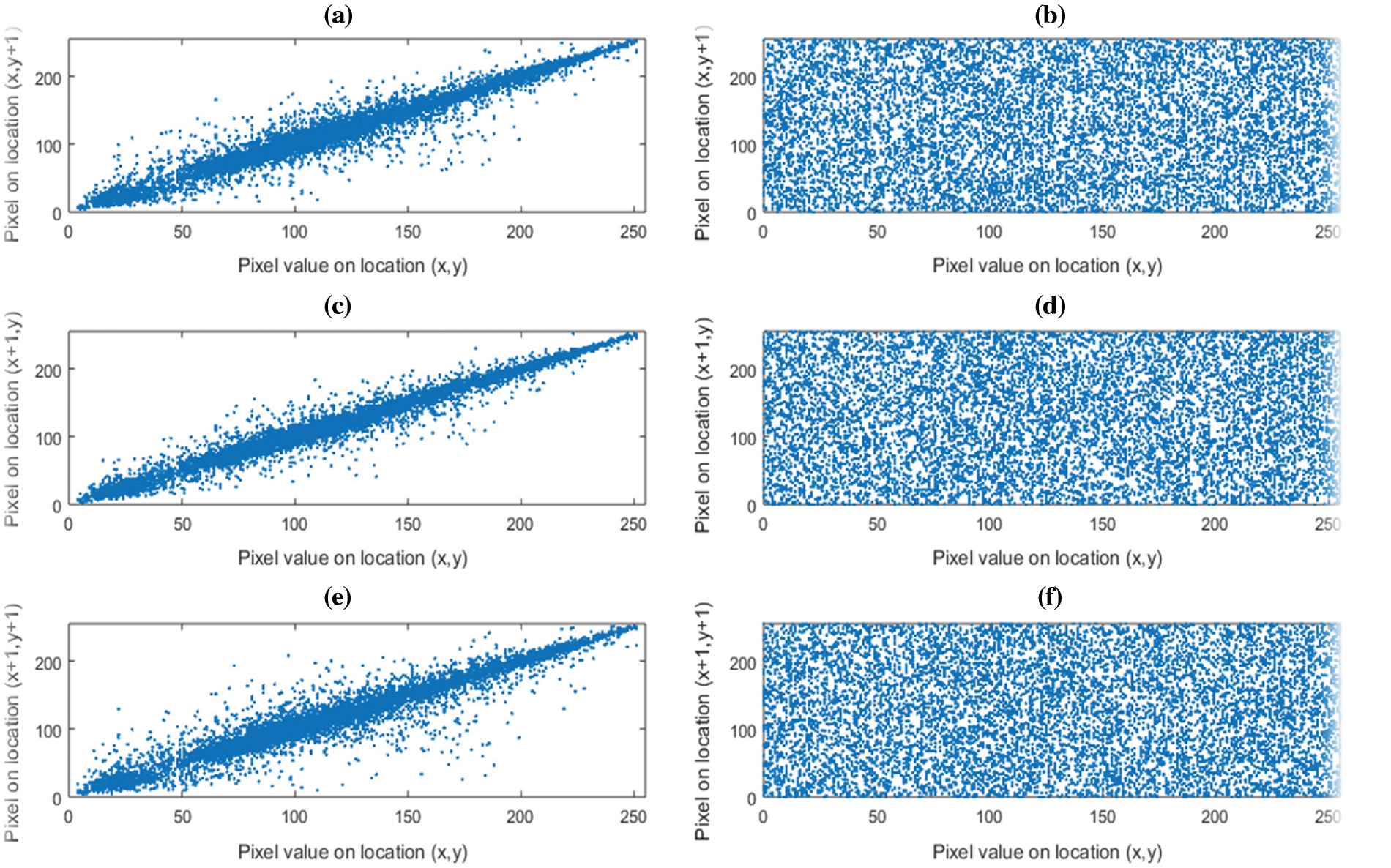
Figure 12: Correlation plots color image Lena. (a) Horizontal direction plain image, (b) Horizontal direction encrypted image, (c) Vertical direction plain image, (d) Vertical direction encrypted image, (e) Diagonal direction plain image, (f) Diagonal direction

5.2.5 Information Entropy

Entropy is a thermodynamics quantity that measures the degree of disorder or randomness within the system. The degree of randomness can be computed within the encrypted image. In an 8-bit image, a value closer to 8 indicates the ideal score of an encrypted image. Entropy can be computed by Eq. (5) [55]:

Entropy(CI)=−∑i=02k−1⁡p(intensity(CIi))  log2(p(intensity(CIi))),(5)

where intensity(CIi) is the ith intensity value of an encrypted image. p(⋅) is the probability function and k=8 for the gray level image. Tab. 7, shows the entropy results closer to 8, hence the encrypted image has maximal randomness thus leading to insignificant information leakage.

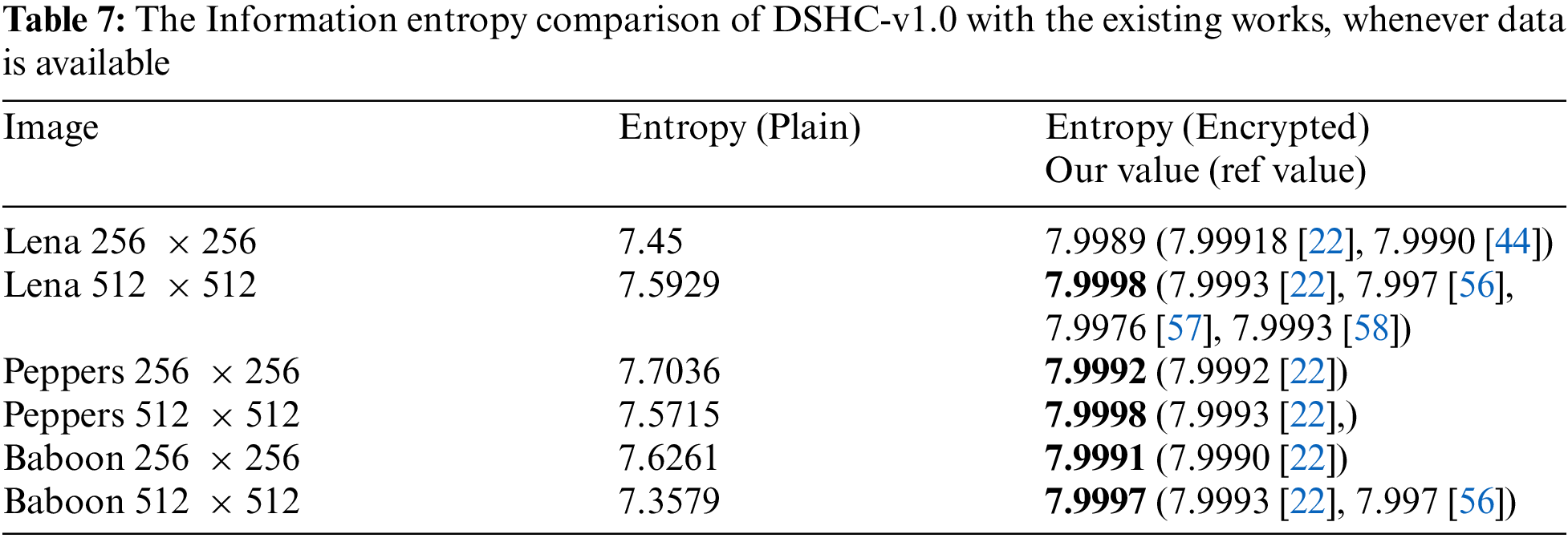
5.2.6 Differential Attack Analysis

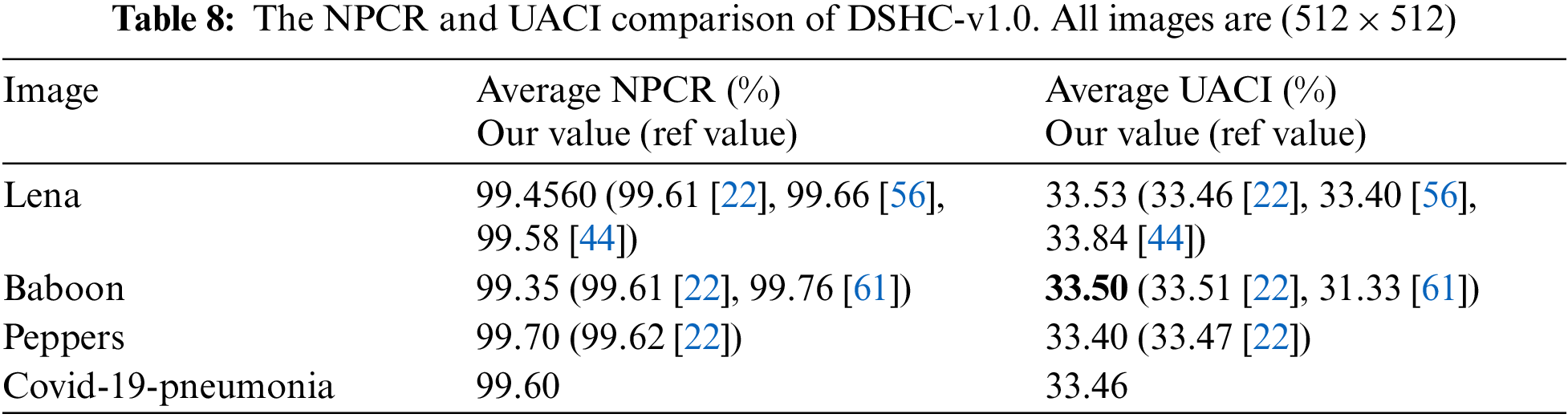
If a 1-bit or 2-bit change in the plain image can lead to a significant change in the encrypted image, then the proposed scheme is considered resistant to differential attacks. In this regard, the Number of Pixel Changing Rate (NPCR) and Unified Average Changing Intensity (UACI) quantitative tests are used to evaluate the differential attack [50–59]. For an image (M × N), NPCR and UACI [60] are calculated as:

NPCR(CI1,CI2)=∑1≤i≤M1≤j≤N⁡D(i,j)M×N×100,(6)

where D(i,j)={0ifCI1(i,j)=CI2(i,j)1ifCI1(i,j)≠CI2(i,j), and

UACI(CI1,CI2)=1M×N[∑1≤i≤m1≤j≤n⁡|CI1(i,j)−CI2(i,j)|255]×100,(7)

where CI1(i,j),  CI2(i,j) are the encrypted versions of plain image before and after n bit change in the plain image at location (i,j) and M×N is the height and width of plain image. The average values of NPCR and UACI (multiple runs) listed in Tab. 8 are comparable to existing results and the improved results are illustrated with bold. Therefore, the proposed scheme shows the resistance against the differential attacks.

5.2.7 Robustness Analysis

Occlusion and salt & pepper noise are used to test the robustness of DSHC-v1.0. The PSNR between plain and decrypted images is used to quantify the quality of the decrypted images after applying attacks. The PSNR can be defined by [62]:

PSNR(PI,DI∗)=10  log10(MAX2MSE(PI,DI∗)),(8)

where MSE(PI,DI∗)=∑1≤i≤m1≤j≤n⁡[PI(i,j)−DI∗(i,j)]2M×N and PI,DI∗, MAX are the plain image, decrypted image after the attack, maximum pixel intensity in the plain image respectively and M×N is the dimension of plain image. Quantitative analysis in terms of PSNR and visual analysis are given in Tab. 9 and Fig. 13 respectively. Whereas, the occlusion attacks on encrypted images and their recovery are shown in Fig. 14. The occluded part is not recovered while the freed part is recovered without adding noise.

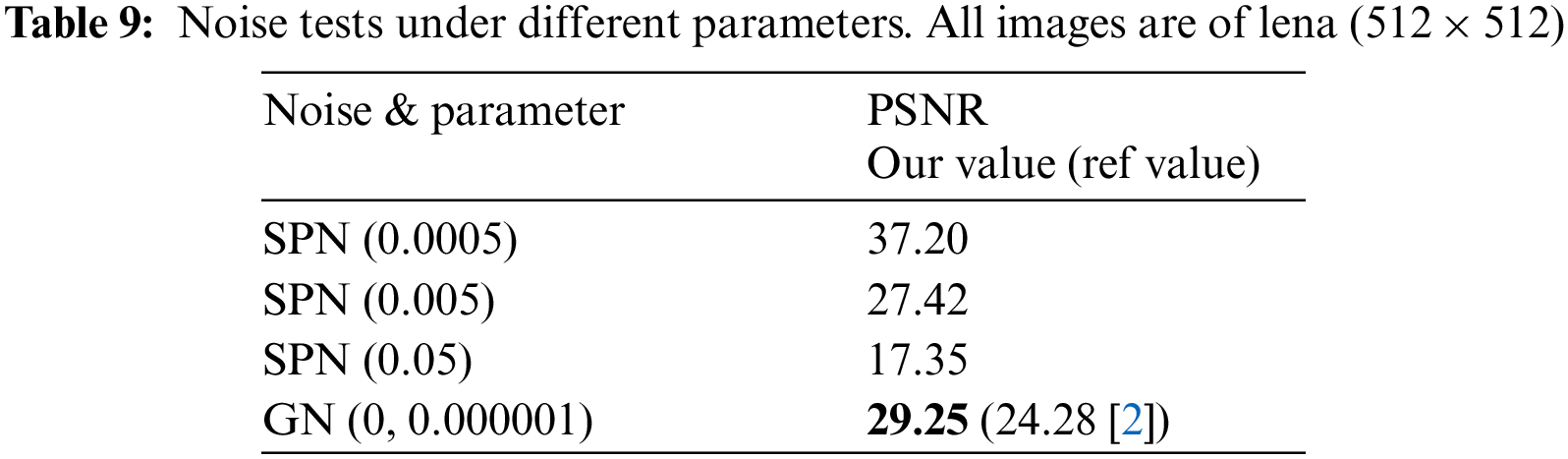
Figure 13: Salt & pepper noise analysis. (a)-(c) Lena encrypted attacked with 0.005, 0.05 and 0.1 noise, (d)-(e) Corresponding decrypted of (a)-(c)

Figure 14: Visual Analysis of occlusion attacks. (a)-(c) Encrypted images with 1/16, 1/4 and 1/2 occlusions, (d)-(f) Decrypted images of (a)--(c). PSNR between (a) and (d) = 20.7797, PSNR between (b) and (e) = 12.40, PSNR between (c) and (f) = 9.33

5.3 Performance Analysis

With the improvement of trend setting innovations in information security, designing the secure ciphers along with the consideration of encryption time, decryption time, and encryption efficiency remains one of the key problems. Therefore, along with security considerations, encryption and decryption time of an image cipher for a real life application must be considered. In this respect, the empirical and theoretical are the 2 ways for assessing the time complexity of a cipher. In empirical evaluation, algorithm is run on some platform and execution time is observed or measured through stopwatch or any other tool. Whereas, in theoretical assessment, asymptotic notation is commonly used to assess the computational complexity. In this research work, we are employing empirical assessments.

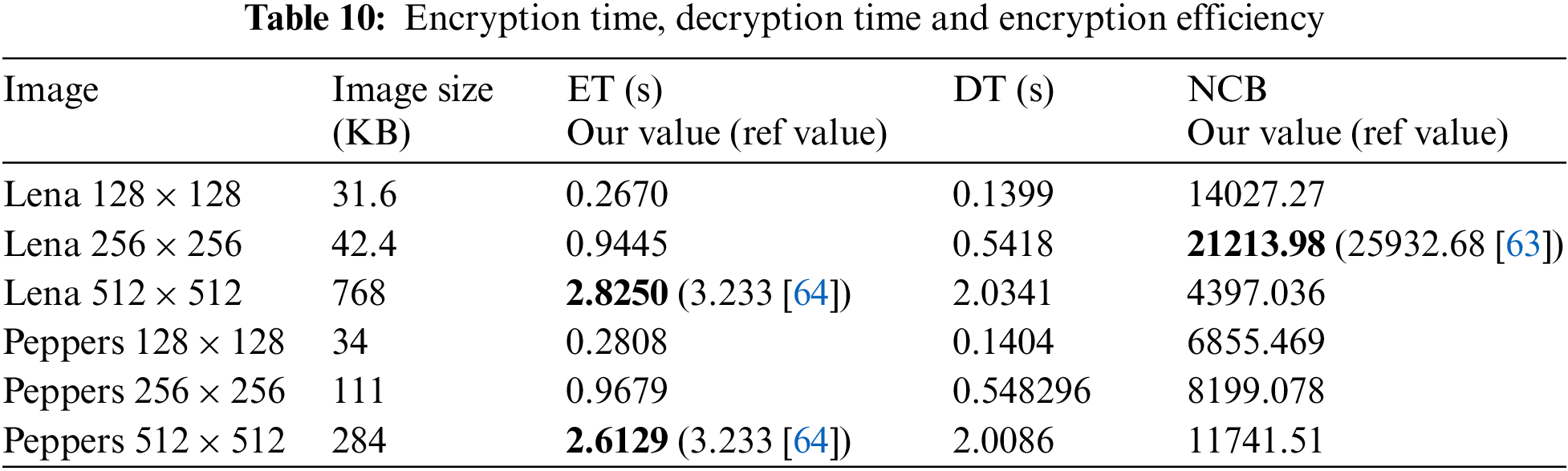
The RGB image of Lena and peppers with different dimensions (128 × 128, 256 × 256, 512 × 512) are taken as input. The average time (10 times execution of an algorithm) for encryption and decryption is computed. Based on the average encryption time of images, the encryption efficiency [63] in terms of encryption throughput (ENC−T) and a number of cycles per byte (NCB) is calculated by:

ENC−T=PIsizeET,(9)

NCB=CPUspeedENC−T,(10)

where PIsize, ET, CPUspeed are the plain image size in bytes, encryption time in seconds, and processor speed in hertz respectively while NS is the number of cycles per byte.

Encryption and decryption time with encryption efficiency is listed in Tab. 10. It can be observed that the encryption time (ET) and decryption time (DT) increases with the increase of RGB image sizes and encryption efficiency is also better for large size images.

6  Conclusions and Future Directions

In this research study, we proposed a genuine cipher for the encryption of color images of different dimensions and sizes by using the SHA-256, MD5, and hyperchaotic system jointed with DNA operations and DNA-based S-box. This scheme takes hardly less than a second for the encryption of color image up to the dimensions of 256 × 256. The proposed scheme's larger keyspace can resist brute force attacks. The scheme showed better security analysis results such as entropy, NPCR, UACI, correlation coefficients, PSNR, histogram, and key sensitivity. Thus the proposed scheme is more effective in terms of security and efficiency for encrypting color images. The proposed solution doesn't work for binary, DICOM and gray scale images. In addition, our proposed cipher outperforms existing ciphers in terms of gray-level co-occurrence matrix evaluations and key sensitivity. The performance of proposed cipher is consistent while changing color image sizes.

The future work includes its improvement in terms of encryption efficiency for encrypting/decrypting medical as well as larger color images. Escalation towards the encryption of selected faces from the images is also included in future work.

Funding Statement: This work was supported in part by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education under Grant NRF-2019R1A2C1006159 and Grant NRF-2021R1A6A1A03039493.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  S. Mohammad Seyedzadeh and S. Mirzakuchaki, “A fast color image encryption algorithm based on coupled two-dimensional piecewise chaotic map,” Signal Processing, vol. 92, no. 5, pp. 1202–1215, 2012. [Google Scholar]

 2.  X. Chai, X. Fu, Z. Gan, Y. Lu and Y. Chen, “A color image cryptosystem based on dynamic DNA encryption and chaos,” Signal Processing, vol. 155, pp. 44–62, 2019. [Google Scholar]

 3.  A. Arab, M. J. Rostami and B. Ghavami, “An image encryption method based on chaos system and AES algorithm,” Journal of Supercomputing, vol. 75, no. 10, pp. 6663–6682, 2019. [Google Scholar]

 4.  C. Li, D. Lin, J. Lu and F. Hao, “Cryptanalyzing an image encryption algorithm based on autoblocking and electrocardiography,” IEEE Multimedia, vol. 25, no. 4, pp. 46–56, 2018. [Google Scholar]

 5.  W. Feng and Y. G. He, “Cryptanalysis and improvement of the hyper-chaotic image encryption scheme based on DNA encoding and scrambling,” IEEE Photonics Journal, vol. 10, no. 6, pp. 1–15, 2018. [Google Scholar]

 6.  A. Belazi, M. Talha, S. Kharbech, W. E. I. Xiang and S. Member, “Novel medical image encryption scheme based on chaos and DNA encoding,” IEEE Access, vol. 7, pp. 36667–36681, 2019. [Google Scholar]

 7.  S. Sun, “A novel hyperchaotic image encryption scheme based on DNA encoding, pixel-level scrambling and bit-level scrambling,” IEEE Photonics Journal, vol. 10, no. 2, pp. 1–15, 2018. [Google Scholar]

 8.  Z. Liu, C. Wu, J. Wang and Y. Hu, “A color image encryption using dynamic DNA and 4D memristive hyper-chaos,” IEEE Access, vol. 7, pp. 78367–78378, 2019. [Google Scholar]

 9.  K. C. Jithin and S. Sankar, “Colour image encryption algorithm combining, Arnold map, DNA sequence operation, and a Mandelbrot set,” Journal of Information Security and Applications, vol. 50, pp. 1–22, 2020. [Google Scholar]

10. X. Zhu, H. Liu, Y. Liang and J. Wu, “Image encryption based on Kronecker product over finite fields and DNA operation,” Optik, vol. 224, no. December, pp. 1–27, 2020. [Google Scholar]

11. C. Li, Y. Zhang and E. Yong, “When an attacker meets a cipher-image in 2018: A year in review,” Journal of Information Security and Applications, vol. 48, pp. 1–9, 2019. [Google Scholar]

12. L. Chun-Lai and Y. Si-Min, “A new hyperchaotic system and its adaptive tracking control,” Acta Phys. Sin, vol. 61, no. 4, pp. 040504-1–040504-7, 2012. [Google Scholar]

13. S. Doss, J. Paranthaman, S. Gopalakrishnan, A. Duraisamy, S. Pal et al., “Memetic optimization with cryptographic encryption for secure medical data transmission in IoT-based distributed systems,” Computers, Materials and Continua, vol. 66, no. 2, pp. 1577–1594, 2021. [Google Scholar]

14. A. H. Al-wattar, R. Mahmod, Z. A. Zukarnain and N. I. Udzir, “A new DNA-based s-box,” International Journal of Engineering & Technology, vol. 15, no. 4, pp. 1–10, 2015. [Google Scholar]

15. D. R. Stille, “Measurement, monitoring and control of fluidized bed combustion and gasification,” in Fluidized Bed Technologies for Near-Zero Emission Combustion and Gasification, 1st ed., Philadelphia, USA: Woodhead Publishing, pp. 813–864, 2013. [Google Scholar]

16. O. E. Rossler, “An equation for hyperchaos,” Physics Letters A, vol. 71, no. 2–3, pp. 155–157, 1979. [Google Scholar]

17. J. Ma and Y. Yang, “Hyperchaos numerical simulation and control in a 4D hyperchaotic system,” Discrete Dynamics in Nature and Society, vol. 2013, pp. 1–16, 2013. [Google Scholar]

18. D. R. Stille, “Genes and DNA,” in DNA: The Master Molecule of Life, 1st ed., Minneapolis, Minn: Compass Point Books, pp. 1–48, 2006. [Google Scholar]

19. L. Adleman, “Molecular computation of solutions to combinatorial problems,” Science, vol. 266, no. 5187, pp. 1021–1024, 1994. [Google Scholar]

20. K. C. Jithin and S. Sankar, “Colour image encryption algorithm combining, Arnold map, DNA sequence operation, and a Mandelbrot set,” Journal of Information Security and Applications, vol. 50, pp. 102428, 2020. [Google Scholar]

21. O. Sengel, M. A. Aydin and A. Sertbas, “An efficient generation and security analysis of substitution box using fingerprint patterns,” IEEE Access, vol. 8, pp. 160158–160176, 2020. [Google Scholar]

22. E. Z. Zefreh, “An image encryption scheme based on a hybrid model of DNA computing, chaotic systems and hash functions,” Multimedia Tools and Applications, vol. 79, pp. 24993–25022, 2020. [Google Scholar]

23. M. Yildirim, “DNA encoding for RGB image encryption with memristor based neuron model and chaos phenomenon,” Microelectronics Journal, vol. 104, pp. 104878, 2020. [Google Scholar]

24. J. K. Myers, “Recombination site-specific recombination: Biological functions, reaction mechanisms, and applications,” in Encyclopedia of Biological Chemistry, 3rd ed., Elsevier vol. 296, pp. 170–180, 2021. [Google Scholar]

25. X. Tian and B. Zhou, “Strategies for site-specific recombination with high efficiency and precise spatiotemporal resolution,” Journal of Biological Chemistry, vol. 296, pp. 100509, 2020. [Google Scholar]

26. H. Liu, A. Kadir and Y. Niu, “Chaos-based color image block encryption scheme using S-box,” AEU-International Journal of Electronics and Communications, vol. 68, no. 7, pp. 676–686, 2014. [Google Scholar]

27. W. Gao, B. Idrees, S. Zafar and T. Rashid, “Construction of nonlinear component of block cipher by action of modular group PSL(2, Z) on projective line PL(GF(2 8)),” IEEE Access, vol. 8, pp. 136736–136749, 2020. [Google Scholar]

28. A. Razaq, H. Alolaiyan, M. Ahmad, M. A. Yousaf, U. Shouaib et al., “A novel method for generation of strong substitution-boxes based on coset graphs and symmetric groups,” IEEE Access, vol. 8, pp. 75473–75490, 2020. [Google Scholar]

29. S. S. Jamal, M. U. Khan and T. Shah, “A watermarking technique with chaotic fractional s-box transformation,” Wireless Personal Communications, vol. 90, no. 4, pp. 2033–2049, 2016. [Google Scholar]

30. F. Özkaynak and S. Yavuz, “Designing chaotic S-boxes based on time-delay chaotic system,” Nonlinear Dynamics, vol. 74, no. 3, pp. 551–557, 2013. [Google Scholar]

31. F. Özkaynak, V. Çelik and A. B. Özer, “A new s-box construction method based on the fractional-order chaotic chen system,” Signal Image Video Process, vol. 11, no. 4, pp. 659–664, 2017. [Google Scholar]

32. F. Özkaynak, “Construction of robust substitution boxes based on chaotic systems,” Neural Computing Applications, vol. 31, no. 8, pp. 3317–3326, 2019. [Google Scholar]

33. Y. Tian and Z. Lu, “Six-dimensional compound hyperchaotic map and artificial bee colony algorithm,” Journal of Systems Engineering and Electronics, vol. 27, no. 1, pp. 232–241, 2016. [Google Scholar]

34. Y. Tian and Z. Lu, “Chaotic s-box: Six-dimensional fractional Lorenz–duffing chaotic system and o-shaped path scrambling,” Nonlinear Dynamics, vol. 94, no. 3, pp. 2115–2126, 2018. [Google Scholar]

35. E. Al Solami, M. Ahmad and C. Volos, “A new hyperchaotic system-based design for efficient bijective substitution-boxes,” Entropy2, vol. 20, no. 3, pp. 525, 2018. [Google Scholar]

36. F. A. Kadhim, G. H. A. Majeed and R. S. Ali, “Proposal new s-box depending on DNA computing and mathematical operations,” in Al-Sadiq Int. Conf. on Multidisciplinary in IT and Communication Techniques Science and Applications (AIC-MITCSA), Iraq, pp. 1–6, 2016. [Google Scholar]

37. A. F. Webster and S. E. Tavares, “On the design of S-boxes,” Advances in Cryptology—CRYPTO, vol. 218, pp. 523–534, 1986. [Google Scholar]

38. J. Pieprzyk and G. Finkelstein, “Towards effective nonlinear cryptosystem design,” IEE Proceedings E-Computers and Digital Techniques, vol. 135, no. 6, pp. 325–335, 1988. [Google Scholar]

39. W. Zhang and E. Pasalic, “Highly nonlinear balanced S-boxes with good differential properties,” IEEE Transactions on Information Theory, vol. 60, no. 12, pp. 7970–7979, 2014. [Google Scholar]

40. H. Ghazanfaripour and A. Broumandnia, “Designing a digital image encryption scheme using chaotic maps with prime modular,” Optics and Laser Technology, vol. 131, no. December 2019, pp. 106339, 2020. [Google Scholar]

41. J. Zhou, N. -R. Zhou and L. -H. Gong, “Fast color image encryption scheme based on 3D orthogonal latin squares and matching matrix,” Optics & Laser Technology, vol. 131, no. December 2019, pp. 106437, 2020. [Google Scholar]

42. N. B. A. Ghani, M. Ahmad, Z. Mahmoud and R. M. Mehmood, “A pursuit of sustainable privacy protection in big data environment by an optimized clustered-purpose based algorithm,” Intelligent Automation and Soft Computing, vol. 26, no. 6, pp. 1217–1231, 2020. [Google Scholar]

43. O. Thinnukool, T. Panityakul and M. Bano, “Double encryption using trigonometric chaotic map and XOR of an image,” Computers, Materials & Continua, vol. 69, no. 3, pp. 3033–3046, 2021. [Google Scholar]

44. N. Sanam, A. Ali, T. Shah and G. Farooq, “Non-associative algebra redesigning block cipher with color image encryption,” Computers, Materials and Continua, vol. 67, no. 1, pp. 1–21, 2021. [Google Scholar]

45. Q. Lu, C. Zhu and X. Deng, “An efficient image encryption scheme based on the LSS chaotic map and single s-box,” IEEE Access, vol. 8, pp. 25664–25678, 2020. [Google Scholar]

46. A. Hadj Brahim, A. Ali Pacha and N. Hadj Said, “Image encryption based on compressive sensing and chaos systems,” Optics and Laser Technology, vol. 132, no. July, pp. 106489, 2020. [Google Scholar]

47. A. Sahasrabuddhe and D. S. Laiphrakpam, “Multiple images encryption based on 3D scrambling and hyper-chaotic system,” Information Sciences, vol. 550, pp. 252–267, 2021. [Google Scholar]

48. T. Wang and M. Hui Wang, “Hyperchaotic image encryption algorithm based on bit-level permutation and DNA encoding,” Optics and Laser Technology, vol. 132, no. May, pp. 1–13, 2020. [Google Scholar]

49. A. Alghafis, F. Firdousi, M. Khan, S. I. Batool and M. Amin, “An efficient image encryption scheme based on chaotic and deoxyribonucleic acid sequencing,” Mathematics and Computers in Simulation, vol. 177, pp. 441–466, 2020. [Google Scholar]

50. X. Wu, J. Kurths and H. Kan, “A robust and lossless DNA encryption scheme for color images,” Multimedia Tools and Applications, vol. 77, no. 10, pp. 12349–12376, 2018. [Google Scholar]

51. F. Meneghello, M. Calore, D. Zucchetto, M. Polese and A. Zanella, “IoT: Internet of Threats? A survey of practical security vulnerabilities in real IoT devices,” IEEE Internet of Things Journal, vol. 6, no. 5, pp. 8182–8201, 2019. [Google Scholar]

52. X. Wu, H. Kan and J. Kurths, “A new color image encryption scheme based on DNA sequences and multiple improved 1D chaotic maps,” Applied Soft Computing Journal, vol. 37, pp. 24–39, 2015. [Google Scholar]

53. K. A. K. Patro and B. Acharya, “An efficient colour image encryption scheme based on 1-D chaotic maps,” Journal of Information Security and Applications, vol. 46, pp. 23–41, 2019. [Google Scholar]

54. S. Kandar, D. Chaudhuri, A. Bhattacharjee and B. Chandra, “Image encryption using sequence generated by cyclic group,” Journal of Information Security and Applications, vol. 44, pp. 117–129, 2019. [Google Scholar]

55. K. A. K. Patro and B. Acharya, “Secure multi level permutation operation based multiple colour image encryption,” Journal of Information Security and Applications, vol. 40, pp. 111–133, 2018. [Google Scholar]

56. G. Bachira and N. Khan, “A new hybrid image encryption algorithm based on 2D-CA, FSM-DNA rule generator, and FSBI,” IEEE Access, vol. 7, pp. 81333–81350, 2019. [Google Scholar]

57. Y. G. Yang, B. W. Guan, Y. H. Zhou and W. M. Shi, “Double image compression-encryption algorithm based on fractional order hyper chaotic system and DNA approach,” Multimedia Tools and Applications, vol. 80, pp. 691–710, 2020. [Google Scholar]

58. E. Hasanzadeh and M. Yaghoobi, “A novel color image encryption algorithm based on substitution box and hyper-chaotic system with fractal keys,” Multimedia Tools and Applications, vol. 79, no. 11–12, pp. 7279–7297, 2020. [Google Scholar]

59. A. Belazi, A. A. Abd El-Latif and S. Belghith, “A novel image encryption scheme based on substitution-permutation network and chaos,” Signal Processing, vol. 128, no. 11, pp. 155–170, 2016. [Google Scholar]

60. S. Sun, Y. Guo and R. Wu, “A novel image encryption scheme based on 7D hyperchaotic system and row-column simultaneous swapping,” IEEE Access, vol. 7, pp. 28539–28547, 2019. [Google Scholar]

61. S. Janakiraman, K. Thenmozhi, J. B. B. Rayappan and R. Amirtharajan, “Lightweight chaotic image encryption algorithm for real-time embedded system: Implementation and analysis on 32-bit microcontroller,” Microprocessors and Microsystems, vol. 56, pp. 1–12, 2018. [Google Scholar]

62. S. N. Lagmiri, J. Elalami, N. Sbiti and M. Amghar, “Hyperchaos for improving the security of medical data,” International Journal of Engineering & Technology, vol. 7, no. 3, pp. 1049–1055, 2018. [Google Scholar]

63. G. Zhang, W. Ding and L. Li, “Image encryption algorithm based on tent delay-sine cascade with logistic map,” Symmetry, vol. 12, no. 3, pp. 1–14, 2020. [Google Scholar]

64. Z. Li, C. Peng, W. Tan and L. Li, “A novel chaos-based image encryption scheme by using randomly DNA encode and plaintext related permutation,” Applied Sciences (Switzerland), vol. 10, no. 21, pp. 1–19, 2020. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.