Computers, Materials & Continua DOI:10.32604/cmc.2022.024500
Article

Metaheuristic Based Data Gathering Scheme for Clustered UAVs in 6G Communication Network

Ahmed S. Almasoud1, Siwar Ben Haj Hassine2, Nadhem NEMRI2, Fahd N. Al-Wesabi2,3, Manar Ahmed Hamza4,*, Anwer Mustafa Hilal4, Abdelwahed Motwakel4 and Mesfer Al Duhayyim5

1Department of Information Systems, College of Computer and Information Sciences, Prince Sultan University, Saudi Arabia
2Department of Computer Science, College of Science & Arts at Mahayil, King Khalid University, Saudi Arabia
3Faculty of Computer and IT, Sana'a University, Sana'a, Yemen
4Department of Computer and Self Development, Preparatory Year Deanship, Prince Sattam bin Abdulaziz University, AlKharj, Saudi Arabia
5Department of Natural and Applied Sciences, College of Community-Aflaj, Prince Sattam bin Abdulaziz University, Saudi Arabia
*Corresponding Author: Manar Ahmed Hamza. Email: ma.hamza@psau.edu.sa
Received: 20 October 2021; Accepted: 22 November 2021

Abstract: The sixth-generation (6G) wireless communication networks are anticipated in integrating aerial, terrestrial, and maritime communication into a robust system to accomplish trustworthy, quick, and low latency needs. It enables to achieve maximum throughput and delay for several applications. Besides, the evolution of 6G leads to the design of unmanned aerial vehicles (UAVs) in providing inexpensive and effective solutions in various application areas such as healthcare, environment monitoring, and so on. In the UAV network, effective data collection with restricted energy capacity poses a major issue to achieving high quality network communication. It can be addressed by the use of clustering techniques for UAVs in 6G networks. In this aspect, this study develops a novel metaheuristic based energy efficient data gathering scheme for clustered unmanned aerial vehicles (MEEDG-CUAV). The proposed MEEDG-CUAV technique intends in partitioning the UAV networks into various clusters and assign a cluster head (CH) to reduce the overall energy utilization. Besides, the quantum chaotic butterfly optimization algorithm (QCBOA) with a fitness function is derived to choose CHs and construct clusters. The experimental validation of the MEEDG-CUAV technique occurs utilizing benchmark dataset and the experimental results highlighted the better performance over the other state of art techniques interms of different measures.

Keywords: 6G network; mobile communication; uav networks; energy efficiency; clustering; metaheuristics

1  Introduction

The cutting edge wireless communication networks towards 6G are imagined to empower intellectual, secure, dependable, and boundless availability [1]. It is anticipated that 6G will bring an undeniable structure for connected things and computerization framework from independent vehicles to unmanned aerial vehicles (UAVs) with tough and various prerequisites such as dependability, inertness, data rate, and energy proficiency. UAVs, normally known as drones, act as a vital part of a broad scope of utilization cases and situations that can go past 5G and 6G [2]. The instances of UAV applications incorporate bundle conveyance, media creation, surveillance, and distant developments. The organization of UAVs is consistently expanding and, as anticipated by the Federal Aviation Administration (FAA), the quantity of business UAV armadas can reach up to 1.6 million by 2024. In the meantime, unmanned aircraft system (UAS) traffic management (UTM) frameworks are being created to provide danger free activity of low-height UAVs with their conceivably high traffic thickness. In an associated sky, the help of a huge scope arrangement of UAVs requires solid and secure remote correspondences that guarantee safe control and activity of UAVs [3]. This will require productive framework plan for remote correspondence, canny calculation, and solid control instruments. Fig. 1 illustrates the process of 5G.

Figure 1: Process of 5G

In multiUAV systems, UAV-to-UAV (U2U) and UAV-to-base station (U2BS) data sharing is a successful answer for excellent organization correspondence. Inferable from the high portability of UAVs, UAV localization is a significant specialized issue. UAV localization is acknowledged utilizing GPS; be that as it may, GPS experiences a normal area blunder of 10–30 m [4]. Much of the time, for example, rural environments check under terrible climate conditions, the GPS signal has been inadequate or totally missing. Subsequently, a few techniques are presented for addressing this localization issue in UAV networks [5]. The vast majority of these techniques, which utilize the distance estimation strategy, depend on bilateration and trilateration. Be that as it may, flip ambiguity (FA) is a significant issue in distance-estimation based localization techniques [6]. Nonetheless, GPS is costly and energy burning-through [7].

In multi-UAV systems, clustering is utilized to control the organization of UAVs in the network. Due to energy limits, the network lifespan has been critical boundary in UAV systems [8]. Additionally, attributable to the high versatility of UAVs, geography control is fundamental to decrease correspondence impedance [9]. The clustering approach addresses the significant distance correspondence issue, expands network versatility, improves network lifetime, and builds the unwavering quality of the whole organization. Moreover, clustering can furnish proficient and consistent courses with low correspondence overhead during the course disclosure and sending measures [10]. It can be result of their effortlessness, adequacy in taking care of complicated streamlining issues, and neighborhood least aversion [11]. A greater part of these calculations is motivated by creature conduct, developmental ideas, and actual wonders.

Pustokhina et al. [12] proposed a novel energy-efficient cluster based UAV network with DL based scene classification technique. The presented technique contains a clustering with parameter tuned residual network (C-PTRN) technique that functions on 2 important stages namely cluster construction as well as scene classification. Primarily, the UAV is clustered, and selected CH transfer the taken images to BS. Secondary level, a DL-based ResNet50 approach was utilized to scene classification. For tuning the hyperparameter of ResNet50 technique, water wave optimization (WWO) technique was utilized.

In Turgut et al. [13], an analytical structure has been given for analyzing the SINR coverage probabilities of UAV helped cellular networks by clustered user equipment (UE). The place of UAVs as well as ground BS have been demonstrated as Poison point procedures, and UE has been considered distributed based on Poisson cluster technique about the predictions of UAV on the ground. Primarily, the complementary cumulative distribution purpose and probabilities density purpose of path losses to combine of UAV as well as ground BS tiers are resultant.

In Na et al. [14], an efficient iterative technique was presented for addressing it. Initially, to set UAV path, every terminal is clustered and sub-slot allocation technique dependent upon Lagrange multiplier and bisection technique was presented. Afterward, to set clustering state and sub-slot time, it can optimize the UAV path. Spyridis et al. [15] regarded the aim of locating mobile IoT devices of unknown places, utilizing the set of UAVs which are equipped by RSSI sensor. The UAV utilized measurement of objective's radio frequency (RF) signal power for modelling the objective as rapidly as feasible. In DL technique carried out clustering from the UAV networks at regular intervals depending upon graph convolutional network (GCN) framework that utilized data on RSSI and UAV places.

In Liu et al. [16], a new non-stationary multi-mobility UAV-to-ship channel technique was presented, containing 3 types of modules, for instance, the line-of-sight (LoS), single-bounce (SB) modules resultant in the variation of seawater, and multi-bounce (MB) modules presented by waveguide result on sea surface. Minhas et al. [17] proposed the Reinforcement Learning (RL) and UAV helped multipath routing technique to PSN. The goal is for increasing network lifespan by enhancing the energy-efficiency of PSN. Initial, network configurations have been created utilizing varying clustering methods. The RL is then implemented for configuring the routing topology which regards combined immediate energy cost and entire distance cost of communication path.

1.1 Objective of the Paper

The major objective of the study is to design an intelligent data gathering scheme for clustered UAVs in such a way that the energy efficiency is accomplished.

1.2 Contribution of the Paper

This article presents a novel metaheuristic based energy efficient data gathering scheme for clustered unmanned aerial vehicles (MEEDG-CUAV). The proposed MEEDG-CUAV technique intends in partitioning the UAV networks into various clusters and assign a cluster head (CH) to reduce the overall energy utilization. Besides, the quantum chaotic butterfly optimization algorithm (QCBOA) with a fitness function is derived to choose CHs and construct clusters. The experimental validation of the MEEDG-CUAV technique takes place using benchmark dataset and the experimental results highlighted the better performance over the other state of art techniques interms of different measures.

1.3 Organization of the Paper

The rest of the paper is organized as follows. Section 2 offers the detailed discussion of the MEEDG-CUAV technique and Section 3 provides a brief performance validation process. Finally, Section 4 draws the conclusion.

2  The Proposed MEEDG-CUAV Technique

In this study, a MEEDG-CUAV technique is derived for energy efficient data collection in UAV enabled 6G networks. The MEEDG-CUAV technique involves the design of QCBOA technique by integrating the concepts of quantum theory and chaotic map into the classical BOA. In addition, the QCBOA technique derives a fitness function involving three input variables to elect CHs like residual energy (RDE), average distance to neighboring UAVs (ADTN), and UAV degree (DEG). Fig. 2 demonstrates the overall process of presented MEEDG-CUAV technique.

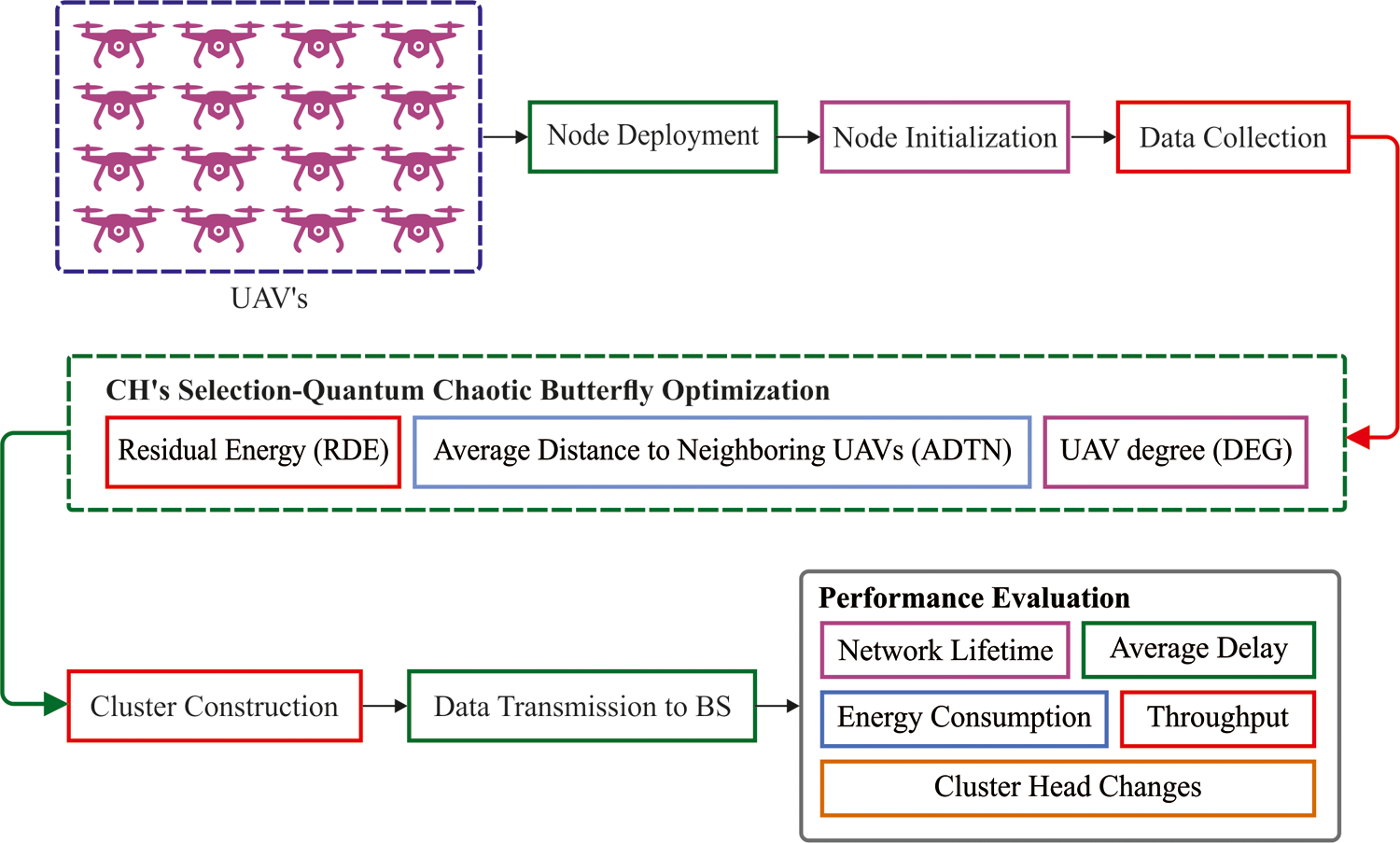
Figure 2: Overall process of MEEDG-CUAV model

2.1 Algorithmic Design of QCBOA Technique

The nature simulated metaheuristic technique is presented, called BOA that reproduces the foraging as well as mating performance of the butterfly. The most essential feature of BOA altered in other metaheuristics is which all butterflies have their individual unique scent. The fragrance was expressed as:

fi=cIa(1)

where fi implies the supposed magnitude of smell, c signifies the sensory modalities, and I refers the stimulation intensities, and a defines the power exponents dependent upon degree of smell absorption. In theory, some value of sensory morphologies coefficient c from the range of 0 and ∞ is taken. But, their value has been defined as the particularity of optimized issues from the iterative procedure of BOA. The sensory modality c from the optimum search phase of technique is expressed as:

ct+1=ct+[0.025/(ct⋅Tmax)](2)

where Tmax represents the maximal amount of iterations during this technique, and the primary value of parameter c has been fixed to 0.01.

Besides, there are 2 important steps from the technique, it can be correspondingly, global as well as local search phases [18]. The mathematical process of butterfly global search movement is written as:

xit+1=xit+(r2×gbest−xit)×fi(3)

where xit indicates the solution vector xi of ith butterfly from t iteration and r signifies an arbitrary number from 0 and 1. At this point, gbest refers the present optimum solution establish amongst every solution from the present stage. Mostly fi defines the smell of ith butterfly. The local search phase is written as:

xit+1=xit+(r2×xik−xjt)×fi(4)

where xjt and xik are jth and kth butterflies selected arbitrarily under the solution spaces. When xjt and xik affect the similar iterations, it implies that butterfly develops local random walk. Otherwise, this type of arbitrary effort alters the solutions.

Combined of global as well as local searches to food and mating partner with butterfly by its nature is taking place. So, the switch probability p has been fixed to change the usual global search and intensive local search. During all the iterations, the BOA arbitrarily creates the number from 0 and 1 that is related to switch probability p for deciding that for conducting global/local searches.

The chaos model is a division of mathematics which acts on non-linear dynamical system. Non-linear represents that it can be inconceivable for predicting the system response with relating the input, and dynamical mean alters from the system in one state to another over time. The chaos purpose signifies the dynamic model with deterministic formula. But, according to the primary condition, chaotic functions are generated wildly unpredictable and divergent feature performances [19]. Therefore, the chaos function is improve the intensification as well as diversification of optimized techniques that is prevent local optimal solutions and change nearby global optimal. These purposes follow very easy principles and have some interrelating parts; but, during all iterations, the created value was based on the earlier value and primary condition.

During this case, it can be executed 3 varying chaotic maps such as logistic mapping, iterative mapping, and tent mapping with sensory modality (c) and power exponents (p) computations from the BOA. The chaos purposes have been established for exhibiting higher efficiency related to other chaos purposes.

Logistic map:

xt=rxt−1(1−xt−1)(5)

At this point, xt implies the value from some iterations t, and r denotes the rate of growth that is proceeds values in [3.0–4.0].

Iterative map:

xt=sin(Pπxt−1)(6)

During the iterative map, the value of P is chosen amongst [0,1], and the outcome xt has been chaotic variable which takes values in [0–1].

Tent map:

xt={xt−10.7,xt−1<0.7103(1−xt−1),xt−1≥0.7(7)

The tent map has 1D map which similar to logistic map. At this point, the outcome xt has been chaotic variable which takes values in [0,1].

During the presented QCBOA, the sensory modality value was changed with more disturbance to c value under the new BOA utilizing a chaos function. It can change the sensory modality value as:

c−mod(t)=[c−mod(t−1)+0.025c−mod(t−1)∗T]∗xt(8)

where c−mod(t) refers the changed sensory modality value from some iterations t. For implementing the logistic, iterative, and tent chaos maps, (5), (6), and (7) are utilized for replacing xt in (8) correspondingly. Also, the constant value of power exponents on every iteration from the original BOA has been exchanged as:

a−mod(t)=0.15∗xt(9)

The variances in the sensory modality and power exponent amongst the new BOA and presented QCBOA with logistic map. The c−mod and a−mod values don't differ linearly, and these values aren't constants on every iteration.

The change of sensory-modality value is affected by premature convergence. In addition, the implementation of constant value to the power exponents are generate a locally minimal output. The intensification as well as diversification of exploring manner is intensified and diversified with more chaotic disturbance and so help the effort near global solutions.

Besides, the quantum computing technique increases the solutions of many real world issues from soft computation methods. Most of their important application was enhancing optimized techniques for exploring the search space further effectively and efficiently. During this technique, every particle is considered for moving in quantum mechanical procedures before typical Newtonian arbitrary movement. During the quantum wave model, a particle has been considered for moving from 1D well δ, and the place of particle X is computed as:

Xi,jt+1=pi,jt+12Lijtln(1u)(10)

In Eq. (10), pi,jt refers the local attractor points (also named as particle motion center) at time t. The convergence to better solution is attained rapidly when all particles move nearby their local attractors. The local attractor point is determined as arbitrary average of global as well as local optimum particles from the swarm as:

pi,jt=φPi,jt+(1−φ)Gjt(11)

At this point, φ represents the arbitrary number with uniform distribution function on the interval amongst [0,1], Pi,jt denotes the local optimum, and Gjt indicates the global optimum amongst every particle. Besides, u signifies the arbitrary number from the range of [0,1], and Li,jt defines the typical length of potential well δ at time t, and this value has been directly compared with convergence speed and search capability of technique. Li,jt is written as:

Lijt=2α|Ct−Xi,jt|(12)

At this time, Ct demonstrates the mean optimum place, for instance, the mean of optimum places of every particle contributing from the quantum computing.

Ct=(C1t,C2t,……CDt)={1M∑i=1M⁡Pi,1t,1M∑i=1M⁡Pi,2t,…1M∑i=1M⁡Pi,Dt}(13)

Now, M represents the population size, and Pit implies the personal optimum place of particles i. Moreover, α stands for tunable parameter (for instance, the contraction-expansion (CE) coefficient) for controlling the convergence speed of technique. Noticeable parameter α can be decreased under the development of iterations as:

α=α0+(T−t)∗(α1−α0)T(14)

At this point, α1 and α0 defines the last and primary values of α correspondingly, T refers the entire amount of iterations, and t signifies the present iteration number.

2.2 Process Involved in the QCBOA Based Clustering Technique

The presented MEEDG-CUAV based clustering is mostly dependent upon the QCBOA technique. The aim of MEEDG-CUAV approach has for dividing nUAVnodes as to existing or optimal amount of clusters Copt. During the clustering, the adjacent nodes have been selected to CH with means of Euclidean distance that generate user which minimal transmission range outcomes from decreased energy consumption. However, it can be tedious for identifying the distance from extremely mobile conditions. In order to resolve the problem, the distance for neighboring UAVs is defined with utilize of MEEDG-CUAV approach. For selecting CH and creating cluster, the MEEDG-CUAV manner considers this issue as maximization issue and derive as FF containing RDE, ADTN, and DEG. The fitness function (FF) has been determined as:

F(i)=α×REL+β×ADTN+γ×DEG,(15)

where α+β+γ=1. Primarily, the RDE of UAV(x) in the communication of k bit data for getting UAV(y) that is placed at distance d, has demonstrated in Eq. (16):

REL=E−(ET(k,d)+ER(k))(16)

where E refers to the current energy level of UAV and ET stands for the energy spent on data broadcast.

ET(k,d)=kEe+KEad2(17)

where Ee defines the energy of electrons and Ea signifies the vital amplified energy, ER(k) indicates the energy spent on data receptions that are defined in Eq. (18):

ER(k)=kEe(18)

In addition, the AADTN signifies the average value of distance of the neighbroing UAV from their 1-hop communication range [20]. It is determined in Eq. (19):

ADTN=∑j=1NBi⁡dist(i,nbj)NBi,(19)

where dist(i,nbj) refers the distance in the UAV to closer jth UAV.

At a time t, the DEG implies the UAV degree representing the amount of adjacent nodes current to UAV that is formulated as:

DEG=|N(x)|(20)

where N(x)={ny/dist(x,y)<transrange}x≠y, and dist(x,y) demonstrates the distance among 2 UAVs nx and ny, transrange implies the transmission range of UAVs.

3  Experimental Validation

The performance validation of the MEEDG-CUAV technique takes place under varying dimensions.

Tab. 1 and Fig. 3 offer the energy consumption (EC) analysis of the MEEDG-CUAV technique with existing approaches under distinct UAV count. The outcomes depicted that the MEEDG-CUAV technique has gained effective outcomes with minimal EC.

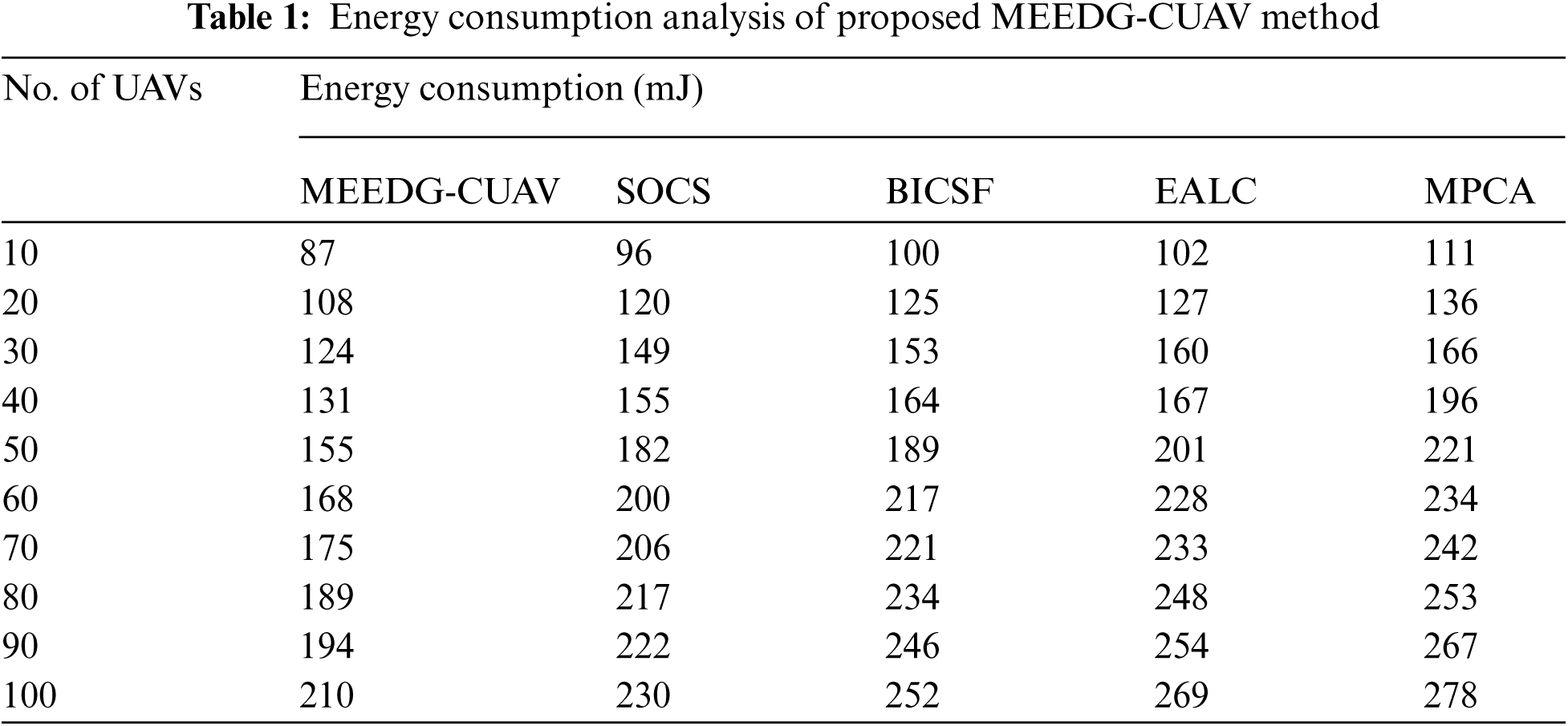
For instance, with 10 UAVs, the MEEDG-CUAV technique has attained a lower EC of 87 mJ whereas the SOCS, BICSF, EALC, and MPCA techniques have obtained higher EC of 96, 100, 102, and 111 mJ respectively. In line with, with 40 UAVs, the MEEDG-CUAV system has reached a minimum EC of 131 mJ whereas the SOCS, BICSF, EALC, and MPCA techniques have gained superior EC of 155, 164, 167, and 196 mJ correspondingly. At the same time, with 80 UAVs, the MEEDG-CUAV approach has achieved a lesser EC of 189 mJ whereas the SOCS, BICSF, EALC, and MPCA methods have obtained higher EC of 217, 234, 248, and 253 mJ respectively. Finally, with 100 UAVs, the MEEDG-CUAV technique has gained a lower EC of 210 mJ whereas the SOCS, BICSF, EALC, and MPCA methodologies have obtained maximal EC of 230, 252, 269, and 278 mJ correspondingly.

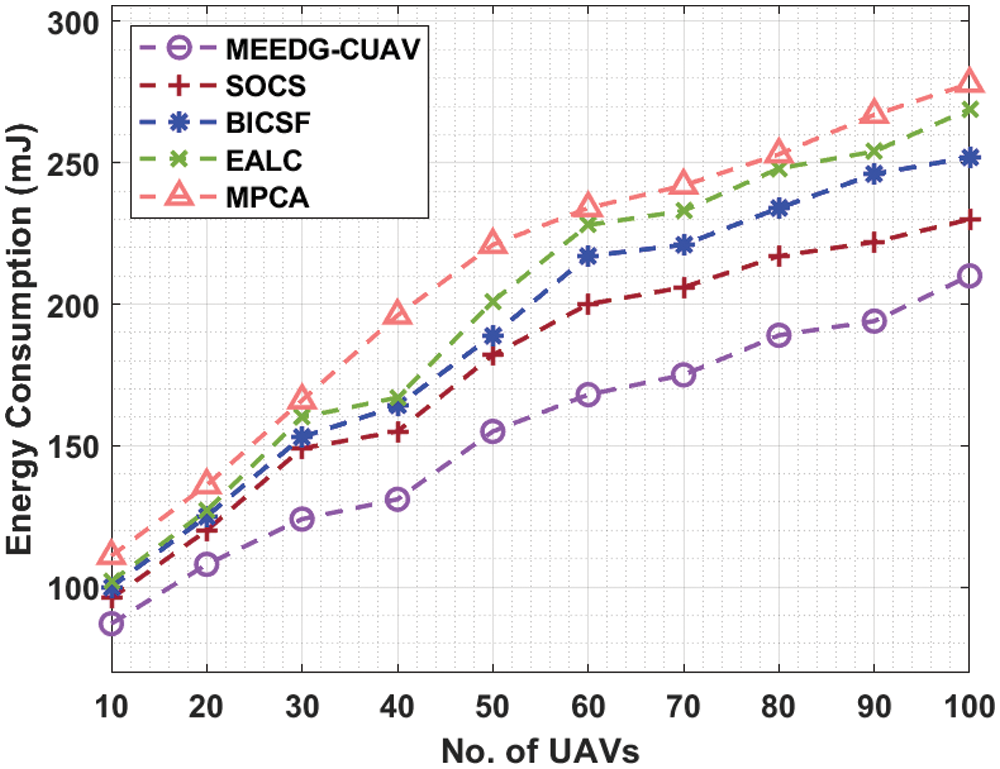
Figure 3: Energy consumption analysis of MEEDG-CUAV model

A brief NLT analysis of the MEEDG-CUAV technique with recent approaches takes place in Tab. 2 and Fig. 4. The experimental results portrayed that the MEEDG-CUAV technique has accomplished improved NLT over the other techniques. For instance, with 10 UAVs, the MEEDG-CUAV technique has resulted in an increased NLT of 5920 rounds whereas the SOCS, BICSF, EALC, and MPCA techniques have attained reduced NLT of 5570, 5520, 5330, and 4770 rounds respectively. Likewise, with 40 UAVs, the MEEDG-CUAV system has resulted in an enhanced NLT of 5410 rounds whereas the SOCS, BICSF, EALC, and MPCA techniques have achieved reduced NLT of 5250, 4950, 4600, and 4180 rounds correspondingly. Moreover, with 80 UAVs, the MEEDG-CUAV approach has resulted in an improved NLT of 4430 rounds whereas the SOCS, BICSF, EALC, and MPCA techniques have attained lower NLT of 4080, 3840, 3760, and 3590 rounds respectively. Furthermore, with 100 UAVs, the MEEDG-CUAV method has resulted in an increased NLT of 4160 rounds whereas the SOCS, BICSF, EALC, and MPCA systems have attained reduced NLT of 3550, 3380, 3280, and 3210 rounds correspondingly.

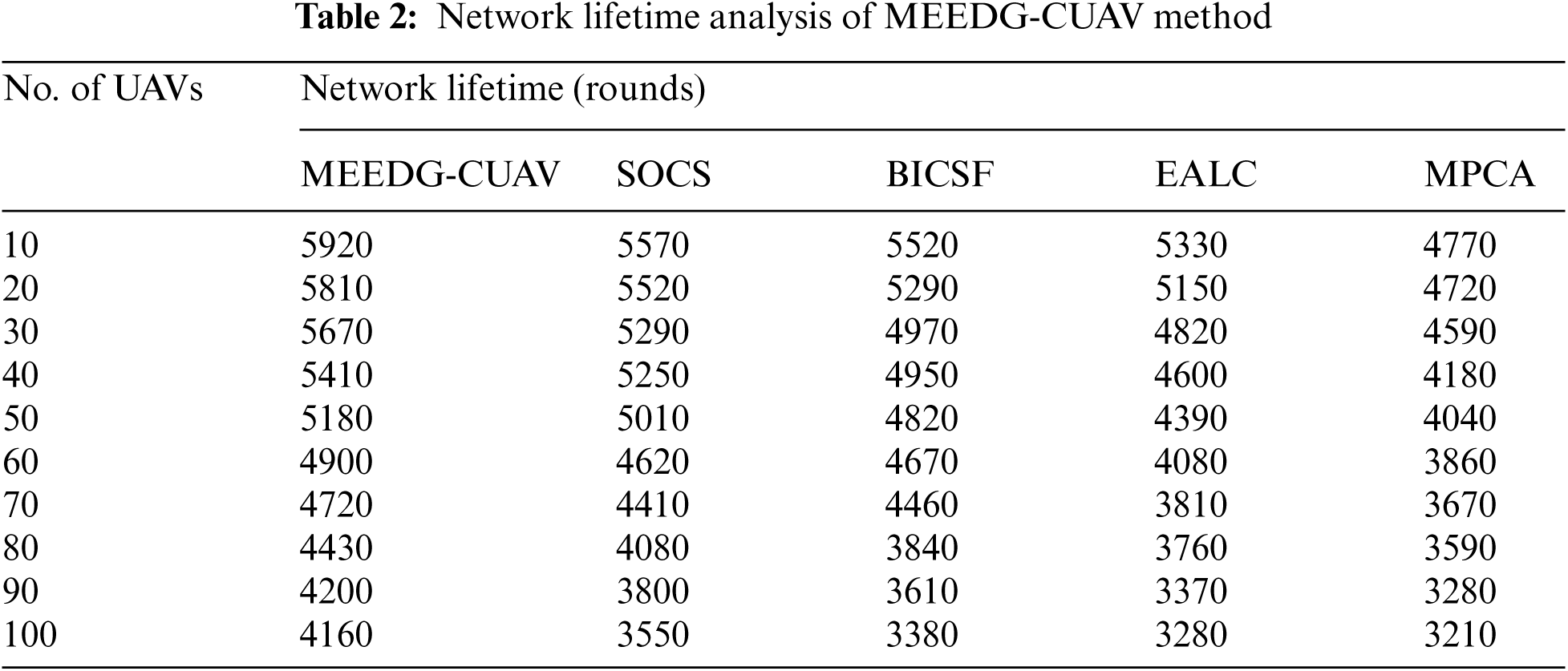
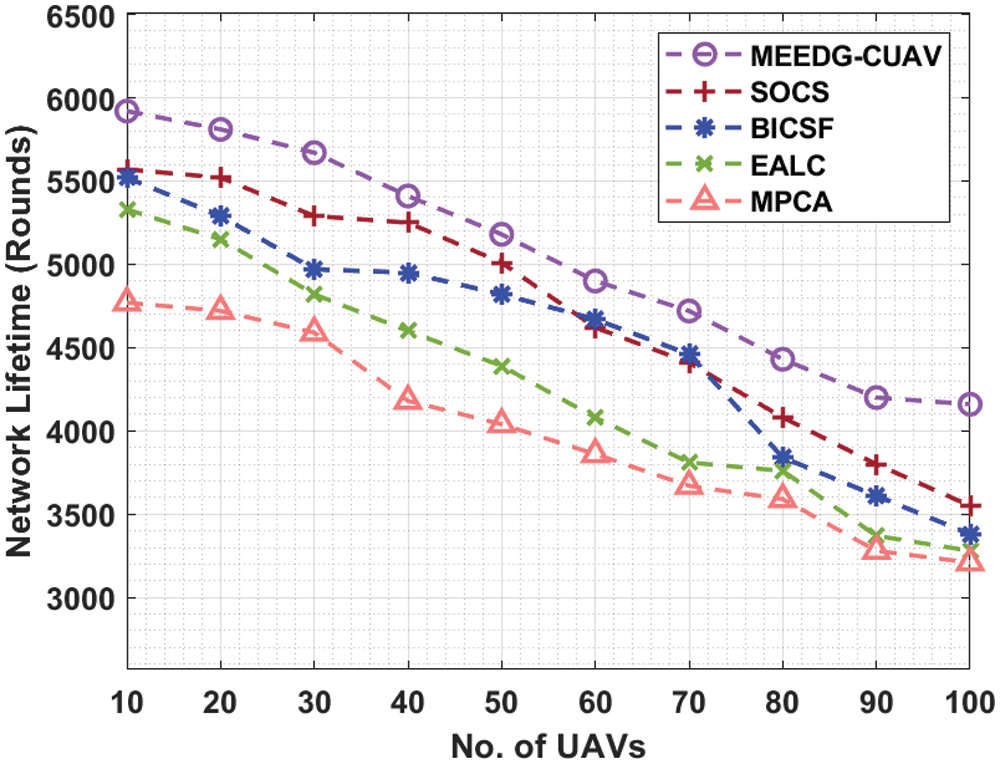
Figure 4: NLT analysis of MEEDG-CUAV model

Detailed throughput analysis of the MEEDG-CUAV manner with recent algorithms occurs in Tab. 3 and Fig. 5. The experimental results portrayed that the MEEDG-CUAV technique has accomplished increased throughput over the other algorithms. For instance, with 10 UAVs, the MEEDG-CUAV manner has resulted in a higher throughput of 99 Mbps whereas the SOCS, BICSF, EALC, and MPCA methods have attained lesser throughput of 93, 92, 90, and 86 Mbps correspondingly. In addition, with 40 UAVs, the MEEDG-CUAV technique has resulted in maximal throughput of 87 Mbps whereas the SOCS, BICSF, EALC, and MPCA techniques have attained reduced throughput of 72, 66, 60, and 53 Mbps respectively. Followed by, with 80 UAVs, the MEEDG-CUAV technique has resulted in a higher throughput of 78 Mbps whereas the SOCS, BICSF, EALC, and MPCA techniques have attained reduced throughput of 61, 53, 52, and 42 Mbps correspondingly. Finally, with 100 UAVs, the MEEDG-CUAV system has resulted in an increased throughput of 74 Mbps whereas the SOCS, BICSF, EALC, and MPCA techniques have attained minimum throughput of 57, 49, 48, and 39 Mbps correspondingly.

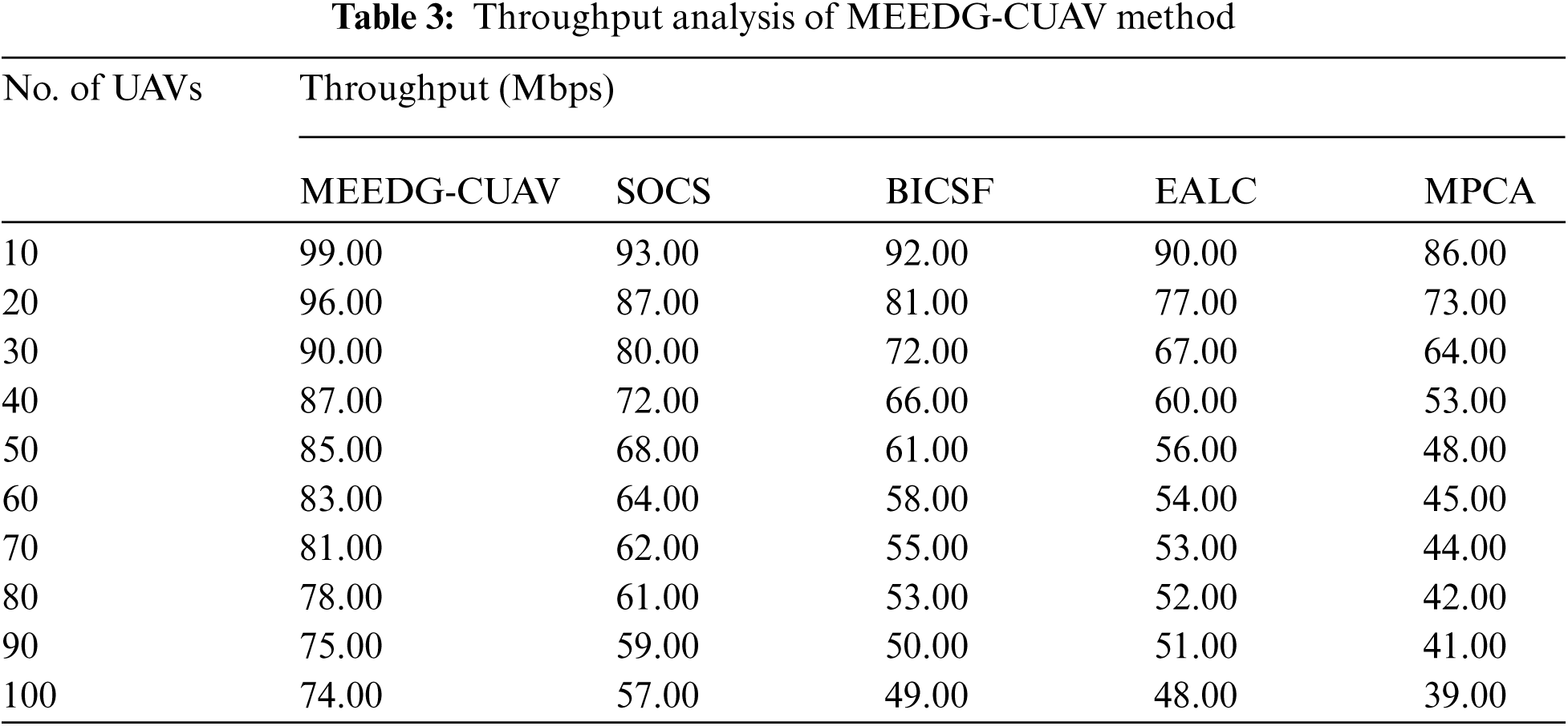
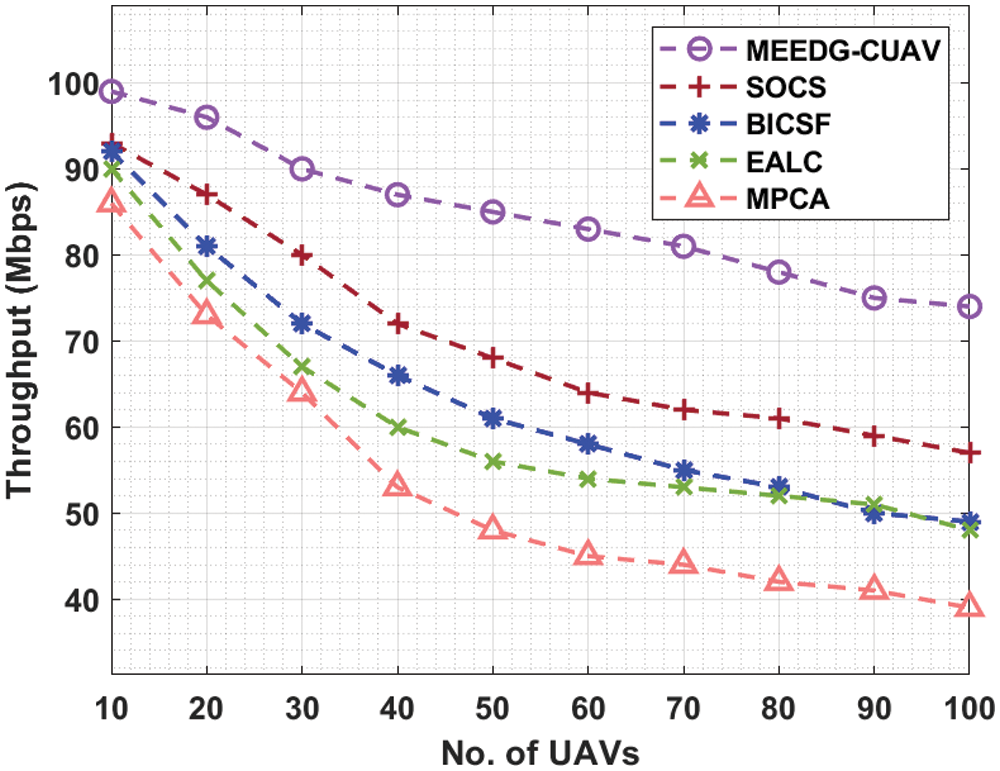
Figure 5: Throughput analysis of MEEDG-CUAV model

Tab. 4 and Fig. 6 provide the ARD analysis of the MEEDG-CUAV system with existing approaches in different UAV counts. The results depicted that the MEEDG-CUAV algorithm has gained effective outcomes with a minimum ARD. For instance, with 10 UAVs, the MEEDG-CUAV manner has reached a lesser ARD of 4.04 s whereas the SOCS, BICSF, EALC, and MPCA techniques have obtained maximum ARD of 4.17, 4.20, 4.27, and 4.86 s correspondingly. Along with that, with 40 UAVs, the MEEDG-CUAV technique has attained a decreased ARD of 5.76 s whereas the SOCS, BICSF, EALC, and MPCA techniques have obtained increased ARD of 6.27, 6.85, 7.67, and 9.86 s correspondingly. Simultaneously, with 80 UAVs, the MEEDG-CUAV approach has attained a reduced ARD of 8.43 s whereas the SOCS, BICSF, EALC, and MPCA manners have obtained improved ARD of 9.17, 9.82, 10.36, and 12.39 s respectively. At last, with 100 UAVs, the MEEDG-CUAV method has attained a lower ARD of 8.98 s whereas the SOCS, BICSF, EALC, and MPCA systems have reached superior ARD of 10.16, 10.92, 11.19, and 13.89 s correspondingly.

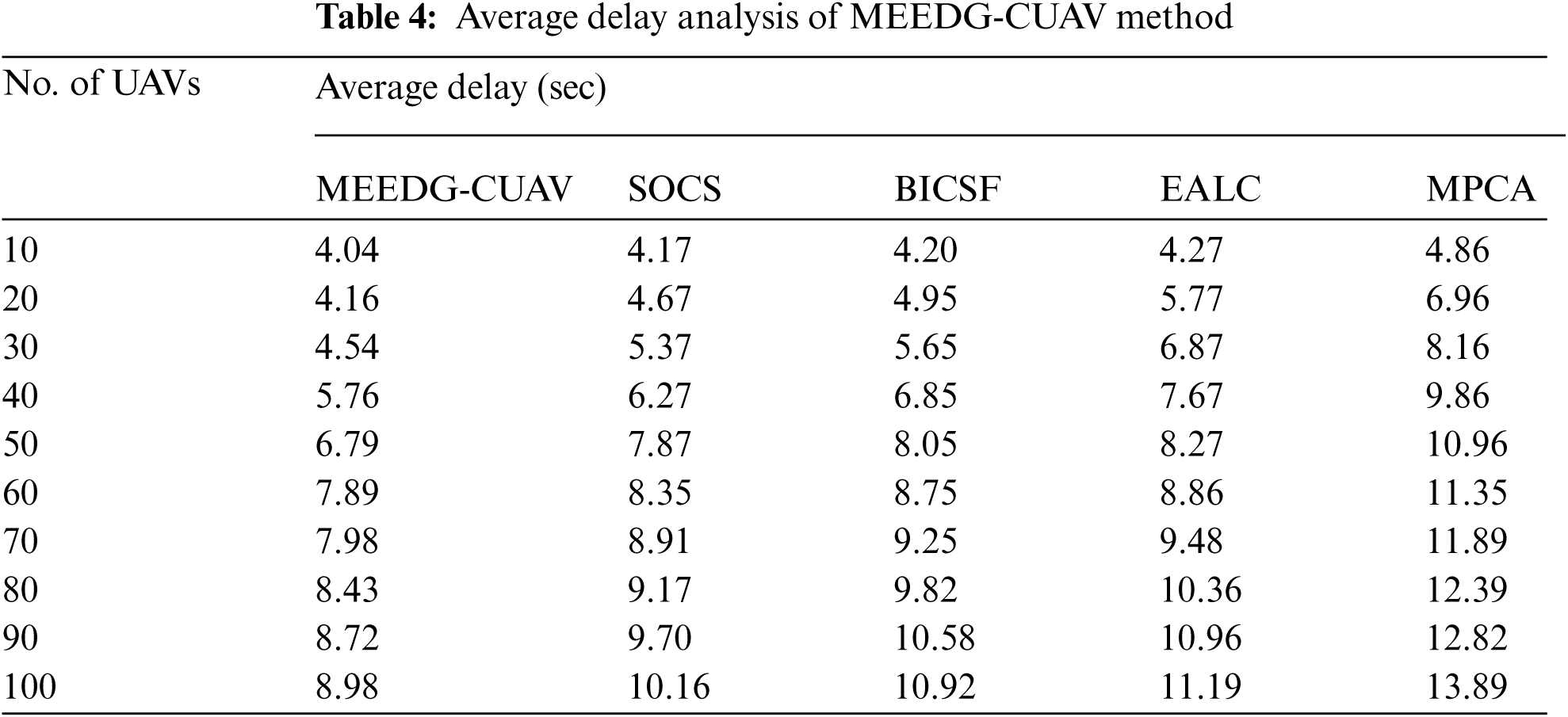
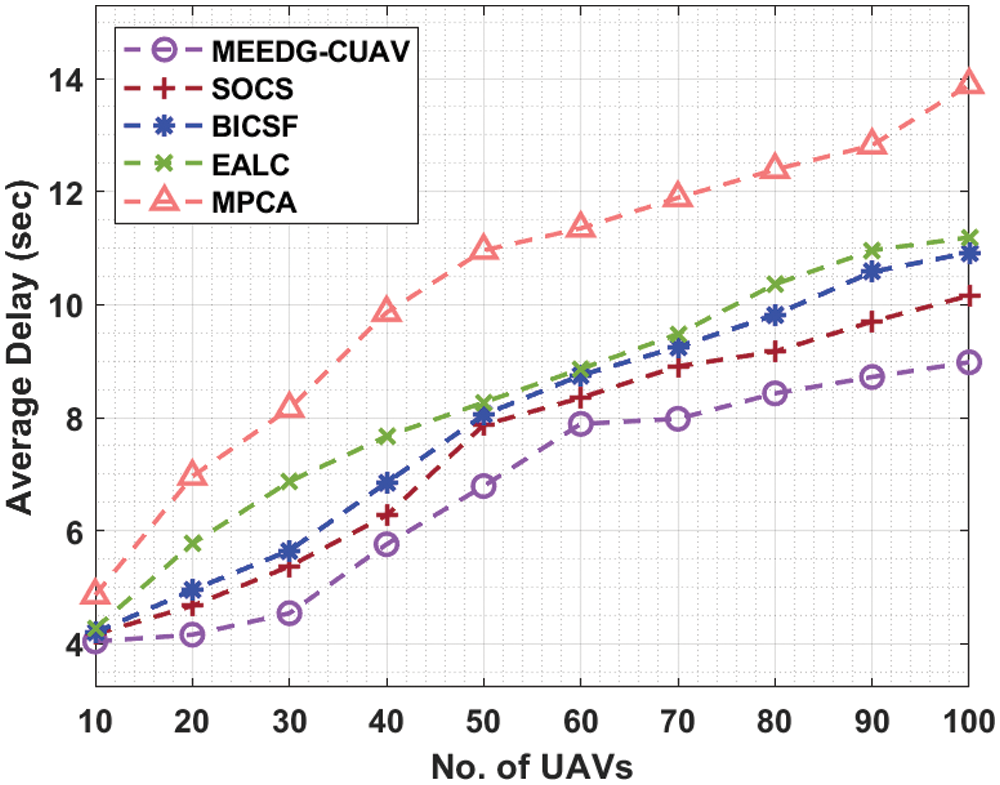
Figure 6: Average delay analysis of MEEDG-CUAV model

Tab. 5 and Fig. 7 gives the NCHC analysis of the MEEDG-CUAV method with existing manners under varying UAV speed rate. The outcomes demonstrated that the MEEDG-CUAV technique has reached effective outcomes with minimal NCHC. For instance, with 2 m/s speed rate, the MEEDG-CUAV system has reached a lower NCHC of 9 whereas the SOCS, BICSF, EALC, and MPCA techniques have achieved higher NCHC of 11, 13, 16, and 19 respectively. Also, with 4 m/s speed rate, the MEEDG-CUAV system has attained a lower NCHC of 8 whereas the SOCS, BICSF, EALC, and MPCA methods have obtained higher NCHC of 10, 15, 18, and 22 correspondingly. Moreover, with 8 m/s speed rate, the MEEDG-CUAV algorithm has attained a lower NCHC of 15 whereas the SOCS, BICSF, EALC, and MPCA systems have obtained higher NCHC of 19, 22, 25, and 28 respectively. Eventually, with 10 m/s speed rate, the MEEDG-CUAV system has attained a minimal NCHC of 17 whereas the SOCS, BICSF, EALC, and MPCA manners have obtained superior NCHC of 20, 24, 29, and 33 correspondingly.

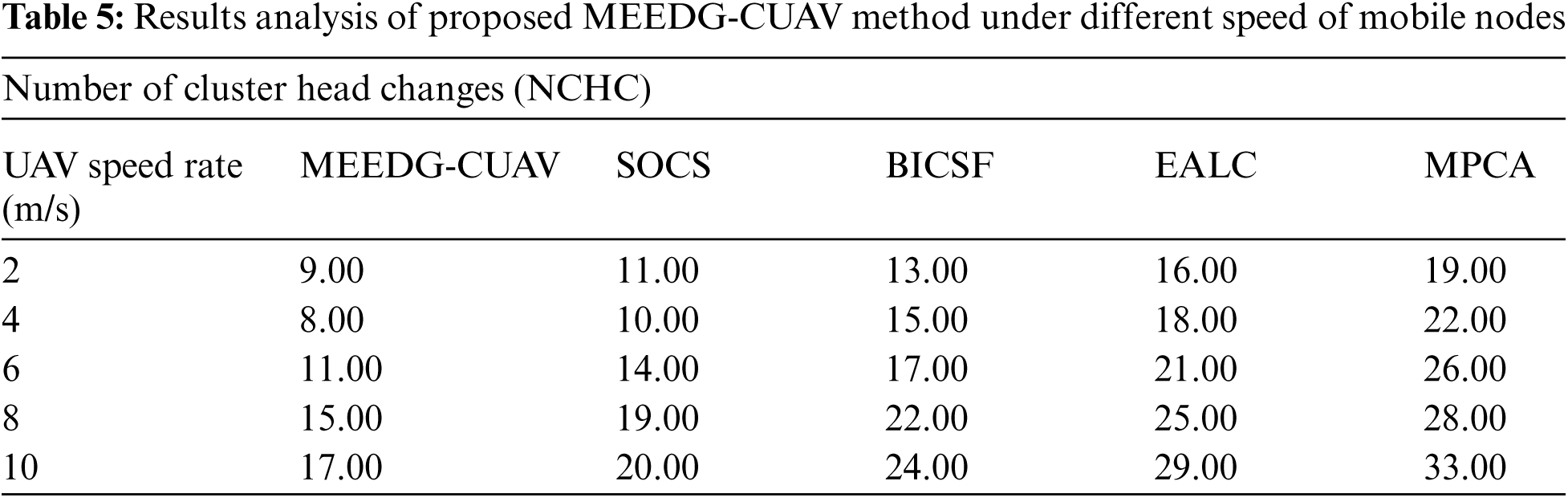
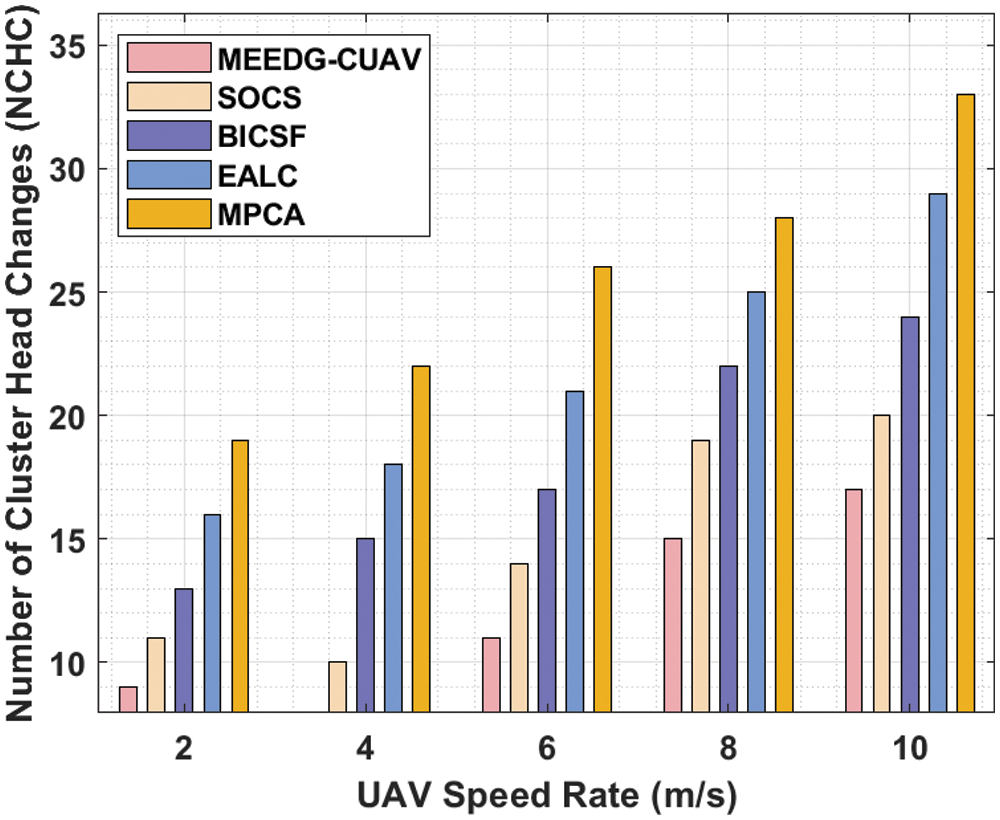
Figure 7: NCHC analysis of MEEDG-CUAV model

4  Conclusion

In this study, a MEEDG-CUAV technique is derived for energy efficient data collection in UAV enabled 6G networks. The MEEDG-CUAV technique involves the design of QCBOA technique by integrating the concepts of quantum theory and chaotic map into the classical BOA. In addition, the QCBOA technique derives a fitness function involving three input variables to elect CHs namely RDE, ADTN, and DEG. The experimental validation of the MEEDG-CUAV technique occurs utilizing benchmark dataset and the experimental results highlighted the better performance over the other state of art techniques interms of different measures. Therefore, the MEEDG-CUAV technique can be utilized as a proficient tool for data collection in clustered UAV enabled 6G networks. In future, task scheduling and resource allocation strategies can be developed for UAV enabled 6G networks.

Acknowledgement: The authors would like to acknowledge the support of Prince Sultan University for paying the Article Processing Charges (APC) of this publication.

Funding Statement: The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work under Grant Number (RGP 1/279/42). https://www.kku.edu.sa.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  M. Y. Arafat and S. Moh, “Location-aided delay tolerant routing protocol in UAV networks for post-disaster operation,” IEEE Access, vol. 6, pp. 59891–59906, 2018. [Google Scholar]

 2.  M. Y. Arafat and S. Moh, “Bio-inspired approaches for energy-efficient localization and clustering in uav networks for monitoring wildfires in remote areas,” IEEE Access, vol. 9, pp. 18649–18669, 2021. [Google Scholar]

 3.  B. A. Y. Alqaralleh, S. N. Mohanty, D. Gupta, A. Khanna, K. Shankar et al., “Reliable multi-object tracking model using deep learning and energy efficient wireless multimedia sensor networks,” IEEE Access, vol. 8, pp. 213426–213436, 2020. [Google Scholar]

 4.  N. H. Motlagh, T. Taleb and O. Arouk, “Low-altitude unmanned aerial vehicles-based Internet of Things services: Comprehensive survey and future perspectives,” IEEE Internet Things Journal, vol. 3, no. 6, pp. 899–922, 2016. [Google Scholar]

 5.  Q. Guo, Y. Zhang, J. Lloret, B. Kantarci and W. K. G. Seah, “A localization method avoiding flip ambiguities for micro-UAVs with bounded distance measurement errors,” IEEE Transactions on Mobile Computing, vol. 18, no. 8, pp. 1718–1730, 2019. [Google Scholar]

 6.  A. K. Dutta, M. Elhoseny, V. Dahiya and K. Shankar, “An efficient hierarchical clustering protocol for multihop internet of vehicles communication,” Transactions on Emerging Telecommunications Technologies, vol. 31, no. 5, pp. 1–12, 2020. [Google Scholar]

 7.  E. C. Strinati and S. Barbarossa, “6G networks: Beyond shannon towards semantic and goal-oriented communications,” Computer Networks, vol. 190, pp. 107930, 2021. [Google Scholar]

 8.  M. Mozaffari, A. T. Z. Kasgari, W. Saad, M. Bennis and M. Debbah, “Beyond 5G with uavs: Foundations of a 3d wireless cellular network,” IEEE Transactions on Wireless Communications, vol. 18, no. 1, pp. 357–372, 2019. [Google Scholar]

 9.  M. Elhoseny and K. Shankar, “Reliable data transmission model for mobile ad hoc network using signcryption technique,” IEEE Transactions on Reliability, vol. 69, no. 3, pp. 1077–1086, 2020. [Google Scholar]

10. S. Yang, D. Enqing, L. Wei and P. Xue, “An iterative method of processing node flip ambiguity in wireless sensor networks node localization,” in 2016 Int. Conf. on Information Networking (ICOIN), Kota Kinabalu, Malaysia, pp. 92–97, 2016. [Google Scholar]

11. Y. Chen, X. Lin, T. Khan and M. Mozaffari, “Efficient drone mobility support using reinforcement learning,” in 2020 IEEE Wireless Communications and Networking Conf. (WCNC), Seoul, Korea (Southpp. 1–6, 2020. [Google Scholar]

12. I. V. Pustokhina, D. A. Pustokhin, P. K. Pareek, D. Gupta, A. Khanna et al., “Energy-efficient cluster-based unmanned aerial vehicle networks with deep learning-based scene classification model,” International Journal of Communication Systems, vol. 34, no. 8, pp. 1–15, 2021. [Google Scholar]

13. E. Turgut and M. C. Gursoy, “Downlink analysis in unmanned aerial vehicle (uav) assisted cellular networks with clustered users,” IEEE Access, vol. 6, pp. 36313–36324, 2018. [Google Scholar]

14. Z. Na, Y. Liu, J. Shi, C. Liu and Z. Gao, “UAV-Supported clustered noma for 6g-enabled internet of things: Trajectory planning and resource allocation,” IEEE Internet Things Journal, vol. 8, no. 20, pp. 15041–15048, 2021. [Google Scholar]

15. Y. Spyridis, T. Lagkas, P. Sarigiannidi, V. Argyriou, A. Sarigiannidis et al., “Towards 6G IoT: Tracing mobile sensor nodes with deep learning clustering in uav networks,” Sensors, vol. 21, no. 11, pp. 3936, 2021. [Google Scholar]

16. Y. Liu, C. X. Wang, H. Chang, Y. He and J. Bian, “A novel non-stationary 6g uav channel model for maritime communications,” IEEE Journal on Selected Areas in Communications, vol. 39, no. 10, pp. 2992–3005, 2021. [Google Scholar]

17. H. I. Minhas, R. Ahmad, W. Ahmed, M. Waheed, M. M. Alam et al., “A reinforcement learning routing protocol for uav aided public safety networks,” Sensors, vol. 21, no. 12, pp. 4121, 2021. [Google Scholar]

18. M. Zhang, D. Long, T. Qin and J. Yang, “A chaotic hybrid butterfly optimization algorithm with particle swarm optimization for high-dimensional optimization problems,” Symmetry, vol. 12, no. 11, pp. 1800, 2020. [Google Scholar]

19. A. Prasanthi, H. Shareef, R. Errouissi, M. Asna and A. Wahyudie, “Quantum chaotic butterfly optimization algorithm with ranking strategy for constrained optimization problems,” IEEE Access, vol. 9, pp. 114587–114608, 2021. [Google Scholar]

20. S. Kouroshnezhad, A. Peiravi, M. S. Haghighi and A. Jolfaei, “Energy-efficient drone trajectory planning for the localization of 6g-enabled iot devices,” IEEE Internet Things Journal, vol. 8, no. 7, pp. 5202–5210, 2021. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.