Computers, Materials & Continua DOI:10.32604/cmc.2022.024273
Article

Elite Opposition Based Metaheuristic Framework for Load Balancing in LTE Network

M. R. Sivagar1,* and N. Prabakaran2

1Department of Computer Science and Engineering, Sathyabama Institute of Science & Technology, Chennai, 600119, India
2Department of Electronics and Communication Engineering, Koneru Lakshmaiah Education Foundation, Guntur, 522502, Andhra Pradesh, India
*Corresponding Author: M. R. Sivagar. Email: sivagar.ramki@gmail.com
Received: 11 October 2021; Accepted: 22 November 2021

Abstract: In present scenario of wireless communications, Long Term Evolution (LTE) based network technology is evolved and provides consistent data delivery with high speed and minimal delay through mobile devices. The traffic management and effective utilization of network resources are the key factors of LTE models. Moreover, there are some major issues in LTE that are to be considered are effective load scheduling and traffic management. Through LTE is a depraved technology, it is been suffering from these issues. On addressing that, this paper develops an Elite Opposition based Spider Monkey Optimization Framework for Efficient Load Balancing (SMO-ELB). In this model, load computation of each mobile node is done with Bounding Theory based Load derivations and optimal cell selection for seamless communication is processed with Spider Monkey Optimization Algorithm. The simulation results show that the proposed model provides better results than exiting works in terms of efficiency, packet delivery ratio, Call Dropping Ratio (CDR) and Call Blocking Ratio (CBR).

Keywords: Spider monkey optimization; load balancing; long term evolution; optimal cell selection; handover; LTE networks; QoS

1  Introduction

Research in newer updates of wireless communications is one of the fastest emerging domains in network engineering for providing higher rate of Quality of Service (QoS). Moreover, in the next-generation of wireless communications, scheduling methods are effectively used for fair resource allocation and utilization among distinctive nodes in heterogeneous traffic scenarios. That concern in providing promising scheduling model, LTE based models are implemented for making the mobile devices that are cumulative at hassled speediness. In general, Long Term Evolution is the mobile communication standard that is an advancement of 4G communications, approved by International Telecommunication Union [1]. The major objective of Fourth Generation networks is to preserve the existence of developed technologies and reduce the complexities with the device and the user equipment (UE) that permits flexible spectrum allocation [2,3].

The consent of mobile communication models to increase the services with various job scheduling models to significantly balance the load distribution among nodes. Furthermore, the performance of the load balancing and scheduling models are based on the corresponding network type, dynamics in the traffic flow, because of the varied time and frequency slots that shows different channel features, which influences the performance of the overall network model. Hence, handling with the several flow requirements for providing maximal QoS is always been a great confrontation in LTE based models. And, there are several conventional scheduling models with service classification techniques have been designed and the model performances are analyzed using the distinctive features of LTE. Some of the majorly used algorithms are Round Robin, Proportional Fair, Fairness model and maximal SNR (Signal to Noise Ratio), performs, intra and inter class scheduling patterns, throughput and so on [4–6]. The typical communication scenario in LTE based model is presented in Fig. 1.

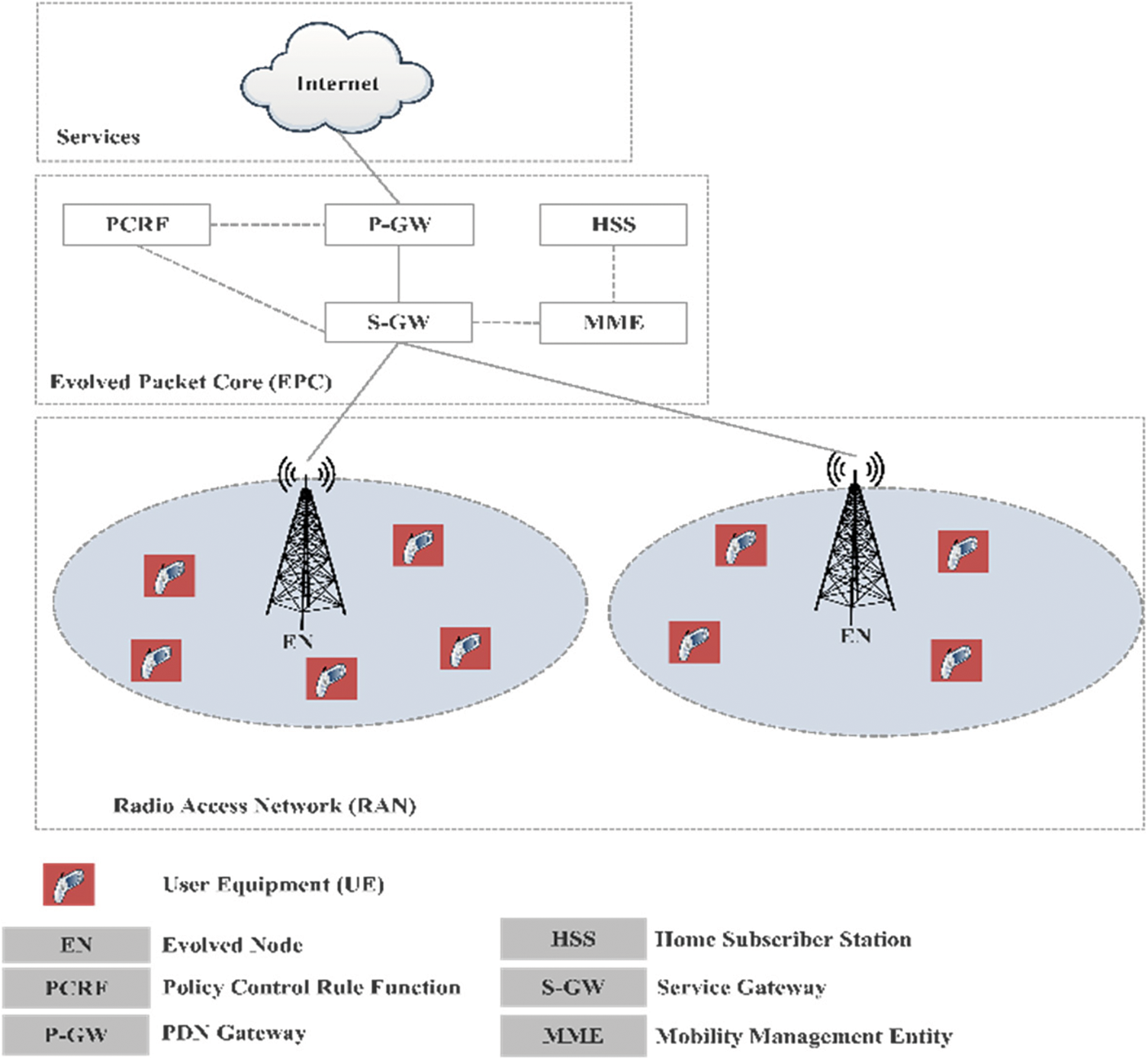
Figure 1: LTE based communication model

In the above figure, the service connectivity layer in the LTE based communication model is presented. In that, the UEs are connected with the evolved node, which is the base station. In LTE, the significance of distribution low power nodes such as micro base stations, relays, home nodes, for increasing the network performance with respect to network coverage, capacity and service knowledge of users are developing huge in present decade [7]. Moreover, because of the dynamic nature and less node co-ordination with the low power nodes, network optimization with balanced load is a great challenge in LTE based models, as mentioned. Additionally, Cell Coverage control is another challenge in LTE based model that is to be considered in developing an efficient communication model. The coverage region of low power nodes is very sensitive to find their corresponding location, status of radio signal distributions and signal strength of neighbour nodes. Hence, the size of each cell in the network is varied, dependent on the previous factors.

Because of receiving higher rate of power from neighbour cells, the coverage region of mobile nodes can be too small to provide services to the nodes that are nearer to their traffic spot. In such scenario, the coverage rate can be enlarged with the combined cell selection for some of the UEs. That means, the user node is permitted to perform handover operation to a weaker cell, by organizing the common cell factor called cell reselection offset function. Nevertheless, the higher rate of offset is not allowed to process with, since, the cell become fragile to process with the intrusions. Subsequently, the node cells can be overloaded in areas with high traffic and hot-spots. Here, load balancing is the important factor in resource management in LTE communications [8–10]. For solving the load balancing issues in LTE based network environment, this paper designs a new work called Elite Opposition based Spider Monkey Optimization Framework for Efficient Load Balancing (SMO-ELB). And, the contributions of this work are provided as follows.

i.   Initially, optimal framework is defined with the deployed low power nodes (PNs) in LTE based model.

ii.   Bounding Theory based Load derivations are incorporated for load balancing among nodes

iii.   Based on the computations, optimal cell selection is processed with Elite Opposition based Spider Monkey Optimization process.

iv.   Cell-edge nodes are estimated for processing handover operations for seamless communications

v.   Model evaluations are carried out based on factors such as efficiency, throughput, packet delivery ratio, Call Dropping Ratio (CDR) and Call Blocking Ratio (CBR)

The remaining part of the work is organized as follows, Chapter 2 discusses about the related works in LTE based models providing effective communications. Research background about the Spider Monkey optimization and problem statement is presented in Chapter 3. In Chapter 4, the complete working process of proposed model is explained with computations. The results and evaluations are presented with comparison graphs in Chapter 5. Finally, the conclusion is given in Chapter 6 with some directions for future work.

2  Related Works

For providing efficient load balancing among base stations, Handover Parameter Control (HPC) model that involves in shifting the user equipment from one cell to another and the process has been noted as Mobility Load Balancing (MLB) [11]. In MLB, the handover factors are adjusted with the offset values, and the radio ranges of UE is derived with the own and neighbour cells. Moreover, the works in [12–14] also discussed about the methods on deriving efficient handover offset. The work presented in [15] discussed about the traffic distribution based congestion issues in Long Term Evolution models in FEMTOCELL scenario. In that work, the femtocell attributes are adjusted with the Fuzzy Logic Controller for balancing the transmission ranges and handover functions. But, problems on overloading were not discussed in the work. For effectively reducing the handovers and CBRs, load balancing model has been designed in [16]. Further, the studies in [17–20], based on user positions, the self-optimization model has been developed that also provided cost reduction. But, the model was not effective with Mobility Load Balancing scenarios.

The work presented in [21] developed a model for cellular optimization using Received Signal Strength (RSS) finger print model. Another femtocell based traffic balancing model has been proposed in [22]. The model used RSS and node location by reframing the cell area, but failed to evaluate about the number of active nodes at an instance. Load balancing techniques are used in LTE based downlink network in the work [23]. The load vector rate has been reduced by the developed model called Load Vector Minimization based Load Balancing Model (LVMLB). The model has not defined the handover technique for providing seamless communications over the network. Further, in the work [24], Distributed Load Balancing Algorithm (DLBA) has been developed for solving the issues of utility maximization in LTE models. The handover operations were processed when the users are negatively utilizing the utility sum.

The authors of [25] presented an optimal cell selection model for LB in heterogeneous network. By the work, the throughput rate has been increased by maximizing the data rate in the macro cells. Further, in [26], a fuzzy Q-learning based handover optimization model has been derived. And, the optimizations were done with addressing two issues, ping pongs and failures of radio links. For reducing the network congestion, in [27], the authors derived a fuzzy logic and reinforcement learning model. A different load balancing model has been derived for increasing the Quality of Service in LTE network. The model used multi-objective based optimization model to achieve the objective.

3  Research Background

In Long Term Evolution, the seamless communication is provided with respect to the corresponding base station and their user equipment. Because of the mobility nature of UE, it moves for one coverage cell to another, which may have maximal load by now. Therefore, the required service for the new UE has not been provided, because of overload. The aforementioned models presented in previous section discussed about various load balancing models in LTE. For processing efficient load balancing, optimal cell selection is very much important, which is processed here with Elite Opposition based Spider Monkey Optimization Algorithm. The algorithm has been implemented for enhancing the CBR with efficient handover probability.

In Spider Monkey Optimization Algorithm, the process works on the food seeking procedure (FSP) of spider monkeys with their Fission-Fusion Social Structure (FFSS). The main four phases of the algorithm are give as,

When the spider monkeys begin with food scrounging, group measures are carried out for food divisions.

The positions of local objects are updated

Group leaders are intended to update the best position to other locals for food search

The optimal best position is updated by the global leader

The larger groups are divided into number of smaller groups, in which the Local Leader Limit (LLL) and Global Leader Limit (GLL) are considered for processing optimal position determinations. Further, the population distribution of spider monkeys with random initialization in FSP is given as,

F(S,d)={1,r<p0,Else(1)

where, F(S,d) is the population distribution function, in which, ‘S’ denotes the spider monkey at the position ‘d’, ‘r’ represents the random number, ranges from [0, 1] and ‘p’ is the probability rate.

Further, fitness rate is computed for each solution and the ‘S’ with best fitness rate is elected as the local leader. Based on the following phases, the search space solution is processed.

3.1 Local_Leader (LL) Phase

Based on the local leader (LL) and local members, the new positions of spider monkey are determined. The new position of the spider monkey is computed as,

P(S+1,d)={F(S,d)+r1×(LL(m,d)−F(S,d))+r2×(F(N,d))−(F(S,d)),ifr1≥PRF(S,d)),Otherwise(2)

From the above equation, ‘r1’ and ‘r2’ are the random numbers in the range between [0, 1] and [−1, 1], respectively. And, the position of the ‘m'th LL in ‘d'th dimension is given as ‘LL(m,d)’. ‘PR’ represents perturbation rate in FSP.

3.2 Global Leader (GL) Phase

In this phase, the positions of all the objects are updated with respect to the local members and global leader. Here, the new position is computed as follows,

P(S+1,d)=F(S,d)+r1×(GL(d)−F(S,d))+r2×(F(N,d)−(F(S,d))(3)

where, GL(d) denotes the GL in ‘d'th position. This is processed with computing the probability rate with fitness rate (FR). It is given as,

PYS=FRSFRmax×0.9+0.1(4)

where, ‘FRS′ denotes the fitness rate of ‘S'th object and ‘FRmax’ denotes the maximal fitness rate.

3.3 GL Learning Phase

In this section, the position of GL is updated and the object with the Best Fitness Value (BFV) among the population is elected as GL. If the GL position is not updated, the number of best solution rate is incremented by 1.

3.4 LL Learning Phase

The member with BFV is elected as the local leader and updated. When the LL position is not updated, the number of global best solution is incremented by 1.

3.5 LL Decision Phase

If the LL number is greater than the local leader limit, then all object positions are updated and the new position of spider monkey is computed as,

P(S+1,d)=F(S,d)+r1×(GL(d)−F(S,d))+r2×(F(N,d)−(LL(S,d))(5)

3.6 GL Decision Phase

Here, the total population is divided into number of smaller groups, when the global member count is larger than the GL limit. When the GL position is not updated, the GL connects all combines together and frames a single group.

4  Working Procedure

In this section, the optimized model for Elite Opposition based Spider Monkey Optimization Framework for Efficient Load Balancing (SMO-ELB) implementations. Here, the macro cells and low power nodes (PNs) are defined as, ‘C1’ and ‘C2’. Let C=C1∪⁡C2 and n=|C| and the set of user equipments are represented as ‘E’. The notation that denotes load here as, ‘γi’ for each macro cell ‘i’ and the load is to measure the resource utilization rate of the cell. In Long Term Evolution, the unit is dependent on the average rate of resource blocks that are processed for data transmission, corresponding to frequency-time domain. And, the load vector is presented as, γ={γ1,γ2,γ3,…..,γn}T. Further, it is assumed that the cell-based offset optimization is employed to the low power node cells in the class C2 and the zero offset value is provided to the regions in C1. And, the value for candidate offset values are considered as ‘V’, which is considered as positive offset value.

The network assignment range ‘R’ is given as Riv, to fins that the cell ‘i∈C2’ and utilizes the offset rate v∈V and the allocation of user equipment is given as U(R), with the equation Ui,j(R)=1, where the ‘i'th cell belongs to ‘C’ and the candidate cell of UEj∈J. For each user equipment, cell selection rule is followed for allocations based on the receiving signal rate and offset value. Further, it is to be stated that load ‘γi’ is dependent on the load factor of remaining cells and the user equipments served by the macro cell ‘i’. The load balancing based optimization derivations for virtual cell allocation is given as follows.

MaxF(γU(R))=(∑i∈C⁡γiU(R))2n.∑i∈C⁡(γiU(R))2(6)

where, ‘γU(R)’ denotes the solid function for load factor for the Ui,j(R) and with the following conditions.

∑i∈C⁡Ui,j(R)=1,∀j∈J(6.1)

∑v∈V⁡Riv=1,∀i∈C2(6.2)

Riv∈{0,1},∀i∈C2,v∈V(6.3)

γiU(R)∈[0,1],∀i∈C(6.4)

Here, the objective function, given in (6.1) is the fairness index of Jain Theorem, which is in the range, [1n,1.0]. The model achieves the maximal range, when all the cells in the communication area are with equal loads. Henceforth, the model intends to attain balanced load among distributed cells.

4.1 Incorporation of Bounding Theory Based Load Derivations in LTE

In this section, load of each communication cell is derived using the bounding principles. The load computation for the considered offset range ‘R’ is computed here. Further, the load coupling factor is derived as,

γi=fiγ=∑jϵJ:Ui,j(R)⁡τj(1+1k∈C/{t}bikjγk+Ni,j)(7)

where, ‘τj’ defines the standardized traffic rate of a user equipment (UEi) based on the time-frequency allocations in one resource unit. And, ‘bikjγk’ is the factor that defines the ratio between the ‘k's interfering signal to the i's servicing cell, when the communication is active for UEi, the noise factor is given as ‘Ni,j’. The feasibility of the Eq. (7) is proved with the property, the solution is found if and only if the system in linear, which is given as, γ=M0γ+f(0) has a solution with Mii=0,i∈C, ‘M’ defines the matrix. When the system is non-linear, the solution is derived, if C−M0 has non-zero eigen values. If the solution for (7) is infeasible, it can be negotiated for further processing.

Based on the bounding concept, the higher and lower bound values are effectively derived for determining the definite rate of convergence called γ∗. Moreover, the upper bound and lower bound rates are computed as ‘γm^’ and ‘γm∨’, respectively, where ‘m’ denotes the number of iterations. When the system is feasible, the initiation point of lower bound value γ˘ is considered as γ0. After processing ‘m’ number of iterations, there is only one ‘i’ cell is presented, having the current load rata as, γ˘im is lesser than the load estimated for remaining cells as, γ˘im<fi(γ˘m), else γ˘m=γ∗. The increasing load rate is updated with the Gauss-Seidal function, which is calculated as,

γ˘im+1=fi(γ˘m)(8)

From the above equation, it is observed that, γ˘im+1≤γ∗, thereby, the series of lower bound rates are computed and for enhancing the system performance, load factor elements are updated in series or parallel manner as presented. Further, the error rate in lower bound rates are computed based on the following Euclidean norm, as,

e˘m=||γ∗−γ˘m||(9)

For higher bound computations, the load function is considered to be concave and has non-negative point. The values are computed based on solving the equivalent linear system and the series of higher bound rates are computed by employing ‘γ˘m’ values and the pseudo code for load estimation is presented below. The complete work flow of the proposed model is presented in Fig. 2.

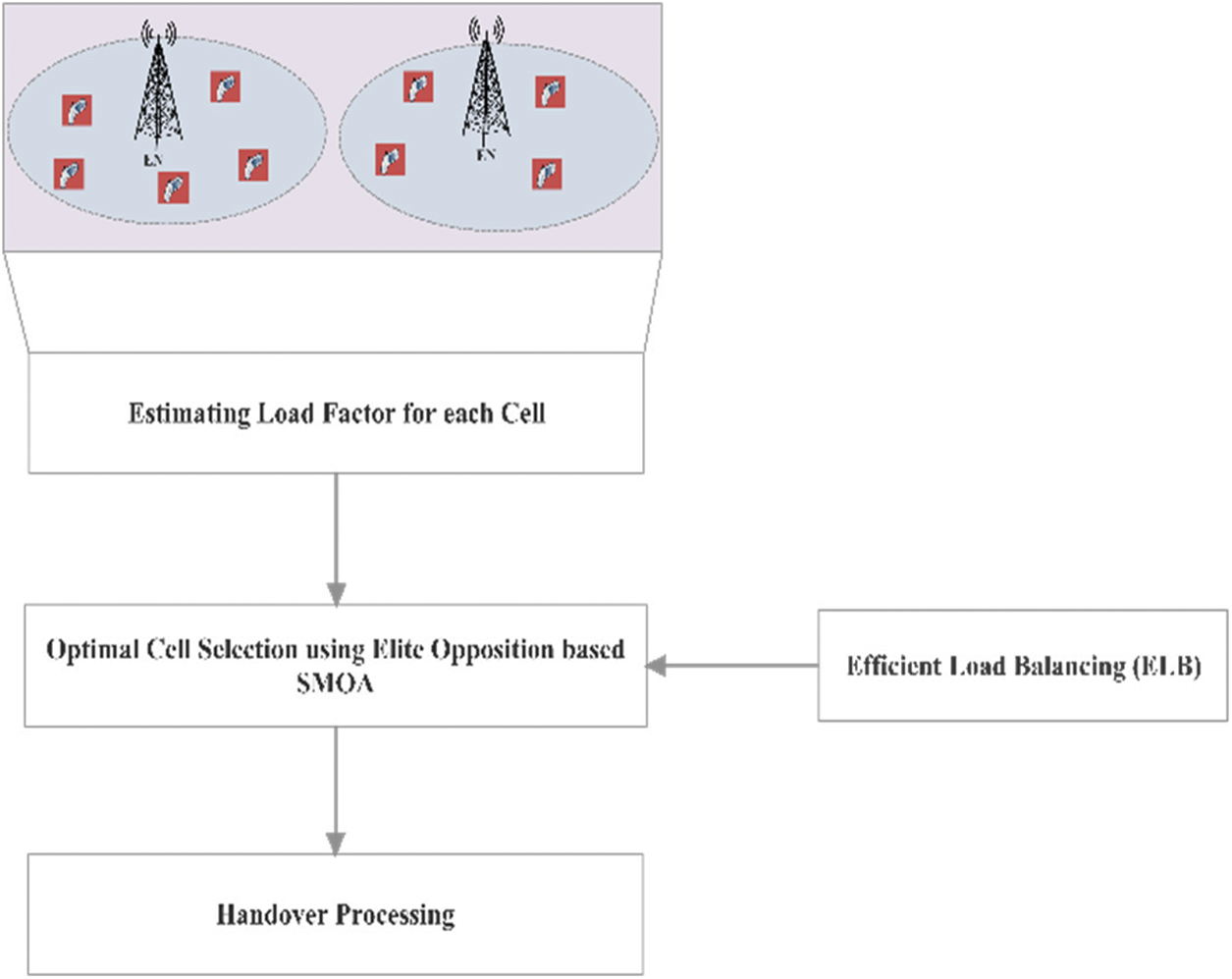
Figure 2: Work flow of SMO-ELB

4.2 Load Balancing with Elite Opposition Based SMO Model

Based on the above derivations, load is computed and compared with the threshold load rate called γth. When the estimated load is greater than the threshold rate, the ser_request from the UE is handovered to another EN of neighbouring cells. In the hand over process, the user equipment is connected with the cell having minimal load. Hence, the optimal cell selection based on load estimation is done here with Elite Opposition based Spider Monkey Optimization Algorithm. The process optimization is employed with enhanced Opposition based Learning (OBL) method. For each derived solution in search space, OBL based solution is framed for reaching the optimal solution in shortest distance. The phases towards selection optimal cell for handover are provided below.

4.2.1 Migration Behavior (Exploration)

The parameter initialization is processed in this phase. The LLL range is considered as [L/2,2×L], where ‘L’ represents the swarm size. And, GLL is taken as d×W, where ‘d’ is the dimensional space. Further, the perturbation rate is given as [0.1, 0.9]. The initial position of the spider monkey (Si) in dth dimension is initiated. And, the candidate solution is given as,

S(n)={S(1,d),S(2,d),….,S(n,d)}(10)

where, ‘S(n,d)’ denotes the nth cell availability in dth dimensional space.

4.2.2 Opposition Based SMO

For each ‘S(n,d)’ initialization, the opposition factor is derived with the OBL method, as in the following equation.

S′(n,d)=ln+hn−S(n,d)(11)

where, ‘ln’ is the lower limit and ‘hn’ is the higher limit of ‘S(n,d)’.

4.2.3 Deriving Fitness Function

The optimal cell for handover is selected by measuring the best solution in each search space. And, the fitness function is derived as,

FRs=(γi(t))(12)

The FF with minimal rate is considered to be the best solution, which is the optimal cell for handover from an overloaded one. When the optimal solution is not achieved, the process is iterated until to reach optimal solution.

4.2.4 Updating Phase

After deriving the fitness function for each solution, it is updated with Global Leader (GL) and Local Leader (LL) for further processing. The complete work process of Efficient Load balancing in selecting optimal cell is presented in Fig. 3.

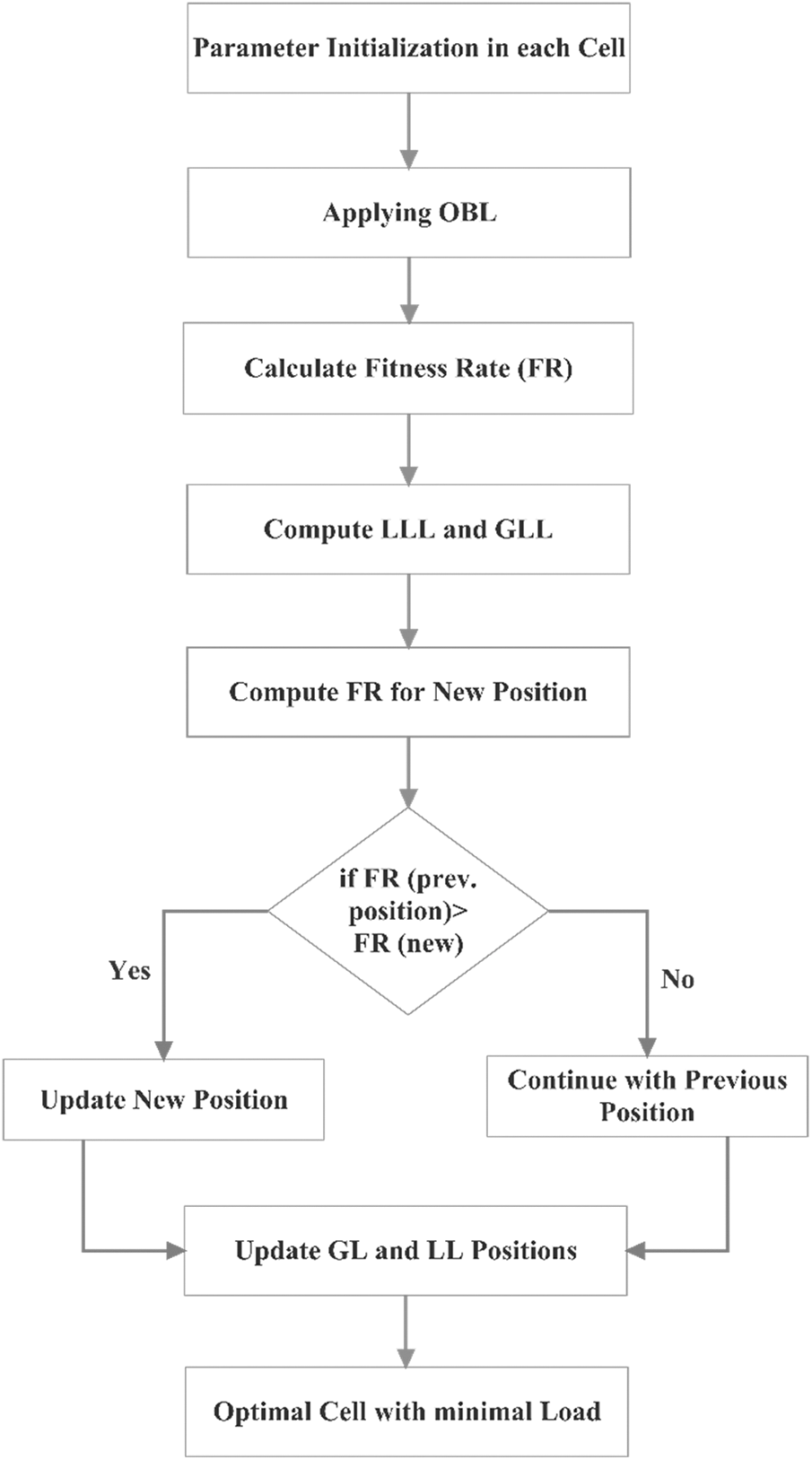
Figure 3: Functions in SMOA for optimal cell selection

5  Results and Discussions

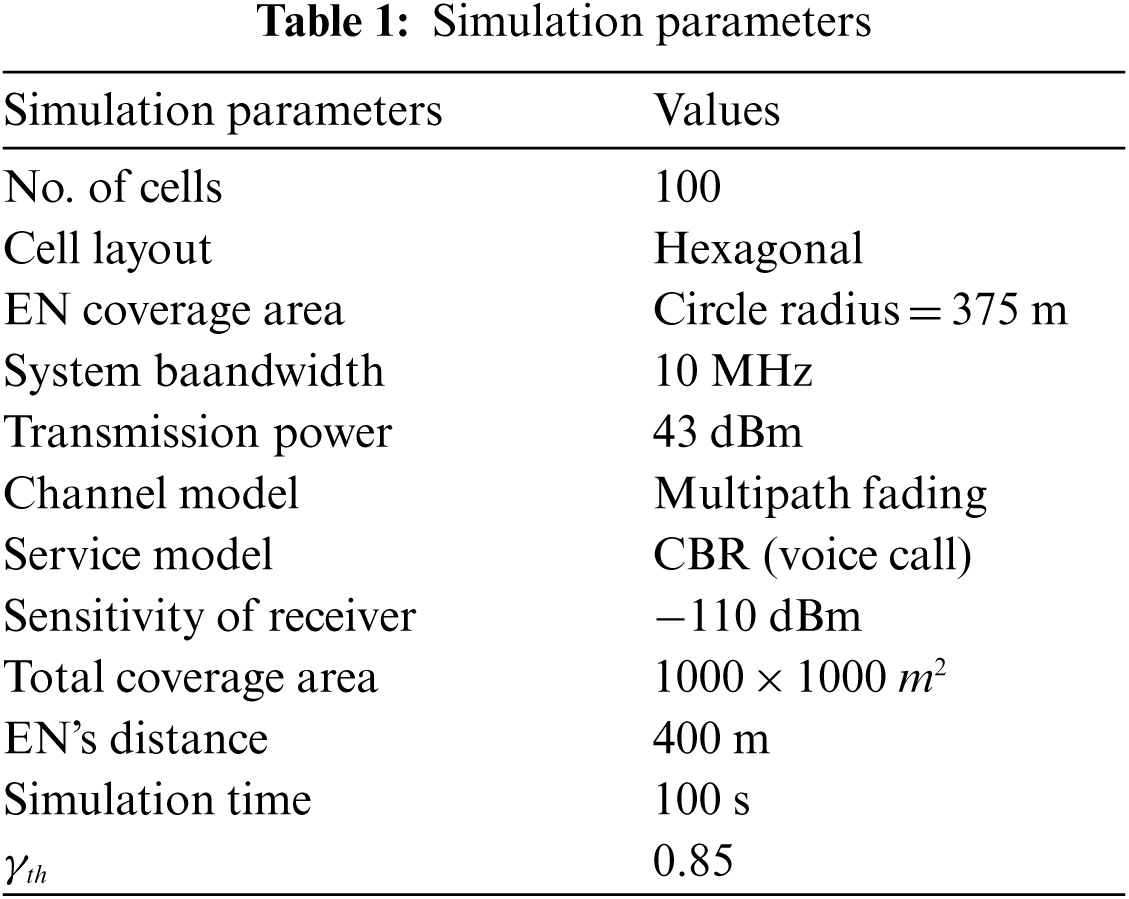
For evidencing the efficiency of the proposed model, implementation is carried out with Network Simulator (NS2) in the area 1000 m × 1000 m. Moreover, it is assumed that there are 100 number of cells, which are hexagonal in shape. And, the area of coverage for each EN is considered to be 375 meters and distance between two subsequent ENs is taken as 400 m. The threshold load rate γth is taken as 0.85, when the cell crosses its threshold, handover is processed. Further, the evaluations are carried out with two factors called number of varying cells and simulation time. The performance metrics taken here for analysis are, delay, Packet Delivery Rate (PDR), Call Dropping Rate (CDR), Call Blocking Rate (CBR) and Handover Probability. Further, the obtained results are compared with the existing models such as, Load Vector Minimization based Load Balancing Model (LVMLB) [23] and Distributed Load Balancing Algorithm (DLBA) [24]. The significant simulation parameters that are considered for implementing SMO-ELB in LTE communication are presented in Tab. 1.

5.1 Evaluation Factors and Comparisons

5.1.1 Packet Delivery Ratio

Another important factor for evaluating the network performance, Packet Delivery Ratio (PDR), which is calculated as the ratio of the amount of successful reception of data packets to the total amount transmitted, presented in (13).

PDR=AmountofPacketsReceivedAmountofPacketsTransmitted(13)

The corresponding results of PDR are provided in Fig. 4. It is observed from the figure that the proposed work attained 66.7%, which is greater than the existing models. The proposed work uses SMOA for optimal cell selection, thereby, the PDR is effectively improved.

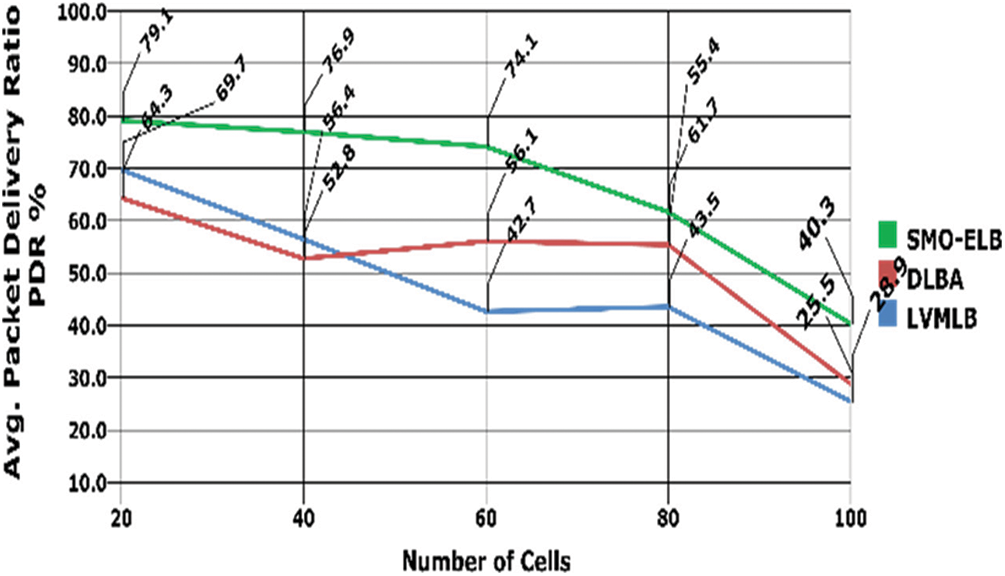
Figure 4: Packet delivery rate with no. of cells

5.1.2 Call Blocking Ratio

Call Blocking Ratio (CBR) is defined as the rate of number of blocked calls among the number of received calls. The calculation is presented as,

CBR=No.ofblockedcellsNo.ofreceivedcells(14)

Here, the CBR is evaluated with varying number of cells and simulation time and the comparison charts are presented in Figs. 5 and 6, respectively. In both cases, it is observed that the proposed model achieves minimal CBR than LVMLB and DLBA. In average, the model achieved 0.06% of CBR, with respect to number of cells and 0.27% of CBR with varying time, respectively.

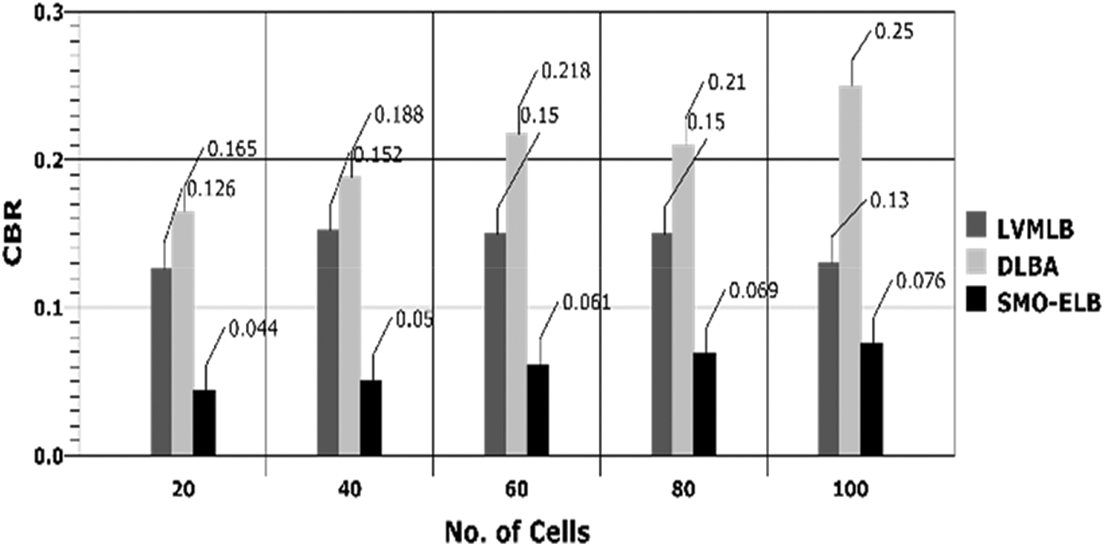
Figure 5: CBR vs. no. of cells

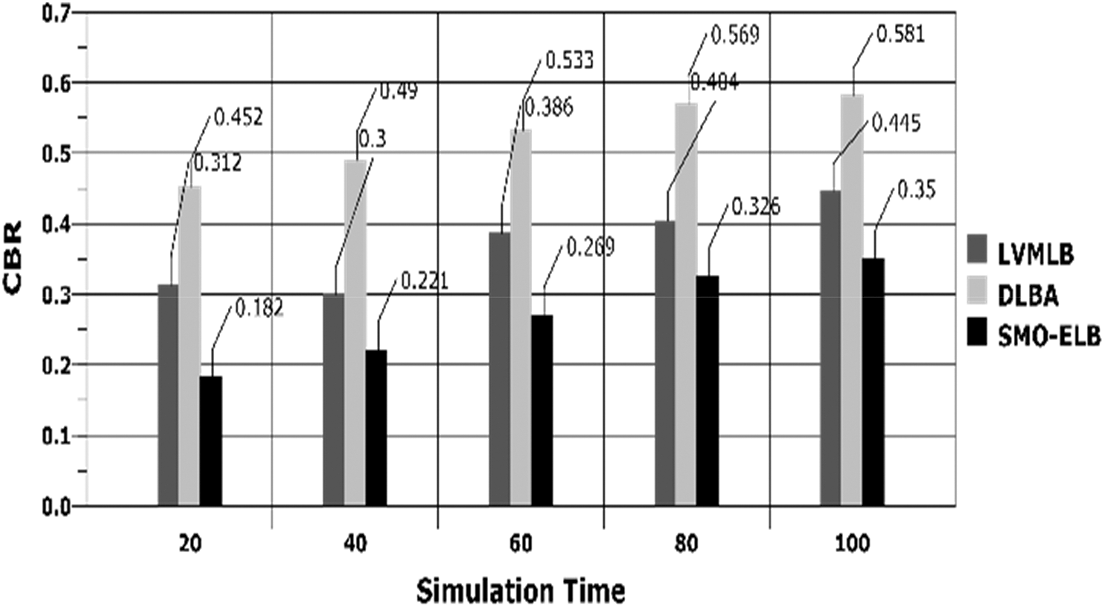
Figure 6: CBR vs. simulation time

5.1.3 Call Dropping Ratio

Call Dropping Ratio is defined as the rate of number of dropped calls to the number of completed calls. The equation is given as,

CDR=NumberofDroppedCallsNumberofCompletedCalls(15)

The corresponding results based on varying cells and time is portrayed in Figs. 7 and 8. By the efficient incorporation of SMOA in optimal cell selection with accurate load estimation, the proposed model achieves minimal rate of CBR and CDR than the compared works.

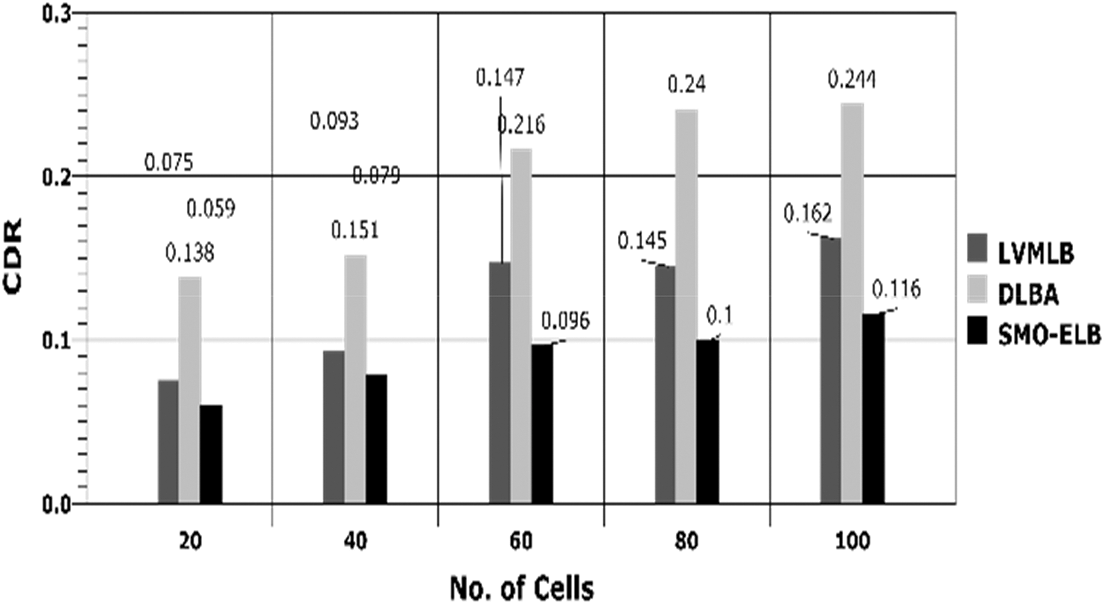
Figure 7: CDR vs. number of cells

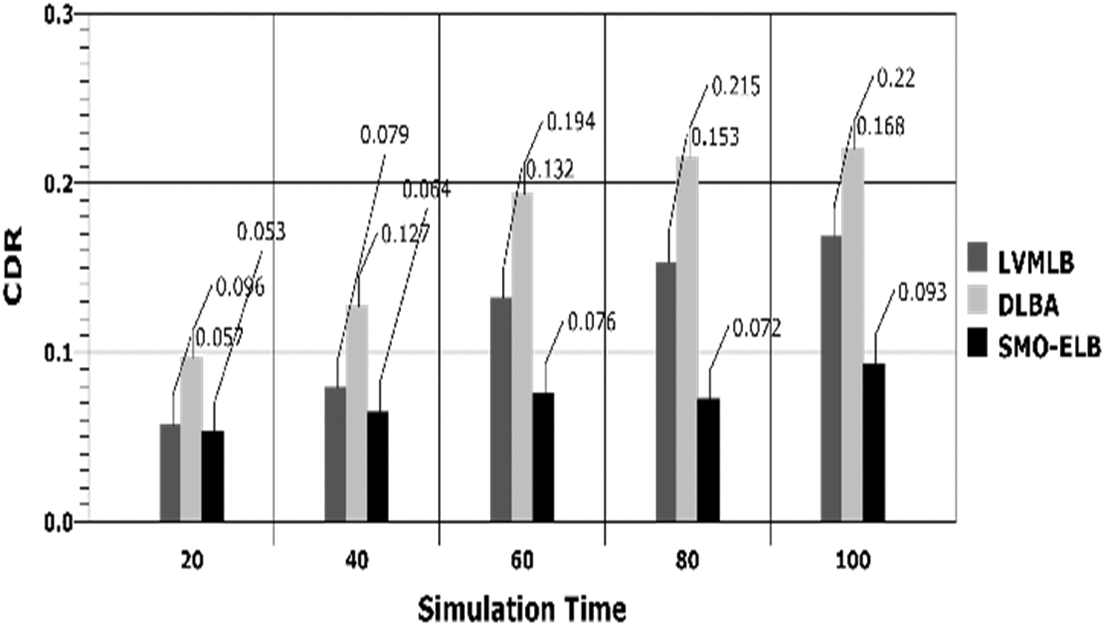
Figure 8: CDR vs. simulation time

When the load of a cell is found to be greater than the threshold load rate, handover takes place to provide seamless communication. Hence, the handover probability is higher in the proposed model than other compared works and the evidence is provided in Fig. 9.

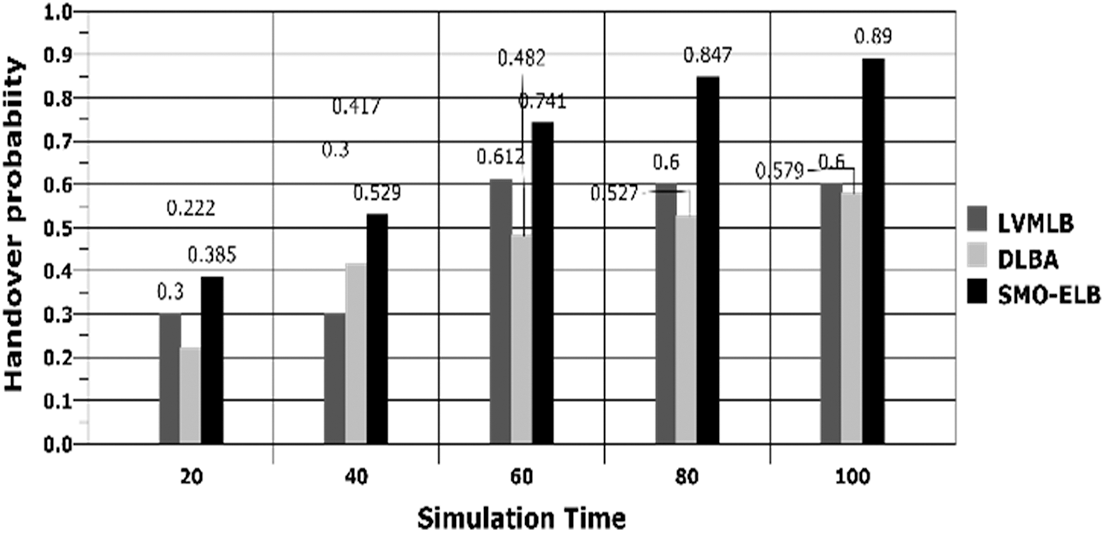
Figure 9: Handover probability vs. simulation time

6  Conclusion

In this paper, a novel method called Elite Opposition based Spider Monkey Optimization Framework for Efficient Load Balancing (SMO-ELB). Moreover, load estimations are processed with bounding theorem, which accurately determines the load factor for each cell in the defined network. Based on the estimated loads, the SMO algorithm is processed for optimal cell selection with minimal load. By effective determination of load derivations, the UE is allotted to the cell with minimal load, provides effective communication with minimal CBR and CDR. The results show that the SMO-ELB model provides better results in Packet Delivery Ratio and handover probability with minimal delay.

In future, the work can be enhanced by deriving efficient model for handover, concerning about power settings. Another direct for extending this work is to frame models for scheduling services in resource allocation.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  J. M. Meredith, “3gpp technical specification group radio access network-study on downlink multiuser superposition transmission (must) for lte (release 13),” Online Document, 3GPP, Technical Report, 2015. [Google Scholar]

 2.  M. Faulkner, “Long term evolution (LTEA technical overview,” Motorola, 2010. [Google Scholar]

 3.  D. Astely, E. Dahlman, A. Furuskar, Y. Jading, M. Lindstrom et al., “LTE: The evolution of mobile broadband,” IEEE Communications Magazine, vol. 47, no. 4, pp. 44–51, 2009. [Google Scholar]

 4.  M. Gidlund and J. C. Laneri, “Scheduling algorithms for 3gpp long-term evolution systems: From a quality of service perspective,” in 2008 IEEE 10th Int. Symp. on Spread Spectrum Techniques and Applications, Bologna, Italy, pp. 118–123, 2008. [Google Scholar]

 5.  R. Basukala, H. A. M. Ramli and K. Sandrasegaran, “Performance analysis of EXP/PF and M-LWDF in downlink 3GPP LTE system,” in 2009 First Asian Himalayas Int. Conf. on Internet, Kathmundu, Nepal, pp. 1–5, 2009. [Google Scholar]

 6.  Y. Wang, G. Li, T. Wu and F. Gong, “Adaptive proportional fair scheduling in multihop ofdma systems,” in 2010 IEEE 71st Vehicular Technology Conf., Taipei, Taiwan, pp. 1–5, 2010. [Google Scholar]

 7.  K. Hiltunen, “Comparison of different network densification alternatives from the lte downlink performance point of view,” in 2011 IEEE Vehicular Technology Conf. (VTC Fall), San Francisco, CA, USA, pp. 1–5, 2011. [Google Scholar]

 8.  I. Siomina and D. Yuan, “Optimization of pilot power for load balancing in WCDMA networks,” in IEEE Global Telecommunications Conf., 2004. GLOBECOM ‘4, Dallas, TX, USA, vol. 6, pp. 3872–3876, 2004. [Google Scholar]

 9.  K. Valkealahti, A. Hoglund, J. Parkkinen and A. Hamalainen, “WCDMA common pilot power control for load and coverage balancing,” in the 13th IEEE Int. Symp. on Personal, Indoor and Mobile Radio Communications, Pavilhao Altantico, Lisboa, Portugal, pp. 1412–1416, 2002. [Google Scholar]

10. H. Zhu, T. Buot, R. Nagaike and S. Harmen, “Load balancing in WCDMA systems by adjusting pilot power,” in the 5th Int. Symp. on Wireless Personal Multimedia Communications, Honolulu, HI, USA, vol. 3, pp. 936–940, 2002. [Google Scholar]

11. 3GPP TR 36.902, “Self-configuring and self-optimizing network (SON) use cases and solutions,” Technical report (TRV9.2.0, 2010. [Google Scholar]

12. A. Lobinger, S. Stefanski, T. Jansen and I. Balan, “Load balancing in downlink lte self-optimizing networks,” in 2010 IEEE 71st Vehicular Technology Conf., Taipei, Taiwan, pp. 1–5, 2010. [Google Scholar]

13. R. Kwan, R. Arnott, R. Paterson, R. Trivisonno and M. Kubota, “On mobility load balancing for lte systems,” in 2010 IEEE 72nd Vehicular Technology Conf.-Fall, Ottawa, ON, Canada, pp. 1–5, 2010. [Google Scholar]

14. Z. Liu, P. Hong, K. Xue and M. Peng, “Conflict avoidance between mobility robustness optimization and mobility load balancing,” in 2010 IEEE Global Telecommunications Conf. GLOBECOM 2010, Miami, FL, USA, pp. 1–5, 2010. [Google Scholar]

15. J. M. R. Avilés, S. L. Ramírez, M. Toril and F. Ruiz, “Traffic steering by self-tuning controllers in enterprise LTE femtocells,” EURASIP Journal on Wireless Communications and Networking, vol. 2012, no. 1, pp. 337, 2012. [Google Scholar]

16. J. Steuer and K. Jobmann, “The use of mobile positioning supported traffic density measurements to assist load balancing methods based on adaptive cell sizing,” in the 13th IEEE Int. Symp. on Personal, Indoor and Mobile Radio Communications, Lisbon, Portugal, vol. 1, pp. 339–343, 2002. [Google Scholar]

17. N. A. Amirrudin, S. H. S. Ariffin, N. N. N. A. Malik and N. E. Ghazali, “User's mobility history-based mobility prediction in LTE femtocells network,” in 2013 IEEE Int. RF and Microwave Conf. (RFM), Penang, Malaysia, pp. 105–110, 2013. [Google Scholar]

18. A. Freedman, D. Dilmon, A. Assayag and E. Deutscher, “Prediction based RSS fingerprinting for positioning and optimization in cellular networks,” in 2012 IEEE 27th Convention of Electrical and Electronics Engineers in Israel, Eilat, Israel, pp. 1–4, 2012. [Google Scholar]

19. F. Guidolin, I. Pappalardo, A. Zanella and M. Zorzi, “A Markov-based framework for handover optimization in hetnets,” in 2014 13th Annual Mediterranean Ad Hoc Networking Workshop (MED-HOC-NET), Slovenia, pp. 134–139, 2014. [Google Scholar]

20. H. Li, S. Habibi and G. Ascheid, “Handover prediction for long-term window scheduling based on SINR maps,” in 2013 IEEE 24th Annual Int. Symp. on Personal, Indoor, and Mobile Radio Communications (PIMRC), London, UK, pp. 917–921, 2013. [Google Scholar]

21. D. Shin and S. Choi, “Dynamic power control for balanced data traffic with coverage in femtocell networks,” in 2012 8th Int. Wireless Communications and Mobile Computing Conf. (IWCMC), Limassol, Cyprus, pp. 648–653, 2012. [Google Scholar]

22. X. Yu, H. Wang and J. Wu, “A method of fingerprint indoor localization based on received signal strength difference by using compressive sensing,” J Wireless Com Network, vol. 2020, no. 1, p. 72, 2020. [Google Scholar]

23. F. Zhou, L. Feng, P. Yu and W. Li, “A load balancing method in downlink LTE network based on load vector minimization,” in 2015 IFIP/IEEE Int. Symp. on Integrated Network Management (IM), Ottawa, ON, Canada, pp. 525–530, 2015. [Google Scholar]

24. D. C. Hernandez and R. Paranjape, “Dynamic analysis of load balancing algorithms in LTE/LTE-a HETNETS,” Wireless Personal Communications, vol. 96, no. 3, pp. 3297–3315, 2017. [Google Scholar]

25. Y. Aghazadeh, H. Kalbkhani, M. Shayesteh and V. Solouk, “Cell selection for load balancing in heterogeneous networks,” Wireless Personal Communications, vol. 101, no. 1, pp. 305–323, 2018. [Google Scholar]

26. R. D. Hegazy, O. A. Nasr and H. A. Kamal, “Optimization of user behavior based handover using fuzzy Q-learning for LTE networks,” Wireless Networks, vol. 24, no. 2, pp. 481–495, 2018. [Google Scholar]

27. P. Muñoz, R. Barco and I. de la Bandera, “Load balancing and handover joint optimization in LTE networks using fuzzy logic and reinforcement learning,” Computer Networks, vol. 76, pp. 112–125, 2015. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.