DOI:10.32604/cmc.2022.024232

| Computers, Materials & Continua DOI:10.32604/cmc.2022.024232 |  |
| Article |
Quantum Particle Swarm Optimization Based Convolutional Neural Network for Handwritten Script Recognition
1School of Computer Science and Engineering, SMVDU, J&K, India
2College of Computing and Informatics, Saudi Electronic University, Riyadh, Saudi Arabia
*Corresponding Author: Muhammad Tahir. Email: m.tahir@seu.edu.sa
Received: 10 October 2021; Accepted: 29 November 2021
Abstract: Even though several advances have been made in recent years, handwritten script recognition is still a challenging task in the pattern recognition domain. This field has gained much interest lately due to its diverse application potentials. Nowadays, different methods are available for automatic script recognition. Among most of the reported script recognition techniques, deep neural networks have achieved impressive results and outperformed the classical machine learning algorithms. However, the process of designing such networks right from scratch intuitively appears to incur a significant amount of trial and error, which renders them unfeasible. This approach often requires manual intervention with domain expertise which consumes substantial time and computational resources. To alleviate this shortcoming, this paper proposes a new neural architecture search approach based on meta-heuristic quantum particle swarm optimization (QPSO), which is capable of automatically evolving the meaningful convolutional neural network (CNN) topologies. The computational experiments have been conducted on eight different datasets belonging to three popular Indic scripts, namely Bangla, Devanagari, and Dogri, consisting of handwritten characters and digits. Empirically, the results imply that the proposed QPSO-CNN algorithm outperforms the classical and state-of-the-art methods with faster prediction and higher accuracy.
Keywords: Neuro-evolution; quantum particle swarm optimization; deep learning; convolutional neural networks; handwriting recognition
With the rapid development and exponential usage of imaging technology, digital cameras, and other intelligent devices, the need for automatic character recognition in document images has drawn the attention of many researchers in this domain. Extensive comprehensive research work is available on the printed character recognition, and the recognition accuracy of printed characters has been potentially considered as a solved problem. However, the recognition of handwritten characters is still a challenging task in the field of pattern recognition. The challenging part of handwritten character recognition is the diversity in individual writing styles, patterns, size, and thickness of characters [1]. Even the handwriting style of the same person may vary at different times. The already difficult task of handwritten character recognition eventually gets more complicated in the case of stylistically distinct Indic scripts. Over the past decades, a large number of research studies have been published on the recognition of handwritten characters in scripts like Arabic, Chinese, Japanese, and Latin. Though, the research on handwritten Indic scripts is still in its infancy due to the presence of several challenging issues [2]. Most Indic script characters have an unconstrained language domain, complex structure, large character sets, and similar shaped characters.
Deep neural networks (DNN) have demonstrated their remarkable performance in recent years to solve pattern recognition problems [3], for instance, handwritten character recognition. Specifically, deep convolutional neural networks (CNN) have witnessed tremendous achievements and proven to be particularly powerful in this domain [4]. Nonetheless, it remains a cumbersome, error-prone, and time-consuming process to design a meaningful CNN topology. Most successful CNNs architectures, such as DenseNet [5], ResNet [6], Inception [7], AlexNet [8], etc. were manually handcrafted. However, designing a successful CNN topology right from scratch is a complex and meticulous process that requires specialists with a lot of problem domain knowledge. As a result, to deal with this unwieldy process of designing CNN topologies, one can get the idea from nature to automatically evolve meaningful CNN representations. This approach belongs to a field known as Neuro-evolution [9], which uses evolutionary computation methods to automatically search and design the CNN topologies without any human expertise.
The rest of this article is organized as follows. Section 2 briefly describes the background of CNN, Binary Particle Swarm Optimization (BPSO), Quantum Computing (QC) and summarizes the related work. Section 3 delineates the proposed algorithm. Section 4 outlines the experimental design, which includes a brief description of the datasets, algorithm parameters, and implementation details. Section 5 presents the computational results and compares the performance of the proposed algorithm with the traditional state-of-the-art techniques. Finally, Section 6 concludes the article.
2.1 Convolutional Neural Networks
CNN was firstly introduced by LeCun et al. [10] in 1998 and used in many applications [11–14]. In CNN, the feature learning unit replaces the traditional feature engineering stage. In fact, CNNs are designed to handle raw data, i.e., data with very little or no pre-processing. In CNN, layers are arranged consecutively in such a practice that the output obtained from one layer will be supplied as input to the next layer. Conventionally, the CNN classifier generally contains three kinds of layers, viz. the convolution layer, the pooling layer, and the fully-connected layer.
2.2 Binary Particle Swarm Optimization
The BPSO suggested by Kennedy et al. [15] in 1997 allows the conventional Particle Swarm Optimization (PSO) to work in binary spaces. The BPSO has potentially the same structure as the real-valued PSO except the position vector of each particle has a binary representation. Furthermore, the velocity of every
In BPSO, the position vector is determined by selecting a number
If
The concept of QC is evolved from Quantum Physics. A quantum bit (Q-bit) is the smallest amount of information in QC [16]. Unlike conventional computing in which a bit is observed either in state 1, or state 0, a Q-bit may reside in state 1, state 0, or superposition of 0 & 1. With the ability to be in more than two states, QC provides a faster and better local exploitation and global exploration of the search space. So, the algorithms designed using QC are more efficient and powerful.
A Q-bit is denoted with a pair of complex numbers
where
In literature, neuro-evolution during its early inception has been applied to encode connection weights and topologies of artificial neural networks (ANN). Stanley et al. [17] initially proposed Neuro-Evolution Augmenting Topologies (NEAT) scheme for learning weights and evolving efficient ANN topologies using variable-length chromosome. Later, Stanley et al. [18] introduced hyperNEAT to overcome the deficiencies of NEAT. Along with the indirect encoding strategy of NEAT, the hyperNEAT approach was also build using connective compositional pattern producing networks (CPPN) [19]. Fernando et al. [20] proposed differentiable CPPN (DPPN) using microbial genetic algorithm (GA) in 2016, capable of searching for feasible CNN representation. A Large-scale evolution of images classifier technique developed by Google in 2017, to evolve CNN topologies achieving state-of-the-art results over several benchmark datasets [21]. In recent times, neuro-evolution based techniques, influenced by the fundamental theory of PSO, have also been used as solution mechanism for regression [22,23] and image classification tasks [24]. Among these techniques, Wang et al. [25] designed an PSO based neurocomputing approach with variable-length encoding strategy, to evolve CNN topologies for handwritten recognition problems. Sun et al. [26] designed an algorithm using PSO to create flexible convolutional autoencoders for the classification of images.
In this section, we describe the proposed quantum particle swarm optimization based convolutional neural network (QPSO-CNN) technique in detail. To be specific, the framework of the proposed QPSO-CNN is elucidated in Section 3.1.
The proposed QPSO-CNN algorithm applies quantum PSO, to automatically evolve meaningful CNN architectures. Algorithm 1 manifests the overall framework of the proposed technique. Firstly, the algorithm is initiated by randomly initializing the position corresponding to each particle and quantum bit (Q-bit) individuals. After this, the evolution of particles will start to take effect before the termination conditions, for instance, the given number of iterations, are met. Lastly, the global best solution is picked up and decoded into the corresponding CNN architecture for the final deep training in order to perform the jobs at hand. During the evolution, the evaluation of the particles is performed, and the corresponding recognition accuracy is employed as a fitness measure of individual particles. Consequently, the

In the proposed QPSO-CNN, a binary encoding strategy is used to encode the potential CNN architectures into particle vectors. Each particle is composed of a different number of convolutional, pooling, and fully-connected layers. Therefore, these layers should be encoded in a single particle vector for the evolution process to proceed further. Each particle vector with D dimensions accommodates the details about CNN layers. To be more specific, in the binary encoding scheme, the particle vector consists of x number of fixed-length binary strings where each string represents the configuration of a single CNN layer, i.e., the layer parameters. The parameters corresponding to the convolutional layer are Kernel size, stride size, and number of feature maps. Secondly, parameters corresponding to the pooling layer are pooling window size, stride size and pooling type (maximal pooling or average pooling). Finally, parameters corresponding to the fully-connected layer are the number of neurons.
Depending on the chosen benchmark datasets size and conventions used in the traditional deep learning community, the range for all the parameters is elucidated in Tab. 1. On the basis of aforementioned range, the maximum number of bits required for binary encoding can be found in Tab. 1. The maximum number of bits describes the length of binary strings. Furthermore, taking the non-zero parameter into account, there is a need to add one in the decimal value convinced out of the binary string. For instance, as depicted in Tab. 1, for the convolutional layer, the Kernel size of 4, the number of feature maps of 64, and stride size of 2 are transformed into corresponding binary strings with values 011, 00111111, and 1. Finally, after transforming the parameters’ values into individual binary strings, these binary strings are concatenated, as illustrated in the summary row corresponding to the convolutional layer. Consequently, the sample binary strings for other layers are obtained by following the same series of steps, as depicted in Tab. 1.
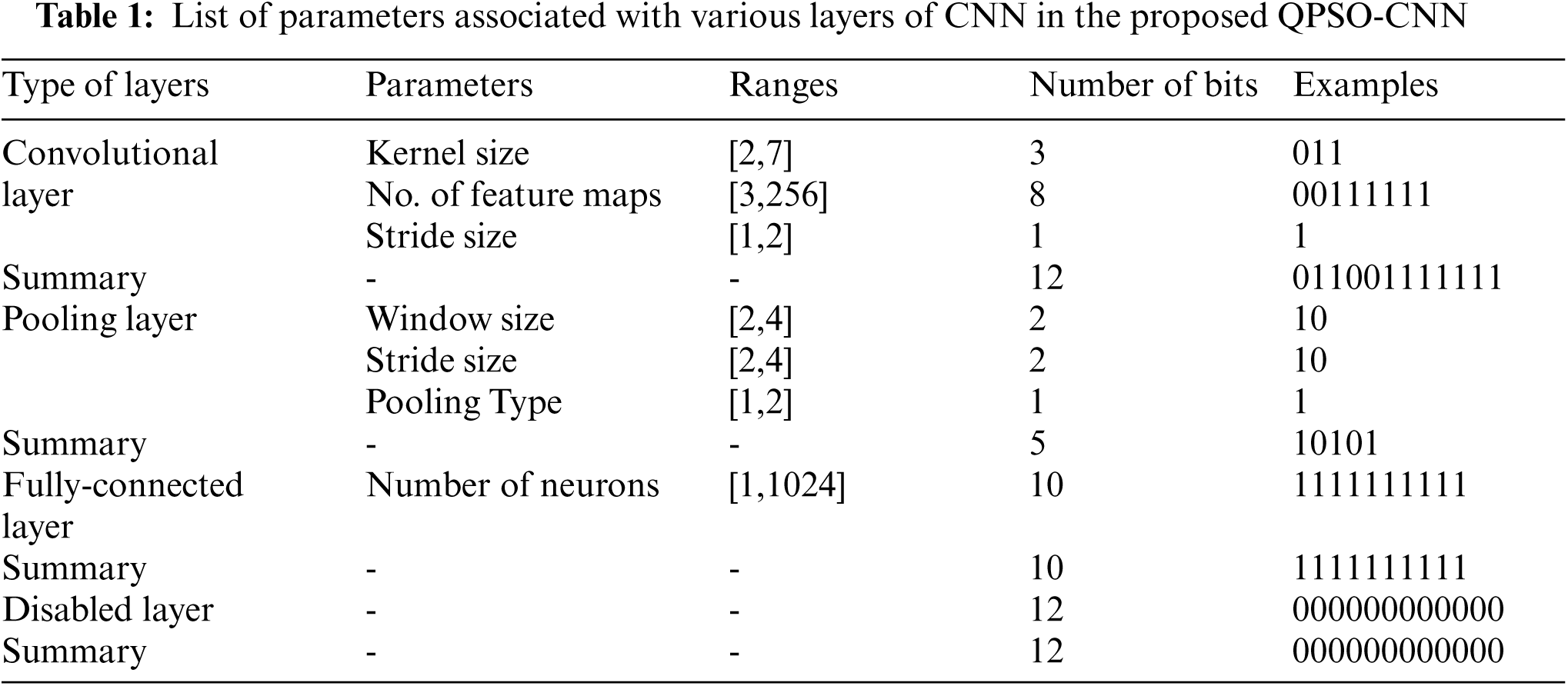
Since the maximum number of bits used to encode a single layer is 12; therefore, for each layer, the binary string is filled with zeros till the length approaches 12 bits, as illustrated in Tab. 2. During initialization, the length of the particles is defined in advance; therefore, to obtain variable-length particles, the disabled layer is employed in the encoded particle. The disabled layer is similar to the other three kinds of layers, except it has no parameters.
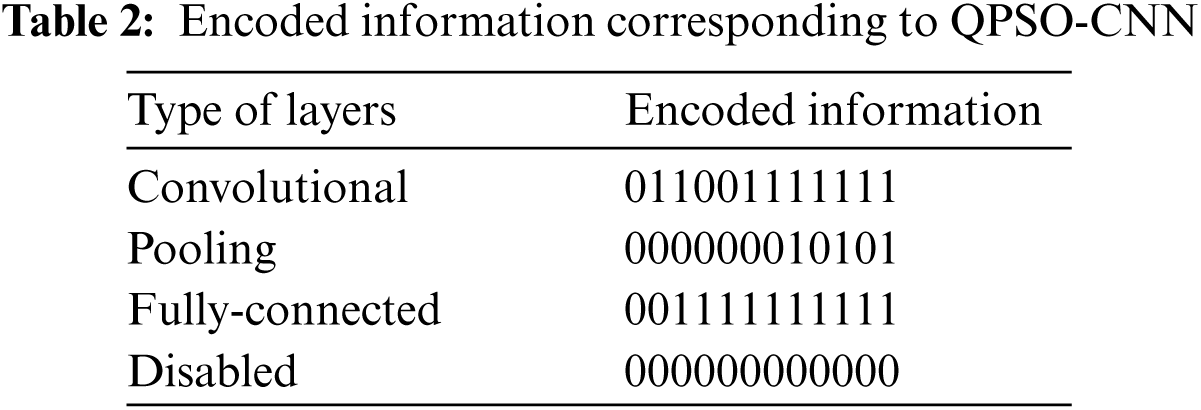
The initialization of the swarm begins with creating individual particles based on the precedent encoding strategy until the pre-determined population size is reached. This process will generate M particles having arbitrary CNN architectures. In the corresponding scheme, each particle will contain a random number of layers. According to the deep learning convention, the first element of each particle is always a convolutional layer. However, the remaining elements of each particle can be supplied by any number of convolutional layers, pooling layers, and disabled layers until the first fully-connected layer is added. Thus, the algorithm should ensure that once a fully-connected appears, then every other succeeding layer ought to be a fully-connected layer or disabled layer. Finally, the last element corresponding to every particle is always a fully-connected layer. Furthermore, during the initialization phase, the values of α and β corresponding to each Q-bit individual are specified to be
Once the position of the particles is obtained, the fitness evaluation is performed by training the particles representing full-fledged CNN architectures on the training dataset (
The proposed QPSO-CNN algorithm uses a rotation operator to update the Q-bit individual. The rotation operator employs a rotation angle (
where
where
Finally, the rotation operator is applied to update the
The condition
3.6 Update Position of Particles
The position vector of every
where r stands for uniformly distributed pseudo-random number from [0, 1].
After the evolution of QPSO-CNN is completed, the global best solution obtained by picking the best particle out of all the particles in the swarm is selected for the final deep training. The deep training process is similar to the fitness evaluation process discussed in Section 3.4, apart from the fact that a substantially huge number of epochs are employed for training the optimal CNN architecture, for example, 100 or 200.
4.1 Datasets Used in Present Work
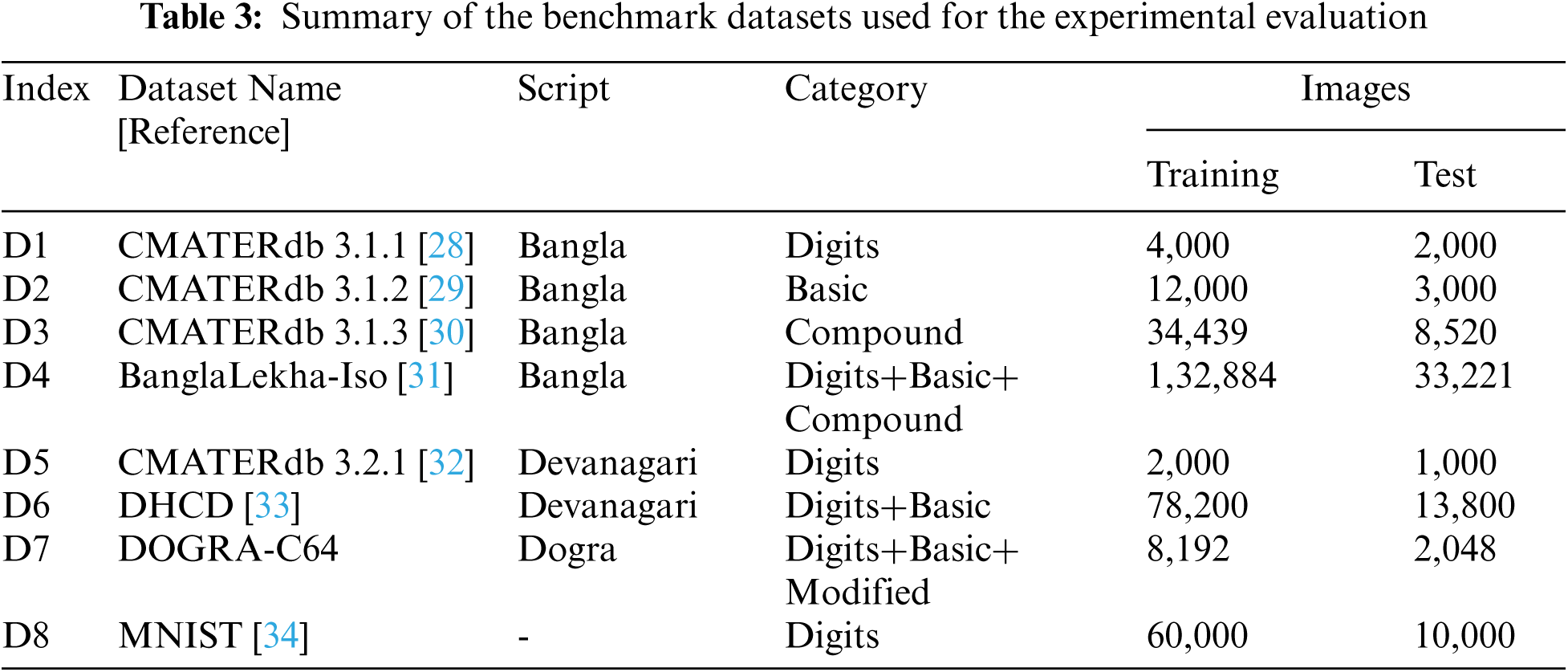
The designed QPSO-CNN algorithm has been evaluated on benchmark handwritten character datasets belonging to three popular Indic scripts (Devanagari, Bangla, and Dogri). These scripts are genealogically different from each other and highly used by the majority of people in India [27]. Some typical samples corresponding to each chosen dataset are depicted in Fig. 1 for reference, and a summary enclosing the dataset name, category, script type, training set, and test set sizes are elucidated in Tab. 3.

Figure 1: Sample images from the chosen benchmark datasets (a) Examples from the CMATERdb 3.1.1 Dataset. (b) Examples from the CMATERdb 3.1.2 Dataset. (c) Examples from the CMATERdb 3.1.3 Dataset. (d) Examples from the BanglaLekha-Iso Dataset. (e) Examples from the CMATERdb 3.2.1 Dataset. (f) Examples from the DHCD Dataset. (g) Examples from the DOGRA C-64 Dataset. (h) Examples from the MNIST Dataset
4.2 Pre-Processing of Datasets
The original handwritten character images in the datasets are not normalized to a uniform size and have numerous pixel resolutions. Therefore, for training and testing, some pre-processing steps are applied to the datasets. The grayscale isolated handwritten character images are first transformed into subsequent binary format. Then the handwritten character images for datasets (D2, D3, D4, and D7) are normalized to a size of 32 × 32 pixels with the aspect ratios preserved.
In the proposed QPSO-CNN algorithm, the parameters are primarily classified into three groups, i.e., parameters related to QPSO, CNN initialization, and CNN training. The parameters used in the present investigation have been compiled in Tab. 4. The parameters associated with the first group, are set according to the conventions applied in the community of evolutionary algorithms. The first group includes seven parameters, namely, the swarm size (
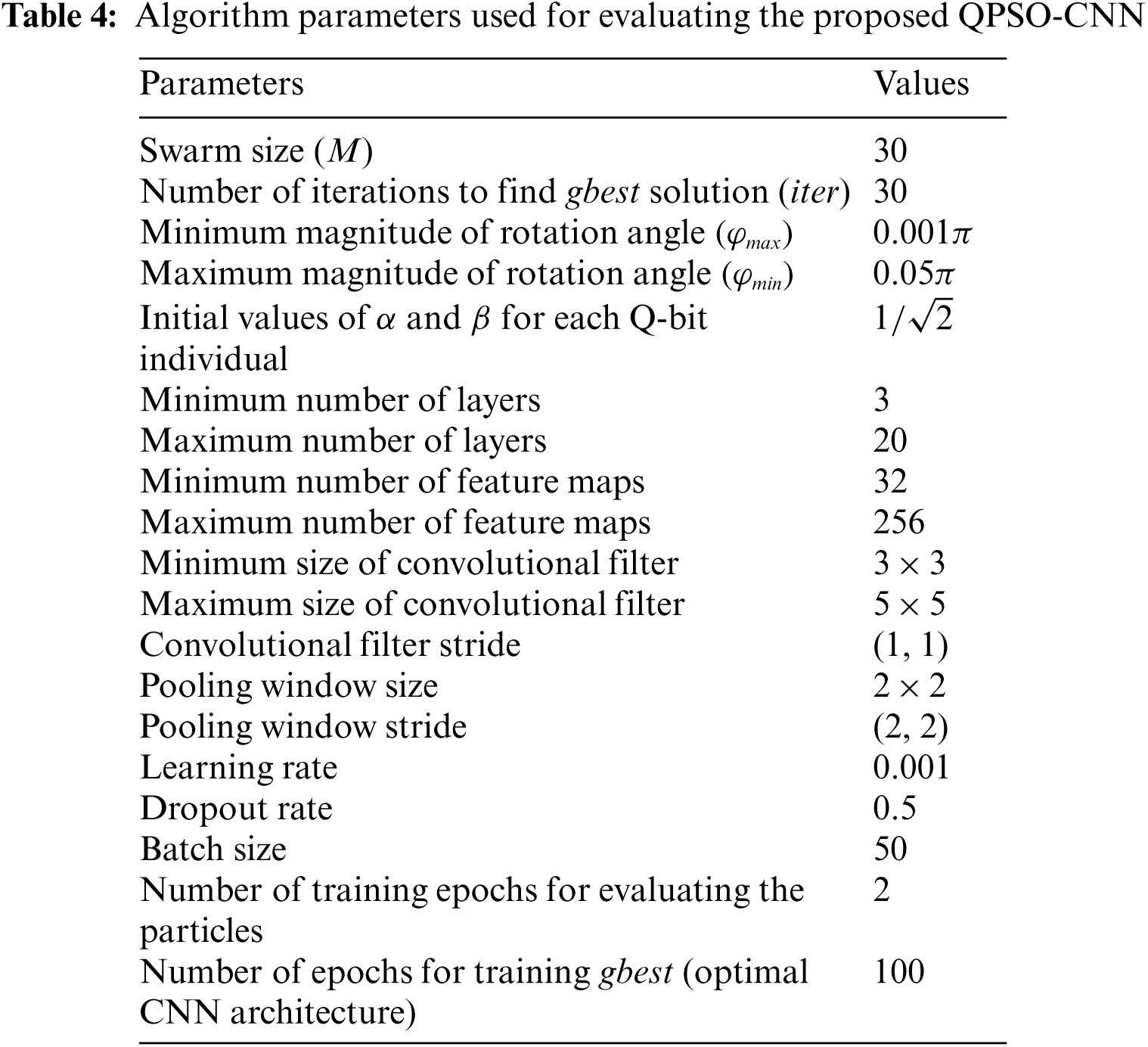
The parameters associated with the second group regulate the diversity of initial particles’ architectures. The second group includes seven parameters, namely, the minimum number of feature maps, the maximum number of feature maps, the minimum size of a convolutional filter, the maximum size of a convolutional filter, the convolutional filter stride size, the pooling window size, and the pooling window stride size. The improper setting of parameters in the convolutional and pooling layers would make the CNN architecture incompetent and result in unaffordable computational costs. Therefore, according to the deep learning conventions, during the exploration of each particle, the minimum and the maximum number of feature maps is set as [32,256]. On the basis of state-of-the-art CNNs conventions, squared convolutional filters are used with a filter size ranging from 3*3 to 5*5. In the convolutional layer, the (width, height) of stride is taken as (1, 1). Analogously, the pooling layer uses squared kernels with a pooling window of size 2*2. The (width, height) of stride in the pooling layer is taken to be (2, 2).
Finally, the parameters associated with the third group regulate the training process of each particle in the swarm. The third group includes five parameters, viz, the training epochs for particle evaluation, learning rate, dropout rate, batch size, and number of epochs for training optimal CNN architecture (
The experiments on the proposed QPSO-CNN model have been performed using a Nvidia Tesla V100 GPU with 16 GB of memory and Ubuntu 16.04.6 LTS operating system. Due to the stochastic nature of the proposed QPSO-CNN algorithm, 10 independent experimental runs are conducted on each handwritten dataset in order to maintain the consistency in the results.
5 Experimental Results and Discussion
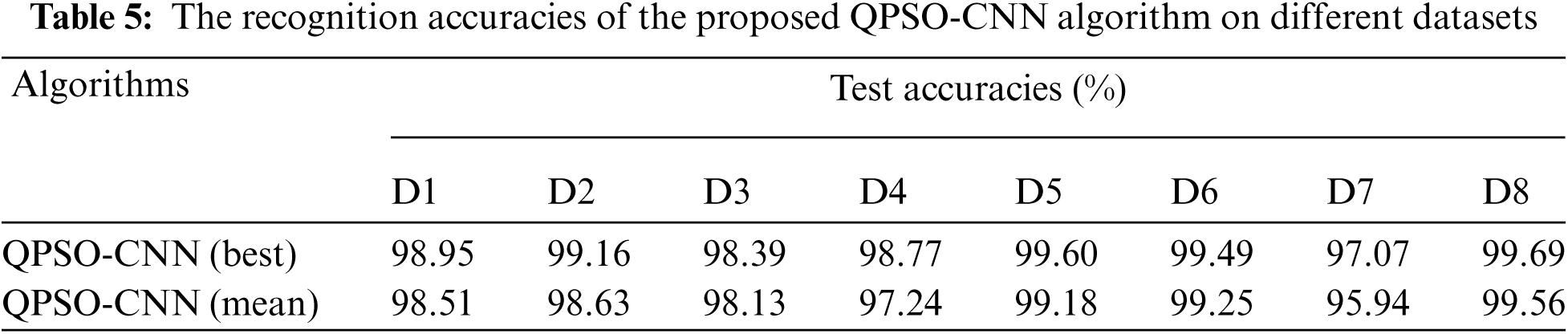
The overall recognition performance of the proposed QPSO-CNN algorithm in terms of the best recognition accuracies and the mean recognition accuracies obtained from 10 independent experimental runs on each chosen benchmark dataset is outlined in Tab. 5. The computational experimental results illustrate that the proposed algorithm obtains promising recognition accuracies on all the conventional Indic script benchmark datasets (i.e., D1, D2, D3, D4, D5, D6, D8), while it exhibits moderately inferior recognition accuracy on the collected DOGRA C-64 dataset. This difference in recognition accuracy demonstrates the complexities and challenges associated with the D7 dataset. These complexities arise due to the presence of complex structures and a potentially large number of visually similar shaped characters in the Dogra script, which eventually brings ambiguities and leads to misrecognition error. Overall, the experimental results clearly reveal that the proposed algorithm yields satisfactory performance on all the chosen datasets.
In this section, to demonstrate the effectiveness of the proposed algorithm, the overall performance has been compared with the conventional techniques that are widely used for handwritten Indic scripts recognition. The existing state-of-the-art techniques that have claimed propitious recognition accuracy on the chosen benchmark Indic script datasets are considered as the peer competitors. The evaluation results of the QPSO-CNN algorithm, along with the existing peer competitors on all the benchmark datasets, have been compiled in Tab. 6.

For the Bangla script datasets, viz, D1, D2, D3, and D4, the deep learning based techniques used to compare our results are unified CNN [40], AlexNet [41], DenseNet [43], Multi-column Multi-scale CNN (MMCNN) [45], Residual Network (ResNet-50) [47], BornoNet [48], and modified ResNet-18 [49]. Moreover, for the Devanagari script datasets, viz, D5 and D6, the deep learning based techniques used to compare our results are MMCNN [45], CNN [50], ResNet-50 [51], and Inception V3 [52]. Furthermore, the classical machine learning based techniques used to compare our results are Sparse Concept Coding with Tetrolet transform and Nearest Neighbor method [42], Opposition-based Multiobjective Harmony Search with SVM [44], and Advanced Feature Sets with SVM [46]. Additionally, to comprehensively evaluate the robustness of the proposed neuroevolutionary algorithm, the standard MNIST dataset is also used since it is a well-known dataset specifically for investigating the population-based neural architecture search (NAS) approaches. For MNIST handwritten digit recognition dataset viz, D8, the NAS approaches used for comparison are Internet Protocol based variable-length PSO-CNN [25], Flexible Convolutional Auto-Encoder [26], Deep Convolutional Variational Autoencoder [53], and Genetic algorithm based EvoCNN [54]. Empirically, it is clearly shown in Tab. 6 that the proposed algorithm achieves the best results in terms of the best classification performance on all the chosen benchmark datasets and thereby outperforms all the existing peer competitors for the handwritten Indic scripts recognition.
In this section, we show some typical examples of misclassified samples on each chosen benchmark dataset, as delineated in Fig. 2.
From the experimental analysis, we have noticed that there are two prominent reasons that contribute to the failure cases for handwritten Indic scripts recognition.
• The main reason is the confusion of similar shaped characters, i.e., some characters’ pairs are written in such a manner that they have similar structural constructs, which are quite challenging to recognize even for humans.
• Also, we observed that it is difficult to correctly identify the cursive and nonstandard writing habits in hooks and circles. Furthermore, the erroneous characters’ samples, which are either degraded or severely polluted, have broken architecture, brought great ambiguities, and directly led to misclassification.

Figure 2: Illustration of frequently misclassified samples for the chosen benchmark datasets. (a) CMATERdb 3.1.1 (b) CMATERdb 3.1.2 (c) CMATERdb 3.1.3 (d) BanglaLekha-Iso (e) CMATERdb 3.2.1 (f) DHCD (g) DOGRA C-64 (h) MNIST
The experimental results in this paper clearly indicate that the meta-heuristic evolutionary approach is proven to be feasible in designing the promising CNN architectures for handwritten Indic scripts recognition. The proposed algorithm provides competitive performance without using complicated architectures and data augmentation, and the results are comparable to the existing handcrafted models. In the past, most of the works have contributed hand-designed architectures for CNNs, explicitly designed for solving a particular problem. This process of manually creating the architecture is expensive and entails a significant amount of trial and error in determining the solution quality. Therefore, this proposed neuro-evolution approach is way more robust and simpler than the existing state-of-the-art techniques.
The proposed algorithm integrates the traditional PSO with the principles and ideology of quantum computing. Unlike classical computing, in which a bit may exist in either state 0 or state 1, in quantum computing, the Q-bit may exist in state 0, state 1, or superposition two states. This ability of quantum computing to have more than two states contributes to a better and faster exploration and exploitation of search space. Since the exploration and the exploration should complement each other, so the appropriate tuning of them could improve the performance. In this regard, the rotation angle is introduced for updating the position of particles. The proper selection of rotation angle controls and upholds a good balance between exploitation and exploration of the search space and obtain the competing solutions with shorter computation time and smaller swarm size. In consequence, this approach remarkably promotes the computation efficiency of the proposed algorithm. Furthermore, QPSO with D-dimensional Q-bit representation provides a better population diversity as it covers the search space faster than the traditional PSO. Thus, quantum computing supplements much more to the performance of PSO, which further intensifies the efficacy of the technique. In addition, the training curves of the global best solution representing the optimal CNN topology for dataset D3 are illustrated in Fig. 3. For this experiment, 15% of the data in the training set is randomly sampled to create the validation set. We noticed that the training and validation accuracies do not exhibit any indications of overfitting, and they are getting improved steadily and smoothly with time. This clearly corroborates that the proposed QPSO-CNN algorithm is sophisticated enough and indeed capable to exploit promising CNN architecture for any given script recognition dataset.
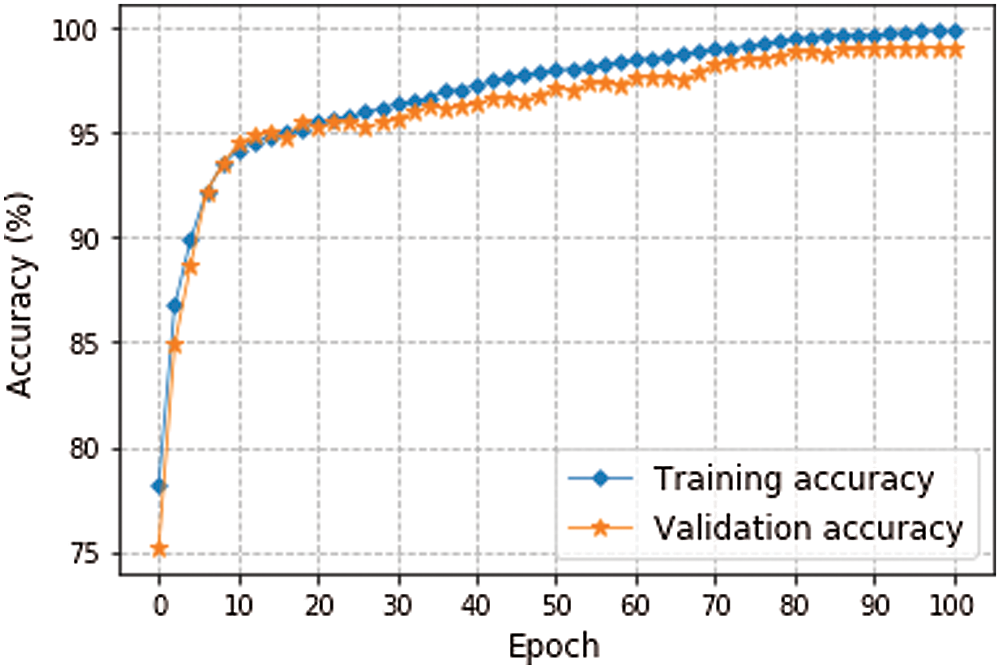
Figure 3: The training process for the
Moreover, in the existing neural architecture search approaches, the final recognition accuracy is considered as a fitness measure while evaluating the particles. The final recognition accuracy usually needs a large number of training epochs. So, this process will eventually take a considerable amount of time. Therefore, to design the complete architecture with the above fitness evaluation plan, it is essential to exercise a significant number of computational resources for speeding up the process. Additionally, this process also demands further professional assistance, for example, task scheduling and synchronization, which is far from the expertise of most of the researchers. Hence, during the evolution, the particles do not need to check the final recognition accuracy; however, it is sufficient to predict the tendency that could reveal the future quality of the solution. In this context, the particles in the proposed scheme are trained with small numbers of epochs during the evaluation. In summary, it concludes that the proposed technique with the simplistic fitness evaluation scheme and well-designed encoding strategies lends the researchers to discover potential CNN architectures without prior domain knowledge.
In this paper, a QPSO-CNN algorithm has been proposed for the recognition of handwritten Indic scripts. The proposed hybrid neuroevolutionary approach integrates particle swarm optimization with the concept of quantum computing to automatically evolve promising CNN architectures. The QPSO has a different operational procedure and is an amended version of conventional PSO. It is strengthened via an additional operator, i.e., the rotation angle. The proper selection of rotation angle controls and upholds a good balance between exploitation and exploration of the search space and obtain the competing solutions, even with a smaller swarm size. Also, we deduce that with the effective use of heuristics, the proposed algorithm avoids wasting too much computational time in vain search and hence provides an enhanced searching efficiency. The superiority of the proposed QPSO-CNN algorithm has been evaluated on a variety of Indic script datasets. The comprehensive experimental results demonstrate that the proposed algorithm performs significantly better than the existing state-of-the-art techniques.
Funding Statement: This research received no external funding.
Conflicts of Interest: The authors declare that they have no conflicts of interest.
1. S. Karthik and K. S. Murthy, “Deep belief network based approach to recognize handwritten kannada characters using distributed average of gradients,” Cluster Computing, vol. 22, no. 2, pp. 4673–4681, 2019. [Google Scholar]
2. R. Sharma and B. Kaushik, “Offline recognition of handwritten indic scripts: A state-of-the-art survey and future perspectives,” Computer Science Review, vol. 38, pp. 100302, 2020. [Google Scholar]
3. M. Tahir, S. Anwar, A. Mian and A. W. Muzaffar, “Deep localization of subcellular protein structures in fluorescence microscopy images,” arXiv:1910.04287, 2021. [Google Scholar]
4. J. Gu, Z. Wang, J. Kuen, L. Ma, A. Shahroudy et al., “Recent advances in convolutional neural networks,” Pattern Recognition, vol. 77, pp. 354–377, 2018. [Google Scholar]
5. G. Huang, Z. Liu, L. V. D. Maaten and K. Q. Weinberger, “Densely connected convolutional networks,” in Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition, Honolulu, HI, USA, pp. 4700–4708, 2017. [Google Scholar]
6. K. He, X. Zhang, S. Ren and J. Sun, “Deep residual learning for image recognition,” in Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, pp. 770–778, 2016. [Google Scholar]
7. C. Szegedy, W. Liu, Y. Jia, P. Sermanet, S. Reed et al., “Going deeper with convolutions,” in Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition, Boston, MA, USA, pp. 1–9, 2015. [Google Scholar]
8. A. Krizhevsky, I. Sutskever and G. E. Hinton, “Imagenet classification with deep convolutional neural networks,” Advances in Neural Information Processing Systems, vol. 25, pp. 1097–1105, 2012. [Google Scholar]
9. H. Jin, Q. Song and X. Hu, “Auto-keras: an efficient neural architecture search system,” in Proc. of the 25th ACM SIGKDD Int. Conf. on Knowledge Discovery & Data Mining, Anchorage, AK, USA pp. 1946–1956, 2019. [Google Scholar]
10. Y. LeCun and Y. Bengio, “Convolutional networks for images, speech, and time series,” in The Handbook of Brain Theory and Neural Networks, 55 Hayward St., Cambridge, MA, United States: MIT Press, pp. 255–258, 1998. [Google Scholar]
11. K. Bhalla, D. Koundal, S. Bhatia, M. K. I. Rahmani and M. Tahir, “Fusion of infrared and visible images using fuzzy based siamese convolutional network,” CMC-Computers,” Materials & Continua, vol. 70, no. 3, pp. 5503–5518, 2021. [Google Scholar]
12. B. Ali, S. A. Lashari, W. Sharif, A. Khan, K. Ullah et al., “An efficient learning weight of elman neural network with chicken swarm optimization algorithm,” Procedia Computer Science, vol. 192, pp. 3060–3069, 2021. [Google Scholar]
13. M. Mahrishi, S. Morwal, A. W. Muzaffar, S. Bhatia, P. Dadheech et al., “Video index point detection and extraction framework using custom yolov4 darknet object detection model,” IEEE Access, vol. 9, pp. 143378–143391, 2021. [Google Scholar]
14. M. Tahir and S. Anwar, “Transformers in pedestrian image retrieval and person Re-identification in a multi-camera surveillance system,” Applied Sciences, vol. 11, no. 19, pp. 14, 2021. [Google Scholar]
15. J. Kennedy and R. C. Eberhart, “A discrete binary version of the particle swarm algorithm,” in IEEE Int. Conf. on Systems, Man, and Cybernetics, Computational Cybernetics and Simulation, Orlando, FL, USA, pp. 4104–4108, 1997. [Google Scholar]
16. Y. W. Jeong, J. B. Park, S. H. Jang and K. Y. Lee, “A new quantum-inspired binary pso: Application to unit commitment problems for power systems,” IEEE Transactions on Power Systems, vol. 25, no. 3, pp. 1486–1495, 2010. [Google Scholar]
17. K. O. Stanley and R. Miikkulainen, “Evolving neural networks through augmenting topologies,” Evolutionary Computation, vol. 10, no. 2, pp. 99–127, 2002. [Google Scholar]
18. K. O. Stanley, D. B. D'Ambrosio and J. Gauci, “A Hypercube-based encoding for evolving large-scale neural networks,” Artificial Life, vol. 15, no. 2, pp. 185–212, 2009. [Google Scholar]
19. K. O. Stanley, “Compositional pattern producing networks: A novel abstraction of development,” Genetic Programming and Evolvable Machines, vol. 8, no. 2, pp. 131–162, 2007. [Google Scholar]
20. C. Fernando, D. Banarse, M. Reynolds, F. Besse, D. Pfau et al., “Convolution by evolution: differentiable pattern producing networks,” in Proc. of the Genetic and Evolutionary Computation Conf., Denver, Colorado, USA, pp. 109–116, 2016. [Google Scholar]
21. E. Real, S. Moore, A. Selle, S. Saxena, Y. L. Suematsu et al., “Large-scale evolution of image classifiers,” in Proc. of the Int. Conf. on Machine Learning, Sydney, NSW, Australia, pp. 2902–2911, 2017. [Google Scholar]
22. K. A. Rashedi, M. T. Ismail, N. N. Hamadneh, S. A. Wadi, J. J. Jaber et al., “Application of radial basis function neural network coupling particle swarm optimization algorithm to classification of Saudi Arabia stock returns,” in Journal of Mathematics, vol. 2021, pp. 1–8, 2021. [Google Scholar]
23. N. N. Hamadneh, M. Tahir and W. A. Khan, “Using artificial neural network with prey predator algorithm for prediction of the COVID-19: the case of Brazil and Mexico,” in Mathematics, vol. 9, no. 2, pp. 1–14, 2021. [Google Scholar]
24. B. Wang, B. Xue and M. Zhang, “Particle swarm optimisation for evolving deep neural networks for image classification by evolving and stacking transferable blocks,” in IEEE Congress on Evolutionary Computation (CEC), Glasgow, UK, pp. 1–8, 2020. [Google Scholar]
25. B. Wang, Y. Sun, B. Xue and M. Zhang, “Evolving deep convolutional neural networks by variable-length particle swarm optimization for image classification,” in IEEE Congress on Evolutionary Computation (CEC), Rio de Janeiro, Brazil, pp. 1–8, 2018. [Google Scholar]
26. Y. Sun, B. Xue, M. Zhang and G. G. Yen, “A particle swarm optimization-based flexible convolutional autoencoder for image classification,” IEEE Transactions on Neural Networks and Learning Systems, vol. 30, no. 8, pp. 2295–2309, 2018. [Google Scholar]
27. R. Sharma, B. N. Kaushik and N. K. Gondhi, “Devanagari and gurmukhi script recognition in the context of machine learning classifiers: mini review,” Journal of Artificial Intelligence, vol. 11, no. 2, pp. 65–70, 2018. [Google Scholar]
28. N. Das, R. Sarkar, S. Basu, M. Kundu, M. Nasipuri et al., “A genetic algorithm based region sampling for selection of local features in handwritten digit recognition application,” Applied Soft Computing, vol. 12, no. 5, pp. 1592–1606, 2012. [Google Scholar]
29. N. Das, R. Sarkar, S. Basu, P. K. Saha, M. Kundu et al., “Handwritten bangla character recognition using a soft computing paradigm embedded in two pass approach,” Pattern Recognition, vol. 48, no. 6, pp. 2054–2071, 2015. [Google Scholar]
30. N. Das, K. Acharya, R. Sarkar, S. Basu, M. Kundu et al., “A benchmark image database of isolated bangla handwritten compound characters,” International Journal on Document Analysis and Recognition (IJDAR), vol. 17, no. 4, pp. 413–431, 2014. [Google Scholar]
31. M. Biswas, R. Islam, G. K. Shom, M. Shopon, N. Mohammed et al., “Banglalekhaisolated: A multi-purpose comprehensive dataset of handwritten bangla isolated characters,” Data in Brief, vol. 12, pp. 103–107, 2017. [Google Scholar]
32. N. Das, J. M. Reddy, R. Sarkar, S. Basu, M. Kundu et al., “A statistical–topological feature combination for recognition of handwritten numerals,” Applied Soft Computing, vol. 12, no. 8, pp. 2486–2495, 2012. [Google Scholar]
33. S. Acharya, A. K. Pant and P. K. Gyawali, “Deep learning based large scale handwritten devanagari character recognition,” in 9th Int. Conf. on Software, Knowledge, Information Management and Applications (SKIMA), Kathmandu, Nepal, pp. 1–6, 2015. [Google Scholar]
34. Y. LeCun, L. Bottou, Y. Bengio and P. Haffner, “Gradient based learning applied to document recognition,” in Proc. of the IEEE, vol. 86, no. 11, pp. 2278–2324, 1998. [Google Scholar]
35. R. Sharma, R. Bangroo, M. Kumar and N. Kumar, “A model for resource constraint project scheduling problem using quantum inspired pso,” in Int. Conf. on Next Generation Computing Technologies, Dehradun, India, pp. 75–87, 2017. [Google Scholar]
36. X. Glorot and Y. Bengio, “Understanding the difficulty of training deep feedforward neural networks,” in Proc. of the thirteenth Int. Conf. on Artificial Intelligence and Statistics, Chia Laguna Resort, Sardinia, Italy, pp. 249–256, 2010. [Google Scholar]
37. D. P. Kingma and J. Ba, “Adam: A method for stochastic optimization,” arXiv Preprint arXiv:1412.6980, 2014. [Google Scholar]
38. N. Srivastava, G. Hinton, A. Krizhevsky, I. Sutskever and R. Salakhutdinov, “Dropout: A simple way to prevent neural networks from overfitting,” The Journal of Machine Learning Research, vol. 15, no. 1, pp. 1929–1958, 2014. [Google Scholar]
39. S. Ioffe, “Batch renormalization: towards reducing minibatch dependence in batch-normalized models,” in Proc. of the 31st Int. Conf. on Neural Information Processing Systems, Long Beach, California, USA, pp. 1942–1950, 2017. [Google Scholar]
40. P. Keserwani, T. Ali, and P. P. Roy, “Handwritten bangla character and numeral recognition using convolutional neural network for low-memory gpu,” International Journal of Machine Learning and Cybernetics, vol. 10, no. 12, pp. 3485–3497, 2019. [Google Scholar]
41. D. Gupta and S. Bag, “CNN-Based multilingual handwritten numeral recognition: A fusion-free approach,” Expert Systems with Applications, vol. 165, pp. 113784, 2021. [Google Scholar]
42. K. S. Dash, N. B. Puhan and G. Panda, “Sparse concept coded tetrolet transform for unconstrained odia character recognition,” arXiv Preprint arXiv:2004.01551, 2020. [Google Scholar]
43. M. Z. Alom, P. Sidike, M. Hasan, T. M. Taha and V. K. Asari, “Handwritten bangla character recognition using the state-of-the-art deep convolutional neural networks,” Computational Intelligence and Neuroscience, vol. 2018, pp. 1–13, 2018. [Google Scholar]
44. A. Gupta, R. Sarkhel, N. Das and M. Kundu, “Multiobjective optimization for recognition of isolated handwritten indic scripts,” Pattern Recognition Letters, vol. 128, pp. 318–325, 2019. [Google Scholar]
45. R. Sarkhel, N. Das, A. Das, M. Kundu and M. Nasipuri, “A Multi-scale deep quad tree based feature extraction method for the recognition of isolated handwritten characters of popular indic scripts,” Pattern Recognition, vol. 71, pp. 78–93, 2017. [Google Scholar]
46. M. R. Kibria, A. Ahmed, Z. Firdawsi and M. A. Yousuf, “Bangla compound character recognition using support vector machine (SVM) on advanced feature sets,” in IEEE Region 10 Symposium (TENSYMP), Dhaka, Bangladesh, pp. 965–968, 2020. [Google Scholar]
47. S. Chatterjee, R. K. Dutta, D. Ganguly, K. Chatterjee and S. Roy, “Bengali handwritten character classification using transfer learning on deep convolutional network,” in Int. Conf. on Intelligent Human Computer Interaction, Daegu, Korea, pp. 138–148, 2019. [Google Scholar]
48. A. S. A. Rabby, S. Haque, S. Islam, S. Abujar and S. A. Hossain, “Bornonet: Bangla handwritten characters recognition using convolutional neural network,” Procedia Computer Science, vol. 143, pp. 528–535, 2018. [Google Scholar]
49. M. A. R. Alif, S. Ahmed and M. A. Hasan, “Isolated bangla handwritten character recognition with convolutional neural network,” in 20th Int. Conf. of Computer and Information Technology (ICCIT), Dhaka, Bangladesh, pp. 1–6, 2017. [Google Scholar]
50. A. K. Tushar, A. Ashiquzzaman, A. Afrin and M. R. Islam, “A novel transfer learning approach upon hindi, arabic, and bangla numerals using convolutional neural networks,” in Proc. of the Computational Vision and Bio Inspired Computing, Coimbatore, India, pp. 972–981, 2018. [Google Scholar]
51. M. Mhapsekar, P. Mhapsekar, A. Mhatre and V. Sawant, “Implementation of residual network (resnet) for devanagari handwritten character recognition,” in Proc. of 2nd Int. Conf. on Advanced Computing Technologies and Applications, Mumbai, India, pp. 137–148, 2020. [Google Scholar]
52. N. Aneja and S. Aneja, “Transfer learning using cnn for handwritten devanagari character recognition,” in 1st Int. Conf. on Advances in Information Technology (ICAIT), Chikmagalur, India, pp. 293–296, 2019. [Google Scholar]
53. X. Chen, Y. Sun, M. Zhang and D. Peng, “Evolving deep convolutional variational autoencoders for image classification,” IEEE Transactions on Evolutionary Computation, vol. 25, no. 5, pp. 815–829, 2020. [Google Scholar]
54. Y. Sun, B. Xue, M. Zhang and G. G. Yen, “Evolving deep convolutional neural networks for image classification,” IEEE Transactions on Evolutionary Computation, vol. 24, no. 2, pp. 394–407, 2019. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |