Computers, Materials & Continua DOI:10.32604/cmc.2022.023685
Article

Text Encryption Using Pell Sequence and Elliptic Curves with Provable Security

Sumaira Azhar1, Naveed Ahmed Azam2,* and Umar Hayat1

1Department of Mathematics, Quaid-i-Azam University, Islamabad, 45320, Pakistan
2Department of Applied Mathematics and Physics, Graduate School of Informatics, Kyoto University, Kyoto, 606-8501, Japan
*Corresponding Author: Naveed Ahmed Azam. Email: azam@amp.i.kyoto-u.ac.jp
Received: 17 September 2021; Accepted: 11 November 2021

Abstract: The demand for data security schemes has increased with the significant advancement in the field of computation and communication networks. We propose a novel three-step text encryption scheme that has provable security against computation attacks such as key attack and statistical attack. The proposed scheme is based on the Pell sequence and elliptic curves, where at the first step the plain text is diffused to get a meaningless plain text by applying a cyclic shift on the symbol set. In the second step, we hide the elements of the diffused plain text from the attackers. For this purpose, we use the Pell sequence, a weight function, and a binary sequence to encode each element of the diffused plain text into real numbers. The encoded diffused plain text is then confused by generating permutations over elliptic curves in the third step. We show that the proposed scheme has provable security against key sensitivity attack and statistical attacks. Furthermore, the proposed scheme is secure against key spacing attack, ciphertext only attack, and known-plaintext attack. Compared to some of the existing text encryption schemes, the proposed scheme is highly secure against modern cryptanalysis.

Keywords: Text encryption; pell numbers; elliptic curves; key sensitivity; statistical cryptanalysis

1  Introduction

There is a high demand for data security schemes due to the recent advancement in the fields of computation and communication technologies. Cryptography and steganography are the two main branches of data security schemes. Cryptography is the study of data security schemes where secret data is transformed into an unreadable data [1]. Steganography is the study of data security schemes where secret data is embedded into host data so that the attackers cannot detect the existence of secret data [2].

Different data security schemes have been proposed based on different mathematical structures such as elliptic curves [3–9], algebraic structures [10–15], chaotic maps [16–21] and fuzzy set theory [22,23]. Security and privacy of the text messages are major concerns of the users while communicating on popular messaging platforms such as WhatsApp and Signal. So, the security of the text messages gained great attention now a days. We briefly review some of the recent text encryption schemes. Abdullah et al. [23] proposed a cryptosystem based on fuzzy logic where triangular fuzzy numbers are used to represent plain text and ciphertext. Gupta et al. [24] proposed a data security algorithm based on logical and shifting operations. Pattanayak et al. [25] used linear congruences and extended Euclidean algorithm to design a text encryption scheme. By utilizing 8-bit code values of alphabets, Agrawal et al. [26] proposed an efficient algorithm for text encryption. Ghrare et al. [27] designed a hidden encrypted symmetric key algorithm by hiding the secret key inside the ciphertext. Linear recurrences such as generalized Fibonacci numbers, Pell numbers and Pell-Lucas numbers have many applications in the field of mathematics and computer science [28–30]. The schemes in [31–33] used linear recurrences for cryptography purpose. Luma et al. [31] explored a relationship between Fibonacci and Lucas sequence and used it for encryption and decryption purpose. Overmars et al. [32] proposed an efficient method to compute the golden ratio to avoid cryptographic breaches. Agarwal et al. [33] proposed a data encryption scheme based on Fibonacci numbers. Recently, DNA sequences are also used to generate secret keys for data security [34–36]. Clelland et al. [34] combined a DNA based technique and the microdot to send messages secretly. Abbasy et al. [36] employed useful features of DNA sequences for data hiding. Chaotic maps are used to develop new security schemes due to their high sensitivity to the initial condition [37–42]. Murillo-Escobar et al. [37] proposed a new text encryption scheme based on a logistic map. Similarly, elliptic curves (ECs) received great attention in the field of cryptography for image encryption [43–47], text encryption [48–53] and signcryption [54–56] due to comparable security against modern cryptanalysis with low key size. Sunneetha et al. [48] proposed a secure algorithm using elliptic curves and algebraic operations to transmit messages. Naji et al. [49] proposed a novel text encryption scheme by representing characters of the plain text with the affine points on an EC. Agrawal et al. [50] designed a text encryption method using ECC and Hill cipher with better security and complexity. Keerthi et al. [51] proposed a novel text encryption scheme where the hexadecimal form of the ASCII values of plain text are mapped to affine points of an ECs. Kumar et al. [52] used paired ASCII values corresponding to the plain text as an input for the elliptic curve. Singh and Singh developed an algorithm that can be used for encryption and decryption of any size of text message with given ASCII values. Ullah et al. [54] provided a critical review of hyper elliptic curves based signcryption algorithms. A hyper elliptic curve based signcryption scheme more suitable for emerging resource constraints environment is proposed by Ullah et al. [56].

Most of the text encryption schemes available in the literature such as the schemes presented in [23–27,33,34,36,37,48–51,53] are not secure against well know attacks including key spacing, key sensitivity, statistical attack, ciphertext only attack and known-plaintext attack. The aim of this paper is to propose a novel text encryption scheme that has high security against modern cryptanalysis including key spacing, key sensitivity, statistical attack, ciphertext only attack and known-plaintext attack as compared to the existing text encryption schemes [23–27,33,34,36,37,48–51,53]. The proposed scheme is based on the Pell sequence and elliptic curves and has three main steps, where we first diffuse the plain text. Then an encoding procedure is applied to the diffused plain text based on the Pell sequence instep 2. Finally, the encoded diffused plain text is confusedin step 3 based on ECs. The rest of the paper is organized as follows. Section 2 contains some preliminaries. We discuss a novel text encryption scheme in Section 3. Security analysis and a detailed comparison of the proposed scheme with the existing text encryption schemes [23–27,33,34,36,37,48–51,53] is discussed in Section 4. A conclusion is drawn in Section 5.

2  Preliminaries

2.1 Pell Sequence

For initial values P0=0 and P1=1, the n-th term Pn of the Pell sequence is defined with the recurrence relation

Pn=2Pn−1+Pn−2.(1)

The first six terms of the Pell sequence are 0, 1, 2, 5, 12, and 29. By [30] it is known that for

i→∞itholdsthatPiPi−1→1+2.

2.2 Elliptic Curves (EC)

For a finite prime field Fp with characteristic other than 2 and 3, prime p and two integers a,b∈[0,p−1] such that 4a3+27b2≠0(modp), the short Weiestrass form elliptic curve Ep,a,b over the field Fp is the set

{(x,y)∈Fp×Fp∣(y2=x3+ax+b)(modp)}∪⁡{δ},(2)

where δ is the identity element of the EC. We call the integers p,a and b the parameters of the EC Ep,a,b.

By [57], when a=0 and p≡2(mod3), the EC Ep,a,b has exactly p+1 points with no repetition in their y-coordinates. Azam et al. [4] defined three orderings on an EC Ep,a,b that have good cryptographic properties. These orderings are natural ordering N, diffusion ordering D, and modulo diffusion ordering M such for any two points (x,y) and (x′,y′) on an EC Ep,0,b it holds that

(x,y)N(x′,y′)⇔‘‘x<x′'' or‘‘x=x′andy<y′'';(3)

(x,y)D(x′,y′)⇔‘‘x+y<x′+y′'' or‘‘x+y=x′+y′andx<x′'';(4)

(x,y)M(x′,y′)⇔‘‘x+y<x′+y′(modp)'' or\;‘‘x+y=x′+y′(modp)andx<x′'';(5)

The key features of these orderings are: (i) they diffuse the y-coordinates of the ordered EC; and (ii) the ordered ECs generated by these orderings are highly uncorrelated. Furthermore, it can be observed from Fig. 1 that the three orderings are non-equivalent and are capable of generating randomness. Due to these properties, Azam et al. [4,5] showed that these orderings are cryptographically suitable for generating a large number of secure permutations over ECs.

Figure 1: EC E29,0,1 and the effect of the natural, diffusion and modulo ordering on the EC E29,0,1: (a) Points of the EC E29,0,1 are shown w.r.t. non-decreasing x-coordinate from left to right; (b) y-coordinates of the points of the ordered EC E29,0,1 with natural ordering; (c) y-coordinates of the points of the ordered EC E29,0,1 with diffusion ordering; (d) y-coordinates of the points of the ordered EC E29,0,1 with modulo ordering

3  The Proposed Scheme

For an encryption scheme, it is essential to diffuse and confuse the plain text up to a certain level [2]. Therefore, our scheme consists of three main steps where we first diffuse the plain text followed by an encoding procedure and then create confusion in the encoded diffused plain text. The diffusion step is performed by permuting the symbol set of the plain text. We use a restricted Pell sequence, a weight function, and a binary sequence to encode each element and its position in the diffused plain text with real numbers. Due to the sensitivity of the ECs over its parameters, we generate permutations over ECs to create confusion in the encoded diffused plain text. We discuss these three steps in detail below.

Let S be a finite symbol set of size m, and for i∈[0,m−1], let S(i) denote the i-th element of S. Suppose that the sender wants to send the plain text T=T(1)⋯T(i)⋯T(n) of length n which is a sequence over S where T(i),i∈[1,n] denotes the i-th element of T and T(i)∈S. In this scheme, we encode plain text to real numbers in the interval [−1,1] with at most β≥14 digits after the decimal.

3.1 Encryption Procedure

Step 1. Diffuse plain text: We select an integer k∈[0,m−1] and permute the entries of S by using the permutation ψk:S→S defined as

ψk(S(i))=S((i+k)(modm)),(6)

i.e., ψk maps the i-th entry of S on its (i+k)(modm)-th entry. Now generate a diffused plain text T′=T′(1)⋯T′(i)⋯T′(n) by using the permutation ψk such that the i-th element T′(i)=ψk(T(i), i∈[1,n]. The diffusion step is similar to the Caesar cipher [58].

Step 2. Encode diffused plain text: To encode the elements of the diffused plain text T′, we generate a restricted Pell sequence, a weight function, and a binary sequence as follows.

Select two positive integers h and h′ such that h<h′ and h′−h+1≤β, and generate the restricted Pell sequence Qh,h′=q1⋯qi⋯qm, if it exists, such that for each integer i∈[1,m] the following hold:

-   qi=log(Pi/Pi−1) and qi has exactly h′−h+1 digits from h-th digit to h′-th digit after the decimal, where Pi is the i-th entry of the Pell sequence, and

-   all entries of Qh,h′ are distinct, i.e., for any two distinct i,j∈[1,m], it holds that qi≠qj. We apply this condition so that each symbol in the diffused plain text can be encoded uniquely.

Observe that the entries of the restricted Pell sequence Qh,h′ are in the closed interval [0,1] since Pi/Pi−1→1+(2)1/2 as i→∞ by [30]. We added the constraint h′−h+1≤β to generate a restricted Pell sequence to control the length of the ciphertext and increase the key size, since for a fixed integer τ, there exists different pairs h,h′ such that h′−h+1=τ, and hence different restricted Pell sequences.

Generate a weight function w:{1,2,⋯,n}→[−1,1] which is an injection, i.e., for any two i,j∈{1,2,⋯,n} such that i≠j, it holds that w(i)≠w(j). The aim of this weight function is to uniquely encode the position of each element of T′.

Generate a binary sequence α=α1⋯αi⋯αn. Based on the i-th entry αi of α, decide if we use weight w(i) with qj or qj−1, j∈[1,n] during the encoding procedure.

Now, generate an encoded diffused plain text (C,D)=(c1,d1)⋯(ci,di)⋯(cn,dn) such that the i-th element T′(i) of T′ is encoded (ci,di) as with

(ci,di)=(q(j+k)(modm)+αiw(i),1−q(j+k)(modm)+(1−αi)w(i)),(7)

where T(i)=S(j), for some j∈[1,m] and T′(i)=ψk(S(j))=S((j+k)(modm)).

Step 3. Confuse encoded plain text: In this step, we create confusion in the encoded plain text (C,D). For this purpose, we generate two bijections σ:C→C and σ′:D→D by using ordered subsets of two ECs. These ordered subsets are such that each integer in [1,n] appears exactly once as y-coordinates of the points. The existence of such subsets is ensured by considering the ECs with a=0 and p≡2(mod3). Finally, the i-th entries of C and D are mapped on some entries of C and D whose indices are determined by the y-coordinates of the i-th points in the ordered sets. More precisely, select two primes p,p′≥n with p≡2(mod3) and p′≡2(mod3), two integers b∈[1,p−1] and b′∈[1,p′−1], and two orderings ≺ and ≺′. Compute the ordered subsets {(ai,bi)∣bi∈[1,n]and(ai,bi)∈Ep,0,b} and {(ai′,bi′)∣bi′∈[1,n]and(ai′,bi′)∈Ep′,0,b′} ordered w.r.t. the orderings ≺ and ≺′, where for each i∈[1,n−1] it holds that (ai,bi)≺(ai+1,bi+1) and (ai′,bi′)≺′(ai+1′,bi+1′), respectively. From these ordered subsets, get the sequences H=b1b2⋯bn and H′=b1′b2′⋯bn′. Now, generate a confused encoded plain text (σ(C),σ′(D))(σ(c1),σ′(d1))⋯(σ(ci),σ′(di))⋯(σ(cn),σ′(dn)) by using the permutations σ:C→C and σ′:D→D such that σ(ci)=cbi and σ′(di)=dbi′.

3.2 Ciphertext

Transmit the confused sequence σ(C) as a ciphertext of the plain text T.

3.3 Secret Keys

The integers h,h′ and k, the weight function w and the encoded sequence σ′(D) are the secret keys of our encryption scheme. The integersh,h′ and k are used to get the representation of symbols in S, the weight function w is used to get the index of the symbols in the plain text, and the sequence σ′(D) is used to get w.

Note that for a given β, the proposed scheme can encrypt a plain text over a symbol set S with size at most|Qh=1,h′=β|, i.e., for the proposed scheme it holds that m≤|Qh=1,h′=β|. Furthermore, the proposed scheme can encrypt a plain text T of any arbitrary size, since it encodes each symbol of T individually.

3.4 Decryption Procedure

Assume that the channel between sender and receiver is noiseless, and therefore the receiver receives the ciphertext G=σ(c1)σ(c2)⋯σ(cn). Let g be the l-th element of G. We find the position of g in the plain text by using the keys σ′(D)=σ′(d1)σ′(d2)⋯σ′(dn) and weight function as follows. Compute a real d∈σ′(D) such that

g+d=r+1,(8)

for some r=w(i)∈[−1,1] with i∈[1,n]. Observe that for each g such a real d always exists by Eq. (7). The integer i is the position of the element of the plain text corresponding to the element g of the ciphertext. By using the secret key h, compute the restricted Pell sequence Qh,h′ and compute the inverse ψk−1:S→S defined as

(S(i))=S((i−k)(modm)),(9)

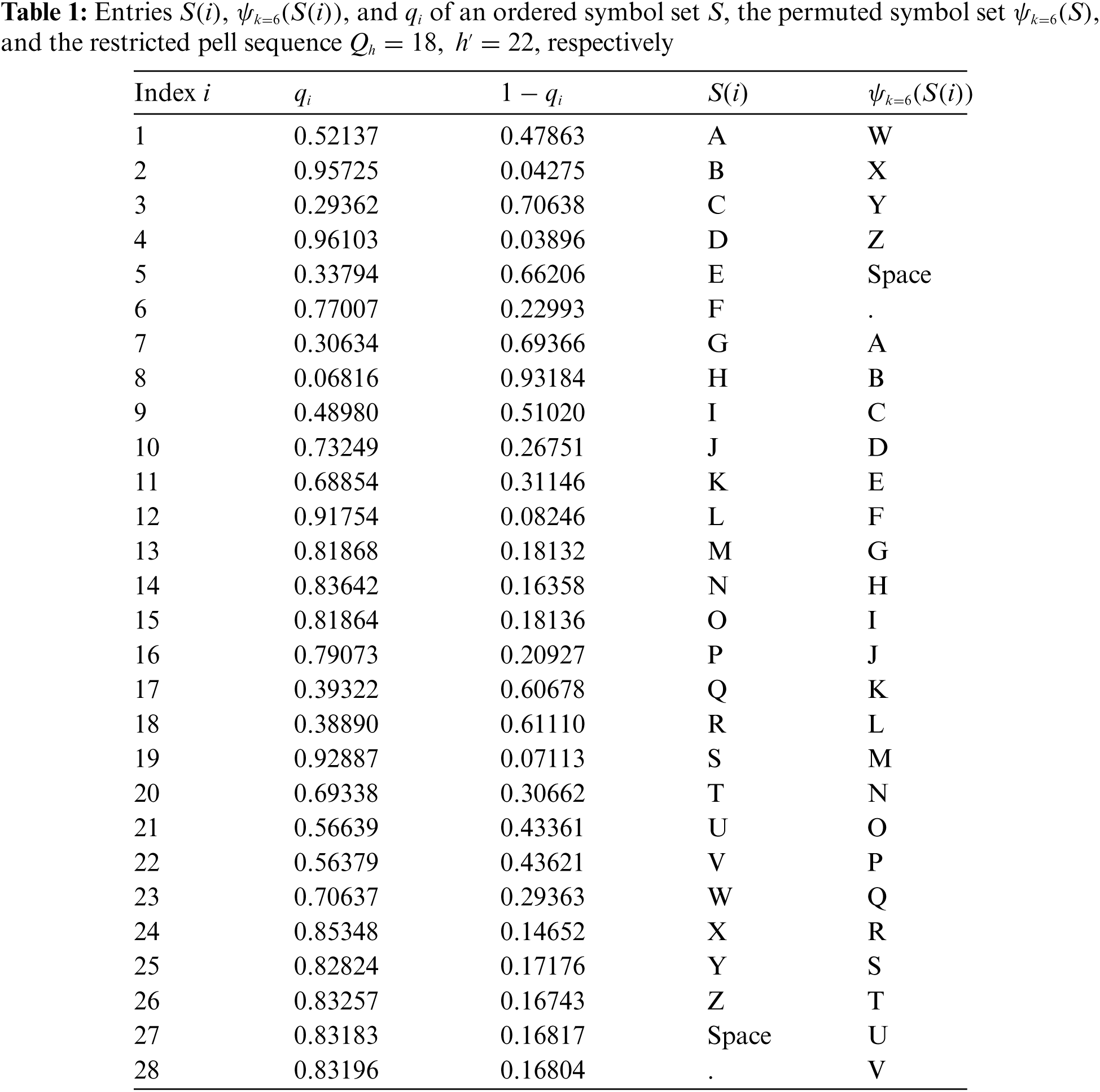
of the permutation by using the secret key k. To get the plain text T(i) at the i-th position of the plain text T, find the real qt∈Qh,h′ such that g=qtord=1−qt for some index t. Find the index t by using Tab. 1, and finally get the i-th plain text T(i) as T(i)=ψk−1(S(t)) corresponding to the l-th element g of G.

By repeating the above procedure for each g∈G, we get the plain text T. The proposed encryption and decryption scheme is illustrated in Fig. 2.

Figure 2: Flowchart of the proposed encryption and decryption scheme

We demonstrate our proposed encryption and decryption procedures in detail in Example 1.

3.5 Example 1

3.5.1 Encryption

Let the ordered symbol set S be the set of the capital English alphabet including blank-space and full-stop. This set is listed in the fourth column of Tab. 1. Let β=14, and for h=18 and h′=22, the entries qi of the restricted Pell sequence Qh,h′ are listed in the second column of Tab. 1, while the third column of Tab. 1 contains 1−qi. Select integer k=6 to generate a permutation ψk=6 on the symbol set S. The entries of ψk=6 are listed in the fifth column of Tab. 1.

Suppose the sender wants to send the plain text T = STAY SAFE with nine elements. For each integer i∈[1,9], the i-th element T(i) of the plain text T, the i-th element T′(i) of the diffused plain text, weight value w(i), binary value αi and i-th element (ci,di) of the encoded plain text are listed in Tab. 2.

To permute the encoded diffused plain text, we generated the ordered ECs E11,0,9 and E11,0,4 using natural and diffusion orderings respectively. The sequences H and H′ generated by these ordered ECs are listed in Tab. 3.

The confused encoded plain text σ(C) and σ′(D) are listed in Tab. 4.

3.5.2 Decryption

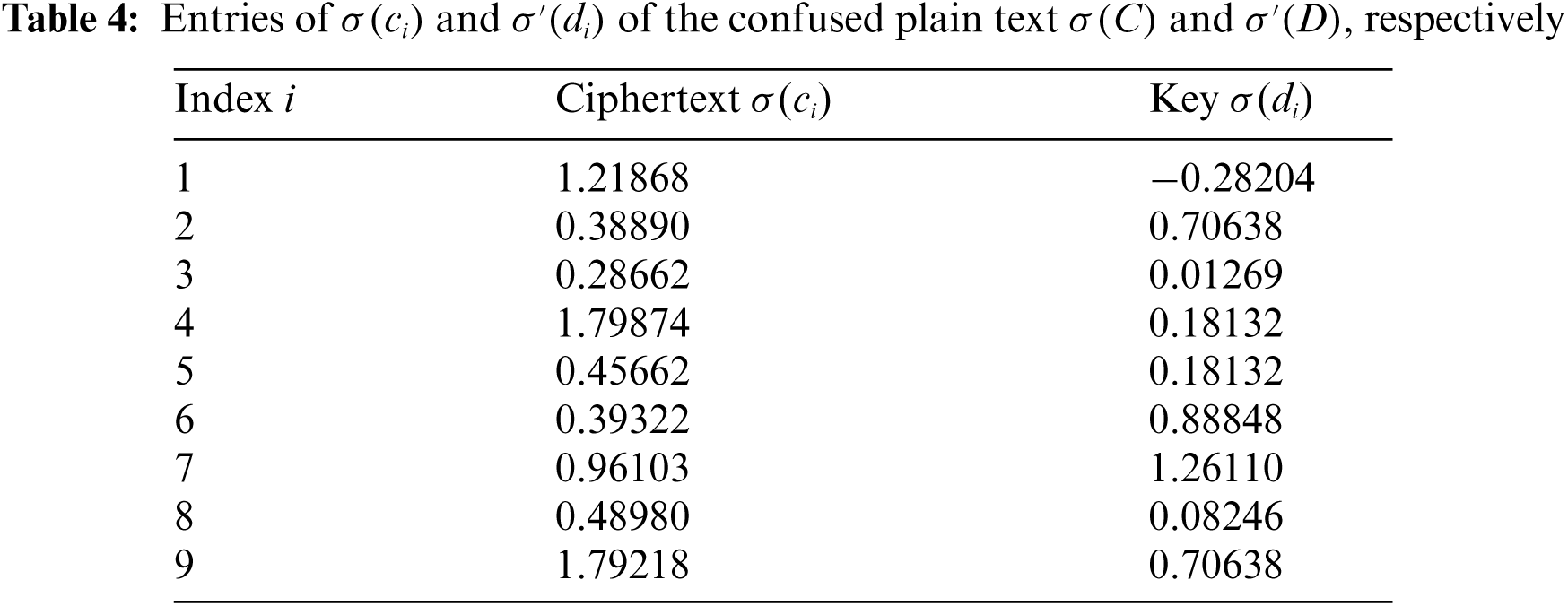
We demonstrate the decryption procedure for the 5-th element g=σ(c5)=0.45662 of the ciphertext G. Note that g+d=r+1 holds for d=σ(d2)=0.70638,r=w(i)=0.163 with i=6. This implies that g is the (i=6)−th element of the plain text. The realqt for which it holds that g=1−qt has index t=3 in the third column Qh=18,h′=22 of Tab. 1. We get the (i=6)-th element T(6)=ψk−1(S(3))=ψk−1(Y)=S of the plain text T from the fourth column of Tab. 1.

4  Security Analysis and Comparison

To analyze the security of the proposed scheme, we apply some well-known security tests including key spacing analysis, key sensitivity analysis, histogram test, information entropy analysis, ciphertext only attack and known-plaintext attack. We briefly explain these tests and their results for the proposed scheme in Sections 4.1–4.5. Furthermore, we give a detailed comparison of the security of the proposed scheme and some of the existing text encryption schemes in Section 4.6.

4.1 Key Spacing Analysis

Brute-force attack is commonly used by cryptanalysts to decrypt ciphertext. Key spacing analysis is used to analyze the security of an encryption scheme against brute-force attack. For an encryption scheme, key spacing is defined to be the number of distinct secret keys that it can generate. An encryption scheme is secure if its key spacing is at least 2100by [59]. The proposed scheme has five secret keys, three integers k,h, and h′, a weight function w and the sequence σ′(D), where the key σ′(D) depends on m,h,h′,k, and w, by Eq. (7). There are m choices for k and (10β)n choices for w, when the plain text is encoded to real numbers with at most β≥14 digits after the decimal and n is the size of the plain text. This implies that the key spacing of the proposed scheme is at least m(10β)n>2100for n≥4,m≥1 and β≥14. This implies that the proposed scheme satisfies key spacing analysis. In particular, when computation accuracy is 10−14,m=5,β=14 and n≥4, then there are 88 choices for selecting a pair of integers h and h′ such that h′−h+1≤β and there exists a restricted Pell sequence. This implies that the key spacing of the proposed scheme in this case is at least 5⋅88⋅(1014)4>2194.

4.2 Key Sensitivity Analysis

An encryption scheme is secure if it can generate a significantly different ciphertext for the same plaintext when the secret keys are slightly changed. In the next lemma, we show that for any plain text our scheme can generate a different ciphertext when any of the secret keysk,h,h′, and w is changed.

Lemma 1. Let T be a plain text of size n over symbol set S of size m and G=σ(c1)σ(c2)…σ(cn) be a ciphertext of T that is obtained by the proposed scheme using the secret keys k,h,h′ and weight function w.

(i)   The ciphertext G′ generated by the proposed scheme by using k′≠k,k′∈[0,m−1],h,h′, and w is not equal to G.

(ii)   The ciphertext G′ generated by the proposed scheme by using k,t≠hort′≠h′ that satisfies conditions of step 2, and w is not equal to G.

(iii)   If αi=1,i∈[1,n], the ciphertext G′ generated by the proposed scheme by using k,h,h′, and w′ such that w′(i)≠w(i), for all i∈[1,n], is not equal to G.

Proof. Let G′=σ(c1′)σ(c2′)…,σ(cn′)

(i)   The integer k′≠k used at step 1 of the proposed scheme is to shift the elements of the symbol set S. Then for all j∈[1,n] it holds that S((j+k′)(modm))≠S((j+k)(modm)). This implies that q(j+k′)(modm)+αiw(i)≠q(j+k)(modm)+αiw(i) for each i∈[1,n] in Eq. (7), where T(i)=S(j). This implies that ci′≠ci for each i∈[1,n], and hence G′≠G.

(ii)   For any integer t≠h or t′′≠h′ that satisfies conditions of Step 2, the restricted Pell sequence Qt,t′′′=q1′q2′⋯qn′≠Qh,h′=q1q2⋯qn, since the length of the elements ofQt,t′′′ is different from the length of the elements of Qh,h′. This implies thatq(j+k)(modm)′+αiw(i)≠q(j+k)(modm)+αiw(i) for each i∈[1,n]. This implies that ci′≠ci, and hence σ(ci′)≠σ(ci), i∈[1,n], from which it follows that G′≠G.

(iii)   Since w′(i)≠w(i) and αi=1 therefore q(j+k)(modm)+αiw(i)≠q(j+k)(modm)+αiw′(i) for each i∈[1,n] in Eq. (7), where T(i)=S(j). This implies that ci′≠ci, and hence G′≠G.

By Lemma 1, our scheme is highly sensitive to the secret keys k,h,h′, and w. We demonstrate Lemma 1 with an example by generating ciphertexts for the plain text T = STAY SAFE by slightly changing one key and fixing all other keys. The ciphertext for k=6,h=18,h′=22, and weight function w listed in Tab. 2, ordered MEC E11,0,4 with diffusion ordering is listed in the first column of Tab. 5. The ciphertext generated by only changing the integer k to 7 following Lemma 1(i) is listed in the third column of Tab. 5. The ciphertext generated by only changing integer h′ to 23 following Lemma 1(ii) listed in the second column of Tab. 5. The ciphertext generated by only changing weight function to w′(i)=w(i)+10−4 following Lemma 1(iii) is listed in the fourth column of Tab. 5. The ciphertext generated by only changing EC E11,0,5 parameter b to 5 with diffusion ordering is listed in the fifth column of Tab. 5. From Tab. 5 it is evident that the ciphertext generated by slight changes in the secret keys are totally different. Hence, the proposed scheme satisfies the key sensitivity analysis.

4.3 Statistical Analysis

An encryption scheme is highly secure against statistical attacks if it can generate a highly random ciphertext. Histogram analysis and entropy analysis are the two commonly used tests to analyze the security of a scheme against statistical attacks. A scheme is secure against statistical attacks if it can generate ciphertexts with uniform histogram and optimal entropy.

Let X be a data set over a symbol set Ω and for ω∈Ω, f(ω) denotes the frequency of w in X. The entropy H(X) of X is defined to be

H(X)=−∑ω∈Ω⁡(f(ω)/|X|)log2(f(ω)/|X|)(10)

In the following result, we show that for each plain text, our scheme can generate a ciphertext with a uniform histogram and optimal entropy.

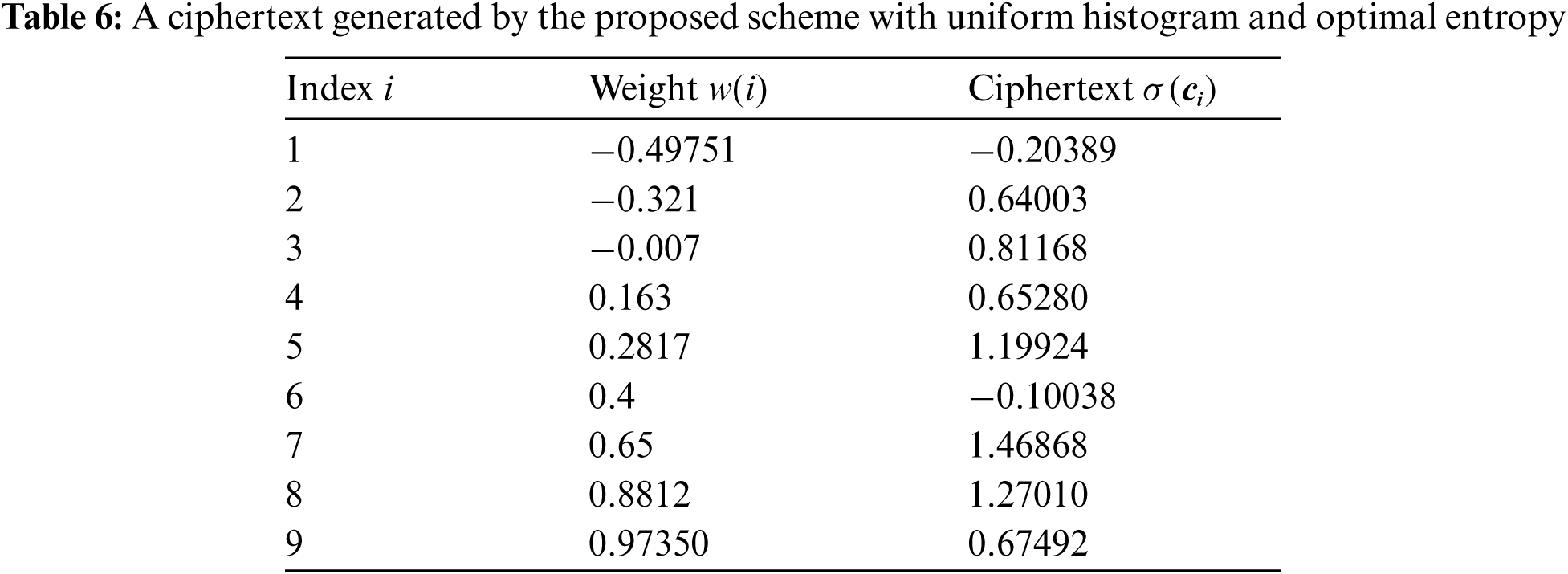
Lemma 2. For any plaint text, there exists at least one weight function w such that the frequency of each element in the ciphertext generated by the proposed scheme is 1.

Proof. Let T be a plain text of size n over a symbol set S and T(i),i∈[1,n] be the i-th element of T. Our proof will complete if we show that there exists at least one weight function w such that for any two distinct i,i′∈[1,n] it holds that the ci≠ci′, where ci and ci′ are generated by Eq. (7). Let gi=q(j+k)(modm)for i∈[1,n], where T(i)=S(j), for some j∈[1,m] and ψk(S(j))=S((j+k)(modm)). Let gi′ be an ordering of g1,g2,…,gn such that gi′≥gi′+1 for i′∈[1,n]. Let w be a mapping such that w(i′+1) is a real in the open interval (−1,w(i′)) and ci′+1=gi′+1+w(i′+1) for i′∈[1,n]. Note that w is an injection since w(i′)>w(i′+1) for each i′∈[1,n−1]. Furthermore, for each i′∈[1,n] it holds that gi′+w(i′)>gi′+1+w(i′+1), since gi′≥gi′+1 and w(i′)>w(i′+1) for each i′∈[1,n]. This implies that ci′>ci′+1 for each i′∈[1,n], and hencec1′c2′…cn′ is a strictly decreasing sequence.This implies that σ(ci)≠σ(cj) for each distinct i,j∈[1,n] from which the proof follows.

By Lemma 2, it follows that for each plain text, the proposed scheme can generate a ciphertext with uniform histogram and optimal entropy by using the weight function w constructed in Lemma 2 and αi=1 for each i. Hence the proposed scheme has provable security against statistical attacks. We demonstrate the claim in Lemma 2 in Tab. 6 by generating a ciphertext for the plain text T = STAY SAFE with secret keys k=6,h=18,h′=22, ordered ECs E11,0,4 with diffusion ordering and weight function w listed in Tab. 6.

4.4 Ciphertext Only Attack

In ciphertext only attack, the cryptanalyst has access to some ciphertexts and try to get secret keys and hence the plain text. The cryptanalyst cannot reveal the plain text without the secret keys of the proposed scheme. Furthermore, there are at least 2100 keys for a fixed plain text of size at least 4, as discussed in Section 4.1, and therefore the brute-force attack requires lots of time to decrypt the ciphertext without keys. Hence by [53] the proposed scheme is secure against ciphertext only attack.

4.5 Known-plaintext Attack

In this attack, the attacker knows a pair of plain text and ciphertext and tries to generate secret keys. In our scheme, the attacker tries to generate h,h′,k,w and σ(D′). The plain text consists of symbols in S and the ciphertext consists of real numbers with at most β digits after the decimal in our scheme, and therefore there is no relationship between the plain text and the keys h,h′,k and w. Recall that w(i)∈[−1,1], and therefore it is not necessary that h′−h+1 is at most the minimum number of digits after the decimal in the ciphertext. Thus, the attacker needs to try all possibilities for h,h′ such that h′−h+1≤β and there exists a restricted Pell sequence of the size |S|, and k to know the representation of symbols in S, the weight function w to know the index of the symbols in the plain text, and σ(D′) which depends on the latter keys. Furthermore, for a given plain text the proposed scheme can generate a completely different ciphertext when keys are changed, as discussed in Section 4.3. Hence the proposed scheme is highly secure against known-plaintext attack by [53].

4.6 Security Comparison

The proposed scheme has five secret keys, the three integers h,h′andk, the weight function w, and the encoded sequence σ′(D). The secret key depends on σ′(D) the choice of h,h′,k,w and the plain text. The main purpose of σ′(D) is to get the weight value w(i), and hence the index i when αi=0. However, if αi=1 for all i, then the weight w(i) are in the ciphertext by Eq. (7), and therefore the key σ′(D) is not necessary to get the weight function. More precisely, when αi=1 for all i, we solve Eq. (8) for d=1−qi, where qi∈Qh,h′ to get w. This implies that in the case of αi=1 for all i,k,h,h′ and w are sufficient keys to decrypt a ciphertext. Note that these keys are independent of the plain text. Furthermore, the proposed scheme also satisfies the key spacing analysis, key sensitivity analysis, statistical analysis, ciphertext only attack and known-plaintext attack for the case of αi=1 for all i as discussed in Sections 4.1–4.5.

We compared the security strength of the proposed scheme when αi=1 for all i, the case where all secret keys are independent of the plain text, and the schemes in [23–27,33,34,36,37, 48–51,53] against key spacing attack, key sensitivity attack, statistical attack, ciphertext only attack and known-plaintext attack in Tab. 7. We write “No” (resp. “NA”) in the second, fifth and sixth columns of Tab. 7 if the corresponding scheme is not secure (resp. the analysis of the scheme against key spacing attack, ciphertext only attack and known-plaintext attack is not available.) Similarly, we write “No” in the third and fourth columns of Tab. 7 if the corresponding scheme does not have provable security against key sensitivity attack and statistical attack. From Tab. 7 observe that the security of the schemes in [23–27,33,34,36,37,48–51,53] is suspected against key spacing attack, key sensitivity attack, statistical attack, ciphertext only attack and known-plaintext attack. Therefore from Sections 4.1–4.5, the proposed scheme is more secure against listed attacks as compared to the schemes [23–27,33,34,36,37,48–51,53].

The schemes in [49] and [53] do not have provable security against key sensitivity attack and statistical attack. By Sections 4.2 and 4.3, the proposed scheme has high security against key sensitivity and statistical attacks as compared to the security of the schemes in [49] and [53].

5  Conclusion

We proposed a secure text encryption scheme. The scheme has three main steps, where we first diffuse the plain text by permuting the symbol set to convert the plain text into a meaningless message. In the second step, the diffused plain text is encoded with real numbers based on the Pell sequence, a weight function, and a binary sequence to hide the diffused plain text. In the third step, the scheme creates confusion in the encoded diffused plain text by generating permutations over ECs. We analyzed the security of the proposed scheme against several modern attacks including key spacing attack, key sensitivity attack, statistical attacks, ciphertext only attack and known-plaintext attack. From the analysis it is clear that the proposed scheme has high resistance against modern attacks. Furthermore, we compared the security strength of the proposed scheme with the existing text encryption schemes in [23–27,33,34,36,37,48–51,53]. It is evident from the comparison that the proposed scheme is more secure as compared to the existing scheme against modern cryptanalysis.

By this scheme, we gave an application of the Pell sequence and ordered ECs in cryptography. In this scheme, we used binary sequence and weight function, which can be generated by any available method.

An interesting future direction would be to generate binary sequence and weight function by using ordered EC and propose an encryption scheme that can provide provable confidentiality and integrity.

Funding Statement: This research is funded through JSPS KAKENHI Grant Number 18J23484, QAU- URF 2015 and HEC project NRPU-7433.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  C. G. Kessler, An Overview of Cryptography, 2010. [Online]. Available: http://www.garykessler.net/library/crypto.html. [Google Scholar]

 2.  C. E. Shannon, “Communication theory of secrecy systems,” The Bell System Technical Journal, vol. 28, no. 4, pp. 656–715, 1949. [Google Scholar]

 3.  U. Hayat and N. A. Azam, “A novel image encryption scheme based on an elliptic curve,” Signal Processing, vol. 155, pp. 391–402, 2019. [Google Scholar]

 4.  N. A. Azam, U. Hayat and I. Ullah, “Efficient construction of a substitution box based on a Mordell elliptic curve over a finite field,” Frontiers of Information Technology and Electronic Engineering, vol. 20, no. 10, pp. 1378–1389, 2019. [Google Scholar]

 5.  N. A. Azam, U. Hayat and I. Ullah, “An injective S-box design scheme over an ordered isomorphic elliptic curve and its characterization,” Security and Communication Networks, vol. 2018, Article ID 3421725, 9 pages, 2018. [Google Scholar]

 6.  U. Hayat, N. A. Azam and M. Asif, “A method of generating 8 x 8 substitution boxes based on elliptic curves,” Wireless Personal Communications, vol. 101, no. 1, pp. 439–451, 2018. [Google Scholar]

 7.  A. A. Khan, V. Kumar and M. Ahmad, “An elliptic curve cryptography based mutual authentication scheme for smart grid communications using biometric approach,” Journal of King Saud University-Computer and Information Sciences, 2019. https://doi.org/10.1016/j.jksuci.2019.04.013. [Google Scholar]

 8.  V. Kumar, M. Ahmad, A. Kumari, S. Kumari and M. K. Khan, “SEBAP: A secure and efficient biometric-assisted authentication protocol using ECC for vehicular cloud computing,” International Journal of Communication Systems, vol. 34, no. 2, pp. 4103, 2019. [Google Scholar]

 9.  Z. E. Dawahdeh, S. N. Yaakob and R. R. B. Othman, “A new image encryption technique combining elliptic curve cryptosystem with hill cipher,” Journal of King Saud University-Computer and Information Sciences, vol. 30, no. 3, pp. 349355, 2018. [Google Scholar]

10. A. Razaq, H. Alolaiyan, M. Ahmad, M. A. Yousaf, U. Shuaib et al., “A novel method for generation of strong substitution-boxes based on coset graphs and symmetric groups,” in IEEE Access, vol. 8, pp. 75473–75490, 2020. [Google Scholar]

11. M. A. Yousaf, H. Alolaiyan, M. Ahmad, M. Dilbar and A. Razaq, “Comparison of pre and post-action of a finite abelian group over certain nonlinear schemes,” IEEE Access, vol. 8, pp. 39781–39792, 2020. [Google Scholar]

12. M. Khan and N. A. Azam, “Right translated AES gray S-boxes,” Security and Communication Networks, vol. 8, no. 9, pp. 1627–1635, 2015. [Google Scholar]

13. M. Khan and N. A. Azam, “S-boxes based on affine mapping and orbit of power function,” 3D Research, vol. 6, no. 2, pp. 12, 2015. [Google Scholar]

14. Ö. Koruoğlu and R. Sahin, “Generalized fibonacci sequences related to the extended hecke groups and an application to the extended modular group,” Turkish Journal of Mathematics, vol. 34, no. 3, pp. 325–332, 2010. [Google Scholar]

15. S. Ullah, L. Zhang, M. W. Sardar and M. T. Hussain, “Τ-Access policy: Attribute-based encryption scheme for social network based data trading,” China Communications, vol. 18, no. 8, pp. 183–198, 2021. [Google Scholar]

16. Z. Hua, S. Yi and Y. Zhou, “Medical image encryption using high-speed scrambling and pixel adaptive diffusion,” Signal Processing, vol. 144, pp. 134–144, 2018. [Google Scholar]

17. O. Vilardy, M. Juan, J. Barba, M. Torres and O. Cesar, “Image encryption and decryption systems using the jigsaw transform and the iterative finite field cosine transform,” Photonics, vol. 6, no. 4, pp. 121, 2019. [Google Scholar]

18. D. Lambić, A. Janković and M. Ahmad, “Security analysis of the efficient chaos pseudo-random number generator applied to video encryption,” Journal of Electronic Testing, vol. 36, no. 4, pp. 709–715, 2018. [Google Scholar]

19. H. A. Ahmed, M. F. Zolkipli and M. Ahmad, “A novel efficient substitution-box design based on firefly algorithm and discrete chaotic map,” Neural Computing and Applications, vol. 31, no. 11, pp. 7201–7210, 2019. [Google Scholar]

20. M. Ahmad, S. Khurana, S. Singh and H. D. AlSharari, “A simple secure hash function scheme using multiple chaotic maps,” 3D Research, vol. 8, no. 28, pp. 13, 2017. [Google Scholar]

21. M. Ahmad, M. N. Doja and M. M. S. Beg, “Security analysis and enhancements of an image cryptosystem based on hyperchaotic system,” Journal of King Saud University-Computer and Information Sciences, vol. 33, no. 1, pp. 77–85, 2021. [Google Scholar]

22. N. A. Azam, “A novel fuzzy encryption technique based on multiple right translated AES Gray S-boxes and phase embedding,” Security and Communication Networks, vol. 2017, Article ID 5790189, 9 pages, 2017. [Google Scholar]

23. K. Abdullah, S. A. Bakar, N. H. Kamis and H. Aliamis, “RSA cryptosystem with fuzzy set theory for encryption and decryption,” in AIP Conference Proceedings, vol. 1905, no. 1, pp. 030001, 2017. [Google Scholar]

24. V. Gupta, G. Singh and R. Gupta, “Advance cryptography algorithm for improving data security,” International Journal of Advanced Research in Computer Science and Software Engineering, vol. 2, no. 1, pp. 1–6, 2012. [Google Scholar]

25. S. Pattanayak and D. Dey, “Text encryption and decryption with extended Euclidean algorithm and combining the features of linear congruence generator,” International Journal of Development Research, vol. 6, no. 7, pp. 8753–8756, 2016. [Google Scholar]

26. E. Agrawal and P. R. Pal, “A secure and fast approach for encryption and decryption of message communication,” International Journal of Engineering Science, vol. 7, no. 5, pp. 11481, 2017. [Google Scholar]

27. S. E. Ghrare, H. A. Barghi and N. R. Madi, “New text encryption method based on hidden encrypted symmetric key,” in Int. Conf., Advanced Computer Information Technologies, Ceske Budejovice, Czech Republic, 2018. [Google Scholar]

28. Q. Mushtaq and U. Hayat, “Horadam generalized Fibonacci numbers and the modular group,” Indian Journal of Pure and Applied Mathematics, vol. 38, no. 5, pp. 345, 2007. [Google Scholar]

29. Q. Mushtaq and U. Hayat, “Pell numbers, Pell-Lucas numbers and modular group,” Algebra Colloquium, Academy of Mathematics and Systems Science, Chinese Academy of Sciences, and Suzhou University, vol. 14, no. 1, pp. 97–102, 2007. [Google Scholar]

30. T. Koshy, Pell and Pell-Lucas Numbers with Applications, New York: Springer, 2014. [Google Scholar]

31. A. Luma and B. Raufi, “Relationship between fibonacci and lucas sequences and their application in symmetric cryptosystems,” in Proc. of the 4th Int. Conf. on Circuits, Systems and Signals, World Scientific and Engineering Academy and Society (WSEAS), Corfu Island, Greece, pp. 146–150, 2010. [Google Scholar]

32. A. Overmars and S. Venkatraman, “An efficient golden ratio method for secure cryptographic applications,” Mathematical and Computational Applications, vol. 23, no. 4, pp. 58, 2018. [Google Scholar]

33. P. Agarwal, N. Agarwal and R. Saxena, “Data encryption through fibonacci sequence and unicode characters,” MIT International Journal of Computer Science and Information Technology, vol. 5, no. 2, pp. 79–82, 2015. [Google Scholar]

34. T. Clelland, V. Risca and C. Bancroft, “Hiding messages in DNA microdots,” Nature, vol. 399, no. 6736, pp. 533–534, 1999. [Google Scholar]

35. M. Borda and O. Tornea, “DNA secret writing techniques,” in 2010 8th Int. Conf. on Communications IEEE, Bucharest, Romania, pp. 451–456, 2010. [Google Scholar]

36. M. R. Abbasy, A. A. Manaf and M. A. Shahidan, “Data hiding method based on DNA basic characteristics,” in Int. Conf. on Digital Enterprise and Information Systems, Springer, Berlin, Heidelberg, pp. 53–62, 2011. [Google Scholar]

37. M. A. Murillo-Escobar, F. Abundiz-Prez, C. Cruz-Hernndez and R. M. Lpez-Gutirrez, “A novel symmetric text encryption algorithm based on logistic map,” in Proc. of the Int. Conf. on Communications, Signal Processing and Computers, Honolulu, Hawaii, USA, vol. 4953, 2014. [Google Scholar]

38. H. Perez-Meana, E. Hernandez-Diaz and V. Silva-Garcia, “Encryption of RGB images by means of a novel cryptosystem using elliptic curves and chaos,” IEEE Latin America Transactions, vol. 18, no. 8, pp. 1407–1415, 2020. [Google Scholar]

39. I. Hussain, N. A. Azam and T. Shah, “Stego optical encryption based on chaotic S-box transformation,” Optics and Laser Technology, vol. 61, pp. 50–56, 2014. [Google Scholar]

40. M. Ahmad and M. S. Alam, “A new algorithm of encryption and decryption of images using chaotic mapping,” International Journal on Computer Science and Engineering, vol. 2, no. 1, pp. 46–50, 2009. [Google Scholar]

41. X. Zhang, Y. Mao and Z. Zhao, “An efficient chaotic image encryption based on alternate circular S-boxes,” Nonlinear Dynamics, vol. 78, no. 1, pp. 359–369, 2014. [Google Scholar]

42. M. Ahmad, M. N. Doja and M. M. S. Beg, “Security analysis and enhancements of an image cryptosystem based on hyperchaotic system,” Journal of King Saud University-Computer and Information Sciences, vol. 33, no. 1, pp. 77–85, 2021. [Google Scholar]

43. A. A. A. El-Latif and X. Niu, “A hybrid chaotic system and cyclic elliptic curve for image encryption,” AEU-International Journal of Electronics and Communications, vol. 67, no. 2, pp. 136–143, 2013. [Google Scholar]

44. R. I. Abdelfatah, “Secure image transmission using chaotic-enhanced elliptic curve cryptography,” IEEE Access, vol. 8, pp. 3875–3890, 2019. [Google Scholar]

45. I. Ullah, U. Hayat and M. D. Bustamante, “Image encryption using elliptic curves and Rossby/drift wave triads,” Entropy, vol. 22, no. 4, pp. 454, 2020. [Google Scholar]

46. S. Toughi, M. H. Fathi and Y. A. Sekhavat, “An image encryption scheme based on elliptic curve pseudo random and advanced encryption system,” Signal Processing, vol. 141, pp. 217–227, 2017. [Google Scholar]

47. L. D. Singh and K. M. Singh, “Image encryption using elliptic curve cryptography,” Procedia Computer Science, vol. 54, pp. 472–481, 2015. [Google Scholar]

48. C. H. Suneetha, T. Surendra and C. H. Neelima, “Implementation of double fold text encryption based on elliptic curve cryptography (ECC) with digital signature,” International Journal of Recent Technology and Engineering (IJRTE), vol. 8, no. 5, pp. 3840–3846, 2020. [Google Scholar]

49. M. A. Naji, D. A. Hammood, H. A. Atee, R. S. Jebur, H. A. Rahim et al., “Cryptanalysis cipher text using new modeling: text encryption using elliptic curve cryptography,” in AIP Conf. Proc., Putrajaya, Malaysia, vol. 2203, no. 1, pp. 020003, 2020. [Google Scholar]

50. K. Agrawal and A. Gera, “Elliptic curve cryptography with hill cipher generation for secure text cryptosystem,” International Journal of Computer Applications, vol. 106, no. 1, pp. 18–24, 2014. [Google Scholar]

51. K. Keerthi and B. Surendiran, “Elliptic curve cryptography for secured text encryption,” in Int. Conf. on Circuit, Power and Computing Technologies (ICCPCT), Kollam, India, IEEE, pp. 1–5, 2017. [Google Scholar]

52. A. Kumar, S. S. Tyagi, M. Rana, N. Aggarwal and P. Bhadana, “A comparative study of public key cryptosystem based on ECC and RSA,” International Journal on Computer Science and Engineering, vol. 3, no. 5, pp. 1904–1909, 2011. [Google Scholar]

53. L. D. Singh and K. M. Singh, “Implementation of text encryption using elliptic curve cryptography,” Procedia Computer Science, vol. 54, pp. 73–82, 2015. [Google Scholar]

54. S. Ullah, X. Li and L. Zhang, “A review of signcryption schemes based on hyper elliptic curve,” in 3rd Int. Conf. on Big Data Computing and Communications (BIGCOM), Chengdu, China, pp. 51–58, 2017. [Google Scholar]

55. S. Ullah, X. Y. Li and Z. Lan, “A novel trusted third party based signcryption scheme,” Multimedia Tools and Applications, vol. 79, pp. 22749–22769, 2020. [Google Scholar]

56. S. Ullah and N. Din, “Blind signcryption scheme based on hyper elliptic curves cryptosystem,” Peer-to-Peer Networking and Applications, vol. 14, no. 2, pp. 917–932, 2021. [Google Scholar]

57. L. C. Washington, Elliptic Curves: Number Theory and Cryptography, New York: CRC Press, 2008. [Online]. Available: https://https://doi.org/10.1201/9781420071474. [Google Scholar]

58. Keith M. Martin, Everyday Cryptography: Fundamental Principles and Applications, Oxford University Press, 2012. [Google Scholar]

59. S. M. Seyedzadeh, B. Norouzi, M. R. Mosavi and S. Mirzakuchaki, “A novel color image encryption algorithm based on spatial permutation and quantum chaotic map,” Nonlinear Dynamics, vol. 81, no. 1–2, pp. 511–529, 2015. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.