DOI:10.32604/cmc.2022.023257

| Computers, Materials & Continua DOI:10.32604/cmc.2022.023257 |  |
| Article |
Hybrid Ensemble-Learning Approach for Renewable Energy Resources Evaluation in Algeria
1Department of Communications and Electronics, Delta Higher Institute of Engineering and Technology, Mansoura, Egypt
2Faculty of Artificial Intelligence, Delta University for Science and Technology, Mansoura 35712, Egypt
3Computer Engineering and Control Systems Department, Faculty of Engineering, Mansoura University, Mansoura, Egypt
4Energies and Materials Research Laboratory, Faculty of Sciences and Technology, University of Tamanghasset, 10034, Tamanghasset, Algeria
5URERMS, Centre de Développement des Energies Renouvelables (CDER), 01000, Adrar, Algeria
6Mechanical Power Engineering Department, Faculty of Engineering, Cairo University, Giza, 12613, Giza, Egypt
7Department Computer Sciences, Universidad Rey Juan Carlos, Móstoles, 28933, Madrid, Spain
8Department of Civil, Environmental and Natural Resources Engineering, Lulea University of Technology, 97187, Lulea, Sweden
*Corresponding Author: Nadjem Bailek. Email: prbailek@gmail.com
Received: 01 September 2021; Accepted: 09 October 2021
Abstract: In order to achieve a highly accurate estimation of solar energy resource potential, a novel hybrid ensemble-learning approach, hybridizing Advanced Squirrel-Search Optimization Algorithm (ASSOA) and support vector regression, is utilized to estimate the hourly tilted solar irradiation for selected arid regions in Algeria. Long-term measured meteorological data, including mean-air temperature, relative humidity, wind speed, alongside global horizontal irradiation and extra-terrestrial horizontal irradiance, were obtained for the two cities of Tamanrasset-and-Adrar for two years. Five computational algorithms were considered and analyzed for the suitability of estimation. Further two new algorithms, namely Average Ensemble and Ensemble using support vector regression were developed using the hybridization approach. The accuracy of the developed models was analyzed in terms of five statistical error metrics, as well as the Wilcoxon rank-sum and ANOVA test. Among the previously selected algorithms, K Neighbors Regressor and support vector regression exhibited good performances. However, the newly proposed ensemble algorithms exhibited even better performance. The proposed model showed relative root mean square errors lower than 1.448% and correlation coefficients higher than 0.999. This was further verified by benchmarking the new ensemble against several popular swarm intelligence algorithms. It is concluded that the proposed algorithms are far superior to the commonly adopted ones.
Keywords: Renewable energy resources; hybrid modeling; tilted solar irradiation; arid region
The performance of photovoltaic or thermal energy conversion systems depends on the orientation and the inclination angle of their collection fields compared to the horizon. Usually (for technical and economic considerations), these systems are installed in a fixed tilted position according to the considered site location for maximum solar energy collection. On the other hand, the inclination angle of photovoltaic arrays or solar thermal collectors could also be adjusted few times a year according to optimum tilt angles defined for specific periods or seasons [1]. The energy gain of these systems is dependent on the availability of solar irradiation on the inclined surface. As a result, determining the generated power requires knowledge of solar irradiance on a photovoltaic (PV) panel in the plane-of-Array (POA). Even though global radiation on a horizontal plane is measured at many meteorological stations around the world, direct measurements of solar radiation on inclined surfaces are very scarce [2]. Over the years, various mathematical models have been developed to calculate solar radiation on tilted surfaces from measured data on the horizontal surface. Evaluation of some of the most widely used such models can be found in [3]. Demain et al. [4] compared 14 models for transposing horizontal radiation to inclined surfaces. They utilized the data for eight months (April to November 2011) from the Royal Meteorological Institute of Belgium in Uccle. The performance of the models was validated against the measured solar radiation data on an inclined surface held at 50.79˚. It was reported that the discrepancies appearing in the models’ outputs could be attributed to intermediate sky conditions, which were found to be very small in case of clear or overcast situations. It was further reported that the isotropic sky consideration yields better results against the anisotropic sky assumption. Notton et al. [5] used ANNs to estimate the hourly solar radiation on the inclined surface from the global horizontal solar radiation using three models for the Mediterranean site of Ajaccio, France. They used five years of measured data (2006–2010). Optimization of the ANN structure was performed for the number of layers, the number of neurons per layer, and the input data size. They also performed a comparison of empirical models with the newly developed ANN model. It was finally concluded that the ANN method produces more reliable results than the conventional models and that the modeling and optimization of PV equipment can rely on the performance estimation of ANN techniques. Shaddel et al. [6] analyzed the performance of the ANN technique to estimate global solar irradiance on tilted surfaces for application in PV and photothermal applications in the city of Mashhad (Iran). Several input parameters were considered, such as the global solar irradiation, extraterrestrial horizontal irradiation, number of days, collector angle, solar altitude angle, and latitude of the location. The ANN was analyzed and optimized for performance for various tilts 0°, 45° and 60° at an interval during the day length of 6:00 to 17:00 h for the year 2013. The performance of the ANN was verified against the ground measured data for inclined surfaces. It was reported that ANN could effectively be used as a reliable tool for estimating solar radiation on inclined surfaces. Takilalte et al. [7] proposed a new methodology to estimate global irradiation on inclined surfaces at five-minute intervals from the data of global horizontal irradiation. They combined the traditional Liu and Jordan model with Perrin Brichambau with an ANN technique to optimize the model and introduced sky-related conditions to transform the isotropic model into an anisotropic model. They compared the newly developed model with the similar form available in the literature previously. It was reported that the new model, tested under complex sky conditions, has smaller errors and better estimation accuracy due to the effective combination of the ANN model with the conventional ones. Dahmani et al. [8] transposed the 5-min interval measured solar radiation data (obtained for two years) for an inclined surface using the ANN technique for the region of Bouzareah, Algeria. The optimization of the number and types of input data was accomplished using sensitivity analysis. One hidden layer was deemed to be sufficient for estimating the 5-min interval data on the inclined surface. Notton et al. [9] presented the neural network approach to estimate solar radiation on a tilted plane from horizontal ones at a 10-min interval using three models. The ANN was based on the Levenberg-Marquardt algorithm (LM). It was developed and optimized using five years of solar data obtained from the “Sciences for Environment” laboratory at the University of Corsica Pascal Paoli with a meteorological station installed at Ajaccio. The accuracy of the optimal configuration was reported to be around 9% in terms of root mean square error (RMSE) and around 5.5% for the relative mean absolute error (RMAE), and it was concluded that these errors are indeed lower in comparison for those obtained from empirical correlations available in the literature and used for the estimation of hourly data.
Hybrid-learning methods have attracted increasing attention amongst researchers. In recent years, various hybrid-learning techniques have been proposed and used to evaluate solar energy resources. Alrashidi et al. [10] proposed a framework by hybridizing Support Vector Regression (SVR) with the Grasshopper Optimization Algorithm (GOA) and the Boruta-based feature selection algorithm (BA), abbreviated as (VR-GOA-BAK), for forecasting global solar radiation values at different locations of Saudi Arabia. It was reported that the proposed algorithm has a lower mean absolute percentage error (MAPE) and outperforms the classical SVR models by 32.15–39.69% for the selected locations of the study. Demircan et al. [11] improved the performance of the empirical Angstrom-Prescott model for solar radiation estimation using the Artificial Bee Colony (ABC) algorithm for the city of Muğla, Turkey. Both annual and semi-annual models were developed, and the performance was enhanced using the computational algorithm. It was also reported that the models solely relying on sunshine duration do not exhibit reliable performances, and therefore, sunset-sunrise hour angle should also be included in the models to enhance the performance. Zhou et al. [12] presented a review of machine learning models based on 232 previously reported research articles. They focused on the type of input parameters included, the kind of feature selection method, and the model development procedure. Seven classes of machine-learning models were defined based on the pre-processing data algorithms, output ensemble methods, and the purpose of the models. It was suggested that the quality control of data used for developing the model should be performed to remove the solar radiation measurement errors and account for instrument failure. Further, it was recommended that novel and combined machine-learning models be the focus of studies in the future. Pang et al. [13] investigated the use of deep learning techniques for solar radiation estimation for the region of Alabama. An ANN model and a recurrent neural network (RNN) were analyzed with different sampling frequencies and moving window algorithms to verify accuracy and efficiency. It was reported that RNN outperforms the ANN algorithm and has a 26% higher accuracy. The performance of RNN was further improved from 0.9% normalized mean bias error (NMBE) to 0.2% using a moving window algorithm. Bellido-Jimenez et al. [14] developed and compared different machine learning models to estimate solar radiation at various locations of southern Spain and the USA. Intrahourly inputs were used to improve the performance of the models. It was suggested that machine learning models outperform the self-calibrated empirical models. It was reported that the multi-layer perceptron (MLP) algorithm outperforms the other algorithms and exhibits the best performance using the new proposed variables for the locations considered with medium aridity values. Further, SVR and random forest (RF) models were suggested to be better for the aridest and most humid sites.
In most aforementioned papers, the climate variables are used to estimate solar radiation on a horizontal plane, or the horizontal solar radiation is used as an input variable to estimate radiation on a tiled surface [15–17]. In this paper, we estimated hourly tilted solar irradiation using climate variables. Moreover, irradiance is estimated by hybrid ensemble-learning approach, hybridizing Advanced Squirrel Search Optimization Algorithm (ASSOA) and Support Vector Regression methods, which to the best of our knowledge, has not been used for solar radiation modeling. In addition, the results are compared to those of several other popular swarm intelligence algorithms, including the genetic algorithm, particle swarm optimization [18], and Grey Wolf Optimizer [19].
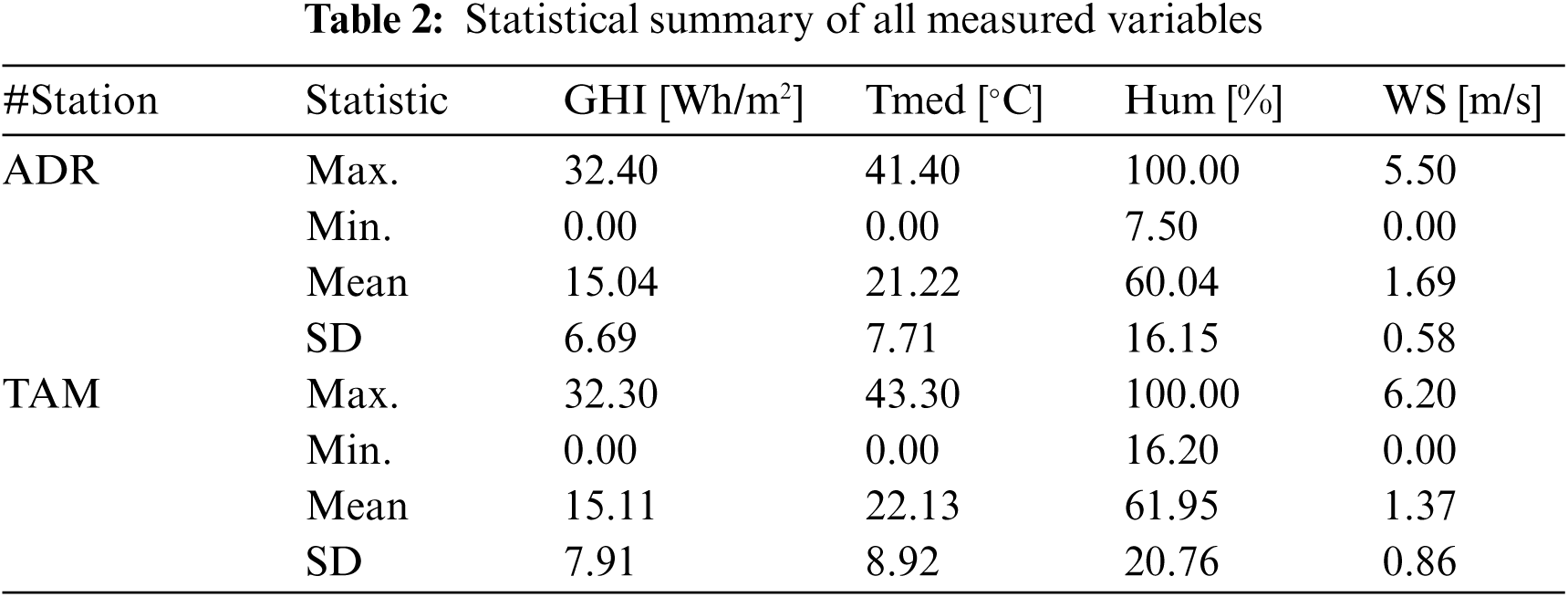
Hourly solar radiation on tilted surfaces measured at the ground is processed in this study. Data were collected from two radiometric stations located in the southern region of Algeria. Tab. 1 presents the station list, including the geographical coordinates and the measurement period. According to Köppen's climate classification, Tamanrasset (TAM) and Adrar (ADR) have a hot desert (BWh) climate with distinct wet and dry seasons. A statistical summary of all measured variables is given in Tab. 2. In this table, GHI, Tmed, Hum, and WS respectively represent the global horizontal irradiation, mean air temperature, relative humidity, and wind speed.

3.1 The ASSOA Regression Algorithm
The Advanced Squirrel Search Optimization Algorithm (ASSOA) was first proposed in [20] for the classification purpose based on two stages to classify chest X-ray images. In this paper, the ASSOA algorithm is applied for the regression problem for the evaluation of renewable energy resources in the Saharan Algeria region. The ASSOA algorithm considers that the agents/individuals are changing their positions in the search space between three kinds of places named-normal, oak, and hickory trees. The optimal solution (nuts food sources) are represented as oak-and-hickory trees. In a mathematical form, the ASSOA algorithm assumes the searching agents are moving to search for the best solution (hickory tree) and next best solutions (three oak trees) for n agents (
The initial locations of
The best solution value of the objective function indicates a hickory tree. The calculated values are sorted in ascending order. The first best solution is
Case 1: Location of
Case 2: Location of
Case 3: Location of
where
Case 4: Location of
where
Case 5: Location of
where
Case 6: Location of
where b is a random number
The constant of seasonal,
The value of
The ASSOA algorithm is explained step-by-step in Algorithm 1. Steps 1 and 2 initialize the algorithm parameters. The objective function is then calculated for each agent to sort them and get the first, second, and third best agents and normal agents in Steps 3 and 4. From Step 5 to Step 44, the algorithm is working to update the agents’ positions. Steps from 45 to 50 calculate and update positions based on the seasonal constant to avoid local minima. The best solution is obtained by the end of the algorithm at Step 53.

The performance metrics used for the classification measurements are RRMSE, MBE, RMSE, MAE, and R. The mean absolute error (MAE) determines the average of absolute errors. The mean bias error (MBE) indicates whether the tested model is under-or over-predicting the actual measurements. The correlation coefficient (R) indicates the strength of the correlation between actual and estimated values. The root mean square error (RMSE) and the relative RMSE (RRMSE) provide estimates of the absolute and relative random error components [21–23].
4.1 Ensemble Selection Scenario
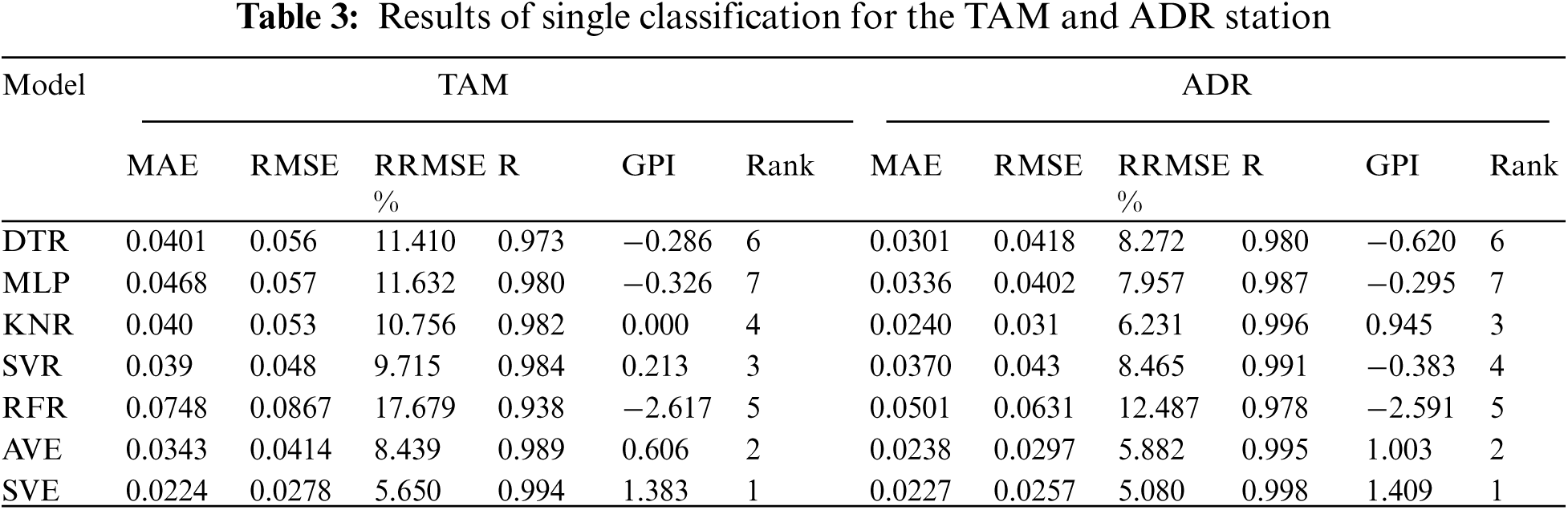
The experiments are divided into two parts. First, the effectiveness of the five models is evaluated for technique selection based on the long-term measured meteo-solar datasets including mean air temperature, relative humidity, wind speed, and global horizontal irradiation, alongside extra-terrestrial horizontal irradiance, for the two Algerian stations. Second, an ensemble-learning method is selected to be used for the estimation of solar radiation. Each investigated dataset is divided randomly into three subsets for training, validation, and testing (60%, 20%, and 20%, respectively). The training set is used to train a k-nearest neighbors (KNN) classifier during the learning phase, the validation set is used when calculating the fitness function for a specific solution, and the testing set is used to evaluate the efficiency of the used techniques. For the KNN classifier, the number of k-neighbors is 5, and the k-fold cross-validation value is set to 10. The selected methods are Decision Tree Regressor (DTR), MLP Regressor (MLP), K-Neighbors Regressor (KNR), Support Vector Regression (SVR), and Random Forest Regressor (RFR). In addition, Average Ensemble (AVE) and Ensemble using SVR (SVE) are two new proposed ensembles for developing solar radiation estimators.
The evaluation of the accuracy of the five selected methods is provided based on the testing dataset, i.e., to determine their capability of handling input data. Fig. 1 shows a comparison between the RMSE values for the different models in each station based on the testing data. It is observed that the KNR approach presents the lowest RMSE values, followed by the MLP approach at ADR and the SVR approach at TAM.
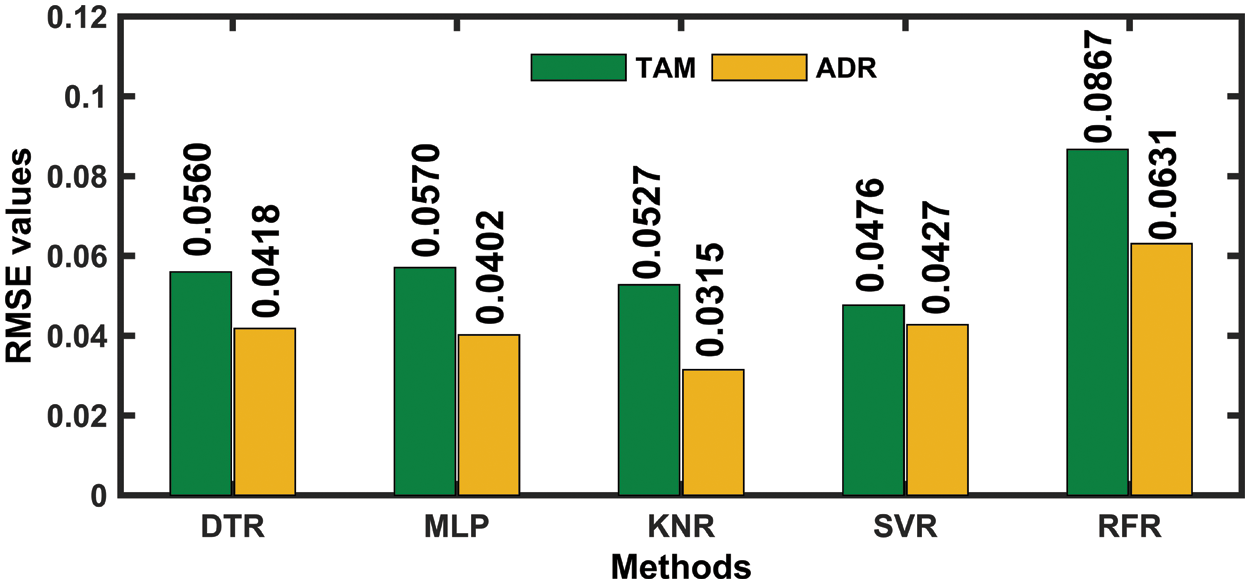
Figure 1: RMSE for five selected methods and each station
Tab. 3 presents the main error metrics of the five selected machine-learning techniques used to select the new ensemble-learning approach. In general, MAE ranges between 0.0260 and 0.0867 for the two sites. The obtained RMSE values also imply a good performance, with high positive correlations, as expected. Although each statistical parameter can evaluate the performance of the model from a specific point of view, it is very difficult for a single statistical parameter to comprehensively evaluate the performance of models. We, therefore, propose to use a supplement statistical score, namely the Global Performance Index (GPI), which has been extensively employed in recent years because of its comprehensiveness and wide applicability. GPI considers different statistical parameters to evaluate the performance of models [24,25] The GPI calculation method is given by Eq. (13).
Here,
4.2 Proposed Hybrid Model Results
The ability of the proposed SVR ensemble-based ASSOA algorithm for improving the accuracy is investigated vs. other algorithms. The parameters of
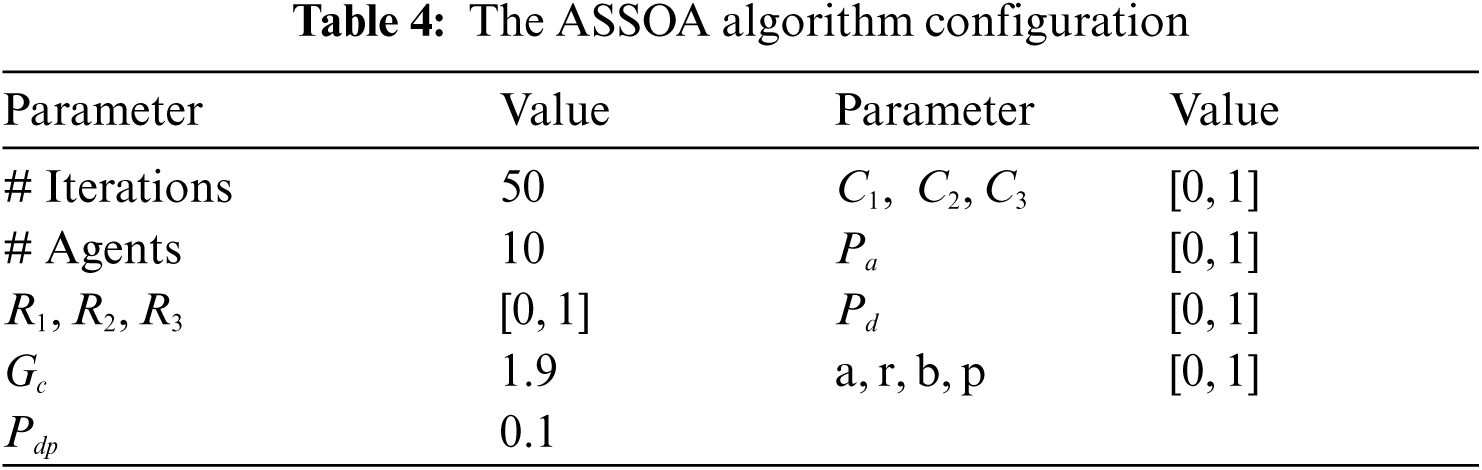
Fig. 2 presents a graph of the measured and predicted hourly tilted irradiance for the combined ASSOA approach. The figure shows a high degree of agreement between actual values and the estimates, which suggests that the proposed model in the study is more reliable than the available approaches. ANOVA statistical tests are performed to ensure the quality of the proposed ASSOA algorithm. The results are shown in Tabs. 5 and 6. On the other hand, Fig. 3 depicts the distributions of estimated residuals at the two locations.
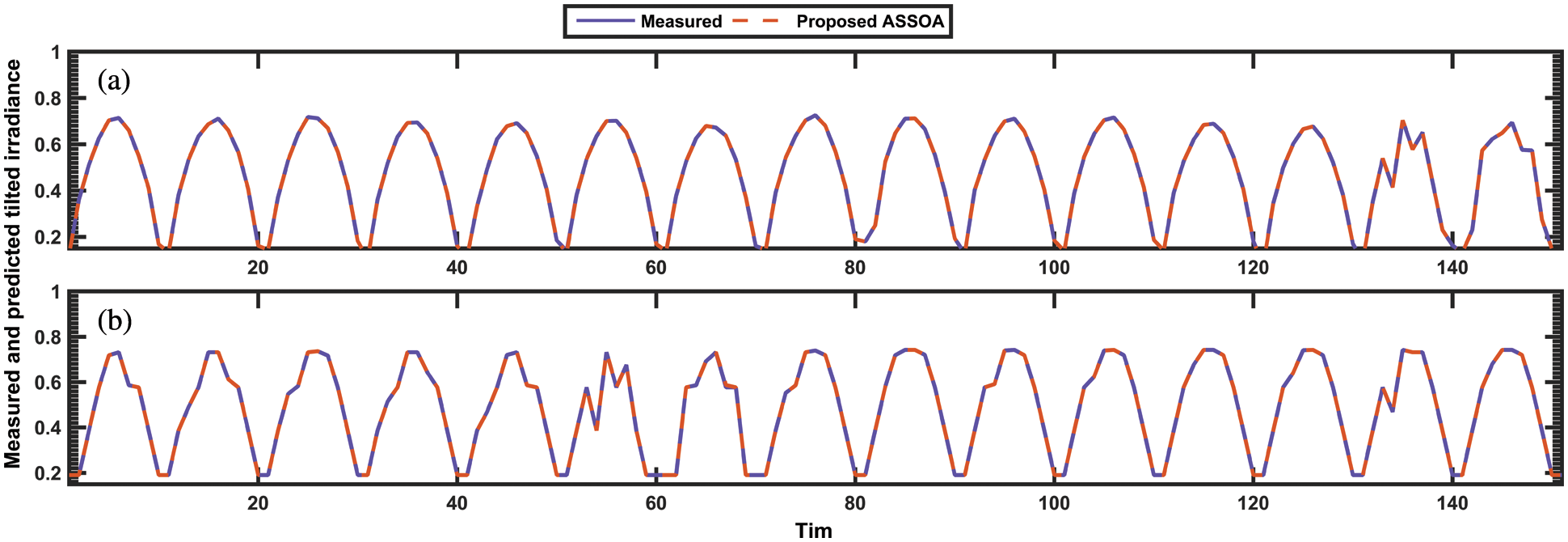
Figure 2: Optimized weights predicted values by the proposed model during 15 consecutive days at (a) ADR, and (b) TAM stations
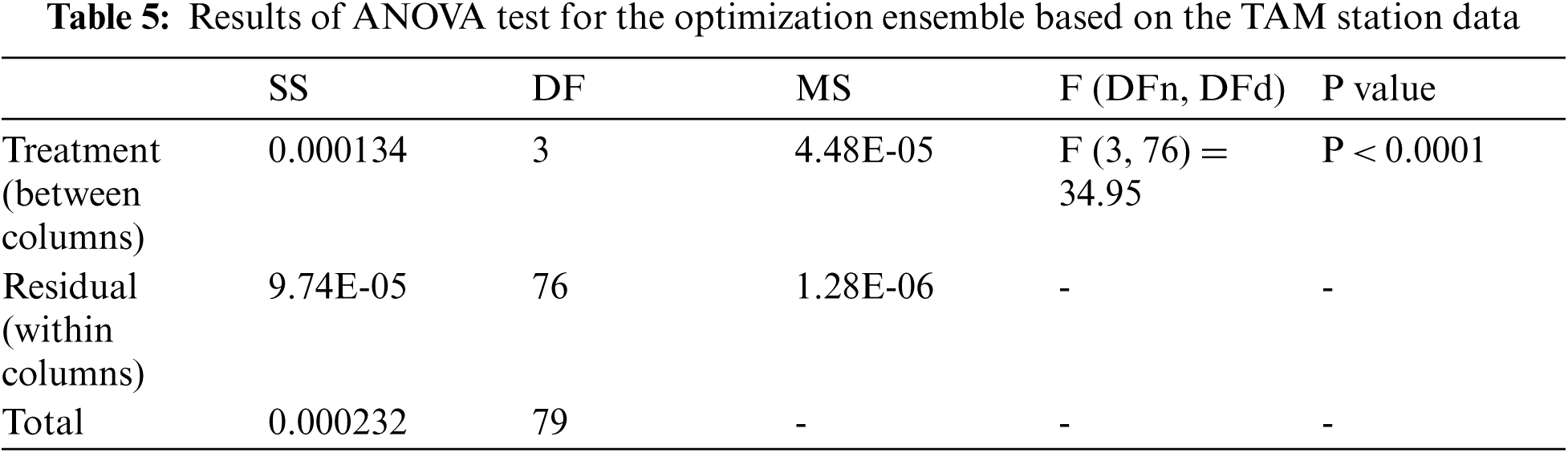
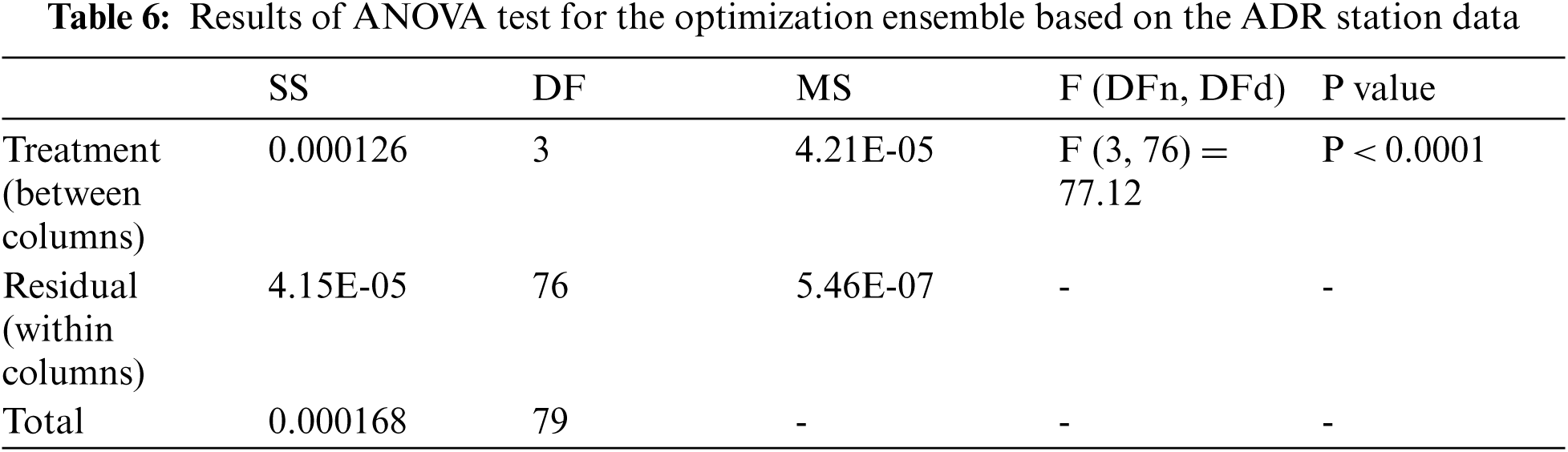
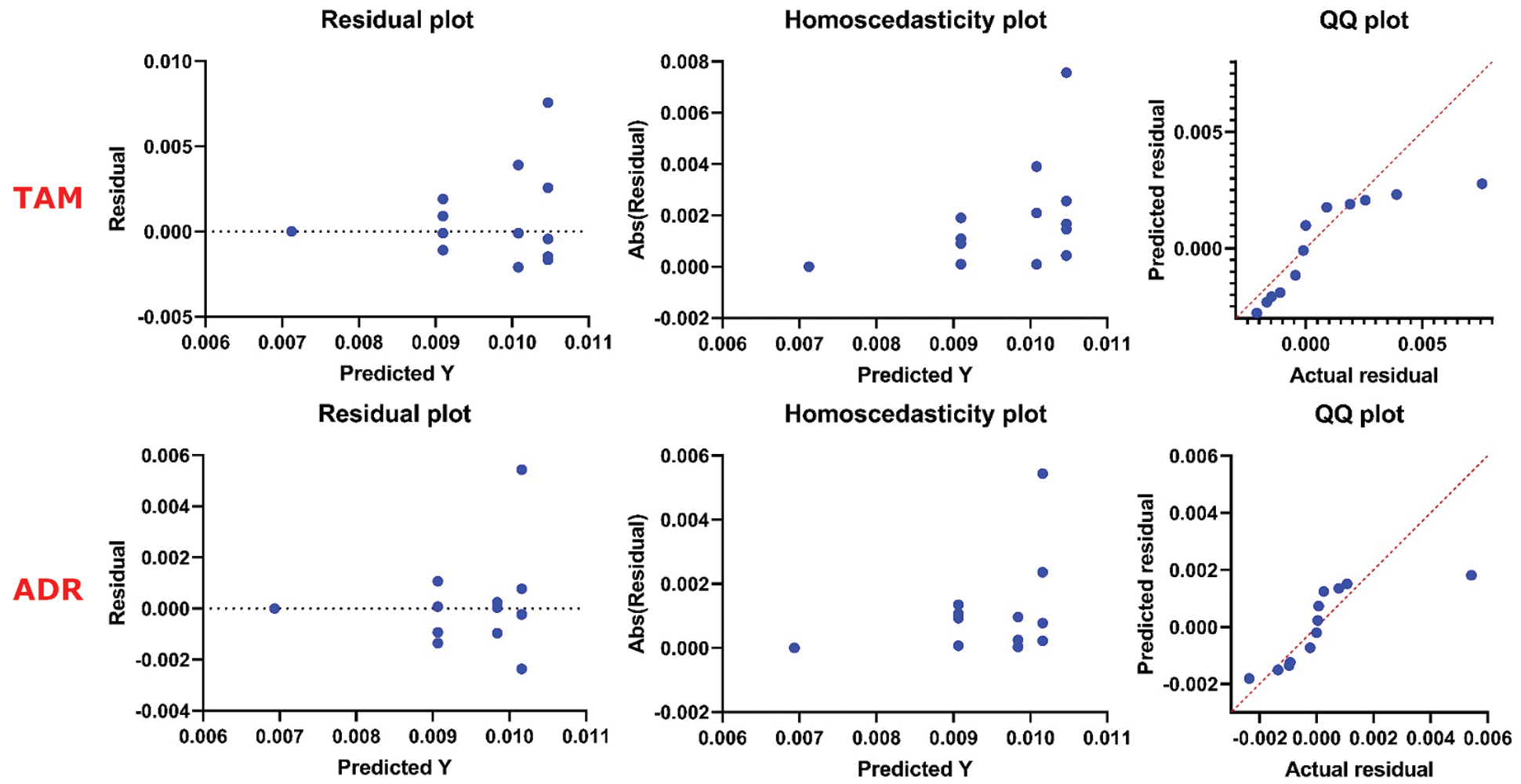
Figure 3: Residual plots of the proposed model at the two stations
To check the sensitivity of the proposed model to the weather conditions, different sky conditions (cloudiness) were considered. This time, the database was divided into three sub-databases according to the cloudiness index value, namely clear sky (CRS), partly cloudy sky (PCR), and complete overcast sky (OTS). The Box plots given in Fig. 4 represent the corresponding results of testing in each class of sky conditions. Without exception, the proposed model performs better under CRS conditions. The model achieves a quite similar accuracy for the PCR and OTS conditions at ADR.
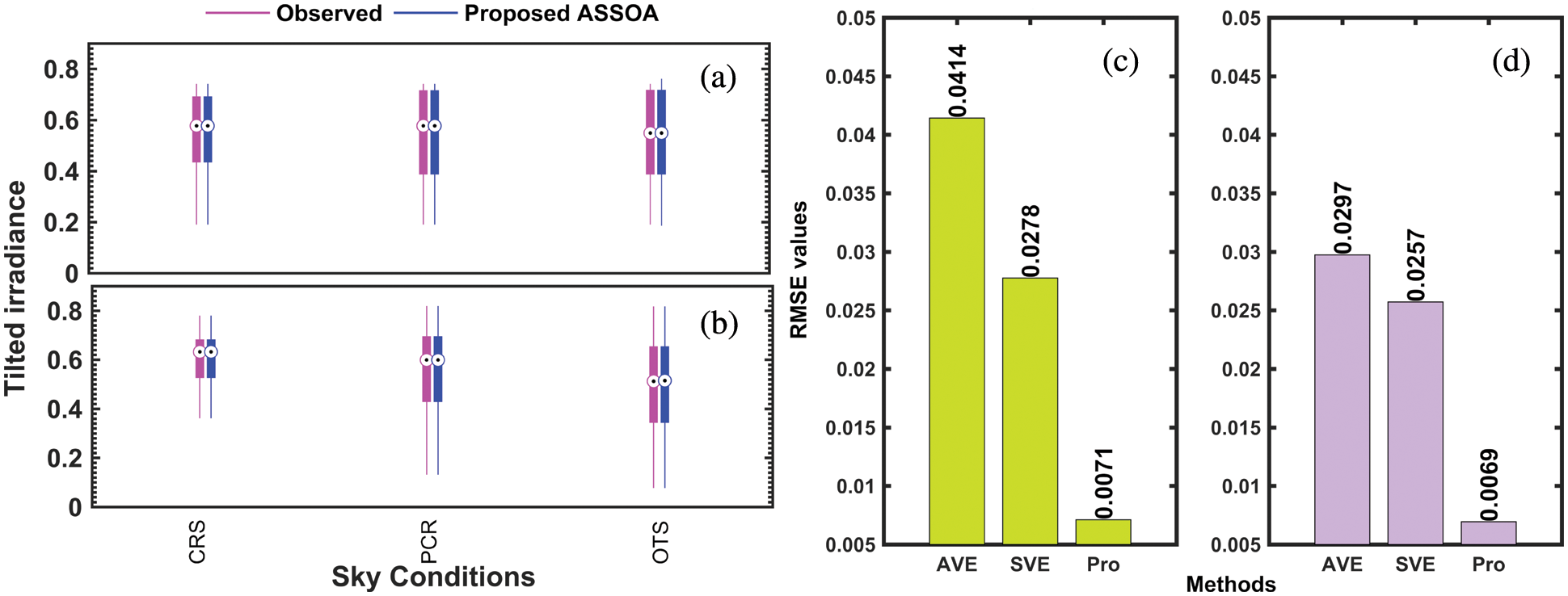
Figure 4: Boxplot for the proposed model test for different sky conditions at (a) ADR and (b) TAM, and comparison between the proposed SVR ensemble-based ASSOA algorithm and two selected ensembles models based on overall RMSE-score at (c) ADR and (d) TAM
4.3 Proposed Optimization Ensemble vs. Other Algorithms
This experimental test is used to investigate how the ASSOA optimization algorithm helps to improve the accuracy of solar radiation prediction models. To verify the effectiveness of the proposed prediction model, the following groups of comparative experiments are carried out using previously described ensembles models (AVE and SVE). The verification experiments are carried out based on measurement at ADR and TAM. The corresponding RMSEs are depicted in Fig. 4. It is found that the RMSE values for the proposed model are extremely less than the corresponding values for the two-best ensemble models from the previous investigation.
Next, to verify the superiority of the proposed method, several other popular swarm intelligence algorithms including the genetic algorithm (GA), particle swarm optimization (PSO), and Grey Wolf Optimizer (GWO) are used as the benchmark algorithms. The configurations of the GA, PSO, and GWO algorithms, including the number of iterations (generations), population size, and other parameters, are shown in Tab. 7.
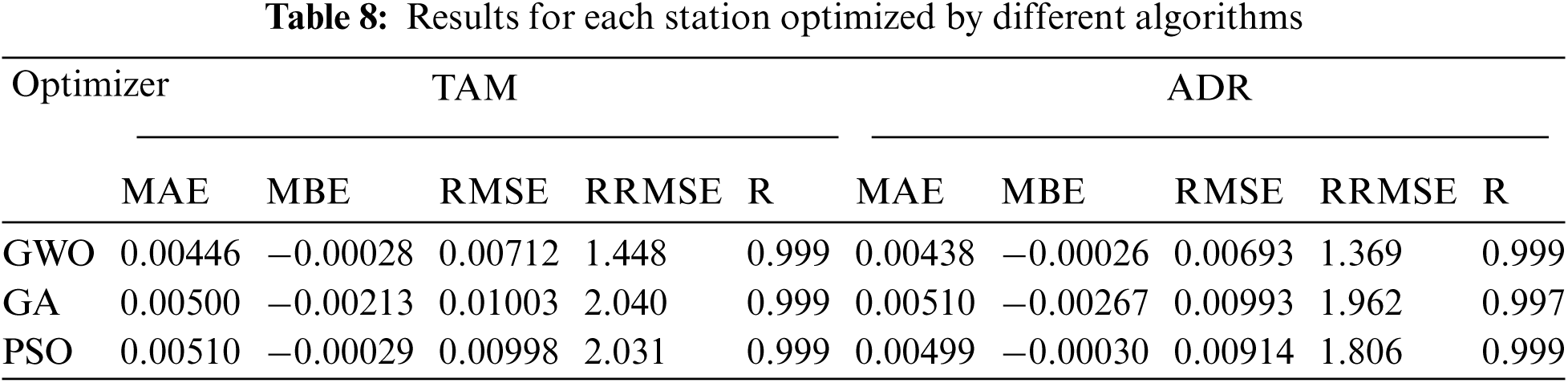
The testing results of the selected swarm intelligence algorithms in this study are presented in Tab. 8 in terms of the performance indicators described in Section 3.2. Among these algorithms, GA's estimates are characterized by the highest uncertainty (roughly the RRMSE ranges between 1.96% and 2.04%) while PSO achieves the smallest uncertainty (RRMSEs range between 1.37% and 1.45%). In fact, PSO takes the first position in three swarm intelligence algorithms. GWO performs comparable or slightly better than GA in terms of RMSE and REMSE.
The variability of the RMSE indicators of the proposed approach, compared to the benchmark algorithms, is shown in Fig. 5. By integrating the proposed hybrid ensemble-learning approach using ASSOA, the model estimates better the hourly solar radiation on tilted surfaces than using PSO, GWO, or GA algorithms (RMSE inferior to 0.008). The Histograms of RMSEs obtained by employing different swarm intelligence algorithms are shown in Fig. 6. It can be noticed that the proposed algorithm using ASSOA can achieve a maximum frequency of error roughly around 0.007 for the two studied sites, which signifies that the ASSOA outperforms the other algorithms. The proposed ASSOA Algorithm's output results in comparison to other algorithms using Wilcoxon's Rank-Sum Based on Average Error Metric are listed in Tabs. 9 and 10, which show that ASSOA is the optimal solution in solving optimization problems in the solar radiation estimation.
Another evaluation is conducted for further assessment of the proposed model against the state-of-the-art models. From Tab. 11, we can see that the proposed hybridization approach yields plausible scores with respect to several prior contributions. The novel adopted approach hybridizing ASSOA and SVR in this study shows high performance in the estimation of hourly solar radiation on tilted surfaces.
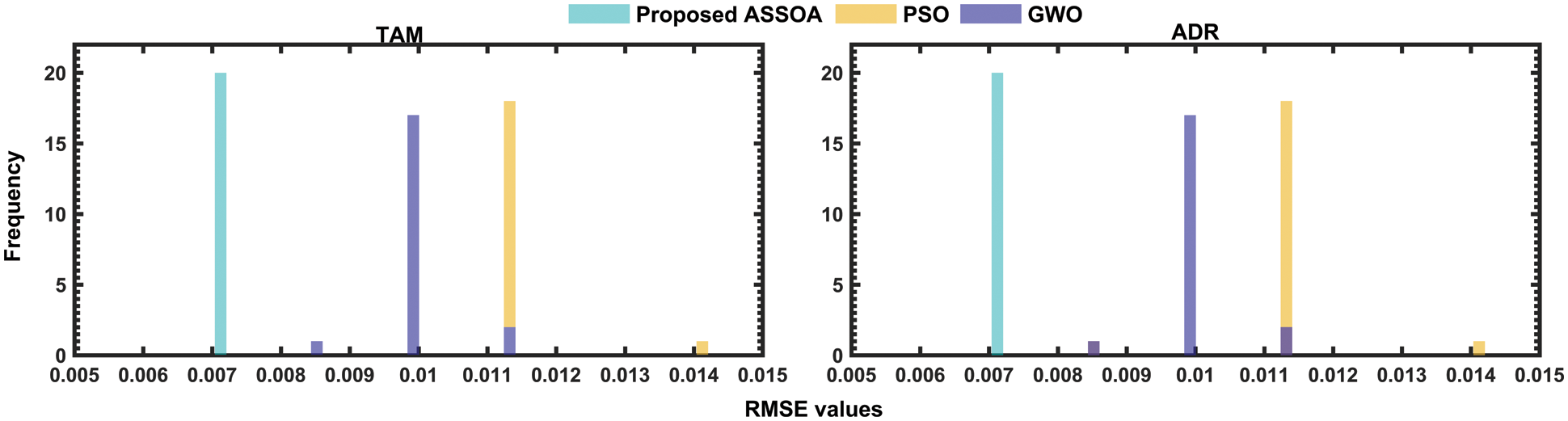
Figure 5: Histogram of RMSE for different algorithms for the TAM and ADR stations
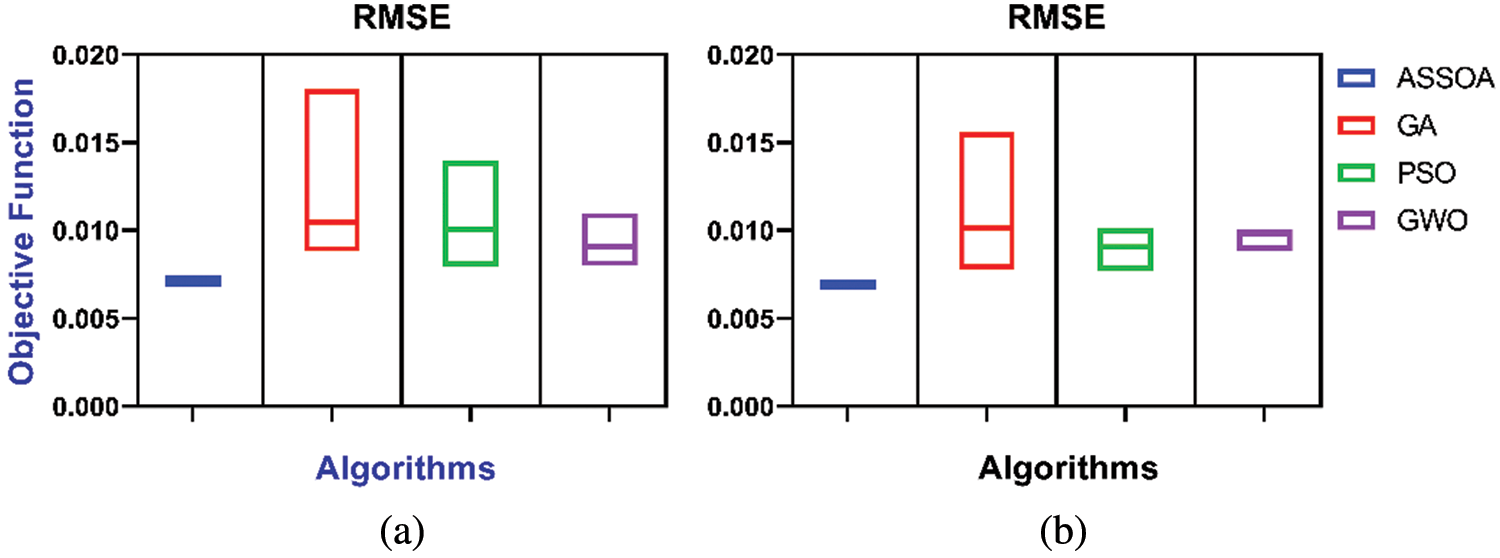
Figure 6: Algorithms, performance vs. the objective function for the TAM and ADR stations. (a) TAM station (b) ADR station
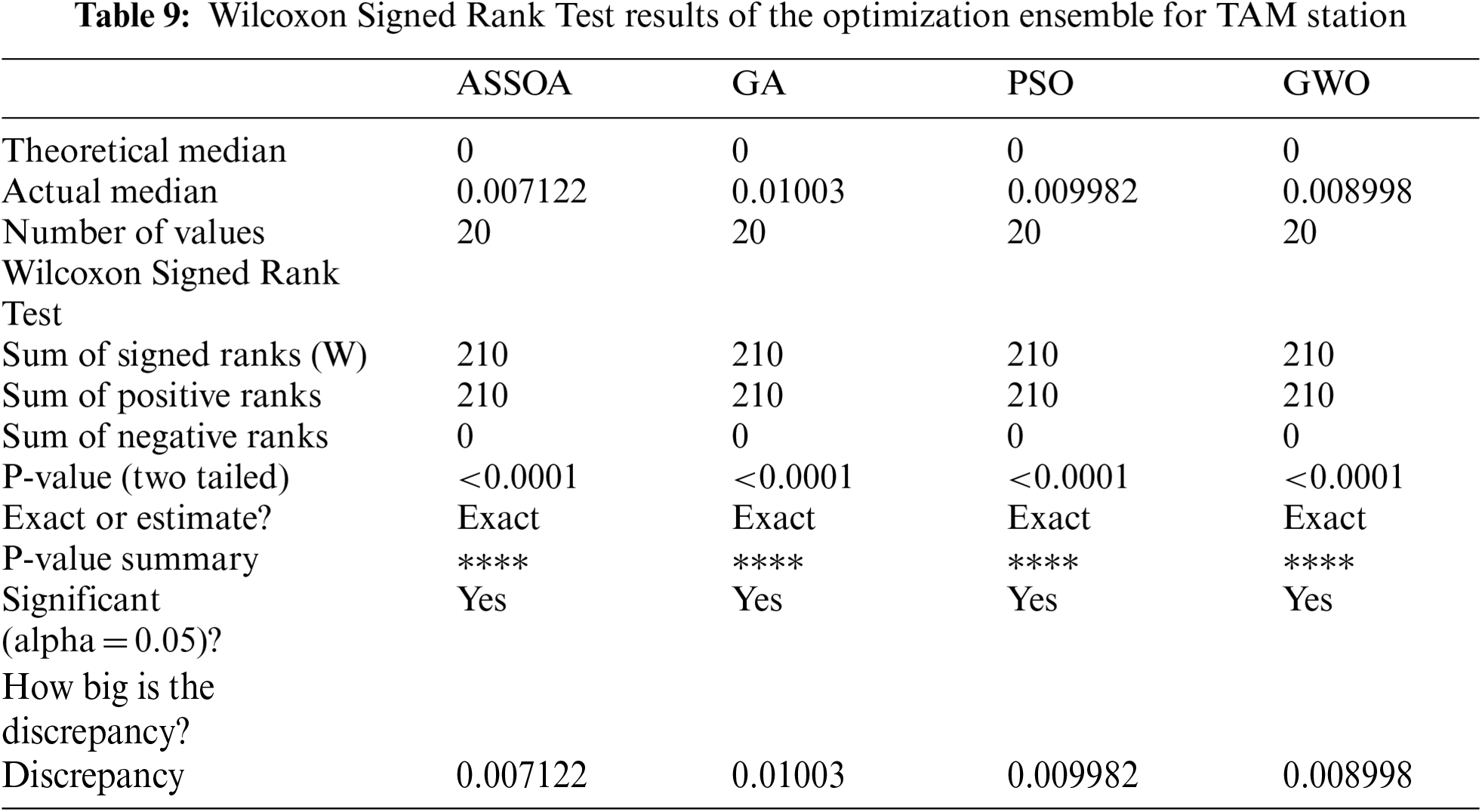
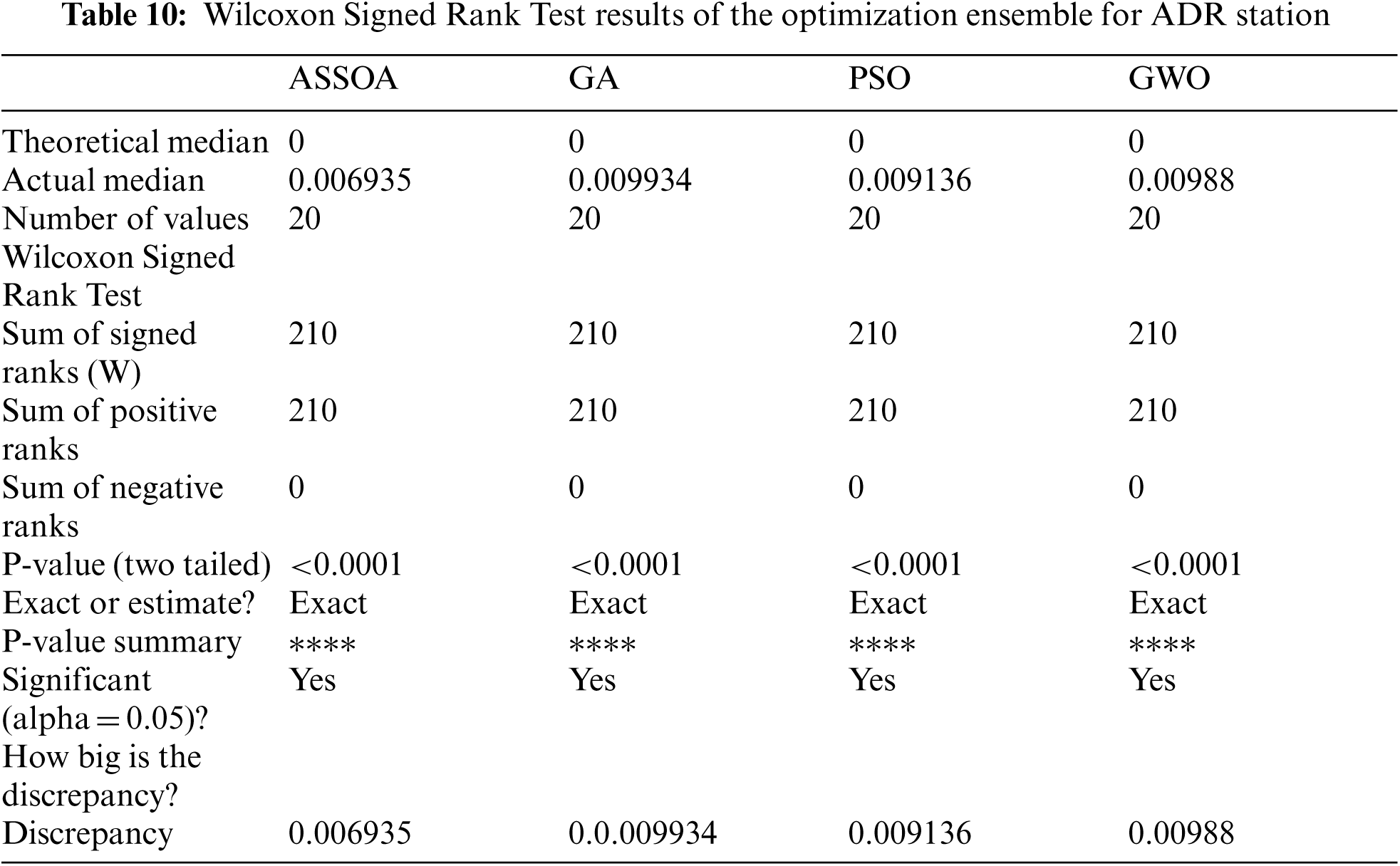
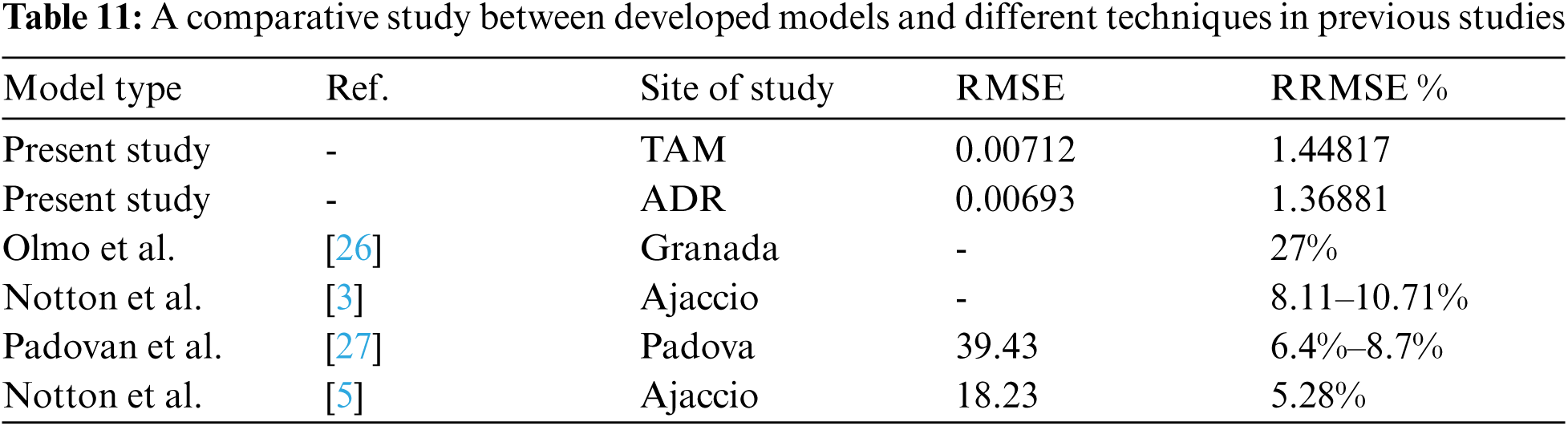
In this paper, a novel combined approach using the ASSOA optimization algorithm is proposed. For this purpose, measurements of hourly solar irradiation on inclined surfaces covering 2002–2006 in Tamanrasset and 2009–2012 in Adrar, Algeria, were used. The proposed model accuracy was assessed based on MBE, MAE, RMSE, RRMSE, and R.
Different experiments are performed using the mentioned data; firstly, five models of technique selection were considered (DTR, MLP, KNR, SVR, and RFR) in developing solar radiation estimating models. The estimation is based on the long-term measured meteorological datasets, including relative humidity, mean air temperature, maximum air temperature, minimum air temperature, and daily temperature range. The performance is evaluated and compared to two new proposed ensembles known as Average Ensemble (AVE) and Ensemble using SVR (SVE). The identification of model performance rankings is then conducted based on the Global Performance Index (GPI). The results of the comparative analysis show the superiority of the AVE and the SVE models.
In the second experimentation, the ASSOA optimization algorithm effect on improving the accuracy results, in the estimation of the solar, was investigated. Comparative analyses were carried out using previously described ensembles models (AVE and SVE). It was concluded that the proposed is more successful than the two better ensemble-based models, AVE and SVE.
Thirdly, to check the proposed model's sensitivity to the climate condition, the proposed evaluation at different sky conditions is conducted. The results show that the ASSOA perform better in CRS condition than in PCR end OTS. The model achieves a quite similar accuracy for the PCR end OTS condition in the ADR site.
The proposed ASSOA algorithm was also compared to GA, PSO, and GWO optimizers for feature selection to validate its efficiency. Compared to the other swarm intelligence algorithms, the proposed ASSOA shows superior performance. When the proposed model in this study is compared against the state-of-the-art models, it can be said that the model offers high performance in the estimation of estimate the hourly solar radiation on tilted surfaces classified as arid climate.
The present work demonstrated the potential of estimating solar radiation on tilted surfaces while also considering the influential meteorological parameters. Thus, it will help in decision-making. Combining the proposed optimization algorithm with more accurate estimation models can be further improved in the future. Moreover, regional models can be established. This study can contribute to enhancing solar design and the facilitation of implementing solar technologies for remote areas.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. N. Bailek, K. Bouchouicha, N. Aoun, M. EL-Shimy, B. Jamil et al., “Optimized fixed tilt for incident solar energy maximization on flat surfaces located in the algerian big south,” Sustainable Energy Technologies and Assessments, vol. 28, pp. 96–102, 2018. [Google Scholar]
2. C. K. Pandey and A. K. Katiyar, “Hourly solar radiation on inclined surfaces,” Sustainable Energy Technologies and Assessments, vol. 6, pp. 86–92, 2014. [Google Scholar]
3. G. Notton, P. Poggi and C. Cristofari, “Predicting hourly solar irradiations on inclined surfaces based on the horizontal measurements: Performances of the association of well-known mathematical models,” Energy Conversion and Management, vol. 47, no. 13–14, pp. 1816–1829, 2006. [Google Scholar]
4. C. Demain, M. Journée and C. Bertrand, “Evaluation of different models to estimate the global solar radiation on inclined surfaces,” Renewable Energy, vol. 50, pp. 710–721, 2013. [Google Scholar]
5. G. Notton, C. Paoli, S. Vasileva, M. L. Nivet, J. L. Canaletti et al., “Estimation of hourly global solar irradiation on tilted planes from horizontal one using artificial neural networks,” Energy, vol. 39, no. 1, pp. 166–179, 2012. [Google Scholar]
6. M. Shaddel, D. S. Javan and P. Baghernia, “Estimation of hourly global solar irradiation on tilted absorbers from horizontal one using artificial neural network for case study of mashhad,” Renewable and Sustainable Energy Reviews, vol. 53, pp. 59–67, 2016. [Google Scholar]
7. A. Takilalte, S. Harrouni, M. R. Yaiche and L. Mora-López, “New approach to estimate 5-min global solar irradiation data on tilted planes from horizontal measurement,” Renewable Energy, vol. 145, pp. 2477–2488, 2020. [Google Scholar]
8. K. Dahmani, R. Dizene, G. Notton, C. Paoli, C. Voyant et al., “Estimation of 5-min time-step data of tilted solar global irradiation using ANN (Artificial Neural Network) model,” Energy, vol. 70, pp. 374–381, 2014. [Google Scholar]
9. G. Notton, C. Paoli, L. Ivanova, S. Vasileva and M. L. Nivet, “Neural network approach to estimate 10-min solar global irradiation values on tilted planes,” Renewable Energy, vol. 50, pp. 576–584, 2013. [Google Scholar]
10. M. Alrashidi, M. Alrashidi and S. Rahman, “Global solar radiation prediction: Application of novel hybrid data-driven model,” Applied Soft Computing, vol. 112, pp. 107768, 2021. [Google Scholar]
11. C. Demircan, H. C. Bayrakçı and A. Keçebaş, “Machine learning-based improvement of empiric models for an accurate estimating process of global solar radiation,” Sustainable Energy Technologies and Assessments, vol. 37, pp. 100574, 2020. [Google Scholar]
12. Y. Zhou, Y. Liu, D. Wang, X. Liu and Y. Wang, “A review on global solar radiation prediction with machine learning models in a comprehensive perspective,” Energy Conversion and Management, vol. 235, pp. 113960, 2021. [Google Scholar]
13. Z. Pang, F. Niu and Z. O'Neill, “Solar radiation prediction using recurrent neural network and artificial neural network: A case study with comparisons,” Renewable Energy, vol. 156, pp. 279–289, 2020. [Google Scholar]
14. J. A. Bellido-Jiménez, J. Estévez Gualda and A. P. García-Marín, “Assessing new intra-daily temperature-based machine learning models to outperform solar radiation predictions in different conditions,” Applied Energy, vol. 298, pp. 117211, 2021. [Google Scholar]
15. E. -S. M. El-Kenawy, “Solar radiation machine learning production depend on training neural networks with ant colony optimization algorithms,” International Journal of Advanced Research in Computer and Communication Engineering (IJARCCE), vol. 7, no. 5, pp. 1–4, 2018. [Google Scholar]
16. J. Almorox, J. A. Arnaldo, N. Bailek and P. Martí, “Adjustment of the Angstrom-Prescott equation from Campbell-Stokes and Kipp-Zonen sunshine measures at different timescales in Spain,” Renewable Energy, vol. 154, pp. 337–350, 2020. [Google Scholar]
17. K. Bouchouicha, M. A. Hassan, N. Bailek and N. Aoun, “Estimating the global solar irradiation and optimizing the error estimates under algerian desert climate,” Renewable Energy, vol. 139, pp. 844–858, 2019. [Google Scholar]
18. A. Ibrahim, M. Noshy, H. A. Ali and M. Badawy, “PAPSO: A power-aware VM placement technique based on particle swarm optimization,” IEEE Access, vol. 8, pp. 81747–81764, 2020. [Google Scholar]
19. E. -S. M. El-Kenawy, M. M. Eid, M. Saber and A. Ibrahim, “MbGWO-SFS: Modified binary grey wolf optimizer based on stochastic fractal search for feature selection,” IEEE Access, vol. 8, pp. 107635–107649, 2020. [Google Scholar]
20. E. -S. M. El-Kenawy, S. Mirjalili, A. Ibrahim, M. Alrahmawy, M. El-Said et al., “Advanced meta-heuristics, convolutional neural networks, and feature selectors for efficient COVID-19 x-ray chest image classification,” IEEE Access, vol. 9, pp. 36019–36037, 2021. [Google Scholar]
21. K. Bouchouicha, N. Bailek, M. E. -S. Mahmoud, J. A. Alonso, A. Slimani et al., “Estimation of monthly average daily global solar radiation using meteorological-based models in adrar, algeria,” Applied Solar Energy, vol. 54, no. 6, pp. 448–455, 2018. [Google Scholar]
22. B. Jamil and A. T. Siddiqui, “Estimation of monthly mean diffuse solar radiation over India: Performance of two variable models under different climatic zones,” Renewable Energy, vol. 25, pp. 161–180, 2018. [Google Scholar]
23. F. J. Olmo, J. Vida, I. Foyo, Y. Castro-Diez and L. Alados-Arboledas, “Prediction of global irradiance on inclined surfaces from horizontal global irradiance,” Energy, vol. 24, pp. 689–704, 1999. [Google Scholar]
24. N. Bailek, K. Bouchouicha, Z. Al-Mostafa, M. El-Shimy, N. Aoun et al., “A new empirical model for forecasting the diffuse solar radiation over sahara in the Algerian Big south,” Renewable Energy, vol. 117, pp. 530–537, 2018. [Google Scholar]
25. N. Bailek, K. Bouchouicha, M. A. Hassan, A. Slimani and B. Jamil, “Implicit regression-based correlations to predict the back temperature of PV modules in the arid region of south algeria,” Renewable Energy, vol. 156, pp. 57–67, 2020. [Google Scholar]
26. F. J. Olmo, J. Vida, I. Foyo, Y. Castro-Diez and L. Alados-Arboledas, “Prediction of global irradiance on inclined surfaces from horizontal global irradiance,” Energy, vol. 24, pp. 689–704, 1999. [Google Scholar]
27. A. Padovan and D. Del Col, “Measurement and modeling of solar irradiance components on horizontal and tilted planes,” Solar Energy, vol. 84, no. 12, pp. 2068–2084, 2010. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |