Computers, Materials & Continua DOI:10.32604/cmc.2022.023172
Article

A BPR-CNN Based Hand Motion Classifier Using Electric Field Sensors

Hunmin Lee1, Inseop Na2, Kamoliddin Bultakov3 and Youngchul Kim3,*

1Department of Computer Science, Georgia State University, Atlanta, 30302, USA
2Nat'l Program of Excellence in Software Centre, Chosun University, Gwangju, 61452, Korea
3Department of Computer Inf. & Communication Eng., Chonnam Nat'l Univ., Gwangju, 61186, Korea
*Corresponding Author: Youngchul Kim. Email: yckim@jnu.ac.kr
Received: 30 August 2021; Accepted: 18 November 2021

Abstract: In this paper, we propose a BPR-CNN (Biometric Pattern Recognition-Convolution Neural Network) classifier for hand motion classification as well as a dynamic threshold algorithm for motion signal detection and extraction by EF (Electric Field) sensors. Currently, an EF sensor or EPS (Electric Potential Sensor) system is attracting attention as a next-generation motion sensing technology due to low computation and price, high sensitivity and recognition speed compared to other sensor systems. However, it remains as a challenging problem to accurately detect and locate the authentic motion signal frame automatically in real-time when sensing body-motions such as hand motion, due to the variance of the electric-charge state by heterogeneous surroundings and operational conditions. This hinders the further utilization of the EF sensing; thus, it is critical to design the robust and credible methodology for detecting and extracting signals derived from the motion movement in order to make use and apply the EF sensor technology to electric consumer products such as mobile devices. In this study, we propose a motion detection algorithm using a dynamic offset-threshold method to overcome uncertainty in the initial electrostatic charge state of the sensor affected by a user and the surrounding environment of the subject. This method is designed to detect hand motions and extract its genuine motion signal frame successfully with high accuracy. After setting motion frames, we normalize the signals and then apply them to our proposed BPR-CNN motion classifier to recognize their motion types. Conducted experiment and analysis show that our proposed dynamic threshold method combined with a BPR-CNN classifier can detect the hand motions and extract the actual frames effectively with 97.1% accuracy, 99.25% detection rate, 98.4% motion frame matching rate and 97.7% detection & extraction success rate.

Keywords: BPR-CNN; dynamic offset-threshold method; electric potential sensor; electric field sensor; multiple convolution neural network; motion classification

1  Introduction

The EF (Electric Field) sensor extracts information by sensing the variations of the electric charge near the surface of the sensor and converts the signal into voltage-level output. Today, EF sensors are mainly categorized by two modes, contact mode and non-contact mode. The contact mode has widely been applied in the area of healthcare and medical applications by sensing bioelectric signals such as electrocardiogram, electromyogram and electroencephalogram [1–5]. Meanwhile, non-contact type measures the electric potential signal on the surface of EF sensors induced by the disturbance of the surrounding electric field which is caused by movement of dielectric substances such as human bodies or hands due to coupling effect [6]. A few of non-contact EF sensor systems have been applied in commercial products, while several studies in academic institutions have been reported in application areas of proximity sensing, placement identification, etc [7–10]. As EF proximity sensing systems are gaining attention, recent studies have been published regarding the area of hand or body motion detection and recognition [11–21]. Our past studies [11–14] were focused on non-contact EF sensing, extracting and processing the signals through EF sensors. Moreover, by utilizing deep learning algorithms such as LSTM and CNN, multiple hand gesture classification mechanisms were proposed after a series of signal processing steps. Wimmer et al. [22] introduced the ‘Thracker’ device that utilized capacitive sensing, which encouraged the possibility of interaction between human and computer systems through non-contact capacitive sensing. Singh et al. [15] suggested a gesture recognition system called Inviz for paralysis patients that implemented textile-built capacitive sensors, measuring the capacitance interaction between the patient's body and the sensor. Aezinia et al. [16] designed a three-dimensional finger tracking system through a capacitive sensor, which was functional within 10 cm range from the sensor.

In this paper, we present a real-time hand motion detection and classification system adopting Biometric Pattern Recognition-Convolution Neural Network (BPR-CNN) classifiers combined with a dynamic threshold method for automatic motion detection and motion-frame extraction (Fig. 1) in EF signals. Our proposed system is fully automated with real-time motion detections, extracting the true frame and classifying motion types occurring at the range of up to 30 cm near the EF sensors. Accuracies of detecting hand motions and extracting signal frames were quantitatively rated through our suggested metrics. Furthermore, we suggest the simulation results of our CNN architectures; Multiple CNN (MCNN) and BPR-CNN with other classification algorithms and empirically evaluate the hand gesture classification performance.

Figure 1: A proposed hand motion extraction and classification process

This paper is organized as follows. Section 2 describes our suggested methods of computing the dynamic threshold for motion detection and frame extraction by analyzing the intrinsic features of the EF signals. We also explain the two CNN-based motion classifiers that were designed and thus applied into our system. In Section 3, we present the results of four hand gesture classifications through multiple experiments. In conclusion, we conclude our study and suggest the future works.

2  Discussion

In this section, we explain our dynamic threshold method for motion detection and frame extraction in the EF sensor signals. After setting the optimal signal frame, we conduct normalization followed by transforming the dimensions of normalized data in order to be trained into our proposed CNN model. We implement the MCNN and BPR-CNN to effectively train the features of the transformed signals thus classifying the inputs into corresponding gestures. Note that we handle the signals that have been already processed through Low-Pass-Filter (LPF) and Simple Moving Average (SMA). Since natural frequency from the human hand or arm is known to have 5∼10 Hz [23], which is a domain of extremely low frequency, thus we use the 10 Hz as a cut-off frequency in the LPF. The readers can refer to our previous studies [11–14] for more information regarding the implementation of LPF to filter out unnecessary noises and conduct the Moving Average to smoothen the filtered gesture signal from the sensor.

2.1 Dynamic Offset and Threshold

One of the challenging problems in dynamic thresholding in order to detect the signal and to locate the “genuine” signal frame is to compute an offset voltage for each Electric Potential Sensor (EPS) and adjust the threshold values periodically before detecting the target hand motion. As most hand motions and gestures are being done within a short period of time, we set the update cycle time unit to be a second. We implemented two EPS (Sensor A, B, sensor type PS25401) [14,23], and each sensor started with unidentical initial offset due to the various electric charging and discharging states near the sensors according to diverse environmental conditions in the moment of time.

Through our empirical past simulations, the initial voltage vinit∈R (unit: V) ranges from −0.2≤vinit≤0.02 with μ(∀vinit)=−0.08 and σ(∀vinit)=0.03 where μ denotes average and σ is standard deviation, when implementing EPS to measure the capacitance changes when the subject is proximally located. The statistics were acquired from four distinct hand gesture types (Tab. 1), each conducting 600 trials; n(∀vinit)=600, and the distribution visualization of vinit is shown in Fig. 2a. Let S={vn|1≤n≤T⋅1000,n∈N} be a set of time series raw sensor (voltage) data vn, where the sampling rate fs=1T=0.001sec which n(S)=1000 when T=0.001sec.

While a sensor is operational, which would constantly generate S, two thresholds εu, εℓ are being computed dynamically in every T=0.5sec, having εu=v(n,T)+τ and εℓ=v(n,T)−τ^ where εu, εℓ each indicates upper and lower threshold, v(n,T) is signal value on index n and time T. Through 12,000 trials of Monte Carlo simulation, we empirically estimated the optimal τ,τ^= 0.02 when the distance between the EPS and the subject's hand is 10∼30 cm, as 0.02 is sufficient enough to encompass the signals in order to detect the actual hand gesture signal. To prove this, we measured the Correct Detection Rate (CDR) which is suggested in Section 3. Note that the signal decreases exponentially as the distance increases linearly, since density of the electromagnetic signal are inverse proportional to the squared distance; E(V/m)=Q4πε0R2aR and F(N/C)=Q1Q24πε0R2 where Q indicates an electric charge, R is a distance, ε0 is a dielectric constant and aR is an unit vector. S1 and S2 produces similar signal patterns while each set was produced from single analogous hand motion, however the starting signal offset and their gradient Δv=vn−vn−1 in both identical index could be disparate as amount of the internal charges of the subject could vary; ε(S1,u,ℓ)(T1)≠ε(S2,u,ℓ)(T2) and ΔvS1≠ΔvS2 where T1≠T2 and (T1,T2)=0.5⋅c with constant c∈N.

Likewise, due to heterogeneous property of S, dynamic ε(S,u,ℓ)(T) tracks the discrete variant vn(T) and its upper and lower bound, which maintains the robustness regardless of time-variant offset value. As for the time-varying signal pattern which is the electric field disturbances due to hand motion, charging and discharging the electrics triggers the voltages to display waveform. Figs. 2b and 2c shows the typical output signal that charges and discharges the sensor plate which soars up (otherwise falls down), reaching its peak (bottom), then descends to bottom point (vice versa) and finally returns to an initial level when there was a hand gesture near the sensor plate.

Figure 2: (a) distribution of vinit in 800 trials. (b, c) the produced EF signals, each with sensor A, B and A–B, where is (b) after the LPF and (c) after LPF & SMA

Due to these features, dynamic ε(S,u,ℓ)(T) are considered to be effective in order to detect our targets which limits the possible starting point of a next hand motion, and we empirically show its detection rate in Section 3.

2.2 Motion Detection and Extraction

Each individual hand motion generates unidentical signal phases depending on various conditions such as hand movement speed, distance and direction. In order to detect and extract the corresponding motion frames, we considered not only the duration, but also the time frame that could be divided into the stages of motion. The detection is composed of 4 steps where the left and right term enclosed with braces each indicate the two contrasting cases (case 1, 2). The detection steps are indicated as follows;

Step1.{(vn−1(T)≤ε(S,u)(T))&&(vn(T)≥ε(S,u)(T))}||{(vn−1(T)≥ε(S,ℓ)(T))&&(vn(T)≤ε(S,ℓ)(T))}

Step2.{(vn−1(T)≥ε(S,u)(T))&&(vn(T)≤ε(S,u)(T))}||{(vn−1(T)≤ε(S,ℓ)(T))&&(vn(T)≥ε(S,ℓ)(T))}

Step3.{(vn−1(T)≥ε(S,ℓ)(T))&&(vn(T)≤ε(S,ℓ)(T))}||{(vn−1(T)≤ε(S,u)(T))&&(vn(T)≥ε(S,u)(T))}

Step4.{(vn−1(T)≤ε(S,ℓ)(T))&&(vn(T)≥ε(S,ℓ)(T))}||{(vn−1(T)≥ε(S,u)(T))&&(vn(T)≤ε(S,u)(T))}

Note that when vn(T)∈S satisfies the first step, it halts updating the ε(S,u,ℓ)(T) and continues to update after step 4. Once the set of input S fully satisfies the above conditions, we acknowledge that the motion has been detected. An initial motion frame size is computed based on the vn′(T′) of Step 1 to vn′′(T′′) of the Step 4; [vn′(T′),vn′′(T′′)]. The initial frame Finit={vi|n′≤i≤n′′,i∈N}.

However, this would trigger to lose the intrinsic features as this frame merely includes the partial actual motion signals as there may be more features on vn(T^) where T^⟨T′&&T^⟩T′′. Thus, the final frame F^ is determined by extending additional 10% of the |n′′−n′| to the Finit in each preliminary left and right directions; F^={vj|(n′−|n′′−n′|⋅0.1)≤j≤(n′′+|n′′−n′|⋅0.1),j∈N}. Fig. 3 shows the motion detection and frames extraction visualization result, which were automatically performed in real-time through dynamic threshold ε(S,u,ℓ)(T) as the sensors were consistently generating the dataset.

In Fig. 3, a signal of hand gesture moved from left to right (LR) is shown. As we make another hand gesture, it detects the motion and locates the following frame continuously. Fig. 3 contains two motion signals; each signal obtained from two different sensors (A-red and B-blue), where the dotted lines intersected with the signals show the starting point of the frame (magenta dot) and ending point of the frame (black dot). Each red and blue dot indicates the intersection point where ε(S,u,ℓ)(T)= vi. Through these steps we could successfully distinguish the hand motions and compute the significant frame that encompasses the authentic motion signals.

Figure 3: Motion frame extraction visualization

2.3 Normalization of an Extracted Motion Frame

When hand motions are identified by the sensor, the time period of the extracted frame is diverse even if the motions were the same types, due to the speed or distance range of the motion. Likewise, the amplitude of the motion signal also tends to change on every new motion since the subject's potential electrostatic state varies through numerous conditions such as textile of the cloth, location, or nearby machines, etc [4,9,11,12]. Thus, it is imperative to conduct normalization in order to be properly trained in deep learning models as normalizing input data is known to be a productive measure to enhance the performance. In our signal, the time (X-axis) and voltage (Y-axis) are the two axes that are to be normalized. For Y-axis, standardization was applied and let F^(Y)={v^j|1≤j≤d,j∈N,v^j=vj−μ(F^)σ(F^)} where d=(n′′−|n′′−n′|⋅0.1)−(n′+|n′′−n′|⋅0.1), F^(Y)∼N(μ(F^)=0,σ(F^)=1). For X-axis, we normalized n(F^(Y)) into 1000, deleting d−1000 data in k-periodical sequence, where k=[dd−1000]. This leads to d⋅(k−1)k+m=1000, computing F^(X,Y)={v^λ|1≤λ≤1000,λ∈N}, where 0≤m<(d−1000). The normalized signal is shown in Fig. 4, where the dotted line indicates the extracted frame of clockwise (CW) hand gesture, meanwhile solid line is the result after the normalization. Note that even if the identical subject performs the same motion type in a homogeneous environment such as time and location, the phase of the signal is distinctive due to the constantly varying charging state.

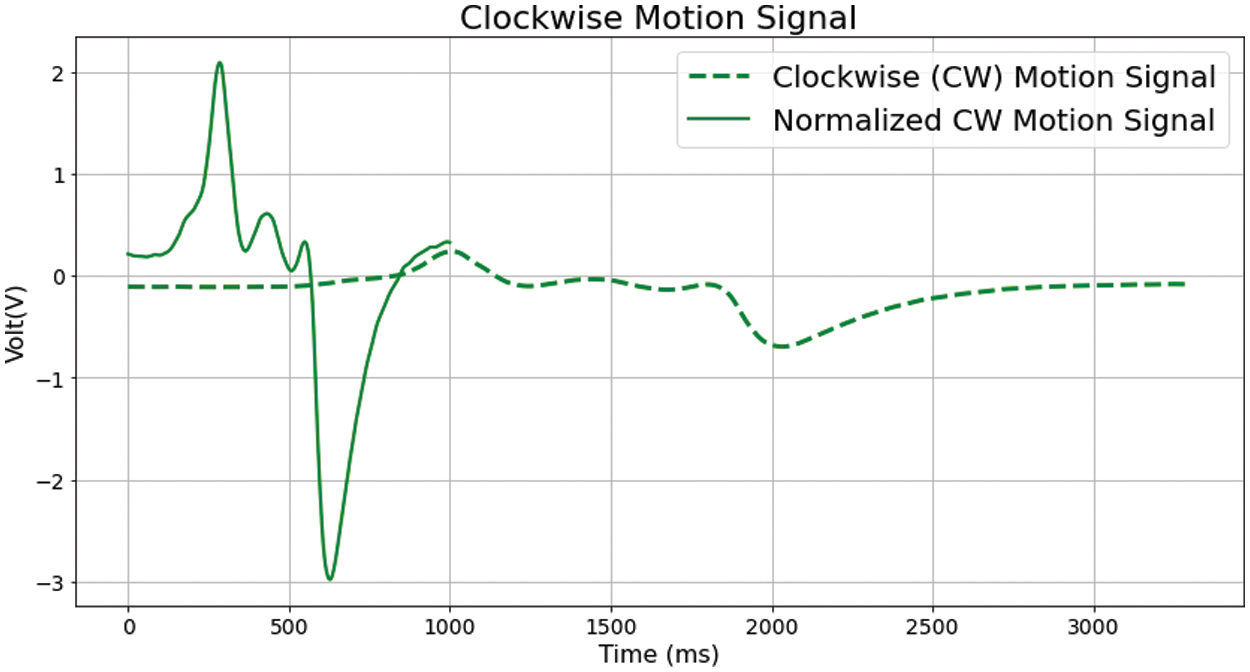
Figure 4: Visualization of original clockwise hand motion frame signal and normalized frame signal

2.4 Signal Dimension Transformation

After applying the normalized motion frame, the signal frame must be transformed from 1-dimension voltage signal to 2-dimension image in order to train the CNN model. Based on F^(X,Y), where n(F^(X,Y))=1000, we primarily reduce n(F^(X,Y)) into 900, deleting the v^1∼50 and v^950∼1000 in order to compute the 30 × 30 × 1 image (900=30⋅30). Fig. 5 shows the schematization of transforming the motion frame into the 30 × 30 × 1 image format.

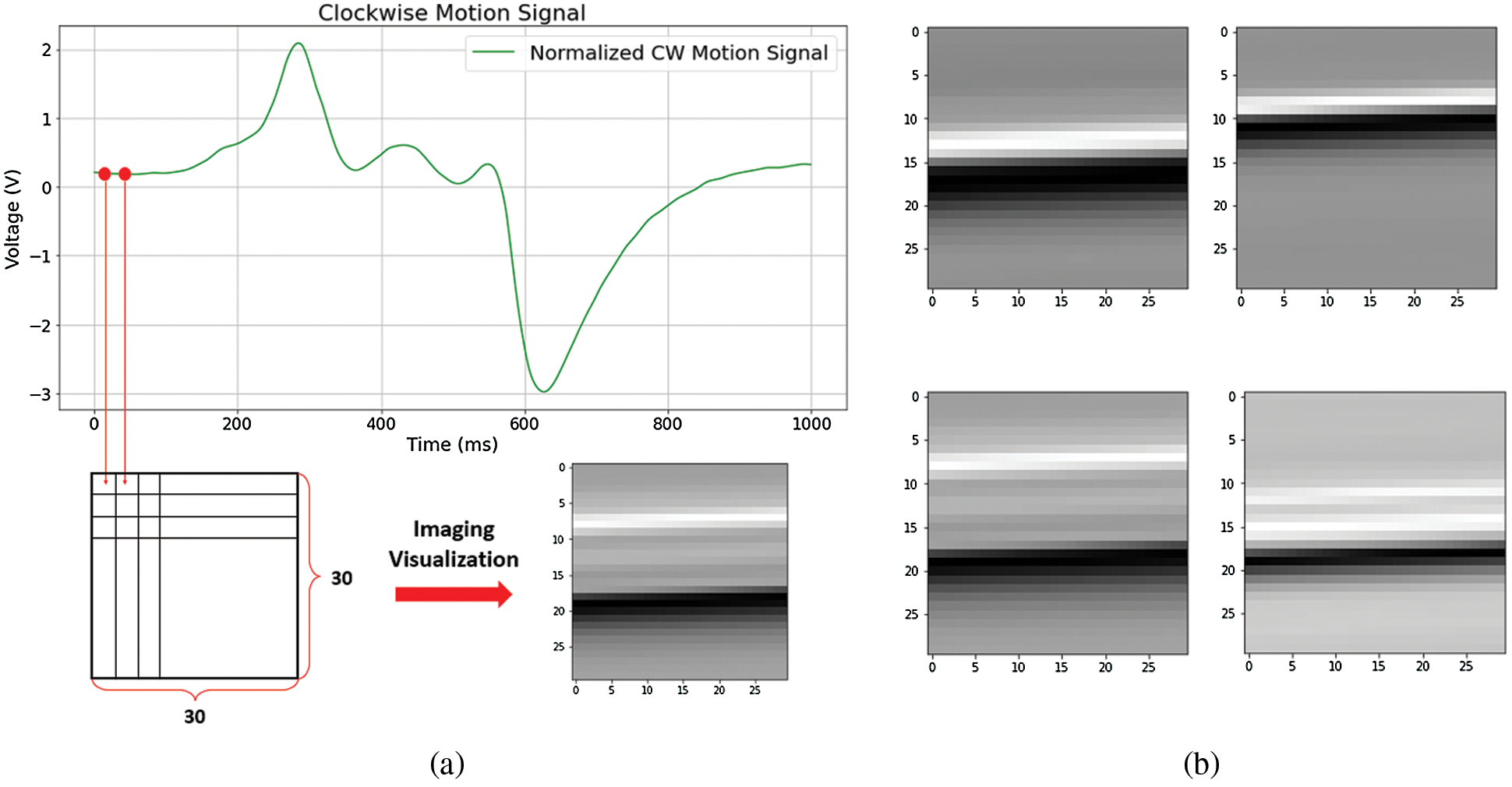
Figure 5: Dimensional transformation of a motion frame: (a) the transformation schematization reshaped into (30 × 30 × 1) grayscale image, (b) the transformed images for 4 hand gestures

2.5 Motion Classification Through CNN Models

In this section, we define the structure of our two CNN-based classifiers; MCNN and BPR-CNN that were implemented to effectively categorize the types of input hand motion signal images.

2.5.1 Multiple CNN Classifiers with Voting Logics

The first classifier is composed of five pre-trained CNN models, which are operated in parallel with unidentical filter size in their convolution layer. Fig. 6 shows a five-layer CNN structure that was applied in our MCNN.

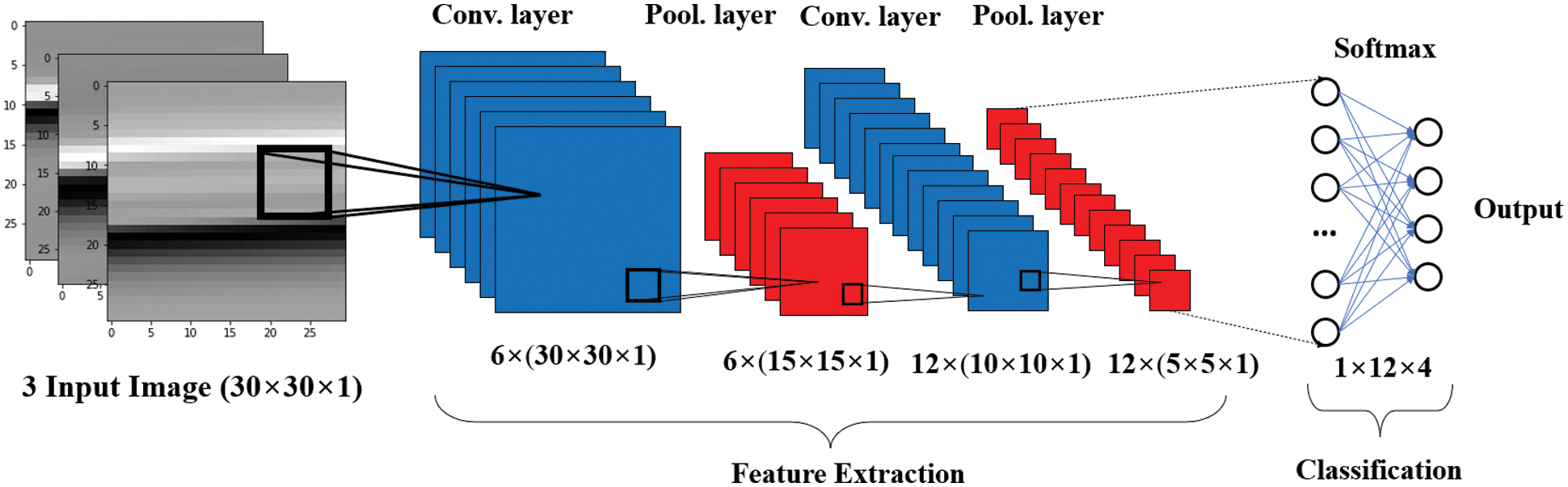
Figure 6: An example of implemented CNN structure

This model was trained through the extracted feature patterns from convolution layers learning local features to global features. After the fully-connected layer and softmax function, it outputs the class probability p(f(x)|x) (soft label). Once the CNN classifiers have been trained, each CNN predicts the input into a single category. Fig. 6 represent that an example of implemented CNN structure. The kernel size of each Ch in ℓ is as follows; δ(C1,∀ℓ) = (5 × 5), δ(C2,∀ℓ) = (7 × 7), δ(C3,∀ℓ) = (3 × 3), δ(C4,1) = (5 × 5), δ(C4,2) = (3 × 3), δ(C5,1) = (7 × 7) and δ(C5,2) = (3 × 3).

The outputs from the five CNNs are considered in order to make the final classification prediction through majority voting as shown in Fig. 7. Each input data consists of three 30 × 30 × 1 images, which represents three channels for sensor A, B and A-B signals. These three motion signal images are extracted in real-time and inserted into pre-trained CNN classifiers in Fig. 6.

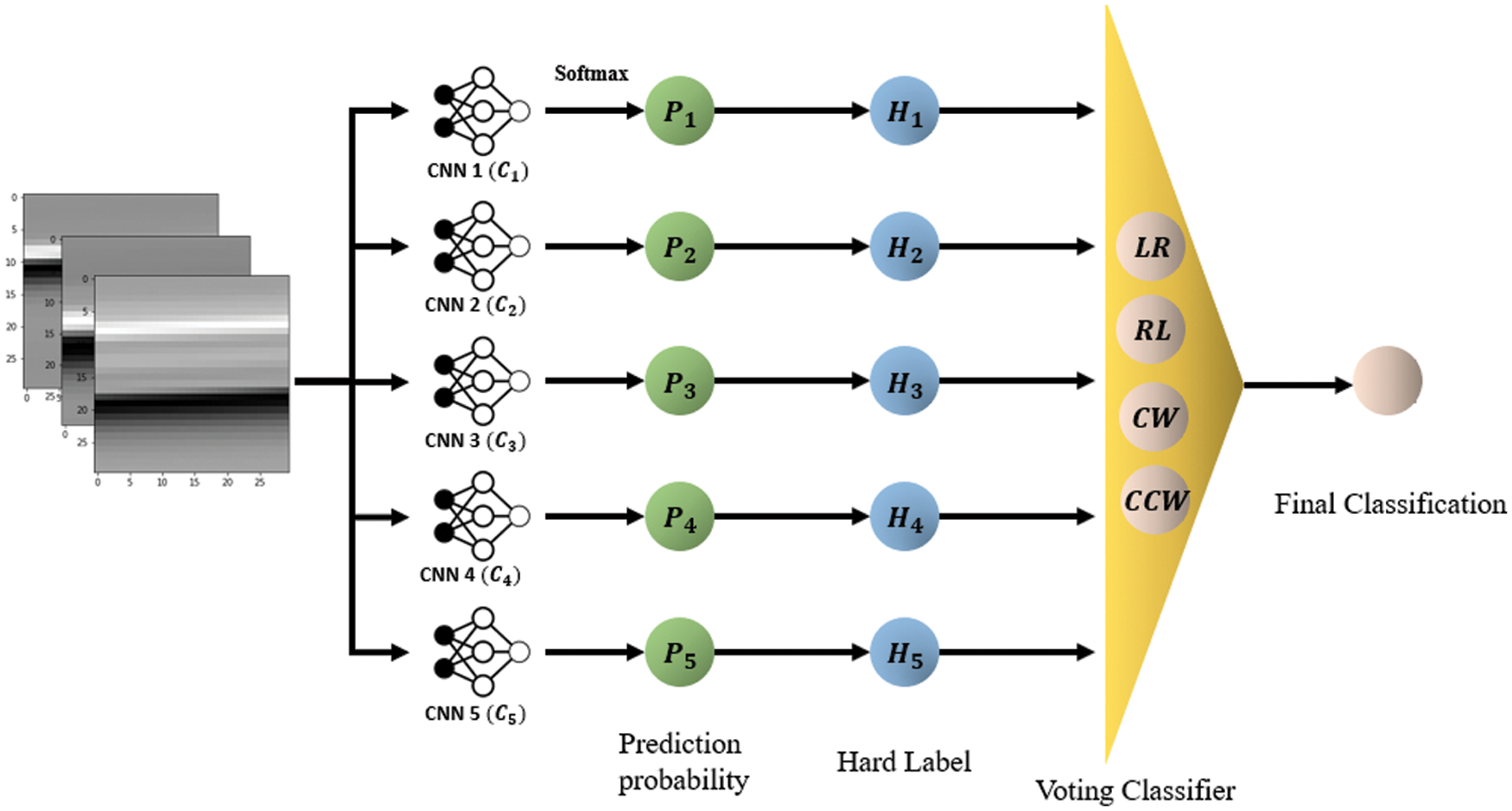
Figure 7: Parallel multiple CNN with majority voting classifier

Our ultimate goal is to successfully classify the four types of hand motions (Tab. 1) with high accuracy. Recall that the five CNN contains different kernel sizes, (refer to Fig. 6 for detailed kernel sizes in each layer) and MCNN classifier conducts majority voting (Fig. 7) between soft labels. Let H={Ch|1≤h≤5,h∈N} and let δ(Ch,ℓ) a kernel size on convolution layer Ch∋ℓ={1,2}, where Ch denotes a CNN model, and h is an index of the model. Ch(y,f(x),L(w,b,x))=Ph(x), where y denotes the true class, f(x) is a prediction class and loss function L(⋅) based on set of weight w, bias b and input x. Ch(⋅) calculates a label prediction probability Ph and eventually computing hard label H(x)=argmax4i=1,i∈N⁡Ph(x). Voting classifier aggregates the H∀h(x), and final classification y^=argmax(φ(H∀h(x))) where φ(Hh(x))={γi|1≤i≤4,i∈N,(Hh(x)=g(i))→γi+1} where initial γ∀i=0.

2.5.2 BPR-CNN Classifier

Biomimetic Pattern Recognition (BPR) [16,23–25] utilizes high-level topology features from biomimetic signals to discover certain patterns, which focuses on the concept of cognizing feature topology. Combining BPR with CNN (BPR-CNN) triggers higher performance as features are extracted from the CNN model, and BPR computes the topological manifold properties in given Euclidean parameter space based on Complex Geometry Coverage (CGC) [26] as shown in Fig. 8. Manipulating the prediction probability P(x), it computes the η number of distance-based clusters ϑη, ϑη∋P(x𝕚) where 1≤𝕚≤n(x), 𝕚∈N, η=n(classes)=n(P(x)). Since the set of trained w and b itself are not permutationally invariant, we cannot implement the distance-based geometry coverage based on the w and b.

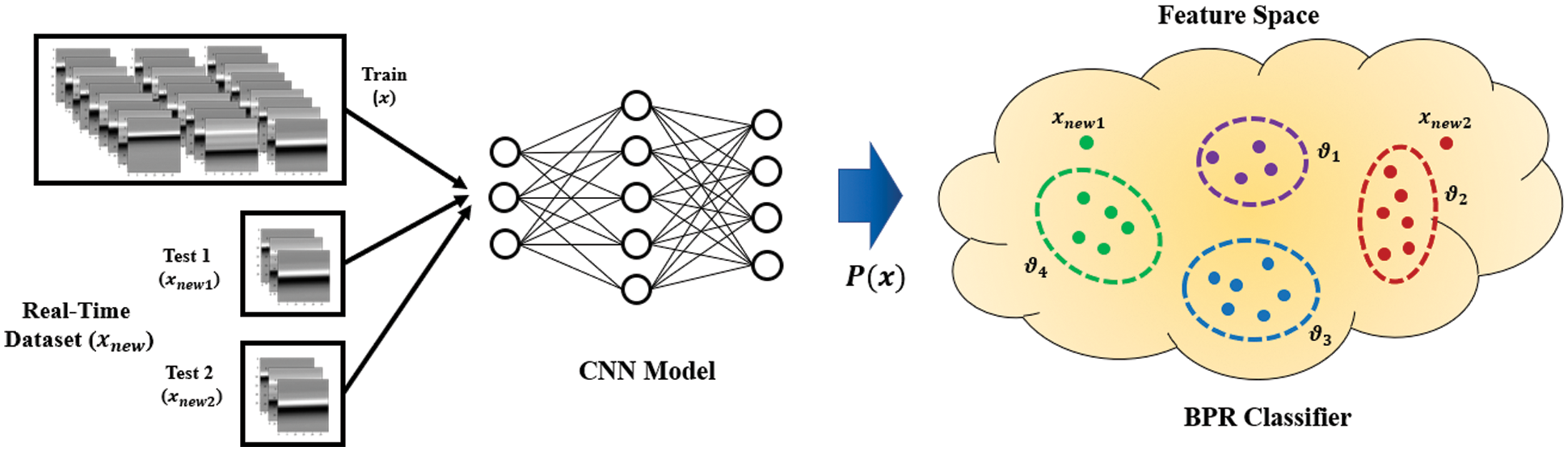
Figure 8: Visualization of the BPR-CNN mechanism

However, P(x) would indicate the proximity between the classes and the output of x, which guarantees the closest single class in the Euclidean space. Based on the proximity of class-wise topological space, it cognizes the matter using the high-level features. The processed input image set is abstruse to distinguish the classes or interpret the meanings of the indicated number of the pixels in the human eye, thus high-level robust features are preferred to accurately compute the decision boundary instead of using low-level features. To elaborate, input images that clearly show an object for CNN to classify the target such as cat or dog, their intrinsic features are distinct such as its eye, nose, or other parts of the subject, whereas our case doesn't.

Our case specifically requires the robust features in high-level feature space where the trend of each hand motion signal image could be found. Implementing the BPR-CNN, we could derive better input signal classification performance compared to conventional CNN, and we validate this through experiments in Section 3. In BPR classifier, pre-trained CNN model C~, C~(y,f(x),L(w,b,x))=P(x) and φ(∀P(xi))=ϑη, where φ(⋅) indicates pairwise distance-based clustering such as K-means (K= η) [27]. In Euclidean space Rη, where Rη∋ϑη∋P(xi), K(xnew)=argmin1≤k≤η,k∈N⁡dL2(μ(ϑk),P(xnew)), which allocates xnew to ϑK where xnew≠x𝕚. The layer structure of the CNN was set with Conv-MaxPooling-Conv-MaxPooling- Conv-MaxPooling-Dense-Dense. The kernel size of each convolution and maxpooling layers were set with 5 × 5 and 2 × 2 respectively.

3  Experimental Results

3.1 Experiment Setting

Through the empirical experiments, we evaluate the performance of our designed methodology. Utilizing the EPS sensor [14,28], four hand motion types indicated in Tab. 1 were extracted from each of six subjects, 100 gestures for each motion, collecting a total of 2400 motion samples. Among the dataset, we randomly split the 2160 samples for training and 240 for test data. The extracted raw signal was processed through consecutive signal processing methods starting from the LPF and SMA, followed by automatically detecting hand motions and setting signal frame by dynamic threshold, and normalizing the signal. Next, we transform the signal into an image and a pre-trained classifier determines its label. Note that η=4, since our objective is to classify the four motion types (Tab. 1). All this process (Fig. 1) is operated in real-time and test dataset were generated and classified (Less than second when computing through CPU i7–7500U RAM 8GB). The performance has been measured through our metrics of Correct Detection Rate (CDR), Motion Frame Matching Rate (MFMR) and Detection & Extraction Success Rate (DESR). CDR shows the degree of correspondence between the signal and the actual motion, and the MFMR quantitatively assesses the matching rate of the computed motion frame. Finally, DESR is obtained by CDR multiplied by MFMR to indicate their combined accuracy level. The training epoch was set with 20 and learning rate of 0.01, with relu activation function in each convolution layer.

3.2 Experiment Result

Following Tab. 2 shows the result of our three designated metrics, which validates that the proposed method of our study works with high accuracy of around 98% on average.

Following Tab. 3 displays the experiment results of the four classifier algorithms. Their performances were evaluated with classification accuracy based on identical test data of four specific hand motions in Tab. 1. We denote the average of four motion accuracy as Classification Correction Rate (CCR), which is computed in Tab. 3. From each motion in Tab. 1, three distinct output signals are produced; sensor A value, sensor B value and subtracted value (A-B). Performance of the two CNN classifiers (MCNN and BPR-CNN) were also compared with other algorithms such as HMM and SVM. Our experiment results show that the suggested motion detection and frame extraction based on the two threshold works with high CDR and MFMR, and also the classification accuracy of BPR-CNN classifier outperformed other competitive models.

4  Conclusion and Future Works

In this paper, we proposed the dynamic thresholding and framing algorithms in order to set the accurate motion EF signal frame in real-time, and evaluated its performance using the following metrics; 99.4% in CDR, 98.4% in MFMR, 97.8% in DESR. Moreover, we implemented the MCNN and BPR-CNN motion classifiers and compared the accuracy with other algorithms. Based on the extracted features of the 3 channel (sensor A, B, A-B) input signal images, BPR-CNN had shown the highest performance of 97.1% in CCR. Utilizing EF sensing is regarded as a prospective research domain and accommodates practical usage in industry due to diverse advantages such as low computation & price, high sensitivity & recognition speed. Our future work is to adopt the introduced methods to mobile devices and apply the algorithms to control the interface through non-contact hand motions. Training and classifying the diverse and detailed gestures in order to gain algorithmic robustness and versatility is a part of our future work. Combining our studies into interface technologies such as Human Computer Interaction (HCI) or Natural User Interface (NUI), we expect the further utilizations of controlling the various applications through user-friendly interfaces based on EF sensing.

Funding Statement: This work was supported by the NRF of Korea grant funded by the Korea government (MIST) (No. 2019 R1F1A1062829).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  R. J. Prance, A. Debray, T. D. Clark, H. Prance, M. Nock et al., “An ultra-low-noise electrical potential probe for human body scanning,” Measurement Science and Technology, vol. 11, no. 3, pp. 291–297, 2000. [Google Scholar]

 2.  E. Rendon-Morales, R. J. Prance, H. Prance and R. Aviles-Espinosa, “Non- invasive electrocardiogram detection of in vivo zebrafish embryos using electric potential sensors,” Applied Physics Letters, vol. 107, no. 19, pp. 3701, 2015. [Google Scholar]

 3.  R. K. Rajavolu and K. Sakumar, “Fetal ECG extraction on light of adaptive filters and wavelet transform approval and application in fetal heart rate variability analysis of low power IOT platform,” International Journal of Pure and Applied Mathematics, vol. 118, no. 14, pp. 307–313, 2018. [Google Scholar]

 4.  T. G. Zimmerman, J. R. Smith, J. A. Paradiso, D. Allport and N. Gershenfeld, “Applying electric field sensing to human-computer interfaces,” International Journal of Smart Home, vol. 11, no. 4, pp. 1–10, 2017. [Google Scholar]

 5.  H. Prance, “Sensor developments for electrophysiological monitoring in healthcare,” Applied Biomedical Engineering, pp. 265–286, 2011. [Online]. Available: https://www.intechopen.com. [Google Scholar]

 6.  M. Nath, S. Maity, S. Avlani, S. Weigand and S. Sen, “Inter-body coupling in electro-quasistatic human body communication: Theory and analysis of security and interference properties,” Scientific Reports, vol. 11, no. 1, pp. 1–15, 2021. [Google Scholar]

 7.  X. Tang and S. Mandal, “Indoor occupancy awareness and localization using passive electric field sensing,” IEEE Transactions on Instrumentation and Measurement, vol. 68, no. 11, pp. 4535–4549, 2019. [Google Scholar]

 8.  B. Fu, F. Kirchbuchner, J. V. Wilmsdorff, T. Grosse-Puppendahl, A. Braun et al., “Performing indoor localization with electric potential sensing,” Journal of Ambient Intelligence and Humanized Computing, vol. 10, no. 2, pp. 731–746, 2018. [Google Scholar]

 9.  D. R. Roggen, A. P. Yazan, F. Javier, O. Marales, R. J. Prance et al., “Electric field phase sensing for wearable orientation and localization applications,” in Proc. of 15th Int. Semantic Web Conf. 2016, Heidelberg, Germany, pp. 52–53, 2016. [Google Scholar]

10. S. Beardsmore-Rust, P. Watson, P. B. Stiffell, R. J. Prance, C. J. Harland et al., “Detecting electric field disturbances for passive through wall movement and proximity sensing,” in Proc. of Smart Biomedical and Physiological Sensor Technology, Orlando, USA, vol. 7313, 2009. [Google Scholar]

11. Y. R. Lee, “EPS gesture signal pattern recognition using multi-convolutional neural networks,” M.S. thesis, Chonnam National University, Gwangju, Korea, 2017. [Google Scholar]

12. S. I. Jeong and Y. C. Kim, “Hand gesture signal extraction and application to light controller using passive electric sensor,” in Proc. 5th Int. Conf. on Next Generation Computing 2019, ChiangMai, Thailand, pp. 130–132, 2019. [Google Scholar]

13. S. I. Jung, V. Kamoliddin and Y. C. Kim, “Automatic hand motion signal extraction algorithm for electric field sensor using dynamic offset and thresholding method,” in Proc. Korean Institute Smart Media 2021, Busan, Korea, pp. 169–172, 2021. [Google Scholar]

14. H. M. Lee, S. I. Jung and Y. C. Kim. “Real-time hand motion frame extraction using electric potential sensors,” in Proc. 9th Int. Conf. on Smart Media and Applications 2020, Guam, USA, pp. 1–5, 2020. [Google Scholar]

15. G. Singh, A. Nelson, R. Rubocci, C. Patel and N. Banerejee, “Inviz: low-power personalized gesture recognition using wearable textile capacitive sensor arrays,” in Proc. 2015 IEEE Int. Conf. on Pervasive Computing and Communications, St. Louis, MO, USA, pp. 198–206, 2015. [Google Scholar]

16. F. Aezinia, Y. Wang and B. Bahreyni, “Three dimensional touchless tracking of objects using integrated capacitive sensors,” IEEE Transactions on Consumer Electronics, vol. 58, no. 3, pp. 886–890, 2012. [Google Scholar]

17. D. N. Tai, I. S. Na and S. H. Kim, “HSFE network and fusion model based dynamic hand gesture recognition,” KSII Transactions on Internet and Information Systems, vol. 14, no. 9, pp. 3924–3940, 2020. [Google Scholar]

18. I. S. Na, C. Tran, D. Nguyen and S. Dinh, “Facial UV map completion for pose-invariant face recognition: A novel adversarial approach based on coupled attention residual UNets,” Human-centric Computing and Information Sciences, vol. 10, no. 45, pp. 1–17, 2020. [Google Scholar]

19. P. N. Huu, Q. T. Minh and H. L. The,“An ANN-based gesture recognition algorithm for smart-home applications,” KSII Transactions on Internet and Information Systems, vol. 14, no. 5, pp. 1967–1983, 2020. [Google Scholar]

20. S. Y. Lee, J. K. Lee and H. J. Cho, “A hand gesture recognition method using inertial sensor for rapid operation on embedded device, “KSII Transactions on Internet and Information Systems, vol. 14, no. 2, pp. 757–770, 2020. [Google Scholar]

21. H. M. Lee, I. S. Na and Y. C. Kim, “A multiple CNN hand motion classifier with a dynamic threshold method for motion extraction using EF sensors,” in Proc. of 16th Asia Pacific Int. Conf. on Information Science and Technology 2021, Busan, Korea, pp. 34–36, 2021. [Google Scholar]

22. R. Wimmer, P. Holleis, M. Kranz and A. Schmidt, “Thracker-using capacitive sensing for gesture recognition,” in proc. of 26th IEEE Int. Conf. on Distributed Computing Systems Workshops, Lisboa, Portugal, pp. 64–64, 2006. [Google Scholar]

23. “Plessy semiconductors, datasheet for PS25014,” “PS25014A, PS25014B Application Boards for EPIC sensor PS25401,” [Online]. Available: https://www.mouser.com/datasheet/2/613/PS25201-EPIC-sensor-electrophysiology-high-gain-Da-1387263.pdf. [Google Scholar]

24. L. Zhou, Q. Li, G. Huo and Y. Zhou, “Image classification using biomimetic pattern recognition with convolutional neural networks features,” Computational Intelligence and Neuroscience, vol. 2017, pp. 1–12, 2017. [Google Scholar]

25. S. Wang and X. Chen, “Biomimetic (topological) pattern recognition-a new model of pattern recognition theory and its application,” in Proc. Int. Joint Conf. on Neural Networks, Portland, OR, USA, vol. 3, pp. 2258–2262, 2003. [Google Scholar]

26. S. Wang and X. Zhao, “Biomimetic pattern recognition theory and its applications,” Chinese Journal of Electronics, vol 13, no. 3, pp. 373–377, 2004. [Google Scholar]

27. L. Aristidis, N. Vlassis and J. Verbeek, “The global k-means clustering algorithm,” Pattern Recognition, vol. 36, no. 2, pp. 451–461, 2003. [Google Scholar]

28. D. Mariama and J. Wessberg. “Human 8-to 10-hz pulsatile motor output during active exploration of textured surfaces reflects the textures’ frictional properties,” Journal of Neurophysiology, vol. 122, no. 3, pp. 922–932, 2019. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.