Computers, Materials & Continua DOI:10.32604/cmc.2022.022759
Article

A Provably Secure and Efficient Remote Password Authentication Scheme Using Smart Cards

Fairuz Shohaimay1,2 and Eddie Shahril Ismail1,*

1Department of Mathematical Sciences, Faculty of Science and Technology, Universiti Kebangsaan Malaysia, UKM Bangi, 43600, Selangor, Malaysia
2Department of Mathematics, Faculty of Computer and Mathematical Sciences, Universiti Teknologi MARA Pahang, Raub Campus, Raub, 27600, Pahang, Malaysia
*Corresponding Author: Eddie Shahril Ismail. Email: esbi@ukm.edu.my
Received: 18 August 2021; Accepted: 06 December 2021

Abstract: Communication technology has advanced dramatically amid the 21st century, increasing the security risk in safeguarding sensitive information. The remote password authentication (RPA) scheme is the simplest cryptosystem that serves as the first line of defence against unauthorised entity attacks. Although the literature contains numerous RPA schemes, to the best of the authors’ knowledge, only few schemes based on the integer factorisation problem (IFP) and the discrete logarithm problem (DLP) that provided a provision for session key agreement to ensure proper mutual authentication. Furthermore, none of the previous schemes provided formal security proof using the random oracle model. Therefore, this study proposed an improved RPA scheme with session key establishment between user and server. The design of the proposed RPA scheme is based on the widely established Dolev-Yao adversary model. Moreover, as the main contribution, a novel formal security analysis based on formal definitions of IFP and DLP under the random oracle model was presented. The proposed scheme's performance was compared to that of other similar competitive schemes in terms of the transmission/computational cost and time complexity. The findings revealed that the proposed scheme required higher memory storage costs in smart cards. Nonetheless, the proposed scheme is more efficient regarding the transmission cost of login and response messages and the total time complexity compared to other scheme of similar security attributes. Overall, the proposed scheme outperformed the other RPA schemes based on IFP and DLP. Finally, the potential application of converting the RPA scheme to a user identification (UI) scheme is considered for future work. Since RPA and UI schemes are similar, the proposed approach can be expanded to develop a provably secure and efficient UI scheme based on IFP and DLP.

Keywords: Authentication scheme; discrete logarithm; factorisation; password; provable security

1  Introduction

In the 21st century, anything is possible on the internet by using applications and services, like operational networks, databases, banking services, and e-commerce, that are available to anyone, anywhere. Although users can enjoy access to the services remotely, the convenience offered is not without a cost. The communication between users and service providers often involves sensitive data dan messages being transmitted through insecure public channel. Furthermore, communication technology has progressed rapidly, thereby increasing the security risk security to protect private information. The remote password authentication (RPA) scheme is a cryptosystem that allows authorised users access to securely communicate with the service providers. Therefore, the RPA scheme serves as the first line of defence against dangerous security threats.

1.1 Related Works

In 1999, Yang et al. [1] proposed two RPA schemes with smart cards, using timestamp and nonce (random number used once). The schemes adopted the concept of an ID-based signature scheme by Shamir [2] without the need to maintain a password verification table. Furthermore, the schemes enabled users to easily select their passwords and demonstrated resistance to replay and forged login attacks. The schemes’ security foundation was grounded on two cryptographic primitives: Integer Factorisation Problem (IFP) and Discrete Logarithm Problem (DLP). Nevertheless, some improved schemes [3–9] have been proposed to overcome the security concerns of Yang et al. [1] scheme while still maintaining the cryptographic primitives of IFP and DLP.

Fig. 1 presents the literature development of RPA schemes based on Yang et al. [1] scheme. The related works are defined as studies that have proposed improvements of RPA schemes and maintained the security foundation of IFP and DLP. These works are selected from the lists of citations and references of the previous studies. As an example, from Fig. 1, the enhancement scheme proposed by Shen et al. [4] was designed based on cryptanalysis of Yang et al. [1] scheme.

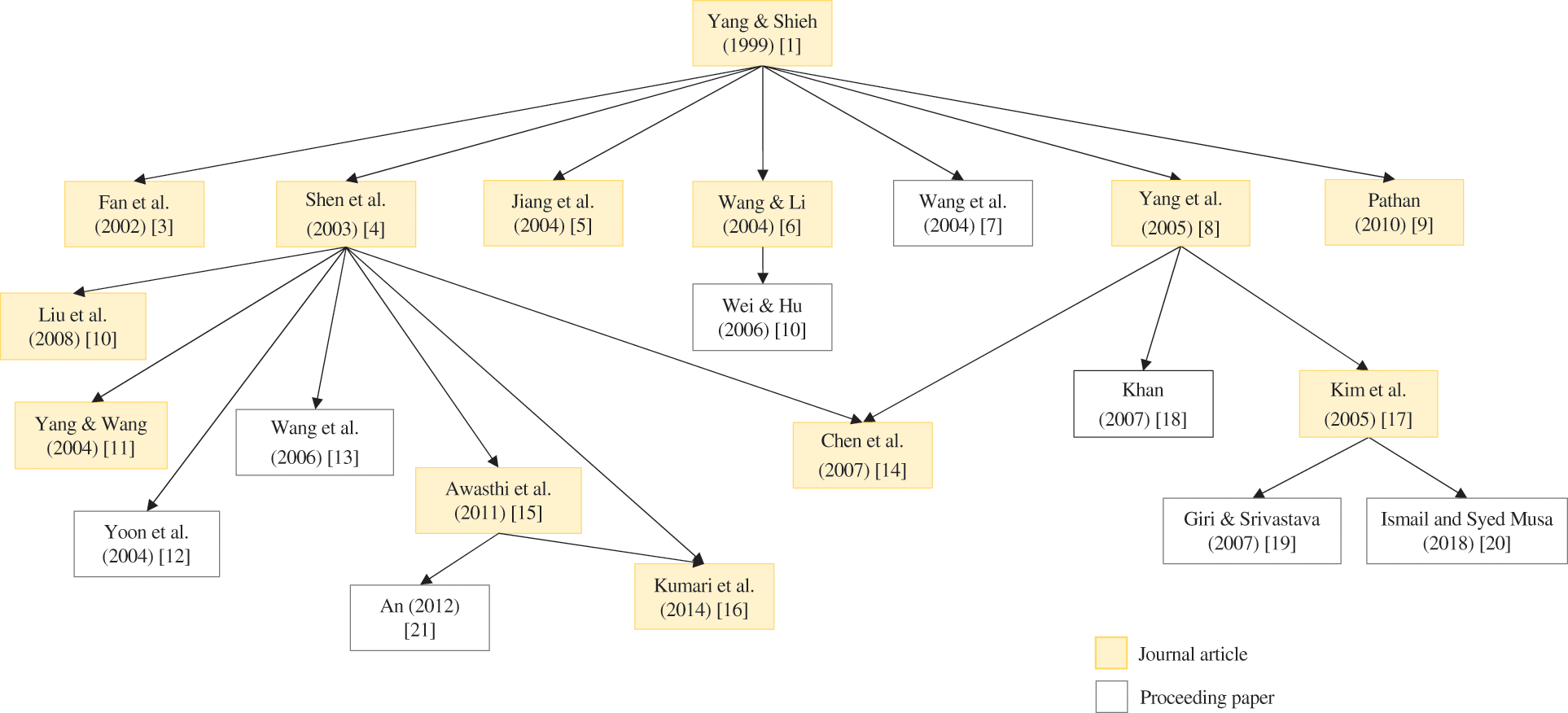
Figure 1: Development of RPA schemes based on Yang et al. [1] scheme using two cryptographic primitives (IFP and DLP)

Shen et al. [4] provided one of the most significant enhancements to scheme by Yang et al. [1], arguing that adversaries could exploit users’ sensitive data through fake servers. As a result, the problem was rectified by incorporating mutual authentication between user and server. Nevertheless, the scheme was shown to be vulnerable to existing and novel security attacks, such as replay, secret-key guessing, and forgery attacks [10–13]. From there, numerous modifications [10–16] have been proposed. These studies reported their schemes to be more practical and efficient than earlier comparable schemes while maintaining a security basis of similar cryptographic primitives (i.e., IFP and DLP) during mutual authentication. Notably, Liu et al. [10] developed a novel nonce-based RPA scheme that could prevent forged login without incurring additional computational cost on the smart card.

Another notable contribution is the improved scheme by Yang et al. [8], which could withstand forgery, password-guessing, smart card loss, and replay attacks. Subsequently, Kim et al. [17] demonstrated that Yang et al. [8] scheme could not withstand previous forgery attacks. Later, Khan [18] demonstrated the vulnerabilities in [8] and presented an enhanced scheme with mutual authentication to address the problem. Nevertheless, other studies [19], [20] have shown that Kim et al. [17] is vulnerable to forgery attacks. As a result, Giri et al. [19] proposed a new scheme to resist the forgery attacks, as well as other types of threats, such as password-guessing, smart card loss, and replay attacks. The most recent related study by Ismail et al. [20] presented a new attack and proposed modifications to address the new threats.

Awasthi et al. [15] demonstrated that the scheme by Shen et al. [4] is vulnerable to forged login attacks and presented additional security concerns about the scheme by Liu et al. [10]. Hence, Awasthi et al. [15] proposed an enhanced scheme for resisting forgery attacks with reduced smart card memory storage cost. Unfortunately, the scheme was shown to be vulnerable to impersonation, insider, and password-guessing attacks by An [21], which also suggested improvements to make the scheme more secure to resist all of the mentioned attacks while supporting mutual authentication. Furthermore, Kumari et al. [16] highlighted that scheme proposed by Awasthi et al. [15] could not resist the claimed attacks. Therefore, they recommended a three-factor scheme authentication improvement with the added security of the user's fingerprint.

Kumari et al. [16] proposed the latest RPA scheme construction based on IFP and DLP. The study was the first to introduce a scheme that included a shared session key between the user and the server to eliminate the man-in-the-middle attack, accompanied by the most comprehensive and informal security analysis. The proposed scheme was shown to be resistant to many security attacks, including the smart card loss, replay, impersonation, forgery, offline password-guessing, denial-of-service, insider, and stolen verifier attacks. Nevertheless, the scheme's computational and communication costs were the highest among all the schemes in Fig. 1.

1.2 Motivation and Contributions

Security analysis, like that of other cryptosystems, is imperative in developing new RPA schemes. Although numerous RPA schemes based on IFP and DLP have been proposed in the literature, none of them provides security proof under the random oracle model. The security proof requirement has been fulfilled by many schemes constructed based on other cryptographic primitives in the literature, such as IFP [22], Elliptic Curve Discrete Logarithm Problem (ECDLP) [23], and chaotic maps [24]. Although the study by Kumari et al. [16] featured many security attributes, no formal security proof of its scheme was presented. Consequently, despite being the most secure among similar works, the proposed scheme had to sacrifice its performance efficiency. Therefore, the purpose of this study is two-fold. First, the aim of this study is to propose an efficient RPA scheme with session key agreement based on two cryptographic primitives (IFP and DLP). Next, the main contribution of this study is to present a formal security analysis based on the formal definitions of IFP and DLP under the random oracle model to prove the security of the proposed scheme.

1.3 Organisation of the Paper

The remainder of this paper is organised as follows. Section 2 presents the mathematical and security preliminaries. Section 3 then explains the newly proposed scheme. Section 4 presents the proposed scheme's formal and informal security analyses. Section 5 provides a comparative study of the previous schemes of [4,15,16], and the present scheme. Section 6 discusses how the RPA scheme could be used to develop a user identification (UI) scheme. Finally, Section 7 presents the conclusion and recommendation.

2  Preliminaries

This section provides a brief overview of the mathematical concepts that served as the security foundation in the development of the proposed scheme in this study, including the definitions of IFP [25], DLP [26], and the one-way hash function (e.g., MD5 [27] or SHA-256 [28]). The adversary model and security goals were also considered. Tab. 1 shows the notations and descriptions used in this paper.

2.1 IFP

Given a 2048-bit integer n=p×q, find the primes p and q that are each at least 1024-bit length. If p and q are known, it will be easy to compute n. Finding p and q given n, on the other hand, is a computationally intractable problem.

2.2 DLP

Assume that g is a primitive element of a finite field Fp with order p. Consider the equation,

β=gαmodp,for1≤α≤p−1.(1)

Given g, α, and p, calculating the modular exponentiation β=gαmodp is trivial. However, finding the exponent α given g, β, and p, it is computationally infeasible.

DLP is defined over a multiplicative group Zn∗ where n=p×q of order ϕ(n)=(p−1)(q−1). Consider the equation,

β=gαmodn,for1≤α≤ϕ(n).(2)

If the factorisation of order ϕ(n) is known and ϕ(n) has (small) prime factors, an instance of the DLP in Zn∗ can be reduced to two instances of the DLP in Zp∗ and Zq∗ using Pohlig et al. [29] algorithm. Nevertheless, it is believed that finding the exponent α is intractable for DLP in the multiplicative groups of finite fields [30].

2.3 Hash Function

A cryptographic one-way hash function h:X={0,1}∗→Y={0,1}l has the following properties.

■ The function h takes an arbitrary length input x∈X and returns a fixed l-bit length message digest y∈Y.

■ The function h is one-way; that is, given the input x, computing h(x)=y is trivial. However, given y, it is computationally infeasible to find the inverse h−1(y)=x.

■ The function h is collision-resistant, which means that finding two inputs x1≠x2 such that h(x1)=h(x2) is computationally infeasible.

The SHA-256 hash function was adopted for the proposed scheme. Other secure hash algorithms, such as SHA-1, SHA-224, SHA-384, SHA-512, and SHA-512/256 [28], can also be implemented.

2.4 Adversary Model

For communications over an insecure public channel, the Dolev et al. [31] adversary model was considered. Accordingly, the following assumptions were made.

■ Assumption A1: An adversary A can trap, delete, or alter the transmitted messages.

■ Assumption A2: An adversary A can obtain the stored information in the smart card using power monitoring techniques [32,33].

■ Assumption A3: An adversary A can guess the identity or password using the dictionary attack. However, the adversary A cannot guess the identity and password simultaneously using any online/offline attacks within polynomial time [34].

According to this adversary model, the following two cases as per [35] were also taken into account.

■ Case 1: An adversary A can be a non-registered user who tries to perform various attacks against the authentication system.

■ Case 2: An adversary A can be a registered user who tries to obtain the secret parameters of the server by which he/she can mount various attacks against the authentication system.

2.5 Security Goals

The following are the security goals of an ideal RPA scheme defined in this study that should be achieved, as listed in [36].

■ Mutual authentication: Both the server and the user can verify the legitimacy of each other. Furthermore, no illegal users or servers can impersonate a legal user or server.

■ Session key agreement: A session key should be created at the end of a successful mutual authentication process. Subsequently, the data transmitted between both entities should be encrypted to ensure confidentiality and secrecy.

■ User anonymity: During data transmission over a public channel, a user's valid identity should be concealed. Even if adversary A can analyse login information or gain access to services, user anonymity protects user's sensitive data, such as personal details, financial information, and social circles, from unauthorised parties.

3  Proposed Scheme

This section presents the proposed RPA scheme based on the security of IFP and DLP and consisted of five phases: (1) initialisation phase, (2) registration phase, (3) login phase, (4) authentication phase, and (5) password change phase. Furthermore, three entities were also considered: KIC, user Ui, and server S. In this scheme, the KIC is a trusted authority responsible for generating global parameters, computing user and server secret information, and providing new users with smart cards.

3.1 Initialisation Phase

The KIC sets up the server's public and secret parameters during the initialisation phase.

1.    Generate two large primes p=2p1+1 and q=2q1+1 of 1024-bit length, where p1 and q1 are both primes.

2.    Compute n=p×q and ϕ(n)=(p−1)⋅(q−1).

3.    Find a prime number e and integer d such that e⋅d≡1modϕ(n), where e is the server S's public-key and d is the corresponding private key.

4.    Find an integer g, which is a primitive element for both finite prime fields Fp and Fq.

5.    Decide on a secret parameter x∈Zp1∗ or Zq1∗ for server S and the format for identity ID of a user.

6.    KIC⇒S:{d,x,IDformat}.

The private key d, secret parameter x, and format of a user's ID should be safely provided to the server S. KIC is no longer needed once the system is set up, except during the registration phase when new users request to join. The integer pair p and q will not be used anymore and should be disposed of securely.

3.2 Registration Phase

In the registration phase, a new user Ui performs the following steps.

1.    Choose the identity IDi and the password pwi.

2.    Generate a random integer bi of 160-bit length.

3.    Compute hpwi=h(pwi||bi).

4.    Ui⇒ KIC:{IDi,hpwi}.

The KIC then performs the following steps.

5.   Generate CIDi=h(IDi||x).

6.   Compute w=h(d||x) and vi=w⊕h(IDi||hpwi).

7.   Compute hi=gIDi⋅d⋅xmodn and Si=CIDidmodn.

8.   Compute ji=hi⊕h(IDi||hpwi).

9.   KIC ⇒Ui:SCi={n,e,g,ji,vi,Si,hi}.

After receiving the smart card SCi, Ui performs the following steps.

10.   Compute b^i=h(IDi||pwi)⊕bi.

11.   Update the smart card SCi={n,e,g,ji,vi,Si,hi,b^i}.

Fig. 2 depicts an overview of the proposed RPA scheme's phases.

Figure 2: Overview of the proposed RPA scheme

3.3 Login Phase

When a registered user Ui wants to access the server S, the user Ui inserts the smart card SCi into a remote terminal. The user then enters the identity IDi and password pwi. The following steps are taken by the smart card SCi.

1.    Extract bi by computing bi=h(IDi||pwi)⊕b^i.

2.    Compute hpwi=h(pwi||bi).

3.    Check ji⊕hi=?h(IDihpwi). If the equation holds, server S believes that the user Ui is a valid user. Otherwise, the login request should be aborted.

4.    Extract w by computing w=h(IDihpwi)⊕vi.

5.    Generate a random integer ri of 160-bit length.

6.    Compute dynamic identity of Ui, DIDi=IDi⊕w.

7.    Compute Xi=gIDi⋅ri⋅emodn and Yi=Si⋅hiri⋅h(IDi||TU)modn, where TU is the timestamp of the user Ui when the login request is submitted.

8.    Ui→S: Login message ={n,e,DIDi,Xi,Yi,TU}.

3.4 Authentication Phase

Once the server S receives the login message request at the time TS, it proceeds with the following steps.

1.    Check (TS−TU)<ΔT, where ΔT is the allowed time transmission. If the time difference does not hold, the login request is rejected.

2.    Compute w=h(d||x).

3.    Extract IDi by computing IDi=DIDi⊕w.

4.    Check the validity of the format for IDi. If the format of IDi is invalid, the login request is rejected.

5.    Compute CIDi=h(IDi||x).

6.    Check Yie=CIDi⋅Xih(IDi||TU)⋅d⋅xmodn. If the equation does not hold, the login request is rejected.

7.    Otherwise, compute Zi=h(IDi||TS) and Ri=Zidmodn.

8.    S→Ui: Response message ={Ri,TS}.

Once the user Ui receives the response message at the time Tc, the user then performs the following steps.

9.   Check (Tc−TS)<ΔT. Disconnect from the server S if the time difference does not hold.

10.   Compute Zi=h(IDi||TS).

11.   Check Rie=?Zimodn. Disconnect from the server S if the equation does not hold.

12.   If mutual authentication is successful, the session key SK=h(IDiZiwTUTS) is agreed upon between the user Ui and server S.

Once the session key SK is established, the user Ui and server S can communicate with each other immediately. This step completes the mutual authentication process and eliminates the risk of the man-in-the-middle attack.

3.5 Password Change Phase

This phase enables the user Ui to change or update the password independently without interacting with the KIC or the server S. When changing the password, the user Ui inserts the smart card SCi into the terminal and enters the identity IDi and password pwi. The following steps are conducted by the smart card SCi.

1.    Extract bi by computing bi=h(IDi||pwi)⊕b^i.

2.    Compute hpwi=h(pwi||bi).

3.    Check ji⊕hi=?h(IDi||hpwi). If the equation holds, the smart card SCi believes the user Ui is a valid user and requests for a new password pwi∗. Otherwise, the password change request is rejected.

Once the user Ui enters the new password pwi∗, the smart card SCi performs the following steps.

4.   Generate a random integer bi of 160-bit length.

5.   Compute hpwi=h(pwi∗||bi∗) and b^i∗=h(IDi||pwi∗)⊕bi∗.

6.   Compute ji∗=ji⊕h(IDi||hpwi)⊕h(IDi||hpwi∗) and vi∗=vi⊕h(IDi||hpwi)⊕h(IDi||hpwi∗).

7.   Replace b^i, ji, and vi with b^i∗, ji∗, and vi∗, respectively.

8.   Update the smart card SCi={n,e,g,ji∗,vi∗,Si,hi,b^i∗}.

If user Ui's smart card SCi is lost or stolen, the user Ui must re-register with the KIC. Then, the KIC should issue a new smart card for the user Ui following the steps outlined in the registration phase.

3.6 Proof of Correctness

The propositions and proofs of correctness are presented below for the sake of completeness of the proposed scheme.

Proposition 1. If user Ui enters the correct identity IDi and password pwi, and Steps 1 and 2 of the login phase run well, the local user verification equation in Step 3 of the login phase will always hold. The proof is shown below.

ji⊕hi=(hi⊕h(IDi||hpwi))⊕hi=h(IDi||hpwi)⊕hi⊕hi=h(IDi||hpwi)

Proposition 2. If all the login phase steps and Steps 1–5 of the authentication phase run well, and the login message {n,e,DIDi,Xi,Yi,TU} is properly generated, then the user authentication equation in Step 6 of the authentication phase will always hold, as shown below.

Yie=(Si⋅hiri⋅h(IDi||TU))emodn=(Si)e⋅(hiri⋅h(IDi||TU))emodn=(CIDid)e⋅((gIDi⋅d⋅x)ri⋅h(IDi||TU))emodn=CIDi⋅(gIDi⋅ri⋅e)h(IDi||TU)⋅d⋅xmodn=CIDi⋅Xih(IDi||TU)⋅d⋅xmodn

Proposition 3. If all the steps in the authentication phase (Steps 1–10) run well and the response message {Ri,TS} is properly generated, then the server authentication equation in Step 11 of the authentication phase will always be true, as shown below.

Rie=(h(IDi||TS)d)emodn=h(IDi||TS)modn=Zimodn

4  Security Analysis of the Proposed Scheme

This section presents the formal security proof that the proposed scheme is provably secure against an adversary A for deriving the private key d, secret parameter x, identity IDi, password pwi, and shared session key SK. The proposed scheme is also shown to provide the desired security attributes.

4.1 Formal Security Proof

The formal security analysis of the proposed scheme, which is based on the random oracle model, is explained below. Specifically, the proposed scheme's formal security proof adopted the approach taken by [22,37–39]. To begin, the formal definitions of the collision-resistant cryptographic one-way hash function [39], IFP [22] and DLP [40,41] are given.

Definition 1. A secure collision-resistant one-way hash function

h:{0,1}∗→{0,1}l(3)

is a deterministic algorithm that takes an arbitrary length input x∈{0,1}∗ binary string and yields a fixed-length l-bit binary string output h(x)∈{0,1}l.

An adversary A's advantage in finding a collision is given as

AdvAHash(t1)=Pr[(x1,x2)⇐RA:x1≠x2∧h(x1)=h(x2)],(4)

where Pr[E] is the probability of an event E in a random experiment and (x1,x2)⇐RA denotes a randomly selected pair (x1,x2) by the adversary A. As a result, the adversary A can be probabilistic. The adversary A computes the probability in the advantage over the random choices with the execution time t1. If AdvAHash(t1)≤ε1, for any sufficiently small ε1>0, the one-way function h(⋅) is collision-resistant.

Definition 2. Assume that GenF is a polynomial time algorithm with input security parameter 1ρ and outputs (n,p,q), where n=p×q, and p and q are ρ-bit distinct primes. Given n, the integer factorisation assumption relative to GenF states that it is computationally infeasible to derive the prime factors p and q, except with a negligible probability in ρ.

For any adversary A of probabilistic-polynomial time (PPT), its factorisation advantage is given by

AdvGenF,AIFP(ρ)=Pr[(n,p,q)⇐GenF(1ρ):A(n)={p,q}].(5)

The integer factorisation assumption states that AdvGenF,AIFP(ρ) is negligible in ρ for every PPT adversary A. That is, the (tIFP,εIFP)-IFP assumption holds if AdvGenF,AIFP(ρ)≤εIFP(ρ), for any sufficiently small εIFP>0 with its running time is at most tIFP.

Definition 3. Let G be an order n cyclic group, g be a generator of G, and A be an algorithm that returns an integer in Zn. The following experiment EXPG,gDLP(A) in Algorithm 1 is considered.

The DLP advantage of algorithm A with execution time t is defined as

AdvG,gDLP(t)=Pr[EXPG,gDLP(A)=1].(6)

If the DLP advantage of any adversary A in terms of time complexity is small, the DLP is hard in G. Hence, DLP is computationally infeasible if AdvG,gDLP(t)≤εDLP, for any sufficiently small εDLP>0.

For this security proof, the adversary A is assumed to have access to the following three random oracles listed below.

■ OracleH: This oracle outputs the string x from a hash value y=h(x).

■ OracleF: This oracle outputs the private key d of the server S from the values n and e.

■ OracleD: This oracle outputs the value x∈Zn from the value h=gxmodn, where g is the generator in G of order n.

The three theorems and proof of formal security analysis are then presented as follows.

Theorem 1. If the cryptographic one-way hash function h(⋅) behaves like a true random oracle, and integer factorisation and discrete logarithm are computationally hard problems, then the proposed RPA scheme is provably secure against an adversary A for deriving the private key d and secret parameter x of server S.

Proof. Initially, an adversary A is constructed with the ability to derive private key d and secret parameter x of the server S by running the algorithm ALGA,PASOracle, as shown in Algorithm 2 for the proposed RPA scheme. By Assumption A2, suppose that the adversary A can extract {n,e,g,ji,vi,Si,hi,b^i} from the smart card using power monitoring techniques. By Assumption A1, it is further assumed that the adversary A intercepts login message {n,e,DIDi,Xi,Yi,TU} and response message {Ri,TS} at the time TU and TS, respectively.

The success probability of ALGA,PASOracle is given by SuccA,PASOracle=2Pr[ALGA,PASOracle=1]−1. Additionally, the advantage for ALGA,PASOracle is given by AdvA,PASOracle(t,qH,qF,qD)=maxA{SuccA,PASOracle}, where the maximum of all adversary A is taken with execution time t and the number of queries qH, qF, and qD made to OracleH, OracleF, and OracleD, respectively.

According to ALGA,PASOracle, if an adversary A could obtain the inverse of the cryptographic one-way hash function h(⋅) and solve the IFP and DLP, then the adversary A can successfully find the private key d and secret parameter x of server S using the oracles OracleH, OracleF, and OracleD, and wins the game. However, it is computationally infeasible for the adversary A as the advantage is negligible in polynomial time. By Definitions 1, 2, and 3, AdvA,PASOracleH(t1)≤ε1, AdvA,PASOracleF(t2)≤ε2, and AdvA,PASOracleD(t3)≤ε3, for any sufficiently small ε1,ε2,ε3>0. Since AdvA,PASOracle(t,qH,qF,qD) depends on all AdvA,PASOracleH(t1), AdvA,PASOracleF(t2), and AdvA,PASOracleD(t3), it must be that AdvA,PASOracle(t,qH,qF,qD)≤ε, for any sufficiently small ε>0. As a result, the theorem is proven.

Theorem 2. If the cryptographic one-way hash function h(⋅) behaves like a true random oracle, then the proposed RPA scheme is provably secure against an adversary A for deriving the identity IDi and password pwi of user Ui.

Proof. An adversary A is constructed who can derive the identity IDi and password pwi of user Ui by running the algorithm ALG2A,PASOracle of the proposed RPA scheme, as presented in Algorithm 3. Suppose that the adversary A can obtain the secret values {n,e,g,ji,vi,Si,hi,b^i} stored in a lost or stolen smart card, as shown in Theorem 1.

The success probability of ALG2A,PASOracle is defined as Succ2A,PASOracle=2Pr[ALG2A,PASOracle=1]−1 and its advantage is Adv2A,PASOracle(t,qH)=maxA{Succ2A,PASOracle}, where the maximum of all adversary A is taken with execution time t and the number of queries qH made to OracleH.

Consider ALG2A,PASOracle given in Algorithm 3, the adversary A will successfully obtain identity IDi and password pwi, and will thus win the game only if the adversary A can calculate the inverse of the cryptographic one-way hash function h(⋅). Nevertheless, it is a computationally infeasible problem for any adversary due to the collision-resistant property of h(⋅). Since AdvA,PASOracleH(t1)≤ε1 for any sufficiently small ε1>0 by Definition 1, then it must be that Adv2A,PASOracle(t,qH)≤ε, for any sufficiently small ε>0. Therefore, the proposed RPA scheme is provably secure against an adversary A for deriving identity IDi and pwi of user Ui.

Theorem 3. If the cryptographic one-way hash function h(⋅) behaves like a true random oracle, then the proposed RPA scheme is provably secure against an adversary A for deriving the shared session key SK between user Ui and server S.

Proof. Suppose that an adversary can derive the shared session key SK by running the algorithm ALG3A,PASOracle against the proposed RPA scheme, as described in Algorithm 4. As in Theorem 1 and Theorem 2, suppose that the adversary A can extract the information {n,e,g,ji,vi,Si,hi,b^i} from a lost or stolen smart card, and intercept login message {n,e,DIDi,Xi,Yi,TU} and response message {Ri,TS}.

Given the success probability of ALG3A,PASOracle is Succ3A,PASOracle=2Pr[ALG3A,PASOracle=1]−1, and the advantage as Adv3A,PASOracle(t,qH)=maxA{Succ3A,PASOracle}, where the maximum of all adversary A is taken with execution time t and the number of queries qH made to OracleH.

Based on ALG3A,PASOracle, if the adversary A can evaluate the inverse of a collision-resistant one-way hash function h(⋅), the adversary A can successfully derive the shared session key SK by using OracleH and wins the game. Nevertheless, Definition 1 states that AdvA,PASOracleH(t1)≤ε1 for any sufficiently small ε1>0. Then, it must be that Adv3A,PASOracle(t,qH)≤ε, for any sufficiently small ε>0, since it depends on AdvA,PASOracleH(t1). Hence, the proposed RPA scheme is shown to be provably secure against an adversary A for deriving shared session key SK between the user Ui and server S.

4.2 Security Attributes

This section further analyses the security attributes offered by the proposed RPA scheme.

4.2.1 No Data Storage in Server S

The proposed scheme preserves the “no data storage” feature of Kumari et al. [16] scheme. By using the information provided by the login message request, private key d, and secret parameter x, the server S can perform all the calculations to authenticate the validity of the user Ui.

4.2.2 Mutual Authentication

The proposed scheme includes mutual authentication steps for verifying the legitimacy of the user Ui and server S. The server S authenticates the user Ui by checking the user authentication equation Yie=CIDi⋅Xih(IDi||TU)⋅d⋅xmodn. A valid user Ui will pass the authentication since the identity IDi must follow the specified ID format.

Next, the user Ui checks the legitimacy of server S by verifying Rie=Zimodn. Since the user's identity is not transmitted explicitly in the public channel, the adversary A does not know the value of IDi. Therefore, any malicious user cannot compute the value of Zi=h(IDi||TS). As a result, the proposed scheme can attain mutual authentication.

4.2.3 Session Key Agreement

After completing the mutual authentication process, both the user Ui and server S will establish a shared session key SK=h(IDiZiwTUTS). Since the adversary A does not know IDi, Zi, and w, the session key SK cannot be directly computed due to the cryptographic collision-resistant one-way hash function. As a result, the proposed scheme can protect the secrecy of shared session keys.

4.2.4 User Anonymity

According to Assumption A2, the adversary A may extract information {n,e,g,ji,vi,Si,hi,b^i} from the smart card SCi. The identity IDi is contained in the parameters ji, vi, Si, and hi. Nevertheless, the adversary A is unable to derive identity IDi since the adversary A needs to invert the output of a collision-resistant one-way hash function. This is only possible for an adversary with a negligible probability in polynomial time, as proven in Theorem 2. As a result, the proposed scheme can preserve user anonymity.

4.2.5 Local Password Verification

The proposed scheme offers an incorrect input detection feature. Before logging into the server S, the smart card SCi verifies the legality of identity IDi and password pwi. The verification equation ji⊕hi=h(IDi||hpwi) will detect if a user Ui inputs the identity IDi or password pwi, or both incorrectly by mistake. Without knowing IDi, pwi, and bi, the adversary A is unable to correctly calculate h(IDi||hpwi) and subsequently, the verification ji⊕hi=h(IDi||hpwi) will fail. Therefore, the proposed scheme can block illegal access using local password verification.

4.2.6 Password Changeability

The extra “password change” phase in the proposed scheme grants users the convenience to change or update their passwords locally. This phase can be done without interacting with the KIC or the server S.

4.2.7 User-Friendliness

The proposed scheme permits the user Ui to freely choose the identity IDi and password pwi. The user Ui can easily change or update the password pwi without communicating with server S within minimal time without having to go through the registration phase. As a result, the proposed scheme is hassle-free and user-friendly.

5  Performance Comparison and Analysis

The endorsement of a new RPA scheme should be supported by careful analysis of its performance. For this purpose, the proposed scheme was compared with similar RPA schemes [4,15,16]. These schemes are chosen according to the security attributes offered, which are mutual authentication and no data storage in the server. Furthermore, since the aim of this study is to propose an efficient RPA scheme, it is considerable to compare its performance to the most recent scheme by Kumari et al. [16] that is found in the literature. The security attributes and efficiency of all schemes considered are investigated in this section.

Tab. 2 compares all schemes based on the security attributes discussed in Section 4. According to Tab. 2, the proposed scheme and the scheme by Kumari et al. [16] outperformed the schemes by Shen et al. [4] and Awasthi et al. [15]. All of the security attributes of [16] were retained in the proposed scheme, including no storage of data in server S, mutual authentication, session key agreement, user anonymity, local password verification, password changeability, and user-friendliness. Furthermore, unlike the other schemes, the proposed scheme includes a formal security analysis. As a result, the proposed RPA scheme outperformed other considered schemes in terms of security attributes.

The assessment assumptions for the efficiency analysis were based on [17,29]. Assuming that each value of {IDi,pwi,bi,ri} is 160-bit long, the output message digests of secure one-way hash function (SHA-256 [28]) {CIDi,DIDi,SK,w,hpwi,vi,ji,b^i} are 256-bit long, and the timestamps {TU,TS,Tc} are 32-bit long. The modular operation of modn is 2048-bit long, and the modular exponentiation is regarded as the most expensive operation. Hence, the values {n,e,d,Si,hi,Xi,Yi,Ri} are 2048-bit and {x,g} are 1024-bit. The exclusive OR (⊕) operation involves very few computations and hence is negligible. The time complexity with the exponential operation (Te), modular multiplication operation (Tm), hashing operation (Th), and exclusive OR operation (⊕) can be roughly expressed as Te≫Tm≈Th>⊕. For ease of time complexity comparison between schemes, the approximation of execution time complexity of Te and Th in terms of Tm is assumed as Te≈240Tm and Th≈Tm [42]. Tab. 3 shows the transmission/computational cost and time complexity for all considered schemes.

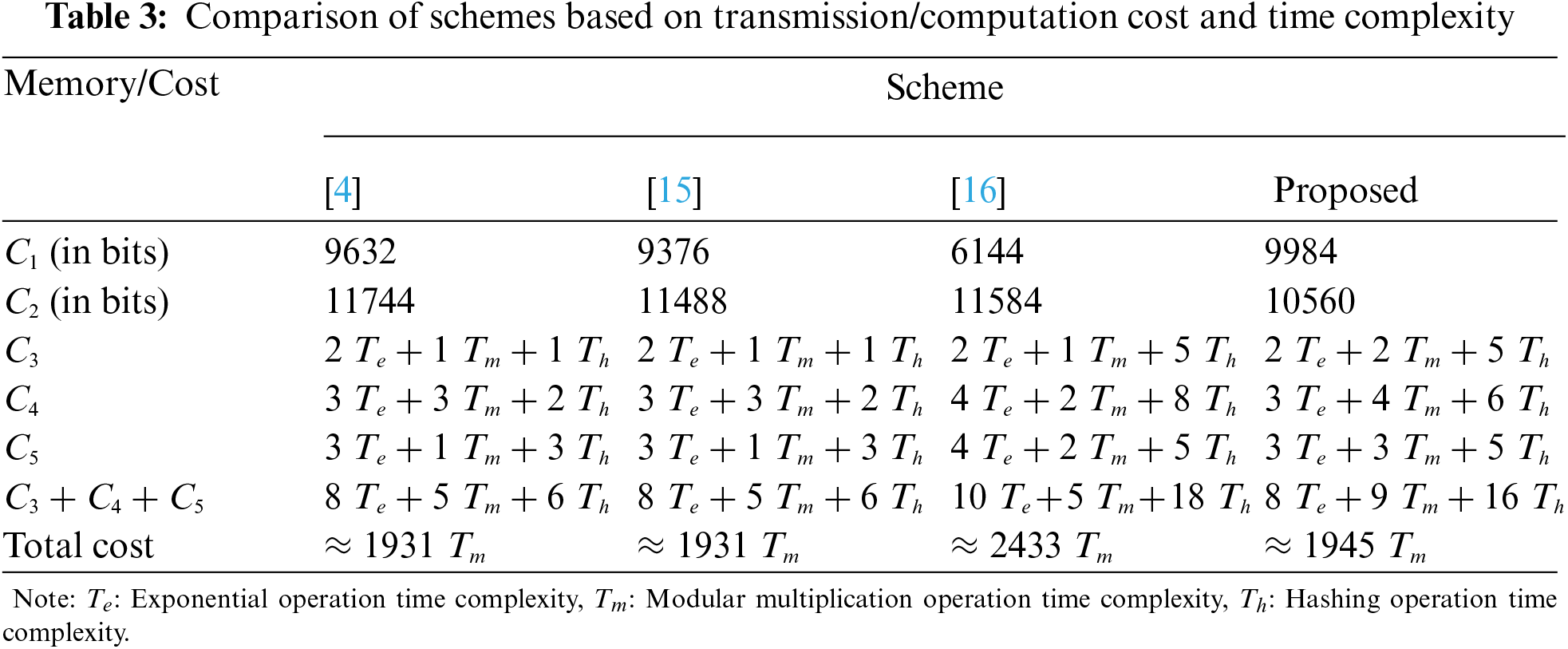
In the proposed scheme, the parameters {n,e,g,ji,vi,Si,hi,b^i} are stored within the smart card SCi. The memory storage required for the smart card is C1=(4×2048)+(1024)+(3×256)=9984-bit, which is the highest among other schemes, particularly 352-bit more than Shen et al. [4]. The transmission cost C2 is the memory space of the login message, {n,e,DIDi,Xi,Yi,TU} and response message, {Ri,TS} that are exchanged during the login and authentication phases. For the proposed scheme, its C2=(5×2048)+(256)+(2×32)= 10560-bit, which is the lowest among other schemes, particularly 928-bit less than Awasthi et al. [15]. The computational cost C3 is the total time complexity of operations executed during the registration phase, C3=2Te+2Tm+5Th. The computational cost of smart card SCi and server S are C4=3Te+4Tm+6Th and C5=3Te+3Tm+5Th, respectively (exhibit the time spent during the authentication phase and session key agreement).

Based on Tab. 3, the total computational costs (C3+C4+C5) of the schemes of Shen et al. [4] and Awasthi et al. [15] are both 8Te+5Tm+6Th≈1931Tm. While, the total computational costs for schemes of Kumari et al. [16] and the proposed scheme are 10Te+5Tm+18Th≈2433Tm and 8Te+9Tm+16Th≈1945Tm, respectively. Compared with the schemes by Shen et al. [4] and Awasthi et al. [15], the proposed scheme is less efficient with 14 Tm higher computational cost. In Fig. 3, the bar chart presents the efficiency of the proposed scheme over other considered schemes. It is clear that the proposed scheme is more efficient than Kumari et al. [16]. The total computational cost of Kumari et al. [16] has been significantly reduced by 20% in the proposed scheme.

Figure 3: Comparison of schemes based on total computational cost (C3+C4+C5)

As provided in Tab. 2, both the proposed scheme and Kumari et al. [16] require extra steps for session key agreement, which explains the higher computational cost when compared to the schemes by Shen et al. [4] and Awasthi et al. [15] in Tab. 3. It is worth noting that, as shown in Tab. 3, the proposed scheme requires larger smart card memory storage, particularly 3480-bit more than Kumari et al. [16]. However, this is justified because the proposed RPA scheme significantly reduced the transmission cost by 1024-bit as compared to Kumari et al. [16]. Additionally, the total computational cost improved to 1945 Tm, which is 488 Tm less than Kumari et al. [16]. Based on the security attributes, communication cost, and time complexity, it can be concluded that the proposed scheme outperformed all other schemes considered.

6  Application

This section discusses the proposed approach's potential applicability in developing a UI scheme. The UI scheme can be considered a simpler algorithm used to distinguish unique users prior to the authentication process. Most RPA schemes require two or more factors (e.g., password, smart card, and fingerprint), whereas UI schemes just need the user's identity. Figs. 4a and 4b show the flowcharts for the RPA and UI schemes, respectively. At a glance, the phases in the RPA and UI schemes appear similar, except that the UI scheme does not require a login phase. Some parameters can be removed while retaining the cryptographic primitives of IFP and DLP, depending on the security goals and purposes. Therefore, it would be interesting to investigate the prospect of converting the proposed RPA scheme into an improved UI scheme with provable security.

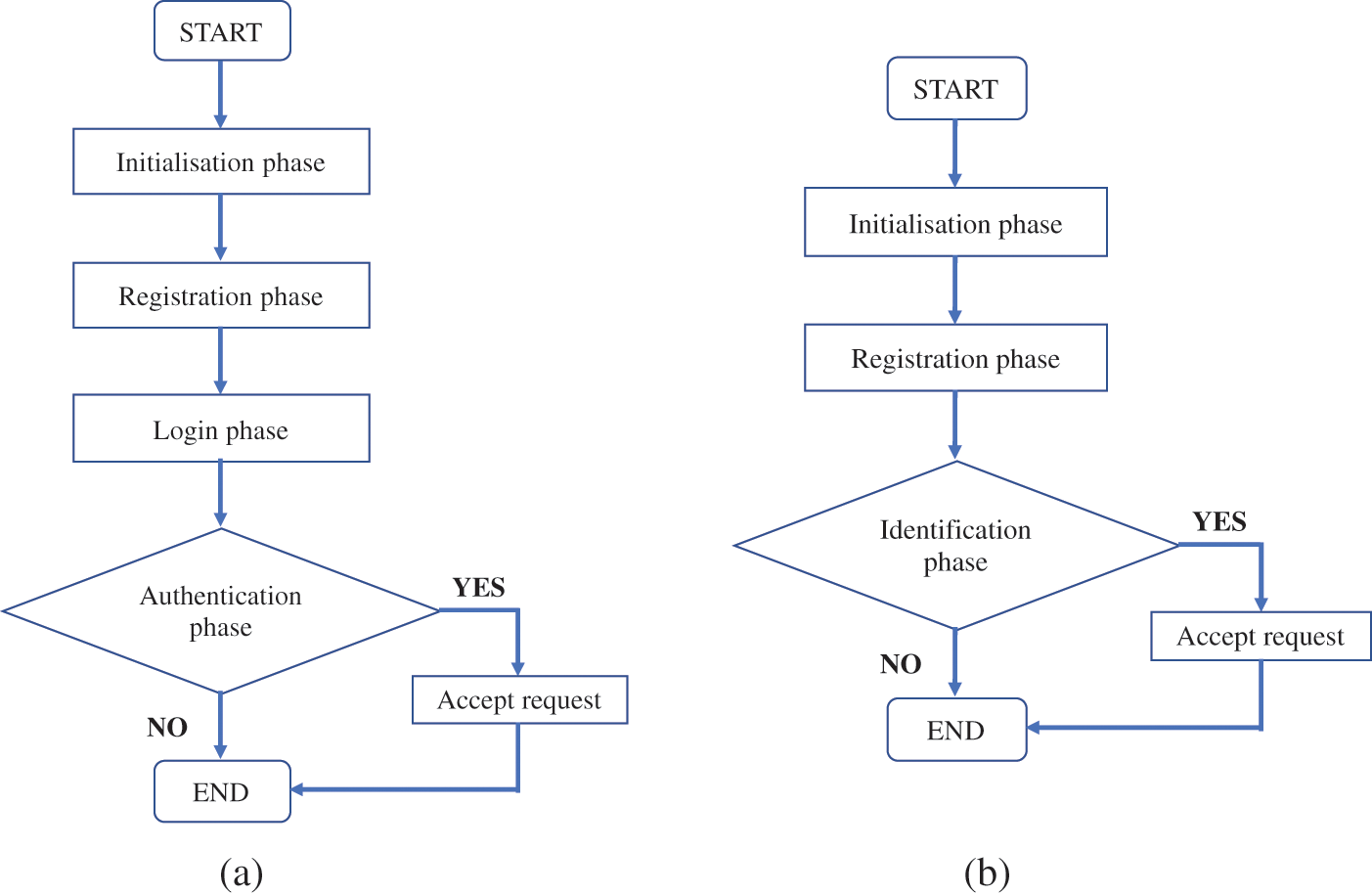
Figure 4: Process flowchart for RPA and UI schemes (a) RPA scheme (b) UI scheme

7  Conclusion

The aim of this study is to primarily propose an efficient RPA scheme that offers session key establishment between user and server. The widely established Dolev-Yao adversary model was considered in the development of the proposed scheme, which attained the desired security attributes of Kumari et al., such as no data storage in server S, user anonymity, local password verification, password changeability, and user-friendliness. Furthermore, as the main contribution, a formal security proof of the proposed scheme was presented based on the random oracle model using formal definitions of IFP and DLP. Although the proposed scheme required higher smart card memory than other similar schemes by Shen et al., Awasthi et al. and Kumari et al., this was acceptable owing to its much-reduced transmission/computation cost and time complexity than Kumari et al.'s scheme. The performance analysis proved that the proposed RPA scheme is noticeably better than Kumari et al., given that it can provide the same security attributes. Future work will investigate the use of two cryptographic primitives (IFP and DLP) in the development of UI schemes. Since the phases in RPA and UI schemes are similar, it would be interesting to examine the potential application, particularly in terms of security and performance. Expectantly, this should aid in the design of an efficient and provably secure UI scheme.

Acknowledgement: Authors are grateful for the support from Universiti Teknologi MARA (UiTM) and Universiti Kebangsaan Malaysia (UKM) for providing the facilities and resources, and UiTM/KPT-SLAB scholarship from the Ministry of Higher Education Malaysia (MOHE). In addition, the authors would like to thank anonymous reviewers for their comments and suggestions to improve this manuscript.

Funding Statement: This research is funded by UKM under Grant No. GUP-2020-029.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  W. H. Yang and S. P. Shieh, “Password authentication schemes with smart cards,” Computers & Security, vol. 18, no. 8, pp. 727–733, 1999. [Google Scholar]

 2.  A. Shamir, “Identity-based cryptosystems and signature schemes,” in Lecture Notes Computer Sciences (Including Subseries Lect. Notes Artificial Intelligence Lecture Notes Bioinformatics), vol. 196 LNCS, Berlin, Heidelberg: Springer, pp. 47–53, 1985. [Google Scholar]

 3.  L. Fan, J. H. Li and H. W. Zhu, “An enhancement of timestamp-based password authentication scheme,” Computers & Security, vol. 21, no. 7, pp. 665–667, 2002. [Google Scholar]

 4.  J. J. Shen, C. W. Lin and M. S. Hwang, “Security enhancement for the timestamp-based password authentication scheme using smart cards,” Computers & Security, vol. 22, no. 7, pp. 591–595, 2003. [Google Scholar]

 5.  R. Jiang, L. Pan and J. H. Li, “Further analysis of password authentication schemes based on authentication tests,” Computers & Security, vol. 23, no. 6, pp. 469–477, 2004. [Google Scholar]

 6.  Y. Wang and J. Li, “Security improvement on a timestamp-based password authentication scheme,” IEEE Transactions on Consumer Electronics, vol. 50, no. 2, pp. 580–582, 2004. [Google Scholar]

 7.  Y. Wang, J. Li and L. Tie, “Security improvement on Yang-Shieh's authentication scheme,” in 2004 Int. Conf. on Communications, Circuits and Systems, Chengdu, China, vol. 1, pp. 4–5, 2004. [Google Scholar]

 8.  C. C. Yang, R. C. Wang and T. Y. Chang, “An improvement of the Yang-Shieh password authentication schemes,” Applied Mathematics and Computation, vol. 162, no. 3, pp. 1391–1396, 2005. [Google Scholar]

 9.  A. S. K. Pathan, “A review and cryptanalysis of similar timestamp-based password authentication schemes using smart cards,” International Journal of Communication Networks and Information Security, vol. 2, no. 1, pp. 15–20, 2010. [Google Scholar]

10. J. Y. Liu, A. M. Zhou and M. X. Gao, “A new mutual authentication scheme based on nonce and smart cards,” Computer Communications, vol. 31, no. 10, pp. 2205–2209, 2008. [Google Scholar]

11. C. C. Yang and R. C. Wang, “An improvement of security enhancement for the timestamp-based password authentication scheme using smart cards,” ACM SIGOPS Operation Systems Review, vol. 38, no. 3, pp. 91–96, 2004. [Google Scholar]

12. E. J. Yoon, E. K. Ryu and K. Y. Yoo, “Security of Shen et al.'s timestamp-based password authentication scheme,” in Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), vol. 3046 LNCS, Berlin, Heidelberg: Springer, pp. 665–671, 2004. [Google Scholar]

13. X. Wang, J. Zhang, W. Zhang and M. K. Khan, “Security improvement on the timestamp-based password authentication scheme using smart cards,” in 2006 IEEE Int. Conf. on Engineering of Intelligent Systems, Islamabad, Pakistan, pp. 1–3, 2006. [Google Scholar]

14. T. H. Chen, G. Horng and K. C. Wu, “A secure YS-like user authentication scheme,” Informatica, vol. 18, no. 1, pp. 27–36, 2007. [Google Scholar]

15. A. K. Awasthi, K. Srivastava and R. C. Mittal, “An improved timestamp-based remote user authentication scheme,” Computers and Electrical Engineering, vol. 37, no. 6, pp. 869–874, 2011. [Google Scholar]

16. S. Kumari, M. K. Gupta, M. K. Khan and X. Li, “An improved timestamp-based password authentication scheme: Comments, cryptanalysis, and improvement,” Security and Communication Networks, vol. 7, no. 11, pp. 1921–1932, 2014. [Google Scholar]

17. K. W. Kim, J. C. Jeon and K. Y. Yoo, “An improvement on yang et al.'s password authentication schemes,” Applied Mathematics and Computation, vol. 170, no. 1, pp. 207–215, 2005. [Google Scholar]

18. M. K. Khan, “Cryptanalysis and security enhancement of two password authentication schemes with smart cards,” in INMIC2007-11th IEEE Int. Multitopic Conf., Lahore, Pakistan, pp. 1–4, 2007. [Google Scholar]

19. D. Giri and P. D. Srivastava, “Cryptanalysis and the improvement of Kim et al.'s password authentication schemes,” in Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), vol. 4812 LNCS, Berlin, Heidelberg: Springer, pp. 156–166, 2007. [Google Scholar]

20. E. S. Ismail and S. M. S. Syed-Musa, “Timestamp-based password authentication scheme,” AIP Conference Proceedings, vol. 1974, pp. 1–5, 2018. [Google Scholar]

21. Y. An, “Security enhancements of an improved timestamp-based remote user authentication scheme,” in Communications in Computer and Information Science, vol. 339 CCIS, pp. 54–61, 2012. [Google Scholar]

22. N. Radhakrishnan and M. Karuppiah, “An efficient and secure remote user mutual authentication scheme using smart cards for telecare medical information systems,” Informatics in Medicine Unlocked, vol. 16, pp. 100092, 2018. [Google Scholar]

23. A. K. Das, S. Chatterjee and J. K. Sing, “A novel efficient access control scheme for large-scale distributed wireless sensor networks,” International Journal of Foundations of Computer Science, vol. 24, no. 5, pp. 625–653, 2013. [Google Scholar]

24. S. H. Islam, “Provably secure dynamic identity-based three-factor password authentication scheme using extended chaotic maps,” Nonlinear Dynamics, vol. 78, no. 3, pp. 2261–2276, 2014. [Google Scholar]

25. R. Amin, T. Maitra, D. Giri and P. D. Srivastava, “Cryptanalysis and improvement of an RSA based remote user authentication scheme scheme using using smart card,” Wireless Personal Communications, vol. 96, no. 3, pp. 4629–4659, 2017. [Google Scholar]

26. W. Diffie and M. Hellman, “New directions in cryptography,” IEEE Transactions on Information Theory, vol. 22, no. 6, pp. 644–654, 1976. [Google Scholar]

27. R. Rivest, “The MD5 message-digest algorithm,” RFC 1321, April 1992. https://ftp://ftp.rfc-editor.org/in-notes/rfc1321.txt. [Google Scholar]

28. NIST, “FIPS PUB 180-4 secure hash standard (SHS),” 2012. [Google Scholar]

29. S. C. Pohlig and M. E. Hellman, “An improved algorithm for computing logarithms over GF(p) and its cryptographic significance,” IEEE Transactions on Information Theory, vol. 24, no. 1, pp. 106–110, 1978. [Google Scholar]

30. J. Katz and Y. Lindell, Introduction to Modern Cryptography, 3rd edition. Boca Raton, USA: CRC Press, 2021. [Google Scholar]

31. D. Dolev and A. C. Yao, “On the security of public key protocols,” IEEE Transactions on Information Theory, vol. 29, no. 2, pp. 198–208, 1983. [Google Scholar]

32. P. Kocher, J. Jaffe and B. Jun, “Differential power analysis,” In: M. Wiener (Ed.) Advances in Cryptology, Berlin, Heidelberg: Springer, pp. 388–397, 1999. [Google Scholar]

33. T. S. Messerges, E. A. Dabbish and R. H. Sloan, “Examining smart-card security under the threat of power analysis attacks,” IEEE Transactions on Computers, vol. 51, no. 5, pp. 541–552, 2002. [Google Scholar]

34. S. K. Sood, A. K. Sarje and K. Singh, “Cryptanalysis of password authentication schemes: Current status and key issues,” in Proc. of Int. Conf. on Methods and Models in Computer Science, ICM2CS09, Delhi, India, 2009. [Google Scholar]

35. T. Maitra, M. S. Obaidat, S. H. Islam, D. Giri and R. Amin, “Security analysis and design of an efficient ECC-based two-factor password authentication scheme,” Security and Communication Networks, vol. 9, no. 17, pp. 4166–4181, 2016. [Google Scholar]

36. F. Wu, L. Xu, S. Kumari, X. Li and A. Alelaiwi, “A new authenticated key agreement scheme based on smart cards providing user anonymity with formal proof,” Security and Communication Networks, vol. 8, no. 18, pp. 3847–3863, 2015. [Google Scholar]

37. A. K. Das, N. R. Paul and L. Tripathy, “Cryptanalysis and improvement of an access control in user hierarchy based on elliptic curve cryptosystem,” Information Sciences, vol. 209, pp. 80–92, 2012. [Google Scholar]

38. A. K. Das, “A secure and effective user authentication and privacy preserving protocol with smart cards for wireless communications,” Networking Science, vol. 2, no. 1–2, pp. 12–27, 2013. [Google Scholar]

39. V. Odelu, A. K. Das and A. Goswami, “An efficient ECC-based privacy-preserving client authentication protocol with key agreement using smart card,” Journal of Information Security Applications, vol. 21, pp. 1–19, 2015. [Google Scholar]

40. M. Bellare and P. Rogaway, Introduction to Modern Cryptography, California, USA, University of California at Davis, 2005. [Online]. https://web.cs.ucdavis.edu/~rogaway/classes/227/spring05/book/main.pdf. [Google Scholar]

41. M. Karuppiah, A. K. Das, X. Li, S. Kumari, F. Fan et al., “Secure remote user mutual authentication scheme with key agreement for cloud environment,” Mobile Networks and Applications, vol. 24, no. 3, pp. 1046–1062, 2018. [Google Scholar]

42. C. H. Tsai and P. C. Su, “Multi-document threshold signcryption scheme,” Security and Communication Networks, vol. 8, no. 13, pp. 2244–2256, 2015. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.