Computers, Materials & Continua DOI:10.32604/cmc.2022.022020
Article

Sum Rate Maximization-based Fair Power Allocation in Downlink NOMA Networks

Mohammed Abd-Elnaby*

Department of Computer Engineering, College of Computers and Information Technology, Taif University, Taif, 21944, Saudi Arabia
*Corresponding Author: Mohammed Abd-Elnaby. Email: maahmed@tu.edu.sa
Received: 25 July 2021; Accepted: 10 November 2021

Abstract: Non-orthogonal multiple access (NOMA) has been seen as a promising technology for 5G communication. The performance optimization of NOMA systems depends on both power allocation (PA) and user pairing (UP). Most existing researches provide sub-optimal solutions with high computational complexity for PA problem and mainly focuses on maximizing the sum rate (capacity) without considering the fairness performance. Also, the joint optimization of PA and UP needs an exhaustive search. The main contribution of this paper is the proposing of a novel capacity maximization-based fair power allocation (CMFPA) with low-complexity in downlink NOMA. Extensive investigation and analysis of the joint impact of signal to noise ratio (SNR) per subcarrier and the channel gains of the paired users on the performance of NOMA in terms of the capacity and the user fairness is presented. Next, a closed-form equation for the power allocation coefficient of CMFPA as a function of SNR, and the channel gains of the paired users is provided. In addition, to jointly optimize UP and PA in NOMA systems an efficient low-complexity UP (ELCUP) method is proposed to be incorporated with the proposed CMFPA to compromise the proposed joint resource allocation (JRA). Simulation results demonstrate that the proposed CMFPA can improve the capacity and fairness performance of existing UP methods, such as conventional UP, and random UP methods. Furthermore, the simulation results show that the proposed JRA significantly outperforms the existing schemes and gives a near-optimal performance.

Keywords: 5G; NOMA; UP; PA; capacity; fairness

1  Introduction

Non-orthogonal multiple access (NOMA) arises as the reliable multiple access technique for the fifth-generation (5G) communication systems to provide the required high data rates and massive connectivity [1,2]. Successive interference cancelation (SIC) enables NOMA to remove the co-channel interference among the users and to efficiently exploit the channel diversity. In NOMA, multiple users can use the same spectrum resources, which leads to achieve higher spectral efficiency and provide higher data rate and latency to a massive number of users compared to conventional orthogonal multiple access (OMA) techniques [3].

The conventional OMA techniques such as orthogonal frequency division multiple access, which are categorized cannot support massive connectivity since each subcarrier can be allocated to a single user to avoid multiple access interference [4]. On the contrary, NOMA allows multiple user equipment (UE) to simultaneously utilize the same frequency by using the SIC technique at the receiver [5], which leads to increase the spectral efficiency [6]. NOMA can also be used to enhance the performance of other communication technologies, such as visible light communication [7], MIMO [8,9], and millimeter-wave communication [10].

Resource allocation represented in power allocation (PA) and channel assignment or user pairing (UP) are the keys to optimize the performance of NOMA systems. The optimal PA was only existed for users on a single channel and only for the maximization of the sum rate. Furthermore, in most of the existing works, the fairness performance was not taken into account, and the PA only depends on the channel gain of the paired users [11–13]. Unfortunately, the joint optimization of PA and UP in NOMA systems requires exhaustive search, which is not applicable or practical solution [14]. In this paper, the resource allocation for downlink NOMA systems is investigated with a focus on PA which is based on SNR per subcarrier and the channel gains of the paired users for optimization of both the sum rate and fairness performance.

The main contributions of this paper are as follows:

1)   Extensive investigation and analysis of the joint impact of SNR per subcarrier and the paired users’ channel gains on the performance of NOMA is presented.

2)   A novel capacity maximization-based fair power allocation (CMFPA) with low-complexity in downlink NOMA is proposed, which represents the main contribution of this paper. In CMFPA, a closed-form equation is proposed for the power allocation coefficient as a function of SNR per subcarrier and the channel gains of the paired users.

3)   In addition, efficient low-complexity UP (ELCUP) method is proposed to be incorporated with the proposed CMFPA to compromise the proposed joint resource allocation (JRA) for the optimization of capacity and fairness performance of NOMA systems with a significantly low computational complexity.

4)   Compared to the existing schemes, CMFPA can significantly improve the capacity and fairness performance of existing UP methods such as conventional UP, and random UP methods.

5)   Finally, simulation results show that the proposed JRA outperforms the existing schemes and gives a near-optimal performance.

The rest of the paper is organized as follows. A discussion of related work is presented in Section 2. Section 3 presents the system model. In Section 4, the investigation and analysis of the joint impact of SNR per subcarrier and the paired users’ channel gains on the performance of NOMA and the proposed CMFPA are provided. The ELCUP method is given in Section 5. The simulation results and discussion are introduced in Section 6. Finally, the conclusion is given in Section 7.

2  Related Work

PA in NOMA depends on several aspects such as the channel conditions and signal-to-noise ratio (SNR), which is related to the total power restriction. The main aim of PA in NOMA is the maximization of the sum-rate (capacity), and there are many related works [14–18].

In [14], the authors develop an optimal joint PA and subcarrier assignment policy using monotonic optimization to maximize the weighted sum rate, which, however, has exponential computational complexity. In [15], a suboptimal PA solution for sum-rate maximization was presented where the nonconvex PA problem was solved using DC programming. Game theory was applied in PA for NOMA systems in several researches for sum-rate maximization [16,17]. The optimal PA is investigated in [18] under QoS constraints for the maximization of the weighted sum rate.

In [19], and [20], sub-optimal solutions for sub-channel and power allocation in multi-user NOMA systems are proposed to enhance energy efficiency. The authors derived a closed form expression to solve the non-convex problem, followed by KKT conditions. An iterative approach is adopted to obtain a solution for the joint problem of power and user allocation to increase the energy efficiency was investigated in [21]. In [22], Lagrangian optimization was used for efficient power allocation, and two-sided matching technique was used for sub-channel assignment to improve the energy efficiency. Besides this, optimal power management and user clustering were performed in [23] to reduce the power consumption in multi-cell NOMA networks.

However, the objective of these researches is the maximization of the sum rate and energy efficiency, where fairness among users is not considered, which is an important issue for NOMA networks. Several works considered the fairness issue in NOMA, e.g., [24–27]. In [24] and [25], optimal PA based on the maximin fairness (MMF) as a fairness indicator was investigated. A proportional fairness scheme for the maximization of the weighted MMF was investigated in [26], for a single channel and two users. The main feature of the suboptimal fractional transmit power control (FTPC) proposed in [27] is that the target performance metric (fairness or sum rate) needs to be determined a priori. In FTPC, the user transmits power depends on the channel gains of the multiplexed users and the decay factor. As the value of decay factor (0 ≤ decay factor ≤ 1) increases, the allocated power to the user with lower channel gain increases, and fairness improves while the sum rate decreases, and vice versa.

Joint sub-channel and power management for downlink heterogeneous NOMA networks were investigated in [28–30]. In addition, the problems of resources in cognitive NOMA networks to increase the spectral efficiency in NOMA were investigated recently in [31–33].

3  System Model

A single-cell based downlink NOMA system scenario is considered, where a base station (BS) simultaneously transmits information to K users (i.e., users’ equipment (UEs)) over M subcarriers, as illustrated in Fig. 1 [34]. Let m = {1,…, M} be the set of subcarriers, and k = {1… K} denotes the set of UEs. In the considered NOMA network system, two users are assigned per subcarrier to reduce the complexity of SIC.

Figure 1: System model for downlink NOMA system [34]

For a subcarrier m, the channel gain of the user1 (UE-1) which is called strong UE is assumed to be larger than the channel gain of the user2 (UE-2), which is called weak UE (|hm,1|2>|hm,2|2). So, the receiver of UE-1 can perform SIC by treating its signal as noise and decoding the signal of UE-2 first. The ratio of weak UE’ channel gain (hm,2) to the strong UE's channel gain (hm,1) is μ=hm,2hm,1 such that hm,2=μhm,1 and hence μ is always <1. The power allocation coefficient for strong UE is denoted by α and must be lower than 0.5 (i.e., α<0.5). So, 1−α of the subcarrier transmitted power is allocated to weak UE.

On a subcarrier m, the superimposed signal transmitted from BS to the paired UEs is

xm=αPmsm,1+(1−α)Pmsm,2(1)

where Pm is the subcarrier allocated power and sm,1 and sm,2 are the transmitted signal to UE-1 and UE-2.

The received signals of the paired UEs are

ym,i=hm,ixm+nm,ii=1,2(2)

where hm,i denotes the channel gain of the subcarrier m between the BS and UE-i, and nm,i refers to the additive white Gaussian noise (AWGN) with zero mean and varianceσ2.

Since |hm,1|2>|hm,2|2, UE-1's receiver can execute SIC and eliminate the interference from UE-2's signal. Assuming that the transmission bandwidth per subcarrier is normalized to 1 Hz, the data rates of the paired UEs will be as follows [35].

Rm,1=log2(1+αPm|hm,1|2σ2)(3)

Rm,2=log2(1+(1−α)Pm|hm,2|2αPm|hm,2|2+σ2)(4)

where (Pmσ2) represents the SNR per subcarrier.

So, the sum-rate over a subcarrier m (i.e., the subcarrier capacity) for NOMA system is Rm,1+Rm,2.

The achievable rate of the UE-i over a subcarrier m for OMA system is

Rm,iOMA=12log2(1+Pm|hm,1|2σ2)i=1,2.(5)

So, the sum-rate over a subcarrier m for OMA system is Rm,1OMA+Rm,2OMA, where the factor 12 is since the OMA system produces a multiplexing loss of 12 [35].

4  The Proposed Capacity Maximization Based Fair Power Allocation (CMFPA)

In this section, extensive investigation and analysis of the joint impact of SNR per subcarrier and the channel gains of the paired users on the performance of NOMA with respect to the capacity and the user fairness are firstly introduced in Section 4.1. After that, the proposed CMFPA, which is based on this investigation, will be presented in Section 4.2 as a function of the following three parameters:

1.    SNR per subcarrier (Pmσ2)

2.    The channel gain of strong UE (hm,1)

3.    The ratio of the channel gain of weak UE to the channel gain of strong UE (μ=hm,2hm,1).

Where hm,1 and μ represent the channel gain parameters of the paired users.

4.1 The Joint Impact of Subcarrier's SNR and Channel Gains of the Paired UEs with α on the Performance of NOMA

In this section, the joint impact of subcarrier's SNR and the channel gains of the paired UEs with the power allocation coefficient α on the subcarrier capacity (i.e., the sum-rate per subcarrier) and the fairness between the paired UEs will be investigated. The main target of these investigations is to specify the best choices of the power allocation coefficient to optimize the capacity and fairness performance according to the values of subcarrier's SNR and the channel gains of the paired UEs.

The subcarrier capacity (i.e., Rm,1+Rm,2) can be computed using Eqs. (3) and (4) which presented in the previous section. On the other hand, the well-known Jain's fairness index (FI) which measures the fairness among the achieved data rates of UEs [36] is used for fairness performance evaluation according to the following equation.

F=(∑k=1K⁡Rk)2K∑k=1K⁡(Rk)2(6)

where Rk is the achieved data rate of the kth UE and K is the number of UEs.

During the analysis and discussion of results, we will refer to hm,1 by h1 for simplicity. The impact of channel gains on NOMA performance is represented in term of the impact of both h1 and μ (i.e., hm,2hm,1). The discussion of results concentrates on clarifying the best choices for the value of α for capacity maximization with highest achievable FI values. The investigation results are organized as follows:

§ To show the joint impact of both SNR and h1 with α at a fixed value of μ, the investigation results are presented as a function of SNR and α at h1 = 1 and then as a function of h1 and α at SNR = 0 dB

§ To show the impact of μ, the investigation results are taken at a large value of μ (μ = 0.9), a medium value of μ (μ = 0.5), and a small value of μ (μ = 0.1).

4.1.1 Performance Investigation Results at a Large Value of μ (μ = 0.9)

Concerning the capacity, Figs. 2 and 3 demonstrate that there is no significant loss in the capacity as α decreases and it increases as the values of SNR and h1 increase. Concerning the fairness performance, Figs. 4 and 5 show that at h1 = 1 and SNR = 0 dB, the FI values are nearly optimum as α>0.25 and as the values of SNR and h1 increase, α should be gradually decreased to maximize the FI.

Figure 2: Capacity as a function of SNR and α (at h1 = 1 and μ = 0.9)

Figure 3: Capacity as a function of h1 and α (at SNR = 0 dB and μ = 0.9)

Figure 4: Fairness Index (FI) as a function of SNR and α (at h1 = 1 and μ = 0.9)

Figure 5: Fairness Index (FI) as a function of h1 and α (at SNR = 0 dB and μ = 0.9)

4.1.2 Performance Investigation Results at a Medium Value of μ (μ = 0.5)

Concerning the capacity, Figs. 6 and 7 show that it slightly decreases as α decreases and the decrement is significant at small values of SNR and h1. Concerning the fairness performance, Figs. 8 and 9 show that at h1 = 1 and SNR = 0 dB, the FI values are nearly optimum as 0.35≥α≥0.15 and, as the values of SNR and h1 increase, α should be gradually decreased to maximize the FI.

Figure 6: Capacity as a function of SNR and α (at h1 = 1 and μ = 0.5)

Figure 7: Capacity as a function of h1 and α (at SNR = 0 dB and μ = 0.5)

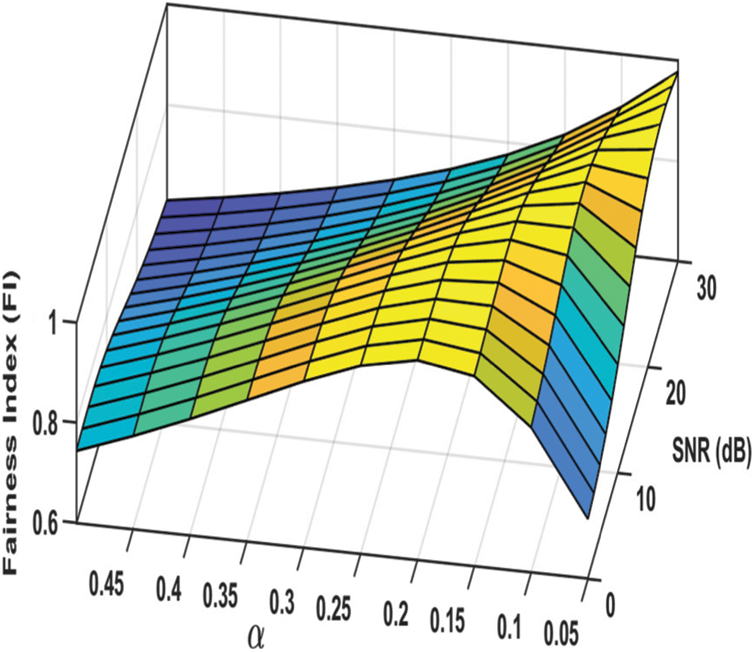
Figure 8: Fairness Index (FI) as a function of SNR and α (at h1 = 1 and μ = 0.5)

Figure 9: Fairness Index (FI) as a function of h1 and α (at SNR = 0 dB and μ = 0.5)

4.1.3 Performance Investigation Results at a Small Value of μ (μ = 0.1)

Concerning the capacity, Figs. 10 and 11 show that the capacity significantly reduces as α decreases, specifically at small values of α. Also, it is clear that increasing the SNR is more effective in improving the capacity rather than increasing h1. Concerning the fairness performance, Figs. 12 and 13 demonstrates that the worst fairness performance occurs at a small value of μ (μ = 0.1), and the FI sharply decreases as α and becomes greater than 0.05. Also, it is shown that fairness performance improves as the SNR and h1 increase and the highest achieved values of FI are obtained at the lowest value of α (α=0.05).

Figure 10: Capacity as a function of SNR and α (at h1 = 1 and μ = 0.1)

Figure 11: Capacity as a function of h1 and α (at SNR = 0 dB and μ = 0.1)

Figure 12: Fairness Index (FI) as a function of SNR and α (at h1 = 1 and μ = 0.1)

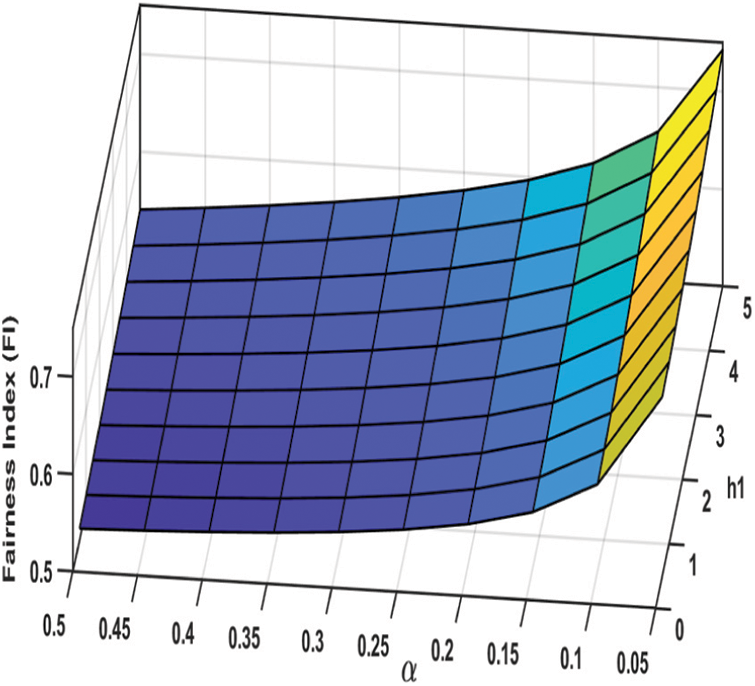
Figure 13: Fairness Index (FI) as a function of h1 and α (at SNR = 0 dB and μ = 0.1)

It is worth mentioning that in case of small values of μ, the optimization of both the capacity and the fairness performance cannot be achieved. Therefore, it is better to maximize the capacity and avoid a large loss in the achieved capacity at the expense of the degradation of the fairness performance by setting α close as possible to its highest possible value (α=0.5).

4.2 The Proposed CMFPA

Based on the extensive investigation results in previous section, the following concepts can be concluded:

1)   In the case of a large value of μ, no capacity loss occurs as α decreases, while to optimize the fairness performance (maximize the FI), α should be greater than 0.25 at h1 = 1 and SNR = 0 dB, and gradually decreased as the values of SNR and h1 increase.

2)   In the case of a medium value of μ (i.e., μ = 0.5), no significant capacity loss occurs as α decreases except at low values of SNR and h1, while to optimize the fairness performance, α should be in the range from 0.15 to 0.35 (0.35 ≥ α ≥ 0.15) at h1 = 1 and SNR = 0 dB, and gradually decreases as the values of SNR and h1 increase.

3)   In the case of a small value of μ (i.e., μ = 0.1), the best choice is setting α close as possible to its highest possible value (α = 0.5) to maximize the capacity and avoid a large loss in the achieved capacity at the expense of the degradation of the fairness performance.

Since the proposed CMFPA targets to maximize the capacity and to achieve the highest possible FI values without capacity loss, α should be adjusted as follows:

§ As the value of μ decreases, α should be increased and be closer to its maximum value αmax.

§ As the values of SNR and h1 increase, α should be monotonically decreased to optimize the fairness performance.

Based on the concluded concepts from the extensive investigation results in the previous section, the following closed-form equations for the adjustment of α according to the values of μ, SNR, and h1 are proposed:

α=αmax−0.25μ−(0.220)(10log10(h1SNR))(7)

αOpt=max(α,αmin)(8)

where

αmax=12(1−θPm|hm1|2),andαmin=0.05(9)

Eq. (9) for αmax is derived from the following equation for the needed gap between the paired UEs’ received powers to perform SIC successfully, where θ is its minimum value [34].

[(1−α)Pm−αPm]|hm,1|2≥θ(10)

During simulation value of θ is set to be 1 Watt.

The proposed equation guarantees that the value of α be in the range required to optimize both the capacity and fairness performance in case of large and medium values of μ and maximize the capacity at the expense of some loss in the fairness performance in case of small values of μ. For example, if αmax is assumed to be 0.5. So, at large values of μ (i.e., μ close to 1), α initially starting at 0.25 at h1 = 1 and SNR = 0 dB since 10log10(h1SNR)=0. Then, α gradually decreases as the values of h1 and SNR increase to reach its minimum value αmin as 10log10(h1SNR) becomes greater than 20 dB. On the other hand, at small values of μ (i.e., μ close to zero), α initially starting at αmax at h1 = 1 and SNR = 0 dB, and gradually decreases as the values of SNR and h1 increase.

5  The Proposed Efficient Low Complexity User Pairing (ELCUP) Algorithm

The UP algorithm is responsible for the selection of the paired UEs according to their channel gains and consequently the selection of h1, and h2 (i.e., the selection of h1, and μ since μ = h2/h1). The impact of h1, and μ on the capacity and user fairness is presented in Figs. 14 and 15, respectively at SNR = 10 dB and α = 0.2. It is clear that the capacity increases as h1increases and decreases as the values of μ become significantly small. With respect to the fairness between the paired users, it is mainly affected by the value of μ and significantly deteriorates as the values of μ become significantly small as shown in Fig. 15. Therefore, the objectives of the proposed Efficient Low Complexity User Pairing (ELCUP) Algorithm are as follows:

•   Maximizing the capacity by increasing the values of h1. Thiscan be achieved by making the order of the UP process bases on the best subcarrier first and selecting the user with the highest channel gain to be the strong user.

•   Improving the fairness among the paired user by avoiding small values of μ.

•   Minimizing the computational complexity of the UP process.

Figure 14: Capacity as a function of h1(at SNR = 10 dB and α = 0.2)

Figure 15: Fairness Index (FI) as a function of h1(at SNR = 10 dB and α = 0.2)

The steps of the user pairing process are proceeded as follows:

•   The average value of the channel gains of all users over each subcarrier is computed to be used as a simple measure of the channel quality per subcarrier, such that, the subcarrier with the highest average value of the channel gains is considered as the best subcarrier.

hmAverage=1K∑k=1K⁡|hm,k|2∀m.(11)

•   The order of subcarriers during the UP process is the highest channel quality subcarrier (i.e., the best subcarrier) first.

•   UP process is performed on two sequential stages; the first stage is the assignment of the strong user for each subcarrier followed by the second stage in which the assignment of the weak user for each subcarrier is performed.

•   During the strong user assignment stage, the user with the largest channel gain over each ordered subcarrier is assigned as the strong user. The selected user is discarded from the subsequent assignment process.

•   During the weak user assignment stage, the user with the most convergent channel gain to the strong user's channel gain is assigned as the weak user to avoid small values of μ. The selected user is discarded from the subsequent assignment process.

The pseudo-code of ELCUP is presented in Algorithm 1.

6  Simulation Results

In this section, the performance of the proposed CMFPA and the performance of the proposed joint resource allocation (JRA), which consists of the proposed ELCUP incorporated with the proposed CMFPA are evaluated via simulations. During the simulation, a frequency selective fading channel with six independent multipath is considered with Rayleigh distributed fading parameters. Link level simulations are performed in MATLAB, and 5000 realizations of channel gains are taken to generate each data point on the forthcoming figures.

The simulation results investigate the performance of the proposed CMFPA compared with that of Fractional Transmit Power Allocation (FTPA) [27] with the conventional user pairing (conventional UP) [37], and random user pairing (random UP) [38]. Also, the performance of the proposed JRA is compared with that of OMA system, and that of conventional UP and random UP NOMA schemes where FTPA and proposed CMFPA are used for power allocation.

Random UP is the easiest method for user pairing, in which the users are randomly selected and allocated into a random empty subcarrier. On the other hand, in conventional UP, the user with the best channel gain is paired with the user with the worst channel gain, which needs exhaustive search to assure that the capacity of the NOMA system is larger than that of OMA system. So, the impact of pairing users whose channel gains are more divergent (i.e., small values of μ) can be investigated in case of conventional UP.

The decay factor of FTPA is chosen to be 0.4 to make a compromise between the capacity and the fairness performance. The minimum power gap θ is set to be 1 W for the proposed CMFPA. The following simulation results are presented as a function of SNR at the number of subcarriers M equals to 32 subcarriers (i.e., K = 64 UEs).

Fig. 16 presents the obtained capacity in bps/Hz and shows that the proposed CMFPA increases the capacity of conventional UP especially as SNR decreases, and makes it outperform random UP for all SNR values. It is also shown that the proposed JRA achieves the highest capacity with a significant capacity gain compared to other NOMA schemes (i.e., conventional UP and random UP NOMA schemes).

Figure 16: The capacity vs. SNR

Fig. 17 presents the fairness performance and shows that the proposed JRA provides the best fairness performance with FI higher than 0.95 for most of the SNR values. Also, it is clear that the proposed CMFPA significantly improves the fairness performance of random UP especially as SNR increases. For example, at 20 dB, using CMFPA the obtained FI is higher than 0.9, while using FTPA the obtained FI equals to 0.65. On the other hand, for conventional UP, the proposed CMFPA improves its fairness performance as SNR increases and makes its fairness performance better than that with FTPA at high SNR values, while FTPA provides slightly better fairness performance at low SNR values at the expense of the loss in capacity as previously shown in Fig. 16.

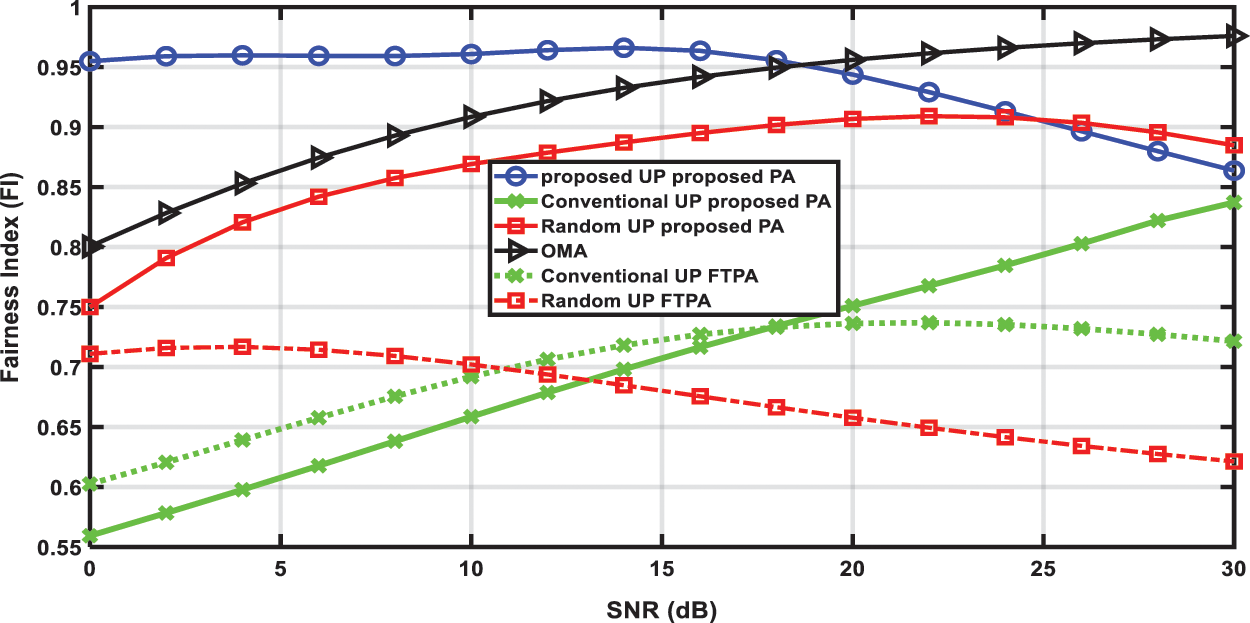
Figure 17: Fairness Index (FI) vs. SNR

One of the important performance metrics is the outage probability which is defined as the probability that the data rate of UE is lower than a certain minimum rate R0. The outage probability for R0 = 1 bps/Hz and R0 = 2 bps/Hz is presented in Figs. 18 and 19, respectively. It is clear that the proposed JRA achieves the lowest outage probability, and its outage probability significantly decreases as SNR increases and it is lower by a factor less than 0.1 than the outage probability of OMA, conventional UP, and random UP for R0 = 1 bps/Hz and R0 = 2 bps/Hz. Also, it is shown that the outage probability of the random UP using the proposed CMFPA is better than that using FTPA especially at R0 = 2 bps/Hz and is always lower than that of OMA. For conventional UP, it provides the worst (i.e., highest) outage probability at R0 = 1 bps/Hz and the proposed CMFPA can improve its outage probability for R0 = 2 bps/Hz at high SNR’ values to outperform random UP using FTPA.

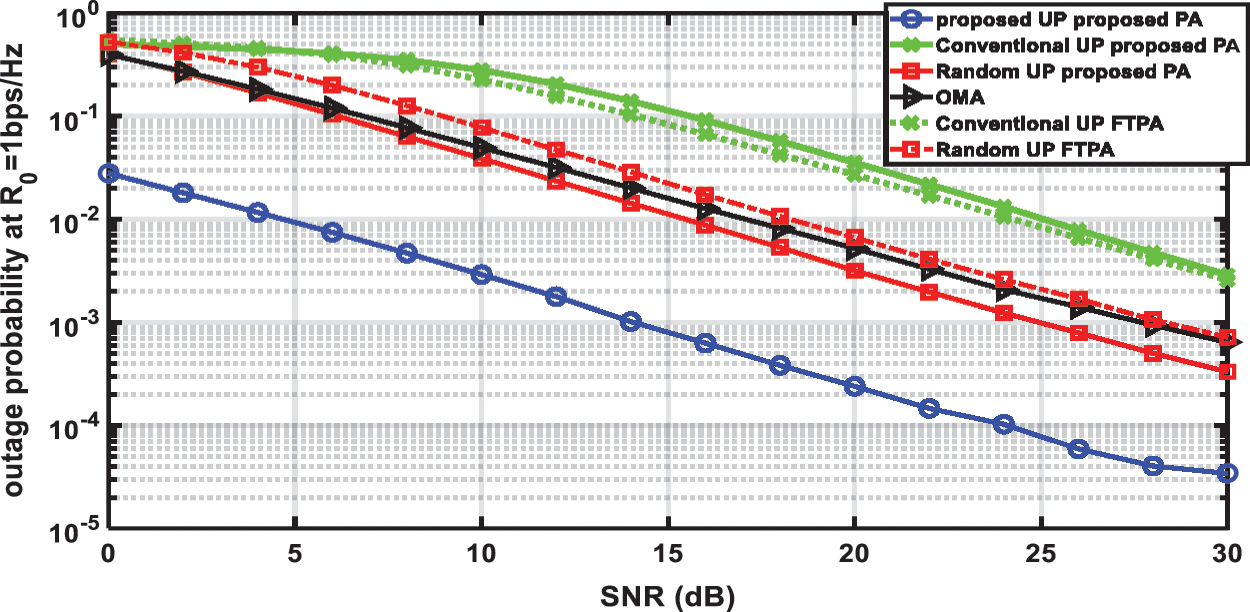
Figure 18: Outage probability at R0 = 1 bps/Hz vs. SNR

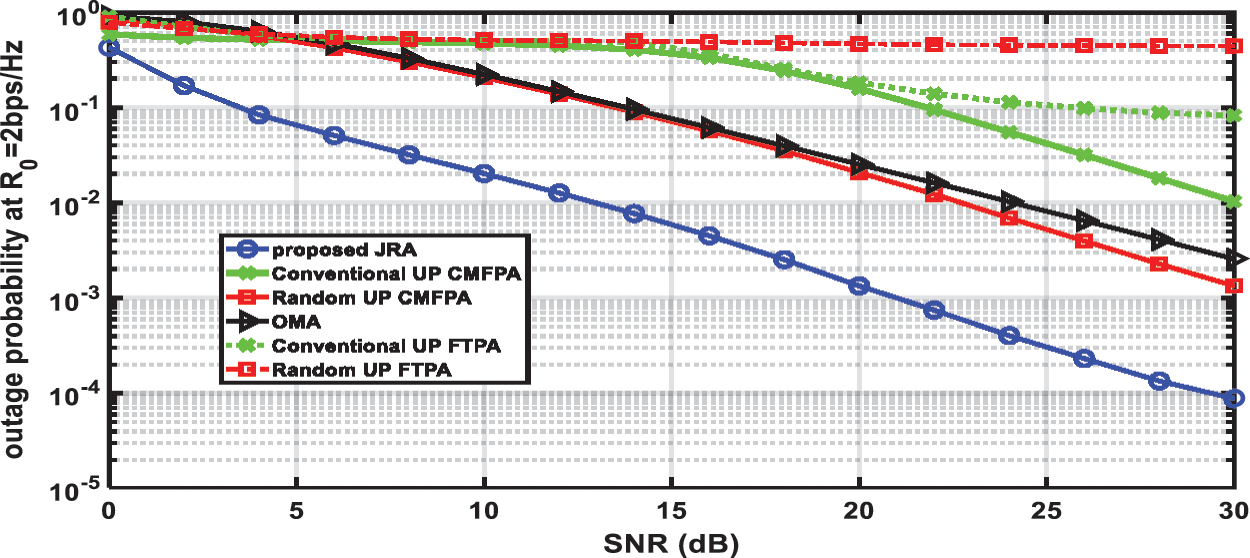
Figure 19: Outage probability at R0 = 2 bps/Hz vs. SNR

7  Conclusion

In this paper, a novel low complexity PA called CMFPA in downlink NOMA is proposed to maximize the capacity while nearly optimize the fairness performance. Extensive investigation and analysis of the joint impact of SNR and paired users’ channel gains on the performance of NOMA is presented. Next, in CMFPA, a closed-form equation is proposed for the power allocation coefficient as a function of SNR and the channel gains of the paired users. In addition, an efficient low-complexity UP (ELCUP) method is proposed to be incorporated with the proposed CMFPA to compromise the proposed joint resource allocation (JRA) for the optimization of capacity and fairness performance of NOMA systems. Compared to FTPC, the proposed CMFPA can significantly improve the capacity and the fairness performance of existing UP methods such as conventional UP, and random UP methods. Also, the proposed JRA outperforms the existing schemes and gives a near-optimal performance.

Acknowledgement: The authors would like to acknowledge the support received from Taif University Researchers Supporting Project Number (TURSP-2020/147), Taif University, Taif, Saudi Arabia.

Funding Statement: This research was supported by Taif University Researchers Supporting Project Number (TURSP-2020/147), Taif University, Taif, Saudi Arabia.

Conflicts of Interest: The author declares that he has no conflicts of interest to report regarding the present study.

References

 1.  J. G. Andrews, S. Buzzi, W. Choi, S. V. Hanly, A. Lozano et al., “What will 5G be?,” IEEE Journal on Selected Areas in Communications, vol. 32, no. 6, pp. 1065–1082, 2014. [Google Scholar]

 2.  V. Jungnickel, K. Manolakis, W. Zirwas, B. Panzner, V. Braun et al., “The role of small cells, coordinated multipoint, and massive MIMO in 5G,” IEEE Communication Magazine, vol. 52, no. 5, pp. 44–51, 2014. [Google Scholar]

 3.  Z. Wei, J. Yuan, D. W. K. Ng, M. Elkashlan and Z. Ding, “A survey of downlink non-orthogonal multiple access for 5G wireless communication networks,” ZTE Communications, vol. 14, no. 4, pp. 17–26, 2016. [Google Scholar]

 4.  W. Peng, X. Jun and L. Ping, “Comparison of orthogonal and nonorthogonal approaches to future wireless cellular systems,” IEEE Vehicular Technology Magazine, vol. 1, no. 3, pp. 4–11, 2006. [Google Scholar]

 5.  Y. Saito, Y. Kishiyama, A. Benjebbour, T. Nakamura, A. Li et al., “Non-orthogonal multiple access (NOMA) for cellular future radio access,” in Proc. IEEE Vehicular Technology Conf., Dresden, Germany, pp, 1–5, Jun 2013. [Google Scholar]

 6.  L. Dai, B. Wang, Y. Yuan, S. Han, I. Chih-lin et al., “Non-orthogonal multiple access for 5G: Solutions, challenges, opportunities, and future research trends,” IEEE Communications Magazine, vol. 53, no. 9, pp. 74–81, 2015. [Google Scholar]

 7.  X. Zhang, Q. Gao, C. Gong and Z. Xu, “User grouping and power allocation for NOMA visible light communication multi-cell networks,” IEEE Commination Letter, vol. 21, no. 99, pp. 777–780, 2016. [Google Scholar]

 8.  Z. Ding, R. Schober and H. V. Poor, “A general MIMO framework for NOMA downlink and uplink transmission based on signal alignment,” IEEE Transactions on Wireless Communications, vol. 15, no. 6, pp. 4438–4454, 2016. [Google Scholar]

 9.  Z. Ding, F. Adachi and H. V. Poor, “The application of MIMO to nonorthogonal multiple access,” IEEE Transactions on Wireless Communications, vol. 15, no. 1, pp. 537–552, 2016. [Google Scholar]

10. Z. Ding, P. Fan and H. V. Poor, “Random beamforming in millimeterwave NOMA networks,” IEEE Access, vol. 5, pp. 7667–7681, 2017. [Google Scholar]

11. G. Nain, S. S. Das and A. Chatterjee, “Low complexity user selection with optimal power allocation in downlink NOMA,” IEEE Wireless Communications Letters, vol. 7, no. 2, pp. 158–161, 2018. [Google Scholar]

12. H. Zhang, F. Fang, J. Cheng, K. Long, W. Wang et al., “Energy-efficient resource allocation in NOMA heterogeneous networks,” IEEE Wireless Communications, vol. 25, no. 2, pp. 48–53, 2018. [Google Scholar]

13. M. Zheng, W. Liang and H. Yu, “Utility-based resource allocation in wireless-powered communication networks,” IEEE Systems Journal, vol. 12, no. 4, pp. 3881–3884, 2018. [Google Scholar]

14. Y. Sun, D. W. K. Ng, Z. Ding and R. Schober, “Optimal joint power and subcarrier allocation for full-duplex multicarrier non-orthogonal multiple access systems,” IEEE Transaction Communication, vol. 65, no. 99, pp. 1077–1091, 2017. [Google Scholar]

15. P. Parida and S. S. Das, “Power allocation in OFDM based NOMA systems: A DC programming approach,” in Proc. IEEE Globecom Workshops, Austin, TX, USA, pp. 1026–1031, Dec 2014. [Google Scholar]

16. C. Li, Q. Zhang, Q. Li and J. Qin, “Price-based power allocation for non-orthogonal multiple access systems,” IEEE Wireless Communications Letters, vol. 5, no. 6, pp. 664–667, 2016. [Google Scholar]

17. Z. Wang, C. Wen, Z. Fan and X. Wan, “A novel price-based power allocation algorithm in non-orthogonal multiple access networks,” IEEE Wireless Communications Letters, vol. 7, no. 2, pp. 230–233, 2018. [Google Scholar]

18. J. Wang, Q. Peng, Y. Huang, H. -M. Wang and X. You, “Convexity of weighted sum rate maximization in NOMA systems,” IEEE Communication Letter, vol. 24, no. 9, pp. 1323–1327, 2017. [Google Scholar]

19. Q. Liu, H. Gao, F. Tan, T. Lv and Y. Lu, “Energy efficient resource allocation in multi-user downlink non-orthogonal multiple access systems,” in Proc. IEEE Global Communications Conf. (GLOBECOM), Singapore, pp. 1–6, Dec 2017. [Google Scholar]

20. Y. Zhang, H. Wang, T. Zheng and Q. Yang, “Energy-efficient transmission design in non-orthogonal multiple access,” IEEE Transactions on Vehicular Technology, vol. 66, no. 3, pp. 2852–2857, 2017. [Google Scholar]

21. F. Fang, H. Zhang, J. Cheng, S. Roy and V. C. M. Leung, “Joint user scheduling and power allocation optimization for energy-efficient NOMA systems with imperfect CSI,” IEEE Journal on Selected Areas in Communications, vol. 35, no. 12, pp. 2874–2885, 2017. [Google Scholar]

22. H. Zhang, B. Wang, C. Jiang, K. Long, A. Nallanathan et al., “Energy efficient dynamic resource optimization in NOMA system,” IEEE Transactions on Wireless Communications, vol. 17, no. 9, pp. 5671–5683, 2018. [Google Scholar]

23. D. Ni, L. Hao, Q. T. Tran and X. Qian, “Transmit power minimization for downlink multi-cell multi-carrier NOMA networks,” IEEE Communications Letters, vol. 22, no. 12, pp. 2459–2462, 2018. [Google Scholar]

24. J. Cui, Z. Ding and P. Fan, “A novel power allocation scheme under outage constraints in NOMA systems,” IEEE Signal Processing Letter, vol. 23, no. 9, pp. 1226–1230, 2016. [Google Scholar]

25. S. Timotheou and I. Krikidis, “Fairness for non-orthogonal multiple access in 5G systems,” IEEE Communications Letters, vol. 22, no. 10, pp. 1647–1651, 2015. [Google Scholar]

26. J. Choi, “Power allocation for max-sum rate and max-min rate proportional fairness in NOMA,” IEEE Communication Letter, vol. 20, no. 10, pp. 2055–2058, 2016. [Google Scholar]

27. A. Benjebbovu, A. Li, Y. Saito, Y. Kishiyama, A. Harada et al., “System-level performance of downlink NOMA for future LTE enhancements,” in Proc. 2013 IEEE Globecom Workshops (GC Wkshps), Atlanta, GA, pp. 66–70, 2013. [Google Scholar]

28. F. Fang, J. Cheng and Z. Ding, “Joint energy efficient subchannel and power optimization for a downlink NOMA heterogeneous network,” IEEE Transactions on Vehicular Technology, vol. 68, no. 2, pp. 1351–1364, 2019. [Google Scholar]

29. B. Xu, Y. Chen, J. R. Carri´on and T. Zhang, “Resource allocation in energy-cooperation enabled two-tier NOMA HetNets toward green 5G,” IEEE Journal on Selected Areas in Communications, vol. 35, no. 12, pp. 2758–2770, 2017. [Google Scholar]

30. X. Song, L. Dong, J. Wang, L. Qin and X. Han, “Energy efficient power allocation for downlink NOMA heterogeneous networks with imperfect CSI,” IEEE Access, vol. 7, pp. 39 329–39 340, 2019. [Google Scholar]

31. L. Xu, W. Yin, X. Zhang and Y. Yang, “Fairness-aware throughput maximization over cognitive heterogeneous NOMA networks for industrial cognitive IoT,” IEEE Transactions on Communications, vol. 68, no. 8, pp. 4723–4733, 2020. [Google Scholar]

32. L. Luo, Q. Li and J. Cheng, “Performance analysis of overlay cognitive NOMA systems with imperfect successive interference cancellation,” IEEE Transactions on Communications, vol. 68, no. 8, pp. 4709–4722, 2020. [Google Scholar]

33. G. Li, D. Mishra and H. Jiang, “Channel-aware power allocation and decoding order in overlay cognitive NOMA networks,” IEEE Transactions on Vehicular Technology, vol. 69, no. 6, pp. 6511–6524, J2020. [Google Scholar]

34. W. U. Khan, F. Jameel, T. Ristaniemi, S. Khan, G. A. S. Sidhu et al., “Joint spectral and energy efficiency optimization for downlink NOMA networks,” IEEE Transactions on Cognitive Communications and Networking, vol. 6, no. 2, pp. 645–656, 2020. [Google Scholar]

35. J. A. Oviedo and H. R. Sadjadpour, “A fair power allocation approach to NOMA in multiuser SISO systems,” IEEE Transactions on Vehicular Technology, vol. 66, no. 9, pp. 7974–7985, 2017. [Google Scholar]

36. F. Capozzi, G. Piro, L. A. Grieco, G. Boggia and P. Camarda, “Downlink packet scheduling in LTE cellular networks: Key design issues and a survey,” IEEE Communications Surveys & Tutorials, vol. 15, pp. 678–700, 2012. [Google Scholar]

37. H. Zhang, D. K. Zhang, W. X. Meng and C. Li, “User pairing algorithm with SIC in non-orthogonal multiple access system,” in Proc. Int. Conf. Communication, KUL, Malaysia, pp. 1–6, May 2016. [Google Scholar]

38. Z. Ding, P. Fan and H. V. Poor, “User pairing in non-orthogonal multiple access downlink transmissions,” in Proc. 2015 IEEE Global Communications Conf. (GLOBECOM), San Diego, CA, pp. 1–5, 2015. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.