Computers, Materials & Continua DOI:10.32604/cmc.2022.023339
Article

Image Dehazing Based on Pixel Guided CNN with PAM via Graph Cut

Fayadh Alenezi*

Department of Electrical Engineering, College of Engineering, Jouf University, Sakaka, Saudi Arabia
*Corresponding Author: Fayadh Alenezi. Email: fshenezi@ju.edu.sa
Received: 04 September 2021; Accepted: 20 October 2021

Abstract: Image dehazing is still an open research topic that has been undergoing a lot of development, especially with the renewed interest in machine learning-based methods. A major challenge of the existing dehazing methods is the estimation of transmittance, which is the key element of haze-affected imaging models. Conventional methods are based on a set of assumptions that reduce the solution search space. However, the multiplication of these assumptions tends to restrict the solutions to particular cases that cannot account for the reality of the observed image. In this paper we reduce the number of simplified hypotheses in order to attain a more plausible and realistic solution by exploiting a priori knowledge of the ground truth in the proposed method. The proposed method relies on pixel information between the ground truth and haze image to reduce these assumptions. This is achieved by using ground truth and haze image to find the geometric-pixel information through a guided Convolution Neural Networks (CNNs) with a Parallax Attention Mechanism (PAM). It uses the differential pixel-based variance in order to estimate transmittance. The pixel variance uses local and global patches between the assumed ground truth and haze image to refine the transmission map. The transmission map is also improved based on improved Markov random field (MRF) energy functions. We used different images to test the proposed algorithm. The entropy value of the proposed method was 7.43 and 7.39, a percent increase of ≃4.35% and ≃5.42%, respectively, compared to the best existing results. The increment is similar in other performance quality metrics and this validate its superiority compared to other existing methods in terms of key image quality evaluation metrics. The proposed approach's drawback, an over-reliance on real ground truth images, is also investigated. The proposed method show more details hence yields better images than those from the existing state-of-the-art-methods.

Keywords: Pixel information; human visual perception; convolution neural network; graph cut; parallax attention mechanism

1  Introduction

Images acquired in an outdoor environment are sometimes affected by degradation due to atmospheric conditions such as fog, rain, snow, or wind-blown sand. Such haze is a type of degradation that affects the image quality more or less homogeneously and persistently, making the visibility of details very difficult. This inevitably reduces the performance of high-level tasks such as the interpretation of the content of the observed scene [1].

The haze phenomenon is due to the presence of water droplets suspended in the air. These droplets cause the phenomenon of light scattering, the distribution and photometric appearance of which depends on the size of the water particles scattering and the wavelength of light. Weather conditions can cause fluctuations in the particles that in turn causes the haze in the atmosphere [2]. These particles’ collective effect arises due to the illumination effect in the image at any given pixel. These effects can be dynamic (snow or rain) or steady (haze, mist, and fog) [2].

Dehazing aims at removing the light-scattering effect from the image by making it more exploitable in various image processing and analysis tasks. However, dehazing methods generally try to reduce or eliminate this phenomenon in a global way without taking into account local aspects, and in particularly typically fail to account for spatial structures and inter-pixel interactions [3]. Thus, this proposal takes into account local aspects to yield a better result.

In order to restore the salient and essential feature regions in the images, the existing image dehazing algorithms tend to use specific points in the image region to approximate the atmospheric light [4]. The majority of the proposed image dehazing algorithms based on atmospheric scattering models, aim at deriving a haze-free image from the observed image [5] by estimating the transmission map. Atmospheric light and the transmission map are estimated in some dehazing methods through the use of physical maps such as color-attenuation on some non-local priors or through the observation of haze-free outdoor images as in the dark-channel prior approach [6]. Despite the huge successes born from these methods, they do not work well in certain cases. For example, in the case of Fattal et al. [5], transmission fails in the presence of white objects in the background. Similarly, non-local prior-based methods like that of Berman et al. [6] have failed in cases of heavy hazed regions as the transmission designed becomes irrelevant. Cai et al. [7] has also suggested color-attenuation prior underestimates the transmission of distant region.

The traditional proposed dehazing methods have been recently combined with CNNs [8]. This has been facilitated by the success of CNNs in the majority of the image processing tasks. CNNs have been combined with other filters to estimate transmission maps, while conventional methods such as Retinex theory have been used to estimate atmospheric light [8]. However, the existing dehazing methods still lack accuracy in the estimation of transmission maps. For instance, Alenezi et al. [9] disregard the physical model of the imaging principle while improving the image quality. Other models such as saliency extraction [10], histogram equalization [11] and Retinex theory [12] have yielded images with color distortion due to incomplete recovery effects [13]. Even promising state-of-the-art methods like that developed by Salazar-Colores et al. [14] yield inaccurate results since their procedures are based on many assumptions.

Image dehazing methods based on supplementary haze removal have various shortcomings. For instance, Wang et al. [1] proposed a method in which final images having a washed-out effect in darker regions due to atmospheric light failures. Middleton [15] have exaggerated contrast on the final images. Vazquez-Corral [16] proposed dehazing technique yields final images with poor information content. Feng et al. [17] proposed using sky and non-sky regions regions as the basis to improve hazy images. The method's strength lies in its bright sky regions, where the results generated have superior edges and good robustness. However, the results from the other sky regions are darker and have a hazed background. These results are similar to those from Wang et al. [1].

Fattal et al. [5,18] dark channel prior contribution in image dehazing has found numerous usages. The soft matting employed in Zhou et al. [18] algorithm makes its computation extensive. The use of a guided filter in soft matting in the first step reduces calculation-and application-related costs. However, He et al. technique has produced outcomes with deprived edges and discriminatory dehazing, which are only sound in non-sky area images [5,8]. He et al. [19] proposed method introduces wavelet transform, assuming haze effects solitarily affect low-frequency element of the image. Yet He et al. [19] proposed technique has not accounted for the differential light from the scene and the atmospheric light, subsequently making the results darker.

Some methods combine traditional existing dehaze methods and Artificial Neural Networks (ANN) to yield promising results. For instance, the multilayer perceptron (MLP), which has nurtured usage in numerous areas in image processing applications such as skin divisions and image denoising [20], has been used by Guo et al. [20]. Guo et al. [20] suggested method was based on the MLP, which draws the transmission map of the haze image directly from the dark channel. The results indicate extended contrast and intensified dynamic range of the dehazed image. However, visual inspection shows that Guo et al. [20] proposed outcomes retain haze towards the horizon, yielding imperfect edges. Other existing hybrid methods of CNNs with traditional methods have also produced imperfect images. For instance, Alenezi et al. [9] estimate a transmission map via DehazeNet. Their method has produced superior results against existing state-of-the-art methods but the CNN functions were limited in predicting the transmission map.

O'Shea et al. [21] proposed a method where the attention block captures the informative spatial and channel-wise features. A visual analysis of the dehazed image results reveals a haze towards the horizon in both simulated and natural images. Unlike the existing methods, a more recent method by Zhu et al. [8] considers the existence of differential pixel-values. This method [8] combines graph-cut with single-pass CNN algorithms estimating transmission maps via global and local patches. However, the proposed method yielded images where the over-bright areas tended to lose some final image features. A more recent study by Zhao et al. [22] merged the merits of prior-based and learning-based approaches. The method [22] combines visibility restoration and realness improvement sub-tasks using two-staged weakly supervised dehazing network. The results of the work had little washed-out effects despite having better performance than existing state-of-the art methods.

In summary, the existing image dehazing techniques have varied drawbacks, which necessitates further research into the topic. The proposed paper uses global and local Markov random fields and graph cuts to [8] improve the transmission map, exploiting the geometric-variance pixel-based guided local and global relationships between the ‘assumed’ ground truth and hazed image. This helps to estimate the transmittance medium and to extract a dehaze image accurately. Thus, this paper's proposed method uses the local and global pixel variance within the local and global image neighborhoods to estimate the transmittance medium. This is achieved by comparing the corresponding local and global pixels between the haze and its assumed ground truth. The energy variations in the global and local Markov fields function as a proposed extension based on corresponding high-low pixel gradient and variance-based boundary in between the two images, and to help smooth and constrain the connection between local and global pixel neighborhoods. These proposed geometric-based methods improve the dehazed image features. The rest of the paper is as follows: Section 2 outlines the contribution of the paper. Section 3 outlines the proposed method, then offers a description of the experiments in Section 4. Finally, Section 5 offers the conclusion.

2  Contribution

This paper makes three significant contributions: it presents a novel combination of CNNs with a parallax attention mechanism and graph-cut algorithms which results in a novel dehazed image; a transmittance medium dependent on pixel variance corresponding to local-and global-based neighborhood between the ground truth and haze image, which serves to strengthen local and global image features; and a local and global correspondence between the ground truth and haze image pixel-based energy function based on the pixel variance restraints of corresponding neighborhoods that enhances the transmission map, which has the effect of enhancing the finer details of the dehazed image. The later stages (the global and local Markov random fields and the graph cut) are an extension of existing work [8].

3  Proposed Method

3.1 Atmospheric Scattering Model

Fig. 1 shows a hazy condition with numerous particles suspended in the environment, resulting in a scattering effect on the light [8,13,17]. Scattered particles during hazy weather conditions allow the attenuation of reflected light on the surfaces of objects. The attenuated light deteriorates the image's brightness and decreases the image's resolution as a forward scattering consequence substantially persists between the particles and surfaces [13]. The ultimate hazed image differs from the ground truth image locally and globally based on their pixels’ information. The back-scattering of atmospheric particles in ordinary light yields images with reduced contrast, hue deviation, and image saturation, contrasting with the ground truth image [23]. These irregular scattering effects on sensor light and natural light in hazy images are broadly demonstrated via a dark channel prior prototype as follows [8,13,17]:

Υ(γ)=Ω(γ)ω(γ)+Ψ(1−ω(γ)).(1)

Figure 1: A summary of formation of scattering effect diagram showing environment radiance Ω, atmospheric light ϕ, attenuation or transmission ω, and observed intensity Υ

In (1), Υ(γ) is the observed image or brightness of the hazy image as established by the observer at pixel γ; Ω(γ) is the scene or environment radiance of the haze-free image; Ψ is the atmospheric light; and ω(γ) is the attenuation or transmittance medium, which ranges between 0 and 1. Thus can be redefined as,

(ω(γ)=e−ηξ(γ)|ω(γ)∈[0,1]),(2)

where η is the scattering coefficient of the atmosphere, and ξ(γ) is the depth of the scene. Eq. (2) is related to homogeneity in the atmosphere; otherwise, ω(γ) is given by (3).

The observed image brightness, Υ(γ) can be obtained by eliminating atmospheric light, Ψ, while rewarding attenuation of the light, ω(γ), to reinstate haze-free scenes, Ω(γ). RGB color space vectors Ω(γ),Ψ, and Υ(γ) in (2) are coplanar from a geometric point of view. The terminal points of vectors Ω(γ),Ψ, and Υ(γ) are collinear and the transmission, ω(γ), is relative to the length of the two lines, as defined in (3)

ω(γ)=‖Ψ−Υ(γ)Ψ−Ω(γ)‖,(3)

Eq. (4) emanates from (2) and shows that haze removal is based on accurate retrieval of Ω(γ), Ψ, and ω(γ) from Υ(γ). Ω(γ)ω(γ), which shows emissivity decay of the natural environment in the medium, represents direct attenuation. Ψ(1−ω(γ)) is air-light based on previously scattered light, leading to alteration of natural environment color. Therefore, the greater the distance between the sensor and the object the larger the attenuation (Ω(γ)ω(γ)) and scattering effect (Ψ(1−ω(γ))), suggesting the exponential transmission that is shown in (2).

Ω(γ)=Υ(γ)−Ψω(γ)+Ψ.(4)

3.2 Convolution Neural Network

CNN is similar to ordinary neural networks: they are composed of learnable weights and biases [24]. In CNN's, each neuron receives an input, such as an image that performs a dot product and may follow a non-linear computation. CNNs are expressed as a single differentiated score function, scoring input image pixel to one another. CNN also has a loss function on the last layer of the network [24]. ConvNets explicitly assumes image inputs, making it possible to encode image properties such as texture and information content into the architecture. This feature makes the forward function in the architecture of ConvNet more efficient during implementation, thus reducing the number of parameters in the network [25]. The rest of the literature on the structure and architecture of Convolution Neural Network (CNNs/ConvNets) is widely presented in papers [26].

4  Image Dehazing Based on Pixel Guided CNN with PAM via Graph Cut

4.1 Transmission Map

We define the mapping of pixel value fluctuations along the smallest regions of the hazed and ground truth image as ΔpH and that of ground truth as ΔpG. The pixel fluctuations also replicate changes in image features. If we symbolize the variance of these deviations with ζ=(Δpi)2, where i=H,G for H (haze) and G (ground truth), when ζ→0, the variation is invisible. Since pixel values are between 0 and 1, then variance in the neighboring pixels, qi is given by ∥Δpi−Δqi∥2, where, ∥.∥ is the magnitude of the pixels. We designate threshold process in input images Id (haze) and ground truth IG as

Ithreshold=∥Δpi−Δqi∥2pi−qi.(5)

Eq. (5) is analogous to (3), that is,

Ithreshold=‖Δpi−Δqi‖2pi−qi≃‖Ψi−Υ(γi)Ψi−Ω(γi)‖=ω(γi).(6)

Thus, the transmittance medium defined by (2) becomes

‖Δpi−Δqi‖2pi−qi≃(ω(γ)=e−ηξ(γi)|ω(γi)∈[0,1]).(7)

(7) is substituted into (1) leads

Υ(γi)=Ω(γi)(∥Δpi−Δqi∥2pi−qi)+Ψi(1−(∥Δpi−Δqi∥2pi−qi)).(8)

Eq. (8) shows that a major challenge of image dehazing is solved. In contrast, while in the beginning there were three unknowns present, (8) shows that only two unknowns are left; Ψi and Υ(γi). However, Ψi can be estimated based on Retinex theory [12], which derives the atmospheric light of the brightest pixel from Ψi=[max(R),max(G),max(B)]t, where R, G, B are the three-color channels in the image and t regulates the weights of the colors.

4.2 Global and Local Markov Random Fields

Scene depth changes gradually and entails variation in local and global neighborhood pixels. Thus, accurate depth variation estimation depends on features including color, texture, location and shape as well as both the local and global neighborhood pixels between the haze and ground-truth images. This paper proposes that these are attainable via a novel energy function in the depth estimation network. The energy function is based on a novel global-local Markov chain already discussed in detail in [8]. The resultant energy function is optimized by the graph-cut as discussed in Zhu et al. [8]. However, in this model, we use the color channel features as representative of both global and local color moments, proposed by [27]. This opposes the super-pixels in global and local neighborhoods as presented in [1]. Thus, the ambient light used epitomizes the connection between global and local pixels and super-pixels. The approach extends the global and local consistency, which helps to protect the proposed convolution neural network from the problem of smoother far apart pixels. It also assists in evading over-saturation of color and produces sharper boundaries. The relationship between the global and local neighborhood pixels and super-pixels is modeled via the long and short-range interaction. This is achieved by considering the global relationship between neighboring local pixels as proposed by Song et al. [27]. The results are extended to the global and local pixels to map the relationship between haze and ground truth image. The constructed Markov Random Fields have edge costs representative of the neighboring pixel's consistency in overlapping regions based on high gradient boundary.

The graph cut and parallax attention mechanism (PAM), which has already been proposed by Zhu [8], helps in optimizing MRF. Furthermore, it protects against over-saturation of color and sharpens boundaries. PAM helps in estimating the correspondences between haze and ground truth pixel values [28]. It also helps in the computation of occlusion maps and warps ground truth image features into the final dehazed image. PAM has inputs from feature maps FMG and FML denoting global and local features, respectively (see Fig. 4). FMG,FML∈RR,G,B represent color channels from the feature extraction based on pixel information. The onset of the PAM has two residual blocks with shared weights adapting input features for transmission estimation and generation of feature maps FMG0 and FML0. This helps in maximization of the training process to avoid training conflicts [29]. A 1×1 convolution layer converts FMG0 into a query feature map QFM∈RR,G,B and another 1×1 layer converts FML0 into a feature map FM∈RR,G,B which is reshaped to RR,G,B, a feature map depending on the shared global and local features of the haze and ground truth image. QFM and FM are multiplied and graph cut with softmax (see Fig. 6). The results are then applied to obtain a parallax attention map MFMG→FML∈RR,G,B. MFML→FMG is seen as a cost matrix encoding the correspondence along with pixel correlations between the haze and ground truth images. The proceeding step sees FML processed by 1×1 convolution layer to obtain R∈RR,G,B, which is multiplied by MFMG→FML to generate O∈RR,G,B (the warping of FML into FMG). PAM also helps in estimation occlusion maps, VFML→FMG, to help refine the transmission medium between ground truth and haze image. During estimation of the occlusion map, a second PAM MFML→FMG is estimated by exchanging FMG and FML. The rest of the details about the occlusion maps are presented in [30]. The literature on the functionality of the PAM about its applicability in image processing is extensively presented in the following existing papers [30]. Graph cut is widely illustrated by Zhu et al. [8] and extensively discussed and described by [9,31]. The two main components of the graph cut are data and regularization [32]. The data part assesses the image data compliance, such as image features, while the regularization part polishes the boundaries of the different conformity areas.

5 Experiments

5.1 Data and Implementation

The proposed technique (summarized in Fig. 3 and comprehensive in Figs. 2 and 6) was applied to various images (presented in Figs. 4, 5 and 7–12) obtained from different databases. These images were resized to reduce computational complexities. The images presented in Figs. 4, 5 and 7–12 are examples obtained from a dataset of 56 examples used in the experiment. The performance metrics presented in Tab. 2 are constructed from the results, whose parameter values are represented in Tab. 1. We used a total of 24640 images to train the network using 440 partitions from 56 image samples. We validated the network results with 11000 images. These were generated from simulated clear images from the images presented in Figs. 4, 5 and 7–12. We extracted images (see Fig. 9 (validation images)) from regions with rich textures. Thus, the quality could be compromised for these set of results due to the absence of ground truth to validate the images. We constructed the final images outputs from 440 partitioned images to yield the results presented in Figs. 4, 5 and 7–12. The partition helped organize images into patches of similar local and global neighborhoods for the corresponding haze and ground truth images. A BIZON X5000 G2 with 16 GB RAM pc was used to train the process for the proposed dehazing technique.

5.2 Evaluation Metrics

The proposed method's performance evaluation was conducted using five image quality criteria, including: (i). Entropy [33]; (ii). e (visible edges) [11]; (iii). r (edge preservation performance) [11]; (iv). Contrast, and (v). Homogeneity [28]. These criteria were chosen based on the proposed method's objective: improving information content, measuring human visual quality and textural features, and comparing the similarities between a dehazed image with the ground truth.

Fig. 6a is comprised of input, encoder, and decoder. The encoder consists of convolution neural networks which extract global and local features from the hazy images and compare their corresponding features to the ground truth images. The decoder functions like the encoder except for its residual functions which contain PAM with graph cut (see Figs. 6b and 6c). The residual decoder function permits full connection with other neurons, thus enhancing the learning rate and merging the training models. Fig. 6c is a build graph designed to minimize the energy problem. The graph consists of nodes corresponding to image pixels and pixel labels. The pixels are weighted based on their label. The cut consists of a configuration of pixels at its maximum label based on haze and ground truth image. The cut also ensures the energy is minimal at all configurations.

Figure 2: The schematic detail shows the proposed architecture with seven neurons in the second hidden layer, eight neurons in the third hidden layer, and a single output. The series contains alternating global and local feature extraction before full connection and PAM via graph cut to obtain the final dehazed image

Figure 3: A detail of the proposed image dehazing using ground truth-based geometric-pixel guided CNN with PAM via graph cut

5.3 Results Analysis and Comparison

Figure 4: Comparison of the effect of proposed energy function on the image features (a) Tan [33] (b) Zhu et al. [8] and the proposed method in the last column. The effectiveness of the proposed method has visibly extracted extra features in the dehazed image compared with existing dehaze cut method's results ([35] and [8])

Figure 5: Comparison showing dehaze-cut results (the first image) and results from [8] (the second image) as well as the proposed method's result (the last image). The red and green patches show the effectiveness of the proposed method in terms of detailed information in comparison with the existing dehaze-cut methods [35] and [8]

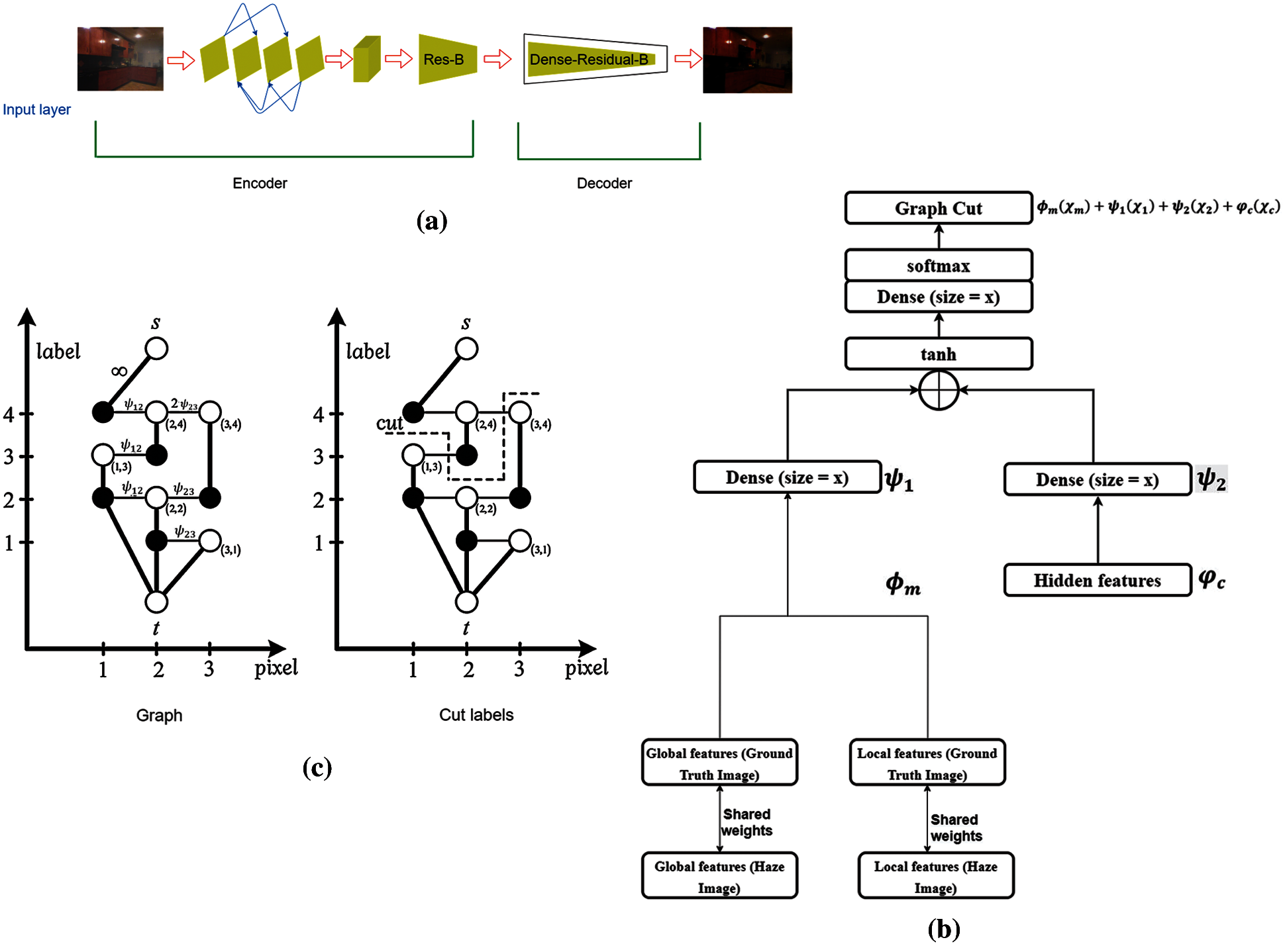
Figure 6: Detailed CNN for the proposed dehazing method with the encoder and decoder, which are similar except in the residual phase. The residual function ensures that each hidden neuron is fully connected, enhances the learning rate, and merges the training data set models. (b) The dense-residual phase is composed of softmax, which feeds information to the (c) PAM via graph-cut algorithm, which conforms image features and smooths the boundaries of varying conformity areas between the corresponding haze and ground truth image

5.4 Quantitative Comparison

Figure 7: Summary of the test comparison with extracted synthetic images from O'Shea et al. [21] showing the original image in the I haze image, and dehazing results from (a) Fattal et al. [5], (b) Barman et al. [6], (c) Zhu et al. [36], (d) Sener et al. [37], (e) Ancuti et al. [4], (f) Meng et al. [31], (g) O'Shea et al. [21], and (h) results from the proposed algorithm, along with T the ground truth in the last column

Figure 8: Summary of the test comparison showing the original haze image in the first column followed by the results from multilayer perceptron [36], residual-based dehazing method [37], the results from the proposed algorithm in the second-to-last column, and the ground truth in the last column

Figure 9: Summary of the test comparison with natural images showing the original image in the I haze image, and dehazing results from (a) Fattal et al. [5], (b) Barman et al. [6], (c) Meng et al. [31], (d) Zhu et al. [38], (e) He et al. [19], (f) Li et al. [39], (g) O'Shea et al. [21] and (h) results from the proposed algorithm in the last column. The patches marked red are the regions of the assumed ground truth for the purposed of training the proposed method

5.5 Comparison Analysis

In all the cases, (see Tab. 2), the images that resulted from the proposed algorithm on average demonstrated higher entropy, e, r, contrast and homogeneity. This suggests that the proposed method resulted in a dehazed image with improved information content, visibility, and with better texture than existing methods (7–12). The difference in the textural properties of the proposed method is compared with those of the state-of-the-art methods in Figs. 11 and 12. The difference in the textures in Figs. 11 and 12 shows that a modification of the combination of PAM via graph cut and CNN with modified energy function and pixel-guided transmission based on ‘assumed ground’ ultimately yields a better dehazed image. The true ground truth and ‘assumed ground truth’ informs the pixel reconstruction to yield an image with cutting edge experience in color correction and visible blue sky (see proposed in the (h) or last column of Fig. 10). A further visual inspection of patched sections of the proposed results in Figs. 11 and 12 compared to the existing methods reveals its strength and weakness.

The proposed method's major strength lies in its capacity to extract more details in the dehazed images (see blue patches in Fig. 12). The areas marked blue tend to have more details than those in Zhu et al. [34]. The extra information can be credited to the proposed pixel differential-based transmittance medium, which emphases the global and local patches’ pixel difference. This explains the addition of some tree leaves in the patched sections. The approximation of transmittance medium via local and global pixels with image neighborhood distinguishes regions, resulting in more information extraction.

Figure 10: Summary of hazed images used in the paper. (a) input image, (b) Zhu et al. [34], and (c) proposed results. The red (d), (e), and (f) patches represent the regions assumed as ground truth and used for training in the proposed method. The blue patches present the visible differences between the proposed method (i) and input similar region (g) and existing state-of-the-art method (h) Zhu et al. [34]

Figure 11: Summary of the proposed method's strength compared to existing state-of-the-art method of Sener et al. [35]. The proposed method preserves light and gives almost similar results to that of ground truth. The green patches show the Sener et al. [35] method tends to exaggerate light, an indication of retention of most of the haze particles. The proposed method in the middle column, although it appears darker, has better visibility than Sener et al. [35]

Figure 12: Summary of hazed images used in the paper. (a) input image, (b) Yousaf et al. [23], and (c) proposed results. The red (d), (e), and (f) patches represent the regions assumed as ground truth and used for training in the proposed method. The blue patches present the visible differences between the proposed method (i) and input similar region (g) and existing state-of-the-art method (h) Yousaf et al. [23]

The visual inspection of patched sections of the proposed results in Fig. 10 compared to the existing methods reveals its weakness. While the proposed method focuses on extracting finer details of the dehazed images (see blue patches), the regions with excess light still retain some light, and hence less information (see also Fig. 5). The red patched areas, for instance, in the areas marked red and black, tend to blur over the entire regions compared to those in Zhu et al. [34] and the input image. This is attributed to the proposed pixel differential-based transmittance medium's reliance on the assumed ground truth, which is not accurate. However, the contrary is true in areas where there exists real ground truth, such as in the simulated image results presented in Figs. 7 and 8. The pixel difference of the global and local patches between the haze and ground truth images functions but fails to extract features with similar pixels within regions as noised, causing a blur in ‘assumed ground truth’ (see Figs. 10 and 12) but correctly extracting details in real ground truth (see Fig. 11). The estimation of transmittance medium via local and global pixels within haze and ground truth image neighborhood distinguishes regions with similar traits, leading to better results, presented in Tab. 2. This also explains the clear visibility of the sky and clouds in (h) Fig. 9, in which a highly textured region is used as ‘assumed ground truth, as well as the conservation of color and light in the green patches in Fig. 11.

In all the examples, extra features of the proposed image results which arose from the proposed novel estimation of transmittance medium are clearly visible in comparison to existing results. The standard deviation values in all cases, as presented in Tab. 2, show lower values than the corresponding benchmark algorithms. Tab. 2 also shows that our proposed algorithm has a higher entropy of 7.43 than Zhu et al. [34] algorithm entropy of 7.12 and Sener et al. [35] algorithm entropy of 6.89. Also, our proposed algorithm has better consistency than others as tabulated in Tab. 2 for Fig. 9. These show that the proposed method gives more consistent and predictable results than existing algorithms. However, the proposed method faces a challenge: some regions of the dehazed image tend to blur instances where the ground truth is assumed since this method relies on the actual ground truth. This is a common problem even in the existing state-of-the-art methods used for comparison.

6  Conclusion

This paper presents a novel method for image dehazing. We propose to solve the dehazing problem using a combination of CNN with PAM via graph-cut algorithms. The method considers the transmittance based on differential pixel-based variance, and uses local and global patches between the ground truth and haze image as well as energy functions to improve the transmission map. Through the outcomes presented presented and demonstrated in given examples, the paper shows that the proposed algorithm yields a better dehazed image than those of the existing state-of-the-art methods, as shown in Figs. 8,10 and 11. Comparison of entropy values in Figs. 7 and 8 suggest the proposed method improved the information content of dehazed image by ≃4.35% and ≃5.42% respectively, compared to the best values. In all the comparison metrics, the proposed method gives consistent results than those of existing methods. These show that our proposed method gives images with better visibility, greater clarity of features, and more features. In general, our results show more details compared to existing benchmark enhancement methods. These improved results can be attributed to strengthening local and global image features by a transmittance medium dependent on image pixel variance. However, the proposed method faces a challenge: some regions of the dehazed image tend to blur instances where the ground truth is assumed since this method relies on the actual ground truth. Future research could consider combining our method with other existing algorithms such as dark channel prior, since at least one-color channel of an RGB image has some pixels of the lowest intensities. This can be achieved via sub-tasking of the CNN framework based on the problems to be solved. This will enhance algorithm complexity while reducing the operational cost. Future research could also test out combining conditions for atmospheric homogeneity and ratio between the ground truth and haze image segments during estimation of transmittance medium. This can be achieved by developing a framework for finding the variation in atmospheric light and the best blend to give optimal results.

Funding Statement: This work was funded by the Deanship of Scientific Research at Jouf University under grant No DSR-2021-02-0398.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  L. Wang, Y. Guo, Y. Wang, Z. Liang, Z. J. Lin et al., “Parallax attention for unsupervised stereo correspondence learning,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 1, pp. 1–18, 2020. [Google Scholar]

 2.  G. Obulesu, M. S. P. Kumar, P. Sowmya and V. T. Reddy, “Single image dehazing using multilayer perceptron and dcp,” International Journal of Engineering and Research, vol. 8, no. 3, pp. 205–209, 2019. [Google Scholar]

 3.  J. Li, G. Li and H. Fan, “Image dehazing using residual-based deep cnn,” IEEE Access, vol. 6, pp. 26831–26842, 2018. [Google Scholar]

 4.  C. O. Ancuti, C. Ancuti and C. De Vleeschouwer, “Effective local airlight estimation for image dehazing,” in 2018 25th IEEE Int. Conf. on Image Processing (ICIPPhoenix, Arizona, USA, IEEE, pp. 2850–2854, 2018. [Google Scholar]

 5.  R. Fattal, “Single image dehazing,” ACM Transactions on Graphics (TOG), vol. 27, no. 3, pp. 1–9, 2008. [Google Scholar]

 6.  D. Berman and S. Avidan, “Non-local image dehazing,” in Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition, Honolulu, Hawaii, USA, pp. 1674–1682, 2016. [Google Scholar]

 7.  B. Cai, X. Xu, K. Jia, C. Qing and D. Tao, “Dehazenet: An end-to-end system for single image haze removal,” IEEE Transactions on Image Processing, vol. 25, no. 11, pp. 5187–5198, 2016. [Google Scholar]

 8.  M. Zhu and B. He, “Dehazing via graph cut,” Optical Engineering, vol. 56, no. 11, pp. 113105, 2017. [Google Scholar]

 9.  F. S. Alenezi and S. Ganesan, “Geometric-pixel guided single-pass convolution neural network with graph cut for image dehazing,” IEEE Access, vol. 9, pp. 29380–29391, 2021. [Google Scholar]

10. S. Chetlur, C. Woolley, P. Vandermersch, J. Cohen, J. Tran et al., “Cudnn: Efficient primitives for deep learning,” arXiv preprint arXiv:1410.0759, 2014. [Google Scholar]

11. D. Zhen, H. A. Jalab and L. Shirui, “Haze removal algorithm using improved restoration model based on dark channel prior,” in Int. Visual Informatics Conf., Bangi, Malaysia, Springer, pp. 157–169, 2019. [Google Scholar]

12. H. Zhang and V. M. Patel, “Densely connected pyramid dehazing network,” in Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition, Salt Lake City, Utah, USA, pp. 3194–3203, 2018. [Google Scholar]

13. B. Li, X. Peng, Z. Wang, J. Xu and D. Feng, “Aod-net: all-in-one dehazing network,” in Proc. of the IEEE Int. Conf. on Computer Vision, Venice, Italy, pp. 4770–4778, 2017. [Google Scholar]

14. S. Salazar-Colores, I. Cruz-Aceves and J. -M. Ramos-Arreguin, “Single image dehazing using a multilayer perceptron,” Journal of Electronic Imaging, vol. 27, no. 4, pp. 043022, 2018. [Google Scholar]

15. W. E. K. Middleton, In Vision Through the Atmosphere, Toronto, Canada: University of Toronto Press, 2019. [Google Scholar]

16. J. Vazquez-Corral, A. Galdran, P. Cyriac and M. Bertalmo, “A fast image dehazing method that does not introduce color artifacts,” Journal of Real-Time Image Processing, vol. 17, no. 3, pp. 607–622, 2020. [Google Scholar]

17. Z. -H. Feng, J. Kittler, M. Awais, P. Huber and X. -J. Wu, “Wing loss for robust facial landmark localisation with convolutional neural networks,” in Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition, Boston, MA, USA, pp. 2235–2245, 2018. [Google Scholar]

18. Y. Zhou, C. Shi, B. Lai and G. Jimenez, “Contrast enhancement of medical images using a new version of the world cup optimization algorithm,” Quantitative Imaging in Medicine and Surgery, vol. 9, no. 9, pp. 1528, 2019. [Google Scholar]

19. K. He, J. Sun and X. Tang, “Single image haze removal using dark channel prior,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 33, no. 12, pp. 2341–2353, 2010. [Google Scholar]

20. Y. Guo and A. S. Ashour, In Neutrosophic Set in Medical Image Analysis, Cambridge, Massachusetts, USA: Academic Press, 2019. [Google Scholar]

21. K. O'Shea and R. Nash, “An introduction to convolutional neural networks,” arXiv preprint arXiv:1511.08458, 2015. [Google Scholar]

22. S. Zhao, L. Zhang, Y. Shen and Y. Zhou, “RefineDNet: A weakly supervised refinement framework for single image dehazing,” IEEE Transactions on Image Processing, vol. 30, pp. 3391–3404, 2021. [Google Scholar]

23. R. M. Yousaf, H. A. Habib, Z. Mehmood, A. Banjar, R. Alharbey et al., “Single image dehazing and edge preservation based on the dark channel probability-weighted moments,” Mathematical Problems in Engineering, vol. 2019, pp. 1–11, 2019. [Google Scholar]

24. E. H. Land, “The retinex theory of color vision,” Scientific American, vol. 237, no. 6, pp. 108–129, 1977. [Google Scholar]

25. Z. Fu, Y. Yang, C. Shu, Y. Li, H. Wu et al., “Improved single image dehazing using dark channel prior,” Journal of Systems Engineering and Electronics, vol. 26, no. 5, pp. 1070–1079, 2015. [Google Scholar]

26. R. Fattal, “Single image dehazing,” ACM Transactions on Graphics (TOG), vol. 27, no. 3, pp. 1–9, 2008. [Google Scholar]

27. Y. Song, J. Li, X. Wang and X. Chen, “Single image dehazing using ranking convolutional neural network,” IEEE Transactions on Multimedia, vol. 20, no. 6, pp. 1548–1560, 2017. [Google Scholar]

28. J. Zhao, Y. Chen, H. Feng, Z. Xu and Q. Li, “Infrared image enhancement through saliency feature analysis based on multi-scale decomposition,” Infrared Physics & Technology, vol. 62, pp. 86–93, 2014. [Google Scholar]

29. V. Sharma and E. Elamaran, “Role of filter sizes in effective image classification using convolutional neural network,” In Cognitive Informatics and Soft Computing, Berlin, Heidelberg, Germany: Springer, pp. 625–637, 2019. [Google Scholar]

30. L. Peng and B. Li, “Single image dehazing based on improved dark channel prior and unsharp masking algorithm,” in Int. Conf. on Intelligent Computing, Wuhan, China, Springer, pp. 347–358, 2018. [Google Scholar]

31. G. Meng, Y. Wang, J. Duan, S. Xiang and C. Pan, “Efficient image dehazing with boundary constraint and contextual regularization,” in Proc. of the IEEE Int. Conf. on Computer Vision, Sydney, Australia, pp. 617–624, 2013. [Google Scholar]

32. S. Yin, Y. Wang and Y. -H. Yang, “A novel image-dehazing network with a parallel attention block,” Pattern Recognition, vol. 102, pp. 107255, 2020. [Google Scholar]

33. K. He, J. Sun and X. Tang, “Guided image filtering,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 35, no. 6, pp. 1397–1409, 2012. [Google Scholar]

34. M. Zhu and B. He, “Dehazing via graph cut,” Optical Engineering, vol. 56, no. 11, pp. 113105, 2017. [Google Scholar]

35. R. T. Tan, “Visibility in bad weather from a single image,” in 2008 IEEE Conf. on Computer Vision and Pattern Recognition, IEEE, pp. 1–8, 2008. [Google Scholar]

36. Q. Zhu, J. Mai and L. Shao, “A fast single image haze removal algorithm using color attenuation prior,” IEEE Transactions on Image Processing, vol. 24, no. 11, pp. 3522–3533, 2015. [Google Scholar]

37. O. Sener and V. Koltun, “Multi-task learning as multi-objective optimization,” arXiv preprint arXiv:1810.04650, 2018. [Google Scholar]

38. Q. Zhu, J. Mai and L. Shao, “A fast single image haze removal algorithm using color attenuation prior,” IEEE Transactions on Image Processing, vol. 24, no. 11, pp. 3522–3533, 2015. [Google Scholar]

39. B. Li, W. Ren, D. Fu, D. Tao, D. Feng et al., “Benchmarking single-image dehazing and beyond,” IEEE Transactions on Image Processing, vol. 28, no. 1, pp. 492–505, 2018. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.