DOI:10.32604/cmc.2022.023004

| Computers, Materials & Continua DOI:10.32604/cmc.2022.023004 |  |
| Article |
A Novel Hybrid Tunicate Swarm Naked Mole-Rat Algorithm for Image Segmentation and Numerical Optimization
1Department of Electronics & Communication Engineering, Chandigarh University, Mohali, 140413, India
2Department of Electronics & Communication Engineering, TIET, Patiala, 147004, India
3Department of Computer Science, College of Computers and Information Technology, Taif University, Taif, 21944, Saudi Arabia
4School of Electrical Engineering and Computer Science, Gwangju Institute of Science and Technology, Gwangju, 61005, Korea
*Corresponding Author: Dilbag Singh. Email: dggill2@gmail.com
Received: 25 August 2021; Accepted: 20 October 2021
Abstract: This paper provides a new optimization algorithm named as tunicate swarm naked mole-rat algorithm (TSNMRA) which uses hybridization concept of tunicate swarm algorithm (TSA) and naked mole-rat algorithm (NMRA). This newly developed algorithm uses the characteristics of both algorithms (TSA and NMRA) and enhance the exploration abilities of NMRA. Apart from the hybridization concept, important parameter of NMRA such as mating factor is made to be self-adaptive with the help of simulated annealing
Keywords: Optimization; NMRA; TSA; image segmentation; thresholding
With the advent of nature inspired computing, a variety of algorithms have been developed in the recent past. The major requirement is that almost every domain research problem including image segmentation [1], scheduling problem [2], industrial engineering design problem [3], routing in wireless sensor network [4] and network distribution [5] is solved/optimized using these algorithms. Various algorithms namely differential evolution (DE) [6], genetic algorithm (GA) [7], grey wolf optimization (GWO) [8], cuckoo search (CS) [9], moth flame optimization (MFO) [10] and others [11] have been proposed to tackle above discussed problems. These algorithms are mainly categorized into two types namely swarm based algorithms and evolutionary algorithms. A large number of new algorithms have been proposed for both these categories and have proved their worthiness for various domain research problems. The major reason for the continuous use of these algorithms is that they require minimal tuning parameters and preserve information over subsequent iterations to find the optimal solution.
Tunicate swarm algorithm (TSA) [12] is a recently introduced algorithm which follows jet propulsion and swarm intelligent behavior of tunicates found in ocean. With the help of these behaviors, tunicates (search agents) become capable to find the location of food (optimal solution).
Naked mole-rat algorithm (NMRA) [13] is another swarm intelligent algorithm proposed in the recent past and based upon matting pattern of mole-rats live in a single colony with size varies from 50 to 295. This colony is leaded by a single female (queen) and categorized into two types of mole-rats (workers and breeders). Here, the queen performs breeding with best performer rats (breeders) while low performer rats (workers) perform some essential tasks.
Both of these algorithms have proved their worthiness and it has been found that TSA has better exploration properties due to avoidance of conflicts among various search candidates and approaching best search candidate. NMRA on the other hand, has better exploitation properties because exploitation phase due to existence of initial best solution and mating factor parameter which controls breeder's frequency to mate with the queen.
As far as the recent literature is concerned, NMRA has been applied to various different optimization problems. These include designing of double notched ultra-wide band antenna [14] and localization problem of wireless sensor networks (WSN) [15]. On the other hand, TSA was also used for economic load dispatch problems [16], parameter optimization of solar cells [17] and multi-path routing protocol in IOT assisted WSN [18].
From the above discussion, it is evident that TSA suffers from the problem of poor exploitation and NMRA has poor exploration properties. In order to deal with this problem, a new hybrid variant combining the added properties of TSA and NMRA has been proposed and named as TSNMRA. Here, exploration properties of TSA are added to the worker phase of NMRA and the breeder phase of NMRA is used as such for better exploration properties. The main contribution of the present work is:
• The concept of TSA and NMRA have been hybridized to propose the new TSNMRA algorithm. The numerical equations of TSA are added in the worker phase of NMRA, while keeping the original structure of both the algorithms intact.
• The concept of
In order to test the efficiency of the proposed TSNMRA, CEC 2019 benchmark problems [19] and real multilevel image thresholding problem [20] have been used. The segmentation of digital images is an open problem that has increasingly attracted the attention of researchers during the last years. Thresholding approaches are often used due to their independence from the resolution of the images and their speed. However, simple thresholding approaches usually generate low-quality images. To achieve a better balance between speed and quality, many criteria are used to select the thresholds that segment the image. Here, TSNMRA is introduced to perform image thresholding by modelling the classes of an image to avoid uncertainty on the selection of the thresholds leading to improvement regarding the quality of the segmented image. From the statistical and experimental results, it has been analyzed that proposed TSNMRA is better than classical NMRA and TSA for CEC 2019 test problems and GA, PSO, MTEMO and BF for image segmentation problem.
The reminder of the paper is organized into 5 sections in which Section 2 deals with background and mathematical model of TSA and NMRA. Section 3 describes proposed algorithm TSNMRA in which hybridization concept of TSA and NMRA has been discussed. Section 4 provides the description of real image thresholding optimization problem. The statistical results along with convergence graphs for CEC 2019 test problems and simulated results for image segmentation problem have been analyzed in Section 5. Finally, conclusion of the article and future prospective are provided in Section 6.
The mathematical model of the TSA has been described in this subsection. TSA is based on tunicate's capability for approaching food source (optimal solution) in the sea. Here, two behaviors are used by tunicates for finding food location such as swarm intelligent behavior and jet propulsion behavior. For implementation of jet propulsion behavior three conditions are taken into consideration such as avoidance of conflicts among search candidates, tunicate approach best candidate position and exist near to best candidate.
Search candidate's avoiding conflicts: For avoiding conflicts among various tunicates, vector
where
where
Approaching best candidate's position: After conflicts avoidance, tunicates start moving towards best neighbour search candidate and calculated as:
where
Converging near to best candidate: The search candidate has to preserved its location near to best search candidate (food's location) and defined as:
where
Swarm intelligent behaviour of tunicates: The search candidates (tunicates) follow swarm intelligent behaviour for position updating and calculated as:
where
NMRA follows the matting behavior of mole rats which are live in a colony and broadly divided into workers and breeders. To develop the mathematical model of NMRA, it is divided into three phases population initialization, exploration (worker phase) and exploitation (breeder) phase.
Initialization of rats: Firstly, initialize the population of rats (n) in a random manner with dimension (d). Here, d represents the problem's variables which are required to be optimized. The equation used for initialization is given as:
where
Worker phase (exploration): The worker rats continuously trying to enhance its fitness in this phase so that they may added into breeder's group and perform breeding with the queen. To develop a new worker's solution, this equation is used:
where
Breeder phase (exploitation): The mole-rats exist in breeder's group also trying to update its fitness so that they become eligible to mate with the queen. The fitness of these breeders is updated with the help of breeding probability (bp) in accordance with initial best solution
where
3 Proposed Algorithm: Hybrid Tunicate Swarm Naked Mole-Rat Algorithm
In the present work, hybridization of TSA and NMRA has been performed to enhance the working capabilities of algorithms. Although, classical TSA and NMRA give reliable results but when these algorithms compared with other improved versions of algorithms, the results are not significant. This is due to poor exploration and local optimum stagnation problem has been observed in basic NMRA whereas TSA performs poor exploitation. Therefore, a new hybrid algorithm TSNMA is proposed without changing the original structure of both NMRA and TSA. This hybrid algorithm starts with initialization of search agents and performed by Eq. (8).
After the initialization, worker phase (exploration) has been performed with properties of both TSA and NMRA. Thus, efficiency of NMRA's worker phase has been enhanced by adding the jet propulsion and swarm behavior equations of TSA. The Eqs. (4)–(7) of TSA have been combined with original worker Eq. (9) of NMRA. Here, it is worth to mention that organization of both the algorithms is kept same and equations of TSA are incorporated in the same way as provided in original TSA.
The nest phase of TSNMRA is breeder phase and has been executed with same structure as given in basic NMRA. This phase is considered as exploitation phase and algorithm converges to global optimal solution. The solution obtained in this phase is provided by Eq. (10) which is same as original NMRA. Here, the selection of breeder's number is very important because limited number of breeders get a chance to mate with the queen (optimal solution). So, proposed TSNMRA breeder phase is similar to original NMRA and no modifications have been added to this phase.
Apart from the hybridization of TSA and NMRA, adaptation of parameters is also included in the present work. Here, mating factor
where
Finally, selection phase of TSNMA is treated as last phase and follows the procedure of greedy selection. Here, if the fitness of newly obtained solution is superior than previous generated solution then the new solution should be adopted as local best solution and previous solution should be discarded. The pseudo-code of proposed TSNMRA is given in Algorithm 1.

4 Real World Image Thresholding Optimization Problem
Image segmentation is a complex area of image processing research that results in a set of segments that cover a set of contours extracted from an image. In an area, each pixel is compared for some distinguishing or calculated attribute, such as colour, texture or intensity. The goal is to make an image's representation more understandable and easier to evaluate by simplifying or changing it. Over the years, a lot of work has been done in this area. The four basic categories of image segmentation techniques now in use are: regional method, border based, clustering based [22] and thresholding based.
In image processing, thresholding is a pre-processing complex task. It's quickest and effective segmentation technique, capable of distinguishing objects from the background using pixel-level criteria. The separation of the foreground object from gray-level pixels in the background is necessary in some image processing examples [22]. It has a wide range of applications in domains such as biomedical imaging, infrared imaging, remote sensing, surveillance, artificial intelligence, for specialized target recognition, and others [23].
Thresholding can be either bi-level or multi-level. In the earlier, image is separated, using single threshold value, into two classes. The entire image is checked for a known threshold value
This bi-level thresholding (BT) not only provides precise regions with low overlap and aggregation effectiveness, but it may also serve as a pre-processing tool for more complex segmentation approaches [24].
In bi-level thresholding, if the threshold value is set incorrectly, the results can be severe. In many circumstances, multi-level thresholding (MT) is utilized to improve the outcomes of segmentation. As shown in Eq. (2), more thresholds are employed to segment the image into a set of classes. MT generates numerous regions [
where i is a certain class and n is the number of classes.
The term “optimization” refers to finding the optimal solution to a problem while keeping certain constraints in consideration [25]. The search for the best threshold values for a given image is considered as constrained optimization problem. To solve the computational inefficient problems of typical thresholding approaches, swarm intelligence (SI) algorithms are widely employed to seek for appropriate threshold values for MT problems using distinct fitness or objective functions. For multi-level designs, many biological evolution-inspired metaheuristic algorithms and their modified algorithms were applied.
Countless thresholding approaches have been documented in the associated literatures over the years [26]. Otsu's method [27], which was introduced in 1979, is a thresholding strategy that maximizes class variance to produce optimal thresholds. Using the 1985 moment-preserving approach, Tsalis [28] suggested a thresholding strategy for a grey image. The Kapur entropy approach, developed by Kapur et al. [28], employed histogram entropy to discover optimal threshold values, and the methodology was widely used to detect the threshold values in image processing. To minimize cross-entropy between the original image and the segmented image, the minimum cross-entropy method is used to detect the appropriate threshold value [29]. These techniques can easily be used to multilevel threshold segmentation applications. When multiple thresholds are to be determined, the computational time increases exponentially as these algorithms look for the best threshold values to optimize objective features.
Image thresholding method: Otsu is nonparametric and unsupervised approach for determining an image's threshold value [6] that seeks to maximize the inter-class variance while reducing the intra-class variance between pixels in each class. Varying classes of image with different threshold values are
where,
For two classes of
If
Function
To extend this method from BT to MT, consider an image with L grey levels (1, 2, …, L), N pixels, and ‘
Between the class value, in this extended form is represented as
If the between-class variance is at its highest, the within-class variable will always be at its lowest, with
The above said problem is a maximization problem in image segmentation optimization. When this method is applied to multilevel thresholding, the computational cost increases exponentially. Using an Intel i7-4770 K CPU, it takes roughly 40 years to identify 8 threshold values using the Otsu approach, and around 10,000 years to find 9 threshold values [30]. Different heuristic-based techniques have been developed to solve this issue, which divide the histogram into multiple sections by selecting appropriate thresholds.
In this work, proposed TSNMRA has been applied to benchmark image set for segmentation based on MT. The objective function for the optimization problem is given as
The initial population of the problem under consideration is determined by
where
To enumerate the effectiveness of each solution utilizing TSNMRA in the image segmentation problem, the fitness values are evaluated using Otsu approach. To construct an evolved population, the population undergoes numerous operators (see Eqs. (1)–(11)) until the termination requirement is satisfied. For the Otsu approach, the solution with the highest fitness value is regarded the best objective function value.
This section deals with the performance evaluation of the proposed new hybrid algorithm TSNMRA for ten 100-digit challenge (CEC 2019) test problems and real image thresholding optimization problem.
5.1 Statical Results for CEC 2019 Test Problems
The CEC 2019 test problems comprise three simple numerical problems (P1 to P3) and seven shifted and rotated numerical problems (P4 to P10) along with scalable properties. A detailed description of CEC 2019 test suite is available in [31]. To check the working capability of the proposed TSNMRA, it is compared with classical NMRA and TSA. The parameters involved in these algorithms are provided in Tab. 1. Here, it should be noted that all the algorithms under test are simulated for 500 iterations with 50 search agents (population size). The statistical results obtained for each algorithm are represented in terms of best, median, worst, mean and standard deviation (Std) for 51 runs and presented in Tab. 2.
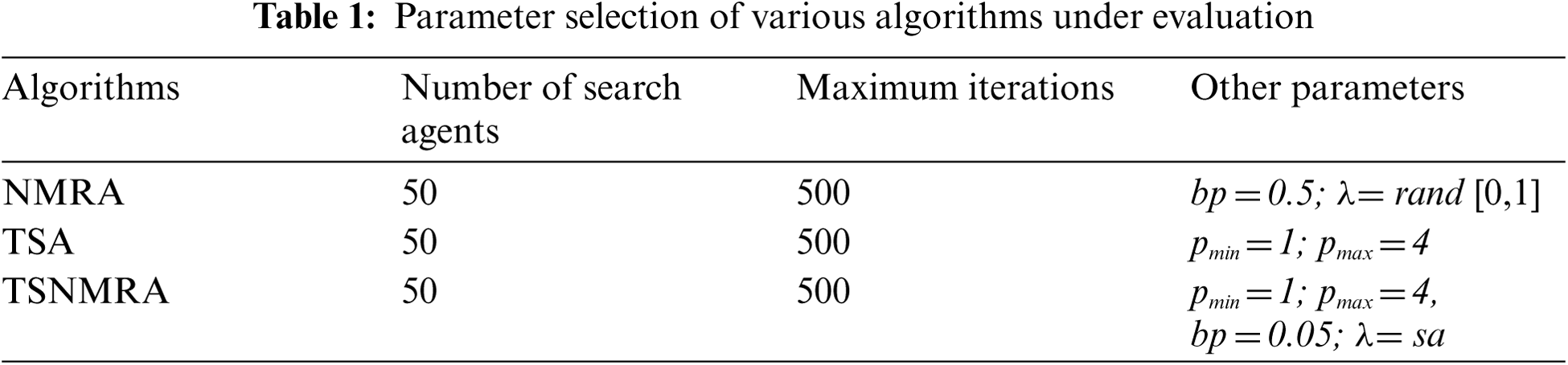
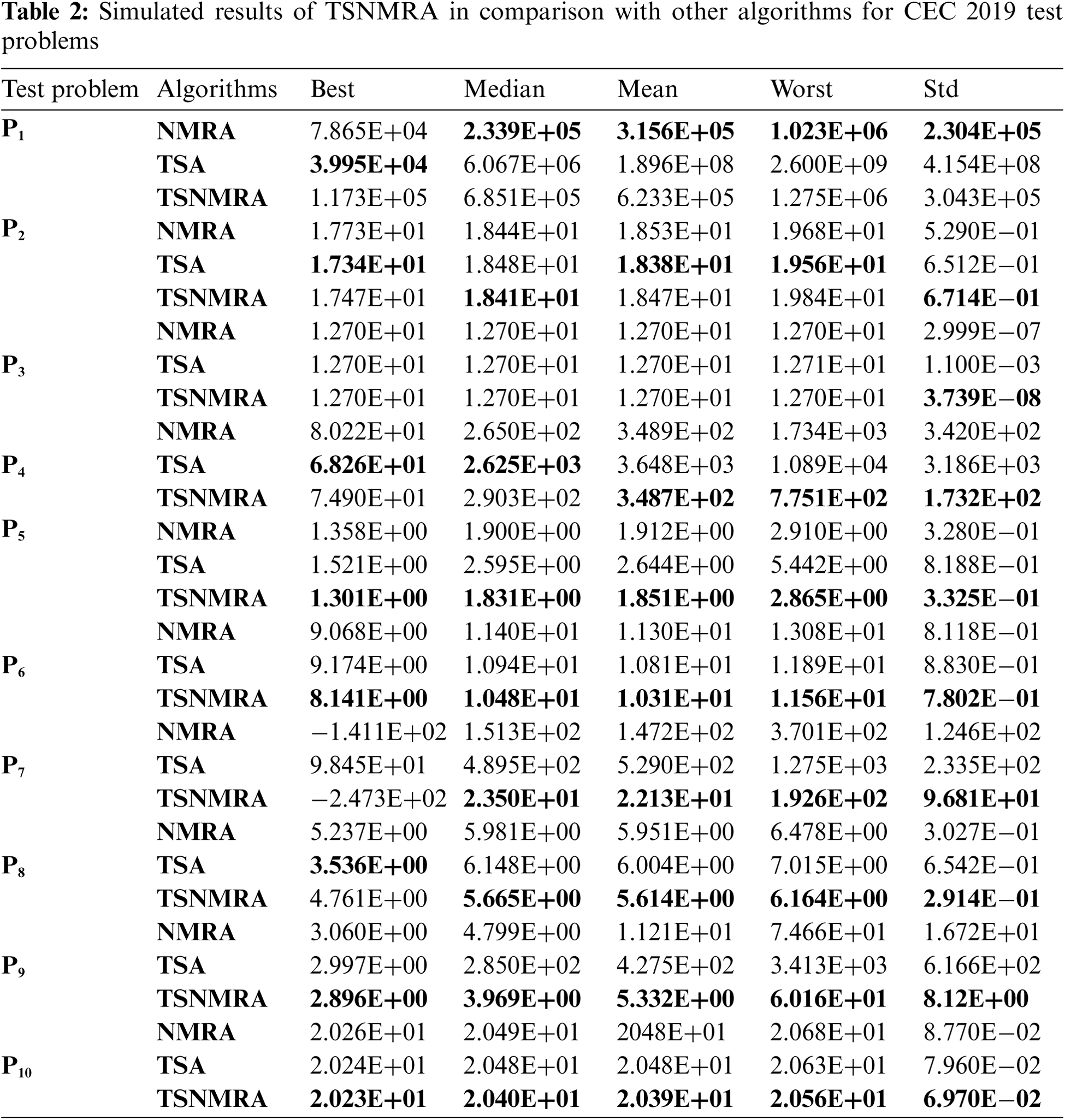
From the results illustrated in Tab. 2, it can be analyzed that classical NMRA's performance is best concerning other competitive algorithms for problems P1 and P2. In case of problem P3, the comparison of algorithm's results is carried out for std values where TSNMRA performs well among all the algorithms under test. For problem P4, TSNMRA gives superior results for all the performance matrices except best values. For problems P5, P6, P7, P8, P9 and P10, results of TSNMRA are best and no other algorithm is capable to match its performance. Therefore, TSNMRA's results are found to be superior for eight numerical test problems and NMRA for two test problems. Apart from the statistical results, convergence of NMRA, TSA and TSNMRA are also drawn and shown in Fig. 1. From the convergence profiles, it has been observed that the proposed algorithm TSNMRA converge to the optimal value for most of the cases with a course of iterations in comparison with TSA and NMRA. So, overall TSNMRA is treated as the best candidate to solve these numerical test problems as compared to other basic competitive algorithms.
5.2 Results for Image Segmentation Problem
To test the efficiency of the proposed method, 4 benchmark images (Hunter, Baboon, Cameraman, and Sea star) from the MT literature are used. Because optimization algorithms are stochastic and reliant on random numbers, there is a chance that there will be error. To circumvent discrepancies, all dataset images are run via TSNMRA 35 times for
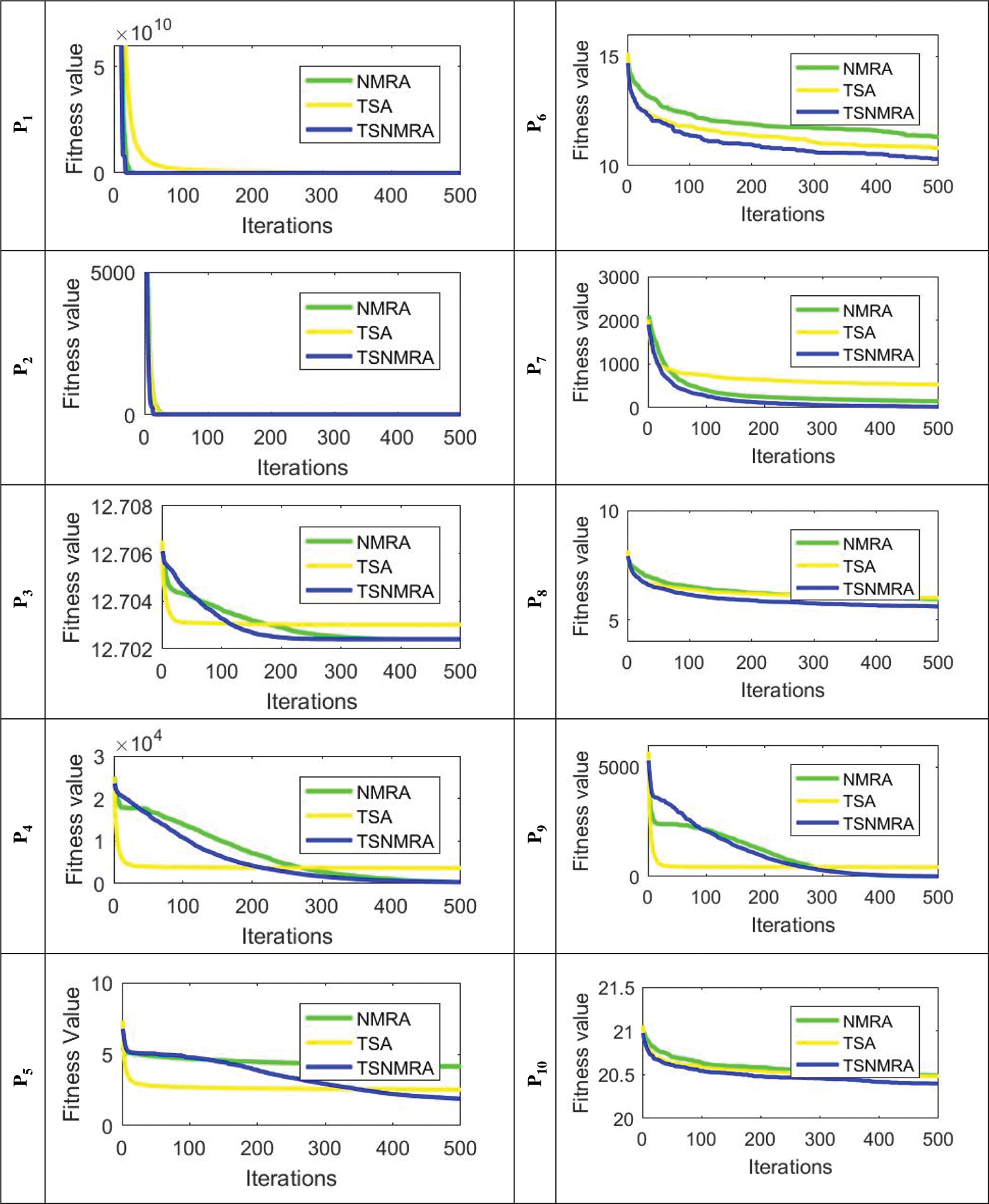
Figure 1: Convergence profiles for CEC 2019 test problems
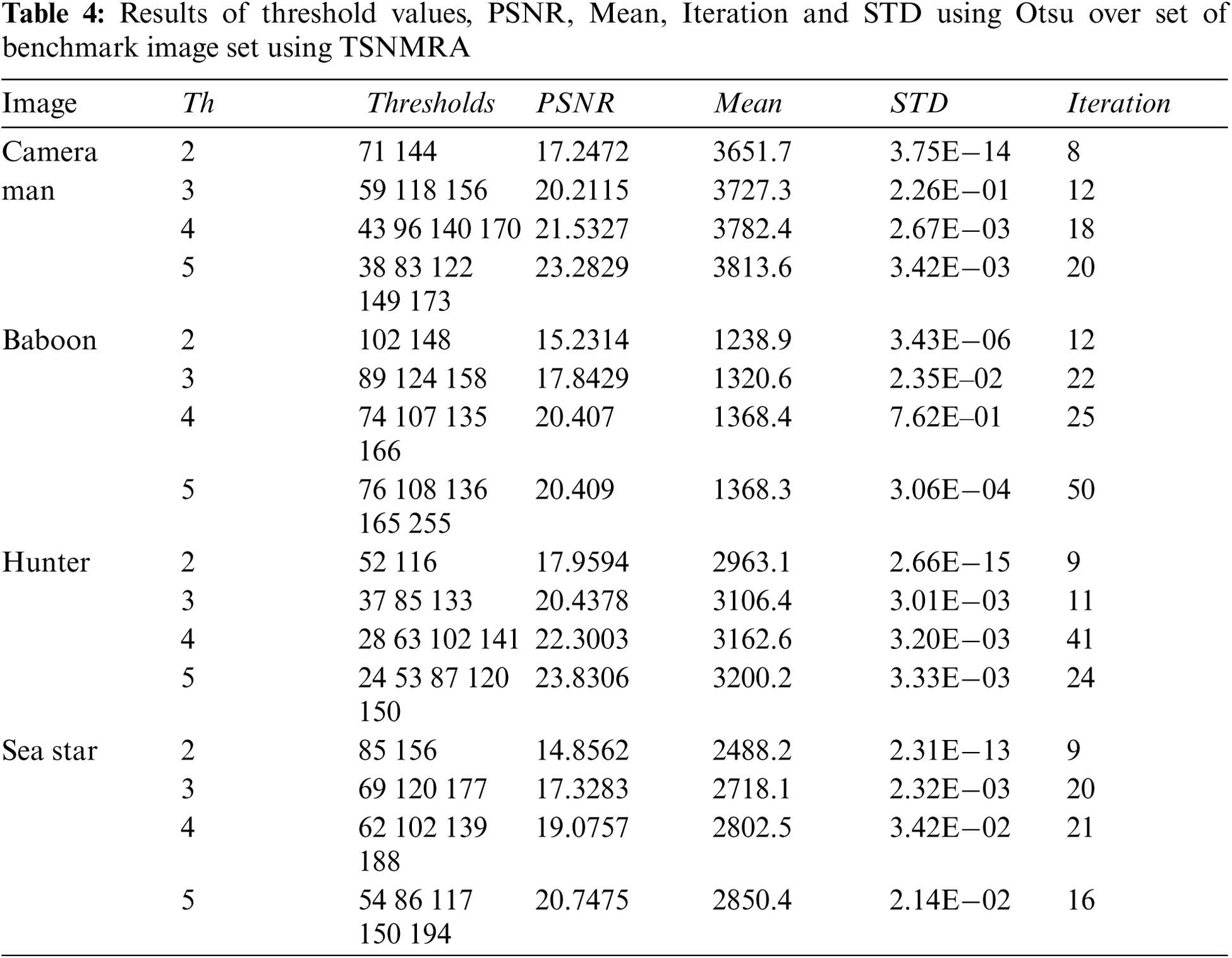
Tab. 3 illustrates the results of applying the TSNMRA to the selected benchmark images using Otsu's technique as an objective function. It can be observed that the TSNMRA method outperforms other algorithms, and majority of the images converge earlier than 30 iterations. On selected dataset images, Otsu's approach is used to determine the optimal thresholds, PSNR, mean, standard deviation and convergence characteristics. Tab. 4 shows the results of threshold values, PSNR, Mean, and STD with iteration count using the Otsu approach on the selected benchmark image set for TSNMRA.
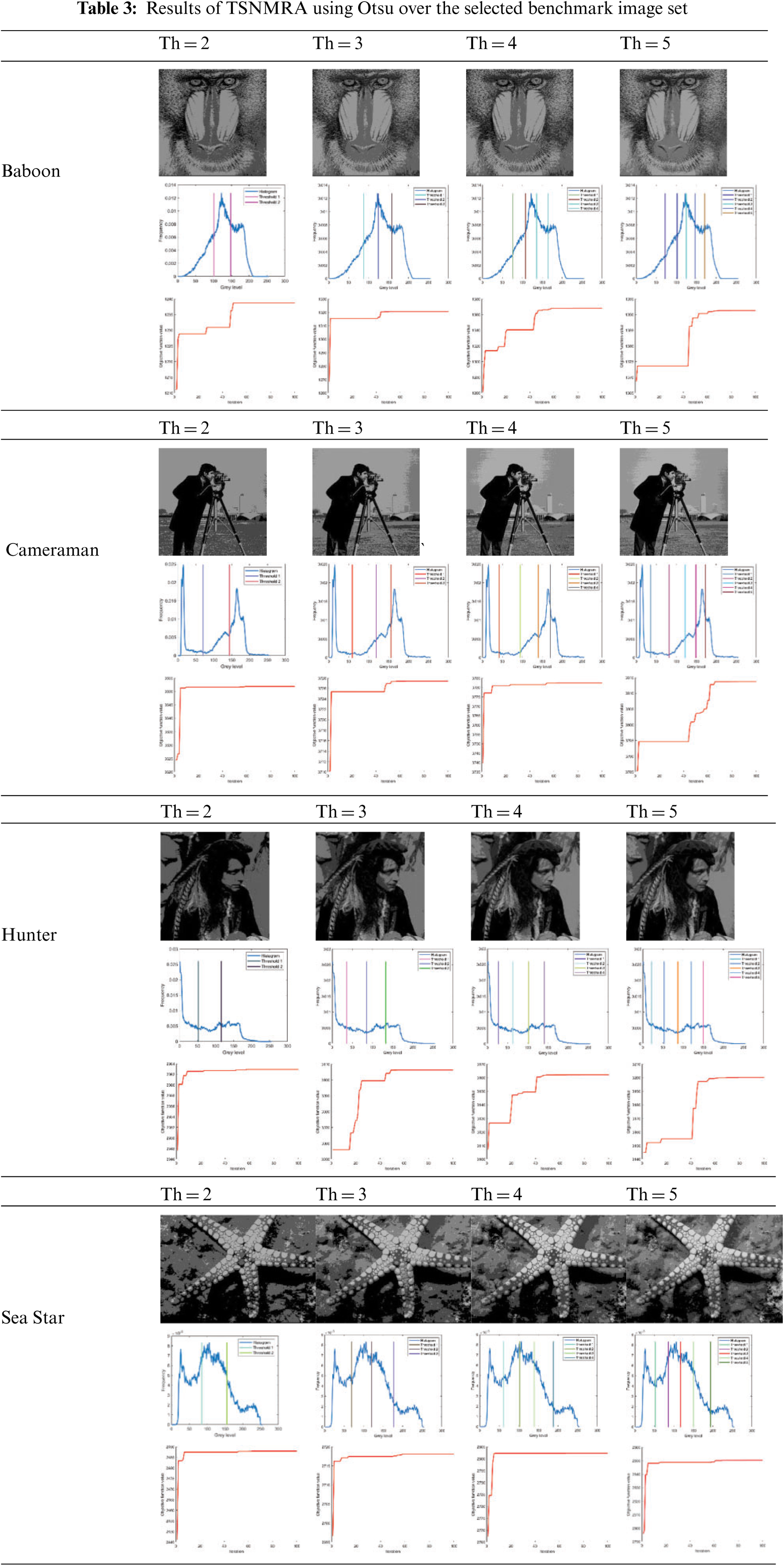
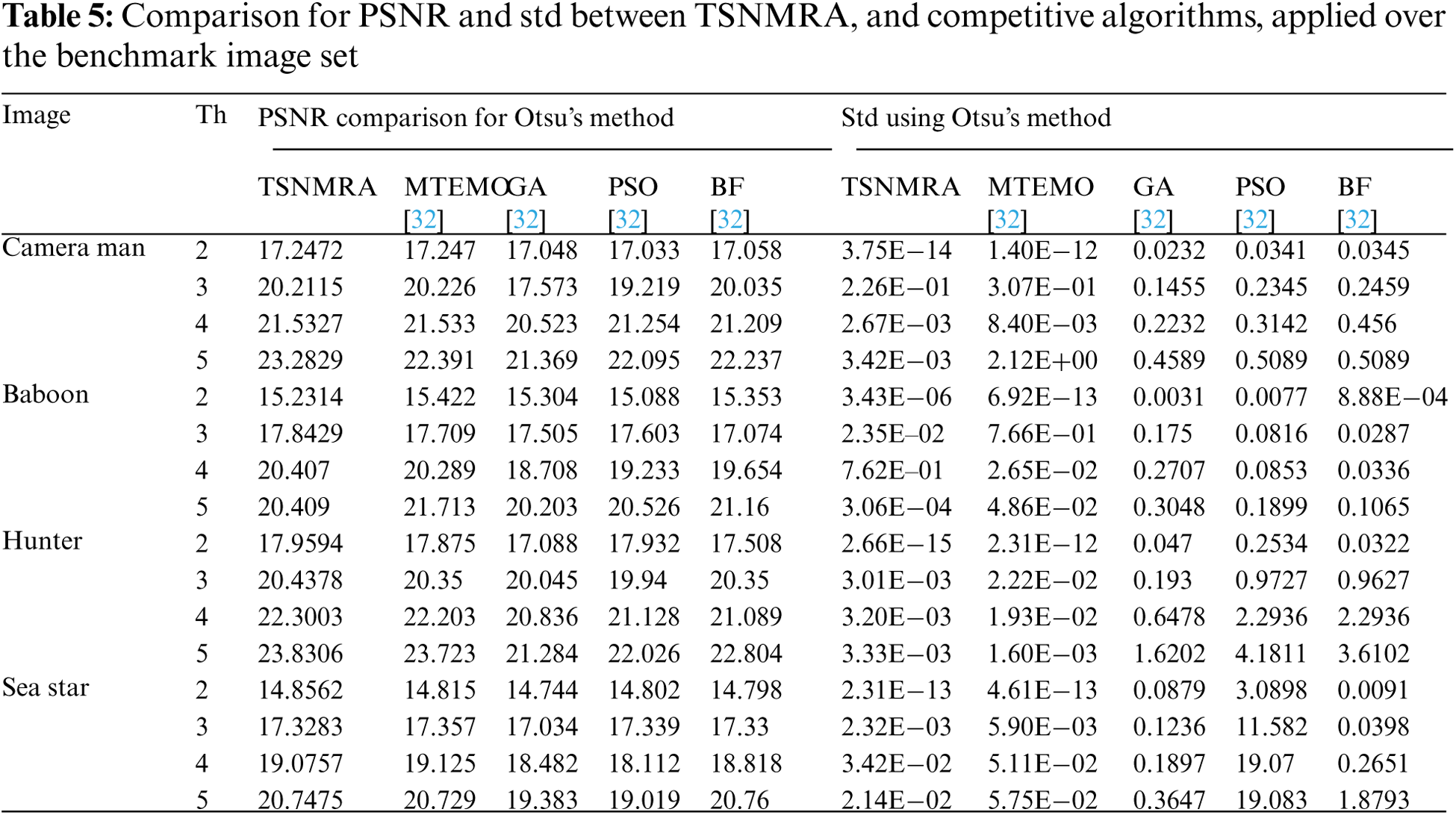
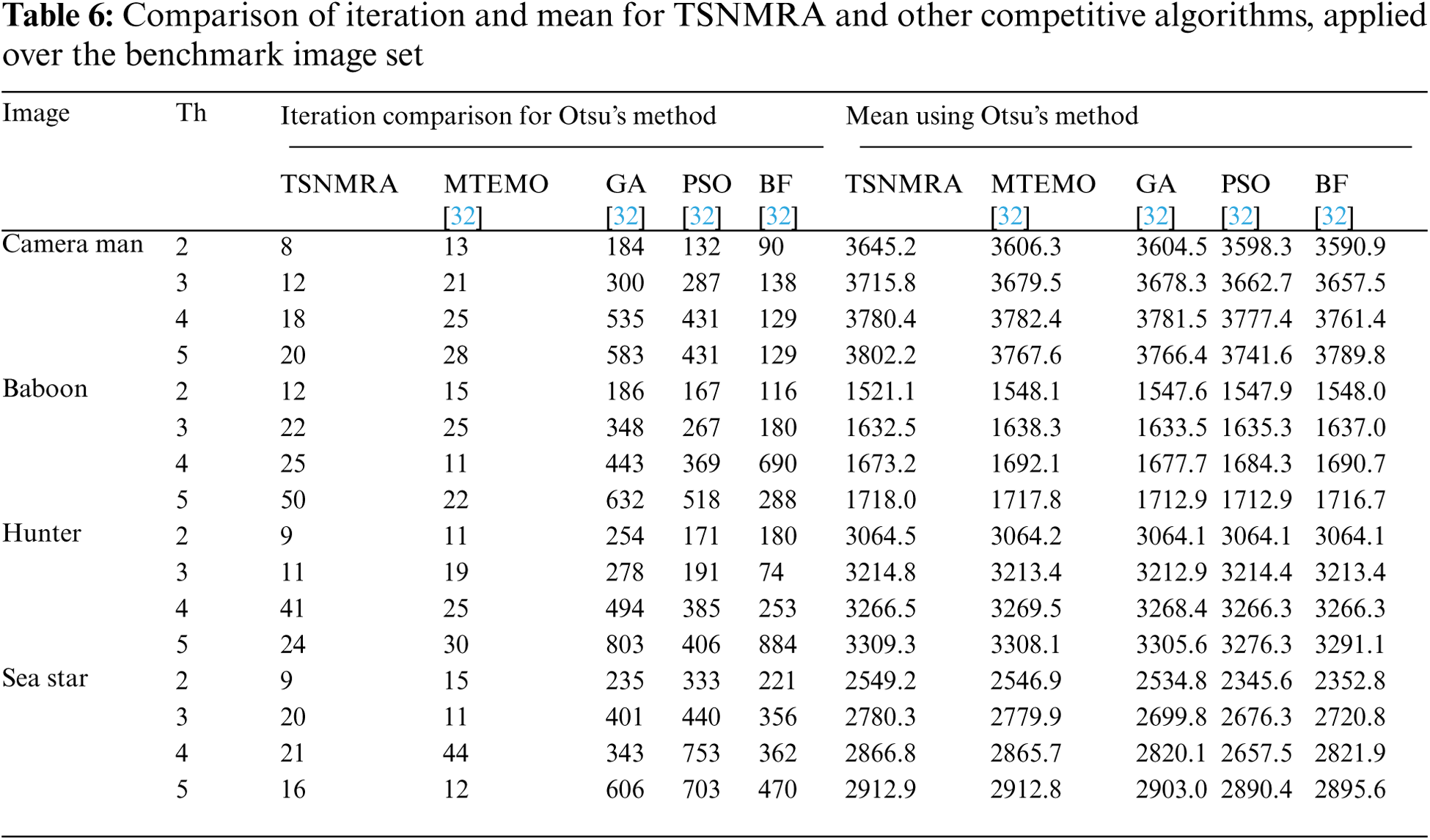
Tab. 5 shows the PSNR, and standard deviation whereas Tab. 6 provides the iteration count and mean error values of TSNMRA, MTEMO, GA, PSO, and BF when applied to the benchmark image set using Otsu's technique. The data illustrates that the TSNMRA technique produces positive results in the majority of cases. It can be seen that TSNMRA offers apparent advantages over GA, PSO, and BF in terms of computation cost across a large number of iterations and excellent segmentation outcomes.
6 Conclusion and Future Directions
This research provides a new hybrid TSNMRA method that combines the qualities of TSA and NMRA algorithms. CEC 2019 benchmark functions are employed to test the effectiveness of proposed algorithm. The performance of the algorithm is evaluated using a new simulated annealing-based mutation operator. It was determined that introducing the mutation operator to the algorithm makes it self-adaptive and enhances its performance. For CEC 2019 benchmarks, it was revealed that TSNMRA outperforms both TSA and NMRA algorithms.
In addition to that, this research proposes a TSNMRA-based image thresholding approach. A collection of benchmark images was used to test the suggested thresholding method. In terms of convergence, accuracy, and quality of the segmented images, the thresholding methodology is compared to competing algorithms. The results show that TSNMRA is a successful image thresholding approach. A better exploration and exploitation operations may be employed to the algorithm as future efforts to increase its performance. To analyze the performance of the TSNMRA method, several chaotic maps and mutation operators can be incorporated. New exploratory and exploitative search equations can be implemented to improve local and global search capabilities. The approach can also be used to solve cancer classification, feature selection, clustering problems, multi-criteria learning, gene expression modelling, and other real-world optimization problems.
Acknowledgement: The authors would like to thank for the support from Taif university Researchers Supporting Project Number (TURSP-2020/114), Taif University, Taif, Saudi Arabia.
Funding Statement: The authors would like to thank for the support from Taif university Researchers Supporting Project Number (TURSP-2020/114), Taif University, Taif, Saudi Arabia.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. S. Singh, N. Mittal, D. Thakur, H. Singh, D. Oliva et al., “Nature and biologically inspired image segmentation techniques,” Archives of Computational Methods in Engineering, vol. 1, pp. 1–28, 2021. [Google Scholar]
2. M. Abdel-Basset, G. Manogaran, D. El-Shahat and S. Mirjalili, “A hybrid whale optimization algorithm based on local search strategy for the permutation flow shop scheduling problem,” Future Generation Computer Systems, vol. 85, pp. 129–145, 2018. [Google Scholar]
3. R. Salgotra, U. Singh, G. Singh, N. Mittal and A. H. Gandomi, “A self-adaptive hybridized differential evolution naked mole-rat algorithm for engineering optimization problems,” Computer Methods in Applied Mechanics and Engineering, vol. 383, pp. 113916, 2021. [Google Scholar]
4. N. Mittal, U. Singh, R. Salgotra and B. S. Sohi, “An energy efficient stable clustering approach using fuzzy extended grey wolf optimization algorithm for WSNs,” Wireless Networks, vol. 25, no. 8, pp. 5151–5172, 2019. [Google Scholar]
5. T. Fetouh and A. M. Elsayed, “Optimal control and operation of fully automated distribution networks using improved tunicate swarm intelligent algorithm,” IEEE Access, vol. 8, pp. 129689–129708, 2020. [Google Scholar]
6. R. Storn and K. Price, “Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces,” Journal of Global Optimization, vol. 11, no. 4, pp. 341–359, 1997. [Google Scholar]
7. S. Mirjalili, “Genetic algorithm,” in Evolutionary Algorithms and Neural Networks, Springer, Cham, pp. 43–55, 2019. [Google Scholar]
8. S. Mirjalili, S. M. Mirjalili and A. Lewis, “Grey wolf optimizer,” Advances in Engineering Software, vol. 69, pp. 46–61, 2014. [Google Scholar]
9. X. S. Yang and S. Deb, “Cuckoo search: Recent advances and applications,” Neural Computing and Applications, vol. 24, no. 1, pp. 169–174, 2014. [Google Scholar]
10. S. Mirjalili, “Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm,” Knowledge-Based Systems, vol. 89, pp. 228–249, 2015. [Google Scholar]
11. R. Salgotra, U. Singh, G. Singh, S. Singh and A. H. Gandomi, “Application of mutation operators to salp swarm algorithm,” Expert Systems with Applications, vol. 169, pp. 114368, 2021. [Google Scholar]
12. S. Kaur, L. K. Awasthi, A. L. Sangal and G. Dhiman, “Tunicate swarm algorithm: A new bio-inspired based metaheuristic paradigm for global optimization,” Engineering Applications of Artificial Intelligence, vol. 90, pp. 103541, 2020. [Google Scholar]
13. R. Salgotra and U. Singh, “The naked mole-rat algorithm,” Neural Computing and Applications, vol. 31, no. 12, pp. 8837–8857, 2019. [Google Scholar]
14. G. Singh, U. Singh and R. Salgotra, “Effect of parametric enhancements on naked mole-rat algorithm for global optimization,” Engineering with Computers, vol. 1, pp. 1–29, 2021. [Google Scholar]
15. P. Singh, N. Mittal, U. Singh and R. Salgotra, “Naked mole-rat algorithm with improved exploration and exploitation capabilities to determine 2D and 3D coordinates of sensor nodes in WSNs,” Arabian Journal for Science and Engineering, vol. 46, no. 2, pp. 1155–1178, 2021. [Google Scholar]
16. L. L. Li, Z. F. Liu, M. L. Tseng, S. J. Zheng and M. K. Lim, “Improved tunicate swarm algorithm: Solving the dynamic economic emission dispatch problems,” Applied Soft Computing, vol. 108, pp. 107504, 2021. [Google Scholar]
17. A. Sharma, A. Sharma, A. Dasgotra, V. Jately, M. Ram et al., “Opposition-based tunicate swarm algorithm for parameter optimization of solar cells,” IEEE Access, vol. 9, pp. 125590–125602, 2021. [Google Scholar]
18. N. Chouhan and S. C. Jain, “Tunicate swarm grey wolf optimization for multi-path routing protocol in IoT assisted WSN networks,” Journal of Ambient Intelligence and Humanized Computing, vol. 1, pp. 1–17, 2020. [Google Scholar]
19. K. V. Price, N. H. Awad, M. Z. Ali and P. N. Suganthan, “The 100-digit challenge: Problem definitions and evaluation criteria for the 100-digit challenge special session and competition on single objective numerical optimization,” Nanyang Technological University, vol. 1, pp. 1–21, 2018. [Google Scholar]
20. S. Singh, N. Mittal and H. Singh, “A multilevel thresholding algorithm using LebTLBO for image segmentation,” Neural Computing and Applications, vol. 32, pp. 16681–16706, 2020. [Google Scholar]
21. W. Al-Hassan, M. B. Fayek and S. I. Shaheen, “Psosa: An optimized particle swarm technique for solving the urban planning problem,” in 2006 Int. Conf. on Computer Engineering and Systems, Cairo, Egypt, IEEE, pp. 401–405, 2006. [Google Scholar]
22. A. Marinoni, A. Plaza and P. Gamba, “A novel preunmixing framework for efficient detection of linear mixtures in hyperspectral images,” IEEE Transactions on Geoscience Remote Sensor, vol. 55, no. 8, pp. 4325–4333, 2017. [Google Scholar]
23. V. K. Bohat and K. V. Arya, “A new heuristic for multilevel thresholding of images,” Expert System with Applications, vol. 117, pp. 176–203, 2019. [Google Scholar]
24. L. Li, L. Sun, J. Guo, C. Han, J. Zhou et al., “A quick artificial Bee colony algorithm for image thresholding,” Information, vol. 8, no. 1, pp. 1–16, 2017. [Google Scholar]
25. P. K. Sahoo and G. Arora, “Image thresholding using two-dimensional Tsallis-Havrda-Charvát entropy,” Pattern Recognition Letters, vol. 27, no. 6, pp. 520–528, 2006. [Google Scholar]
26. J. Shi, N. Ray and H. Zhang, “Shape based local thresholding for binarization of document images,” Pattern Recognition Letters, vol. 33, no. 1, pp. 24–32, 2012. [Google Scholar]
27. N. Otsu, “A threshold selection method from gray-level histograms,” IEEE Transactions on Systems, Man and Cybernetics, vol. 9, no. 1, pp. 62–66, 1979. [Google Scholar]
28. J. N. Kapur, P. K. Sahoo and A. K. C. Wong, “A new method for gray-level picture thresholding using the entropy of the histogram,” Computer Vision, Graphics and Image Processing, vol. 29, no. 3, pp. 273–285, 1985. [Google Scholar]
29. H. Jia, J. U. N. Ma and W. Song, “Multilevel thresholding segmentation for color image using modified moth-flame optimization,” IEEE Access, vol. 7, pp. 44097–44134, 2019. [Google Scholar]
30. M. Tuba, “Multilevel image thresholding by nature-inspired algorithms: A short review,” Computer Science Journal of Moldova, vol. 22, no. 3, pp. 318–338, 2014. [Google Scholar]
31. P. Singh and N. Mittal, “An efficient localization approach to locate sensor nodes in 3D wireless sensor networks using adaptive flower pollination algorithm,” Wireless Networks, vol. 27, no. 3, pp. 1999–2014, 2021. [Google Scholar]
32. S. Singh, N. Mittal and H. Singh, “A multilevel thresholding algorithm using LebTLBO for image segmentation,” Neural Computing and Applications, vol. 32, pp. 16681–16706, 2020. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |