Computers, Materials & Continua DOI:10.32604/cmc.2022.022797
Article

A New Metaheuristic Approach to Solving Benchmark Problems: Hybrid Salp Swarm Jaya Algorithm

Erkan Erdemir1,* and Adem Alpaslan Altun2

1Department of Information Technologies, Tokat Vocational and Technical Anatolian High School, Merkez/Tokat, 60030, Turkey
2Department of Computer Engineering, Faculty of Technology, Konya Selcuk University, Selcuklu/Konya, 42130, Turkey
*Corresponding Author: Erkan Erdemir. Emails: erdemirerkan@gmail.com, erkan.erdemir@lisansustu.selcuk.edu.tr
Received: 19 August 2021; Accepted: 05 October 2021

Abstract: Metaheuristic algorithms are one of the methods used to solve optimization problems and find global or close to optimal solutions at a reasonable computational cost. As with other types of algorithms, in metaheuristic algorithms, one of the methods used to improve performance and achieve results closer to the target result is the hybridization of algorithms. In this study, a hybrid algorithm (HSSJAYA) consisting of salp swarm algorithm (SSA) and jaya algorithm (JAYA) is designed. The speed of achieving the global optimum of SSA, its simplicity, easy hybridization and JAYA's success in achieving the best solution have given us the idea of creating a powerful hybrid algorithm from these two algorithms. The hybrid algorithm is based on SSA's leader and follower salp system and JAYA's best and worst solution part. HSSJAYA works according to the best and worst food source positions. In this way, it is thought that the leader-follower salps will find the best solution to reach the food source. The hybrid algorithm has been tested in 14 unimodal and 21 multimodal benchmark functions. The results were compared with SSA, JAYA, cuckoo search algorithm (CS), firefly algorithm (FFA) and genetic algorithm (GA). As a result, a hybrid algorithm that provided results closer to the desired fitness value in benchmark functions was obtained. In addition, these results were statistically compared using wilcoxon rank sum test with other algorithms. According to the statistical results obtained from the results of the benchmark functions, it was determined that HSSJAYA creates a statistically significant difference in most of the problems compared to other algorithms.

Keywords: Metaheuristic; optimization; benchmark; algorithm; swarm; hybrid

1  Introduction

Optimization problems; signal processing, mathematics, chemistry, computer science, mechanics, economics, etc. it is the expression of real-world problems in fields by converting them into mathematical terms. Purpose in optimization problems; is to find the best available solution by optimizing the value among the possible solutions within a certain solution search range and constraints [1,2].

It may be necessary to use different algorithms to find the best solution to optimization problems. These algorithms are divided into deterministic algorithms, which often use a method of tracking a particular sequence of actions, and stochastic algorithms that contain randomness [3].

In deterministic algorithms, no hesitant result is obtained. As long as the input given to the problem in the algorithm is the same, the solution obtained as the output is always the same, but with a deterministic algorithm, structural difficulties can develop in solving problems, and there is a possibility that the expected solution cannot be obtained [4,5].

For the reasons above; metaheuristic algorithms inspired by nature contained in stochastic algorithms; they are preferred because they can be created in a simple way according to deterministic algorithms, hybrid with multiple metaheuristic algorithms, flexibility in adapting to different problems, solving real problems without derivatives, and avoiding local optimal values [6,7].

Most of the metaheuristic algorithms are population and swarm based high level heuristics; It is one of the methods preferred by researchers in the solution of optimization problems. Cuckoo search algorithm (CS) [8], firefly algorithm (FFA) [9], salp swarm algorithm (SSA) [10], jaya algorithm (JAYA) [11,12], genetic algorithm (GA) [13] can be given as examples to these algorithms.

Metaheuristic algorithms; simple, easy to implement, successful in solving difficult problems, etc. but high computational costs, stuck in local search, uncertainty in reaching convergence, and non-repeatable exact solutions, etc. are among its weaknesses [14,15].

To obtain a stronger metaheuristic algorithm, either new algorithms should be created or new hybrid algorithms should be developed by taking the successful parts of more than one algorithm [16]. While the hybrid algorithm aims to create a better algorithm by combining the advantageous aspects of more than one algorithm, it also aims to reduce or remove the weaknesses of the algorithms that make up the hybrid algorithm [17,18].

Hybrid metaheuristic algorithms developed in studies are also superior in areas such as optimization problems, artificial neural network training, etc. Some of the studies in the literature are;

Li et al. [19] developed a hybrid algorithm with GSA to improve SSA's success in complex problem solutions and improve its search capability. The hybrid algorithm has been tested with CEC2017 functions and has been found by researchers to increase accuracy and convergence rate.

Singh et al. [20] have developed a hybrid salp swarm-sine cosine algorithm for nonlinear optimization problems. They performed the positions of salp swarms in the search space using position equations in the sine cosine algorithm. Researchers noted that the hybrid algorithm tested in optimization and engineering problems reach the best solution in a short time and with high accuracy compared to other algorithms.

Caldeira et al. [21] have designed advanced JAYA to solve flexible workshop scheduling problems. In order for JAYA's solutions to be better, local search methods, new acceptance criteria, etc. they have added innovations such as. The improved JAYA algorithm has been compared with other well-known metaheuristic algorithms based on the makespan criterion on benchmarking samples.

Khamees et al. [22] hybridized the simulated annealing algorithm (SA) with the SSA algorithm. They used it for multi-purpose feature selection. The hybrid algorithm, which has been tested in a total of 16 data sets, has been compared to the original SSA, PSO and ant lion algorithm (ALO). They noted that the accuracy rate in classification according to results is high compared to other algorithms.

Aslan et al. [23] designed JAYA with XOR operator for binary optimization called JayaX. Researchers believe that JAYA is not suitable for binary optimization problems, and have noted that solutions solve this obstacle by using the XOR operator. They aimed to improve the performance of the algorithm by adding a local search section to the algorithm they developed. They noted that the solution quality and stability of the new algorithm, which is compared with other algorithms on various problems, is better.

Ibrahim et al. [24] designed an improved SSA algorithm for PSO-based attribute selection. Researchers have taken advantage of the strengths of the two algorithms to overcome the high-dimensionality problem in attribute selection. The algorithm developed was evaluated in two parts; in the first part, benchmarking functions were evaluated and in the second part, experimental analysis was performed on the selection of the best attributes on different data sets. As a result, they noted that the improved hybrid algorithm results better in performance and accuracy.

Chen et al. [25] proposed a hybrid algorithm that they created using PSO-CS algorithms. They used their proposed algorithms as a new training method for feedforward neural networks. As a result, they found that the proposed hybrid algorithm performed better in feedforward neural networks training than in PSO and CS.

The aim of this study is to develop a new hybrid algorithm by combining the metaheuristic optimization algorithms that exist in the literature. The developed hybrid algorithm has a high accuracy rate, the error rate has been minimized, and at the same time it was desired to develop an algorithm that will succeed from the algorithms that make up the hybrid algorithm.

In this context, a hybrid metaheuristic algorithm (Hybrid Salp Swarm Jaya Algorithm-HSSJAYA) consisting of the SSA and JAYA algorithm was developed. The developed hybrid algorithm was used in unimodal - multimodal benchmarking functions. The hybrid algorithm developed has been compared to SSA, JAYA and several leading algorithms.

In Section 1 (Introduction), information on optimization, metaheuristic algorithms, hybrid algorithms and related studies and the purpose and subject of the study were given.

In Section 2 (Overview), information about SSA and JAYA was given.

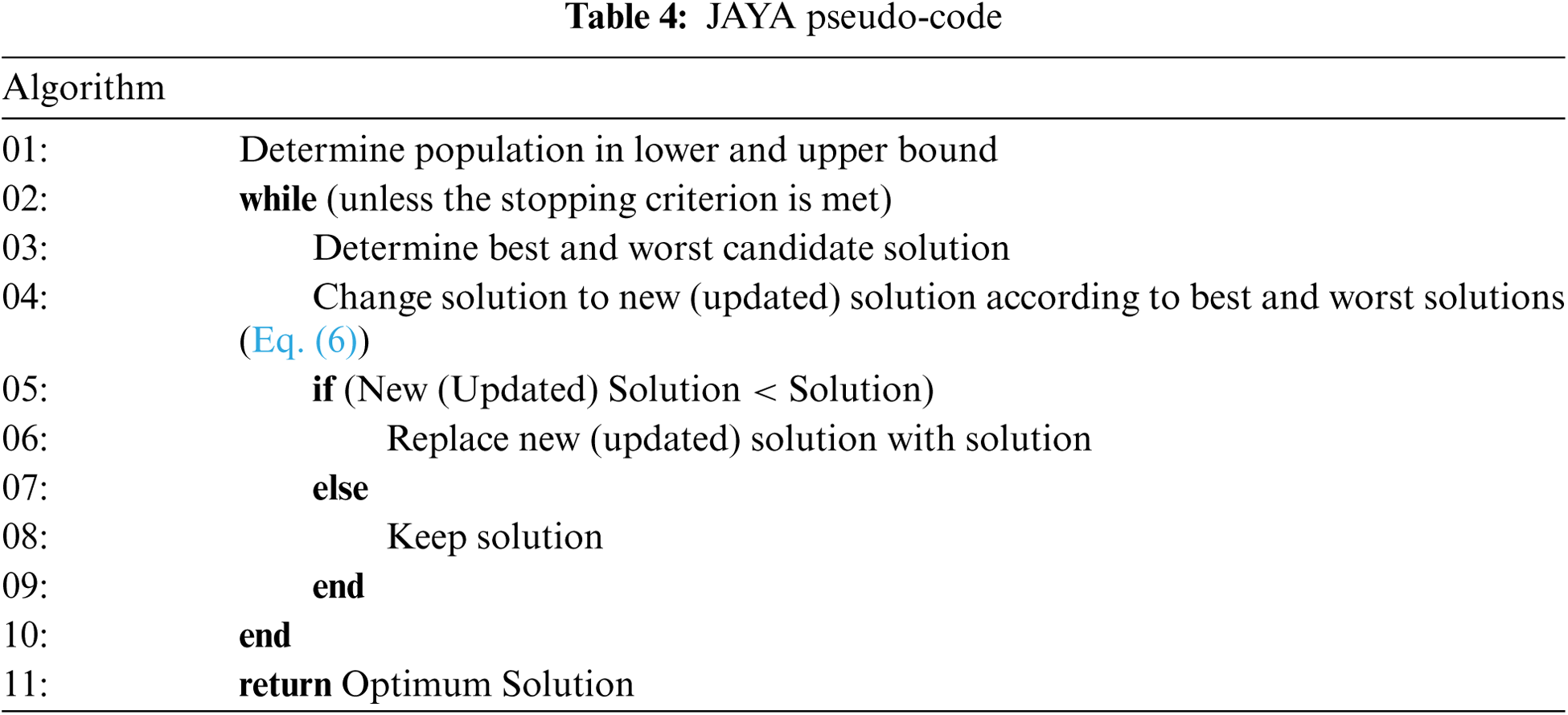
In Section 3 (Proposed Hybrid Approach), information was given about the developed HSSJAYA. Equations, changes and updates of HSSJAYA were tried to be expressed in the best way. Also in this section, there is a detailed pseudo code about HSSJAYA.

In Section 4 (Experimental Results), the solutions obtained by HSSJAYA in unimodal and multimodal benchmark functions were compared with other algorithms and also the results were compared statistically. Many information such as benchmark functions used in the research, search agents, number of iterations, parameters of algorithms used in comparison are also included in this section.

In Section 5 (Conclusions and Future Work), conclusions about the designed HSSJAYA and information that will guide future studies were mentioned.

2  Overview

2.1 SSA

SSA is inspired by salps from the salpedia family, which are structurally similar to jellyfish and live in packs deep in the seas and oceans. At the beginning of this chain, there is a salp in the leader position, and the other salps follow the leader. The leader updates its position relative to food source. The best solution is always in the leader. The salps that follow the leader update their positions relative to each other. SSA, which is easy and simple to implement, is used in many areas, including optimization problems [10,26].

Mirjalili et al. [10] explained the equations used in SSA as follows;

In SSA, the location of salps is located in a d−dimensional search space. N refers search agents. The X matrix where the position of the salps in Nxd size is kept is shown in Eq. (1). Salps are randomly assigned between the lower and upper bounds specified at the beginning.

Xi=[x11x12⋯x1dx21x22…x2d⋮⋮…⋮xN1xN2…xNd](1)

Eq. (2) is used to update the salp position, which is the leader in SSA.

xj1={Fj+c1((ubj−lbj)c2+lbj)c3≥0Fj−c1((ubj−lbj)c2+lbj)c3<0(2)

According to this equation, if i==1, xji shows the position information of the leader salp in the jth dimension, Fj indicates the best solution (food source) of jth dimension. The terms ub and lb refer to the lower and upper limits of the jth dimension. The term c1, which is important for the food source, is calculated according to the equation contained in Eq. (3).

c1=2e−(4itMax_it)2(3)

According to the Eq. (3), the value e shows the number e, the value it shows the current iteration value, and the Max_it shows the maximum number of iterations. According to the literature, the coefficents ​​of c2 and c3 represent random values between 0 and 1. This means that the value of c3 will never fall below zero, and it means that the equation in the c3<0 proposition in Eq. (2) cannot be calculated at all. Ahmed et al. [27], Singh et al. [28] and Faris et al. [29] in their studies, they wrote an equation in which the leader position can be updated according to the situation where the value of c3 can be between 0 and 1, which is shown in Eq. (4).

xj1={Fj+c1((ubj−lbj)c2+lbj)c3≥0.5Fj−c1((ubj−lbj)c2+lbj)c3<0.5(4)

The mathematical expression required to update the position of the salps following the leader is contained in Eq. (5).

xji=12(xji+xji−1)(5)

Tab. 1 contains the pseudo-code of the SSA. In this pseudo-code, the leader is based on a single leader when updating the salp position [10].

In the literature review, if the single leader salp is selected as multiple, the randomness of the algorithm can be increased. This increase affects the stability of the algorithm as a disadvantage, if it is desired to increase the randomness and keep its stability in a balanced state. It has been stated that half of the search agents (N) should be chosen as the leader (N/2) and the other half (N/2) as the follower [30,31]. In addition, when the leader and follower position updates in the codes written by the developers of SSA are examined, it is seen that half of the search agents are leaders and the other half are followers [32,33]. According to the explanations written above, the pseudo-code of SSA is shown in Tab. 2. In our research, the pseudo-code in Tab. 2 was taken as the basis in SSA and HSSJAYA.

2.2 Jaya

JAYA, which means victory in Sanskrit developed by Rao [11], does not have its own extra parameters compared to other optimization algorithms. There are best and worst solutions in this algorithm. It is an algorithm that tries to get as close as possible to the best solution and as far away as possible from the worst solution. In this algorithm, which is easy and simple to implement, the basic parameters are very few. Rao [11] describes the solution updates according to Eq. (6) as follows;

uj,k,i′=uj,k,i+r1,j,i(uj,best,i−|uj,k,i|)−r2,j,i(uj,worst,i−|uj,k,i|)(6)

The terms ​​in Eq. (6) are expressed in Tab. 3 as follows;

r1,j,i(uj,best,i−|uj,k,i|) in equation describes the state of the solution approaching the best solution. −r2,j,i(uj,worst,i−|uj,k,i|) describes the state of the solution moving away from the worst solution. Tab. 4 contains the pseudo-code of Jaya.

3  Proposed Hybrid Approach

Metaheuristic algorithms aim to find global or close to optimal solutions at a reasonable computational cost. By using the global optimum search feature of the salp swarm algorithm and the success of the jaya algorithm in reaching the best solution, a hybrid algorithm that achieves the best result faster than traditional metaheuristic algorithms is aimed.

In SSA, salps update their positions according to the source of the food. During this update, leader and follower salps try to be closest to the food source. Positions that do not give good results in SSA do not have any effect on the calculations. In JAYA, the best and worst candidates are the solutions. These obtained solutions are used to calculate the new solution.

The hybrid algorithm is based on SSA's leader and follower salp system and JAYA's best and worst solution part. HSSJAYA works according to the best and worst food source positions. The best food source refers to the position that the leader and follower salps should reach; the worst food source refers to the position that the leader and follower salps should not reach. When calculating the best food source position, the values obtained from the worst food source position are also included in the calculation. In this way, it is thought that the leader-follower salps will find the best solution to reach the food source. HSSJAYA algorithm has been developed based on the SSA given pseudo code in Tab. 2. The equations developed for HSSJAYA and the descriptions of these equations are as follows.

In HSSJAYA, as in SSA, the location of salps is located in a d−dimensional search space. N refers to search agents. Eq. (7) contains the X matrix in which the position of the salps in Nxd size is kept. Salps are randomly assigned between the lower and upper bounds specified initially.

Xi=[x11x12⋯x1dx21x22…x2d⋮⋮…⋮xN1xN2…xNd](7)

In Eqs. (8)–(10), the d−dimensional best food source, worst food source and new candidate solution positions are defined respectively.

BFPi=bfp1bfp2…bfpd(8)

WFPi=wfp1wfp2…wfpd(9)

Ui′=u1′u2′…ud′(10)

Obtaining a new candidate solution contained in JAYA will be performed in HSSJAYA, as in Eq. (11).

uj′=xji+bwfr(r1i,j(bfpj−|xji|)−r2i,j(wfpj−|xji|))(11)

The terms ​​in Eq. (11) are expressed in Tab. 5 as follows;

bwfr is calculated according to Eq. (12);

bwfr=bfpfv/(bfpfv+wfpfv)(12)

In the equation, bfpfv is the best food fitness value; wfpfv, on the other hand, represents the worst food fitness value. Before the leader and follower salps update the position, the position of the salps is updated according to Eq. (13).

xji=xji−uj′(13)

Updating the leading salp in the HSSJAYA algorithm, provided i≤N/2, is shown in Eq. (14).

xji={bfpj+c1((ubj−lbj)c2+lbj)c3≥0.5bfpj−c1((ubj−lbj)c2+lbj)c3<0.5(14)

The difference of this equation from the position update of the leader salp in SSA is that instead of Fj (food position in the jth dimension), bfpj (the best food position in the jth dimension) is located. Except for the coefficent c1, other coefficents and terms (ubj, lbj, c2, c3) are used as contained in the SSA. There are studies in the literature in which SSA coefficients were used by changing them. One of them is the perturbation weight salp swarm algorithm developed by Fan et al. [34] who proposed a new c1 and c2 value, leader and follower position update technique according to the perturbation weight mechanism. The equation prepared by Fan et al. [34] for c1 is shown in Eq. (15). The value t refers to the iteration; the value T refers to the maximum iteration and u1 refers to the number between 0 and 1.

c1new=u1(1−tT)(15)

In this study, we also made changes to the original c1 coefficient by adding a new parameter and obtained a new c1 coefficient shown in Eq. (16).

c1=iv2e−(4itMax_it)2(16)

The iv value (0 < iv < 1) contained in Eq. (16) is the improvement value of c1, which performs the update process by reducing the difference between positions when updating the leader's position. In the analysis conducted, it was found that the hybrid algorithm gives better results in this way. The iv value is not random; it was considered more appropriate to assign it as a fixed parameter so that researchers who will use the hybrid algorithm can change it at the above-mentioned intervals depending on the type of problems to be solved.

Finally, the equation required for updating the positions of the follower salps in HSSJAYA, provided that it is between i>N/2 and i≤N, is the same as the equation in Eq. (5) used in updating the positions of the follower salps in SSA. In order to update the positions of the leader and follower salps correctly, xji is transposed and processed. After the update process is completed, the positions are restored by transposing again. The pseudo code of HSSJAYA is shown in Tab. 6.

4  Experimental Results

In order to measure the performance of the developed algorithm, some analysis must be performed. In this section, analyzes made with HSSJAYA are included. The hybrid algorithm has been used in solving unimodal and multimodal benchmark functions. The results obtained were compared with the popular CS, GA, FFA algorithms, primarily the SSA and JAYA algorithms that make up the hybrid algorithm. All algorithms have equal number of independent runs, equal search agent, equal iteration. For all algorithms, each operation was run independently 30 times; the number of search agents used in each run was set to 30 and the number of iterations was set to 100.

HSSJAYA has been created by writing in Python (version 3.6). In the study, Evolopy framework was used. The Evolopy framework is an easy-to-use framework developed for optimization problem solving, artificial neural network training, attribute selection, clustering operations [35–37].

Algorithms can include special parameters. These parameters can take constant values and can take different values according to the problem being studied. The iv parameter of HSSJAYA was accepted as 0.1. For the parameter values of other algorithms, the values in the Evolopy Framework were used [33].

In addition, the methods to be used in the comparison between algorithms are included in the subheadings of this section.

4.1 Results of Benchmark Functions

HSSJAYA and other algorithms have optimized a total of 35 benchmark functions, including 14 unimodal and 21 multimodal. In the optimization process, attention was paid to the criteria in Section 4. In order to better compare the results of the algorithms, the results were normalized from between 0 and 1 [10]. Tab. 7 contains the unimodal and multimodal benchmark functions used in the study. In this table, a few benchmark functions; Although it is mentioned as both unimodal and multimodal in the literature, it has been used by choosing one of the unimodal or multimodal types according to the type it is used most frequently [38–43].

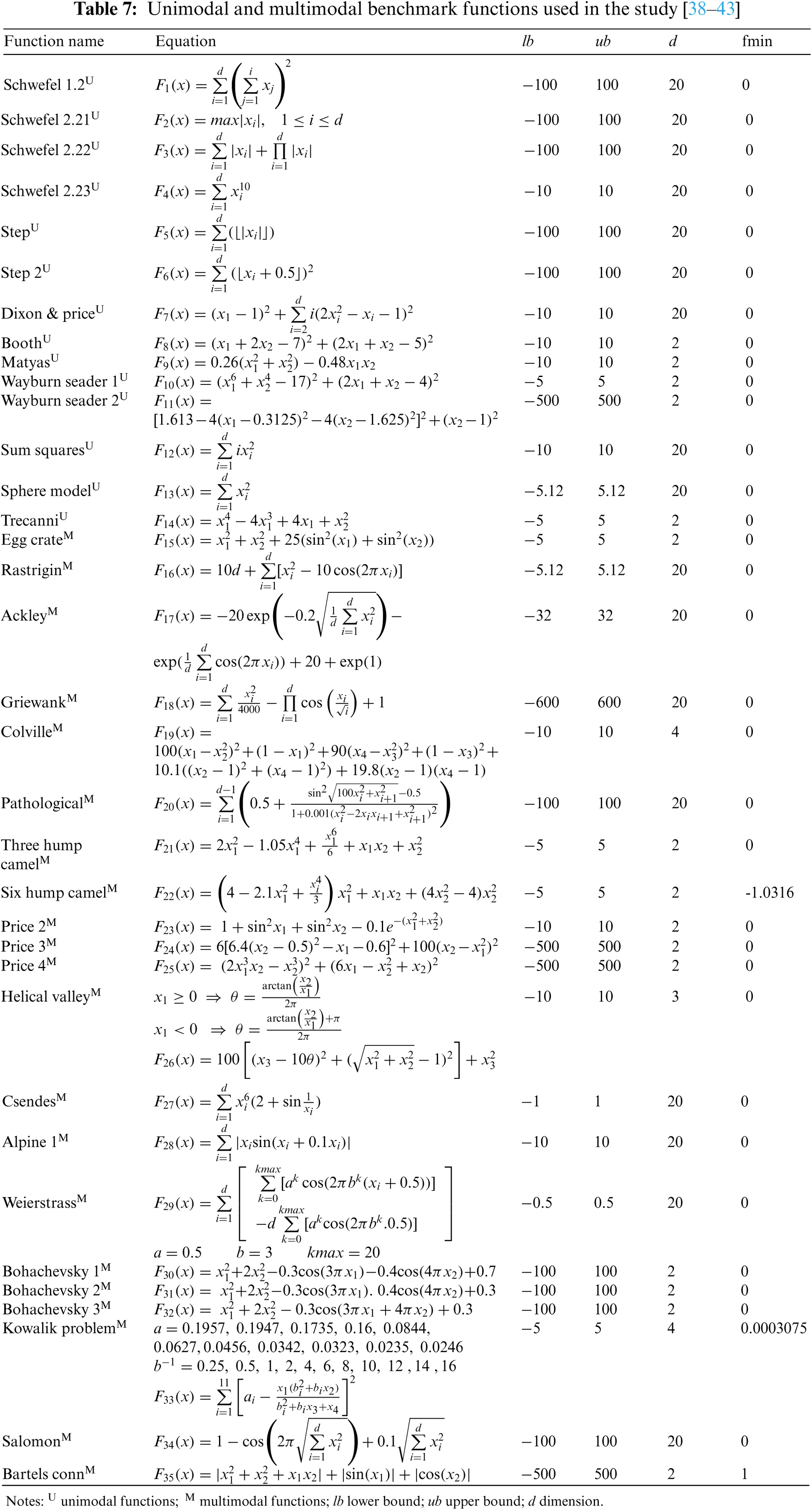
Mean and standard deviation values of benchmark functions according to algorithms are shown in Tab. 8. If the mean and standard deviation values in this table are examined, it is seen that HSSJAYA gets better mean and standard deviation values in most benchmark functions than other algorithms. In addition, the mean convergence curves of some benchmark functions optimized by HSSJAYA are given in Fig. 1.

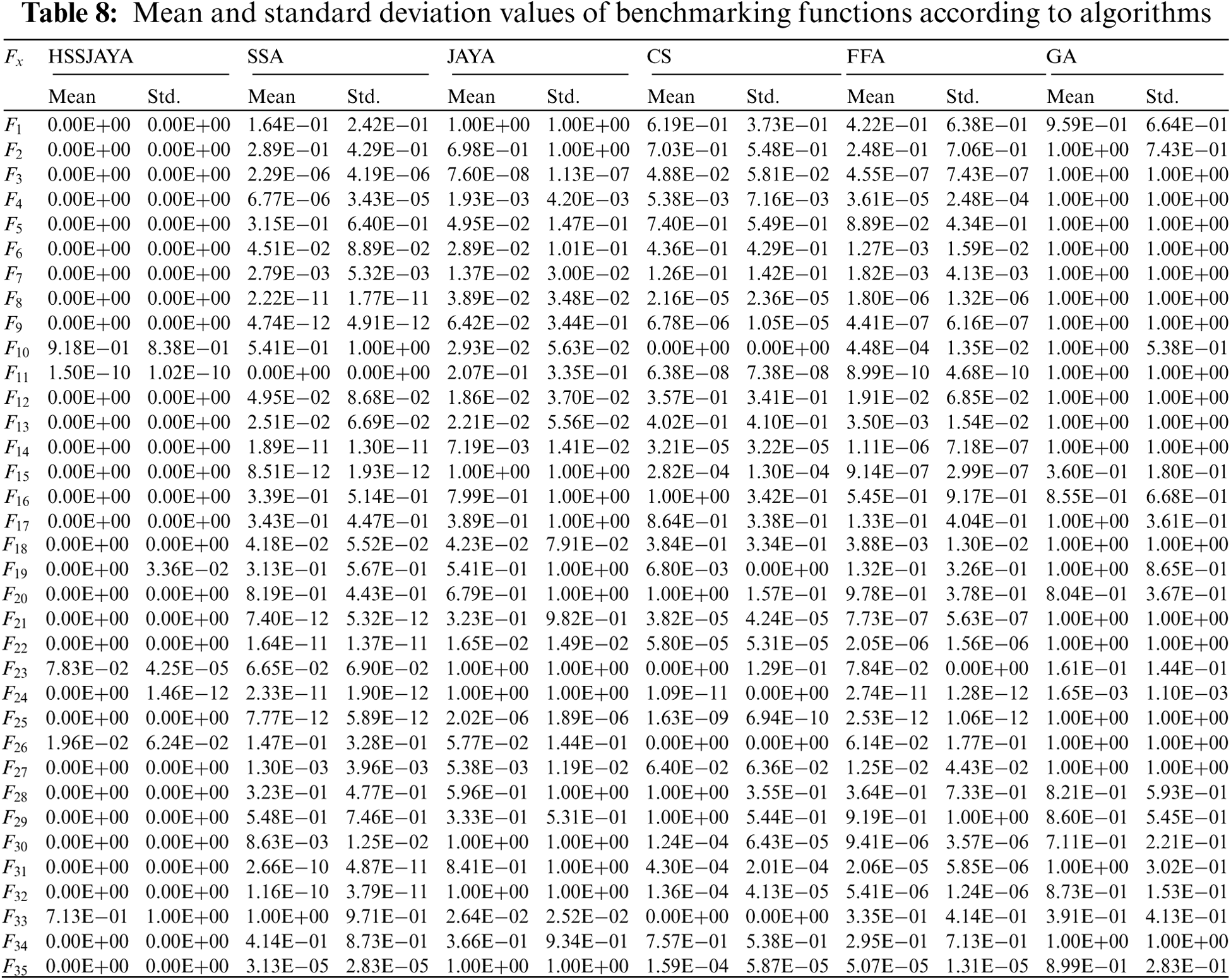
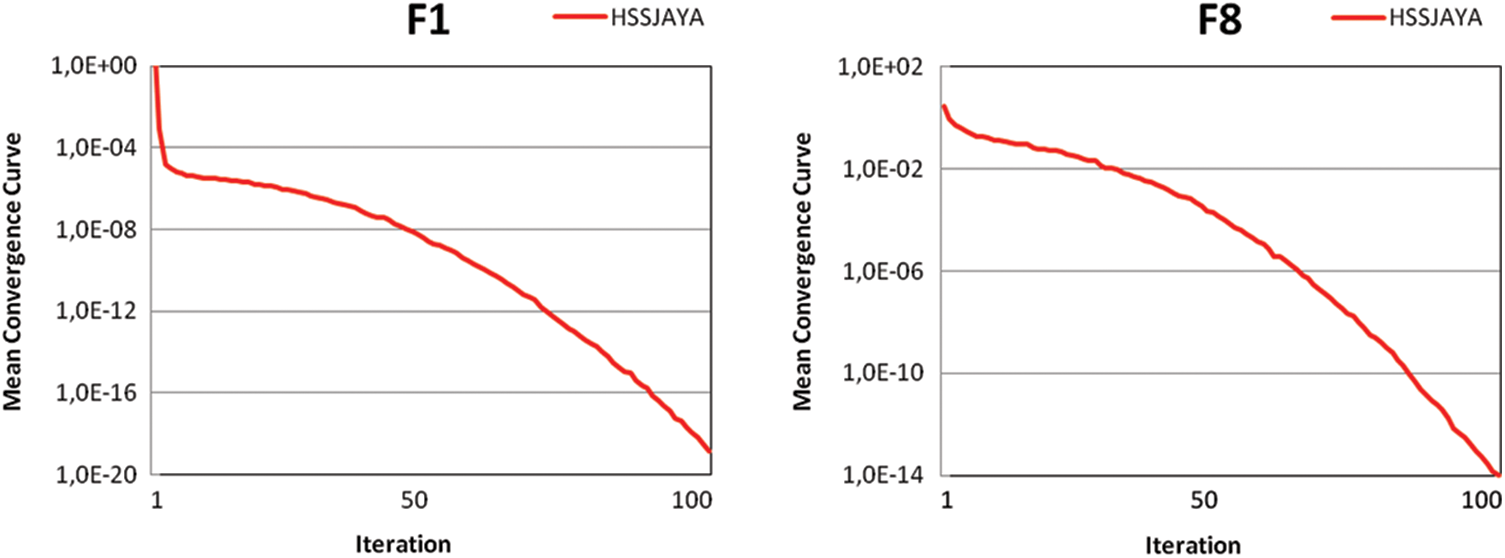
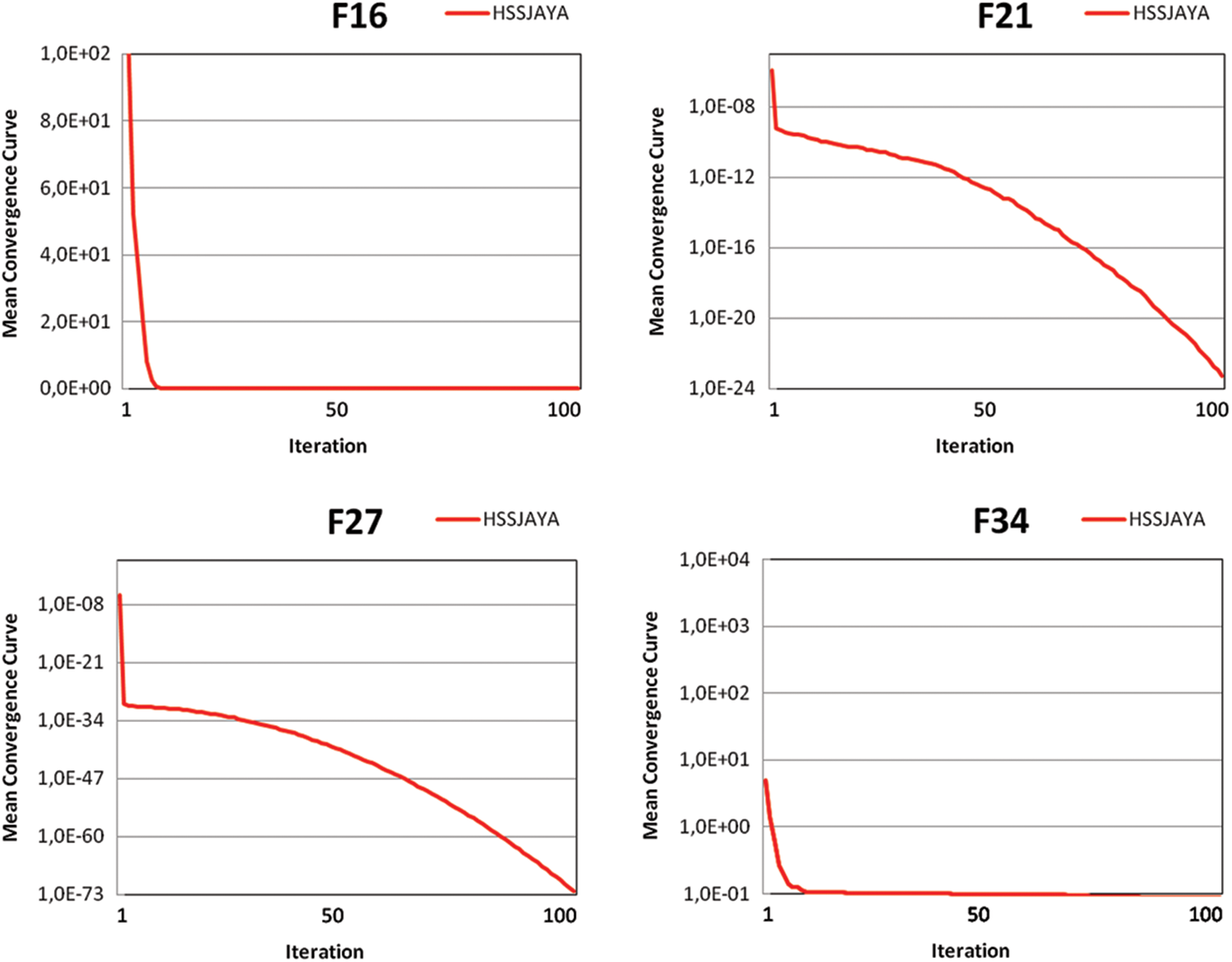
Figure 1: Mean convergence curves for some functions optimized with HSSJAYA

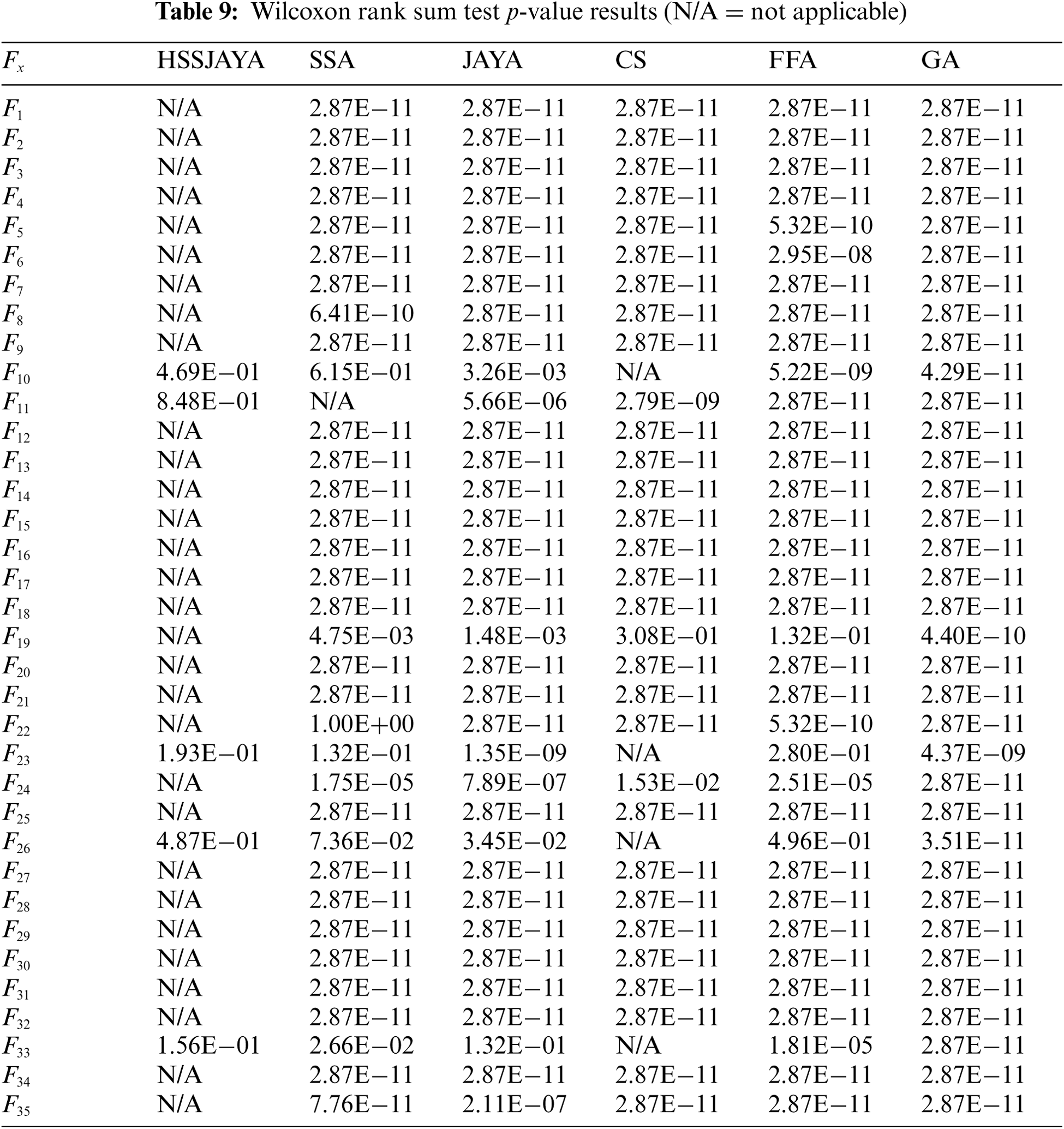
Although HSSJAYA appears to be successful in the optimization of unimodal and multimodal benchmark functions, statistically it is necessary to prove that the algorithm is successful. For this reason, the wilcoxon rank sum test, which is one of the data analysis tests, was applied and the p value was considered less than 0.05 (5E−02) in order to express a statistically significant difference. In each statistical test, the best algorithm was compared with the other algorithm [11,44]. The results of the wilcoxon rank sum test are given in Tab. 9. When the results are examined, it is seen that the hybrid algorithm creates statistically significant differences in unimodal and multimodal benchmark functions and is successful.

5  Conclusions and Future Work

HSSJAYA was inspired by SSA's method of reaching the nutrient of salps and JAYA's method of reaching the desired solution through the best and worst candidate solutions. In other words, a hybrid algorithm has been developed in which the leader salp and the follower salp can reach the food more successfully and efficiently by calculating the positions of the salps that are far/should not reach (worst food solution) and close/should (best food solution) reach the food.

Proposed HSSJAYA appears to be successful in optimization of benchmark functions. HSSJAYA achieved the best mean results in 30 out of 35 benchmark functions compared to other algorithms. Our study is also statistically successful. It has been determined that the hybrid algorithm creates statistically significant differences in most results compared to other algorithms. Other factors in the success of HSSJAYA are due to elements such as the algorithm structure developed, new equations and parameters added. According to these results, it has been proven that HSSJAYA is successful in solving benchmark problems according to the algorithms with which it is compared.

HSSJAYA has been tested by the number of trials, search agents and iterations in the optimization of benchmark functions. It is recommended that it be tested with different number of trials, search agents and iterations, and also using it in different problems or artificial intelligence techniques apart from the problems in the study.

By selecting algorithms that work well in their field from among the metaheuristic algorithms created or developed by researchers. It is believed that new hybrid algorithms will be developed that will give better results if they are hybridized with HSSJAYA developed in our study.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  S. Mukhopadhyay and S. Das, “A system on chip development of customizable GA architecture for real parameter optimization problem,” In: J. K. Mandal, S. Mukhopadhyay and T. Pal (Eds.Handbook of Research on Natural Computing for Optimization Problems, Hershey, PA: IGI Global, pp. 66–102, 2016. [Google Scholar]

 2.  S. Sieniutycz, “Systems design: Modeling, analysis, synthesis, and optimization,” in Complexity and Complex Thermo-Economic Systems, Amsterdam, Netherlands: Elsevier, pp. 85–115, 2020. [Google Scholar]

 3.  X.-S. Yang, “Engineering optimization,” in Engineering Optimization: An Introduction with Metaheuristic Applications, Hoboken, NJ: Wiley, pp. 15–28, 2010. [Google Scholar]

 4.  Ç. Sel, “Genel atama problemlerinin çözümünde deterministik, olasılık temelli ve sezgisel yöntemlerin uygulanması,” M.S. thesis, A Graduate School of Natural and Applied Sciences, Ankara University, Turkey, pp. 8–24, 2013. [Google Scholar]

 5.  T. Keskintürk, “Diferansiyel gelişim algoritması,” İstanbul Ticaret Üniversitesi Fen Bilimleri Dergisi, vol. 5, no. 9, pp. 85–99, 2006. [Google Scholar]

 6.  D. Gupta and V. Gupta, “Test suite prioritization using nature inspired meta-heuristic algorithms,” in Int. Conf. on Intelligent Systems Design and Applications ISDA 2016, Springer, Cham, Porto, Portugal, pp. 216–226, 2016. [Google Scholar]

 7.  S. Mirjalili, S. M. Mirjalili and A. Lewis, “Grey wolf optimizer,” Advances in Engineering Software, vol. 69, pp. 46–61, 2014. [Google Scholar]

 8.  X.-S. Yang and S. Deb, “Cuckoo search via lévy flights,” in 2009 World Congress on Nature & Biologically Inspired Computing (NaBICCoimbatore, India, IEEE Publications, USA, pp. 210–214, 2009. [Google Scholar]

 9.  X. -S. Yang, “Firefly algorithm, stochastic test functions and design optimisation,” International Journal of Bio-Inspired Computation, vol. 2, no. 2, pp. 78–84, 2010. [Google Scholar]

10. S. Mirjalili, A. H. Gandomi, S. Z. Mirjalili, S. Saremi, H. Faris et al., “Salp swarm algorithm: A bio-inspired optimizer for engineering design problems,” Advances in Engineering Software, vol. 114, pp. 163–191, 2017. [Google Scholar]

11. R. V. Rao, “Jaya: A simple and new optimization algorithm for solving constrained and unconstrained optimization problems,” International Journal of Industrial Engineering Computations, vol. 7, no. 1, pp. 19–34, 2016. [Google Scholar]

12. T. Dede, M. Grzywiński and R. V. Rao, “Jaya: A new meta-heuristic algorithm for the optimization of braced dome structures,” In: R. V. Rao and J. Taler (Eds.Advanced Engineering Optimization Through Intelligent Techniques. Advances in Intelligent Systems and Computing, Singapore: Springer, vol. 949, pp. 13–20, 2020. [Google Scholar]

13. J. H. Holland, “Genetic algorithms,” Scientific American, vol. 267, no. 1, pp. 66–72, 1992. [Google Scholar]

14. X. -S. Yang, S. Deb, S. Fong, X. He and Y. Zhao, “From swarm intelligence to metaheuristics: Nature-inspired optimization algorithms,” Computer, vol. 49, no. 9, pp. 52–59, 2016. [Google Scholar]

15. A. Ehsan and Q. Yang, “Optimal integration and planning of renewable distributed generation in the power distribution networks: A review of analytical techniques,” Applied Energy, vol. 210(C), pp. 44–59, 2018. [Google Scholar]

16. F. A. Şenel, F. Gökçe, A. S. Yüksel and T. Yiğit, “A novel hybrid PSO–GWO algorithm for optimization problems,” Engineering with Computers, vol. 35, pp. 1359–1373, 2019. [Google Scholar]

17. T. O. Ting, X. -S. Yang, S. Cheng and K. Huang, “Hybrid metaheuristic algorithms: Past, present, and future,” In: X.-S. Yang (Ed.Recent Advances in Swarm Intelligence and Evolutionary Computation. Studies in Computational Intelligence, Cham: Springer, vol. 585, pp. 71–83, 2015. [Google Scholar]

18. F. J. Rodriguez, C. Garcia-Martinez and M. Lozano, “Hybrid metaheuristics based on evolutionary algorithms and simulated annealing: Taxonomy, comparison, and synergy test,” IEEE Transactions on Evolutionary Computation, vol. 16, no. 6, pp. 787–800, 2012. [Google Scholar]

19. S. Li, Y. Yu, D. Sugiyama, Q. Li and S. Gao, “A hybrid salp swarm algorithm with gravitational search mechanism,” in 2018 5th IEEE Int. Conf. on Cloud Computing and Intelligence Systems (CCISNanjing, China, pp. 257–261, 2018. [Google Scholar]

20. N. Singh, L. H. Son, F. Chiclana and J.-P. Magnot, “A new fusion of salp swarm with sine cosine for optimization of non-linear functions,” Engineering with Computers, vol. 36, no. 1, pp. 185–212, 2020. [Google Scholar]

21. R. H. Caldeira and A. Gnanavelbabu, “Solving the flexible job shop scheduling problem using an improved jaya algorithm,” Computers & Industrial Engineering, vol. 137, article 106064, 2019. [Google Scholar]

22. M. Khamees, A. Albakry and K. Shaker, “Multi-objective feature selection: Hybrid of salp swarm and simulated annealing approach,” in Int. Conf. on New Trends in Information and Communications Technology Applications NTICT 2018, Baghdad, Iraq, pp. 129–142, 2018. [Google Scholar]

23. M. Aslan, M. Gunduz and M. S. Kiran, “Jayax: Jaya algorithm with xor operator for binary optimization,” Applied Soft Computing Journal, vol. 82, article 105576, 2019. [Google Scholar]

24. R. A. Ibrahim, A. A. Ewees, D. Oliva, M. A. Elaziz and S. Lu, “Improved salp swarm algorithm based on particle swarm optimization for feature selection,” Journal of Ambient Intelligence and Humanized Computing, vol. 10, pp. 3155–3169, 2019. [Google Scholar]

25. J. -F. Chen, Q. H. Do and H.-N. Hsieh, “Training artificial neural networks by a hybrid PSO-CS algorithm,” Algorithms, vol. 8, no. 2, pp. 292–308, 2015. [Google Scholar]

26. P. A. V. Anderson and Q. Bone, “Communication between individuals in salp chains. II. physiology,” Proceedings of the Royal Society of London B: Biological Sciences, vol. 210, no. 1181, pp. 559–574, 1980. [Google Scholar]

27. S. Ahmed, M. Mafarja, H. Faris and I. Aljarah, “Feature selection using salp swarm algorithm w ith chaos,” in Proc. of the 2nd Int. Conf. on Intelligent Systems, Metaheuristics & Swarm Intelligence (ISMSI ‘18Phuket, Thailand, pp. 65–69, 2018. [Google Scholar]

28. N. Singh, S. B. Singh and E. H. Houssein, “Hybridizing salp swarm algorithm with particle swarm optimization algorithm for recent optimization functions,” Evolutionary Intelligence, pp. 1–34, 2020. https://doi.org/10.1007/s12065-020-00486-6. [Google Scholar]

29. H. Faris, S. Mirjalili, I. Aljarah, M. Mafarja and A. A. Heidari, “Salp swarm algorithm: Theory, literature review, and application in extreme learning machines,” In: S. Mirjalili, J. Song Dong and A. Lewis (Eds.Nature-Inspired Optimizers. Studies in Computational Intelligence, Cham: Springer, vol. 811, pp. 185–199, 2020. [Google Scholar]

30. Q. Zhang, H. Chen, A. A. Heidari, X. Zhao, Y. Xu et al., “Chaos-induced and mutation-driven schemes boosting salp chains-inspired optimizers,” IEEE Access, vol. 7, pp. 31243–31261, 2019. [Google Scholar]

31. D. Wang, Y. Zhou, S. Jiang and X. Liu, “A simplex method-based salp swarm algorithm for numerical and engineering optimization,” in Int. Conf. on Intelligent Information Processing (IIP 2018Nanning, China, pp. 150–159, 2018. [Google Scholar]

32. S. Mirjalili, “SSA: Salp swarm algorithm, mathworks,” 2018. [Online]. Avaliable: https://www.mathworks.com/matlabcentral/fileexchange/63745-ssa-salp-swarm-algorithm. [Google Scholar]

33. H. Faris, R. Qaddoura, I. Aljarah, J. W. Bae, M. M. Fouad et al., “Evolopy, github,” 2016 (SSA was added in 2018). [Online]. Avaliable: https://github.com/7ossam81/EvoloPy/blob/master/optimizers/. [Google Scholar]

34. Y. Fan, J. Shao, G. Sun and X. Shao, “A modified salp swarm algorithm based on the perturbation weight for global optimization problems,” Complexity, article 6371085, pp. 17, 2020. [Google Scholar]

35. R. Qaddoura, H. Faris, I. Aljarah and P. A. Castillo, “Evocluster: An open-source nature-inspired optimization clustering framework in python,” in Int. Conf. on the Applications of Evolutionary Computation (Part of EvoStarSeville, Spain, pp. 20–36, 2020. [Google Scholar]

36. R. A. Khurma, I. Aljarah, A. Sharieh and S. Mirjalili, “Evolopy-FS: An open-source nature-inspired optimization framework in python for feature selection,” In: S. Mirjalili, H. Faris and I. Aljarah (Eds.Evolutionary Machine Learning Techniques. Algorithms for Intelligent Systems, Singapore: Springer, pp. 131–173, 2020. [Google Scholar]

37. H. Faris, I. Aljarah, S. Mirjalili, P. A. Castillo and J. J. Merelo, “Evolopy: An open-source nature-inspired optimization framework in python,” in Proc. of the 8th Int. Joint Conf. on Computational Intelligence-ECTA (IJCCI 2016Porto, vol. 1, pp. 171–177, 2016. [Google Scholar]

38. M. Jamil and X.-S. Yang, “A literature survey of benchmark functions for global optimization problems,” International Journal of Mathematical Modelling and Numerical Optimisation (IJMMNO), vol. 4, no. 2, pp. 150–194, 2013. [Google Scholar]

39. K. Hussain, M. N. M. Salleh, S. Cheng and R. Naseem, “Common benchmark functions for metaheuristic evaluation: A review,” JOIV: International Journal on Informatics Visualization, vol. 1, no. 4–2, pp. 218–223, 2017. [Google Scholar]

40. R. Fletcher and M. J. D. Powell, “A rapidly convergent descent method for minimization,” The Computer Journal, vol. 6, no. 2, pp. 163–168, 1963. [Google Scholar]

41. P. N. Suganthan, N. Hansen, J. J. Liang, K. Deb, Y.-P. Chen et al., “Problem definitions and evaluation criteria for CEC 2005, special session on real-parameter optimization,” Technical report, Nanyang Technological University (NTUSingapore and KanGAL Report Number 2005005, 2005. [Google Scholar]

42. A. Gavana, “Global optimization benchmarks and AMPGO, test functions index,” 2013. [Online]. Avaliable: http://infinity77.net/global_optimization/test_functions.html. [Google Scholar]

43. M. K. Naik, L. Samantaray and R. Panda, “A hybrid CS–GSA algorithm for optimization,” In: S. Bhattacharyya, P. Dutta and S. Chakraborty (Eds.Hybrid Soft Computing Approaches. Studies in Computational Intelligence, New Delhi: Springer, vol. 611, pp. 3–35, 2016. [Google Scholar]

44. J. Derrac, S. García, D. Molina and F. Herrera, “A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms,” Swarm and Evolutionary Computation, vol. 1, no. 1, pp. 3–18, 2011. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.