Computers, Materials & Continua DOI:10.32604/cmc.2022.022304
Article

Robust Reversible Audio Watermarking Scheme for Telemedicine and Privacy Protection

Xiaorui Zhang1,2,*, Xun Sun1, Xingming Sun1, Wei Sun3 and Sunil Kumar Jha4

1Engineering Research Center of Digital Forensics, Ministry of Education, Jiangsu Engineering Center of Network Monitoring, School of Computer and Software, Nanjing University of Information Science & Technology, Nanjing, 210044, China
2Wuxi Research Institute, Nanjing University of Information Science & Technology, Wuxi, 214100, China
3Jiangsu Collaborative Innovation Center of Atmospheric Environment and Equipment Technology, Nanjing University of Information Science & Technology, Nanjing, 210044, China
4IT Fundamentals and Education Technologies Applications, University of Information Technology and Management in Rzeszow, Rzeszow Voivodeship, 100031, Poland
*Corresponding Author: Xiaorui Zhang. Email: zxr365@126.com
Received: 02 August 2021; Accepted: 03 September 2021

Abstract: The leakage of medical audio data in telemedicine seriously violates the privacy of patients. In order to avoid the leakage of patient information in telemedicine, a two-stage reversible robust audio watermarking algorithm is proposed to protect medical audio data. The scheme decomposes the medical audio into two independent embedding domains, embeds the robust watermark and the reversible watermark into the two domains respectively. In order to ensure the audio quality, the Hurst exponent is used to find a suitable position for watermark embedding. Due to the independence of the two embedding domains, the embedding of the second-stage reversible watermark will not affect the first-stage watermark, so the robustness of the first-stage watermark can be well maintained. In the second stage, the correlation between the sampling points in the medical audio is used to modify the hidden bits of the histogram to reduce the modification of the medical audio and reduce the distortion caused by reversible embedding. Simulation experiments show that this scheme has strong robustness against signal processing operations such as MP3 compression of 48 db, additive white Gaussian noise (AWGN) of 20 db, low-pass filtering, resampling, re-quantization and other attacks, and has good imperceptibility.

Keywords: Telemedicine; privacy protection; audio watermarking; robust reversible watermarking; two-stage embedding

1  Introduction

With the rapid development of Internet communication technology, telemedicine has received more and more attention in the medical field, and the protection of medical data has become the primary problem to be solved in telemedicine. Traditional robust watermarking [1–5] and fragile/semi-fragile watermarking [6,7] will cause permanent distortion of the medical cover audio when extracting the watermark, which makes the doctor unable to diagnose effectively. As a kind of digital watermark, reversible watermark can effectively protect the integrity, authenticity and privacy of medical data; it uses the redundancy of cover audio to embed watermark such as patient privacy, hospital information into the cover audio. When receiving medical data, the receiving end can recover the data content non-destructively while extracting the watermark information, thereby ensuring the integrity and authenticity of the data, which helps doctors more accurately judge the patient's condition. Reversible image watermarking can be divided into the following categories: based on compression technology [8], based on differential expansion (DE) [9–11], based on histogram shift (HS) [12,13], based on prediction error (PEE) [14–16], and based on integer transformation [17,18].

At present, audio, as an important part of medical data, is widely used in telemedicine. A study by MIT [19] showed that new artificial intelligence (AI) can detect asymptomatic patients with new coronaviruses, only through medical audio such as cough recorded on the phone can be diagnosed. Reversible audio watermarking technology, as a protection scheme for this medical audio, can protect the privacy of patients and the integrity of data without affecting the quality of medical data. According to the different embedded domains of watermarks, reversible audio watermarks can be divided into time domain watermarks [20,21], transform domain watermarks [22] and compressed domain watermarks [23].

However, the reversible audio watermark is generally fragile due to lacking enough robustness, especially, when it is interfered and attacked by noise or signal processing operations, the watermark cannot be accurately extracted. In fact, the telemedicine data is inevitably subject to malicious or unintentional attacks during data transmission. Therefore, robust reversible watermarks have more application scenarios in the field of telemedicine and privacy protection. When the watermarked audio file is not attacked during the telemedicine transmission process, the watermark can be extracted accurately and the original medical cover audio can be restored non-destructively, improving the accuracy of doctor’s diagnosis.

There are two mainstream robust reversible watermarking frameworks, based on two-stage embedding (TSW) [24–27] and based on histogram modification [28,29]. Coltuc et al. [24] proposed an image authentication framework based on a two-stage undistorted watermark. In the first stage, a robust watermark is embedded in the DCT coefficients of the image to obtain an intermediate image, and then the difference between the original image and the intermediate images is reversibly embedded in the intermediate image. This method is robust to JPEG and has a high embedding capacity. But the reversible watermark embedding in the second stage weakens the robustness of the watermark in the first stage. Wang et al. [27] proposed an independent two-stage watermark embedding, where haar wavelet transform is used to decompose the original image into two independent embedding domains. By the method, the watermark is embedded into the low-frequency embedding domain as well as the difference between the original image and the intermediate image are reversibly embedded in the high-frequency embedding domain to restore the original cover. Due to the independence of the two stages, the reversible embedding in the second stage will not affect the robust embedding in the first stage, thereby improving the robustness of the watermark.

At present, Research on robust reversible watermarking on images accounts for the majority. Because images are different from audios in the structure, many image-based robust reversible watermarking scheme cannot be effectively applied to audios. In a robust reversible watermarking framework based on histogram displacement, Xiang et al. [30] proposed a reversible robust audio watermarking scheme based on high-order difference statistics. The original audio was divided into several non-overlapping sub-audios, and the high-order difference statistics model was used to construct a histogram. The histogram is regarded as a robust feature, and the watermark is embedded in the audio file by shifting the histogram. This scheme has strong robustness to MP3 compression and AWGN.

In this paper, we propose a robust reversible audio watermarking for telemedicine and privacy protection, which first divides the medical cover audio into two independent embedding domains by the frequency domain transform function F. Robust watermark is embedded into the low-frequency embedding domain Al to obtain the watermarked low-frequency embedding domain Alw, and then the difference between Al and Alw is reversibly embedded in the high-frequency embedding domain Ah to obtain the watermarked high-frequency embedding domain Ahw. Finally, the inverse transform of the frequency domain transform function F−1 is used to synthesize Alw and Ahw into watermarked audio. In the watermark extraction process, if the watermarked audio is attacked by signal processing operations, the watermark can be extracted correctly to protect medical audio. The watermarked audio obtained by this scheme has good audio quality and strong robustness to noise and signal processing operations.

2  Preparatory Work

This section introduces the preparatory work of robust reversible medical audio watermarking in four parts. First, the method of how to decompose medical cover audio will be introduced. Second, we will introduce how to use the Hurst exponent to determine the appropriate watermark embedding position, improving the imperceptibility of the watermark. Then, the method of constructing histogram to hide the watermark will be introduced. Finally, we will introduce method to prevent overflow after embedding watermarks.

2.1 Decomposition of Medical Cover Audio

First, the original medical cover audio A is divided into several sampling points, denoted as {a1,a2…}. The medical cover audio is decomposed into low-frequency embedding domain Al and high-frequency embedding domain Ah, the transformation function F processes the sampling point pair (a1,a2), as shown as follows.

{al=a1+a22ah=a1−a2 (1)

Among them, al represents the low-frequency embedding domain signal, and ah represents the high-frequency embedding domain signal. This decomposition transform decomposes the original medical audio data A into two half-length sub-audio embedding domains: the low-frequency embedding domain Al and the high-frequency embedding domain Ah. The medical cover audio can be reconstructed by the inverse transformation F−1 by using Eq. (2). The decomposition effect is shown in Fig. 1.

{a1=al+ah2a2=al−ah2 (2)

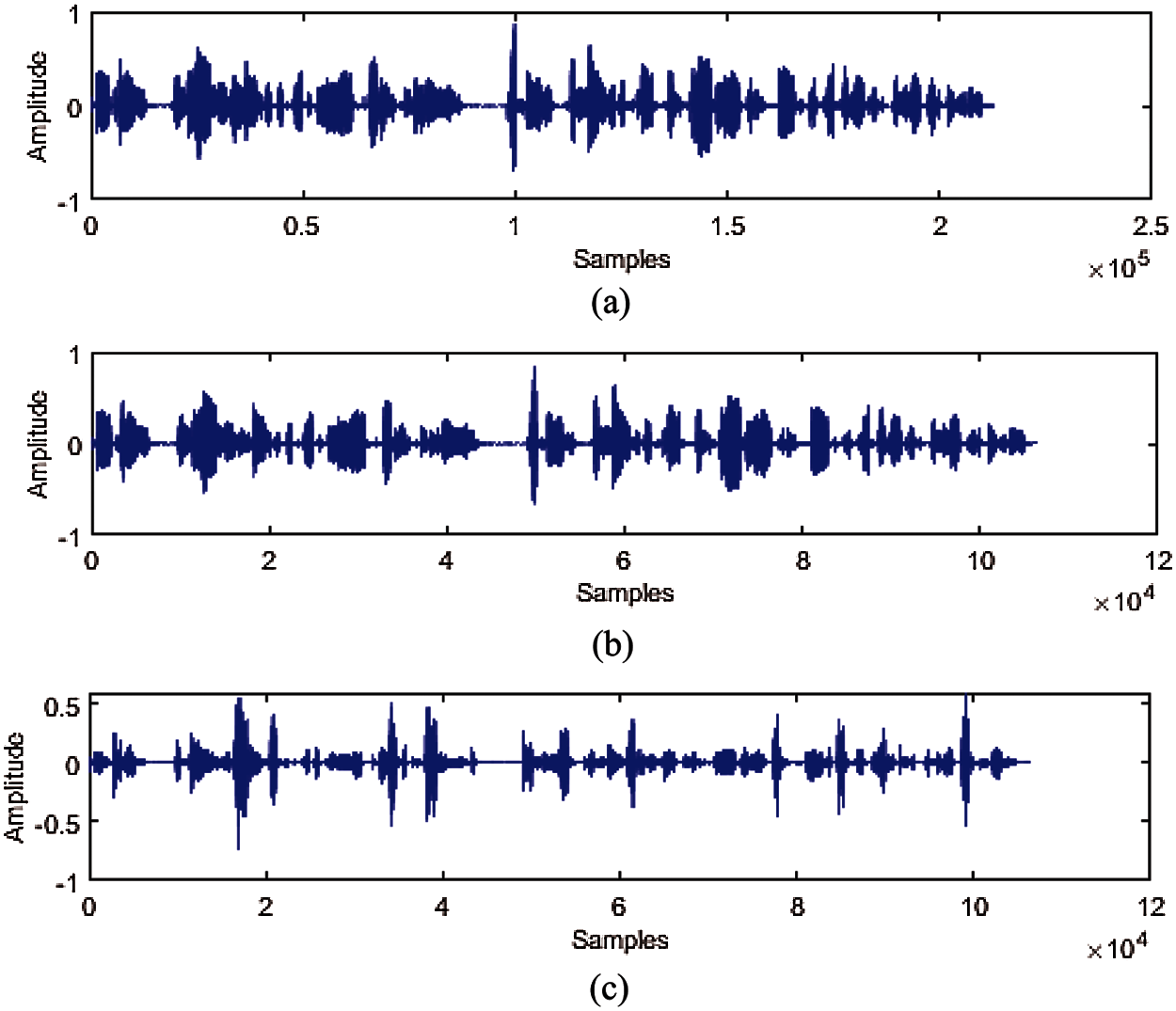
Figure 1: (a) Original medical audio; (b) Decomposed low-frequency embedding domain; (c) Decomposed high-frequency embedding domain

2.2 Hurst Exponent Calculation

In telemedicine, medical audio is a continuous analog signal. Therefore, in the medical audio, the values of adjacent sampling points are generally correlated. Hurst exponent H is an important indicator for judging whether time series data obey random distribution or biased random distribution. The Hurst exponent can be calculated through the range analysis (R/S). The Hurst exponent is proposed by the British hydrologist named H. E. Hurst in 1951. In this paper, the R/S method is used to calculate the Hurst exponent to determine the appropriate watermark embedding position. The specific method is as follows.

The low-frequency embedding domain is decomposed into N non-overlapping sub-audios containing 2n sampling points. For each sub-audios, the statistic t is calculated according to R/S. Thus, the data pair (log⁡ri,log⁡ti)i=1,2,…m is obtained. Take log⁡ri as the independent variable and log⁡ti as the dependent variable to do linear regression, the obtained slope is the Hurst exponent.

When the value of Hurst exponent H falls into the range of (0, 0.5), it implies that the time series has long-term correlation, and the general trend in the future is opposite to the past trend, which is called anti-sustainability: the first period goes up, the next period goes down, and vice versa. Noting that the closer H is to zero, the stronger the negative correlation. When H is equal to 0.5, means that the time series does not have correlation and presents a complete random walk. When H is in the range of (0.5, 1), the general trend of the time series in the future is the same as that in the past, which is called positive continuity. The closer H is to 1, the stronger the positive correlation. When H is 1, the general trend in the future can be predicted by the present, and the time series is a straight line.

Fig. 2 shows the low-frequency embedding domain Al of medical cover audio is divided into several non-overlap sub-audios of the same length. Different sub-audios show different trends. The Hurst exponents of these sub-audios are calculated and displayed in Fig. 2, where the two thresholds H1,H2∈(0,1) of the Hurst exponent are used to determine the embedding position of the watermark towards achieving minimum embedding distortion.

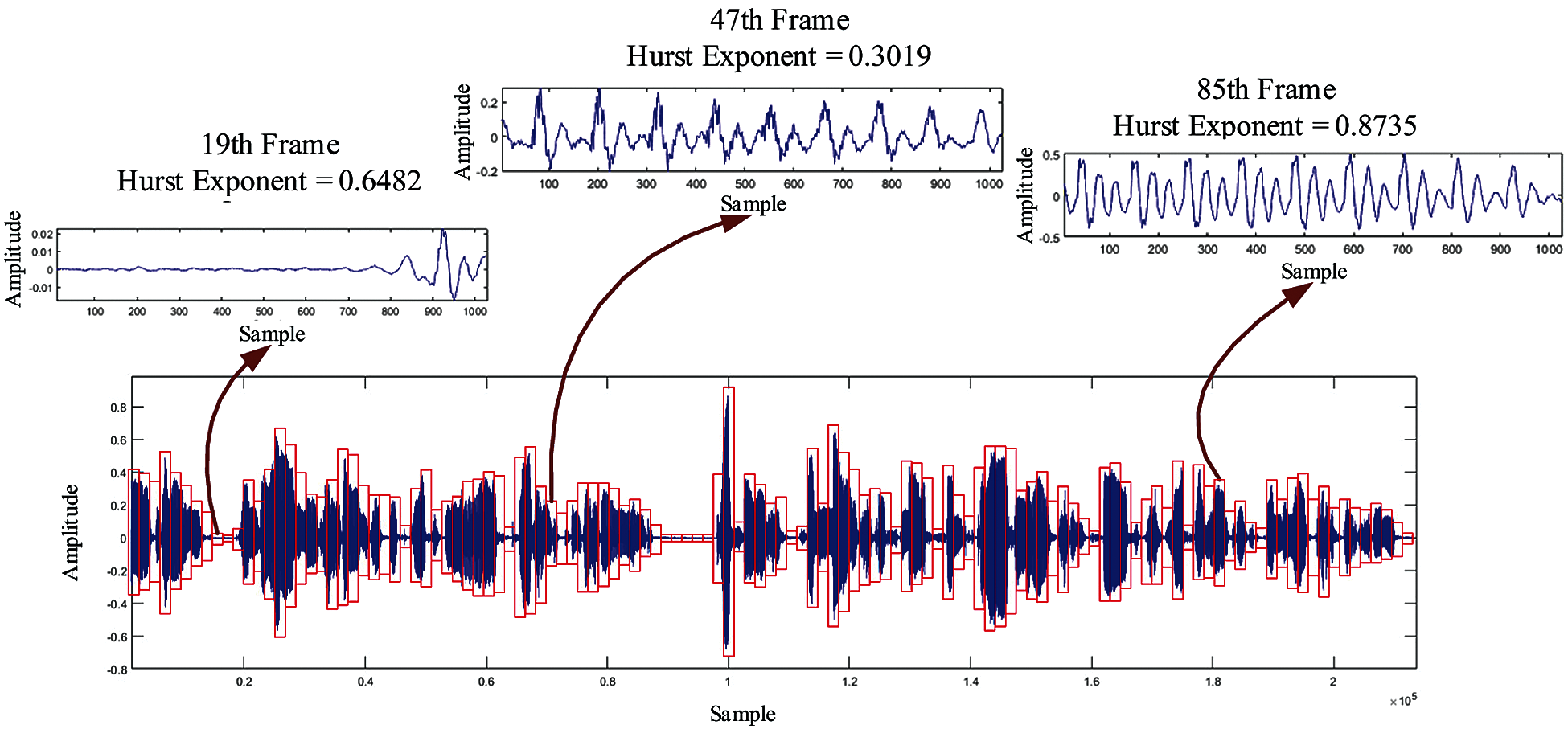
Figure 2: Hurst exponent of different sub-audios in the low frequency embedding domain

2.3 Difference Histogram Shifting

In the second stage of the scheme, the difference between the sampling points is calculated, and the sum of the difference is called the difference statistic. By constructing difference statistics, the correlation between adjacent sampling points can be better utilized. In this paper, the difference statistics model is used to calculate the difference statistics, and then the histogram of the difference statistics is constructed to realize the reversible embedding in the second stage.

For the decomposed high-frequency embedding domain Ah, divide Ah into several non-overlapping sub-audios of equal length. The sampling points in each sub-audio are divided into M groups, and everyone has two sampling points. Let ahp(k,q) represent the q-th sampling point of the k-th sampling point group in the p-th sub-audio, q∈{1,2}; Let dhp(k) represent the difference of the k-th sampling point group of the p-th sub-audio, 1≤k≤M, as show as follows.

dhp(k)=ahp(k,1)−ahp(k,2) (3)

The sum of the difference of all sample points in the p-th sub-audio is called the difference statistic of the sub-audio, denoted as S(p).

S(p)=∑k=1Mdhp(k) (4)

By changing the difference of the k-th sampling point group of the p-th sub-audio, the difference statistic of the p-th sub-audio is changed, so that the watermark is reversibly embedded in it. As shown in Eq. (15).

dhp(k)′=dhp(k)+⌊B+(k−1)M⌋ (5)

In Eq. (5), B represents the shifting quantity of S(p), ⌊x⌋ represents the largest integer without exceeding x, and dhp(k)′ represents the changed value of dhp(k). Because the shifted process is reversible, dhp(k) can be restored. By using Eqs. (4) and (5), the shifted difference statistic S(p)′ of the p-th sub-audio can be obtained.

S(p)′=∑k=1Mdhp(k)′=∑k=1Mdhp(k)+∑k=1M⌊B+(k−1)M⌋=S(p)+B (6)

By shifting the difference statistics dhp(k), the histogram of the difference statistics can be shifted, thereby reversibly embedding the watermark sequence into the sub-audio of the high-frequency embedding domain Ah; Let α(k) be the shifting quantity of dhp(k).

α(k)=⌊B+(k−1)M⌋ (7)

Then dhp(k) is shifted by performing integer transformation on ahp(k,q). The sampling point ahp(k,q) is modified by Eq. (8).

ahp(k,q)′={ahp(k,q)+⌊α(k)2⌋,ifq=1ahp(k,q)−⌊α(k)+12⌋,ifq=2 (8)

where ahp(k,q)′ represents the shifted sampling point. Because the integer transformation is reversible, the original sampling points can be restored after the watermark is extracted.

2.4 Sampling Point Overflow/Underflow

For medical audio data with a sampling depth of 16 bits, the range of the sampling point is [−215,215], and the transformed ahp(k,q)′ may not be in this range, therefore, in the audio the pre-processing is needed to prevent overflow before embedding the watermark. From Eq. (8), we can get.

⌊α(k)2⌋≤|ahp(k,q)′−ahp(k,q)|≤⌊α(k)+12⌋ (9)

And because 1≤k≤M,α(k)=⌊B+(k−1)M⌋, so

⌊α(1)2⌋≤|ahp(k,q)′−ahp(k,q)|≤⌊α(M)∓12⌋ (10)

Define

σ=⌊α(M)+12⌋ (11)

First traverse the sample points containing the watermark, mark the sample values that are not in the range of (−215+σ,215−σ), and then adjust these marked sample points to (−215+σ,215−σ) and record the marked sequence. In actual experiments, due to the large range of sampling point values and small σ, there are few overflow sampling points, which has little impact on audio quality.

3  Proposed Scheme

This section will introduce the embedding process and extraction process of the watermark in detail, including the embedding and extraction of the robust watermark and the embedding and extraction of the reversible watermark. The robust watermark and the reversible watermark are respectively embedded in two different embedding domains of the audio. The medical audio watermark framework is shown in Fig. 3.

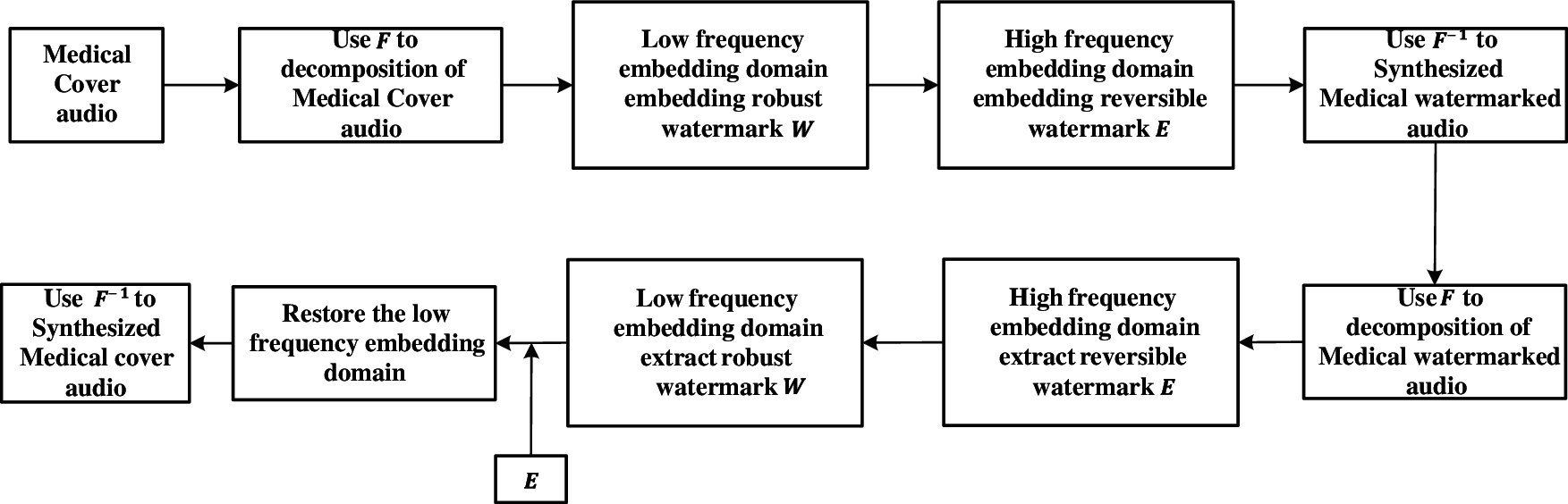
Figure 3: Medical audio watermark frame diagram

3.1 Robust Watermark Embedding

The low-frequency embedding domain Al is divided into several non-overlapping sub-audios with equal length, and the robust watermark is embedded in the sub-audios of Hurst exponent H∈(H1,H2). Every sub-audio contains 2n sampling points, denoted as al(1),al(2),…,al(2n). Define a random mapping relationship {1,2,…,2n}→{φ(1),φ(2),…φ(2n)}, where φ() represents the position sequence of the sampling points after mapping; Define alφ(i) to represent the value of the φ(i)th sampling point in the sub-audio of the low-frequency embedded domain, 1≤i≤2n; every sub-audio is embedded with a 1-bit watermark w∈{0,1}, as shown as follows.

blφ(i)={alφ(i)+(2w−1)(μt−dl2),if 1≤i≤nalφ(i)−(2w−1)(μt+dl2),if n+1≤i≤2n (12)

where blφ(i) represents the φ(i)th sampling point value in the sub-audio of the low-frequency embedding domain after the watermark is embedded, and μ is the watermark embedding strength. In order to ensure the minimum embedded distortion, the minimum masking threshold t is determined by the psychoacoustic model [31]. dl represents the difference between the sample point sets of the two parts before and after the original sub-audio, expressed as.

dl=∑i=1nalφ(i)−∑i=n+12nalφ(i)n (13)

After the watermark is embedded, the sampling point difference dlw of the two parts before and after the sub-audio is modified as Eq. (14).

dlw=∑i=1nblφ(i)−∑i=n+12nblφ(i)n={μt,if w=1−μt,if w=0 (14)

The change of the sampling point may cause overflow. For this reason, it is necessary to mark the sequence of the overflowed sampling points and restore the original sampling point value. In fact, there are few overflow sampling points, which will not affect the extraction of watermark.

3.2 Reversible Embedding

In the reversible embedding stage, the watermarked error E generated by the robust watermark is reversibly embedded into the high-frequency embedding domain as compensation information. Because of the characteristics of reversible watermarking, the high-frequency embedding domain can be restored without loss when extracting compensation information. The watermarked error E consists of four parts: watermark embedding strength μ, Hurst exponent threshold Hϵ{H1,H2}, overflow sampling point mark sequence L, and minimum masking threshold. Let T∈{t(1),t(2)…t(N)}, where N represents the number of sub-audios embedded in the watermark.

The reversible watermark is embedded in the high-frequency embedding domain Ahof the medical audio data A, and Ah is divided into several non-overlapping sub-audios with equal length. The sampling points in each sub-audio are divided into M groups, everyone has two sampling points. Then, calculate the difference statistics of each sub-audio according to Eqs. (3) and (4). Finally, select the secret key T>|S|max, and the movement amount B can be calculated as.

B={T,if S(p)≥0−T,if S(p)<0 (15)

The difference statistic S={S(p)|1≤p≤N}, where N is the number of sub-audios in the high-frequency embedding domain. Then let

α(k)=⌊B+(k−1)M⌋={⌊T+(k−1)M⌋,if S(P)≥0⌊−T+(k−1)M⌋,if S(P)<0 (16)

where k∈[1,M]. According to Eqs. (6) and (8), the sampling point ahp(k,q) in the p-th sub-audio is be modified, and the reversible watermark is embedded into high-frequency embedding domain. Finally, the watermarked high-frequency embedding domain Ahw is obtained.

3.3 Watermark Extracting

Robust reversible audio watermarking can correctly extract and restore medical audio data non-destructively if the watermarked medical audio is not attacked during the telemedicine transmission process. The watermark can still be extracted if the watermarked medical audio is attacked.

In the process of watermark extraction, the frequency domain transform function F is used to decompose the medical audio into two independent embedding domains. If the medical audio is not attacked, the high-frequency embedding domain Ahw of watermark is divided into several non-overlapping domains. For sub-audios with equal length, the sampling points in each sub-audio are divided into M groups, with two sampling points in each group. Next, according to Eqs. (3) and (4), the difference statistic S(p)′ will be calculated, and the p-th sub-audio of the watermark is extracted by the key T by Eq. (17).

w(p)={0,if S(p)′∈(−T,T)1,if S(p)′∈(−2,T)∪(T, 2T) (17)

In the process of extracting the robust watermark, the low-frequency embedding domain Alw of watermark is divided into several non-overlapping sub-audios with equal length. Each sub-audio contains 2n sampling points. The Hurst exponent H∈(H1,H2) is selected. For sub-audios, calculate the difference dlw of the sample point set of the two parts before and after the sub-audio, and extract the watermark through the following as.

w={1,if dlw>00,if dlw<0 (18)

The original low-frequency embedding domain is restored to:

alφ(i)={blφ(i)−(2w−1)(μ−dl2),if 1≤i≤nblφ(i)+(2w−1)(μ+dl2),if n+1≤i≤2n (19)

If the watermarked medical audio data is attacked, the original medical audio data cannot be recovered, but according to Eq. (18), robust watermark can still be extracted.

4  Experimental Results

This section will evaluate the performance of the proposed. The audio data used is taken from LJ Speech Dataset. The selected speech signals are evenly distributed across all age groups and genders. Using 16 bits of audio data as test data to carry out the following experiments. Use Signal-to-Noise Ratio (SNR) to evaluate the imperceptibility of watermarked medical audio. The larger is the SNR, the better is the imperceptibility. The SNR evaluation method is as follows.

SNR=10×lg∑t=1LA(t)2∑t=1L[A(t)−Aw(t)]2 (20)

where L represents the length of the medical audio data A, A(t) represents the value of the t-th sampling point in A, and Aw(t) represents the value of the t-th sampling point in the watermarked medical audio Aw. The accuracy of the watermark and the robustness of the algorithm are evaluated by calculating the bit error rate (BER) of the extracted watermark. The lower is the BER, the higher is the accuracy of the watermark and the stronger is the robustness of the algorithm. The BER is calculated as follows.

BER=WeWc (21)

In Eq. (21), We represents the extracted wrong watermark, and Wc represents the original watermark. The experimental results are shown in Fig.4. Fig. 4a represents the original audio, and Fig. 4b represents the audio after the watermark is embedded, and the SNR is 38.50 db. When the audio is not attacked, the watermark is extracted and the original medical audio is restored, as shown in Fig. 4c, the SNR is +∞. The BER of the extracted watermark is 0, which proves that the watermark can be extracted accurately without being attacked.

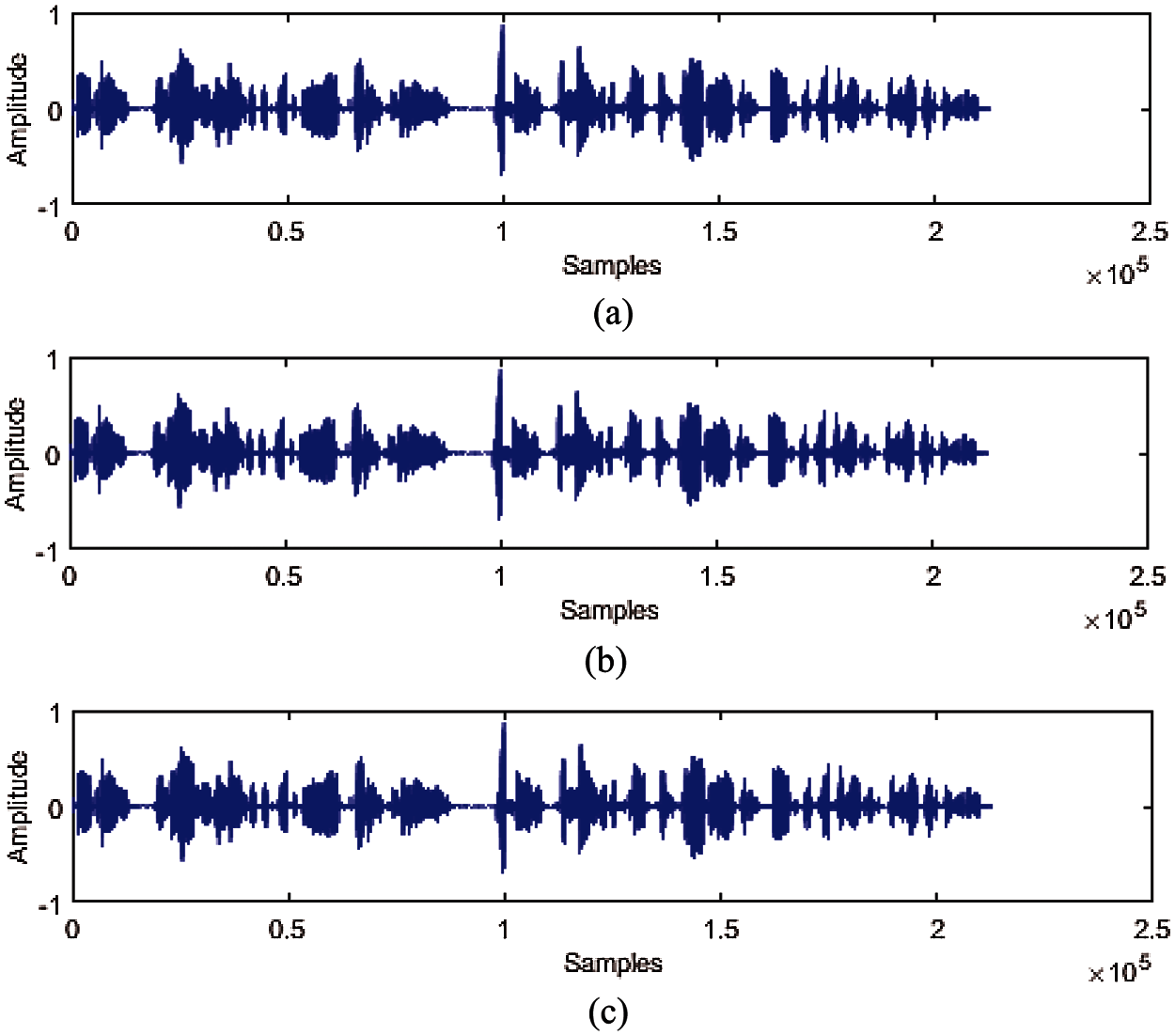
Figure 4: (a) Original audio data LJ00-0001. Wav; (b) Watermarked audio (SNR=38.50db); (c) Recovered audio (SNR=+∞)

4.1 Watermark Imperceptibility and Capacity Test

In order to test the imperceptibility of the proposed, we extracted 5 audio data (LJ001-0001, LJ001-0002, LJ001-0003, LJ001-0004, LJ001-0005) from LJ Speech Dataset for experiments. Intercept 204,800 sampling points, and embed the watermark into the intercepted audio data. The distortion produced by watermark embedding affects the imperceptibility of audio, which is related to embedding strength μ, embedding capacity C, and Hurst exponent threshold H. This section mainly studies the influence of μ, C, and H on audio imperceptibility.

Fig. 5 shows the relationship between different watermark embedding strength μ and SNR. In this experiment, the thresholds H1,H2 are set to 0.3 and 0.4, respectively, and the watermark embedding capacity C is set to 100 bits. It can be seen from Fig. 5 that the imperceptibility of watermarked medical audio data decreases with the increase of the watermark embedding strength μ. This is because according to Eq. (12), the increase of the watermark embedding strength causes the distortion, and thus the SNR value reduces.

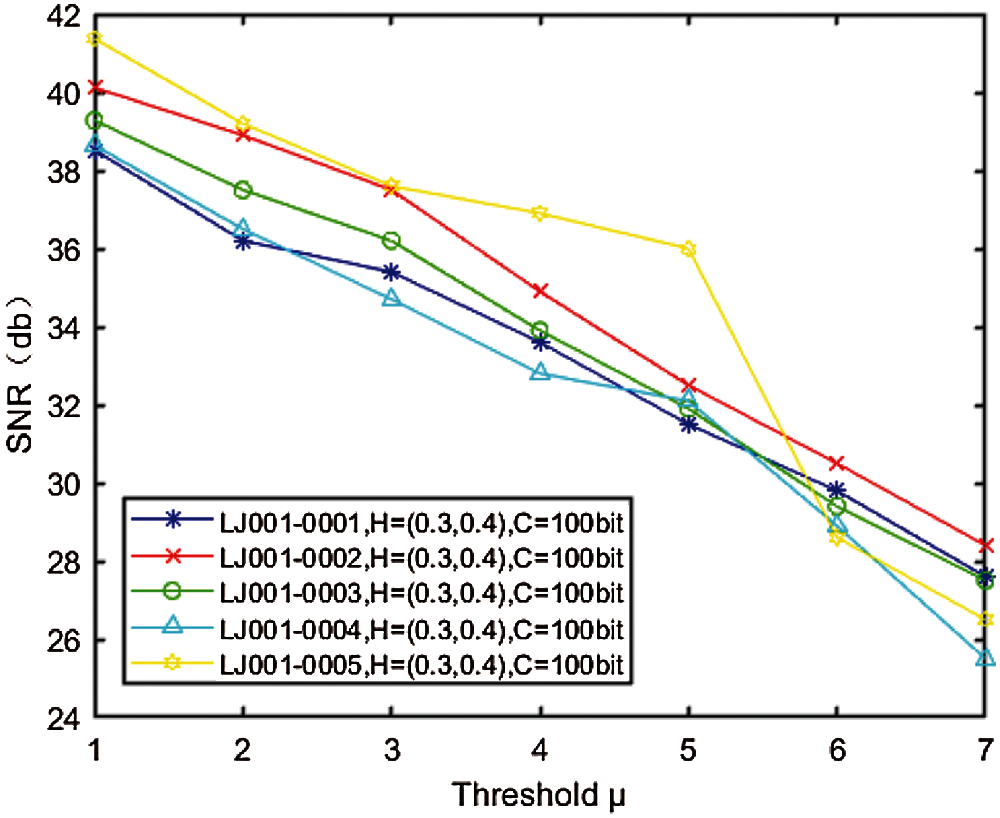
Figure 5: Relationship between μ and SNR value

Fig. 6 shows the relationship between watermark embedding capacity C and SNR. In this experiment, the thresholds H1,H2 are set to 0. 3 and 0. 4 respectively, and the watermark embedding strength μ is set to 1. It can be seen from Fig. 6 that the imperceptibility of watermarked audio decreases as the watermark embedding capacity C increases. The reason is that the larger the embedding capacity, the more sampling points that need to be modified, and the greater the distortion. resulting in reduced imperceptibility.

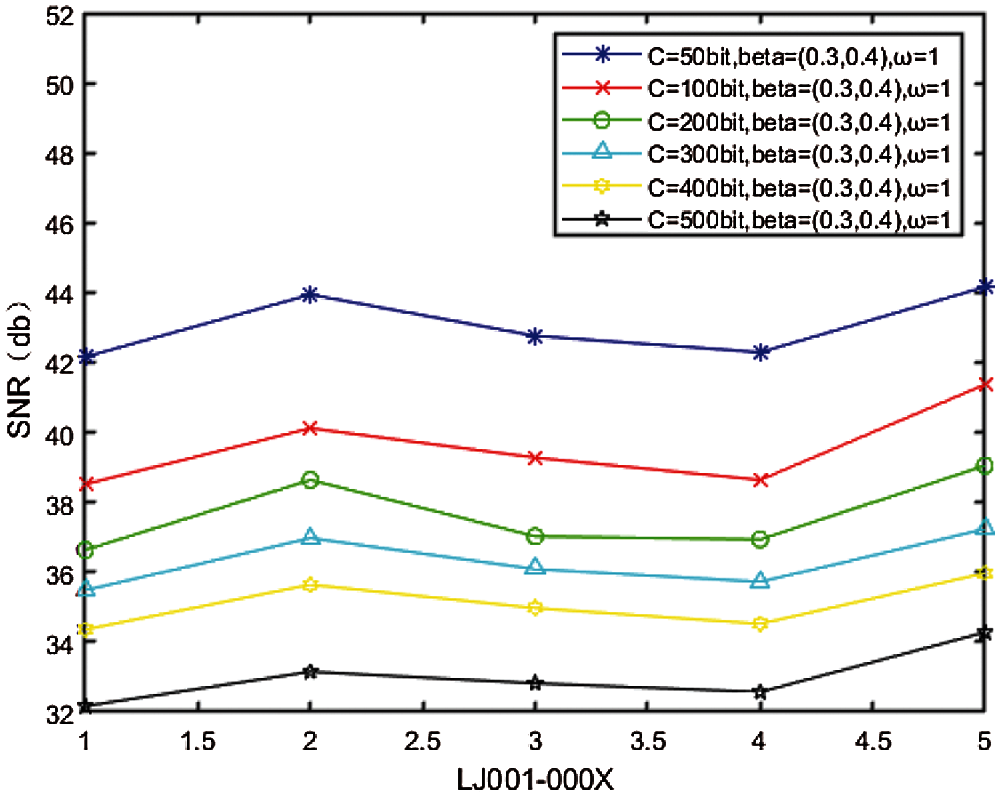
Figure 6: Relationship between C and SNR value

In order to verify the impact of different Hurst exponent thresholds on audio quality, we fixed the watermark embedding strength and the watermark embedding capacity, i.e., let μ= 1, C = 100, and choose different thresholds of H to test the extracted audio data, as can be seen from Tab. 1, When the threshold H∈(0.3,0.4), the signal-to-noise ratio is the highest and the imperceptibility is the best.

4.2 Watermark Robustness Test

Experiments on watermarked medical cover audios of LJ001-0001, LJ001-0002, LJ001-003, LJ001-0004, LJ001-0005 under MP3 compression, resampling, re-quantization, and (AWGN) are carried out to verify the robustness of the watermark. We use the software MATLAB to process the watermarked audio with AWGN, resampling (44.1-22.05-44.1 kHz) and re-quantization (16-8-16 bits). It can be seen from Fig. 7 that all watermarked medical audio has a certain degree of robustness to compression. When the MP3 compression ratio is 48 kbps, watermark information can still be obtained, indicating that the scheme can effectively resist MP3 compression.

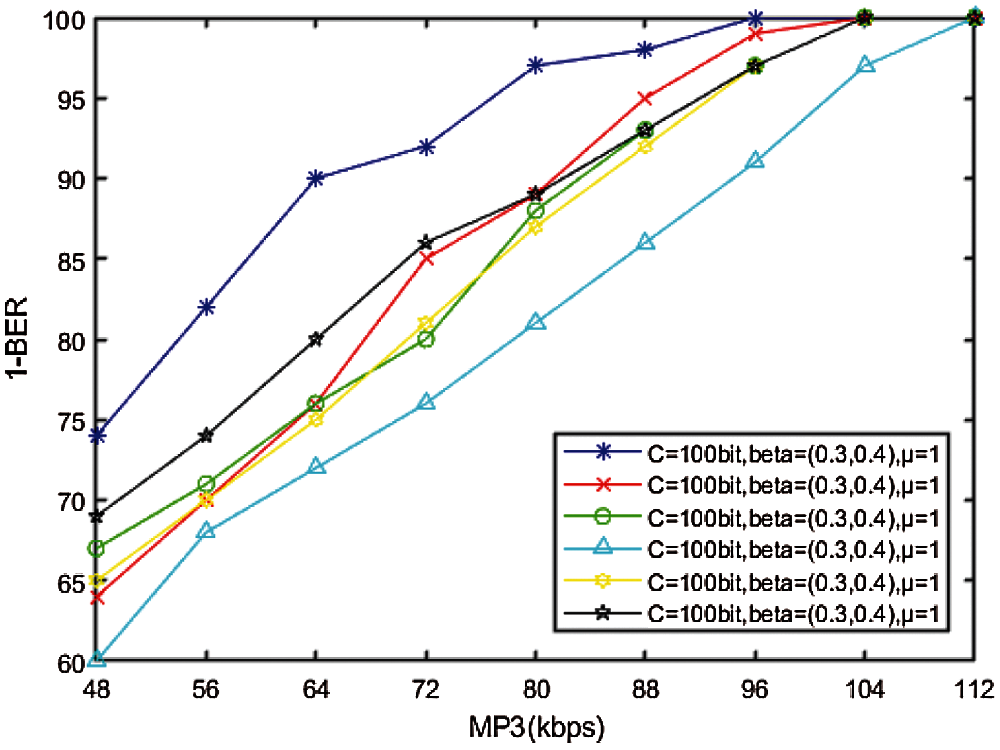
Figure 7: Relationship between MP3 and BER

It can be seen from Fig. 8 that all watermarked audio has strong robustness to AWGN. When the noise where SNR is lower than 20 db, the watermark can be accurately extracted. When the SNR of the noise is lower than 40 db, the watermark can still be extracted at 40 db, which means that the proposed scheme can effectively resist AWGN.

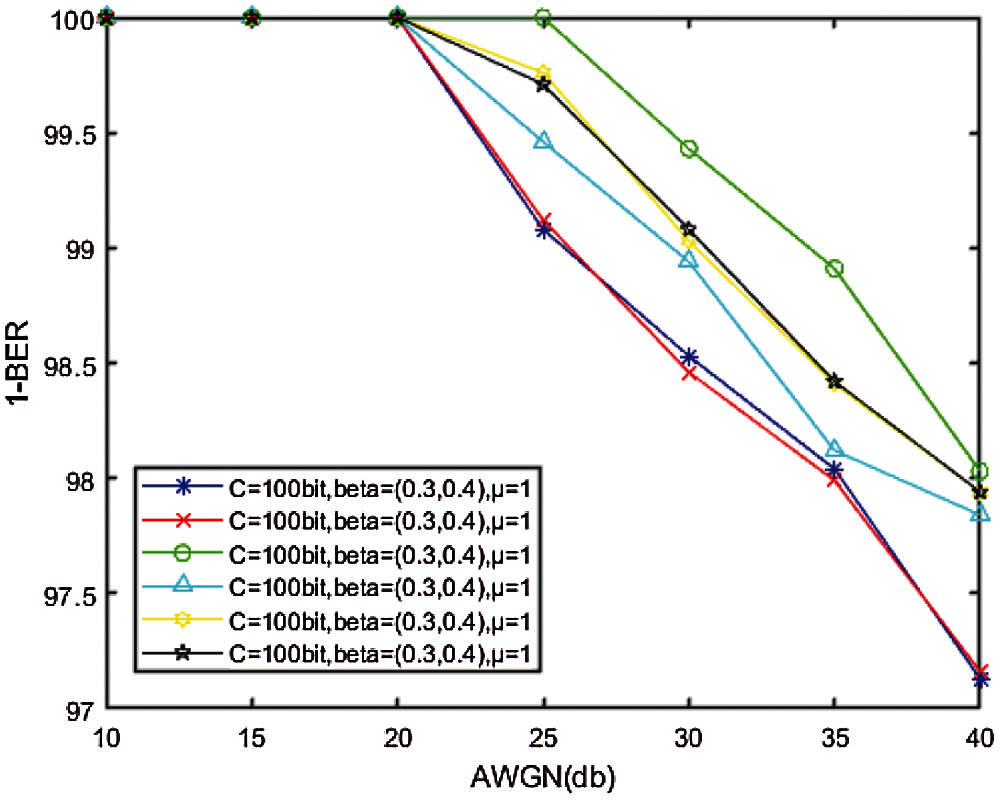
Figure 8: Relationship between AWGN and BER

In order to further verify the performance of this scheme, Tabs. 2 and 3 respectively show the influence of resampling and re-quantization on watermark extraction under different embedding capacities. From Tab. 2, it can be seen that under different embedding capacities, re-sampling has little effect on watermark extraction, and the BER is not higher than 0.0002, indicating that the scheme can effectively resist re-sampling attacks. Tab. 3 also shows that under different embedding capacities, re-quantification has little effect on watermark extraction, which indicates that this scheme can effectively resist quantification attacks.

5  Conclusion

In this paper, we propose a new robust reversible medical audio watermarking scheme. The robust watermark and reversible watermark are embedded into two independent embedding domains respectively, and the reversible watermark embedding does not affect the robust watermark, which improves the robustness of the watermark. In addition, in the stage of reversible watermarking, the correlation between sampling points in medical audio is used to modify the hidden bits of the histogram to reduce the modification of medical audio and reduce the distortion of the medical audio caused by the reversible watermark. When the medical audio is not attacked, the watermark information can be correctly extracted and the medical audio data can be restored without distortion, ensuring the integrity and authenticity of the medical audio. When the medical audio is attacked, the watermark information can still be extracted and the medical audio can be protected by copyright. Simulation experiments show that this scheme has good imperceptibility, and has strong robustness to MP3 compression, AWGN, low-pass filtering, resampling, re-quantization.

Acknowledgement: We thanks NUIST to give us the opportunity for this research work.

Funding Statement: This work was supported, in part, by the Natural Science Foundation of Jiangsu Province under Grant Numbers BK20201136, BK20191401; in part, by the National Nature Science Foundation of China under Grant Numbers 61502240, 61502096, 61304205, 61773219; in part, by the Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD) fund.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  X. R. Zhang, W. F. Zhang, W. Sun, T. Xu and S. K. Jha, “A robust watermarking scheme based on ROI and IWT for remote consultation of COVID-19,” Computers, Materials & Continua, vol. 64, no. 3, pp. 1435–1452, 2020. [Google Scholar]

 2.  L. L. Cui and Y. B. Xu, “Research on copyright protection method of material genome engineering data based on zero-watermarking,” Journal on Big Data, vol. 2, no. 2, pp. 53–62, 2020. [Google Scholar]

 3.  B. Wang and P. Zhao, “An adaptive image watermarking method combining SVD and Wang–Landau sampling in DWT domain,” Mathematics, vol. 8, no. 5, pp. 691, 2020. [Google Scholar]

 4.  B. Wang, W. Kong, W. Li and N. N. Xiong, “A dual-chaining watermark scheme for data integrity protection in internet of things,” Computers, Materials & Continua, vol. 58, no. 3, pp. 679–695, 2019. [Google Scholar]

 5.  F. N. Al-Wesabi, H. G. Iskandar, M. Alamgeer and M. M. Ghilan, “Proposing a high-robust approach for detecting the tampering attacks on english text transmitted via internet,” Intelligent Automation & Soft Computing, vol. 26, no. 6, pp. 1267–1283, 2020. [Google Scholar]

 6.  K. Maeno, Q. Sun, S. F. Chang and M. Suto, “New semi-fragile image authentication watermarking techniques using random bias and nonuniform quantization,” IEEE Transactions on Multimedia, vol. 8, no. 1, pp. 32–45, 2006. [Google Scholar]

 7.  X. Zhang, S. Wang, Z. Qian and G. Feng, “Reference sharing mechanism for watermark self-embedding,” IEEE Transactions on Image Processing, vol. 20, no. 2, pp. 485–495, 2011. [Google Scholar]

 8.  M. U. Celik, G. Sharma, A. M. Tekalp and E. Saber, “Lossless generalized-LSB data embedding,” IEEE Transactions on Image Processing, vol. 14, no. 2, pp. 253–266, 2005. [Google Scholar]

 9.  J. Tian, “Reversible data embedding using a difference expansion,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 13, no. 8, pp. 890–896, 2003. [Google Scholar]

10. Y. Hu, H. Lee, K. Chen and J. Li, “Difference expansion based reversible data hiding using two embedding directions,” IEEE Transactions on Multimedia, vol. 10, no. 8, pp. 1500–1512, 2008. [Google Scholar]

11. I. Dragoi and D. Coltuc, “Local-prediction-based difference expansion reversible watermarking,” IEEE Transactions on Image Processing, vol. 23, no. 4, pp. 1779–1790, 2014. [Google Scholar]

12. W. Tai, C. Yeh and C. Chang, “Reversible data hiding based on histogram modification of pixel differences,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 19, no. 6, pp. 906–910, 2009. [Google Scholar]

13. X. L. Li, W. Zhang, X. Gui and B. Yang, “Efficient reversible data hiding based on multiple histograms modification,” IEEE Transactions on Information Forensics and Security, vol. 10, no. 9, pp. 2016–2027, 2015. [Google Scholar]

14. W. He and Z. Cai, “An insight into pixel value ordering prediction-based prediction-error expansion,” IEEE Transactions on Information Forensics and Security, vol. 15, pp. 3859–3871, 2020. [Google Scholar]

15. V. Sachnev, H. J. Kim, J. Nam, S. Suresh and Y. Q. Shi, “Reversible watermarking algorithm using sorting and prediction,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 19, no. 7, pp. 989–999, 2009. [Google Scholar]

16. A. Roy and R. S. Chakraborty, “Toward optimal prediction error expansion-based reversible image watermarking,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 30, no. 8, pp. 2377–2390, 2020. [Google Scholar]

17. S. W. Weng and J. S. Pan, “Integer transform based reversible watermarking incorporating block selection,” Journal of Visual Communication & Image Representation, vol. 35, no. 8, pp. 25–35, 2016. [Google Scholar]

18. A. Singh and M. K. Dutta, “Wavelet-based reversible watermarking system for integrity control and authentication in tele-ophthalmological applications,” International Journal of Electronic Security and Digital Forensics, vol. 8, no. 4, pp. 392–411, 2016. [Google Scholar]

19. J. Laguarta, H. Puig and B. Subirana, “COVID-19 artificial intelligence diagnosis using only cough recordings,” IEEE Open Journal of Engineering in Medicine and Biology, vol. 1, pp. 275–281, 2020. [Google Scholar]

20. D. Yan and R. Wang, “Reversible data hiding for audio based on prediction error expansion,” in Proc. IIHMSP, Harbin, China, pp. 249–252, 2008. [Google Scholar]

21. J. J. Garcia-Hernandez, “Exploring reversible digital watermarking in audio signals using additive interpolation-error expansion,” in Proc. IIHMSP, Washington, USA, pp. 142–145, 2012. [Google Scholar]

22. X. Huang, N. Ono, I. Echizen and A. Nishimura, “Reversible audio information hiding based on integer DCT coefficients with adaptive hiding locations,” in Proc. IWDW, Auckland, New Zealand, pp. 376–389, 2013. [Google Scholar]

23. D. Xiao, J. Liang, Q. Ma, Y. Xiang and Y. Zhang, “High-capacity data hiding in encrypted image based on compressive sensing for nonequivalent resources,” Computers, Materials & Continua, vol. 58, no. 1, pp. 1–13, 2019. [Google Scholar]

24. D. Coltuc and J. M. Chassery, “Distortion-free robust watermarking: A case study,” in Proc. SPIE, Washington, USA, vol. 6505, pp. 65051N, 2007. [Google Scholar]

25. D. Coltuc, “Towards distortion-free robust image authentication,” Journal of Physics Conference Series, vol. 77, pp. 12005, 2005. [Google Scholar]

26. S. Iftikhar, M. Kamran and Z. Anwar, “RRW—A robust and reversible watermarking technique for relational data,” IEEE Transactions on Knowledge and Data Engineering, vol. 27, no. 4, pp. 1132–1145, 2015. [Google Scholar]

27. X. Wang, X. Li and Q. Pei, “Independent embedding domain based two-stage robust reversible watermarking,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 30, no. 8, pp. 2406–2417, 2020. [Google Scholar]

28. Z. Ni, Y. Shi, W. Ansari, Q. Sun and X. Lin, “Robust lossless image data hiding designed for semi-fragile image authentication,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 18, no. 4, pp. 497–509, 2008. [Google Scholar]

29. X. Gao, L. An, Y. Yuan, D. Tao and X. Li, “Lossless data embedding using generalized statistical quantity histogram,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 21, no. 8, pp. 1061–1070, 2011. [Google Scholar]

30. X. Liang and S. J. Xiang, “Robust reversible audio watermarking based on high-order difference statistics,” Signal Processing, vol. 173, no. 3, pp. 107584, 2020. [Google Scholar]

31. S. Par, A. Kohlrausch, G. Charestan and R. Heusdens, “A new psychoacoustical masking model for audio coding applications,” in Proc. ICASSP, Orlando, USA, pp. 1805–1808, 2002. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.