DOI:10.32604/cmc.2022.021981

| Computers, Materials & Continua DOI:10.32604/cmc.2022.021981 |  |
| Article |
OBSO Based Fractional PID for MPPT-Pitch Control of Wind Turbine Systems
1Department of Electrical and Computer Engineering (ECE), King Abdulaziz University, Jeddah, 21589, Saudi Arabia
2Center of Excellence in Intelligent Engineering Systems (CEIES), King Abdulaziz University, Jeddah, 21589, Saudi Arabia
3Department of Electrical & Electronics Engineering, Universiti Teknologi PETRONAS, Malaysia
*Corresponding Author: Ibrahim M. Mehedi. Email: imehedi@kau.edu.sa
Received: 23 July 2021; Accepted: 01 September 2021
Abstract: In recent times, wind energy receives maximum attention and has become a significant green energy source globally. The wind turbine (WT) entered into several domains such as power electronics that are employed to assist the connection process of a wind energy system and grid. The turbulent characteristics of wind profile along with uncertainty in the design of WT make it highly challenging for prolific power extraction. The pitch control angle is employed to effectively operate the WT at the above nominal wind speed. Besides, the pitch controller needs to be intelligent for the extraction of sustainable secure energy and keep WTs in a safe operating region. To achieve this, proportional–integral–derivative (PID) controllers are widely used and the choice of optimal parameters in the PID controllers needs to be properly selected. With this motivation, this paper designs an oppositional brain storm optimization (OBSO) based fractional order PID (FOPID) design for sustainable and secure energy in WT systems. The proposed model aims to effectually extract the maximum power point (MPPT) in the low range of weather conditions and save the WT in high wind regions by the use of pitch control. The OBSO algorithm is derived from the integration of oppositional based learning (OBL) concept with the traditional BSO algorithm in order to improve the convergence rate, which is then applied to effectively choose the parameters involved in the FOPID controller. The performance of the presented model is validated on the pitch control of a 5 MW WT and the results are examined under different dimensions. The simulation outcomes ensured the promising characteristics of the proposed model over the other methods.
Keywords: Wind turbine; wind energy; pitch control; brain storm optimization; PID controller; maximum power point
Electric power source from wind energy (WE) becomes a main contribution power resource in the electrical system over the world. A substantial emphasis is located on cost-effective usage of the energy source for attaining simultaneous reliable and quality electrical supply [1]. Regarding security and operational factors, wind energy combination in the electrical grid developed as a major problem because of its increased penetration level and variable nature; such factors have a great impact on the control and operation of the electrical systems. Novel electricity grid codes are established in many countries for specifying an appropriate need to combine wind electricity production with the present electrical power scheme. In the novel grid codes, there is a need for wind farms to satisfy similar needs since the traditional power plant and must stay linked to support the grid in the anomalous condition [2]. Conventionally, the wind energy resource system utilizes constant speed wind turbines (WT), a variable pitch that has been combined to the squirrel cage induction generator (SCIG), and fed power straightaway to the grid utilities. The latest variable speed WT system processes energy via power electronic system (PES) have developed a greater acceptance and conquer all share markets. PES technology enhances the control of WT considerably. The Reutilized in the wind power generation (WPG) scheme could efficiently face the challenge of grid connection requirement (GCR) and consecutively, improves the operation and integration of wind farms linked to the grid.
The WT penetrated in novel regions such as power electronic system that is utilized for facilitating the connectivity procedure of a WE scheme with the grid. Moreover, this system helps in improving the extracted energy from the WE scheme and maximizes the entire performance. The maximal power point tracker (MPPT) is a vital controller needed for improving the output power from the WE scheme. Various researchers have been stated in the implementation field of MPPT controller with WT. In previous years, many effective and beneficial controlling methods have been issued for guarantying efficiency when taking into account economic factors. In [3], a relation among traditional PID and H∞ robust controller for regulating the pitch angle is attained and its efficiency in tracking the desirable power output in various wind profiles are examined. The ambiguity of this module and environments are involved. The study ultimately accomplishes the dominance of strong controller on PID because of its lesser oscillation in output power. In [4], by improving several PI controllers in distinct wind speeds overrated, an RBF NN was trained. Thus, in some wind speeds, appropriate benefits are selected for PI controller.
Fuzzy logic controllers (FLCs), because of their strength they can control the system with complex mathematical modules and a higher degree of non-linearity [5]. Alternatively, PID controllers because of their robustness and simplicity have been utilized in industrial applications [6]. Thus, the integration of PID and fuzzy controllers provide a proper background for designing controllers to the high non-linear system with a substantial number of uncertainties. Recently, fractional-order systems and controllers have attained significant interest. In fact, they are common types of integer controllers while their orders are fractional values, hence they could have a high degree of freedom. Fractional order controller is highly efficient for fractional and complex procedures compared to their integer-order equivalents [7]. In recent times, Fractional-Order PID (FOPID) controllers were developed attractive and beneficial for some industrial applications [8]. In contrast, as stated investigation, the efficiency of fuzzy PI exposed an optimum efficiency in minimalizing the error however with further control efforts. The parameter of controllers has been attained using error and trial. This isn't only a direct process however it doesn't provide optimum variables. Though, in engineering application detecting suboptimal or optimal resolutions are required by optimization methods [9].
This paper designs an oppositional brain storm optimization (OBSO) based fractional order PID (FOPID) design for sustainable and secure energy in WT systems. The proposed model focuses on the effective extraction of the maximum power point (MPPT) in the low range of weather condition and save the WT in high wind regions by the use of pitch control. Besides, the OBSO algorithm is derived from the integration of oppositional based learning (OBL) concept with the traditional BSO algorithm in order to improve the convergence rate, which is then employed for the optimal parameter selection of the FOPID controller. For examining the improved outcomes of the proposed model, a simulation process takes place on the pitch control of a 5 MW WT.
The rest of the paper is arranged as follows. The next section examines recent state-of-the-art controller technologies applied to WT systems. Section 3 elaborates the wind energy system model; Section 4 designs an OBSO-based FOPID controller. Section 5 evaluates the results of the proposed model, and Section 6 draws the conclusion.
This section performs a detailed review of existing controller designs for WT systems. In Kumar et al. [10], 2 innovative controllers named FPID and FOFPID are presented for improving pitch control efficiency. In the meantime, to detect variables of the controllers the chaotic evolution optimization techniques are utilized. With this technique, it provides unknown variables of the controller however it assurances the optimality depending upon the selected objective function. For improving the efficiency of this technique chaotic maps are utilized. Maroufi et al. [11] proposed a new hybrid controller called FFPID approach tune by an effective metaheuristic optimization bat algorithm (BA) to control WT armed with WTPMSG. The key control objective is for driving WT-PMSG to MPPT in lower range of climate conditions and in addition to secure the WT in higher wind areas by pitch angle control. The efficiency of presented approach is examined in every area with lower-higher wind speed disturbances.
Fathy et al. [12] proposed a new method depending upon current metaheuristic grasshopper optimization algorithm (GOA) to extract highest energy from a WE scheme functioned in parameter speed condition. This method contains PMSG functioned by WT, a dc-dc boost converter, a 3-phase diode rectifiers, and MPPT implemented by the projected GOA. In Pannu et al. [13], the PSO method is utilized however traditional PSO method could not address the system uncertainties and nonlinearity. Henceforth, the presented PSO method is utilized for calculating the controller's optimum parameter. The projected method is executed on a five MW WT that is implemented by Bladed software.
In Singh et al. [14], a combined tuning of parameter of controller to enhance frequency features of a multi-area interrelated thermal scheme in existence of doubly fed induction generator (DFIG) wind production is proposed. AN extensively utilized 2 area non reheat thermal interrelated scheme is inspired by its 1 area combined with DFIG based wind production. In Civelek [15], fuzzy controller was implemented for controlling WT blades which are improved by GA. Novel features are included for improving AIGA efficiency. One of these is an addition to AEC. The transformation from decimal to binary and from binary to decimal is executed according to a number of this acceptable error. In Bashetty et al. [16], strong adaptive control is implemented for pitch and torque control of the WT functioning in turbulent wind condition. The dynamics of WT are developed by taking into account 5 degrees of freedom systems. Saadatmand et al. [17] proposed a common technique for LFO damping by LPF with the implementation of an optimum PID controller as power oscillation damper in the non-linear control loop of LPF.
Qais et al. [18] proposed a new adaptive control system depending upon PI controller and adaptive filtering method named LMSRE technique. Initially, this technique is employed for unknown scheme detection after it is related to another benchmark technique like LMF, CMPN, and LMS. Next, the LMSRE has employed for self-tuning the parameter of cascaded PI controllers for improving MPPT and FRTA of grid integrated PMSG based WT. Mehedi et al. [19] proposes an execution of membership function and fuzzy rule based fuzzy aided PID controller to AGC in multi area nonlinear power systems. In this work, 3 areas 9 unit installed interconnected networks are considered to improve various dynamic responses concerning AGC analyses. An adapted method called MSCA is presented to tune the gaining parameter of projected fuzzy controller for producing closer optimal gain values.
The existing methodologies of MPPT control in wind turbines extract more efforts of control measures which lead to loss of energy. The loss of energy affects the sustainability in the power generation, thus reducing the efficiency of the power generation system using wind turbines. To overcome the observed pitfalls of the existing methodologies, the objectives of the proposed research work is framed and is listed as follows: Design a novel FOPID controller using OBSO algorithm for MPPT-Pitch Control of WT system
• Aims to achieve sustainable and secure energy in WT systems by the use of optimal pitch control
• Derive an OBSO algorithm by integrating the concepts of OBL with the BSO algorithm in population initialization process
• Validate the efficiency of the OBSO algorithm on a 5 MW WT and examine the results under several measures
The proposed method is an hybrid meta-heuristic method to achieve high level of sustainability and efficiency in power generation system using wind turbines. The Maximum Power Point Tracking (MPPT) is performed effectively using OBL and BSO optimization algorithms.
The overall system model of wind energy is depicted in Fig. 1. The system encompasses a DFIG generator driven by a WT as a prime mover, 3 phase diode rectifier, and dc-dc boost converter controlled by the OBSO algorithm. The MPPT will adjust the duty cycle given to the boost converter to enhance the sustainable and secure energy from the entire system.
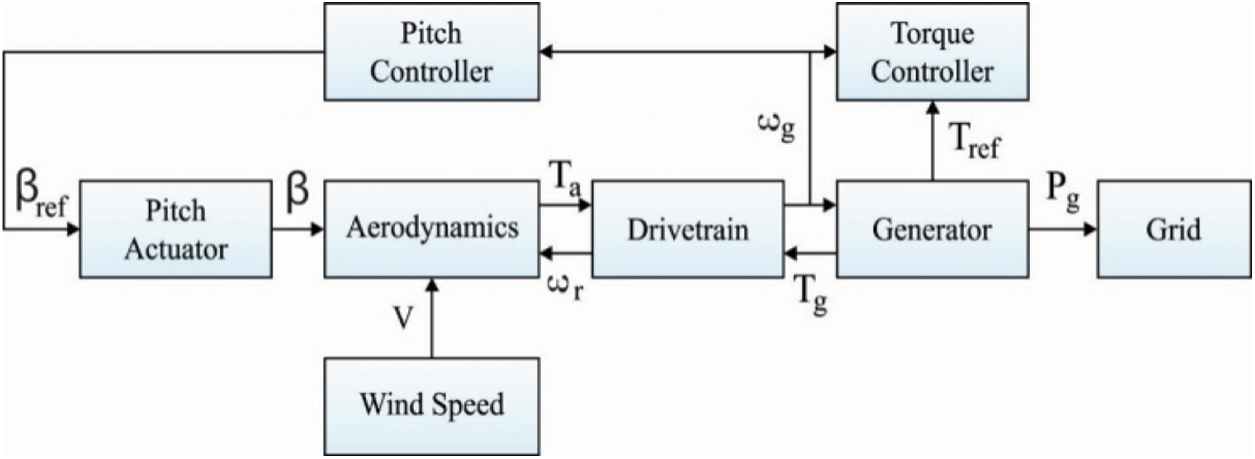
Figure 1: Overall system model of wind energy [10]
WT is employed to convert the wind power into mechanical power, and the wind power is defined in Eq. (1):
where
where
with
The coefficient values are allocated as follows as
where R defines the radius of the WT radius and
The maximal mechanical power generated from the WT is defined in Eq. (7):
Based on Eq. (7), it is noticeable that the MPPT is important for controlling the mechanical speed of the WT to be its optimum value.
A DFIG is employed. The mechanical
where
where
The pitch actuator offers the rotational movements of the blades in the WT over the longitudinal axis. The pitch actuator in WT generally has two restrictions in the amplitude and rate of change of pitch angle. The amplitude and rate limitations are assumed in the range of 0°−90° and −8°/s to +8°/s, correspondingly [21]. In addition, the slew rate is a major impact on the optimization results. The actuator could be treated as a first order low pass filter as defined below:
where
The energy from the wind turbines are extracted by the aerodynamic forces based on the drag and lift operations. In the proposed method, the aerodynamics is controlled by the pitch actuator, which acts as a subsystem for controlling the pitch angle of the overall system. The extracted energy by the aerodynamics is fed to the drive train which converts the mechanical energy to the electrical energy with the combined function of generator, gear box and power electronic converters. The generated energy is transmitted to the power grid/load through the generator and a part of generated power is fed back for the process of pitch controlling and torque controlling process such that to perform an efficient pitch controlling process. The controlling process drives the wind turbine power generation system to the high level of efficiency and the proposed system is composed of FOPID controller to execute this objective which is illustrated in the Section 4.
4 Design of Proposed FOPID Controller
For satisfying the demands of control requirements, an effective FOPID controller is designed. Besides, the optimal parameters of the FOPID controller are tuned by OBSO algorithm.
The PI controller is usually employed in industry procedure control owing to the simplicity and better performance in linear as well as non-linear systems [22–24]. The total control function can be defined using Eq. (13):
where e denotes the feedback error defining the variation among the truly computed values of variables states and the reference values. Afterward,
Another Version of the PID controller design has higher degree of freedom compared to the conventional PID controller. It is evolved from the integrator as well as differentiator with respect to
For implementing the FOPID in simulation and practically, an approximation with integer order transfer function is needed. Here, the Crone approximation is employed in which the approximation utilizes a recursive distribution of N poles and N zeros.
where
Here, the frequency range is chosen as
where
4.3 Algorithm Process of OBSO Algorithm
The BSO technique is inspired using the concept of brainstorming, and it is an extensively utilized tool to increase inspiration in organizations that have attained broad acceptance as means of assisting creativeness [28]. A possible solution in the solution space denotes a BSO idea. The BSO follows the procedure of interchanging ideas by a team and utilizes three processes for producing global optimal generations. In BSO process, initially, N ideas are arbitrarily initiated with the solution space, and later every idea is calculated based on FF. Then m points of cluster centres are chosen arbitrarily and initiated as Nideas, whereas m is lesser compared to N. The BSO procedure is defined in Algorithm 1.

Clustering Individuals: It is a procedure of integrating same objects, and, in every generation, every idea is clustered to m cluster based on individual feature. The optimum concept in every center is selected as cluster center, and its function could improve search field. The K-means technique is a common method utilized in clustering.
Disrupting Cluster Center: It arbitrarily selects a cluster center and gets replaced with the recently created idea using a likelihood of p_replace, that is so called replacing function. The p_replace value is utilized for controlling likelihood to replaces cluster center with arbitrarily created solution. It is utilized for avoiding early convergences and assist individual “jump out” of local optimal.
Creating Individuals: For maintaining population diversity, a novel idea (individual) is created according to one or two ideas in one or two clusters, correspondingly. In generating function, initially, BSO arbitrarily selects more than one cluster based on a likelihood of
Whereas rand denotes arbitrary value among [0, 1].
Afterward selecting one/two ideas, the chosen idea(s) is upgraded by
whereas
whereas
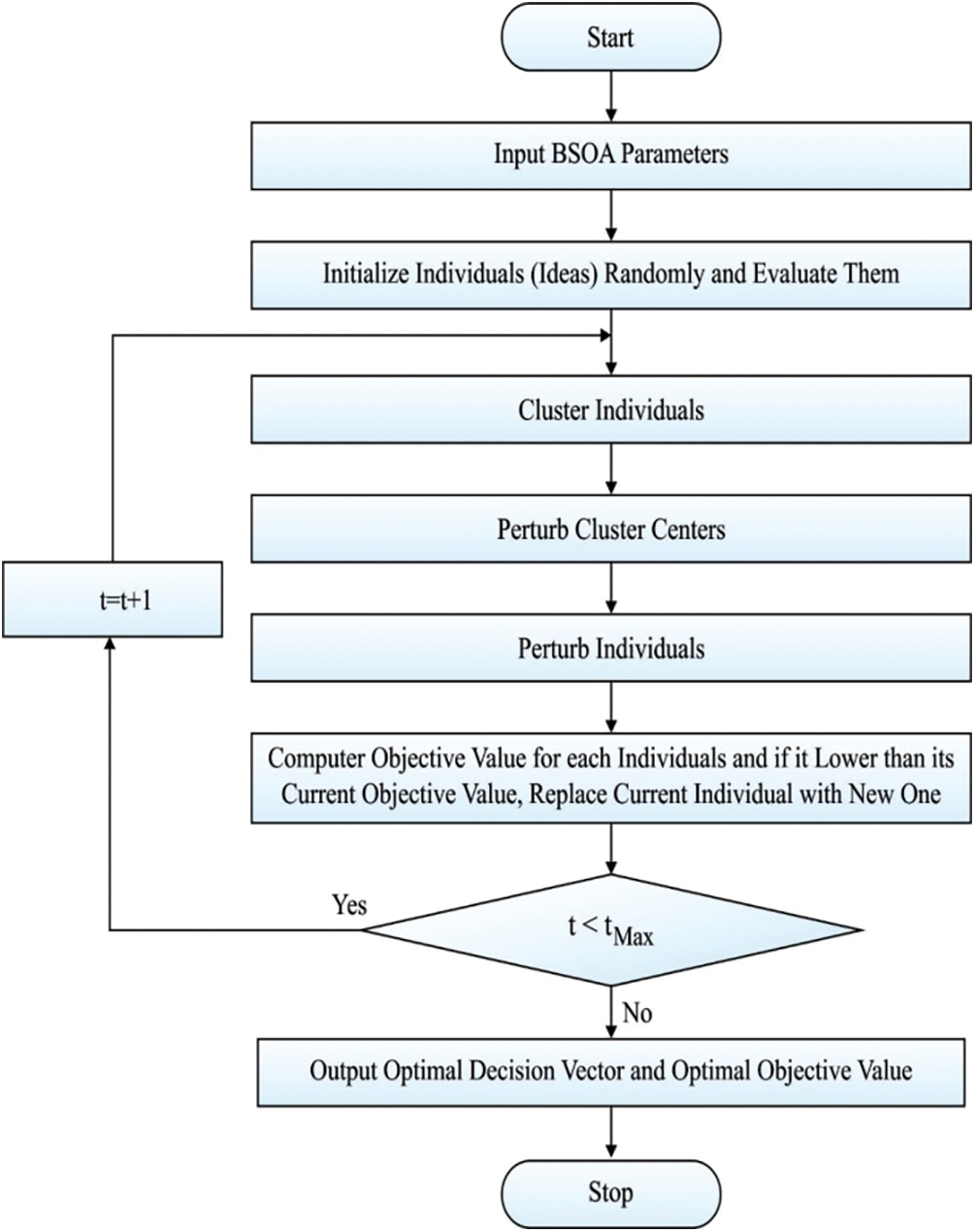
Figure 2: Flowchart of BSO
To boost the convergence performance of the BSO technique, OBL concept is employed. OBL concept is utilized to enhance the quality of the initial population solution by the diversification of the solutions. The OBL scheme searches in all directions in the searching area, namely original solution direction, and opposite solution direction. At last, the OBL concept considers the fittest solution from every solution.
Opposite number x is denoted by a real number over the range
The above equation can be generalized to employ it in a searching area space with multiple dimensions. So, for generalization, each search agent and the corresponding opposite positions can be defined using Eqs. (28)–(29):
The value of every individual element in
Here, the fitness function is
The processes involved in the OBSO algorithm are listed as follows.
1. Population initiation X as
2. Compute the opposite position of individuals OX as
Elect the n fittest individuals from
4.4 Design of FOPID Controller Using OBSO Algorithm
Here, the integral absolute error (ISE) condition is employed for minimizing the error signal. The objective function of the OBSO algorithm can be represented in Eq. (31):
where
In this paper, the WT is modeled and designed by the use of Bladed software. The parameter setting of the WTs is given in Tab. 1. Owing to the non-linear characteristics of aerodynamics and actuators, the WTs are highly non-linear. This paper validates the performance of three controllers as PID, FPID, and FOPID are used to pitch control a 5 MW WT.
The results of the OBSO algorithm under three different controllers are investigated in terms of ISE, NFE, SD, and CPU running time. An ISE analysis of the OBSO with other optimization algorithms under three controllers is made in Tab. 2 [11].
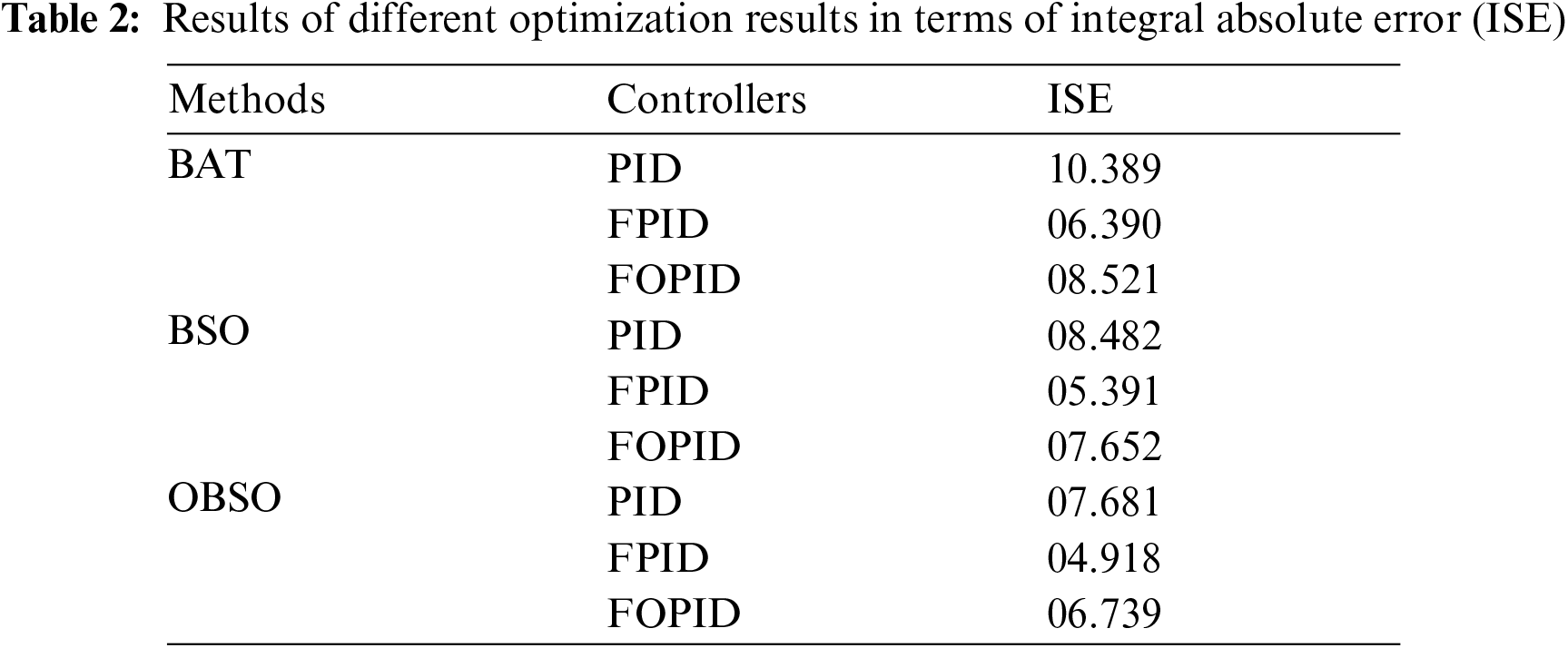
Fig. 3 examines the ISE analysis of the OBSO with other algorithms under PID controller. From the figure, it is apparent that the BAT algorithm has failed to achieve effective outcome and offered a higher ISE of 10.389. At the same time, the BSO algorithm has tried to show slightly improved performance with a moderate ISE of 8.482. However, the proposed OBSO algorithm has accomplished better performance with a minimal ISE of 7.681. Similarly, Figs. 4 and 5 examine the ISE analysis of the OBSO with other algorithms under FPID and FOPID controllers. From the figures, it is stated that the BAT algorithm has failed to attain effective outcome and offered a higher ISE of 6.390. At the same time, the BSO algorithm has tried to show slightly improved performance with a moderate ISE of 5.391. But, the proposed OBSO algorithm has accomplished better performance with the lesser ISE of 4.918.
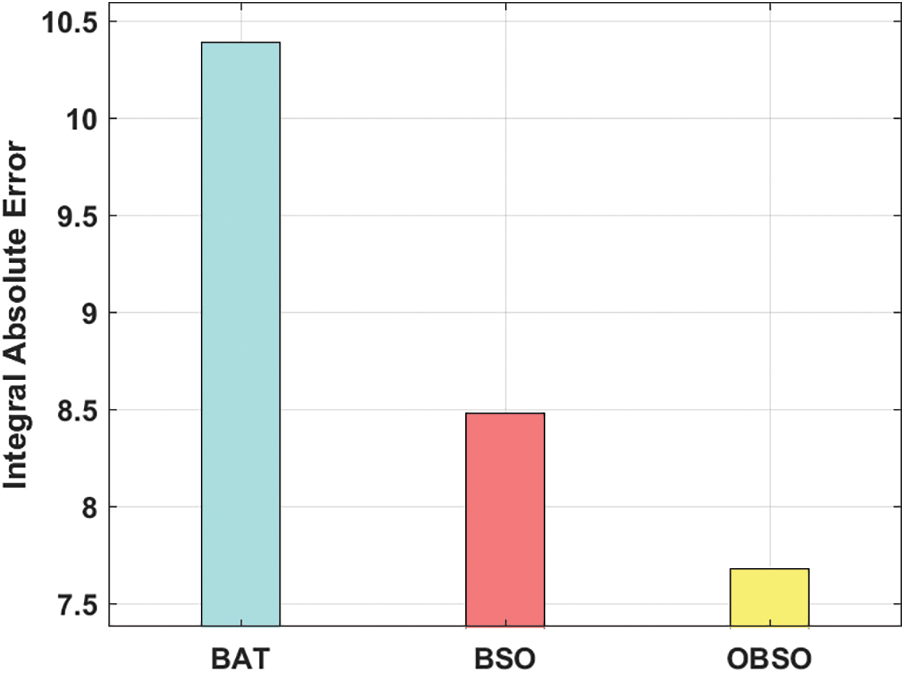
Figure 3: PID controller analysis is of OBSO model
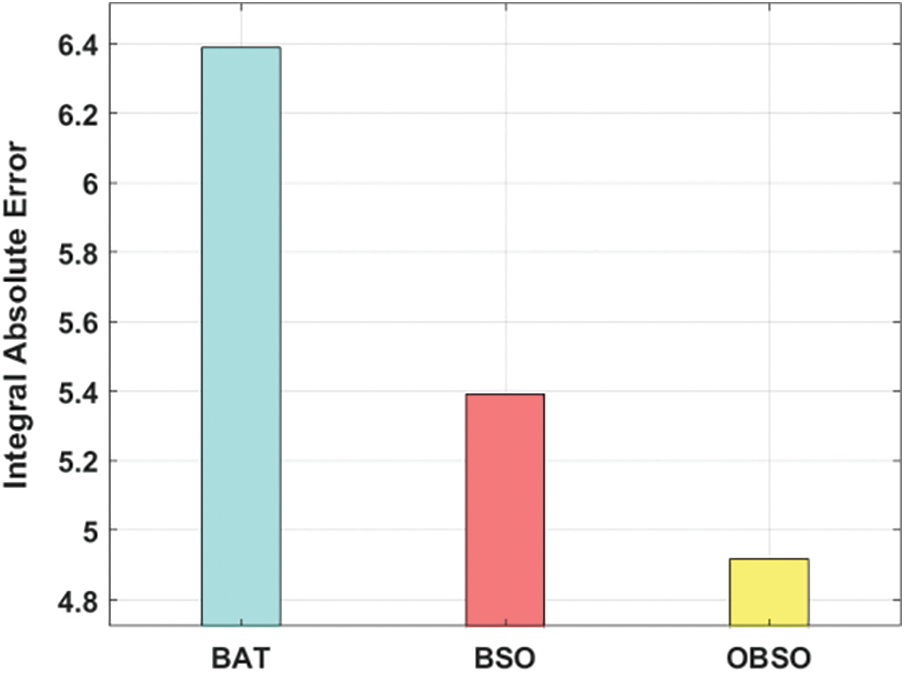
Figure 4: FPID controller analysis of OBSO
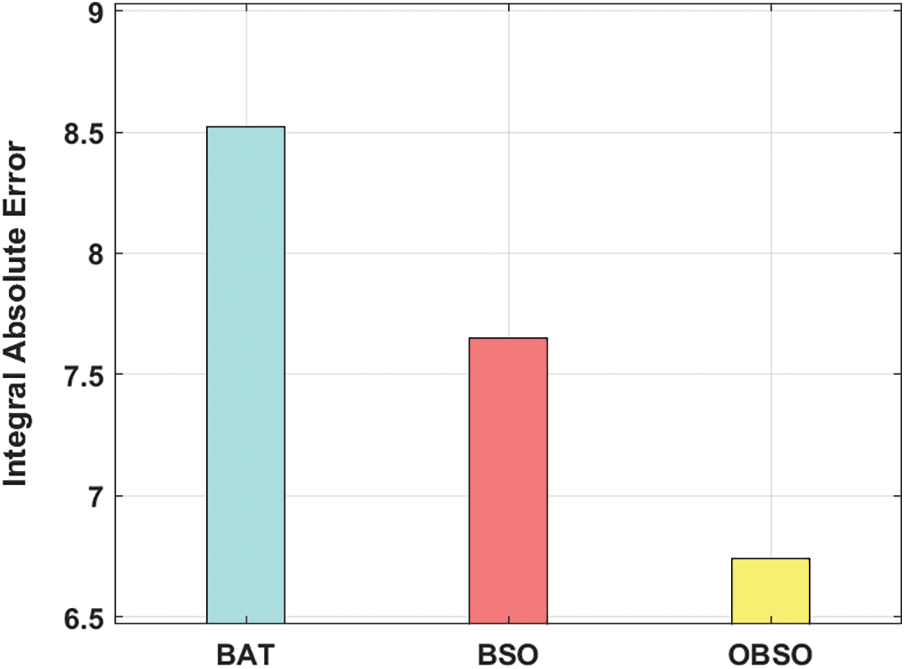
Figure 5: FOPID controller analysis of OBSO model
A detailed comparative results analysis of the OBSO algorithm with other methods in terms of CPU time is given in Tab. 3 and Fig. 6. On examining the performance of the OBSO with other algorithms under PID controller, it is evident that the DE algorithm has shown worse performance by offering a higher CPU time of 34271 s. Eventually, the PSO and CDE algorithms have demonstrated slightly enhanced outcomes with the CPU time of 34218 s and 34189 s respectively. Meanwhile, the CPSO algorithm has demonstrated moderate performance over the other algorithms with a CPU time of 33984 s. Though the BSO algorithm has reached a reasonable CPU time of 32839 s, the proposed OBSO algorithm exhibited superior performance with the least CPU time of 32647 s.
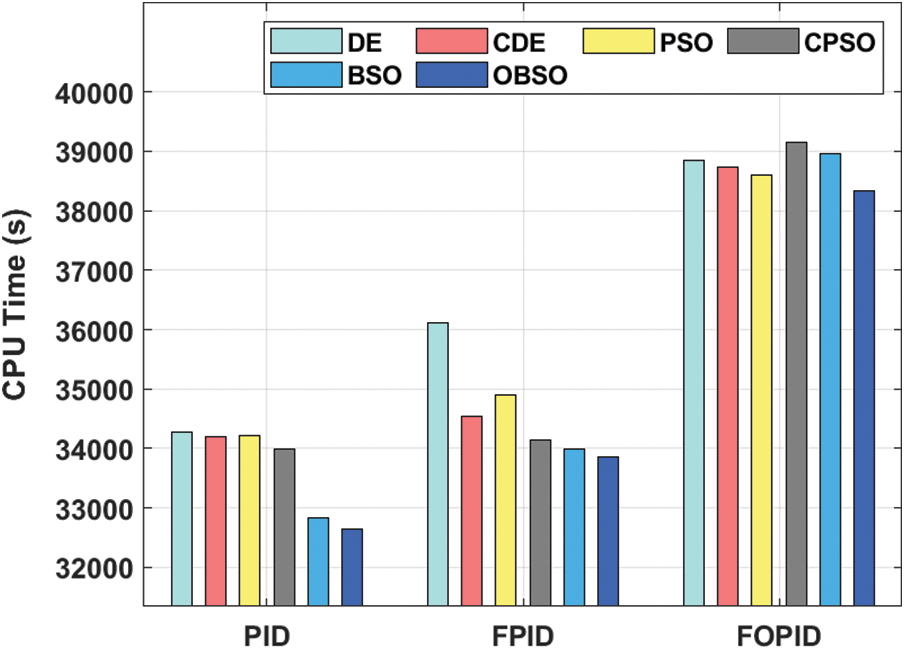
Figure 6: Comparative results analysis of OBSO method with other models
Besides, on investigating the performance of the OBSO with other approaches under FPID controller, it is evident that the DE algorithm has shown worse performance by offering a superior CPU time of 36105 s. Eventually, the PSO and CDE algorithms have demonstrated slightly enhanced outcomes with the CPU time of 34895 s and 34530 s respectively. In the meantime, the CPSO algorithm has revealed moderate performance over the other systems with a CPU time of 34137 s. Though the BSO algorithm has reached a reasonable CPU time of 33998 s, the proposed OBSO algorithm displayed superior performance with the least CPU time of 33864 s. Finally, on inspecting the performance of the OBSO with other algorithms under FOPID controller, it is evident that the DE algorithm has shown worse performance by offering a higher CPU time of 38850 s. Eventually, the PSO and CDE algorithms have demonstrated slightly enhanced outcomes with the CPU time of 38601 s and 38729 s respectively. Meanwhile, the CPSO algorithm has demonstrated moderate performance over the other algorithms with a CPU time of 39146 s. But, the BSO technique has reached a reasonable CPU time of 38953 s, the proposed OBSO system exhibited superior performance with the least CPU time of 38326.
Fig. 7 showcases the convergence analysis of the OBSO algorithm with other optimization algorithms in the design of FOPID controller [10]. From the figure, it is demonstrated that the proposed OBSO algorithm has reached to effective convergence rate over the other algorithms due to the inclusion of OBL concept and opposition based population initialization. From the above-mentioned tables and figures, it is apparent that the proposed model is found to be an effective tool for the design of FOPID controller of pitch control in WT systems. Therefore, it can be employed to achieve sustainable and secure energy from WT systems.
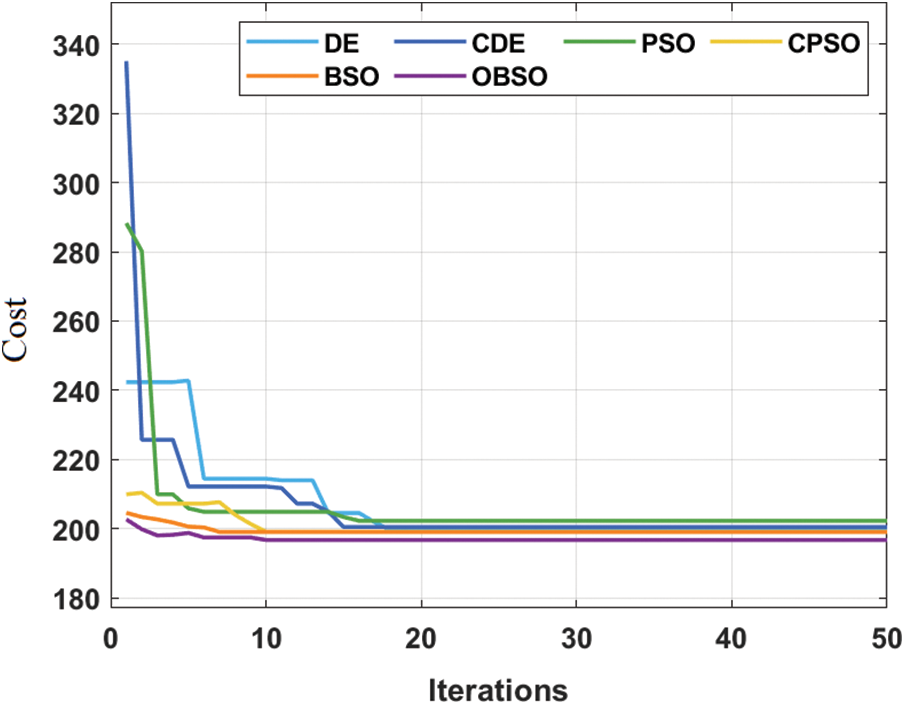
Figure 7: Convergence characteristics for FOPID
This paper has devised an effective OBSO technique in the designing of FOPID controller to accomplish sustainable and secure energy in WT systems. The FOPID controller is proficiently designed with an aim of proficiently extracting the MPPT under different weather conditions using pitch control. The optimal design of FOPID pitch control in WT system results in enhanced performance under different aspects. In addition, the inclusion of OBL concept in the classical BSO algorithm results in improved convergence rate. For examining the improved outcomes of the proposed model, a simulation process takes place on the 5 MW WT. The experimental results highlighted the promising outcomes of the presented technique over the recent methods. In future, the settling time of the WT system can be reduced to boost the system stability. In addition, the multi-objective optimization method to reduce error and rate of control effort two paradoxical objectives could be utilized in future.
Acknowledgement: The authors extend their appreciation to the Deputyship for Research & Innovation, Ministry of Education in Saudi Arabia for funding this research work through the project number IFPRC-040-135-2020 and King Abdulaziz University, DSR, Jeddah, Saudi Arabia.
Funding Statement: Deputyship for Research and Innovation, Ministry of Education in Saudi Arabia, project number (IFPRC-040-135-2020).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. B. Singh, S. N. Singh and E. Kyriakides, “Intelligent control of power electronic systems for wind turbines,” in Wind Power Systems, Berlin, Heidelberg, Germany: Springer, pp. 255–295, 2010. [Google Scholar]
2. I. Erlich, W. Winter and A. Dittrich, “Advanced grid requirements for the integration of wind turbines into the German transmission system,” in 2006 IEEE Power Engineering Society General Meeting, Montreal, QC, Canada, IEEE, pp. 1–7, 2006. https://doi.org/10.1109/PES.2006.1709340. [Google Scholar]
3. H. Moradi and G. Vossoughi, “Robust control of the variable speed wind turbines in the presence of uncertainties: A comparison between H∞ and PID controllers,” Energy, vol. 90, pp. 1508–1521, 2019. [Google Scholar]
4. I. Poultangari, R. Shahnazi and M. Sheikhan, “RBF neural network based PI pitch controller for a class of 5-MW wind turbines using particle swarm optimization algorithm,” ISA Transactions, vol. 51, no. 5, pp. 641–648, 2012. [Google Scholar]
5. B. Han, L. Zhou, F. Yang and Z. Xiang, “Individual pitch controller based on fuzzy logic control for wind turbine load mitigation,” IET Renewable Power Generation, vol. 10, no. 5, pp. 687–693, 2016. [Google Scholar]
6. R. C. Dorf and R. H. Bishop, in Modern Control Systems, Harlow, England: Pearson, 2011. [Google Scholar]
7. S. Das, I. Pan and S. Das, “Performance comparison of optimal fractional order hybrid fuzzy PID controllers for handling oscillatory fractional order processes with dead time,” ISA Transactions, vol. 52, no. 4, pp. 550–566, 2013. [Google Scholar]
8. Z. Chen, X. Yuan, B. Ji, P. Wang and H. Tian, “Design of a fractional order PID controller for hydraulic turbine regulating system using chaotic non-dominated sorting genetic algorithm II,” Energy Conversion and Management, vol. 84, pp. 390–404, 2014. [Google Scholar]
9. M. Kaur, V. Kumar, V. Yadav, D. Singh, N. Kumar et al., “Metaheuristic-based deep COVID-19 screening model from chest X-ray images,” Journal of Healthcare Engineering, vol. 2021, Article ID 8829829, pp. 9, 2021. [Google Scholar]
10. V. Kumar, D. Kumar, M. Kaur, D. Singh, S. A. Idris and H. Alshazly, “A novel binary seagull optimizer and its application to feature selection problem,” in IEEE Access, vol. 9, pp. 103481–103496, 2021. [Google Scholar]
11. O. Maroufi, A. Choucha and L. Chaib, “Hybrid fractional fuzzy PID design for MPPT-pitch control of wind turbine-based bat algorithm,” Electrical Engineering, vol. 102, pp. 2149–2160, 2020. [Google Scholar]
12. A. Fathy and O. El-baksawi, “Grasshopper optimization algorithm for extracting maximum power from wind turbine installed in Al-Jouf region,” Journal of Renewable and Sustainable Energy, vol. 11, no. 3, pp. 033303, 2019. [Google Scholar]
13. H. H. Pannu, D. Singh and A. K. Malhi, “Multi-objective particle swarm optimization-based adaptive neuro-fuzzy inference system for benzene monitoring,” Neural Computing and Applications, vol. 31, pp. 2195–2205, 2019. [Google Scholar]
14. S. P. Singh, T. Prakash and V. P. Singh, “Coordinated tuning of controller-parameters using symbiotic organisms search algorithm for frequency regulation of multi-area wind integrated power system,” Engineering Science and Technology, an International Journal, vol. 23, no. 1, pp. 240–252, 2020. [Google Scholar]
15. Z. Civelek, “Optimization of fuzzy logic (Takagi-Sugeno) blade pitch angle controller in wind turbines by genetic algorithm,” Engineering Science and Technology, an International Journal, vol. 23, no. 1, pp. 1–9, 2020. [Google Scholar]
16. S. Bashetty, J. I. Guillamon, S. S. Mutnuri and S. Ozcelik, “Design of a robust adaptive controller for the pitch and torque control of wind turbines,” Energies, vol. 13, no. 5, pp. 1195, 2020. [Google Scholar]
17. M. Saadatmand, B. Mozafari, G. B. Gharehpetian and S. Soleymani, “Optimal PID controller of large-scale PV farms for power systems LFO damping,” International Transactions on Electrical Energy Systems, vol. 30, no. 6, pp. e12372, 2020. [Google Scholar]
18. M. H. Qais, H. M. Hasanien and S. Alghuwainem, “A novel LMSRE-based adaptive PI control scheme for grid-integrated PMSG-based variable-speed wind turbine,” International Journal of Electrical Power & Energy Systems, vol. 125, pp. 106505, 2021. [Google Scholar]
19. I. M. Mehedi, H. S. M. Shah, U. M. Al-Saggaf, R. Mansouri and M. Bettayeb, “Adaptive fuzzy sliding mode control of a pressure-controlled artificial ventilator,” Journal of Healthcare Engineering, vol. 2021, Article ID 1926711, pp. 1–10, 2021. [Google Scholar]
20. L. Wang and C. Singh, in Wind Power Systems, Berlin, Heidelberg, Germany: Springer-Verlag, 2010. [Google Scholar]
21. J. Jonkman, S. Butterfield, W. Musial and G. Scott, Definition of a 5-MW reference wind turbine for offshore system development (No. NREL/TP-500-38060). National Renewable Energy Lab.(NRELGolden, CO (United States2019. [Google Scholar]
22. M. Dulău, A. Gligor and T. M. Dulău, “Fractional order controllers versus integer order controllers,” Procedia Engineering, vol. 181, pp. 538–545, 2017. [Google Scholar]
23. I. M. Mehedi, U. M. Al-Saggaf, R. Mansouri and M. Bettayeb, “Stabilization of a double inverted rotary pendulum through fractional order integral control scheme,” International Journal of Advanced Robotic Systems, vol. 16, no. 4, pp. 1–9, 2019. [Google Scholar]
24. U. M. Al-Saggaf, I. M. Mehedi, M. Bettayeb and R. Mansouri, “Fractional-order controller design for a heat flow process,” Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering, vol. 230, no. 7, pp. 680–691, 2016. [Google Scholar]
25. I. M. Mehedi, “State feedback based fractional order control scheme for linear servo cart system,” Journal of Vibroengineering, vol. 20, no. 1, pp. 782–792, 2018. [Google Scholar]
26. U. M. Al-Saggaf, I. M. Mehedi, R. Mansouri and M. Bettayeb, “Rotary flexible joint control by fractional order controllers,” International Journal of Control, Automation and Systems, vol. 15, no. 6, pp. 2561–2569, 2017. [Google Scholar]
27. U. M. Al-Saggaf, I. M. Mehedi, R. Mansouri and M. Bettayeb, “State feedback with fractional integral control design based on the bode's ideal transfer function,” International Journal of Systems Science, vol. 47, pp. 149–161, 2016. [Google Scholar]
28. Z. Cao, X. Hei, L. Wang, Y. Shi and X. Rong, “An improved brain storm optimization with differential evolution strategy for applications of ANNs,” Mathematical Problems in Engineering, vol. 2015, Article ID 923698, pp. 18, 2015. [Google Scholar]
29. A. R. Jordehi, “Brainstorm optimization algorithm (BSOAAn efficient algorithm for finding optimal location and setting of FACTS devices in electric power systems,” International Journal of Electrical Power & Energy Systems, vol. 69, pp. 48–57, 2015. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |