Computers, Materials & Continua DOI:10.32604/cmc.2022.022224
Article

Design of Nonlinear Components Over a Mordell Elliptic Curve on Galois Fields

Hafeez ur Rehman*,1, Tariq Shah1, Amer Aljaedi2, Mohammad Mazyad Hazzazi3 and Adel R. Alharbi2

1Department of Mathematics, Quaid-i-Azam University, Islamabad, Pakistan
2College of Computing and Information Technology, University of Tabuk, Tabuk, 71491, Saudi Arabia
3Department of Mathematics, College of Science, King Khalid University, Abha, Saudi Arabia
*Corresponding Author: Hafeez ur Rehman. Email: hrehman@math.qau.edu.pk
Received: 31 July 2021; Accepted: 02 September 2021

Abstract: Elliptic curve cryptography ensures more safety and reliability than other public key cryptosystems of the same key size. In recent years, the use of elliptic curves in public-key cryptography has increased due to their complexity and reliability. Different kinds of substitution boxes are proposed to address the substitution process in the cryptosystems, including dynamical, static, and elliptic curve-based methods. Conventionally, elliptic curve-based S-boxes are based on prime field GF(p) but in this manuscript; we propose a new technique of generating S-boxes based on mordell elliptic curves over the Galois field GF(2n). This technique affords a higher number of possibilities to generate S-boxes, which helps to increase the security of the cryptosystem. The robustness of the proposed S-boxes against the well-known algebraic and statistical attacks is analyzed to classify its potential to generate confusion and achieve up to the mark results compared to the various schemes. The majority logic criterion results determine that the proposed S-boxes have up to the mark cryptographic strength.

Keywords: Galois field; elliptic curve; S-box; nonlinearity

1  Introduction

The rapid growth of digital technology and network communications has improved electronic data transmission across many networks over the last few decades. Since most communication networks are open, the privacy of sensitive data transmission across that network is controversial, raising numerous concerns. The study of cryptography is the study of how to address the challenge of secure transformation. Therefore, Cryptographers have paid close attention to the security of sensitive data in recent decades. The researchers have suggested different types of informative security techniques to combat modern information security attacks. Shift cipher, hill cipher, transposition cipher, and various versions were the most prominent classical cryptosystems. In many well-known cryptosystems, including AES, S-box is used as a nonlinear component [1]. The safety of such cryptosystems is therefore dependent on the cryptographic properties of respective S-boxes. The Rijndael block cipher [2] has been adopted by the National Institute of Standards and Technology (NIST) as an Advanced Encryption Standard (AES). Because of the significance of AES, many researchers investigated the cryptographic characteristics of its S-box. Since S-box plays an essential role in AES, numerous cryptographers have proposed different S-box transformations based on various mathematical structures. An S-boxes passed specific tests, such as nonlinearity, approximation, strict avalanche, and bit independence. In that case, it is cryptographically enough to obtain the desired confusion. Several schemes based on different structures were designed to develop this nonlinear component of the block ciphers [3–7]. So, there is a lack of a parallel and less intricate scheme to design a nonlinear component of the block cipher.

1.1 Related Work

Elliptic curves are also used in the development of powerful cryptosystems. Elliptic curve-based techniques are the most widely deployed to increase the security of information. Specifically, We will concentrate on elliptic curve cryptography (ECC) and the various methods put forward by various researchers throughout this area. Miller [8] proposed the first scheme to use the elliptic curve as a public key cryptosystem in 1985. In addition, a cryptosystem is supplied that is 20% efficient than the Diffie-Hellman algorithm. Reference [9] presents a relationship between the nonlinearity of rational functions over F2n and the number of points on the associated hyperelliptic curve and obtain a lower bound on the nonlinearity of rational typed vector Boolean functions over F2n. The idea of a discrete logarithmic issue is utilized to build a highly safe, fast, and efficient security system in [10]. An efficient approach to multiply the elliptic curve points and their resources are compared with binary and non-adjacent (NAF) methods are presented in [11]. It is observed that ECC with a smaller key length is more secure than RSA with a larger key size. In [12], an elliptic curve is utilized over a prime field to generate elliptic curve points and add the x, y coordinates of each point lying on the elliptic curve followed by modulo function to construct the different number of 4×4 S-boxes. A method for constructing prime field dependent 8×8 substitution boxes (S-boxes) are presented in [13]. In this work, they use the x-coordinate of an elliptic curve followed by the modulo operation to construct the different number of prime field-dependent 8×8 S-boxes. Reference [14] Present novel approaches for creating S-boxes utilizing total order on an elliptic curve (EC) over a prime field. Instead of the more classical group rule that costs computationally, a search method is employed to generate an EC efficiently. The Construction technique for the S-boxes uses the x-coordinates of the points of order elliptic curve (OEC). These techniques are capable of constructing a different number of 8×8 S-boxes. Still, their output is unpredictable because they may or may not generate an S-box for any input parameter and are independent of the underlying elliptic curve. Recently Farwa et al. [15] presented an excellent and novel method for constructing a 4×4 S-box by utilizing an elliptic curve over the Galois fieldGF(24). In this study, they applied group structure on the elements of the elliptic curve having the same order as the order of extension field and used the features of the specified elliptic curve to design a bijective Boolean function.

1.2 Motivation

The following are the primary motivations for this study to improve the strength of S-boxes over elliptic curves and their application in different cryptosystems.

1.    Usually, the elliptic curves are considered over prime fields to construct S-boxes, and the generation of S-box is not possible for each input EC.

2.    Moreover, the prime field dependent S-boxes do not address the maximum number of S-box possibilities.

3.    In [15], they considered elliptic curve over the 16 order Galois field GF(24) and designed a single 4×4 S-box. Whereas the method is given in this study the binary Galois field extension GF(2n),where n=8 or an odd n≥9 is considered and develop an effective scheme for 8 × 8 S-boxes construction. Moreover, rather than prevailing 8×8 S-box designing Galois field GF(28) dependent schemes, this study brings a more comprehensive and complex approach in which one could use the Galois fields GF(2n) of order 256, 512 and higher.

1.3 Our Contribution

The drawbacks of existing schemes prompt us to present this new scheme. The following steps will explain how to sum up the entire manuscript.

1.    We used a simple method instead of arduous S-boxes designing algorithms with outstanding results to construct 8 × 8 S-boxes in the proposed work.

2.    In this work, to generate elliptic curve points, we considered Mordell elliptic curve interpreted over the Galois fields GF(2n) of order 256, 512 and higher.

3.    Inverse function under prescribed Galois field and primitive irreducible polynomial as for the generation of elliptic curve points applied to the pairs of elliptic curve points.

4.    To get the different number of S-boxes, one can vary the parameter b of the Mordell elliptic curve or alter the primitive irreducible polynomial of a degree corresponding to the Galois field over the binary field.

The remaining paperwork is as follows: In Section 2, we offered some preliminary information. Section 3 discusses the proposed algorithm. In Section 4, we evaluated the designed S-boxes performance indices and compared them to other preexisting S-boxes. The application of designed S-boxes in image encryption algorithm and majority logic criterion is also carried out in Section 4. In the end, Section 5 presents some convincing remarks.

2  Preliminaries

Some basic and essential concepts about the elliptic curves, Galois fields, Euler's totient function, irreducible polynomials, and primitive polynomials are reviewed in this section.

2.1 Galois Fields

Galois fields, often known as Finite fields, are the foundations of any cryptographic theory, denoted byGF(pn), where p is any prime and n∈Z+ [16]. Ifn=1, then GF(pn) is known as Prime field. Ifn>1, then GF(pn) is known as the extension field. The order of the Galois fields ispn.

2.2 Euler's Totient Function

Reference [17] presents Euler's phi function, also called Euler's totient function φ(n) gives the numbers not exceeding n and having gcd 1 with n. By convention φ(0)=1, and for the number n, which is not prime.

φ(n)=n(1−1p1)(1−1p2)…(1−1pr) Where the product runs over all primes pdividingn. φ(p)=p−1, where p prime.

2.3 Primitive Polynomials and Galois Fields

In [18], Some basic definitions are stated in this section of reducible, irreducible, and primitive polynomials over the Galois field. In this section, p=2 for GF(pn) if not otherwise mentioned.

2.3.1 Definition

There is precisely one finite field for every prime number p and positive integer n having orderpn. All the elements of this finite field except zero forms a cyclic group under multiplication. As a result, there is an element β which generates all the elements of this finite field except zero andβpn−1=1. The generators of GF(pn) is known as primitive elements.

2.3.2 Definition

If f∗(x) is a polynomial and we cannot factories it into two additional polynomials whose degree is less than f∗(x), then f∗(x) is irreducible in GF(p)[X], and primitive if f∗(x)is irreducible, and all the roots of the polynomial are primitive elements inGF(pn). The total number of binary primitive irreducible polynomials of degree n isφ(2n−1)n, where φ is Euler's totient function.

2.3.3 Definition

If f∗(x) is a polynomial having degree m≥1 such that f∗(0)≠0, Then there exists n∈Z+ and n≤pm−1 such thatf∗(x)|(xn−1). An irreducible polynomial f∗(x)∈GF(p)[X] having degree m satisfying min\; n∈N⁡{n:f∗(x)|xn−1} =pm−1, then the polynomial is called primitive. If a polynomial of degree m is primitive, then n=pm−1.

2.4 Lemma

For any prime p greater than 3 with the condition that p≡2(mod3) the Mordell elliptic curve, which is of the form: y2=x3+b has exactly p+1 points, and there is no repetition in the y-coordinates of points lying on the elliptic curve such that, for each integer y∈[0,1] there exists precisely one integer x∈[0,1] where (x,y) are points lying on the mordell elliptic curve, Washington [19](6.6(c),p.188).

2.5 Construction of GF(2n)

The Galois field GF(2n) is defined as F2[x]⟨f∗(x)⟩, where ⟨f∗(x)⟩ is a maximal ideal of F2[X], generated by irreducible polynomial f(x), having degreen. The order of the field is 2nand each polynomial of the field have degree at most n−1 having coefficients inF2, [15].

2.5.1 Addition and Subtraction in GF(2n)

As we work on the field of characteristic2 so the operation of addition and subtraction is the same. The addition of polynomials is very simple in the Galois field, [16].

2.5.2 Multiplication inGF(2n)

Let f∗(x),g∗(x)∈GF(2n)[X], and let h∗(x) be the primitive polynomial whose degree is n. Then their product denoted by m∗(x) is given as.

m∗(x)=(f∗(x)⋅g∗(x))modh∗(x)

And if

(f∗(x)⋅a∗(x))modh∗(x)=1

Then a∗(x) is called multiplicative inverse of f∗(x).

Note that whenever we multiply two polynomials or to find the multiplicative inverse of polynomial, both require coefficient modulo 2and the polynomials modulo h(x).

3  Proposed S-Box Algorithm

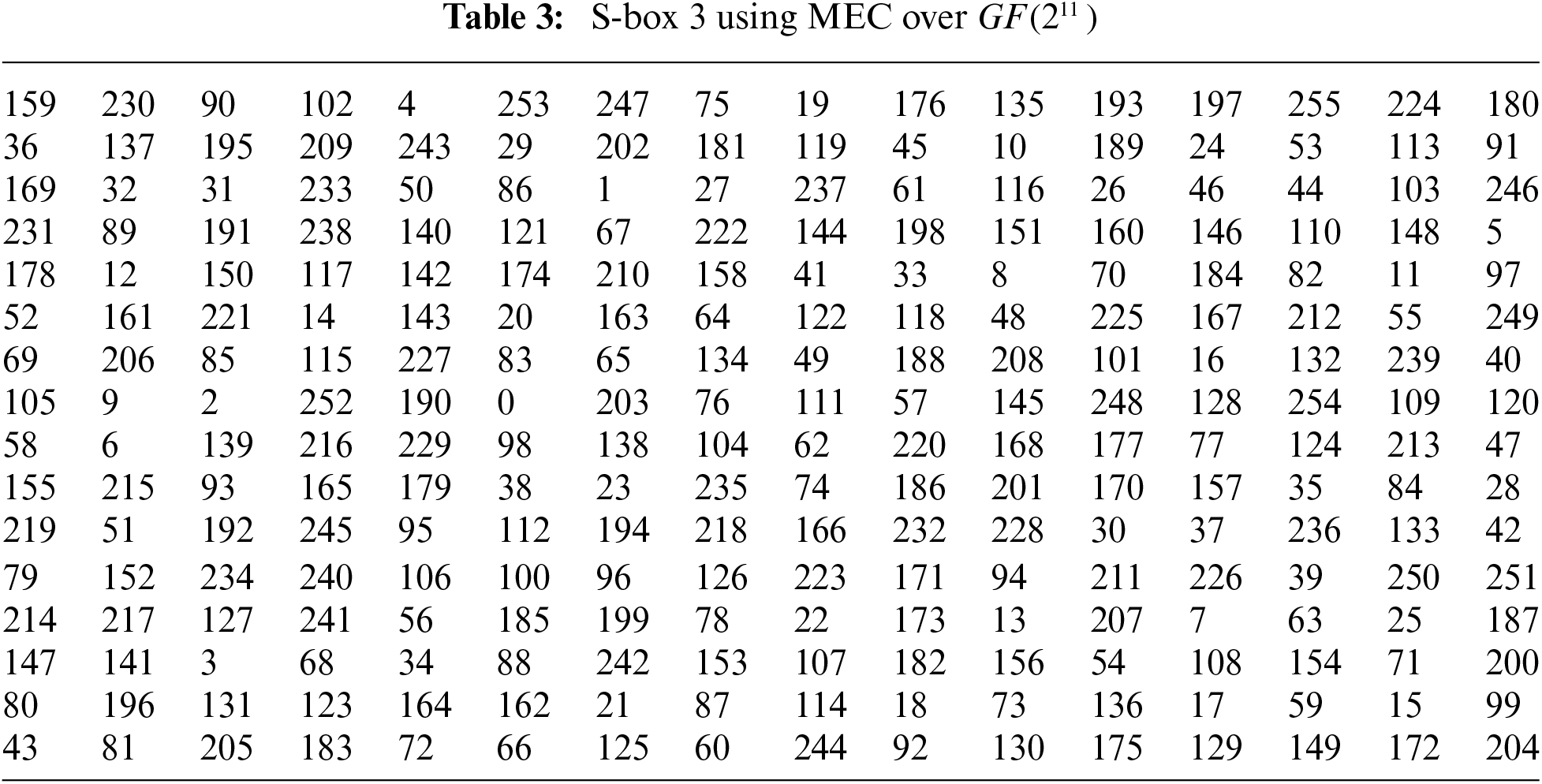
In this section, we discussed two different S-box algorithm approaches. In the first technique, the nonlinear component of a block cipher is developed using Mordell elliptic curve interpreted over 256 order Galois field. In the second technique, instead of deploying 256 order Galois field dependent S-boxes, we construct a different number of 8×8 S-boxes using Mordell elliptic curve over GF(2n), for different odd values ofn≥9.

3.1 Construction of S-Box Using Mordell Elliptic Curve Over Galois Field GF(28)

Choose primitive polynomial

f(x)=x8+x4+x3+x2+1(1)

One can choose independently any other primitive polynomial of degree 8with coefficients in a binary field. Choose an elliptic curve of the form:

E:y2=x3+b(2)

where b is any element of Galois field except zero. The specialty of this curve is that when we choose Mordell elliptic curve over GF(28), the number of elements lying on the elliptic curve is 28+1 including the point at infinity. The other thing we see that whenever we choose Mordell elliptic curve over GF(28), then there is no repetition in the x-coordinates of elliptic curve points, and repetition is accrued in y-coordinates. The strength of this curve is that it has 256 distinct pairs of elements (x,y) excluding the point at infinity over the GF(28). Our requirement to generate an 8 × 8 S-box with 256 distinct numbers is fulfilled by taking the x-coordinates of each ordered pair of elliptic curve points because there is no repetition in the x-coordinates elements and gives us precisely 256 elements. Apply inverse function under GF(28) on each element of x-coordinate except zero elements with primitive irreducible polynomial given in Eq. (1). Finally, we have S-box having nonlinearity 112, which is given in Tab. 1. Fig. 1 depicts the flowchart of the proposed algorithm.

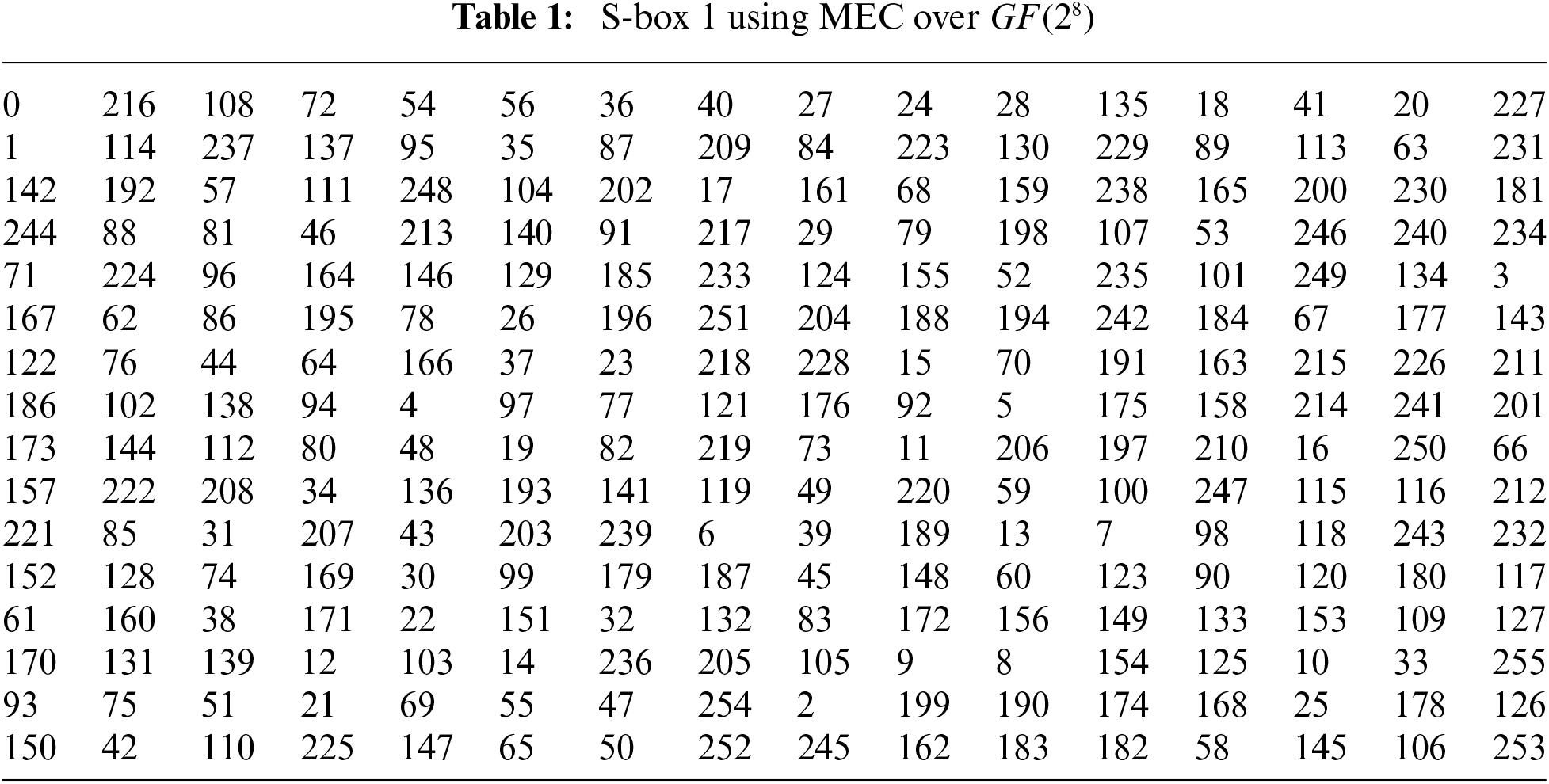
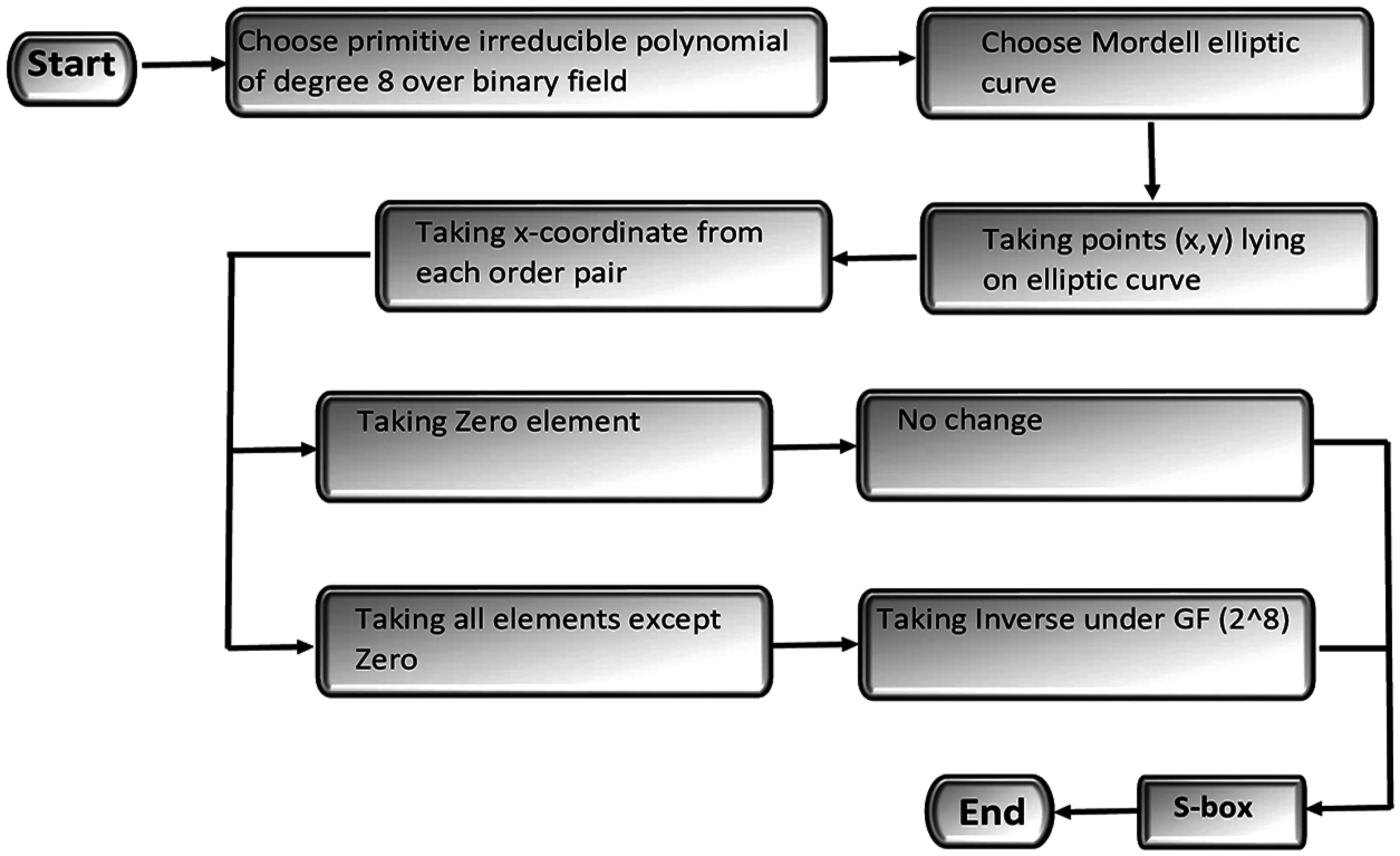
Figure 1: Proposed S-box scheme based on MEC over GF(28)

3.2 Construction of S-Box Using Mordell Elliptic Curve Over Galois Field GF(2n)

The Galois fields GF(2n) of order 512, 1024 are utilized in this work to establish a more comprehensive and effective approach for the designing of a large number of distinct 8×8 S-boxes is developed.

3.2.1 Construction of S-Box Using Mordell Elliptic Curve over Galois fieldGF(29)

Firstly, choose primitive polynomial.

f(x)=x9+x4+1(3)

Over the binary field, any arbitrary primitive polynomial of degree 9 with coefficients in the binary field can be chosen independently. Choose elliptic curve.

E:y2=x3+b(4)

where bis any element of Galois field except zero.

When we choose Mordell elliptic curve over GF(29), the number of elements lying on the elliptic curve is 29+1 including the point at infinity. In this case, there is no repetition in x-coordinates of points lying on elliptic curve and gives us precisely 0−511 elements, and no repetition is accrued in the y-coordinates of elliptic curve points and gives us random numbers. The specialty of this curve is that it has 512 distinct pairs of elements (x,y) except point at infinity over GF(29). Take y-coordinate from each point lying on the elliptic curve because of no repetition and randomness. Apply inverse function under GF(29) on each element of y-coordinates except zero with primitive irreducible polynomial given in Eq. (3) As we required 8×8 S-box which has 256 distinct numbers, takes all elements randomly, which is less than 256. Finally, we get different S-boxes by giving different values to the parameter b. As the number of primitive irreducible polynomials of degree9 over GF(2) is48, so through this technique, we can construct different 511×48 S-boxes. The S-box through this technique is presented in Tab. 2, having nonlinearity106.25. The flow chart of the proposed scheme is given in Fig. 2.

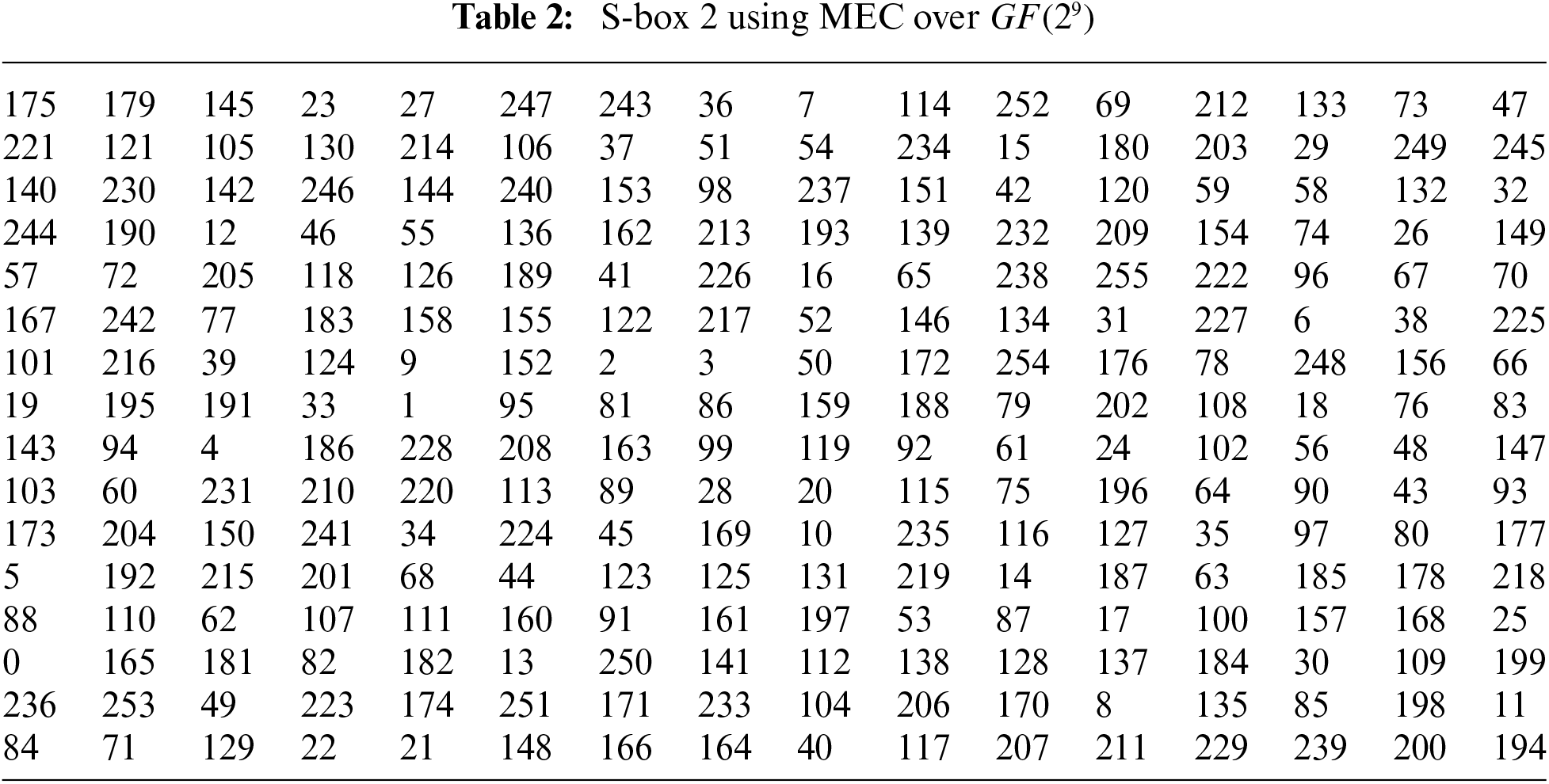
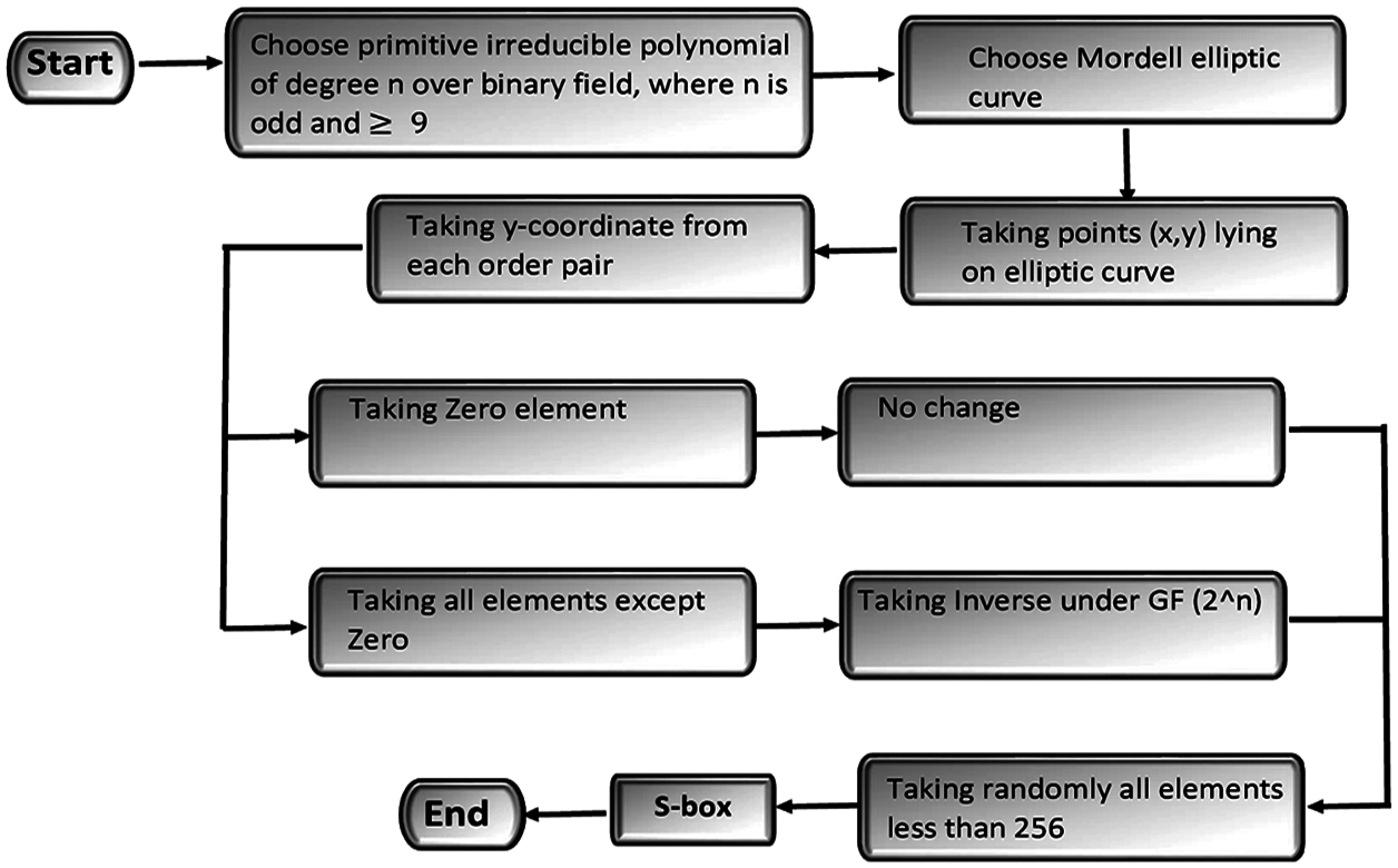
Figure 2: Proposed S-box scheme based on MEC over GF(2n)

3.2.2 Construction of S-Box Using Mordell Elliptic Curve Over Galois Field GF(211)

Choose primitive polynomial.

f(x)=x11+x4+1(5)

In the binary field, any arbitrary primitive irreducible of degree 11with coefficients in the binary field can be selected independently. Choose Mordell elliptic curve.

E:y2=x3+b(6)

where b∈GF(211)−{0}. The specialty of this elliptic curve over GF(211) is that the number of points (x,y) lying on an elliptic curve is 211+1 including the point at infinity. In this case, there is no repetition in y-coordinates of elliptic curve points and random numbers, while in x-coordinates, there is no repetition but in the sequence. Skip the x-coordinates and take y-coordinates of each elliptic curve point to construct the robust S-boxes. Apply inverse function under GF(211) on each y-coordinate of elliptic curve points except zero with primitive irreducible polynomial given in Eq. (5) As we need 256 distinct numbers to construct 8×8 S-boxes, we randomly choose all elements that are lee than 256. To construct a different number of S-boxes, one can vary the value of b. As the total number of primitive polynomials of degree 11 over binary field is176, one can construct the different number of 2047×176 S-boxes through this technique. S-box through technique is given by Tab. 3, and the flow chart is presented in Fig. 2.

4  Security Analysis

In this section, we mainly discussed the algebraic properties of newly designed S-boxes. We analyzed the cryptographic features of our proposed nonlinear component and compared the results to current benchmarks. Our proposed technique has clear advantages as compared to other algorithms as mentioned in the below tables.

4.1 Nonlinearity

To calculate the nonlinearity of a given S-box, one can calculate the smallest distance of Boolean function h from a set of affine functions. An unknown individual might identify the information and actions of concerned Boolean functions if the proposed nonlinearity is insufficient. The nonlinearity of the S-box measures the confusion ability of the S-box over GF(28) in [20]. Our S-box average nonlinearity is the highest among all S-boxes based on the elliptic curve or other chaotic maps. Minimum and maximum nonlinearity are also better than many other S-boxes.

4.2 Strict Avalanche Criterion

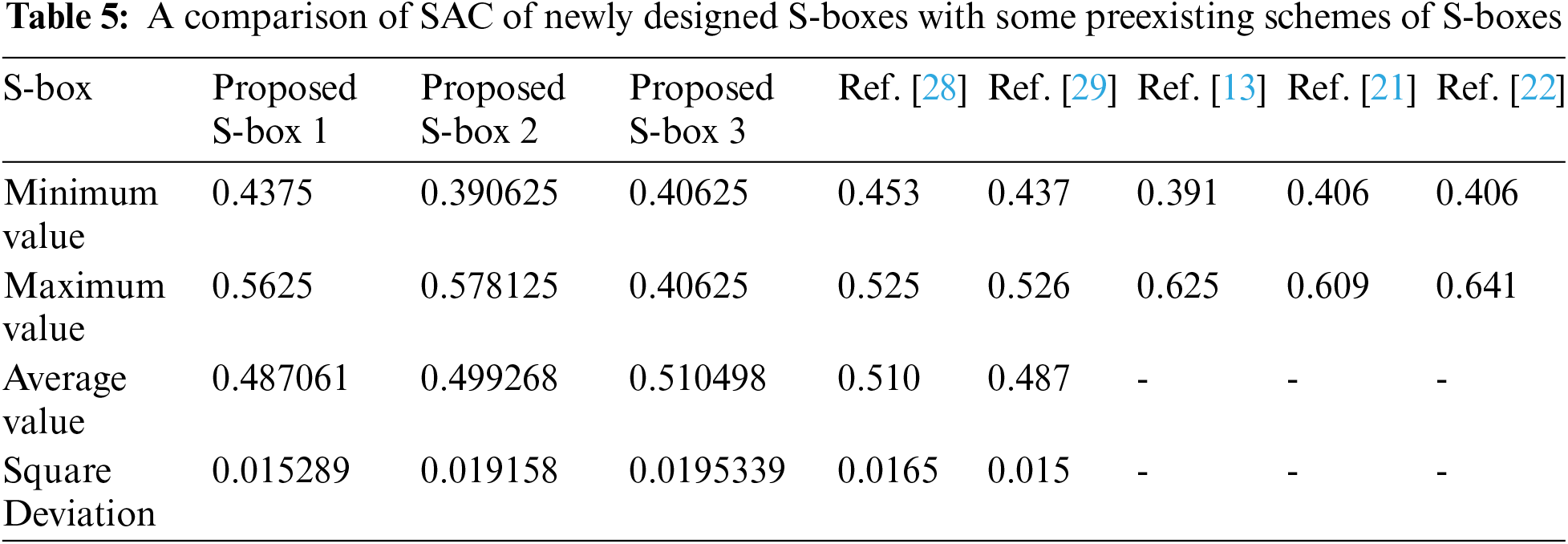
In [27], Webster and Tavares invented the theory of SAC in 1985. The criteria of SAC are fulfilled when the output bits deviation probability is 1/2, in the case when a single input bit is complemented. A 0.5 value of SAC assures that the correlation between input and output bits is minimal and makes the encryption procedure secure against various leakages. The SAC values of our S-boxes are close to 0.5, and the square deviation is also comparable to other existing S-boxes mentioned in Tab. 5. It clearly illustrates that the proposed S-boxes meet the requisite criteria better than different preexisting S-boxes SAC values.

4.3 Bit Independent Criteria

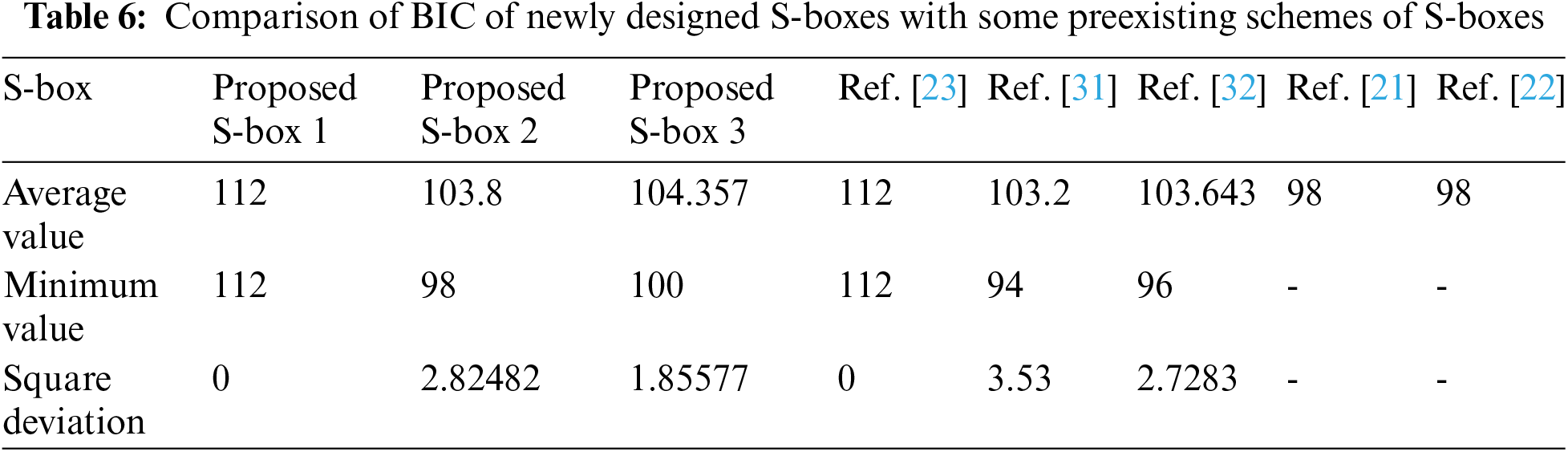
The BIC is an important test to evaluate the diffusion creation capability of the S-box. In [30], BIC is started off to check the dependence of two output bits when a single input bit is placed.

The BIC parameters are as follows:

Leth1∗,h2∗,…,h8∗be the component of Boolean functions of the S-box, then S-box satisfies BIC when the below two conditions are fulfilled:

The function h∗h∗=hi∗⊕hj∗ where (i≠j,1≤i,j≤8) is highly nonlinear.

SAC criteria satisfied.

The BIC of the newly designed S-boxes is calculated using this technique by assessing the nonlinearity and SAC of hi∗⊕hj∗. The average and minimum value of the BIC nonlinearity of the proposed S-boxes is significantly higher than other existing S-boxes mentioned in Tab. 6. The square deviation of our S-boxes is comparatively excellent when compared with different schemes. BIC nonlinearity of designed S-boxes is significantly greater than other preexisting S-boxes, as required.

4.4 Differential Approximation Probability

The DAP of an S-box is used to assess its resistance against differential approximation attacks. Reference [33] Introduces the probability of differential approximation to describe the probability effect of a reasonable difference in the input bit on the resulting output bit difference. The lower the value of DAP, the more secure S-box is against differential approximation attacks. The DAP of the proposed S-boxes is better than the various S-boxes mentioned in Tab. 7.

4.5 Linear Approximation Probability

The linear approximation probability is discussed in [34]. This determines the probability of getting a linear approximation of a given S-box. The LAP of the S-box is calculated by the correlation of input and output bits. If an S-box has a low LAP, it is highly resistant to linear attacks. The LAP value of the proposed S-boxes is very low as compared to other S-boxes mentioned in Tab. 7.

4.6 NPCR and UACI Analysis

Hackers typically attempt to make minor changes to the original image before encrypting it with the proposed technique. Examine the original image with the image with changes after substitution. They discover the relationship between the original and encrypted images using this technique. Two significant studies are used to compute the influence of a one-pixel change in the original image on the image after substitution. The findings of the two most well-known tests, Unified averaged changed intensity (UACI) and several pixels changing rate (NPCR), are described in this part to measure the system's resistance to differential attacks. Mathematically NPCR is defined as

NPCR=∑m∗,n∗⁡B(m∗,n∗)K∗×L∗×100%

And UACI is defined as

UACI=1K∗×L∗[∑m∗,n∗⁡abs(E1∗(m∗,n∗)−E2∗(m∗,n∗))255]×100%

where K∗ presents width and L∗presents the height of the image. The NPCR and UACI values of proposed S-boxes compared to other existing schemes are presented in Tab. 8.

4.7 Majority Logic Criterion Test

Reference [41] provides a detailed description of the majority logic criteria (MLC). These evaluations compare plaintext and encrypted images and so provide an accurate assessment of encryption technology. MLC performs statistical studies on both plain and encrypted data. MLC is essential in statistical feature analysis, such as in the enciphering process manipulation of data, which results in modifications in the plain data. MLC specifies a criterion for evaluating the outcomes of several statistical investigations, such as homogeneity, energy, correlation, contrast, and entropy. Its evaluation determined whether the S-box is appropriate for the use of an image encryption application or not. The 256×256 image of Lena is used for MLC analysis, and the result of the proposed scheme is given in Tab. 9. The MLC analysis indicated that the diffusion level of the newly designed S-boxes is up to the mark. All this can be seen in Fig. 3.

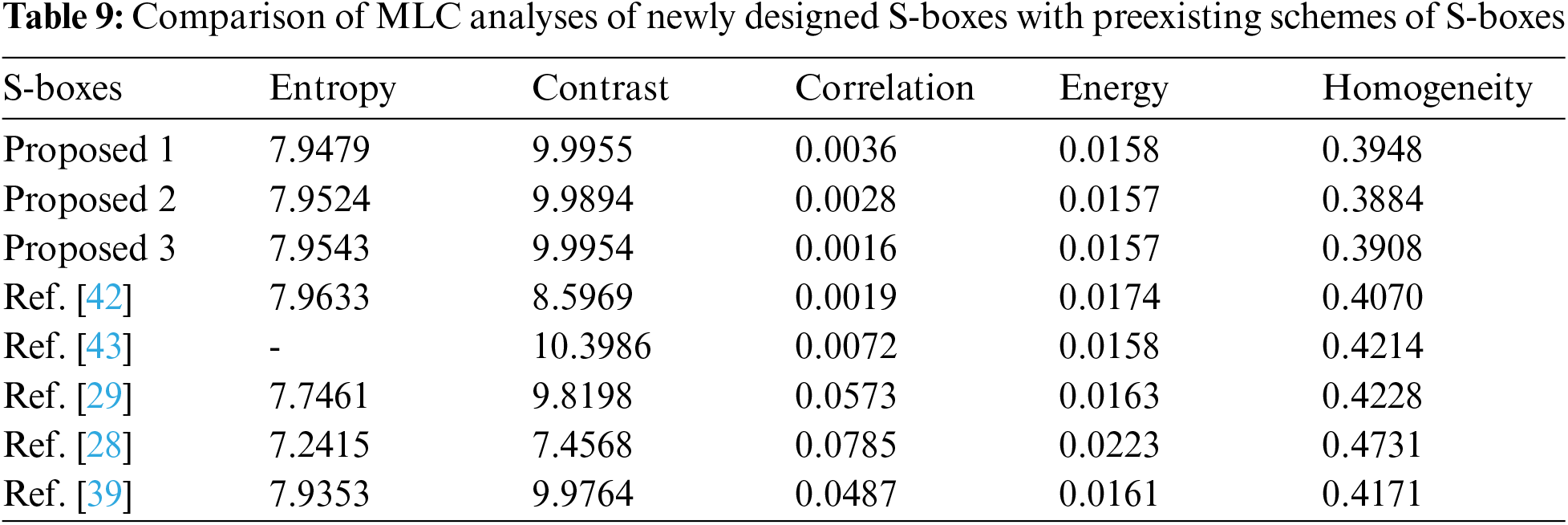
Figure 3: (O) Original lena image (1, 2, 3) Encrypted lena image using S-box 1, S-box 2, and S-box 3

4.8 Comparative Analysis

The proposed algorithms of S-boxes construction are compared with other S-box designing schemes to assess their efficiency and resilience against various cryptographic attacks. The following point by point comparison is presented.

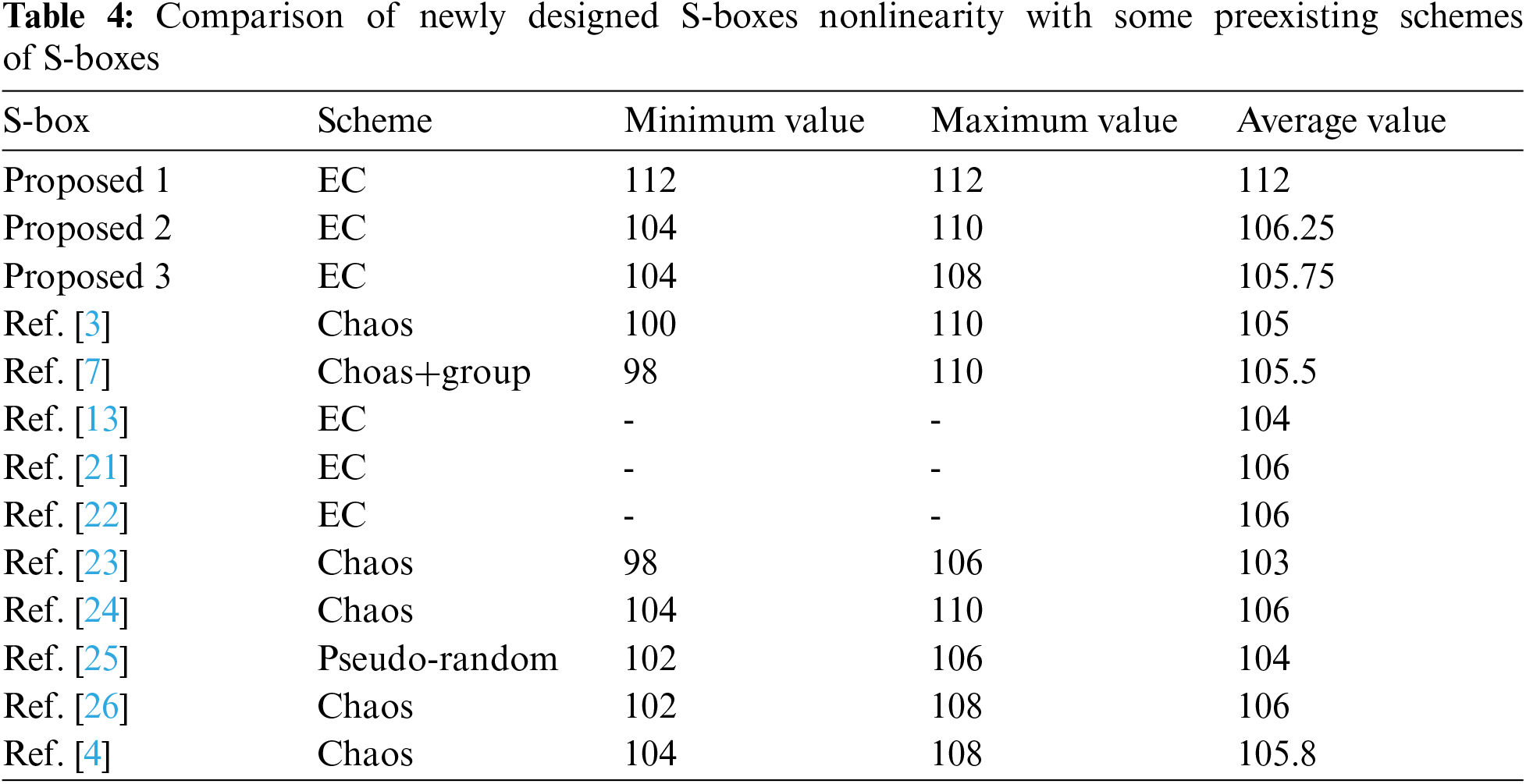
1.    Tab. 4 shows some S-boxes based on chaos and elliptic curves with low nonlinearity compared to the proposed algorithm. The features of elliptic curves are used to construct nonlinear components of a block cipher in [13,21,22], but all work is done over the prime field. Instead of designing prime field dependent S-boxes, we used an innovative technique to consider elliptic curves over binary extension fields, and our results outperformed these algorithms.

2.    The proposed S-boxes BIC and SAC results are much better than the existing algorithms [21–22,28] shown in Tabs. 5 and 6. In addition, our S-box BIC value is the optimal value. Consequently, the proposed S-boxes have a far more impressive diffusion creation power than other S-boxes.

3.    The proposed S-boxes have lower LP values than the other schemes [13,21,28,32] S-boxes values shown in Tab. 7. As a result, the proposed algorithm is highly resistant to linear attacks and generates significant data confusion. Furthermore, the proposed S-boxes have lower DP values than the S-boxes in Tab. 7, making our scheme more resistant to various attacks.

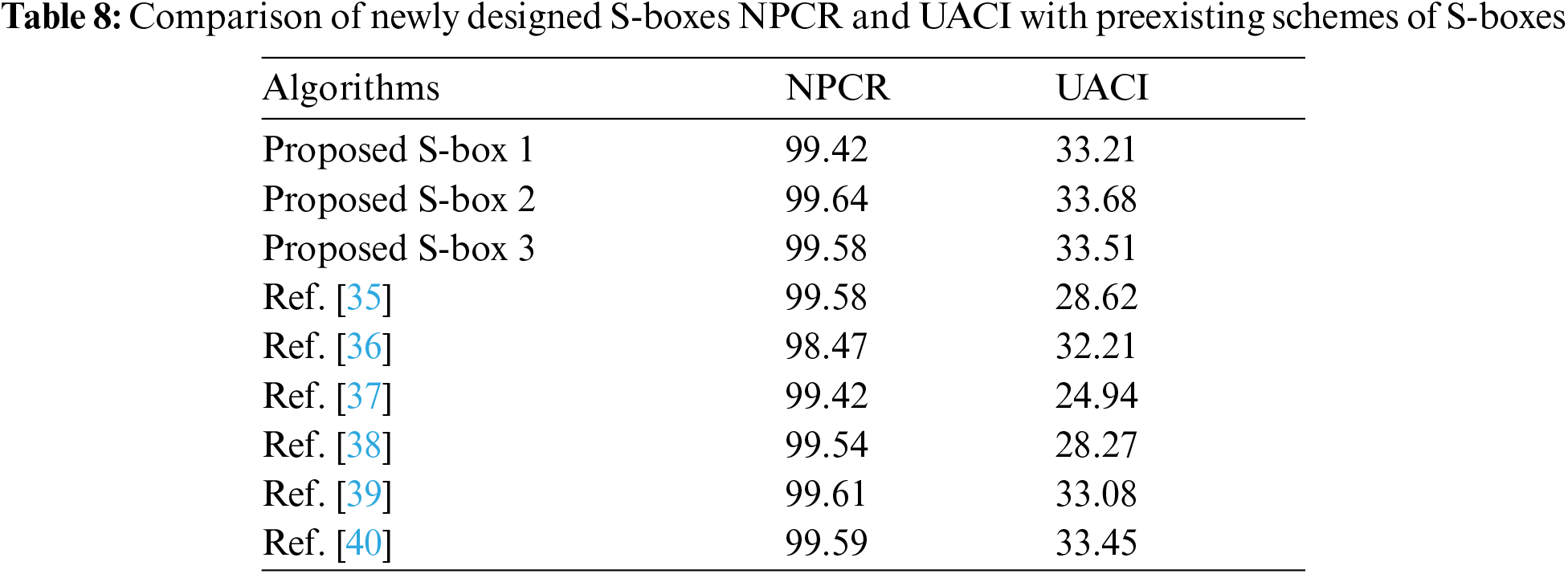
4.    In terms of NPCR and UACI, the proposed S-boxes outperform the schemes presented in Tab. 8. Compared to techniques [28–29,39,42], the MLC analysis of the proposed algorithm provided in Tab. 9 is considerably more refined, making our algorithm excellent for image encryption.

From comparative analysis, we may realize that the proposed S-boxes design method has an upright resistance against cryptanalysis compared to the prevailing S-box algorithms. According to the MLC test, the proposed S-boxes have outstanding image encryption features.

5  Conclusion

In this paper, the complex structure of elliptic curves defined over the binary Galois field extension GF(2n),where n=8 or an odd had been used to develop an efficient method for S-box construction. Generally, the elliptic curves are considered over prime fields. The performance of the newly designed S-boxes over Galois field n≥9GF(2n) showed relatively better results as compared to the prevalent S-box construction schemes. Also, we have utilized S-boxes for the substitution process, and outcomes are considerably better than various existing schemes. From the futuristic point of view, the proposed method can be extended to prove some general results about the Mordell elliptic curve over the Galois field extension GF(pn) of the prime field GF(p).

Funding Statement: The author extends their gratitude to the Deanship of Scientific Research at King Khalid University for funding this work through the research groups program under Grant Number R. G. P. 2/150/42.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  C. E. Shannon, “Communication theory of secrecy systems,” The Bell System Technical Journal, vol. 28, no. 4, pp. 656–715, 1949. [Google Scholar]

 2.  J. Daemen and V. Rijmen, “The Rinjdael block cipher: AES proposal,” in First Candidate Conference (AES1), pp. 343–348, 1999. [Google Scholar]

 3.  A. Belazi, A. Ahmad and A. E. Latif, “A simple yet efficient S-box method based on chaotic sine map,” Optic, vol. 130, pp. 1438–1444, 2017. [Google Scholar]

 4.  G. Liu, W. Yang, W. Liu and Y. Dai, “Designing S-boxes based on 3-D four-wing autonomous chaotic system,” Nonlinear Dynamics, vol. 82, no. 4, pp. 1867–1877, 2015. [Google Scholar]

 5.  U. Çavuşoğlu, A. Zengin, I. Pehlivan and S. Kaçar, “A novel approach for strong S-box generation algorithm design based on chaotic scaled zhongtang system,” Nonlinear Dynamics, vol. 87, no. 2, pp. 1081–1094, 2017. [Google Scholar]

 6.  H. Isa, N. Jamil and M. R. Zaba, “Construction of cryptographically strong S-boxes inspired by bee waggle dance,” New Generation Computing, vol. 34, no. 3, pp. 221–238, 2016. [Google Scholar]

 7.  M. Khan and T. Shah, “An efficient construction of substitution box with fractional chaotic system,” Signal, Image and Video Processing, vol. 9, no. 6, pp. 1335–1338, 2015. [Google Scholar]

 8.  V. S. Miller, “Use of elliptic curves in cryptography,” in Conf. on the Theory and Application of Cryptographic Techniques, Springer, Berlin, Heidelberg, pp. 417–426, 2000. [Google Scholar]

 9.  H. C. Jung, C. Seongtaek and P. Choonsik, “S-boxes with controllable nonlinearity,” in Int. Conf. on the Theory and Application of Cryptographic Techniques, Berlin, Heidelberg, Springer, pp. 286–294, 1999. [Google Scholar]

10. N. Koblitz, A. Menezes and S. Vanstone, “The state of elliptic curve cryptography,” Designs, Codes and Cryptography, vol. 19, no. 2, pp. 173–193, 2000. [Google Scholar]

11. R. K. Kodali, K. H. Patel and N. Sarma, “Energy efficient elliptic curve point multiplication for WSN applications,” in National Conf. on Communications (NCCIEEE, IIT Delhi, pp. 1–5, 2013. [Google Scholar]

12. I. Khalid, S. S. Jamal, T. Shah, D. Shah and M. M. Hazzazi, “A novel scheme of image encryption based on elliptic curves isomorphism and substitution boxes,” IEEE Access, vol. 9, pp. 77798–77810, 2021. [Google Scholar]

13. U. Hayat, N. A. Azam and M. Asif, “A method of generating 8 × 8 substitution boxes based on elliptic curves,” Wireless Personal Communications, vol. 101, no. 1, pp. 439–451, 2018. [Google Scholar]

14. U. Hayat and N. A. Azam, “A novel image encryption scheme based on an elliptic curve,” Signal Processing, vol. 155, pp. 391–402, 2019. [Google Scholar]

15. S. Farwa, A. Sohail and N. Muhammad, “A novel application of elliptic curves in the dynamical components of block ciphers,” Wireless Personal Communications, vol. 115, no. 2, pp. 1309–1316, 2020. [Google Scholar]

16. C. J. Benvenuto, “Galois field in cryptography,” University of Washington, vol. 1, no. 1, pp. 1–11, 2012. [Google Scholar]

17. E. W. Weisstein, “Totient function,” https://Mathworld.Wolfram.Com/, 2003. [Google Scholar]

18. S. Maitra, K. C. Gupta and A. Venkateswarlu, “Results on multiples of primitive polynomials and their products over GF (2),” Theoretical Computer Science, vol. 341, no. 1–3, pp. 311–343, 2005. [Google Scholar]

19. L. C. Washington, “Elliptic curves,” Number Theory and Cryptography, CRC press: Chapman and Hall, CRC, 2008. [Google Scholar]

20. W. Meier and O. Staffelbach, “Nonlinearity criteria for cryptographic functions,” in Workshop on the Theory and Application of Cryptographic Techniques, Springer, Berlin, Heidelberg, pp. 549–562, 1989. [Google Scholar]

21. N. A. Azam, U. Hayat and I. Ullah, “An injective S-box design scheme over an ordered isomorphic elliptic curve and its characterization,” Security and Communication Networks, vol. 18, pp. 9, 2018. [Google Scholar]

22. N. A. Azam, U. Hayat and I. Ullah, “Efficient construction of a substitution box based on a mordell elliptic curve over a finite field,” Frontiers of Information Technology, Electronic Engineering, vol. 20, no. 10, pp. 1378–1389, 2019. [Google Scholar]

23. M. A. Gondal, A. Raheem and I. Hussain, “A scheme for obtaining secure S-boxes based on chaotic baker's map,” 3D Research, vol. 5, no. 3, pp. 17, 2014. [Google Scholar]

24. U. Cavusoglu, A. Zengin, I. Pehlivan and S. Kacar, “A novel approach for strong S-box generation algorithm design based on chaotic scaled Zhongtang system,” Nonlinear Dynamics, vol. 87, no. 2, pp. 1081–1094, 2017. [Google Scholar]

25. K. Kazlauskas, G. Vaicekauskas and R. Smaliukas, “An algorithm for key-dependent S-box generation in block cipher system,” Informatica, vol. 26, no. 1, pp. 5165, 2015. [Google Scholar]

26. F. U. Islam and G. Liu, “Designing S-box based on 4D-4wing hyperchaotic system,” 3D Research, vol. 8, no. 1, pp. 9, 2017. [Google Scholar]

27. A. F. Webster and S. E. Tavares, “On the Design of S-boxes,” in Conf. on the Theory and Application of Cryptographic Techniques, Springer, Berlin, Heidelberg, pp. 523–534, 1985. [Google Scholar]

28. S. Farwa, T. Shah and L. Idrees, “A highly nonlinear S-box based on a fractional linear transformation,” Springer Plus, vol. 5, no. 1, pp. 1–12, 2016. [Google Scholar]

29. Y. Naseer, T. Shah, D. Shah and S. Hussain, “A novel algorithm of constructing highly nonlinear sp-boxes,” Cryptography, vol. 3, no. 1, pp. 6, 2019. [Google Scholar]

30. A. F. Webster and S. E. Tavares, “On the design of S-boxes. advances in cryptology,” Crypt 085 Lncs, vol. 218, pp. 523534, 1986. [Google Scholar]

31. K. F. Zkayna, “Construction of robust substitution boxes based on chaotic systems,” Neural Computing and Applications, vol. 31, no. 8, pp. 33173326, 2019. [Google Scholar]

32. A. Razaq, A. Yousaf, U. Shuaib, N. Siddiqui, A. Ullah et al., “A novel construction of substitution box involving coset diagram and a bijective map,” Security and Communication Networks, vol. 2017, pp. 1–16, 2017. [Google Scholar]

33. E. Biham and A. Shamir, “Differential cryptanalysis of DES-like cryptosystems,” Journal of Cryptology, vol. 4, no. 1, pp. 3–72, 1991. [Google Scholar]

34. T. Helleseth, “Advances in cryptology,” in Workshop on the Theory and Application of Cryptographic Techniques, Lothfus, Norway, Springer, vol. 765, 2003. [Google Scholar]

35. K. Loukhaoukha, J. Y. Chouinard and A. Berdai, “A secure image encryption algorithm based on Rubik's cube principle,” Journal of Electrical and Computer Engineering, vol. 12, no. 7, pp. 7–14, 2012. [Google Scholar]

36. G. A. Sathishkumar and D. N. Sriraam, “Image encryption based on diffusion and multiple chaotic maps,” arXiv preprint arXiv, vol. 10, pp. 1103.3792, 2011. [Google Scholar]

37. C. K. Huang and H. H. Nien, “Multi chaotic system S-Based pixel shuffle for image encryption,” Optics Communications, vol. 282, no. 11, pp. 2123–2127, 2009. [Google Scholar]

38. C. K. Huang, C. W. Liao, S. L. Hsu and Y. C. Jeng, “Implementation of gray image encryption with pixel shuffling and gray-level encryption by single chaotic system,” Telecommunication Systems, vol. 52, no. 2, pp. 563–571, 2013. [Google Scholar]

39. S. Hussain, S. S. Jamal, T. Shah and I. Hussain, “A power associative loop structure for the construction of non-linear components of block cipher,” IEEE Access, vol. 8, pp. 123492–123506, 2020. [Google Scholar]

40. X. Wang, X. Zhu and Y. Zhang, “An image encryption algorithm based on Josephus traversing and mixed chaotic map,” IEEE Access, vol. 6, no. 17, pp. 23733–23746, 2018. [Google Scholar]

41. A. K. Farhan, N. M. Al-Saidi, A. T. Maolood, F. Nazarimehr and I. Hussain, “Entropy analysis and image encryption application based on a new chaotic system crossing a cylinder,” Entropy, vol. 21, no. 10, pp. 958, 2019. [Google Scholar]

42. Y. Naseer, T. Shah, S. Hussain and A. Ali, “Steps towards redesigning cryptosystems by a non-associative algebra of IP-loops,” Wireless Personal Communications, vol. 108, no. 3, pp. 1379–1392, 2019. [Google Scholar]

43. F. A. Khan, J. Ahmad, J. S. Khan, J. Ahmed, M. A. Khan et al., “A new technique for designing 8 × 8 substitution box for image encryption applications,” in 2017 9th Computer Science and Electronic Engineering (CEECIEEE, Colchester, UK, pp. 7–12, 2017. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.