Computers, Materials & Continua DOI:10.32604/cmc.2022.022203
Article

An Improved Sparrow Search Algorithm for Node Localization in WSN

R. Thenmozhi1, Abdul Wahid Nasir2, Vijaya Krishna Sonthi3, T. Avudaiappan4, Seifedine Kadry5, Kuntha Pin6 and Yunyoung Nam7,*

1Department of Computer Science and Engineering, College of Engineering and Technology, SRM Institute of Science and Technology, Kattankulathur, 603203, India
2Department of Electronics Communication and Engineering, CMR Institute of Technology, Bengaluru, 560037, India
3Department of Computer Science and Engineering, Koneru Lakshmaiah Education Foundation, Vaddeswaram, 522502, Andhra Pradesh, India
4Department of Computer Science and Engineering, K. Ramakrishnan College of engineering, Tiruchirappalli, 621112, India
5Department of Applied Data Science, Noroff University College, Kristiansand, Norway
6Department of ICT Convergence, Soonchunhyang University, Korea
7Department of Computer Science and Engineering, Soonchunhyang University, Korea
*Corresponding Author: Yunyoung Nam. Email: ynam@sch.ac.kr
Received: 30 July 2021; Accepted: 30 September 2021

Abstract: Wireless sensor networks (WSN) comprise a set of numerous cheap sensors placed in the target region. A primary function of the WSN is to avail the location details of the event occurrences or the node. A major challenge in WSN is node localization which plays an important role in data gathering applications. Since GPS is expensive and inaccurate in indoor regions, effective node localization techniques are needed. The major intention of localization is for determining the place of node in short period with minimum computation. To achieve this, bio-inspired algorithms are used and node localization is assumed as an optimization problem in a multidimensional space. This paper introduces a new Sparrow Search Algorithm with Doppler Effect (SSA-DE) for Node Localization in Wireless Networks. The SSA is generally stimulated by the group wisdom, foraging, and anti-predation behaviors of sparrows. Besides, the Doppler Effect is incorporated into the SSA to further improve the node localization performance. In addition, the SSA-DE model defines the position of node in an iterative manner using Euclidian distance as the fitness function. The presented SSA-DE model is implanted in MATLAB R2014. An extensive set of experimentation is carried out and the results are examined under a varying number of anchor nodes and ranging error. The attained experimental outcome ensured the superior efficiency of the SSA-DE technique over the existing techniques.

Keywords: Localization; wireless networks; sparrow search algorithm; machine learning; bio-inspired algorithm

1  Introduction

Wireless sensor networks (WSNs) are related closely to the physical phenomena in its environments. The collected data must be related to the location of sensors for providing a precise overview of the analyzed sensory regions. The positioning is significant in many applications, like geographical routing and tracking and environment rescue, sensing, and search; the location of all the nodes need to be recognized [1]. This requirement stimulates the development of effective localizing algorithm for WSN. In previous years, there have been a huge amount of studies on localization for WSN [2]. They share similar concept that nodes with unknown coordinates are used for more than one GPS armed nodes with known coordinates for estimating their position. Almost all of this work considers the static beacon. Initially, GPS accessible for WSN is highly expensive, exceed the cost of sensors. Furthermore, GPS process has a higher power consumption profile that might enforce further limitations on the WSN lifetime. Moreover, WSN is generally static, and localizing algorithm might be needed for running only at the time of network initialization. Subsequently, GPS process mayn’t be inexpensive for various WSN realizations [3]. Hence, for obtaining position data, they require a method that incurs less cost and provides a more precise position. With the known location of anchor nodes, localizing algorithm could be applied for estimating the position of unknown nodes. There exist 2 types of non GPS based localizing processes, such as range-based algorithm and rang-free algorithm [4]. Point-to-point or Angle based distance estimations amongst the sensors are utilized for rang based localizing algorithm. In this algorithm, the position of sensors is estimated using anchors trilateration [5]. Different from range based localizing algorithms, range-free localizing algorithms don’t require range data for estimating the position of unknown nodes. Only it is based on the topological data. Fig. 1 shows the overview of WSN.

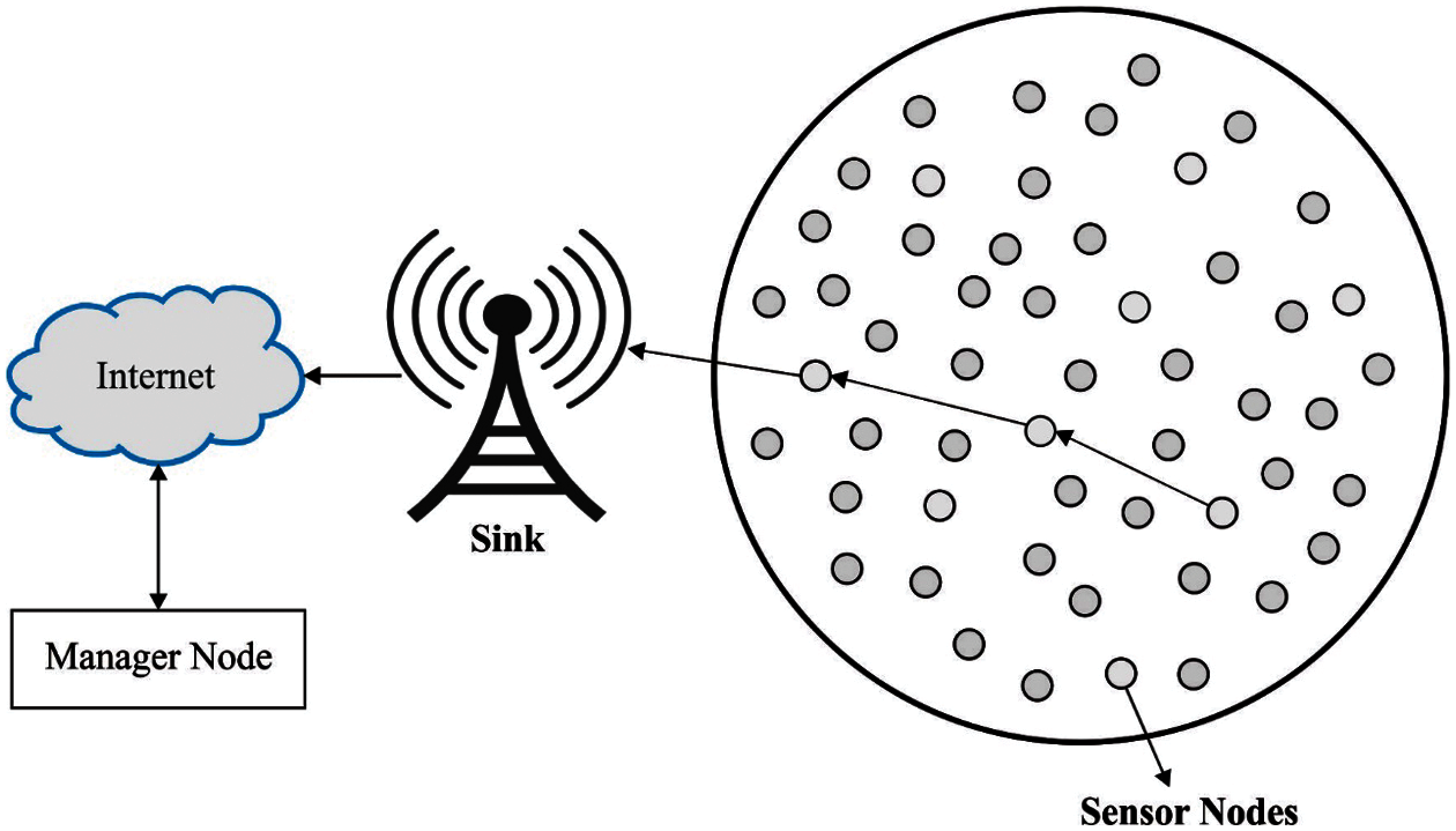
Figure 1: Overview of WSN

In recent times, NL in WSNs is dealing with a multidimensional and multimodal optimization problem which could be resolved by population based stochastic methods. In the study, several Meta heuristic approaches were applied for solving the localization problems in WSN. This algorithm has achieved in decreasing the localization error drastically [6]. This algorithm attempts to resolve optimization problems using error and trial where the possible solution is treated, and the near optimum solution is recognized [7]. Now, several optimization approaches like particle swarm optimization (PSO), cuckoo search (CS), genetic algorithm (GA), artificial bee colony (ABC), gravitational search algorithm (GSA), butterfly optimization algorithm (BOA), and so on, were applied efficiently in representing the position of unknown nodes in WSN.

Kanoosh et al. [8], proposed an NL algorithm that depends on a novel bio-inspired approach named SSA deals with the NL problems as an optimization problem. The presented method was validated and implemented in distinct WSN placements with distinct numbers of anchor and target nodes. Amri et al. [9] implement and propose a novel method for geographic routing. Hence, the presented methods are depending upon a weighted centroid localizing method, in which the positions of unknown node is evaluated by FL approach. In this regard, they proposed a fuzzy localization algorithm which utilizes flow measurement via wireless network for computing the distance splitting the sensor node and anchor node. Consequently, this study is depending upon the centroid algorithms which estimate the positions of unknown nodes by Sugeno inference and fuzzy Mamdani methods for increasing the precision of calculated positions.

Mihoubi et al. [10] proposed an efficient BA approach for the NL problems, the efficacy is depending on the adaption of velocity of Bat using hybridization, using Doppler effects to improve the efficiency, appropriately called Dopeffbat. Therefore, Dopeffbat calculates (via development) the node position iteratively by the Euclidian distance as fitness. Positioning these algorithms on a huge WSN with hundreds of sensor nodes shows better efficiency based on NL. Furthermore, the Dopeffbat parameter is interpreted and simulated in various situations. Miloud et al. [11] proposed a technique for NL, i.e., MFOA. Node is positioned with Euclidean distance, hence it is set as a FF in the optimization method. Positioning these algorithms on a huge WSN with hundreds of sensor nodes demonstrates better efficiency based on NL. Computer simulation shows that MFOA converges quickly to an optimum nodes location.

Wang et al. [12], proposed a new NL approach called KELM-HQ. The presented method applies the real number of hop counts among anchors and unknown nodes as the training input and the location of anchor as the training target to train KELM. Also, the presented technique applies the real number of hop-counts among unknown nodes as the test sample to estimate the positions of unknown nodes to train KELM. Santhosh et al. [13] present a new NMGOA method for NL in WSN. The Nelder–Mead simplex search technique is applied for improving the efficacy of GOA due to its ability of fast convergence. Initially, the node in WSN are arbitrarily located in the target area and later the nodes are initialized. Then, the node performs the NMGOA method to evaluate the places of unknown node and becomes localizing node. Subsequently, the localizing node would be added to the group of anchor nodes for performing the localization procedure. In Li et al. [14], a novel heuristic approach called PCCSO using 3 distinct transmission approaches and the idea of compacts is introduced in this study. The advantages of PCCSO are reflected in improving the capability of local search, as well as storing in the computer memory.

Qi et al. [15] proposed an NWS2CNS for solving the optimization of several bumps in a huge three dimension WSNs. NWS2CNS is presented for improving the position accuracy attained by node inertia weight to precisely estimate the acceleration factors. The suboptimal network segmentation is achieved by precisely recognizing concave nodes which breakdown the three dimension WSNs into various roughly convex subnets. Sekhar et al. [16] designed an efficient Meta heuristic based GTOA NL method for WSN. The aim is to define the positions of unknown nodes using anchors node in the WSN with the help of maximal localizing accuracy and minimal localizing error. The proposed method is inspired by the group teaching approach and it could be utilized to process optimization without losing generalization.

Phoemphon et al. [17] presented a new method, NS-IPSO which separated SNs as to segments for improving the accuracy of calculated distances among pairs of unknown node and anchor node. Firstly, they define candidate nodes which can be possibly utilized for segmenting anchor node in the areas. This sensor node (STs) on the shortest paths among anchor nodes appears frequently compared to the average appearance of each sensor. Later, segmented nodes (SM, sensors to segment the anchor node) is elected from each ST depending on specific condition. Dao et al. [18] proposed an NL recognition in WSN depending upon the integrated ALO with a general method of positioning. The FF is modelled arithmetically depends on evaluating the distance of WSN sensor node. The upgrading solution of populations is designed for correcting positions to enhance the node localization accuracy. The effect of parameters such as transmitting range and node density is tested in the experiment for evaluating the efficiency of this presented technique based on the success ratio and average positioning error.

This paper introduces a new Sparrow Search Algorithm with Doppler Effect (SSA-DE) for Node Localization in Wireless Network. The SSA is generally stimulated by the group wisdom, foraging, and anti-predation behaviors of sparrows. Besides, the Doppler effect is incorporated into the SSA to further improve the node localization performance. In addition, the SSA-DE model defines the position of the nodes in an iterative manner using Euclidian distance as the fitness function. The presented SSA-DE model is implanted in MATLAB R2014. An extensive set of experimentation is carried out and the results are examined under a varying number of anchor nodes and ranging error.

2  The Proposed Model

The proposed SSA-DE technique incorporates the concepts of the SSA and DE in order to proficiently localize the nodes in WSN. The working process of the SSA-DE technique is discussed in the following.

2.1 Overview of SSA

Generally, the sparrows are social in nature and have different types. They are circulating all over the world and attracted to survive in regions near humans. Likewise, they are omnivorous species and mainly eat grain and seeds. It is generally termed as resident in nature. Compared to other birds, it is robust in creativity and memory power. Most importantly they have 2 various kinds of captive house sparrows i.e., producer and scrounger. The producer energetically tries to find the source of food, whereas the scroungers acquire food from the producers. Depending upon the above description of sparrow, a mathematical technique could be evolved as SSA. The virtual sparrows are applied for identifying the improved food source. The place of sparrows are given in the following equation:

X=[χ1,1χ1,2χ2,1χ2,2⋮xn,1⋮xn,2⋯⋯χ1,d⋯⋯χ2,d⋮⋯⋮⋯⋮xn,d](1)

whereas n depicts the amount of sparrows and d denotes the direction of variables that has to be optimized. Hence, the fitness score of each sparrow is given as follows:

FX=[f([x1,1χ1,2⋯f([x2,1χ2,2⋯⋮f([xn,1⋮xn,2⋮⋯⋯χ1,d])⋯χ2,d])⋮⋯⋮xn,d])](2)

In which n defines the count of sparrows, and measure of all rows in FX refers the fitness score. In SSA, the producers have maximum fitness measures to accomplish optimal food in searching process. As well, the producers are in-charge to explore food and help the action of whole population. Therefore, the producers are capable of finding food in wider ranges than scroungers. Depending upon the rules (1) & (2), the location of producers are enlarged by the given equation:

Xj,jt+1={Xi,jt⋅exp⁡(−iα⋅itermax)if R2<STXi,jt+O⋅Lif R2≥ST(3)

whereas t denotes the recent iteration, j=1,2,…,d.Xj,jt indicates the rate of jth dimension of ith sparrows at iteration t.itermax indicates a constant with maximum iteration. α∈(0,1] demonstrates an arbitrary value. R2(R2∈[0,1]) and ST(ST∈[0.5,1.0]) show an alarm value and safety threshold correspondingly. Q signifies a random value which applies simple distribution and L signifies a matrix of 1×d for each element within one. Fig. 2 illustrates the process flow of SSA.

If R2<ST, represents that no predators exist, and producer gets into extensive search mode. If R2≥ST, few sparrows have established the predators, and it is necessary to safeguard them by flying to safer areas. For scroungers, it employs rules (4) & (5). Few scroungers only follow the producer significantly [19]. If the producers detect the best food, it leaves the place to compete for food. If the competition is accomplished, it can obtain the food of producers, otherwise, rules (7) are implemented. The location updating expressions for scroungers are determined below:

Xi,jt+1={0.exp⁡(Xworstt−Xitij2)if i>n/2XPt+1+|Xj,jt−XPt+1|⋅A+⋅Lotherwise(4)

whereas XP implies the optimal position applied by a producer, Xworst refers the recent global worst position, A showcases a matrix of 1×d for elements within 1, and A+=AT(AAT)−1. When i>n/2, it recommends that ith scroungers with ineffective fitness are more starving.

As a result, the sparrow i.e., far from risk will have additional lifetime. The primary location of sparrows is generated randomly in the population. Depends on, the mathematical approach is provided in the following:

Xi,jt+1={Xbestt+β⋅|Xi,jt−Xbestt|if fi>fgXi,jt+K⋅(|Xi,jt−Xworstt|(fj−fw)+ε)if fi=fg(5)

where Xbest represents recent global best location.β, indicates a step size control variable, i.e., a normal distribution of arbitrary values with mean value of zero and a variance of 1. K∈[−1,1] represents a random measure. In this method, fi refers fitness value of recent sparrow. fg and fw signifies recent global best and worst fitness measures. ε depicts a minimum constant and eliminates zero-division-error.

When fi>fg, the sparrows are at border of a group. Xest represents a position of a centre of population i.e., safer. Here, fj=fg denotes that the sparrow, is in between a population i.e., aware of a threat and migrate close to the edge. K is a direction where sparrows move and a step-size control coefficient.

Figure 2: Process flow of SSA

2.2 Design of SSA-DE Technique

The SSA-DE algorithm is defined depending upon the change in frequency of steady events when the viewer moves in related sources. This particular variation is called DE and is represented as the variation in wavelength of a source between two points [20]. The associated development affects the observed frequency which is a growth in the line of sight (LOS) amongst two points. The sparrows encompass improved vision over humans and they can be embedded to a high frequency which results in moving and reaching the food as a chain. The sparrow directs the remaining ones to move in the direction of the food source and the leader sparrow has the ability to determine the distance and place of the source.

The leader sparrow travels arbitrarily and raises the frequency Doppler to be kept in a controlled frequency measuring area. It contains better hearing competence and due to the Doppler shift recompense. The benefit of Doppler shift is employed in the design of the SSA. Totally, two Doppler shifts are used to estimate the place of the sparrows. It is considered that ft/vt and fr/vr are frequencies of two ends. An original frequency comprises a relationship by the use of a wavelength, where f0=C/λ0, λ0 signifies the wavelength of a source, and C outlines the wave frequency. If the source is kept from the observer, then the sparrow leader position update tends to be negative and therefore

f′=f0[C+vrC].(6)

when the source is moving the distance away from observer, the place of the sparrow leader resulted to positive; and thereby:

f′=f0[C−vrC].(7)

f′=f0[C±vrC].(8)

when the source is moved towards the direction of the receiver, the function can be rewritten as follows:

f′=f0[CC−vs].(9)

In case, the source is developed, the maximization of actual frequency take place using Eq. (10):

f′=f0[CC+vs].(10)

Finally, the new frequency can be represented as follows:

f′=f0[CC∓vs].(11)

The +/− signs are overturned as the sign on top can be employed to the relative movement between two points. The estimated DE function can be defined by:

fr=ft[C±vrC∓vr](12)

The actual frequency function is integrated into the SSA algorithm as given below.

fit+1=fit[C±viC∓vi](13)

Likewise, the actual variables (w1,w2) are employed for improving the operation and performance of the method. They are applied for controlling the proportional link between the global and local convergence abilities (w1,w2)∈C[0.7,1].

vit+1=w1∗vit+(xit+1−x∗)×fit+1(14)

xit+1=w2∗xit+vit+1(15)

2.3 Steps Involved in the SSA-DE Technique for Localization Process

The SSA-DE localization approach was mostly utilized for estimating the coordinate points of sensor in WSN. The goal is for determining the coordinate point of target node with minimization of objective function. The procedures contained in the SSA-DE manner are provided in the succeeding:

     i)  Initialized of N unidentified node and M anchor node arbitrarily in the sensing field with broadcast radius R. All anchor nodes define the locating and sending the coordinate point to adjacent nodes. To all iterations, the node which settles down at the end is recognized as reference nodes and its roles as anchor nodes in the succeeding iteration.

    ii)  The group of 3 or superior to 3 anchor nodes occur in the broadcast radius of node was defined as localized node.

   iii)  The distance among the target as well as anchor nodes is defined and obtains altered using additive Gaussian noises. The target node calculates the distance with d^i=di+ni where di refers the actual distance that is defined amongst the places of target nodes (x,y) and place of beacon (xi,yi) utilizing in Eq. (16):

di=(x−xi)2+(y−yi)2(16)

    iv)  The target node is named a localizable node when it contains 3 anchor nodes within broadcast range of target nodes. According to employed trigonometric law of sine/cosine, the coordinate points of target nodes are estimated.

     v)  The SSA-DE manner was utilized to define the coordinate points (x,y) of target nodes which minimizes the localization errors. The primitive employed in localization problem was average square distance among the target as well as anchor nodes that are minimized utilizing Eq. (17):

f(x,y)=1N(∑i=1N(x−xi)2+(y−yi)2−d^)2(17)

    vi)  The optimal measure (x,y) was calculated by utilizing of SSA-DE manner at the end of iteration.

   vii)  The entire localization error was estimated next to estimate of localizable target nodes NL. It can be validated estimated as average square of distance from defined node coordinate points (Xi,Yi) but the original node coordinate points (xi,yi) are determined as:

EL=1N1∑i=1N(xi−Xi)2+(yi−Yi)2(18)

  viii)  Steps 2–5 develop iterated still the place of target node was recognized. The localization method was dependent upon maximum localization error E1 and unlocalized node count NNL that was estimated by the utilize of NNL=M−NL. The minimum score of E1 and NNL outcomes in proficient localization efficiency.

3  Performance Validation

The proposed SSA-DE technique is simulated using MATLAB tool. The results of the SSA-DE technique are inspected interms of different measures under varying anchors, error, and transmission ranges.

A brief analysis of node localization performance of the SSA-DE approach is observed with respect to NLLN under distinct numbers of anchor nodes in Tab. 1 and Fig. 3. The experimental outcomes exhibited that the SSA-DE approach has resulted in an increased NLLN under all anchor counts. For sample, with 10 anchors, the SSA-DE manner has obtainable an improved NLLN of 134 whereas the SSA-NL, CSA-NL, GWO-NL, and PSO-NL manners have reached a lesser PDR of 120, 118, 111, and 108 correspondingly. Followed by, with 30 anchors, the SSA-DE algorithm has accessible an enhanced NLLN of 168 whereas the SSA-NL, CSA-NL, GWO-NL, and PSO-NL techniques have attained a minimal PDR of 148, 144, 127, and 118 respectively. Eventually, with 50 anchors, the SSA-DE technique has offered an enhanced NLLN of 193 whereas the SSA-NL, CSA-NL, GWO-NL, and PSO-NL methodologies have gained a lower PDR of 173, 160, 148, and 137 correspondingly.

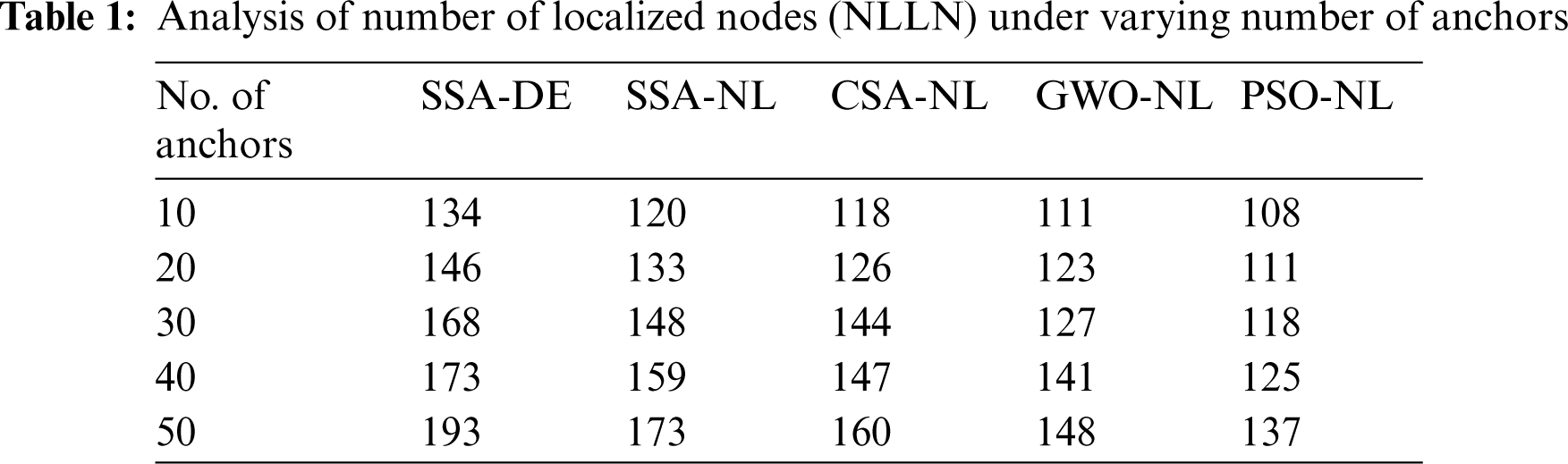
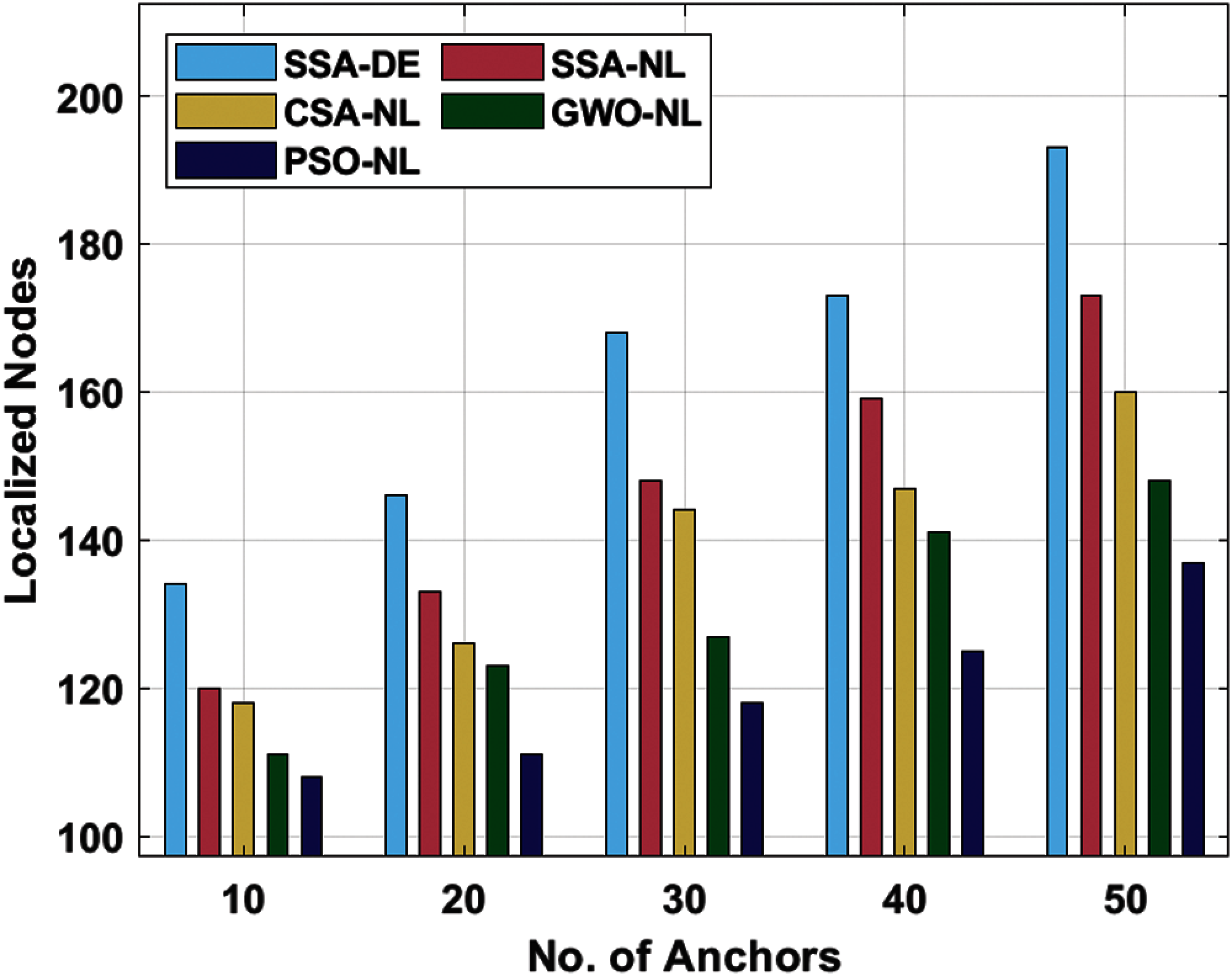
Figure 3: NLLN analysis of SSA-DE model under different anchors

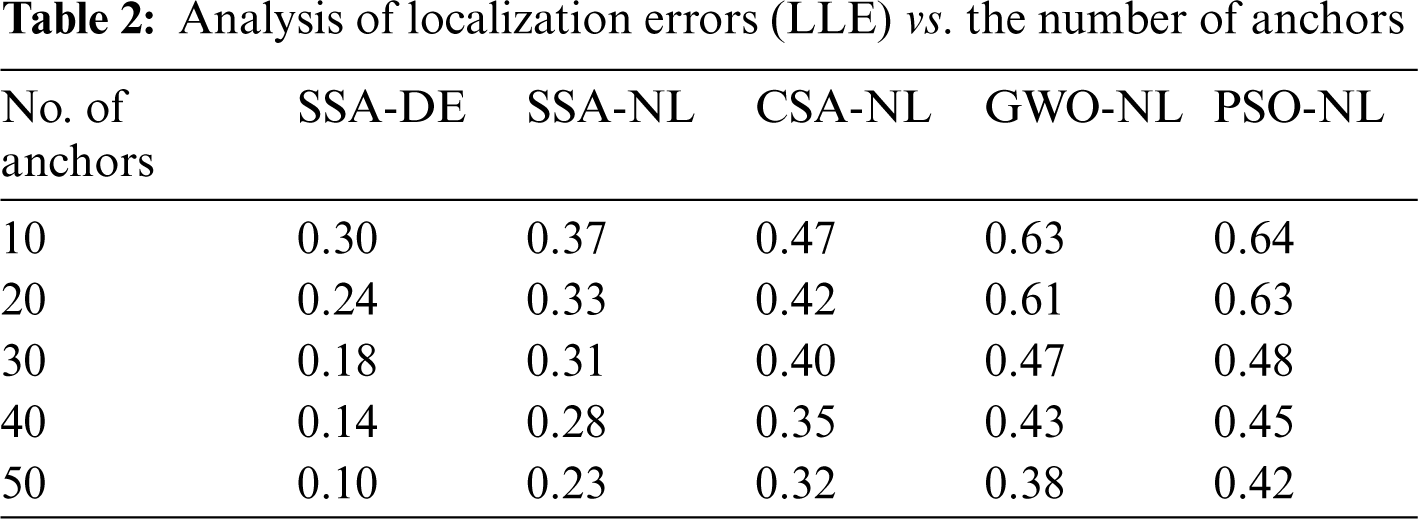
Tab. 2 and Fig. 4 investigates the performance of the SSA-DE technique interms of LLE under varying numbers of anchors. The results showcased the effective localization outcome of the SSA-DE technique with the least LLE value. For instance, with 10 anchors, the SSA-DE technique has offered a minimal LLE of 0.30 whereas the SSA-NL, CSA-NL, GWO-NL, and PSO-NL techniques have attained a maximum LLE of 0.37, 0.47, 0.63, and 0.64 respectively. In line with, with 30 anchors, the SSA-DE approach has offered a lesser LLE of 0.18 whereas the SSA-NL, CSA-NL, GWO-NL, and PSO-NL algorithms have obtained a superior LLE of 0.31, 0.40, 0.47, and 0.48 correspondingly. At the same time, with 50 anchors, the SSA-DE manner has existed a reduced LLE of 0.10 whereas the SSA-NL, CSA-NL, GWO-NL, and PSO-NL techniques have obtained a higher LLE of 0.23, 0.32, 0.38, and 0.42 correspondingly.

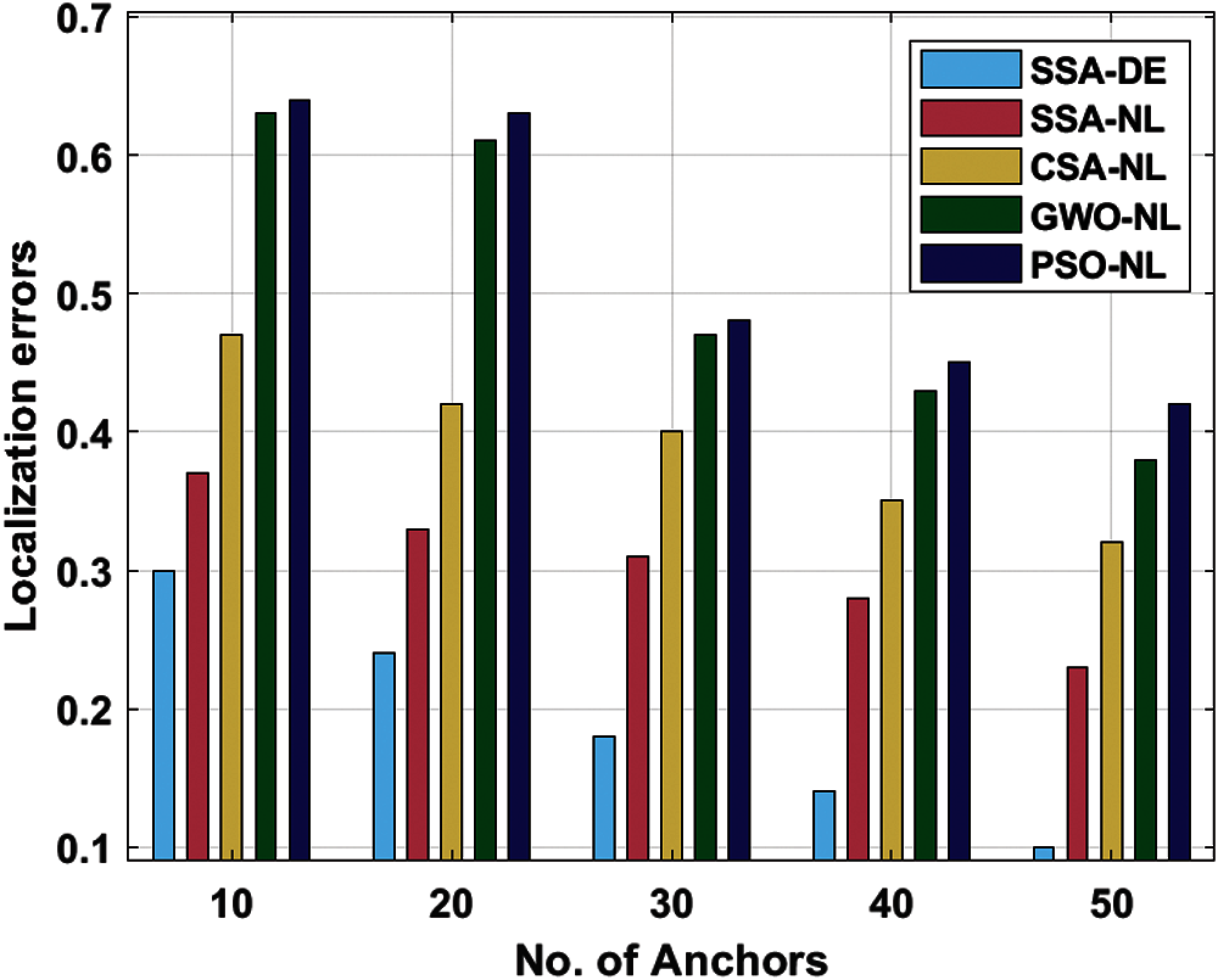
Figure 4: LLE analysis of SSA-DE model under different anchors

Tab. 3 examines the performance of the SSA-DE technique with respect to LLE under different error and transmission ranges. Fig. 5 illustrates the LLE analysis of SSA-DE method under different errors. The outcomes showcased the effectual localization outcome of the SSA-DE manner with the minimal LLE value. For sample, with 10% error, the SSA-DE approach has accessible a lesser LLE of 0.23 whereas the SSA-NL, CSA-NL, GWO-NL, and PSO-NL algorithms have reached a maximal LLE of 0.34, 0.39, 0.59, and 0.60 correspondingly. Similarly, with 20% error, the SSA-DE algorithm has existed a minimal LLE of 0.11 whereas the SSA-NL, CSA-NL, GWO-NL, and PSO-NL manners have gained a superior LLE of 0.29, 0.35, 0.47, and 0.50 correspondingly. Simultaneously, with 30% error, the SSA-DE method has offered a reduced LLE of 0.08 whereas the SSA-NL, CSA-NL, GWO-NL, and PSO-NL techniques have attained an enhanced LLE of 0.25, 0.27, 0.38, and 0.42 correspondingly.

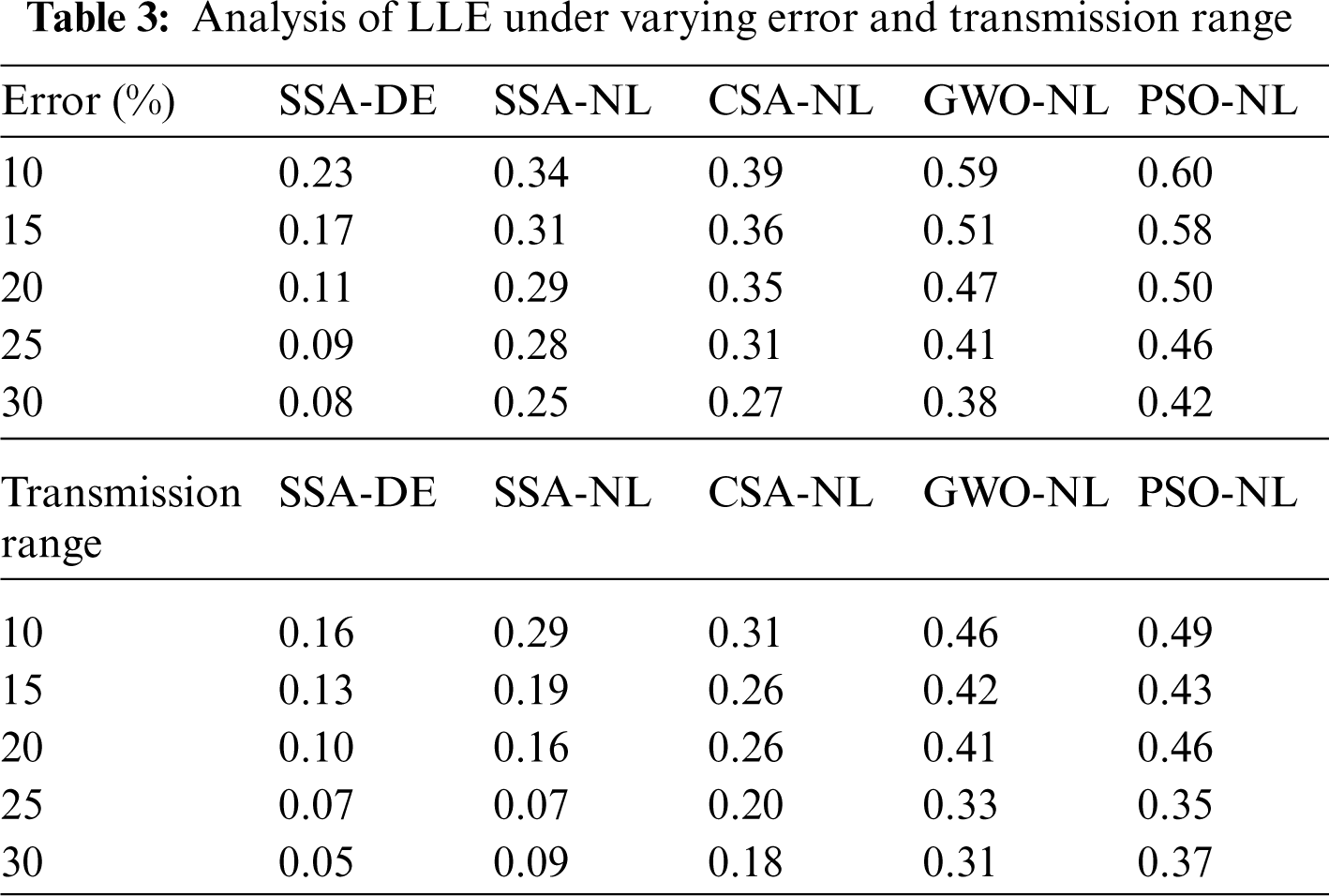
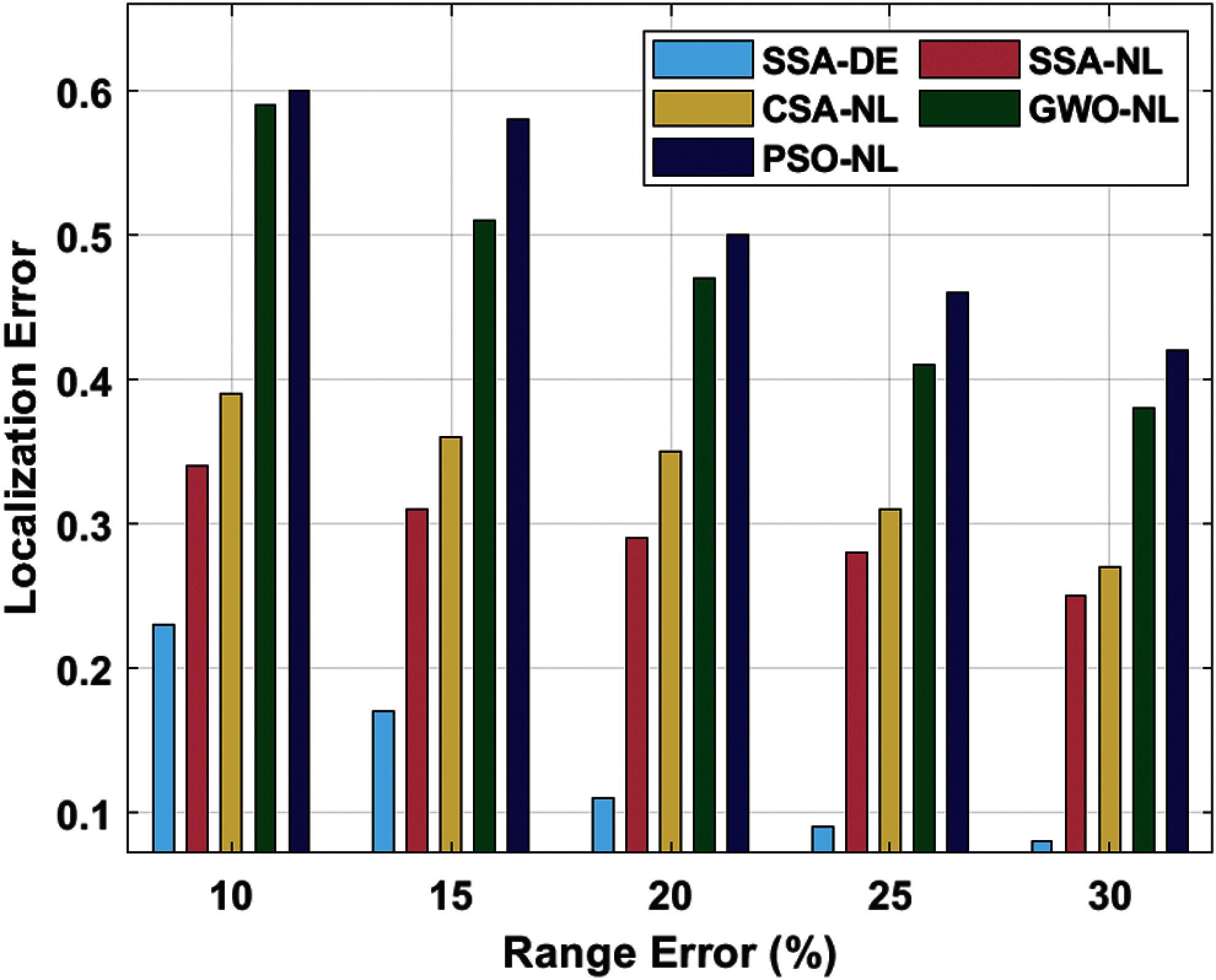
Figure 5: LLE analysis of SSA-DE model under different error

Fig. 6 depicts the LLE analysis of SSA-DE approach under varying transmission ranges. The outcomes demonstrated the effectual localization outcome of the SSA-DE approach with the minimal LLE value. For sample, with 10 transmission range, the SSA-DE approach has obtainable the least LLE of 0.16 whereas the SSA-NL, CSA-NL, GWO-NL, and PSO-NL techniques have reached a higher LLE of 0.29, 0.31, 0.46, and 0.49 correspondingly. Similarly, with 20 transmission range, the SSA-DE method has offered a lower LLE of 0.10 whereas the SSA-NL, CSA-NL, GWO-NL, and PSO-NL methods have achieved a maximal LLE of 0.16, 0.26, 0.41, and 0.46 correspondingly. Eventually, with 30 transmission range, the SSA-DE methodology has existed a lesser LLE of 0.05 whereas the SSA-NL, CSA-NL, GWO-NL, and PSO-NL algorithms have reached an improved LLE of 0.09, 0.18, 0.31, and 0.37 correspondingly.

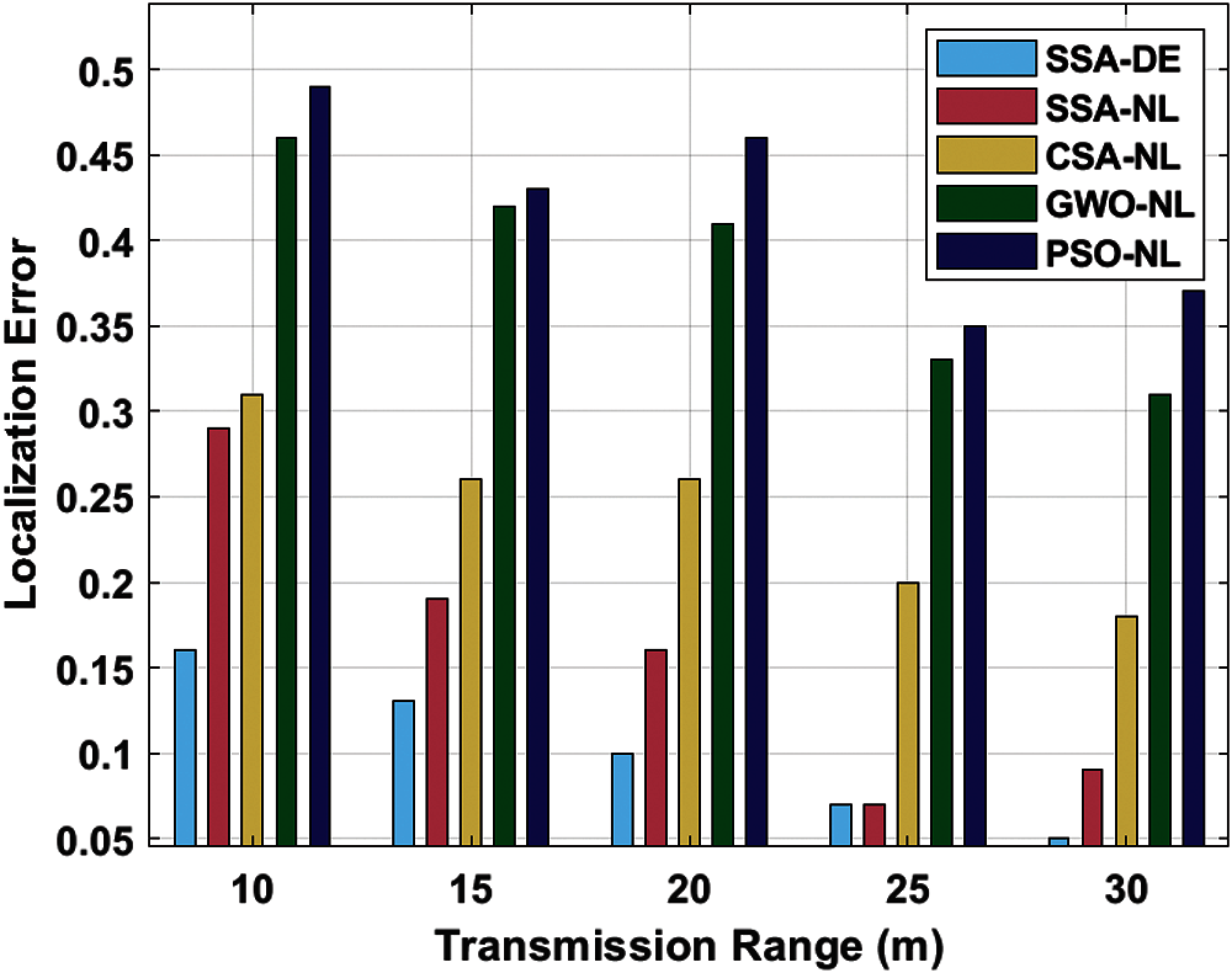
Figure 6: NLLN analysis of SSA-DE model under different transmission range

Finally, the node localization performance of the SSA-DE technique is examined interms of PDR under distinct number of anchor nodes in Tab. 4 and Fig. 7. The experimental outcomes exhibited that the SSA-DE technique has resulted in a minimum PDR under all anchor counts. For instance, with 10 anchors, the SSA-DE technique has offered a lower PDR of 94.15% whereas the SSA-NL, CSA-NL, GWO-NL, and PSO-NL techniques have attained a higher PDR of 96.47%, 97.37%, 98.25%, and 98.67% respectively. In line with, 30 anchors, the SSA-DE manner has existed at least PDR of 90.37% whereas the SSA-NL, CSA-NL, GWO-NL, and PSO-NL approaches have gained an increased PDR of 93.28%, 94.30%, 96.35%, and 97.04% correspondingly. At last, with 50 anchors, the SSA-DE technique has presented a minimum PDR of 86.06% whereas the SSA-NL, CSA-NL, GWO-NL, and PSO-NL algorithms have achieved an improved PDR of 89.55%, 92.41%, 94.26%, and 95.14% correspondingly.

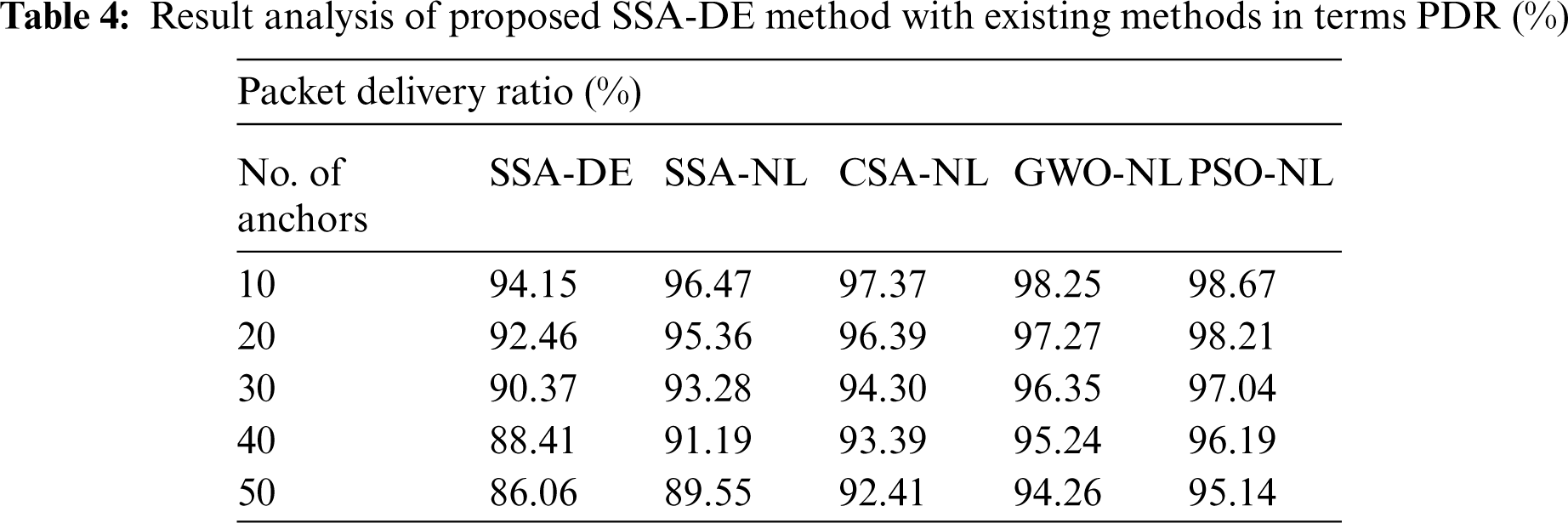
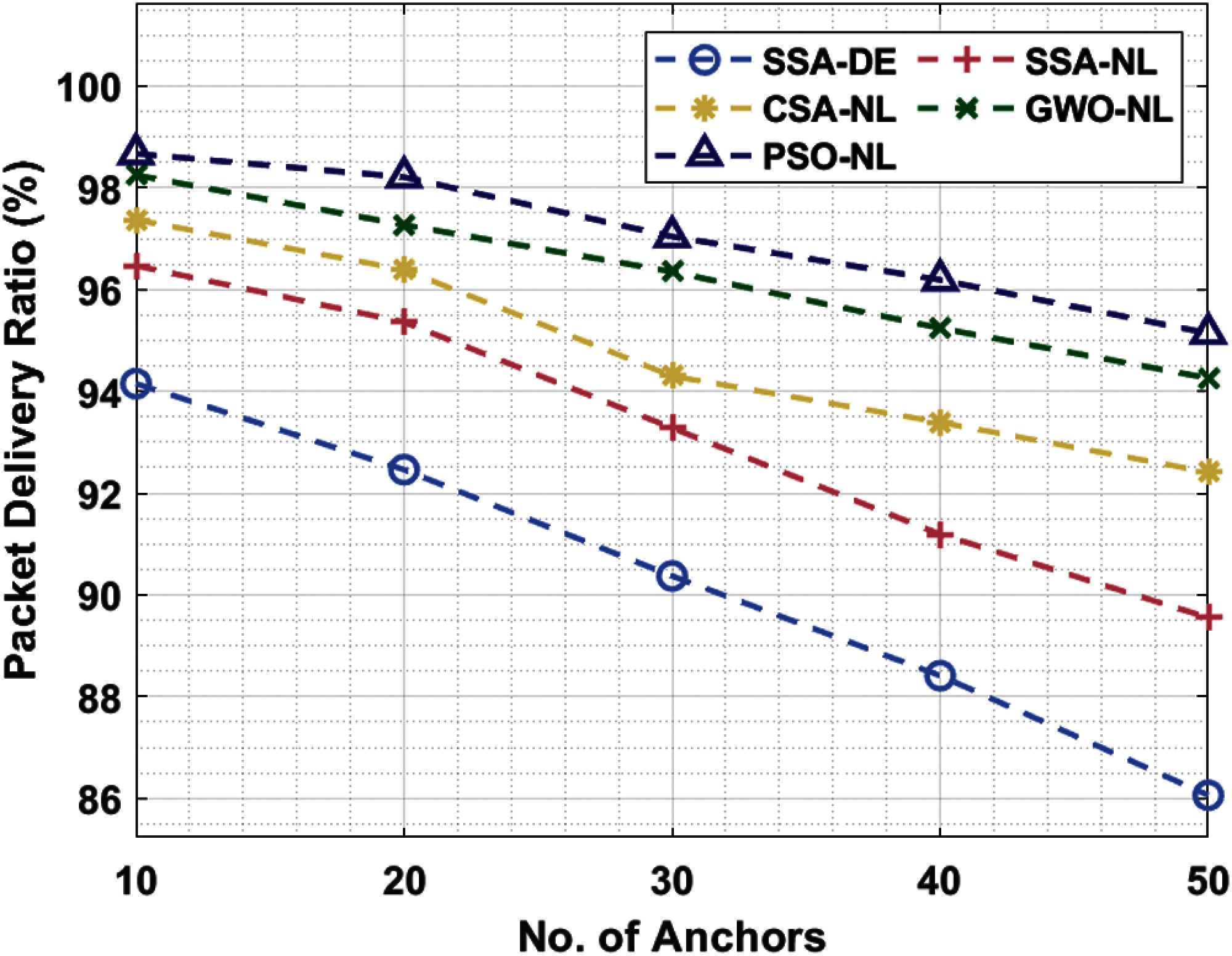
Figure 7: PDR analysis of SSA-DE model with existing techniques

From the above-mentioned results analysis, it is demonstrated that the SSA-DE technique has resulted in an effectual approach for node localization process in WSN. The improved performance is due to the Doppler Effect which is incorporated into the SSA.

4  Conclusion

This paper has developed an SSD-DE technique for WSN. The proposed SSA-DE technique incorporates the concepts of the SSA and DE for proficiently localize the node in WSN. Besides, the Doppler Effect is incorporated into the SSA to further improve the node localization performance. In addition, the SSA-DE model defines the position of node in an iterative manner using Euclidian distance as the fitness function. An extensive set of experimentation is carried out and the outcomes are examined under a different number of anchor nodes and ranging error. The SSA-DE technique has presented a minimum PDR of 86.06% under the presence of 50 anchors. The attained experimental outcome make sure that higher efficiency of the SSA-DE algorithm over the existing algorithms. In future, time synchronization approaches are designed for enhancing the overall performance of the network.

Funding Statement: This research was supported by Korea Institute for Advancement of Technology (KIAT) grant funded by the Korea Government (MOTIE) (P0012724, The Competency Development Program for Industry Specialist) and the Soonchunhyang University Research Fund.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  X. Zhang, J. Fang and F. Meng, “An efficient node localization approach with RSSI for randomly deployed wireless sensor networks,” Journal of Electrical and Computer Engineering, vol. 2016, pp. 1–11, 2016. [Google Scholar]

 2.  P. Sekhar, E. L. Lydia, M. Elhoseny, M. Al-Akaidi, M. M. Selim et al., “An effective metaheuristic based node localization technique for wireless sensor networks enabled indoor communication,” Physical Communication, vol. 48, pp. 101411, 2021. [Google Scholar]

 3.  R. Punithavathi, C. Kurangi, S. P. Balamurugan, I. V. Pustokhina, D. A. Pustokhin et al., “Hybrid BWO-IACO algorithm for cluster based routing in wireless sensor networks,” Computers, Materials & Continua, vol. 69, no. 1, pp. 433–449, 2021. [Google Scholar]

 4.  A. Vempaty, O. Ozdemir, K. Agrawal, H. Chen and P. K. Varshney, “Localization in wireless sensor networks: Byzantines and mitigation techniques,” IEEE Transactions on Signal Processing, vol. 61, no. 6, pp. 1495–1508, 2013. [Google Scholar]

 5.  G. Kadiravan, P. Sujatha, T. Asvany, R. Punithavathi, M. Elhoseny et al., “Metaheuristic clustering protocol for healthcare data collection in mobile wireless multimedia sensor networks,” Computers, Materials & Continua, vol. 66, no. 3, pp. 3215–3231, 2021. [Google Scholar]

 6.  S. N. Mohanty, E. L. Lydia, M. Elhoseny, M. M. G. Al Otaibi and K. Shankar, “Deep learning with LSTM based distributed data mining model for energy efficient wireless sensor networks,” Physical Communication, vol. 40, no. 3, pp. 101097, 2020. [Google Scholar]

 7.  M. S. Maharajan, T. Abirami, I. V. Pustokhina, D. A. Pustokhin and K. Shankar, “Hybrid swarm intelligence based QoS aware clustering with routing protocol for WSN,” Computers, Materials & Continua, vol. 68, no. 3, pp. 2995–3013, 2021. [Google Scholar]

 8.  H. M. Kanoosh, E. H. Houssein and M. M. Selim, “Salp swarm algorithm for node localization in wireless sensor networks,” Journal of Computer Networks and Communications, vol. 2019, no. 4, pp. 1–12, 2019. [Google Scholar]

 9.  S. Amri, F. Khelifi, A. Bradai, A. Rachedi, M. L. Kaddachi et al., “A new fuzzy logic based node localization mechanism for wireless sensor networks,” Future Generation Computer Systems, vol. 93, no. 9, pp. 799–813, 2019. [Google Scholar]

10. M. Mihoubi, A. Rahmoun, P. Lorenz and N. Lasla, “An effective bat algorithm for node localization in distributed wireless sensor network,” Security and Privacy, vol. 1, no. 1, pp. e7, 2018. [Google Scholar]

11. M. Miloud, R. Abdellatif and P. Lorenz, “Moth flame optimization algorithm range-based for node localization challenge in decentralized wireless sensor network,” International Journal of Distributed Systems and Technologies, vol. 10, no. 1, pp. 82–109, 2019. [Google Scholar]

12. L. Wang, M. J. Er and S. Zhang, “A kernel extreme learning machines algorithm for node localization in wireless sensor networks,” IEEE Communications Letters, vol. 24, no. 7, pp. 1433–1436, 2020. [Google Scholar]

13. M. Santhosh and P. Sudhakar, “Nelder mead with grasshopper optimization algorithm for node localization in wireless sensor networks,” Journal of Computational and Theoretical Nanoscience, vol. 17, no. 12, pp. 5409–5421, 2020. [Google Scholar]

14. J. Li, M. Gao, J. S. Pan and S. C. Chu, “A parallel compact cat swarm optimization and its application in DV-Hop node localization for wireless sensor network,” Wireless Networks, vol. 27, no. 3, pp. 2081–2101, 2021. [Google Scholar]

15. X. Qi, X. Liu and L. Liu, “Node localization in wireless sensor networks using swallow swarm optimization algorithm,” Software Engineering, vol. 12, no. 6–8, pp. 117–120, 2020. [Google Scholar]

16. P. Sekhar, E. L. Lydia, M. Elhoseny, M. A. Akaidi, M. M. Selim et al., “An effective metaheuristic based node localization technique for wireless sensor networks enabled indoor communication,” Physical Communication, vol. 48, pp. 101411, 2021. [Google Scholar]

17. S. Phoemphon, C. S. In and N. Leelathakul, “A hybrid localization model using node segmentation and improved particle swarm optimization with obstacle-awareness for wireless sensor networks,” Expert Systems with Applications, vol. 143, pp. 113044, 2020. [Google Scholar]

18. T. K. Dao, J. S. Pan, S. C. Chu, H. T. Tran, T. D. Nguyen et al., Node localization in wireless sensor network by ant lion optimization. in Advances in Smart Vehicular Technology, Transportation, Communication and Applications, Smart Innovation, Systems and Technologies, vol. 226. Springer, Singapore, pp. 97–109, 2021. [Google Scholar]

19. J. Xue and B. Shen, “A novel swarm intelligence optimization approach: Sparrow search algorithm,” Systems Science & Control Engineering, vol. 8, no. 1, pp. 22–34, 2020. [Google Scholar]

20. H. A. Mohammed, M. J. N. Sibley and P. J. Mather, “Investigation of doppler effects on high mobility OFDM-MIMO systems with the support of high altitude platforms (HAPS),” Journal of Physics: Conference Series, vol. 364, pp. 12048, 2012. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.