DOI:10.32604/cmc.2022.022011

| Computers, Materials & Continua DOI:10.32604/cmc.2022.022011 |  |
| Article |
Attribute Weighted Naïve Bayes Classifier
Multimedia University, Cyberjaya, 63100, Malaysia
*Corresponding Author: Lee-Kien Foo. Email: lkfoo@mmu.edu.my
Received: 24 July 2021; Accepted: 13 September 2021
Abstract: The naïve Bayes classifier is one of the commonly used data mining methods for classification. Despite its simplicity, naïve Bayes is effective and computationally efficient. Although the strong attribute independence assumption in the naïve Bayes classifier makes it a tractable method for learning, this assumption may not hold in real-world applications. Many enhancements to the basic algorithm have been proposed in order to alleviate the violation of attribute independence assumption. While these methods improve the classification performance, they do not necessarily retain the mathematical structure of the naïve Bayes model and some at the expense of computational time. One approach to reduce the naïveté of the classifier is to incorporate attribute weights in the conditional probability. In this paper, we proposed a method to incorporate attribute weights to naïve Bayes. To evaluate the performance of our method, we used the public benchmark datasets. We compared our method with the standard naïve Bayes and baseline attribute weighting methods. Experimental results show that our method to incorporate attribute weights improves the classification performance compared to both standard naïve Bayes and baseline attribute weighting methods in terms of classification accuracy and F1, especially when the independence assumption is strongly violated, which was validated using the Chi-square test of independence.
Keywords: Attribute weighting; naïve Bayes; Kullback-Leibler; information gain; classification
The naïve Bayes classifier is one of the widely used algorithms for data mining applications. The naïveté in the classifier is that all the attributes are assumed to be independent given the class. Such assumption simplifies the computation to infer the probability of a class given the data. Although the attribute independence assumption in the naïve Bayes classifier makes it a tractable method for learning, this assumption may not hold in real-world applications.
Various approaches have been proposed to relax the attribute independence assumption. One of the approaches is to combine the naïve Bayes with a pre-processing step. In this approach, an attribute selection is first performed to identify the set of informative attributes before training the naïve Bayes [1–3]. This approach usually relies on some heuristics to evaluate the characteristics of the attributes. The naïve Bayes is only trained on the set of identified informative attributes.
Another approach to mitigate the independence assumption is the structure extension [4–7]. This approach extends the structure in naïve Bayes to represent attribute dependencies by creating edges between the attributes. These edges allow the dependence relationships between attributes to be captured.
Since some attributes have more influences in discriminating the classes, an alternative approach is to apply an attribute weighting method. In this approach, different weights are assigned to different attributes with a higher weight for attributes that have more influences. Although there are many methods proposed to calculate the weights for naïve Bayes learning, these methods incorporate the weights by raising the power of the conditional probabilities. However, incorporating weights in this manner may cause the conditional probabilities to behave inversely. In this paper, we propose a method to address this issue. The proposed method is evaluated on public benchmark datasets and compared to other baseline attribute-weighting methods.
The remainder of this paper is structured as follows. Section 2 reviews the related work. Section 3 presents our proposed method. Section 4 describes the experimental setup. Section 5 discusses the experimental results. Section 6 draws the conclusions of the research.
Attribute weighting methods in naive Bayesian learning can be divided into two methods: wrapper-based and filter-based. The wrapper-based methods use a classifier as an evaluation function to score the attributes based on their classification performance, whereas filter-based methods apply some heuristics to evaluate the characteristics of the attributes.
Among the earlier work that used a filter-based method for attribute weights is the work of Lee et al. [8]. They used a weighted average of Kullback-Leibler measure across the attribute values for calculating weight for each attribute. Hall [9] proposed an attribute weighting method based on decision tree for naïve Bayes. The method first constructs an unpruned decision tree. Attribute weight is calculated by examining the minimum depth at which attributes are tested in the tree. Duan et al. [10] used the information gain measure for attribute weights. They first calculate the information gain for each attribute and then select a set of informative attributes. The information gain from the set of informative attribute is normalized and the weight is assigned for the corresponding attribute.
Yu et al. [11] proposed a weighted adjusted naïve Bayes, where the attribute weights are iteratively adjusted using the wrapper method. Weights are updated by using a threshold to evaluate the performance of the current attribute weights. The final optimised weights are then used to train the attribute weighted naïve Bayes. A similar work was seen in the work of Yu et al. [12] where they proposed a hybrid attribute weighting method that combines filter and wrapper approaches. Rather than initialising a constant weight for each attribute, the correlation-based weight filter is applied to initialise the weights. The wrapper method is then applied to iteratively update the weights. Such methods, however, have high computational cost.
There are works [13,14] that applied a correlation-based attribute weighting method where the weight for each attribute is determined by the difference between attribute-class correlation and average attribute-attribute inter-correlation. To avoid negative weights when calculating the difference between attribute-class correlation and average attribute-attribute inter-correlation, Jiang et al. [13] applied a logistic sigmoid transformation to ensure the weight falls within the range of 0 and 1. Zhang et al. [14] proposed an attribute and instance weighted naïve Bayes that combines attribute weighting with instance weighting methods. They first compute the attribute weight using correlation-filter and applied a frequency-based instance weight filter to each instance. These weights are then applied to naïve Bayes for classification.
In this section, we describe our proposed method and the rationale of our method.
3.1 Naïve Bayes Classifier with Attribute Weights
The naïve Bayes classifier is a probabilistic model that applied the Bayes theorem in classification [15]. Given an instance to be classified based on the values of n attributes, A = (a1, a2, …, an), we can calculate the conditional probability that the class of this instance is C as below:
In practice, we are only interested in the numerator in Eq. (1), which is the joint probability of class C and the attributes. With the strong conditional independence assumption in naïve Bayes classifier, this joint probability can be expressed as the following:
The naïve Bayes classifier classifies the instance by maximizing the probability at the right hand side of Eq. (2). The class of this instance is labelled as cj if
In real application of classification, the assumption of conditional independence between attributes is not always true. One approach to alleviate the independence assumption is to incorporate attribute weights into the naïve Bayes. We propose to incorporate the weight wi of attribute ai into the naïve Bayes classifier as in Eq. (4):
3.2 Rationale of Our Proposed Method
The conditional probability
where
Since the conditional probability is always bounded between 0 and 1,
To further illustrate our proposed method, let us assume that the conditional probability of the attribute ai given the class cj,
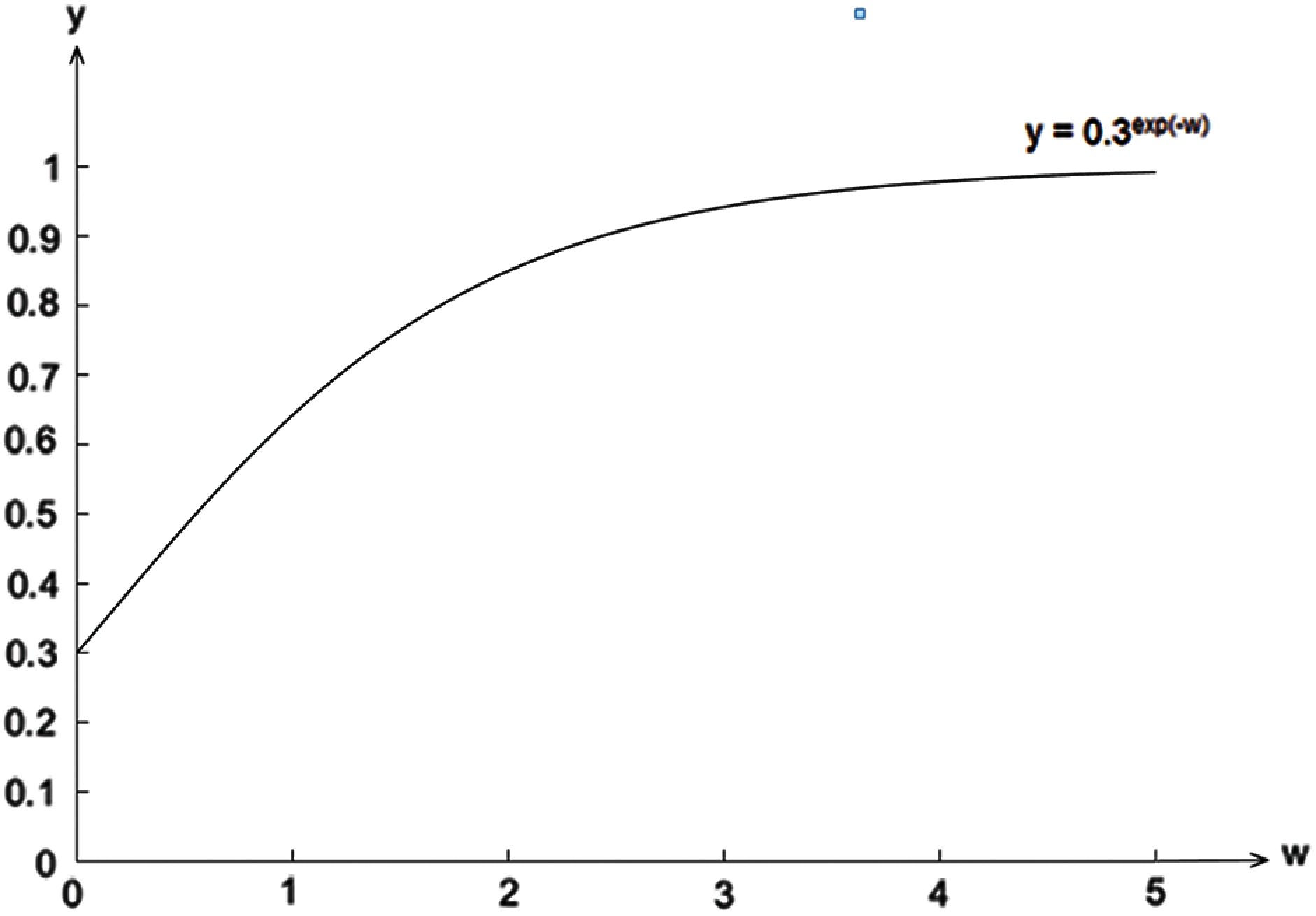
Figure 1: The changes in
The performance of our method is evaluated on a collection of 9 public benchmark datasets obtained from UCI repository [16] and 1 dataset obtained from the United States Food & Drug database (FDA) [17]. The FDA dataset contains 7 attributes to classify the severity of adverse drug events encountered by Osteoporosis patients from year 2004 to 2018. Tab. 1 provides a description of the datasets used in the experiments.
All instances with missing values were removed from the dataset and numerical attributes were discretized using the supervised discretisation method of Fayyad et al. [18]. Numerical attributes that have only one interval after discretization are not included in the modelling process.
To evaluate the performance of our method, these data were cross-validated using a 5-fold cross-validation method. Stratified sampling method is used to sample the training data. The train:test ratio is 70:30 for each class. The classification performance was obtained by averaging the results from the 5 runs. Two measurements were used to evaluate the classification performance: accuracy and F1. Accuracy measures the number of times the model correctly makes the prediction, while F1 is the harmonic mean of precision and recall.
We conducted two sets of experiments. The first experiment compared our method with standard naïve Bayes, i.e., without applying any attribute weighting method. The second experiment compared our method with existing baseline method to incorporate attribute weights. The attribute weights in both experiments are calculated using methods proposed in literature, one based on Kullback-Leibler (KL) measure [8] and another based on information gain (IG) [10].
5.1 Standard Naïve Bayes vs. Proposed Method
The classification performance of our method using KL measure as attribute weights and standard naïve Bayes is presented in Fig. 2. Our method performed better in both accuracy (Fig. 2a) and F1 measures (Fig. 2b) for 6 of the datasets (AB, CC, LP, MR, AD and AE). Both methods achieved the same performance for BC dataset. The standard naïve Bayes performed better for HD, CA and TTT datasets.
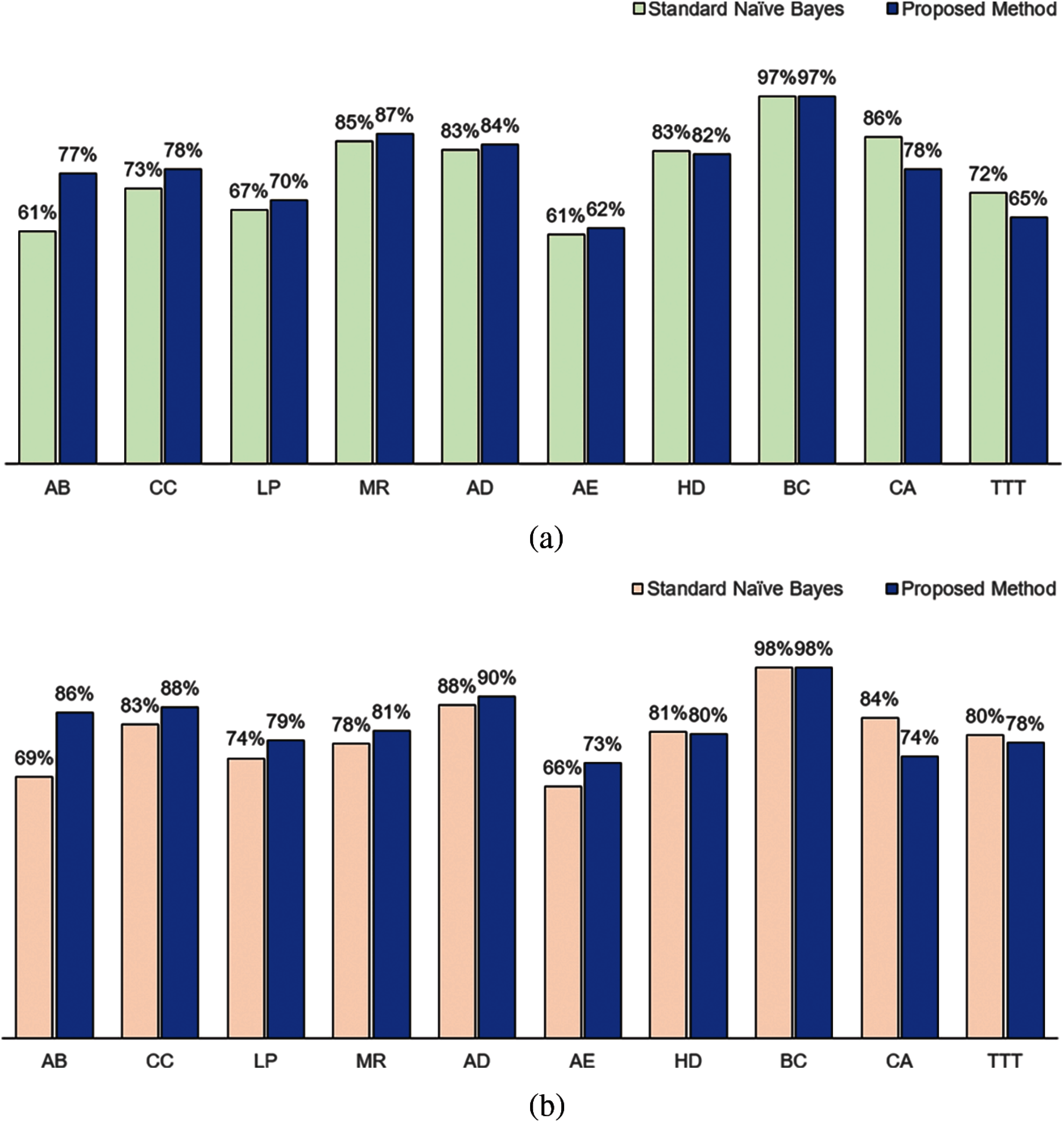
Figure 2: Classification performance in terms of (a) Accuracy and (b) F1 between standard naïve Bayes and proposed method using Kullback-Leibler measure as the attribute weight
When we used IG as the attribute weights, we obtained a similar result as in KL when compared to the standard naïve Bayes for accuracy. As shown in Fig. 3a, our method performed better for AB, CC, LP, MR, AD and AE; performed equivalent for BC, but not as good for HD, CA and TTT. In terms of F1, as shown in Fig. 3b, our method performed better for AB, CC, LP, MR, AD and AE; performed equivalently for BC and HD; but not as good for CA and TTT.
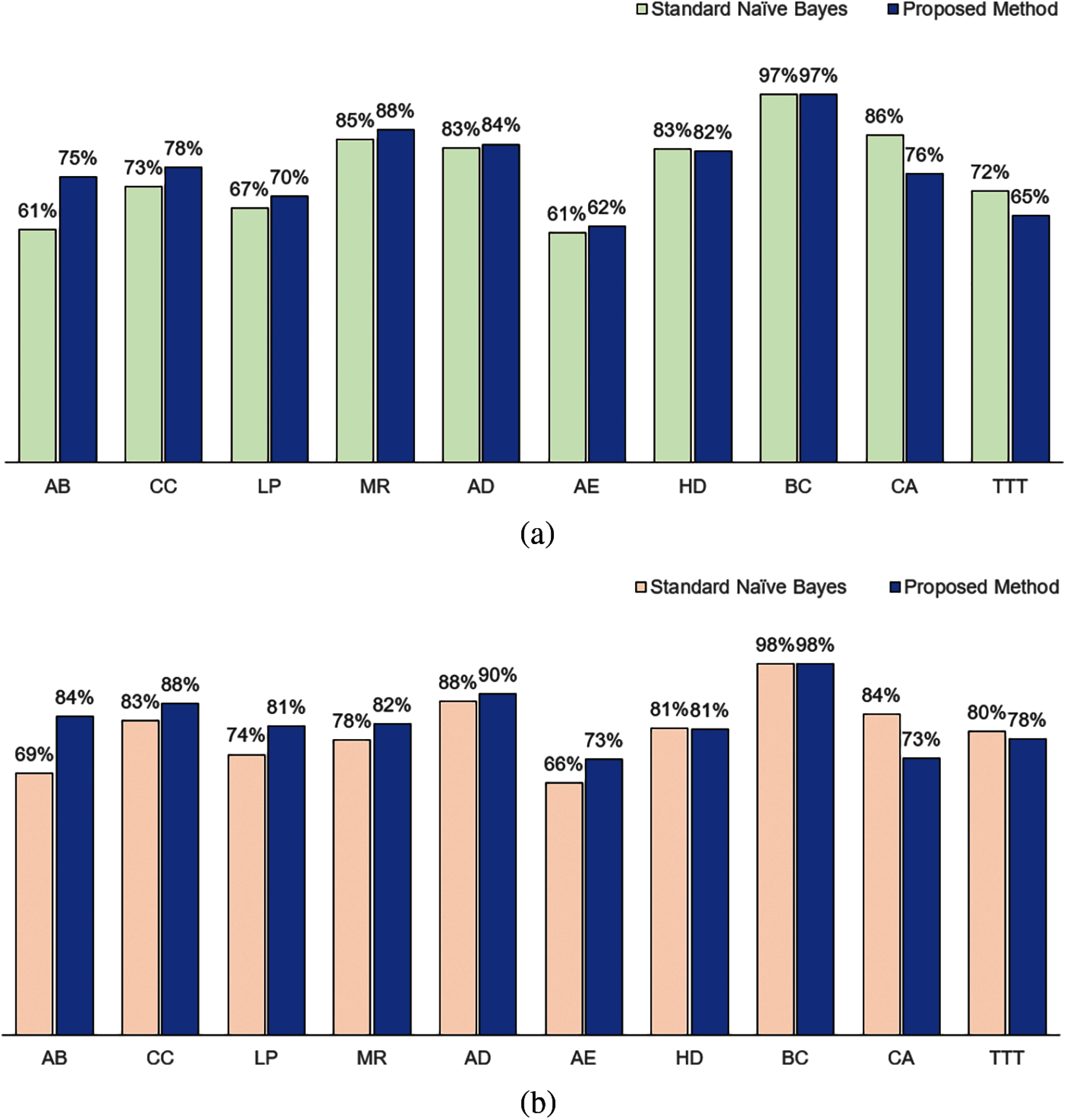
Figure 3: Classification performance in terms of (a) Accuracy and (b) F1 between standard naïve Bayes and proposed method using information gain measure as the attribute weight
5.2 Baseline Method vs. Proposed Method
The majority of the existing work for weighted naïve Bayes [8,9,13,14] incorporate attribute weights using the following formula:
This experiment compares the classification performance of our method to incorporate attribute weights (following Eq. 4) with this baseline method (following Eq. 6). The attribute weights are calculated based on KL and IG measures.
Fig. 4 shows the classification performance of our method and baseline method for attribute weights calculated based on KL measure. In terms of accuracy, our method performed better for 7 datasets (AB, CC, LP, MR, AD, AE and HD). The baseline method performed better in CA and TTT datasets. Both methods performed equivalently for BC dataset. In terms of the F1, our method performed better for 8 datasets (AB, CC, LP, MR, AD, AE, HD and TTT), performed equivalently for BC dataset and not as well for CA dataset.
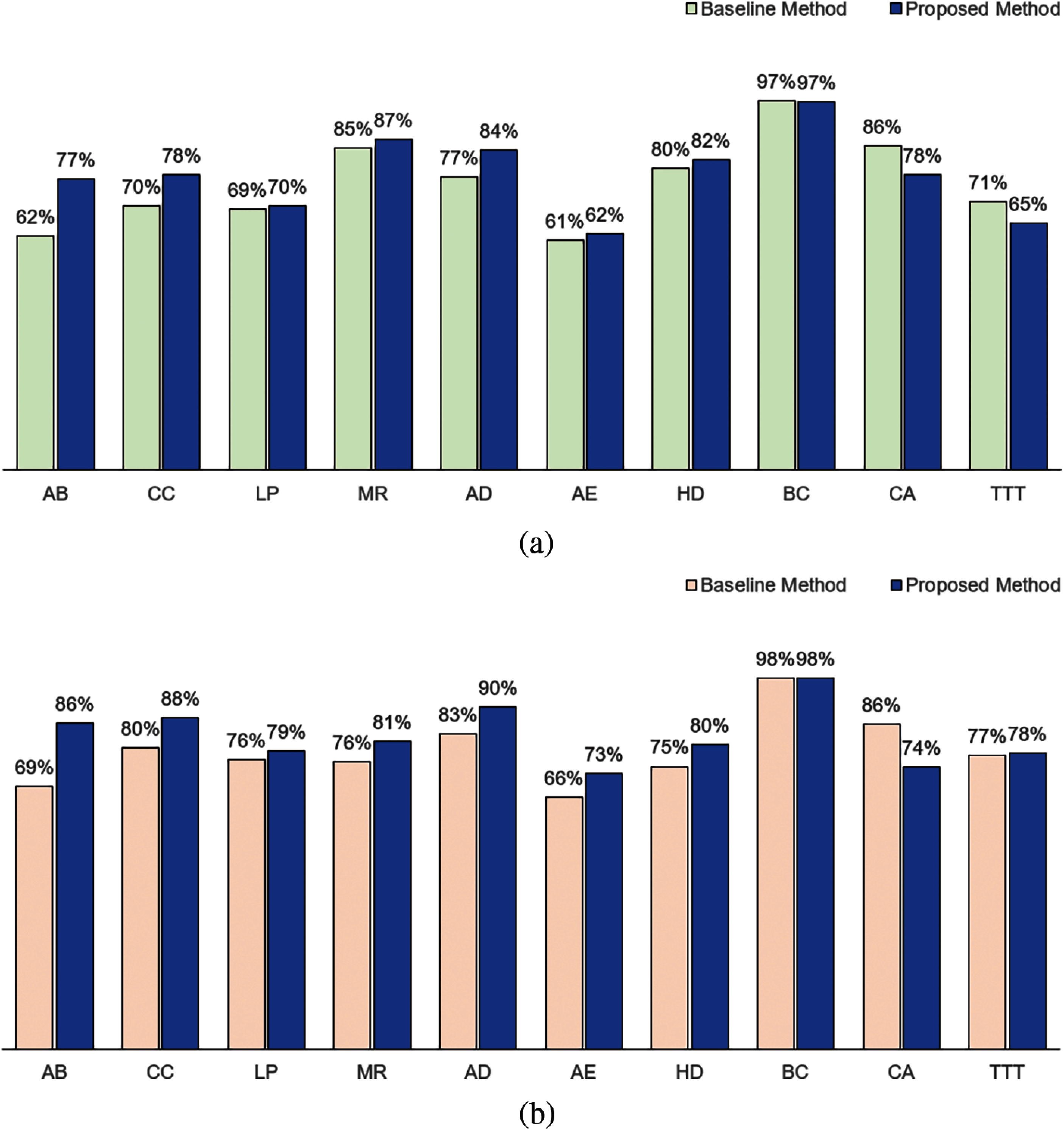
Figure 4: Comparison between baseline method and proposed method based on Kullback-Leibler measure: (a) Accuracy and (b) F1
When IG measure is used as the method to compute attribute weights, we observed the same performance results. As shown in Fig. 5, in terms of accuracy, our method performed better for AB, CC, LP, MR, AD, AE and HD datasets; has an equivalent performance in BC dataset and not as good in CA and TTT datasets as compared to the baseline method. In terms of F1, our method performed better for 8 datasets (AB, CC, LP, MR, AD, AE, HD and TTT), performed equivalently for the BC dataset, and not as well for CA dataset.
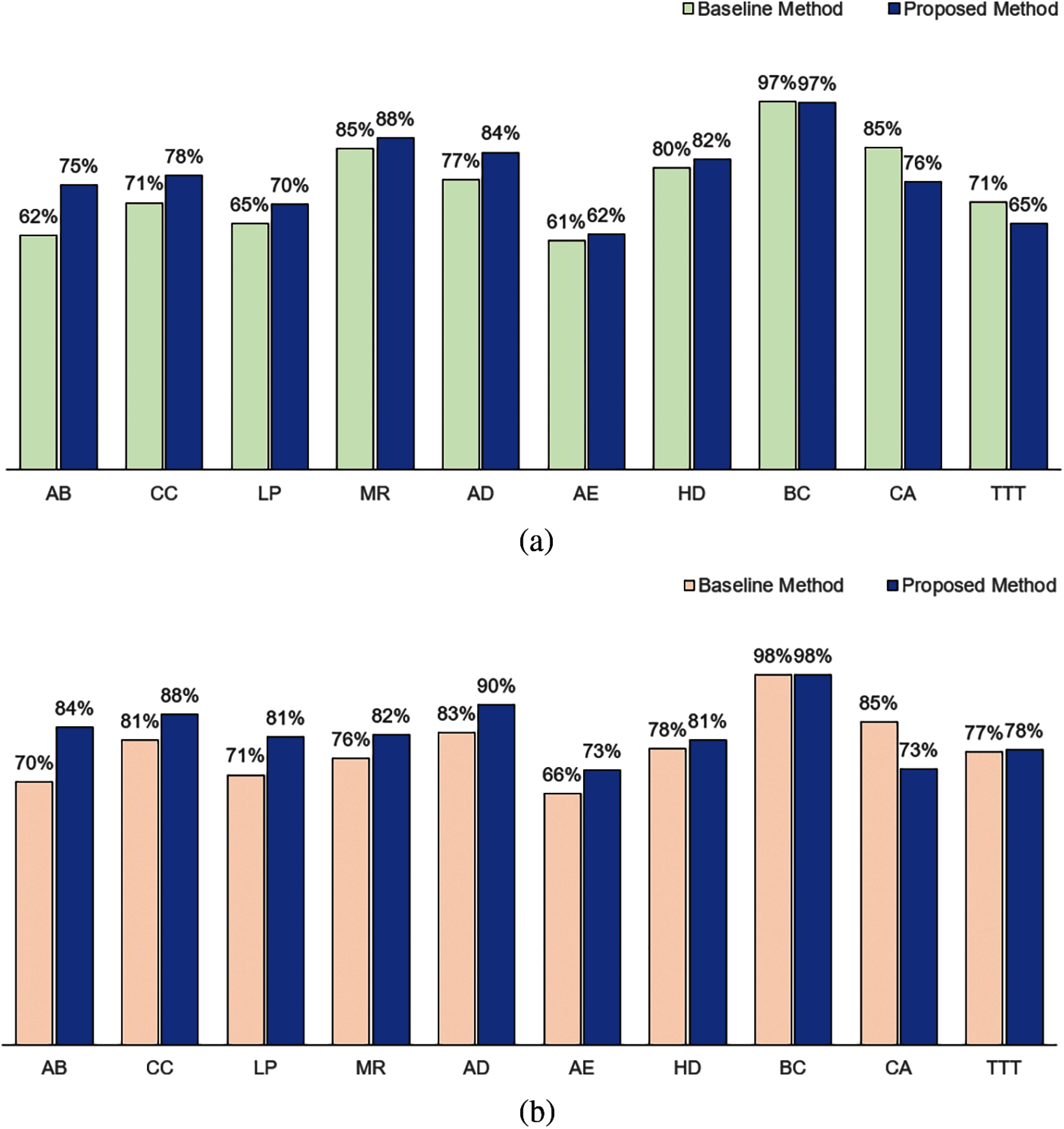
Figure 5: Comparison between baseline method and proposed method based on information gain measure: (a) Accuracy and (b) F1
5.3 Further Investigation on the Classification Performance
In order to better understand the experimental results, we have conducted a test to evaluate the assumption of conditional independence in naïve Bayes. This independence assumption is valid only if all the variables are pairwise independent. The chi-square test of independence is used to verify if a pair of attributes are independent; thus it is a suitable test for the verification of this assumption. Since we are evaluating the independence between attributes condition on the class, each dataset is divided into different subsets according to their classes. The chi-square test is applied on each subset to evaluate pairwise independence between attributes.
The null hypothesis (Ho) of the chi-square test is that a pair of attributes are independent and Ho is rejected if the p-value is smaller than a level of significance (α). We have used α = 0.05 in our test. If the p-value is smaller than 0.05, then the attributes are not independent and thus violate the conditional independence assumption of naïve Bayes.
Tab. 2 presents the results of the pairwise test for 3 attributes (A1, A2 and A3). If an attribute is independent with another attribute, the cell of the intersection of these attributes in the table is labelled as “I”. The cell of intersection is labeled as “NI” if these two attributes are not independent. For readability, the cell with “NI” value is shaded. Tab. 2 showed that A1 is independent with A2, but not independent with A3. A2 and A3 are also not independent. The independence assumption in naïve Bayes is not violated if all the attributes are pairwise independent, which means that all the entries in the table are “I”. The more “NI” values are seen in the table, means that the assumption is violated more seriously.

Tab. 3 shows the results of the chi-square test on AB dataset, where our method performed better than the standard naïve Bayes and baseline methods. In the AB dataset, there are 2 classes: “Larger” and “Smaller”. Tab. 3a is the chi-square test result for class “Larger” and Tab. 3b is the chi-square test result for class “Smaller”. There are 8 attributes in the AB dataset. All the attributes are not pairwise independent for both the classes, which means that the conditional independence assumption is seriously violated for this dataset.

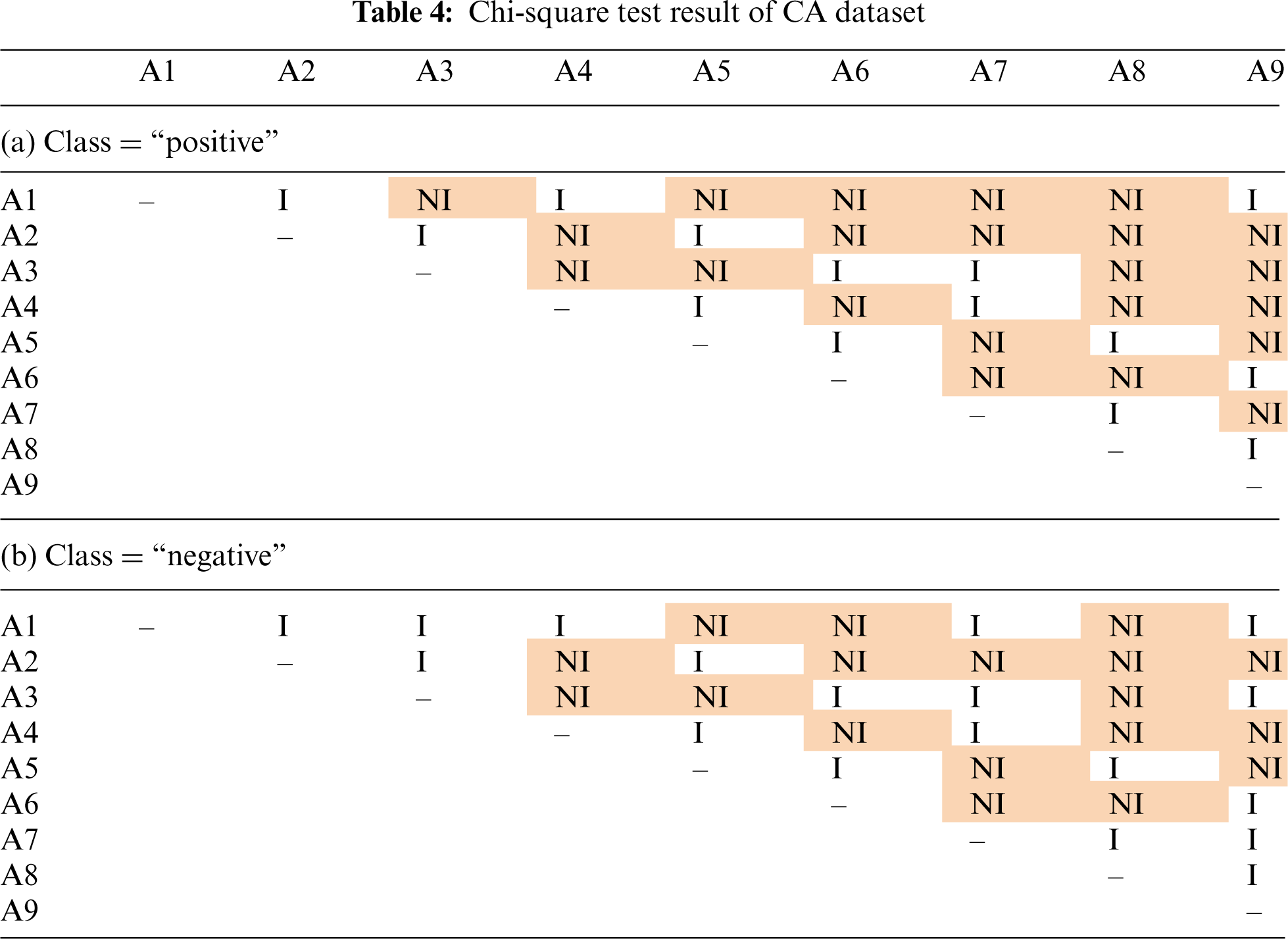
Tab. 4 shows the results of chi-square test on CA dataset, where our method did not perform as good as the standard naïve Bayes and baseline methods. This dataset has 9 attributes with two classes: “positive” and “negative”. Although some “NI” values were observed in Tab. 4, there are also many “I” values. These results showed that some of the attributes in CA dataset are pairwise independent. Although the independence assumption does not hold for all the attributes, the violation is not as serious compared to AB dataset.
For the other datasets where our method performed better, we see a similar results of chi-square test alike the one in AB dataset. For example, out of 55 pairwise chi-square test in MR dataset with 11 attributes, only 2 pairs of attributes are independent in one class and 7 pairs are independent in another. This again means that there is a serious violation on the independence assumption. Our method to incorporate attribute weights is still able to achieve a higher performance even when the independence assumption is seriously violated.
We have also compared the performance of the baseline method to the standard naïve Bayes and the results are presented in Tab. 5. In terms of accuracy, when KL measure is used to calculate the attribute weights, the baseline method performed slightly better for datasets AB and LP, but not as good for 5 datasets (CC, AD, AE, HD and TTT). When IG measure is used, the baseline method only performed better in the AB dataset and not as good for 7 datasets (CC, LP, AD, AE. HP, CA and TTT). In terms of F1, the baseline method with KL performed better for LP and CA datasets, but not as good for 5 datasets (CC, MR, AD, HD and TTT). The baseline method with IG performed slightly better for AB and CA datasets, but not as good for 6 datasets (CC, LP, MR, AD, HD and TTT). The improvement is marginal with only 1 or 2 percent even when the baseline method has a better performance in some datasets.

This paper proposed a new method to incorporate the attribute weights in the computation of conditional probabilities for naïve Bayes classifier. In this paper, we explored two attribute weights based on Kullback-Leibler and information gain measures, and incorporated these weights using our method. We evaluated our method on public benchmark datasets obtained from UCI and FDA repositories. Our attribute weighting method outperformed both the standard naïve Bayes and baseline weighting methods in terms of accuracy and F1. Our method is able to achieve a better performance even when the conditional independence assumption is seriously violated, which is validated with the chi-square test.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. S. Chen, G. Webb, L. Liu and X. Ma, “A novel selective naïve Bayes algorithm,” Knowledge-Based Systems, vol. 192, no. 1, pp. 105361, 2020. [Google Scholar]
2. B. Tang, S. Kay and H. He, “Toward optimal feature selection in naïve Bayes for text categorization,” IEEE Transactions on Knowledge Data Engineering, vol. 28, no. 9, pp. 2508–2521, 2016. [Google Scholar]
3. P. Bermejo, J. Gámez and J. Puerta, “Speeding up incremental wrapper feature subset selection with naïve Bayes classifiers,” Knowledge-Based Systems, vol. 55, no. 1, pp. 140–147, 2014. [Google Scholar]
4. Y. Long, L. Wang and M. Sun, “Structure extension of tree-augmented naïve Bayes,” Entropy, vol. 21, no. 8, pp. 721, 2019. [Google Scholar]
5. L. Yu, L. Jiang, D. Wang and L. Zhang, “Attribute value weighted average of one-dependence estimators,” Entropy, vol. 19, no. 9, pp. 501, 2017. [Google Scholar]
6. L. Jiang, S. Wang, C. Li and L. Zhang, “Structure extended multinomial naïve Bayes,” Information Sciences, vol. 329, no. 2–3, pp. 346–356, 2016. [Google Scholar]
7. J. Wu, S. Pan, X. Zhu, P. Zhang, C. Zhang et al., “Self-adaptive one-dependence estimators for classification,” Pattern Recognition, vol. 51, pp. 358–377, 2016. [Google Scholar]
8. C. Lee, F. Gutierrez and D. Dou, “Calculating feature weights in naive Bayes with Kullback-Leibler measure,” in Proc. of the IEEE 11th Int. Conf. on Data Mining, Vancouver, Canada, pp. 1146–1151, 2011. [Google Scholar]
9. M. Hall, “Decision tree-based attribute weighting filter for naïve Bayes,” Knowledge-Based Systems, vol. 20, no. 2, pp. 120–126, 2007. [Google Scholar]
10. W. Duan and X. Lu, “Weighted naïve Bayesian classifier model based on information gain,” in Proc. of the 2010 Int. Conf. on Intelligent System Design and Engineering Application, Changsha, China, pp. 819–822, 2010. [Google Scholar]
11. L. Yu, L. Jiang, L. Zhang and D. Wang, “Weight adjusted naive Bayes,” in Proc. of the IEEE 30th Int. Conf. on Tools with Artificial Intelligence, Volos, Greece, pp. 825–831, 2018. [Google Scholar]
12. L. Yu, S. Gan, Y. Chen and M. He, “Correlation-based weight adjusted naive Bayes,” IEEE Access, vol. 8, pp. 51377–51387, 2020. [Google Scholar]
13. L. Jiang, L. Zhang, C. Li and J. Wu, “A correlation-based feature weighting filter for naïve Bayes,” IEEE Transactions on Knowledge and Data, vol. 31, no. 2, pp. 201–213, 2019. [Google Scholar]
14. H. Zhang, L. Jiang and L. Yu, “Attribute and instance weighted naive Bayes,” Pattern Recognition, vol. 111, no. 2–3, pp. 107674, 2021. [Google Scholar]
15. D. Berrar, “Bayes’ theorem and naive Bayes classifier,” Encyclopedia of Bioinformatics and Computational Biology: ABC of Bioinformatics, vol. 1, pp. 403–412, 2018. [Google Scholar]
16. D. Dua and C. Graff, “UCI machine learning repository. Irvine, CA: University of California, School of Information and Computer Science, 2019. [Online]. Available: https://archive.ics.uci.edu/ml/index.php. [Google Scholar]
17. U.S. Food and Drug Administration, 2018. [Online]. Available: https://fis.fda.gov/extensions/FPD-QDE-FAERS/FPD-QDE-FAERS.html. [Google Scholar]
18. U. Fayyad and K. Irani, “Multi-interval discretization of continuous-valued attributes for classification learning,” Artificial Intelligence, vol. 13, pp. 1022–1027, 1993. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |