DOI:10.32604/cmc.2022.021793

| Computers, Materials & Continua DOI:10.32604/cmc.2022.021793 |  |
| Article |
Hybrid Cuckoo Search Algorithm for Scheduling in Cloud Computing
CSE Department, DCR University of Science and Technology, Murthal, 131039, Sonepat, India
*Corresponding Author: Manoj Kumar. Email: manojsarasyiya@gmail.com
Received: 15 July 2021; Accepted: 27 August 2021
Abstract: Cloud computing has gained widespread popularity over the last decade. Scheduling problem in cloud computing is prejudiced due to enormous demands of cloud users. Meta-heuristic techniques in cloud computing have exhibited high performance in comparison to traditional scheduling algorithms. This paper presents a novel hybrid Nesterov Accelerated Gradient-based Cuckoo Search Algorithm (NAGCSA) to address the scheduling issue in cloud computing. Nesterov Accelerated Gradient can address trapping at local minima in CSA by updating the position using future approximation. The local search in the proposed algorithm is performed by using Nesterov Accelerated Gradient, while the global search is performed by using levy flights. The amalgamation of NAG and CSA helps in cost reduction and time-saving for users. The simulation has been carried out on the CloudSim tool on three different real datasets; NASA, HPC2N, and SDSC. The results of the proposed hybrid algorithm have been compared with state-of-art scheduling algorithms (GA, PSO, and CSA), and statistical significance is carried on mean, standard deviation, and best for each algorithm. It has been established that the proposed algorithm minimizes the execution cost and makespan, hence enhancing the quality of service for users.
Keywords: Cloud computing; scheduling; quality of service; cuckoo search; cost; makespan
Cloud computing has become a fundamental part of the computing world nowadays. The expansion of cloud computing technology act as the backbone of newly developed technology like Fog Computing [1], Internet of Things (IoT) [2], Cloud of Things [3] etc. Cloud computing provides services to its users through the internet without knowledge of hardware and other infrastructures. Cloud uses on-demand policies, i.e., the services are available to its users as per their demand, and user has to pay to the service provider based on usage of cloud services [4]. However, there are methods of resource provisioning like leased and reserved, which are used by big organizations [5]. The additional benefits of cloud computing are scalability, availability, reliability, flexibility, and sustainability [6,7].
The key technology behind the success of cloud computing is virtualization. Virtualization helps cloud providers to deliver any kind of computing phenomenon by assembling the required hardware and software together on a single platform and minimizing the complexity and burden of buying new hardware and software. Some of the virtualization vendors are Xen [8], Virtual Box [9], VMWare Server [10]. Mostly offered public clouds are owned by Google Cloud [11], Amazon EC2 [12], Microsoft Azure [13].
Resource scheduling is a building block in cloud computing that decides how resources are distributed over time and made available to its users in the best possible way. It helps in providing the best quality of service to its users and the best utilization of resources to increase profits. The fluctuating demands of users are unpredictable concerning the time domain, so it is very difficult to satisfy resource requirements in dynamic nature. Scheduling in cloud computing is done at two levels: users to virtual machines (VM) and VM to the physical host. The first level scheduling is responsible for maintaining the quality of service in terms of makespan, execution cost, and response time while the latter decides load balancing, migrations, energy and resource utilization [14].
As the number of users and virtual machines keeps on changing continuously in cloud computing, so resource scheduling in the cloud system is an NP-Hard problem. Suppose there exit N users and M virtual machines for a broker to satisfy the user’s requirements. The number of schedules for N users for M machines is N2M which increases exponentially in the cloud environment with an increase in the number of machines and number of users. Therefore, resource scheduling is NP-Hard in nature and requires efficient algorithms that satisfy both users and cloud service providers. The fitness function of any scheduling algorithm is focused on cloud service providers and user requirements. The fitness function considers the availability, cost, makespan, energy, throughput, reliability, fault tolerance, etc., for optimal scheduling. An optimization problem can be stated as a fitness function f mapping the candidate solution to fitness measure
Hybrid algorithms always try to conquer all factors in solving any optimization problem. The benefits of combining two or more algorithms are that they always find the best solutions by addressing the limitations of the single algorithm in terms of speed and accuracy. Hybrid algorithms consist of some meta-heuristic techniques, while other methods can achieve optimal scheduling.
Cuckoo Search (CS) algorithm is a population-based meta-heuristic technique that has been widely used by the researcher in various domains of engineering and technology like scheduling, image processing, structural design, speech recognition etc. [16]. The searching behaviour of CS does not guarantee finding an optimal solution for specific problems. CS may trap into local minima and may lead to premature convergence. To solve this problem in CS, the Nesterov Accelerated Gradient technique is used in local search to improve the convergence rate and identify more feasible solutions to schedule activities on virtual machines with the lowest execution cost and time, hence improving the quality of service (QoS) for customers. Therefore, this paper proposes a novel hybrid Nesterov Accelerated Gradient-based Cuckoo Search (NAGCSA) algorithm to enhance QoS in terms of makespan and execution cost.
The vital contributions of this paper are as follows:
• Frame the makespan and execution cost using mathematical models for scheduling as the fitness functions
• Hybridize the Nesterov Accelerated Gradient with Cuckoo Search for scheduling in IaaS cloud
• Design of hybrid NAGCS algorithm to address the proposed scheduling model.
• Proposed hybrid NAGCS algorithm is implemented in the CloudSim simulation tool.
• Comparability of proposed hybrid NAGCS algorithm with CS algorithm and meta-heuristic techniques like GA and PSO in terms of makespan and execution cost.
The remaining sections of this paper are organized as follows: Section 2 review some existing techniques that are used in scheduling for IaaS cloud computing. Problem is formulated in Section 3. Section 4 presents the mathematical models of performance metrics that is used in this research work. Section 5 presents the explanation for CS search, Nesterov Accelerated Gradient and hybrid NAGCS algorithm. Section 6 presents the simulations setups for scheduling. Results and discussions are furnished in Section 7, and finally, we conclude the paper in last with some valuable suggestions.
There is a vast literature on scheduling techniques in cloud computing. Researchers and scientists have applied many computational techniques to perform scheduling in cloud computing considering various constraints like budget, deadlines. The various review articles published in the literature have shown a broad application of heuristic and meta-heuristics techniques to solve various challenges in cloud computing [17]. Some past studies like [18] show various requirements of QoS based on particle swarm optimization. Computational intelligence has been divided into two parts heuristic, and meta-heuristic and how they were applied in cloud computing is very well explained in studies [19].
Genetic Algorithm (GA) has been widely used in cloud computing for performing scheduling, load balancing, and VM allocation. Its modified version and hybrid form with other techniques were also used for efficient scheduling in cloud computing. Author in [20] proposed multi QoS GA-ACO to schedule tasks on VMs to minimize the execution time and improves resource utilization. Alla et al. [21] proposed dynamic dispatch queue-based task scheduling strategies optimized using fuzzy logic and particle swarm optimization (PSO) and simulated annealing with PSO to minimize waiting time, makespan and cost. The algorithms were tested on both synthetic and real data systems while disabling the migration systems. The proposed work was extended to add energy parameters to minimize makespan while deadline as a constraint in [22]. The proposed algorithm improved QoS, minimize energy and improve resource utilization significantly.
Abari et al. [23] enhanced GA to perform static scheduling for a processor in a heterogeneous cloud computing environment by replacing random population with some initial population with relatively optimized solutions to lower repetition. Keshanchi et al. [24] modified GA with Linear Temporal Logic (LTL) formulas to schedule workflow in the cloud. The modified GA helps in prioritizing the tasks and determined the best available resource for execution efficiently. Zhou et al. [25] also modified the GA with a greedy strategy for scheduling the tasks in the cloud computing environment. The proposed method finds the solution very early in few iterations and helps minimise the makespan, response time, and maintain good QoS from the user’s perspective.
Strumberger et al. [26] developed a scheduling algorithm with hybridization of monarch butterfly algorithm with ABC method to minimize the makespan. The algorithm was tested first on standard mathematical benchmark functions and then applied to scheduling problems in cloud sim simulator. Both synthetic and real data set were used to prove the performance of proposed algorithm; however, how priority of task is taken is not explained in work. Author also applied [27] whale optimization algorithm for scheduling of task by modifying the exploration stages of whale optimization with ABC and firefly to remove the weakness of Whale optimization algorithm. The algorithm achieves good QoS in terms of makespan and resource utilization.
Al-Olimat et al. [28] proposed the hybrid PSO-SA based scheduling technique to schedule the tasks in cloud computing environment. The SA helps in adjusting the weights of particles and moved them toward good solution. The proposed method minimizes the makespan however some more parameters need to be tested to find the performance of algorithm in multi-objective nature. Alsaih et al. [6] developed a dynamic job scheduling model to map the jobs with resource based on available resources characteristics and also re-schedule the jobs that get allocated to VM. Proposed method minimizes the makespan, improved CPU utilization and bandwidth utilization. Beegom et al. [29] developed discrete-integer based PSO algorithm to schedule tasks in cloud computing and applied it on single optimization and multiple optimization problem. The algorithm efficiently manages the degree of imbalance, minimize cost and makespan. Attiya et al. [30] designed a hybrid algorithm by combining the Harris Hawks Optimization and Simulated Annealing (SA) technique to minimize the makespan in cloud. The algorithm improves response time and converges early to give good solutions as search spaces increases.
Madni et al. [31] proposed multi-objective cuckoo search based scheduling to find the non-dominant solution in cloud computing to minimize execution cost, makespan and improves resource utilization. The simulations were carried out in CloudSim simulator, and real data set were used to evaluate the performance of algorithm with other meta-heuristic techniques. Author also extended the cuckoo search algorithm with gradient descent to increase the performance in [32]. Gradient descent was used to perform the local search, and levy flight in the cuckoo search was used to perform global search. The proposed hybrid algorithm was tested on both synthetic datasets and real datasets.
Kaur et al. in [33] proposed the hybrid GA-ACO based scheduling mechanism to minimize the execution time and makespan. The proposed algorithm was tested on a synthetic dataset inside Matlab and compare with GA and ACO; however, its performance can be compared with more meta-heuristic techniques.
The analysis of the reviewed articles established that the majority of studies includes meta-heuristic techniques like GA, PSO, ABC, and ACO and their hybridization with some heuristic techniques. These algorithms get trapped in local minima while performing scheduling in cloud computing. The performance of these algorithms is also not compared with other meta-heuristic techniques. This article presents a technique to avoid local optima problem using NAG and also performs better at global minima.
Resource scheduling in cloud computing is NP-Hard in nature. It is defined as mapping the user’s task to the best available virtual machines to fulfill the user’s demand. Suppose a cloud datacenter consists of p physical hosts, represented by set
where
Suppose there is set of Activity cost
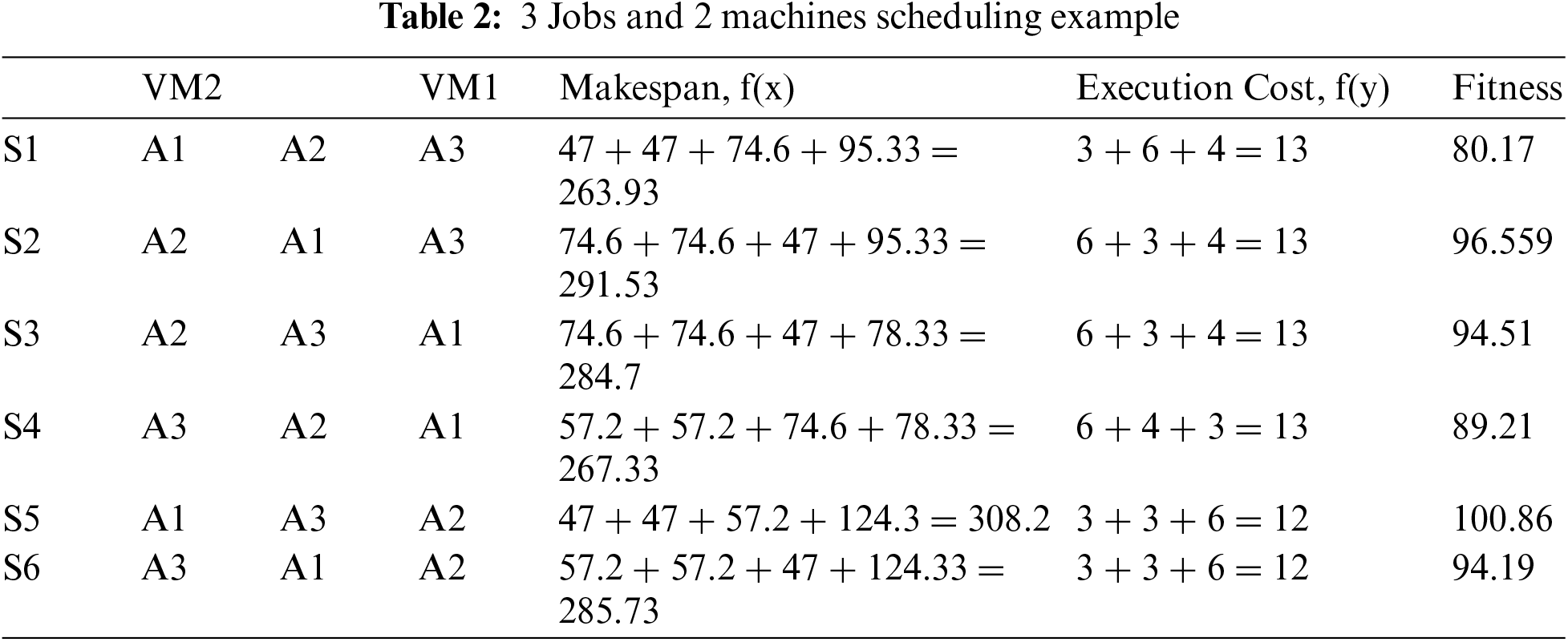
Selecting the best resource for cloud user with minimum cost in less time is very complex problem. To understand the complexity of the problem, a simple example is illustrated in Tab. 1.
Suppose there are two virtual machines available (VM1 and VM2) in the cloud datacenter and three users (A1–A3) requested for resource. The cloud broker can allocate any two users without waiting, but one user has to wait for some time. Considering this there are two choices available to broker, either any two users use machine 1 and one user use machine 2 or any two-user use machine 2 and only one user use machine 1. So, there are multiple decisions available to cloud broker and is responsible to give good quality of service to his users. The multiple decisions are illustrated in Tab. 2 with execution time and cost value. Similarly, more schedule S7 to S8 can also presented in which two users can use VM1 and remaining one will use VM2.
4 Mathematical Model for Scheduling
In this article, makespan time and execution cost are considered as the main objective for scheduling in cloud computing. Therefore, fitness value of hybrid NABCS can be calculated using equation Eqs. (5) and (6).
Makespan is the maximum finishing time of all activities when they mapped on VMs. It is calculated using Eq. (5).
where Ti indicates the completion time of specific activity.
Execution cost is defined as amount paid by cloud users to CSP for executing their activities on VMs as per Service Level Agreement (SLA). Eq. (6) is used for calculating execution cost for specific VM.
where
The two functions of makespan and execution cost can be combined together as weighted-product of two functions respectively. So, combining Eqs. (5), and (6) to into a single objective function:
where w is weight factor, that decides importance to makespan and execution cost, and
The Eq. (8) inherits the characteristics of weighted sum and weighted product performance metrics namely; makespan and execution cost. Combining both weighted sum and weighted product in calculation provides two advantages; firstly, it makes equation analytically tractable and logarithmic expectation is additive over time [34,35]. It helps to analyze makespan-cost trade-offs in much more efficient way to enhance QoS.
In this section, the concepts of CS algorithm and NAG is presented. Then, hybridization of CS with NAG is presented to explain how NAG is helpful in local search.
Cuckoo Search Algorithm [36] is a population-based meta-heuristic technique developed by Xin-She Yang and Suas Deb. The behaviour of various species of Cuckoo of laying their eggs in other’s nests to maximize the hatching probability [36]. CS has significantly proved in global optimization problems for its fast convergence and speed. Various problems of engineering have been solved using CS, including scheduling. The original Cuckoo Search works on three principles: -
• Each Cuckoo lays one egg at a time and places it in a nest that has been selected at random.
• The highest-quality nest will be the carrier of the next generation or solution.
• The number of host nests is fixed, and a host can realize unfamiliar eggs with the probability (0 or 1). In this case, a host can abandon the nest to build a new nest or throw cuckoo egg.
There are three parameters used in CS algorithm.
•
• α > 0 step size, depends on scale of the problem, mostly taken α > 1.
→
Levy flight is most commonly used in terms of step length with CS to update the solution as represented in Eq. (9)
where
Assumptions of CS algorithm
(1) Cuckoo bird lays one egg at a time, which shows one solution.
(2) Nests having the best solution would be most delicate nests, i.e., nest itself represents the solution.
(3) A fixed number of the nests would be available; there are finite numbers of initial solutions, which will remain the same throughout the algorithm [36].
The behaviour of CS algorithm performs local and global search based on switching and discovery probability
5.2 Nesterov Accelerated Gradient (NAG) Approach
Gradient Descent is commonly used optimization method for finding local minima of a function [37]. It has been widely used in machine learning to optimize any network. The gradient states that if a function F(x) is discrete and differentiable near any point a, the value of F(x) decreases if one move from a in negative of gradient of F at point a, −
where a is current position, b is next position,
The concept of the Nesterov Accelerated Gradient [39] approach helps to update the function’s position towards minimum with a look ahead. It helps in the correction of position if function moves away from the optimal solution in any particular iteration. The intuition behind accelerated gradient follows the rule-“look ahead before you leap” for a particular update. Now, applying this rule on Eq. (10),
For particular iteration i.
The updatei can be derived from the momentum-based update rule and can be understood mathematically as follows:
(1) Without momentum
(2) With momentum
Now applying NAG rule on Eqs. (13) and (14), the look-ahead before you move can be calculated and updated as follows:
The updates come in two parts; a partial update and a final update. So, when a function overshoots and goes away from the optimal solution, NAG helps to take a U-turn and comes closely towards minima. The updating of a function from a particular point towards minima is based not only on current position but also on an approximation of future position. This helps in finding more accurate results and can be used with other meta-heuristic techniques with problem of trapping of a function at local minima.
5.3 Hybrid Nesterov Accelerated Gradient-Based Cuckoo Search Algorithm
Resource scheduling issues have been solved by various meta-heuristic techniques. Many scheduling algorithms have been proposed to optimize the scheduling issue in IaaS cloud computing, but every algorithm has limitations like speed or premature convergence. Most of the meta-heuristic techniques use the current position to update its position towards optimal solution. This hybrid algorithm uses the look-ahead position to move towards optimal solution even if it moves away from optimal solution. The proposed hybrid NAGCSA helps in local optimization due to NAG and global search maintains through breeding behaviour of cuckoo search algorithm.
A set of random integers is generated using an array that represents a solution for scheduling. This step finds dimension of solutions, given by number of n activities, lower bound and upper bound of the search space. Therefore, the process of generating
where each value of xi has any integer value in the interval [1, m], where m is number of virtual machines, and Round coverts it to nearest value to whole number. To understand it more clearly, consider an example of twelve activities on five virtual machines. So, generated values for one solution using Eq. (13) are given in xi = [4, 3, 2, 2, 1, 3, 1, 5, 2, 4, 3, 3]. The value “four” indicates the first job will be assigned to fourth machine. So, second, sixth, eleventh and twelfth jobs will be assigned to third machine. Similarly, interpretation of all other values can be done. The Eqs. (3) and (4) will calculate requires amount of execution time and cost initially. This xi also represents cuckoo’s eggs in our algorithm.
After the initialization stage, fitness of all eggs is calculated, the best is selected. All cuckoos now fly towards the optimal solution with step-size variable. NAG is used for performing local search when
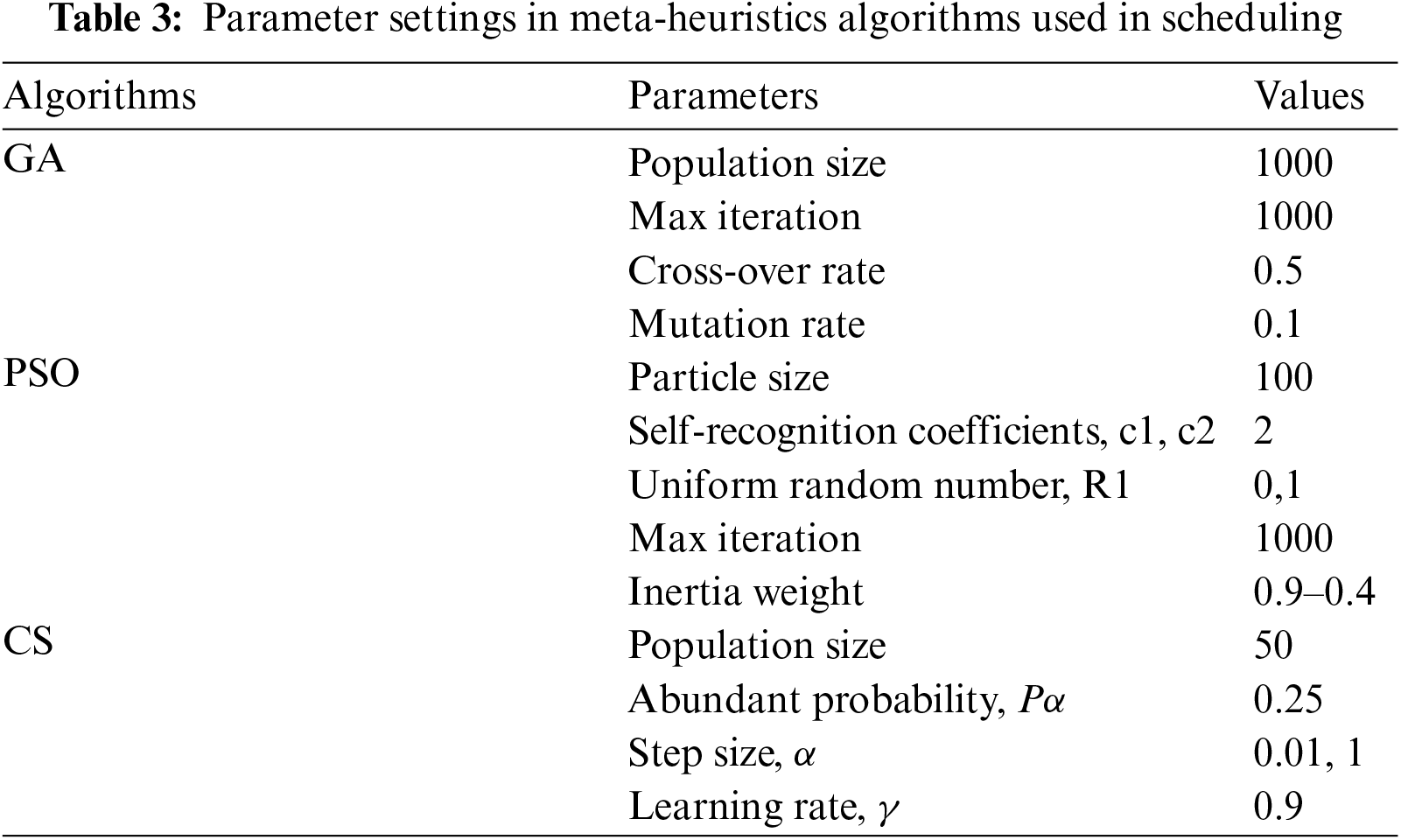
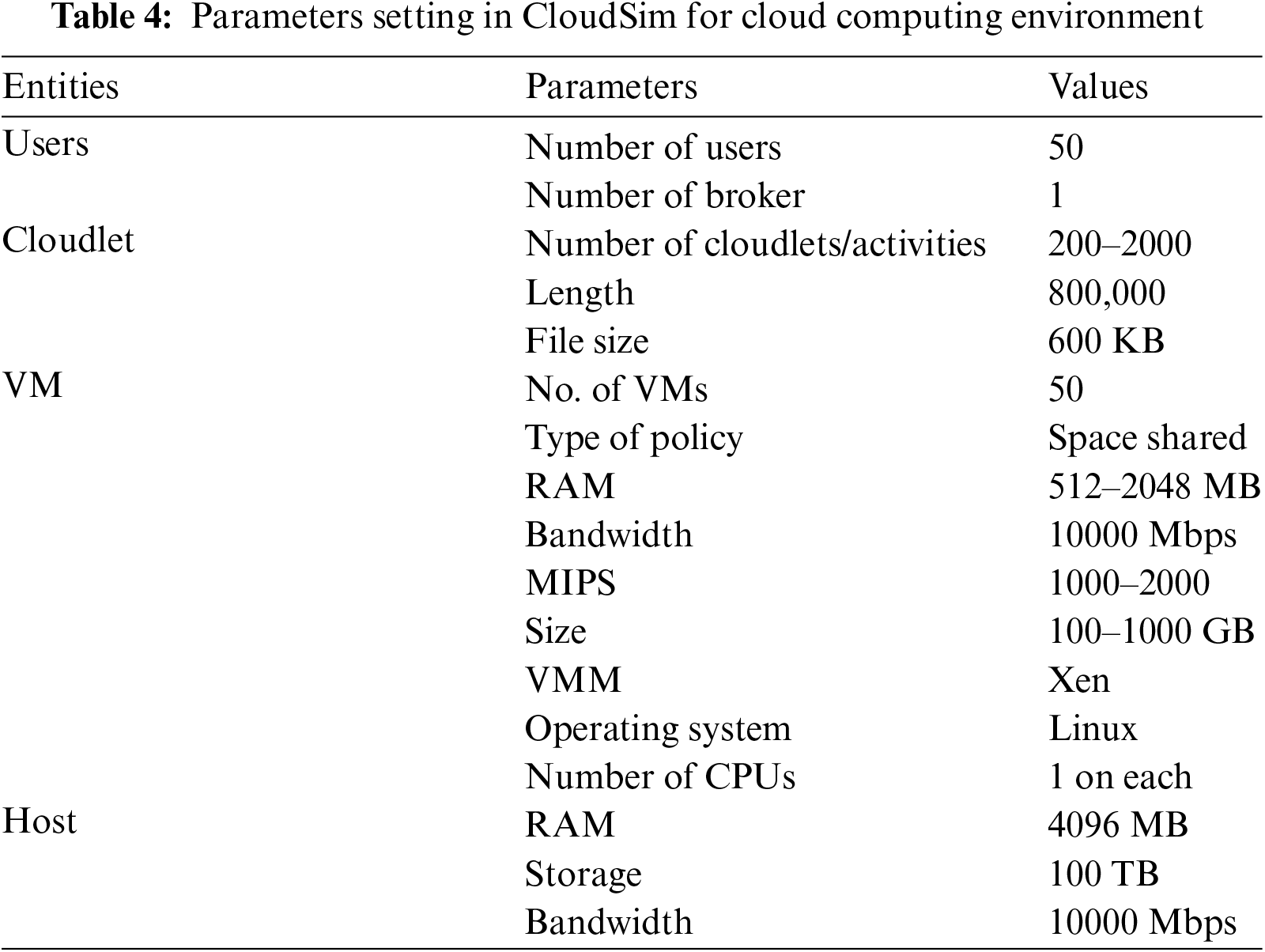
The simulation setup is described in this section. Simulation has been prepared on Apache NetBeans IDE 11.3, supported by CloudSim simulation tool 3.03 [40], which is a Java-based simulator. The software has been installed on the HP ProDesk desktop computer having 64-bit Windows 10, 16 GB RAM, 3.20 GHz CPU, with eight cores. The performance of the proposed hybrid NAGCSA is compared with genetic algorithm (GA), particle swarm optimization (PSO), and standard cuckoo search (CS) algorithms, respectively. Parameter setting of each meta-heuristic technique is presented in Tab. 3. The configuration settings of CloudSim are presented in Tab. 4.

Figure 1: Hybrid nesterov accelerated gradient-based cuckoo search algorithm
The performance of the proposed hybrid NAGCSA is evaluated on real traces from HPC2N (High-Performance Computing Center North) [41], NASA Ames iPCS/860 [42], and SDSC (San Diego Supercomputer Center) [43]. These workload archives are presented by “Ake Sandgren, Bill Nitzberg and Victor Hazlewood”, in the standard workload format (swf) recognized by the CloudSim tool. These workloads are primarily used to evaluate the performance of scheduling algorithms in cloud computing. HPC2N has 527,371 jobs, NASA has 14,794 jobs, and SDSC has 73,496 jobs.
This section presents and discusses the computational outcomes of the simulation performed in CloudSim tool. The makespan time and execution cost are considered to evaluate the Quality of Service of the proposed algorithm.
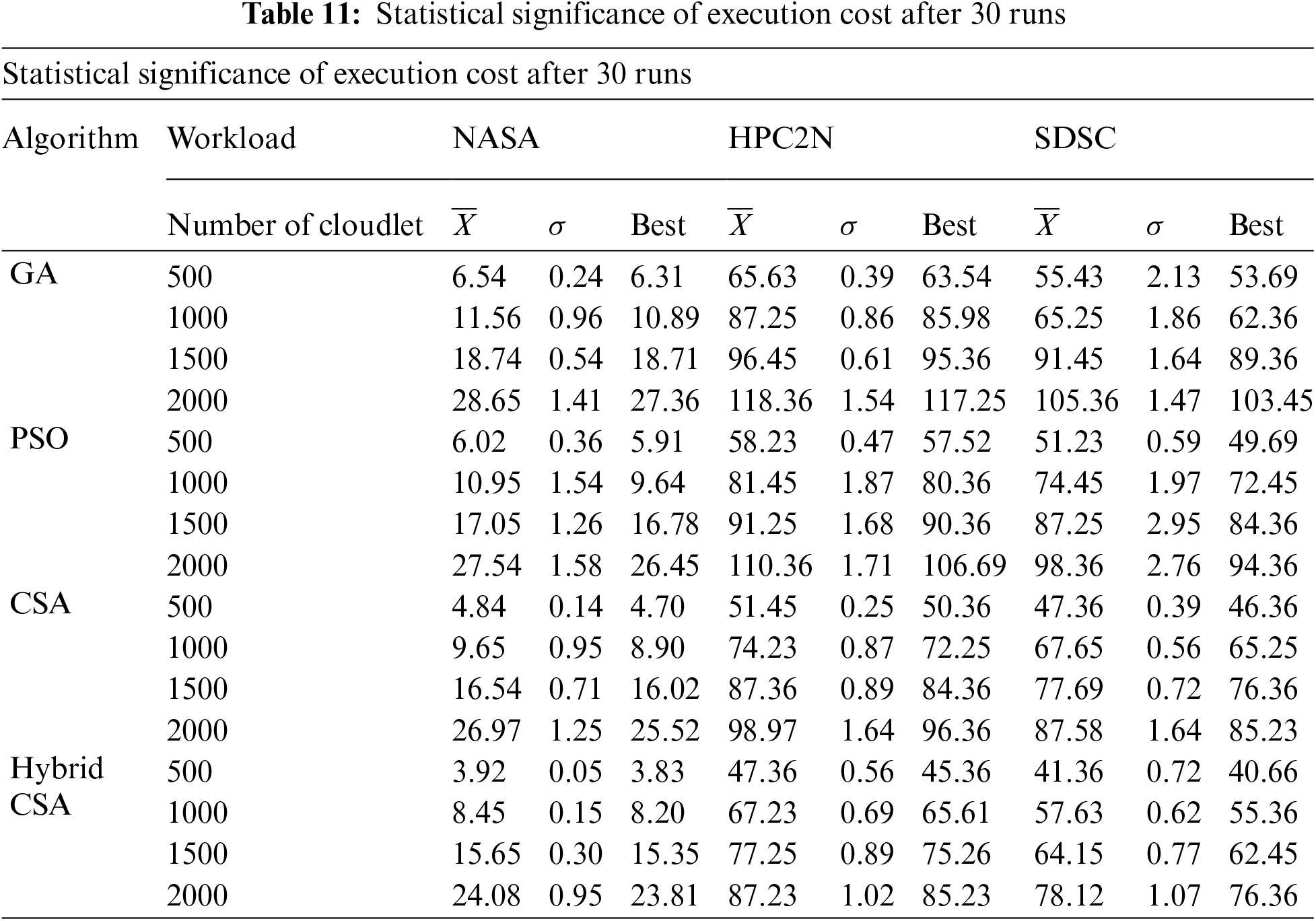
Figs. 2–4 show the execution cost calculated of the hybrid NAGCSA algorithm with the help of NASA, HPC2N and SDSC workload. The simulation has been carried out on a varied number of cloudlets ranging from 500 to 2000. The other meta-heuristic algorithms used in resource scheduling (GA, PSO, and CSA) in cloud computing are used for comparison with the proposed hybrid algorithm. The pricing policy of VMs was taken from Google AppEngine [11], and the unit of cost is dollar ($). The execution cost calculated by the proposed hybrid algorithm is lower than the other algorithms. It can be seen that the proposed hybrid algorithm supports cloud users to save more money in a cloud environment. Execution cost increases while an increase in the number of cloudlets. The performance of the proposed hybrid algorithm is increasing while an increase in the number of cloudlets. The performance improvement rate of the proposed hybrid algorithm is shown in Tabs. 5–7.
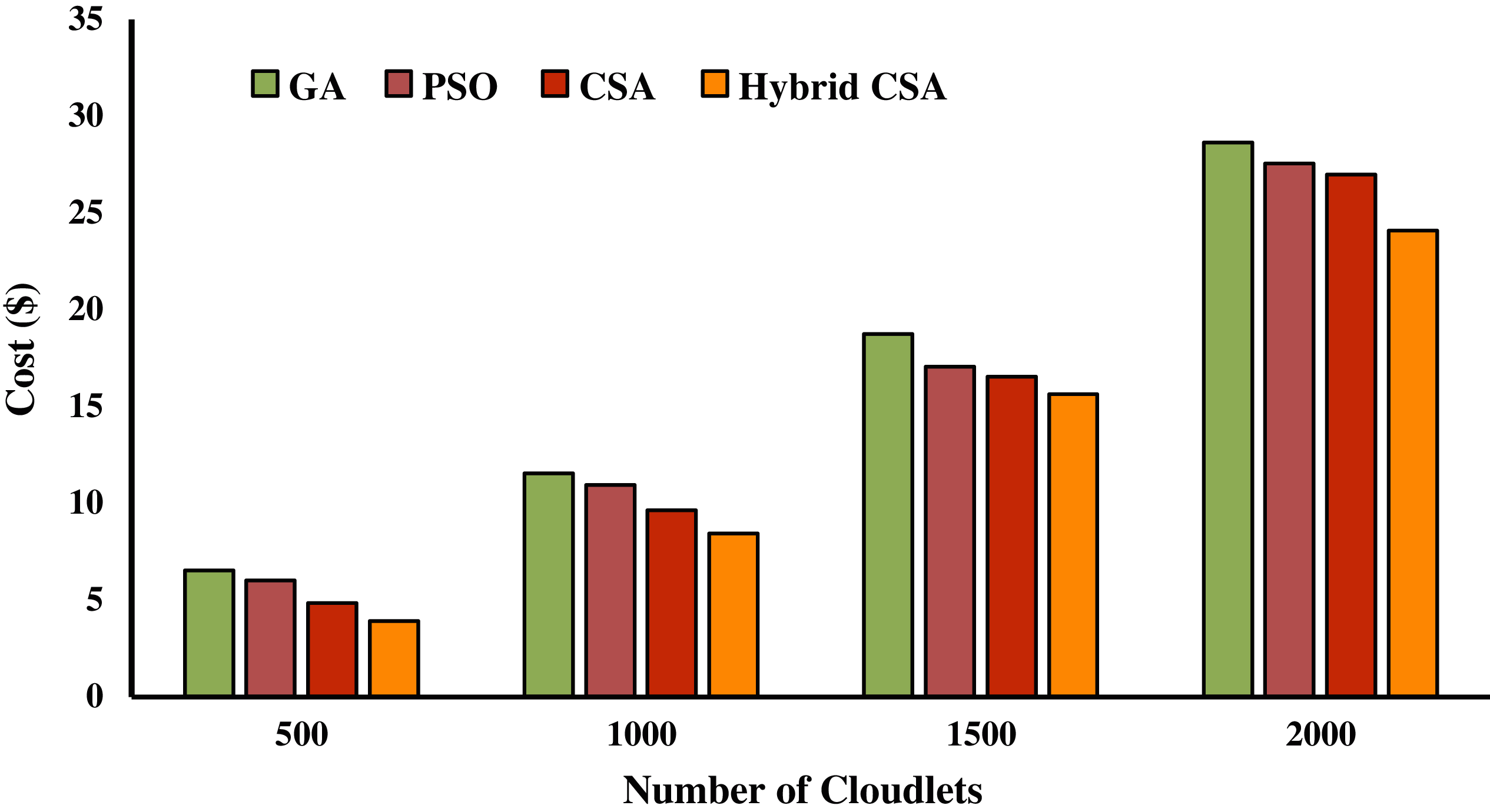
Figure 2: Execution cost on NASA dataset
The performance improvement rate (PIR) is calculated to evaluate the improvement for the xth algorithm as compared to yth algorithm [31,32,44]. It can be calculated using Eq. (19).
PIR (%) is calculated based on makespan on three different datasets shows that proposed hybrid Cuckoo Search Algorithm has a significant performance than GA, PSO, and CSA. Proposed hybrid algorithm minimizes execution cost by 35.59%, 32.22%, and 31.26% as compared to GA; 26.61%, 22.19%, and 24.05% as compared to PSO; and 13.83%, 11.40%, and 16.35% as compared to CSA on NASA, HPC2N, and SDSC workloads respectively, which is presented in Tab. 5–7.
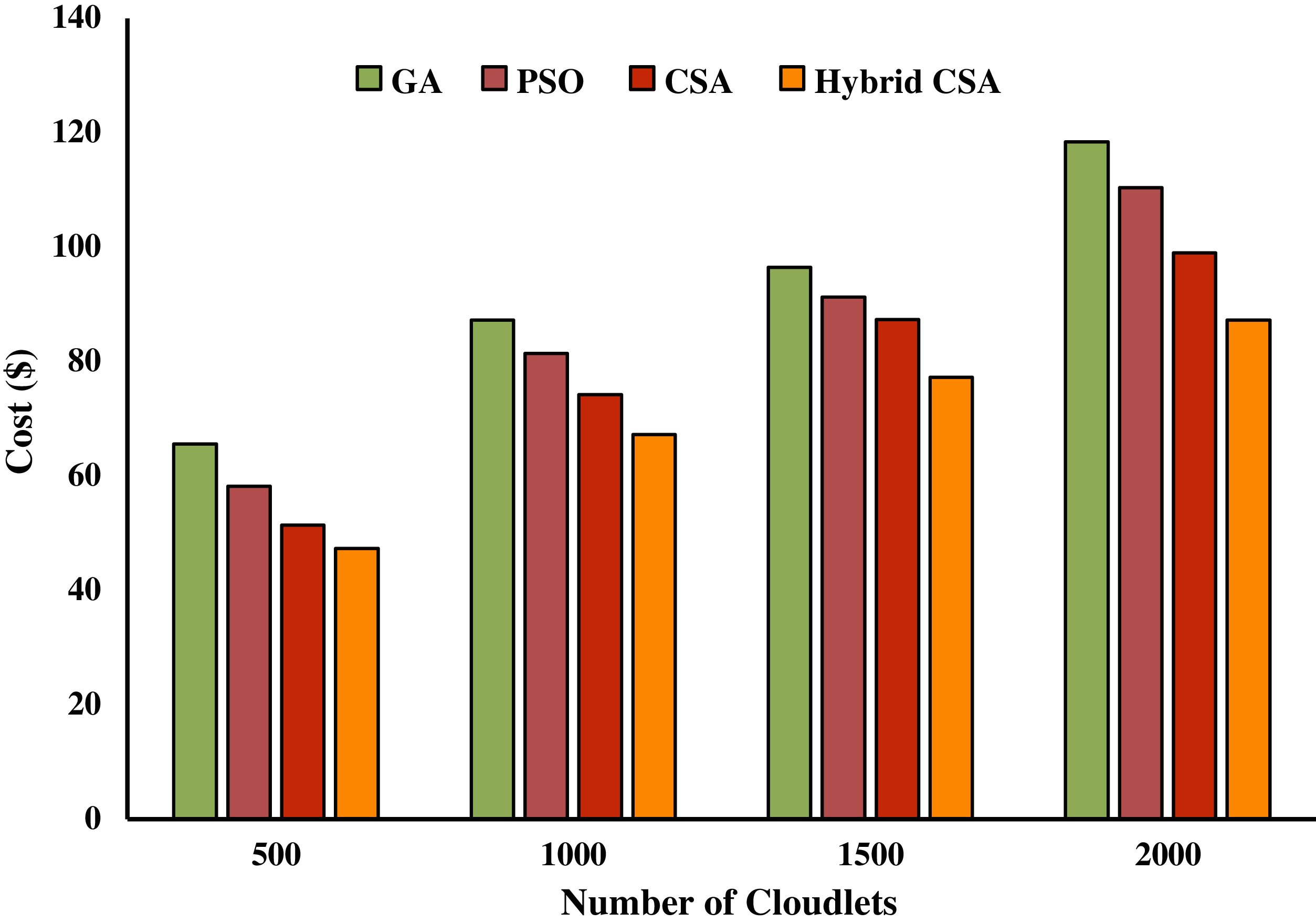
Figure 3: Execution cost on HPC2N dataset
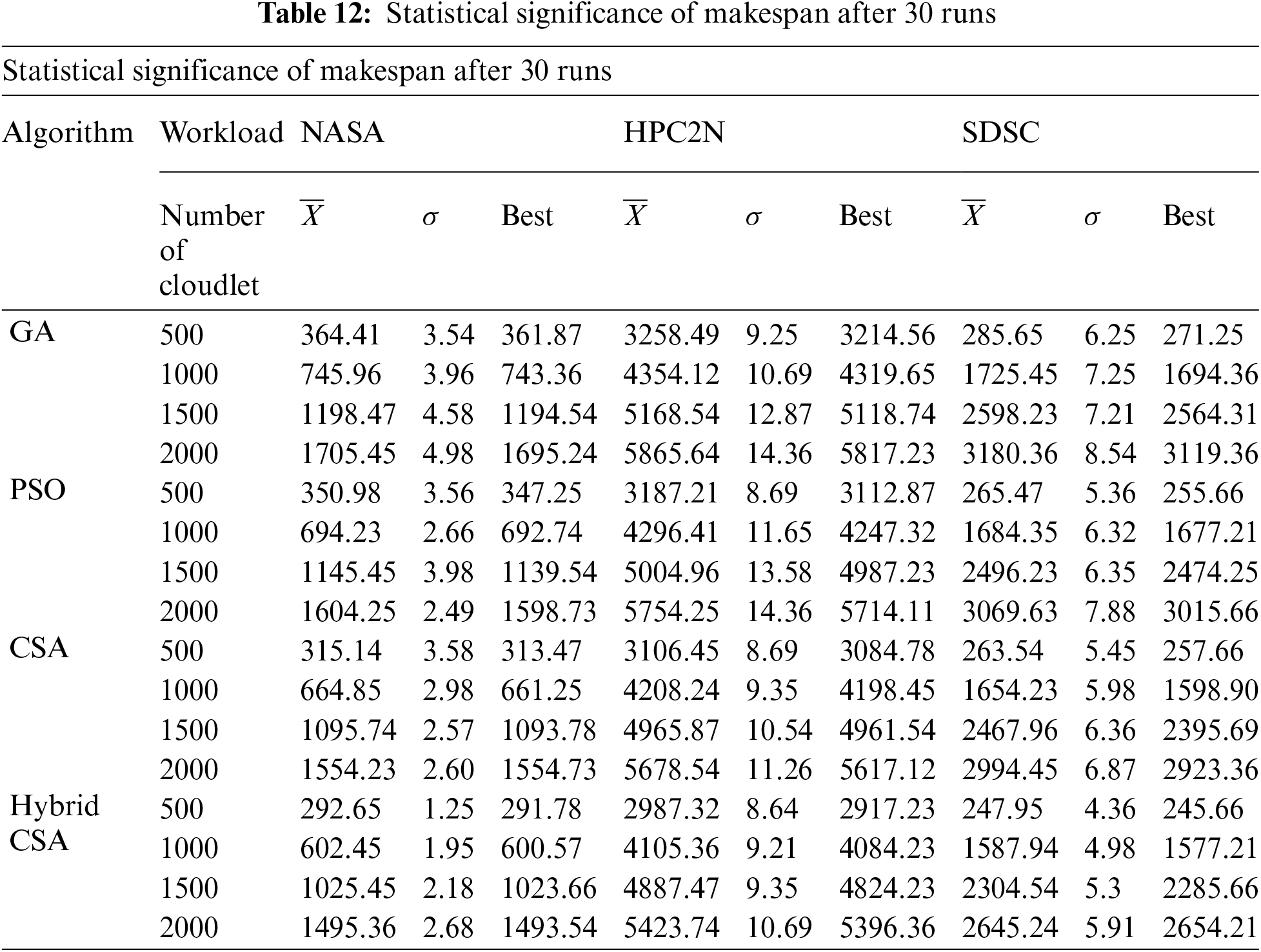
Figs. 5–7 present the makespan calculated by a proposed hybrid algorithm for three different datasets in seconds. The other meta-heuristic algorithms, GA, PSO, and CSA, were also simulated with the same configuration to calculate the makespan. Figs. 5–7 show that our proposed hybrid NAGCSA algorithm minimizes the makespan and finishes the execution of all cloudlets earlier than GA, PSO, and CSA. The simulation has been carried out on a varied number of cloudlets from 500 to 2000, and a mean of 30 simulation results are presented in the form of bar charts. The performance of proposed hybrid algorithm saves more time. The performance improvement rate (%) in makespan is presented in Tabs. 8–10 for each dataset. Proposed hybrid algorithm reduces time and exhibits 19.82%, 13.54%, 7.21% improvement on NASA, 7.26%, 4.96%, and 3.20% improvement on HPC2N, 15.09%, 10.24%, and 8.54% improvement on SDSC over GA, PSO, and CSA respectively.
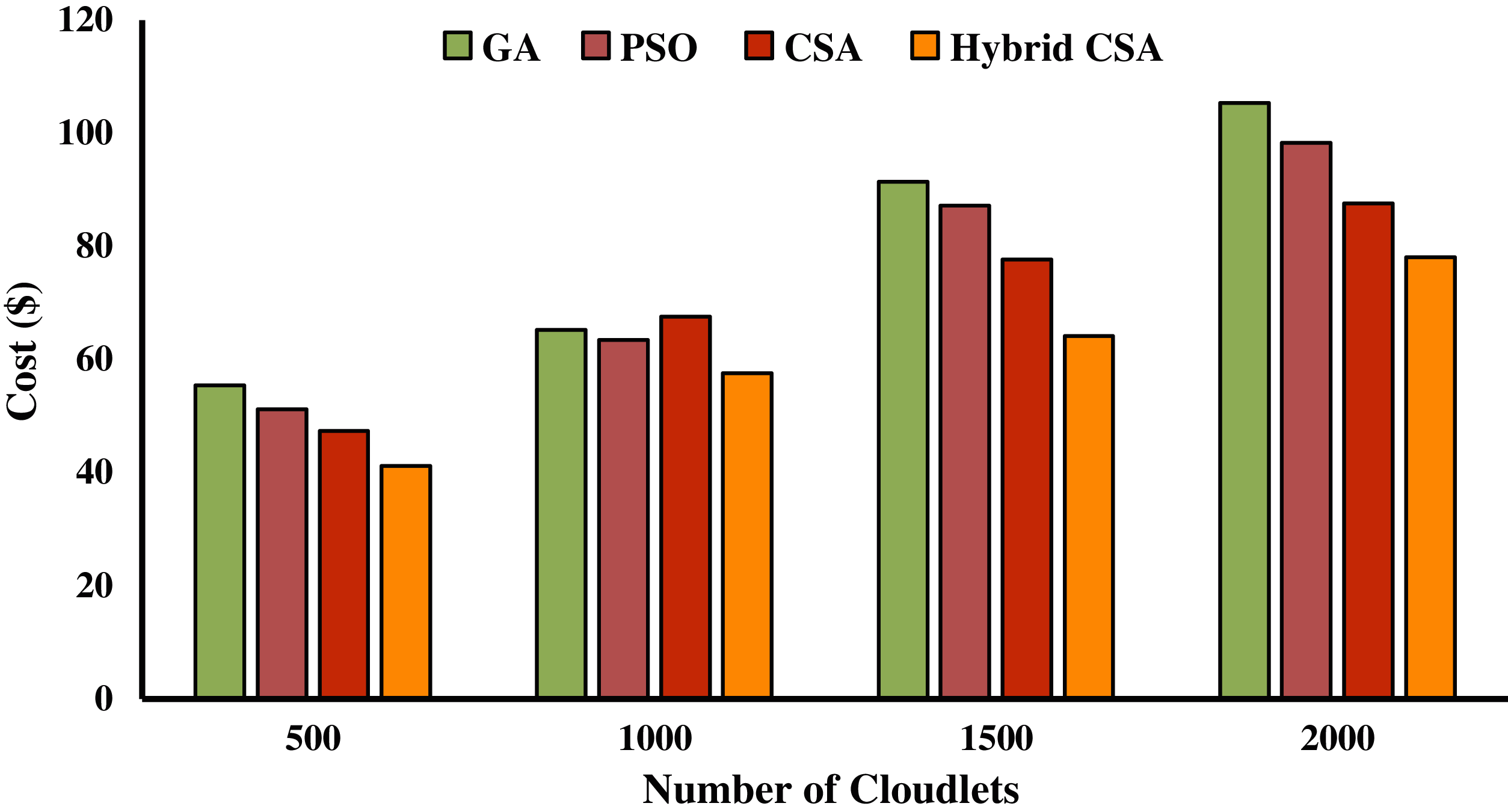
Figure 4: Execution cost on SDSC dataset
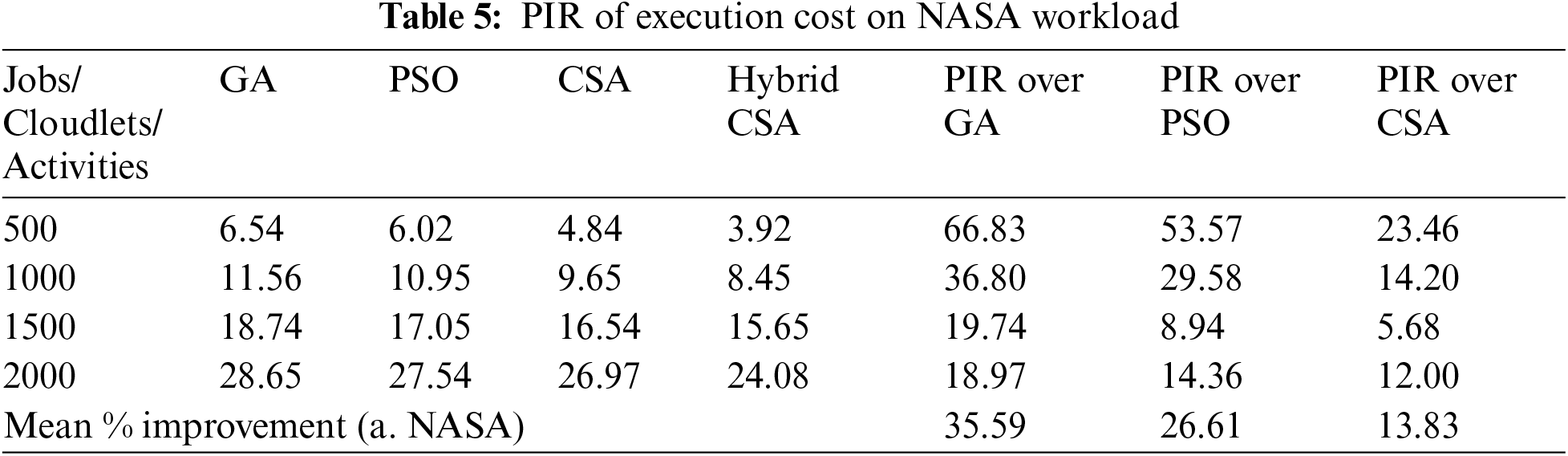
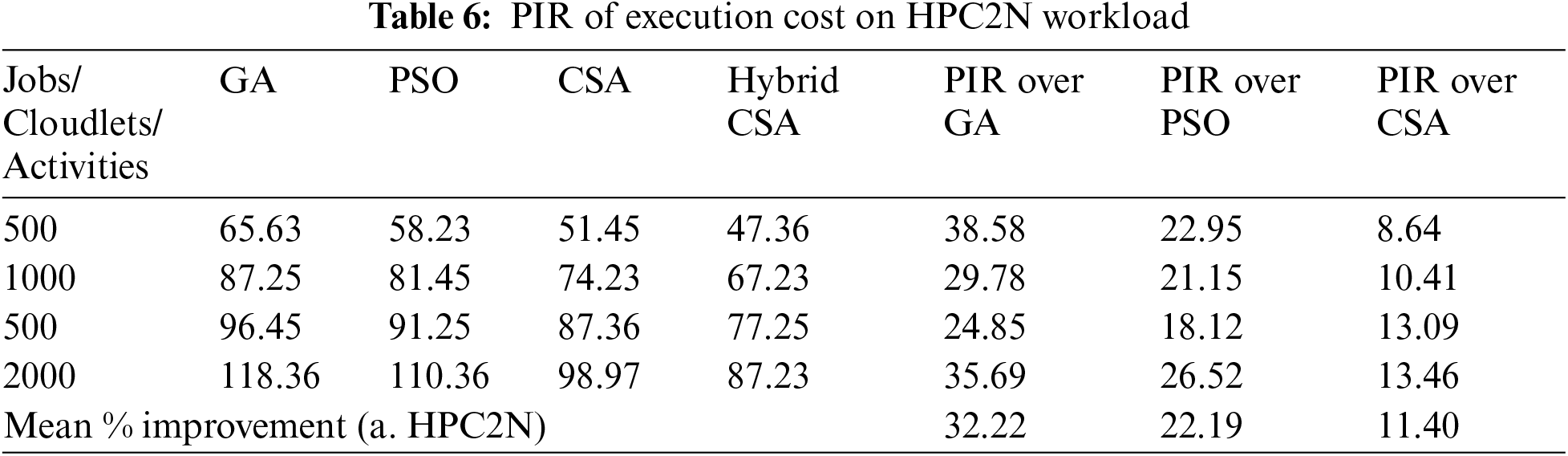
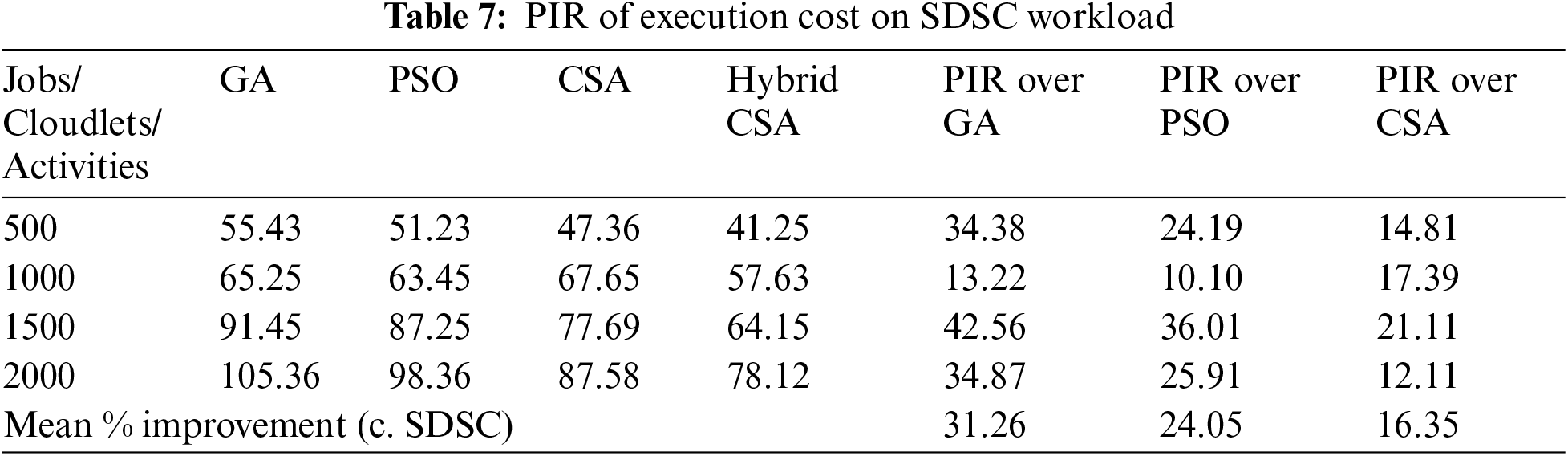
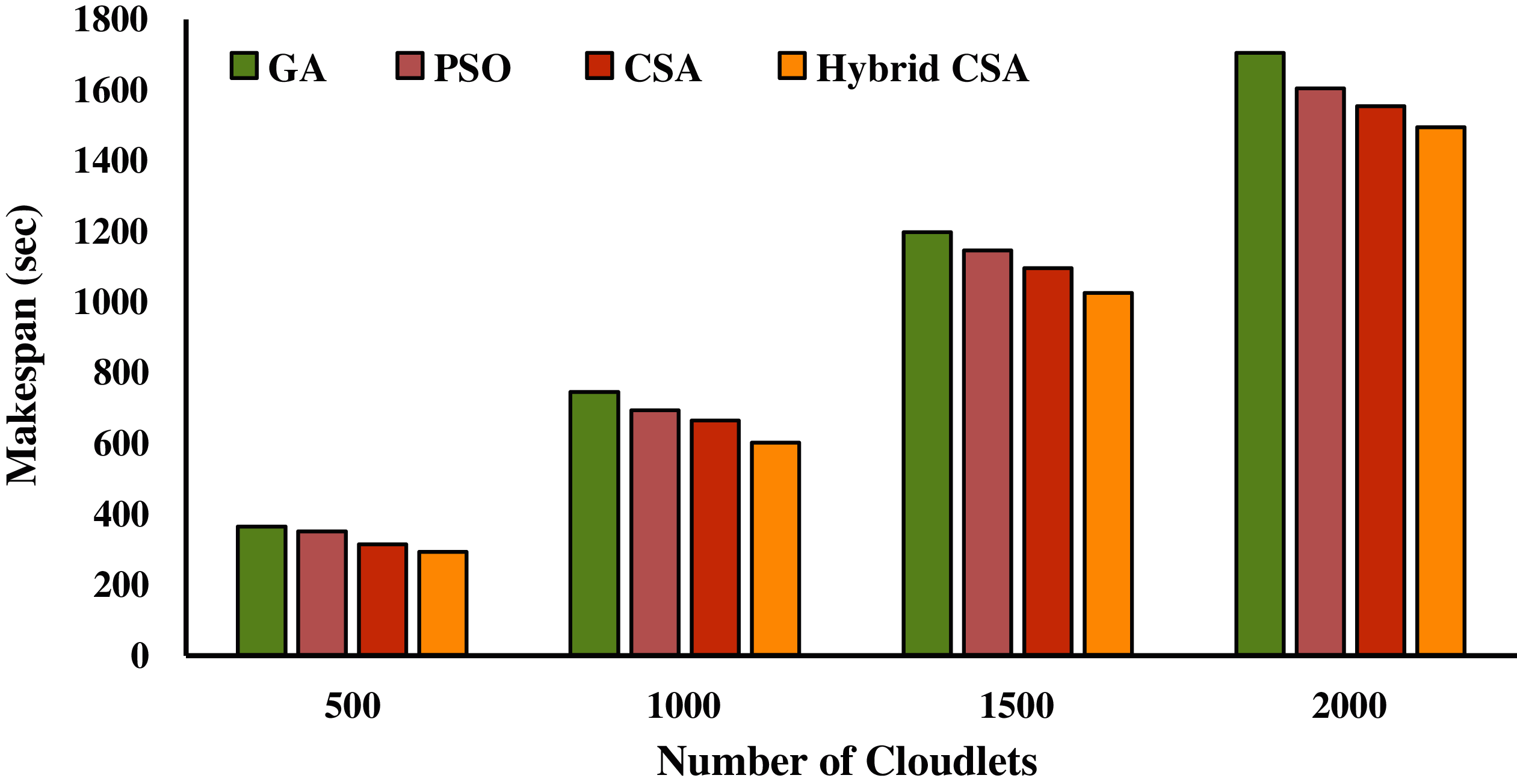
Figure 5: Makespan calculated on NASA dataset
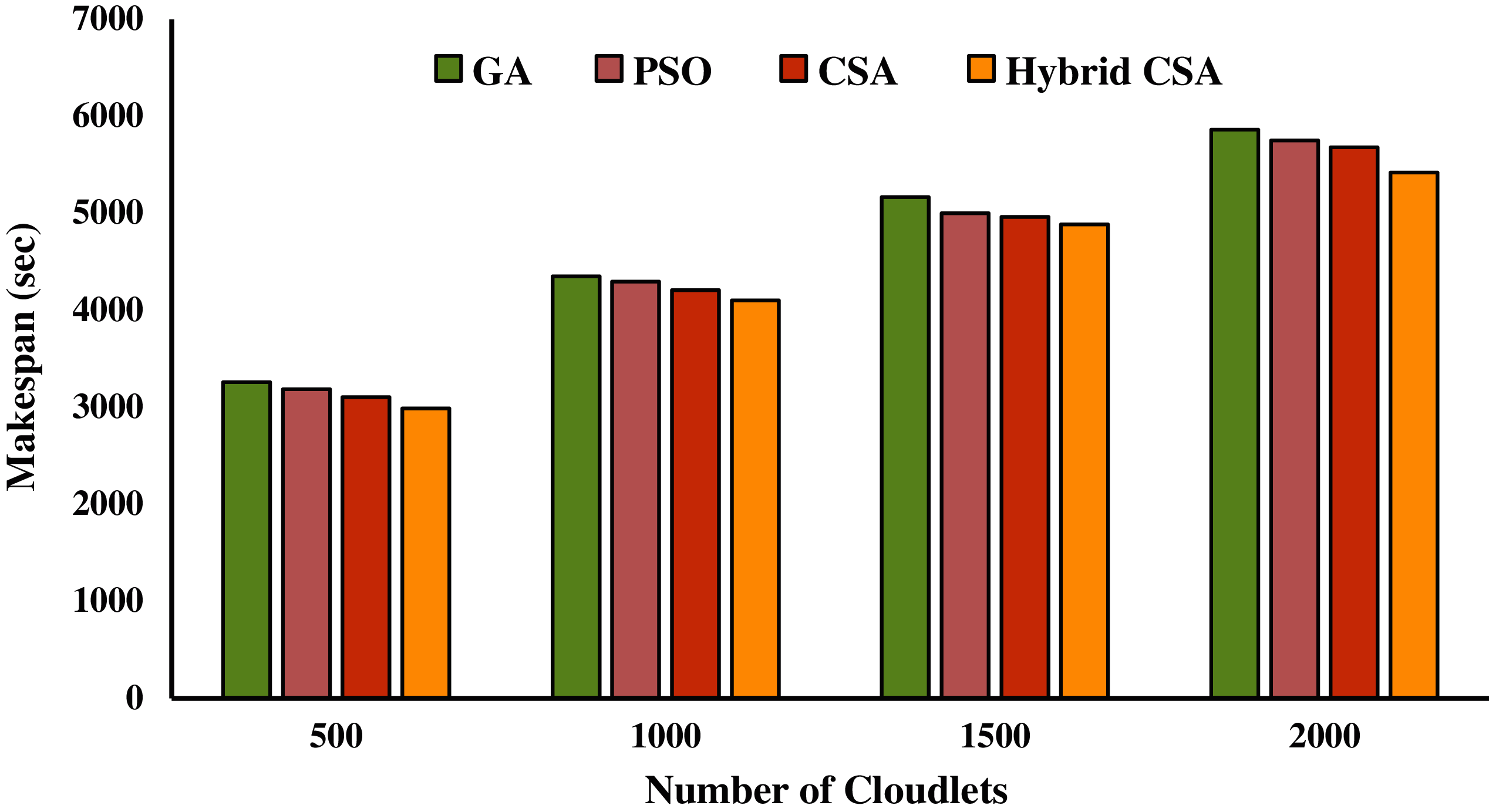
Figure 6: Makespan calculated on HPC2N dataset
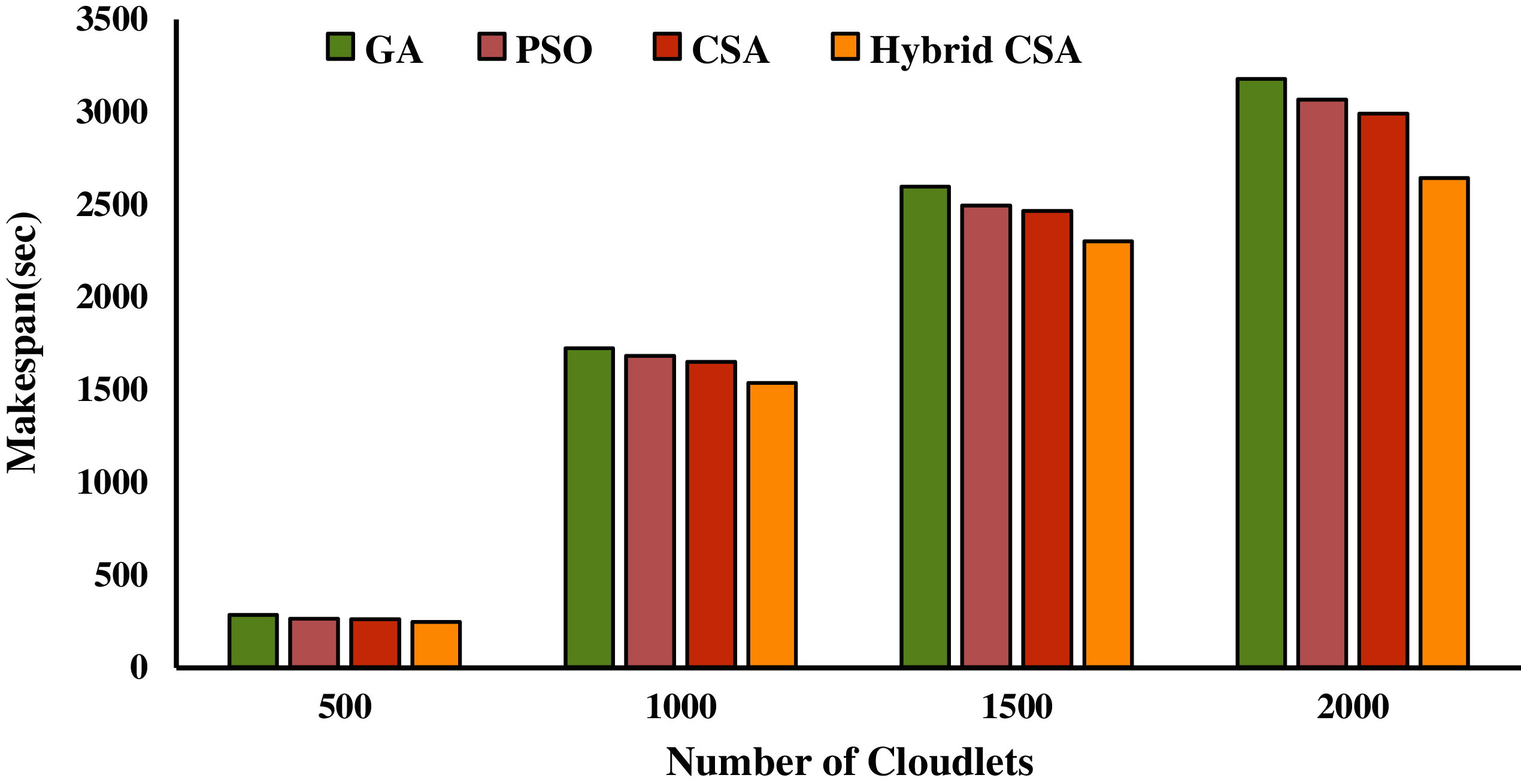
Figure 7: Makespan calculated on SDSC dataset
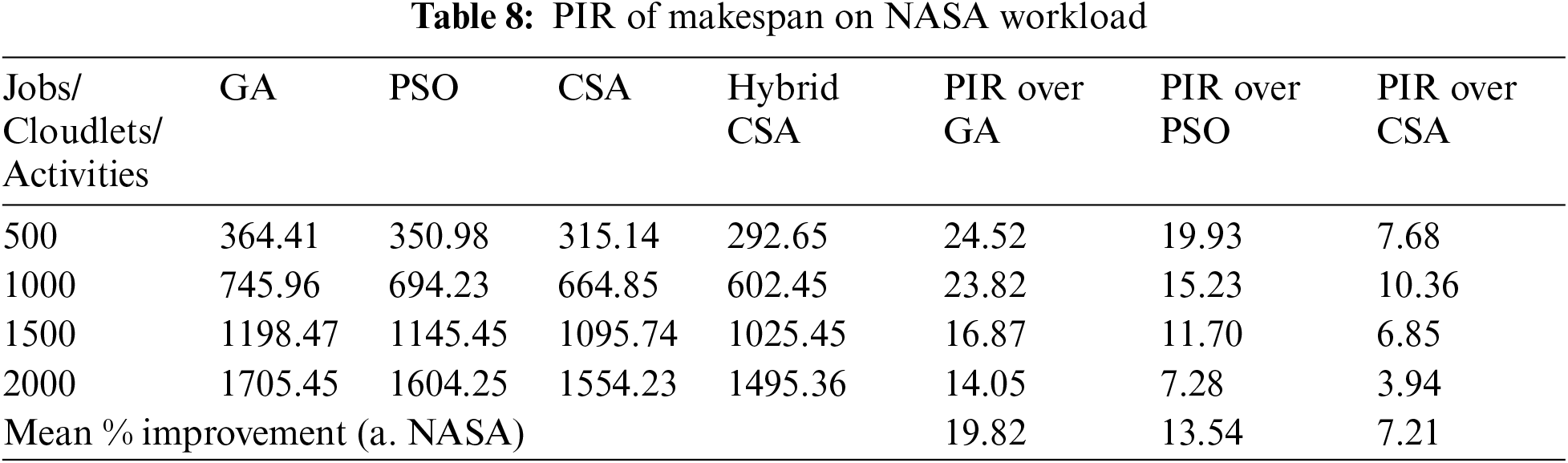
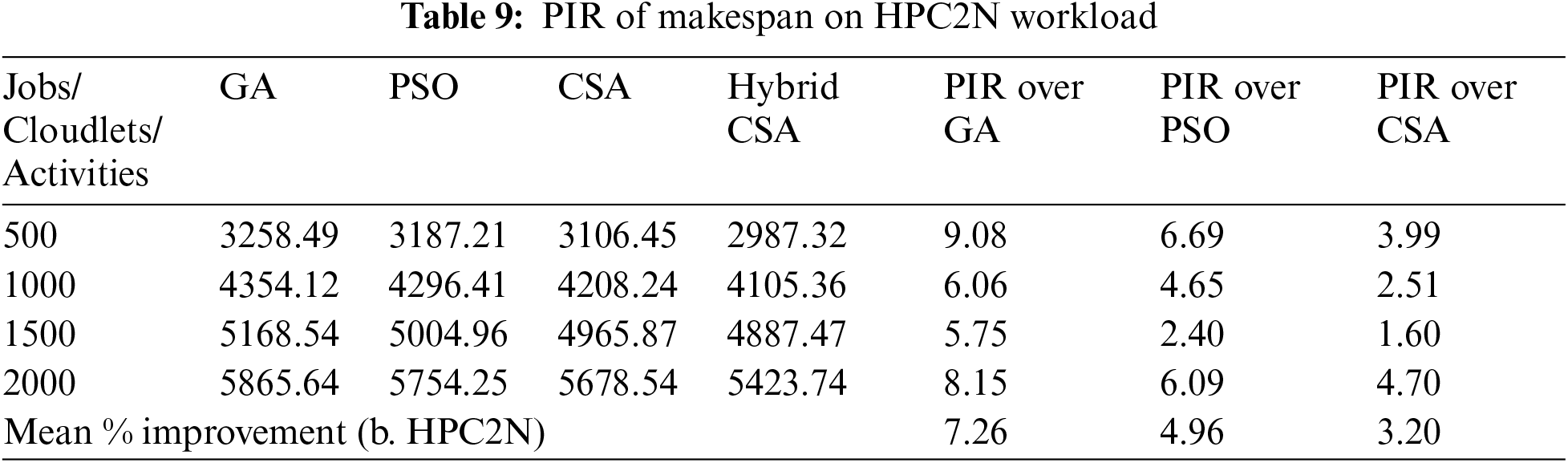
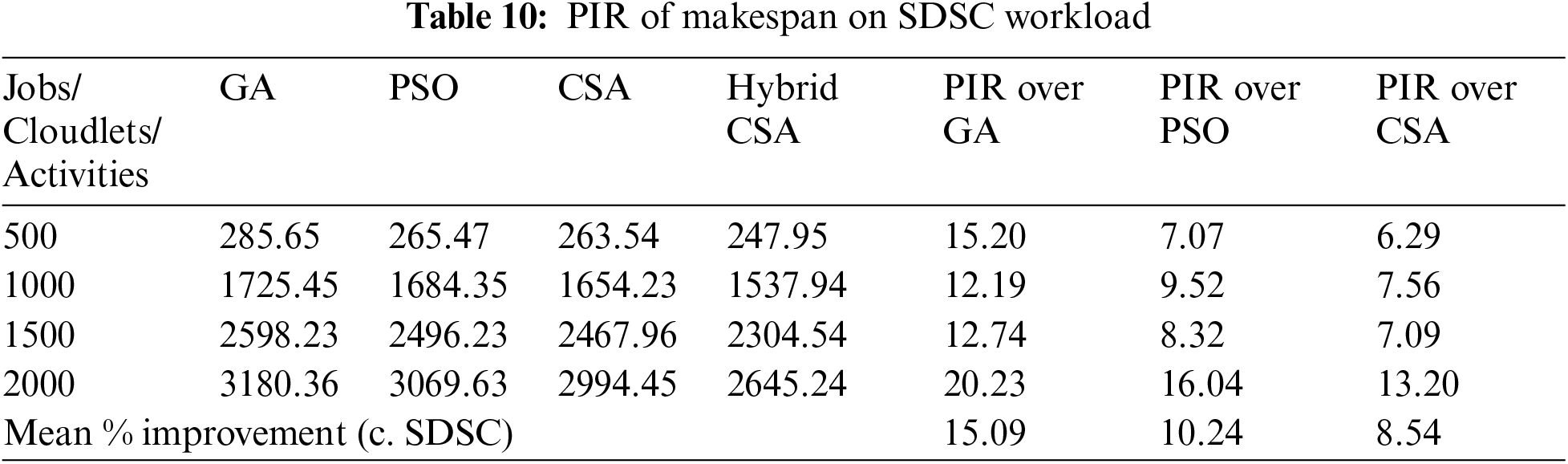
The statistical significance of each algorithm for execution cost and makespan after thirty simulation runs is presented in Tabs. 11 and 12. The comparison is made on mean, standard deviation, and best value is considered. Tabs. 11 and 12 signifies that our proposed hybrid NAGCSA is more significant in terms of execution cost and makespan.
Scheduling in cloud computing is considered an NP-Hard problem to fulfil the demands of all users. It has been explored by most scientists and researchers around the world to increase the performance of scheduling algorithms. The motivation for this paper has explored techniques to study important parameters of quality of service, i.e., makespan and execution cost, for cloud users. This paper proposed a novel hybrid Nesterov Accelerated Gradient-based Cuckoo Search Algorithm to perform the scheduling in the IaaS cloud. The approximation of the future position of using NAG helps to reach the function towards local minima even if gets overshoots in any iteration. The simulation was performed in CloudSim on three different datasets; NASA, HPC2N, and SDSC with GA, PSO, and CSA scheduling algorithms. The results show that our proposed hybrid algorithm helps in saving time and money of users up to 19.20% and 35%, respectively. This work can be extended by adding more parameters like degree of imbalance, energy consumption, and throughput. The proposed hybrid algorithm can be used to resolve other issues in cloud computing like VM allocation and load balancing. More gradient-based optimization algorithms can be hybridized with CSA to evaluate its performance in other engineering optimizations problems.
Acknowledgement: Authors also acknowledge the Computer Science and Engineering Department of Deenbandhu Chhotu Ram University of Science and Technology for providing various facilities in the research lab.
Funding Statement: This research work is funded by University Grant Commission under National Fellowship Programme, Grant No. 2017-18/29146.
Conflicts of Interest: The authors declare that they have conflict of interest to report regarding this research work.
1. H. Gupta, A. V. Dastjerdi, S. K. Ghosh and R. Buyya, “iFogSim: A toolkit for modeling and simulation of resource management techniques in the internet of things, edge and fog computing environments,” Software Practice and Experience, vol. 47, no. 9, pp. 1275–1296, 2017. [Google Scholar]
2. J. Gubbi, R. Buyya, S. Marusic and M. Palaniswami, “Internet of things (IoTA vision, architectural elements, and future directions,” Future Generation Computing System, vol. 29, no. 7, pp. 1645–1660, 2013. [Google Scholar]
3. M. Aazam, I. Khan, A. A. Alsaffar and E.-N. Huh, “Cloud of things: Integrating internet of things and cloud computing and the issues involved,” in Proc. IBCAST, Islamabad, Pakistan, pp. 414–419, 2014. [Google Scholar]
4. E. N. Al-Khanak, S. P. Lee, S. U. R. Khan, N. Behboodian, O. I. Khalaf et al., “A heuristics-based cost model for scientific workflow scheduling in cloud,” Computers, Materials & Continua, vol. 67, no. 3, pp. 3265–3282, 2021. [Google Scholar]
5. M. Kumar, S. C. Sharma, A. Goel and S. P. Singh, “A comprehensive survey for scheduling techniques in cloud computing,” Journal of Network. Computer Applications, vol. 143, no. 2, pp. 1–33, 2019. [Google Scholar]
6. M. A. Alsaih, R. Latip, A. Abdullah, S. K. Subramaniam and K. Ali Alezabi, “Dynamic job scheduling strategy using jobs characteristics in cloud computing,” Symmetry, vol. 12, no. 10, pp. 1638, 2020. [Google Scholar]
7. P. Baldoss and G. Thangavel, “Optimal resource allocation and quality of service prediction in cloud,” Computers, Materials & Continua, vol. 67, no. 1, pp. 253–265, 2021. [Google Scholar]
8. Xen, “Xen Project,” (accessed Apr. 29, 2021). [Online]. Available: https://xenproject.org/. [Google Scholar]
9. Oracle VM VirtualBox, (accessed May 07, 2021). [Online]. Available: https://www.virtualbox.org/. [Google Scholar]
10. VMware India-delivering a digital foundation for businesses | IN, (accessed May 07, 2021). [Online]. Available: https://www.vmware.com/in.html. [Google Scholar]
11. Google AppCloud, (accessed May 07, 2021). [Online]. Available: https://cloud.google.com/. [Google Scholar]
12. Amazon EC2, (accessed May 07, 2021). [Online]. Available: https://aws.amazon.com/. [Google Scholar]
13. Microsoft Azure: Cloud computing services, (accessed May 07, 2021). [Online]. Available: https://azure.microsoft.com/en-in/. [Google Scholar]
14. M. Kumar, Suman and S. Singh, “A survey on virtual machine scheduling algorithms in cloud computing,” International Journal of Computer Sciences and Engineering, vol. 6, no. 3, pp. 485–490, 2018. [Google Scholar]
15. D. D. Zhu, P. M. Pardalos, W. Wu, C. Floudas and P. Pardalos, History of optimization. In: Encyclopedia of Optimization. Berlin: Springer, pp. 1538–1542, 2009. [Google Scholar]
16. N. Dey, X. S. Yang and S. Fong, Applications of Cuckoo Search Algorithm and its Variants. Berlin: Springer, pp. 1–324, 2021. [Google Scholar]
17. M. Kumar and Suman, “Meta-heuristics techniques in cloud computing: Applications and challenges,” Indian Journal of Computer Science and Engineering, vol. 12, no. 2, pp. 385–395, 2021. [Google Scholar]
18. M. Farid, R. Latip, M. Hussin and N. A. W. A. Hamid, “A survey on QoS requirements based on particle swarm optimization scheduling techniques for workflow scheduling in cloud computing,” Symmetry, vol. 12, no. 4, pp. 551, 2020. [Google Scholar]
19. A. R. Arunarani, D. Manjula and V. Sugumaran, “Task scheduling techniques in cloud computing: A literature survey,” Future Generation Computers System, vol. 91, no. 4, pp. 407–415, 2019. [Google Scholar]
20. Y. Dai, Y. Lou and X. Lu, “A task scheduling algorithm based on genetic algorithm and ant colony optimization algorithm with multi-QoS constraints in cloud computing,” in Proc. ICIHMSSC, Hangzhou, China, pp. 428–431, 2015. [Google Scholar]
21. H. B. Alla, S. B. Alla, A. Touhafi and A. Ezzati, “A novel task scheduling approach based on dynamic queues and hybrid meta-heuristic algorithms for cloud computing environment,” Cluster. Computing, vol. 21, no. 4, pp. 1797–1820, 2018. [Google Scholar]
22. S. B. Alla, H. B. Alla, A. Touhafi and A. Ezzati, “An efficient energy-aware tasks scheduling with deadline-constrained in cloud computing,” Computers, vol. 8, no. 2, pp. 46, 2019. [Google Scholar]
23. M. Akbari, H. Rashidi and S. H. Alizadeh, “An enhanced genetic algorithm with new operators for task scheduling in heterogeneous computing systems,” Engineering Applications of Artificial Intelligence, vol. 61, pp. 35–46, 2017. [Google Scholar]
24. B. Keshanchi, A. Souri and N. J. Navimipour, “An improved genetic algorithm for task scheduling in the cloud environments using the priority queues: Formal verification, simulation, and statistical testing,” Journal of Systems and Software, vol. 124, no. 8, pp. 1–21, 2017. [Google Scholar]
25. Z. Zhou, F. Li, H. Zhu, H. Xie, J. H. Abawajy et al., “An improved genetic algorithm using greedy strategy toward task scheduling optimization in cloud environments,” Neural Computing and Applications, vol. 32, no. 6, pp. 1531–1541, 2020. [Google Scholar]
26. I. Strumberger, M. Tuba, N. Bacanin and E. Tuba, “Cloudlet scheduling by hybridized monarch butterfly optimization algorithm,” Journal of Sensor and Actuator Networks, vol. 8, no. 3, pp. 1–39, 2019. [Google Scholar]
27. I. Strumberger, N. Bacanin, M. Tuba and E. Tuba, “Resource scheduling in cloud computing based on a hybridized Whale optimization algorithm,” Applied Sciences, vol. 9, no. 22, pp. 4893, 2019. [Google Scholar]
28. H. S. Al-Olimat, M. Alam, R. Green and J. K. Lee, “Cloudlet scheduling with particle swarm optimization,” in Proc. ICCSNT, Gwalior, India, pp. 991–995, 2015. [Google Scholar]
29. A. S. A. Beegom and M. S. Rajasree, “Integer-PSO: A discrete PSO algorithm for task scheduling in cloud computing systems,” Evolutionary Intelligence, vol. 12, no. 2, pp. 227–239, 2019. [Google Scholar]
30. I. Attiya, M. A. Elaziz and S. Xiong, “Job scheduling in cloud computing using a modified Harris Hawks optimization and Simulated Annealing algorithm,” Computational Intelligence and Neuroscience, vol. 2020, no. 16, pp. 1–17, 2020. [Google Scholar]
31. S. H. H. Madni, M. S. A. Latiff, J. Ali and S. M. Abdulhamid, “Multi-objective-oriented cuckoo search optimization-based resource scheduling algorithm for clouds,” Arabian Journal of Science and. Engineering, vol. 44, no. 4, pp. 3585–3602, 2019. [Google Scholar]
32. S. H. H. Madni, M. S. Abd Latiff, S. M. Abdulhamid and J. Ali, “Hybrid gradient descent cuckoo search (HGDCS) algorithm for resource scheduling in IaaS cloud computing environment,” Cluster Computing, vol. 22, no. 1, pp. 301–334, 2019. [Google Scholar]
33. M. Kaur and M. Agnihotri, “Performance evaluation of hybrid GA-ACO for task scheduling in cloud computing,” in Proc. ICCCI, Greater Noida, India, pp. 168–172, 2016. [Google Scholar]
34. H. Wu and K. Wolter, “Stochastic analysis of delayed mobile offloading in heterogeneous networks,” IEEE Transactions on Mobile Computing, vol. 17, no. 2, pp. 461–474, 2018. [Google Scholar]
35. A. Gandhi, V. Gupta, M. H. Balter and M. A. Kozuch, “Optimality analysis of energy-performance trade-off for server farm management,” Performance Evaluation, vol. 67, no. 11, pp. 1155–1171, 2010. [Google Scholar]
36. X. S. Yang and S. Deb, “Cuckoo search via levy flights,” in Proc. WCNBIC, Coimbatore, India, pp. 210–214, 2009. [Google Scholar]
37. J. A. Snyman, Practical mathematical optimization. In: An Introduction to Basic Optimization Theory and Classical and New Gradient-Based Algorithms. Berlin: Springer, 2005. [Google Scholar]
38. R. Fletcher and M. J. D. Powell, “A rapidly convergent descent method for minimization,” The Computer Journal, vol. 6, no. 2, pp. 163–168, 1963. [Google Scholar]
39. Y. Nesterov, “Gradient methods for minimizing composite functions,” Mathematics Program, vol. 140, no. 1, pp. 125–161, 2013. [Google Scholar]
40. R. N. Calheiros, R. Ranjan, A. Beloglazov, C. A. De Rose and R. Buyya, “CloudSim: A toolkit for modeling and simulation of cloud computing environments and evaluation of resource provisioning algorithms,” Software Practice and Experience, vol. 41, no. 1, pp. 23–50, 2011. [Google Scholar]
41. Parallel workloads archive: HPC2N seth, (accessed May 04, 2021). [Online]. Available: https://www.cs.huji.ac.il/labs/parallel/workload/l_hpc2n/. [Google Scholar]
42. Parallel workloads archive: NASA iPSC/860, (accessed May 04, 2021). [Online]. Available: https://www.cs.huji.ac.il/labs/parallel/workload/1_nasa_ipsc/. [Google Scholar]
43. Parallel workloads archive: SDSC SP2, (accessed May 04, 2021). [Online]. Available: https://www.cs.huji.ac.il/labs/parallel/workload/l_sdsc_sp2/. [Google Scholar]
44. M. Kumar and Suman, “Energy efficient scheduling in cloud computing using black widow optimization,” Journal of Physics: Conference Series, vol. 1950, pp. 12063, 2021. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |