Computers, Materials & Continua DOI:10.32604/cmc.2022.020687
Article

Diabetes Prediction Algorithm Using Recursive Ridge Regression L2

Milos Mravik1, T. Vetriselvi2, K. Venkatachalam3,*, Marko Sarac1, Nebojsa Bacanin1 and Sasa Adamovic1

1Department of Computer Science, Singidunum University, Belgrade, 11000, Serbia
2Department of Computer science and Engineering, K.Ramakrishnan College of Technology, Trichy, 621112, India
3Department of Applied Cybernetics, Faculty of Science, University of Hradec Králové, 500 03, Hradec Králové, Czech Republic
*Corresponding Author: K. Venkatachalam. Email: venkatme83@gmail.com
Received: 03 June 2021; Accepted: 07 August 2021

Abstract: At present, the prevalence of diabetes is increasing because the human body cannot metabolize the glucose level. Accurate prediction of diabetes patients is an important research area. Many researchers have proposed techniques to predict this disease through data mining and machine learning methods. In prediction, feature selection is a key concept in preprocessing. Thus, the features that are relevant to the disease are used for prediction. This condition improves the prediction accuracy. Selecting the right features in the whole feature set is a complicated process, and many researchers are concentrating on it to produce a predictive model with high accuracy. In this work, a wrapper-based feature selection method called recursive feature elimination is combined with ridge regression (L2) to form a hybrid L2 regulated feature selection algorithm for overcoming the overfitting problem of data set. Overfitting is a major problem in feature selection, where the new data are unfit to the model because the training data are small. Ridge regression is mainly used to overcome the overfitting problem. The features are selected by using the proposed feature selection method, and random forest classifier is used to classify the data on the basis of the selected features. This work uses the Pima Indians Diabetes data set, and the evaluated results are compared with the existing algorithms to prove the accuracy of the proposed algorithm. The accuracy of the proposed algorithm in predicting diabetes is 100%, and its area under the curve is 97%. The proposed algorithm outperforms existing algorithms.

Keywords: Ridge regression; recursive feature elimination; random forest; machine learning; feature selection

1  Introduction

Supervised learning methods can be divided into classification and regression problems. A continuous problem can be predicted easily by using regression method. A data set is collection of information with samples and parameters. Ridge regression can be efficiently used to obtain the best solution if we have fewer samples with more number of parameters. Understanding the bias and variance in machine learning context is important. Bias refers to a condition where a model plots the inline nearby samples. Variance refers to the differences between fitted data sets. A graph is considered to be high variance when the lines are squiggly process, whereas it is considered to be low variance when lines are straight. Ridge regression refers to a process where the sum of squares is introduced in linear regression.

Some feature-based models are trained by using machine learning algorithms [1]. The accuracy of feature selection for new data is extremely low. The main problems in new data are underfitting and overfitting.

1.1 Problem Formulation

A training model experiences overfitting problem when it is fitted with huge data features. If a model is trained with less data features, then machine learning is biased [2,3]. This condition leads to underfitting problem. If a model is trained with more number of features, then high variance occurs [4–6]. This condition leads to low efficiency in identifying a suitable model. This problem is defined as overfitting and is widely investigated.

The problem in processing few data features in training the model leads to wrong prediction of unknown data, as shown in Fig. 1a. Some feature selection models are suggested to reduce underfitting [7].

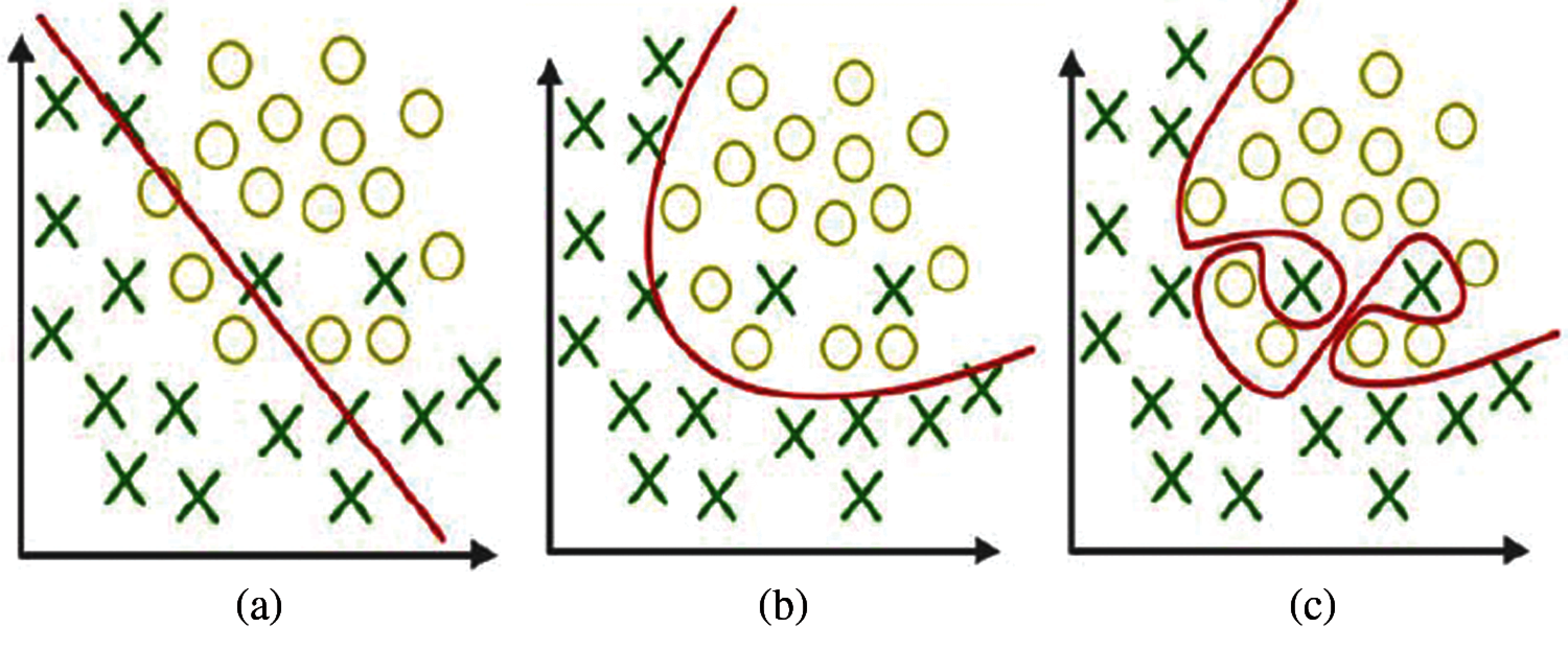
Figure 1: a) Underfitting b) Actual fitting c) Overfitting

Two terms, namely, bias and variance, occur in overfitting and underfitting, as explained in Figs. 1a–1c. Bias is a process used to match the correct value by calculating the differences. Variance is the prediction for given features at various realization views. Model overfitting can be overcome by selecting more features and bias functions. Machine learning algorithms with high bias are required to solve the problems.

The contribution of this research article is as follows:

In this article, we combine ridge regression with recursive feature elimination (RFE) to reduce the overfitting problems. If the training error is less than the testing error, then an overfitting problem is found. Conventional methods, such as L1, L2 regularization, are used to minimize overfitting problems. However, the outcome efficiency is extremely low. To improve the accuracy of feature selection, we combine RFE with L2 regularization. The output feature is classified by using random forest algorithm.

The remainder of this paper is organized as follows: Section 2 conducts a literature survey of existing implementations. Section 3 explains the proposed model. Section 4 discusses the outcome of our proposed model. Section 5 provides the conclusions.

2  Literature Review

Reference [8] conducted a survey on feature selection algorithms, such as k-nearest neighbor (kNN), k means, and Naïve Bayes. This paper uses the common diabetic data set, analyzes the results of the algorithms, and suggests the best algorithm on the basis of performance accuracy. The result shows that the branch and bound algorithm obtains the highest level of accuracy compared with the other eight algorithms, namely, as Naïve Bayes, support vector machine (SVM), C4.5, kNN), k means, randomized hill climb, and simulated annealing.

Reference [9] conducted a survey of various feature selection methods. This paper introduces feature selection based on genetic algorithm (GA) to detect and diagnose biological issues. This paper provides detailed descriptions about the types of feature selection algorithms, such as filter-based, wrapper, and embedded feature selection algorithms. The algorithms are tested on five benchmark data sets from the University of California Irvine (UCI) repository. They conclude that wrapper-based methods perform well to reduce the features among the three feature selection methods. This paper discusses the challenges in feature selection.

Reference [10] proposed a feature selection algorithm based on L1 (Lasso) and classification on microarray cancer data by using random forest. The proposed algorithm is tested on eight standard data sets of microarray cancer data set. The learning proficiency of the classifier is explored by using a learning curve model called fivefold cross-validation during the training phase. The comparative result of the proposed algorithm shows the best accuracy level than the recent research studies. The evaluation is performed in terms of accuracy, recall, precision, F measure, and confusion matrix.

Reference [11] proposed a prediction model with high sensitivity and selectivity. The prediction on diabetes mellitus of Canadian patients is conducted on the basis of their lab results. The proposed model is based on logistic regression and gradient boosting machine (GBM) approaches. The proposed algorithm is implemented with adjusted threshold and class weight to improve its sensitivity. The proposed model is compared with decision tree and random forest in terms of area under the receiving operating characteristic curve (AROC). The proposed GBM and logistic regression shows better accuracy of 87% and 84% compared with other existing algorithms.

Reference [12] focused on the regularization of embedded feature selection algorithms, such as ridge regression, lasso regression, and their combination. The algorithms are evaluated on five large dimensional data sets. They are compared in terms of sparsity, correlation, and execution time. The result shows that L21 performs better in sparse data set, SC has high BSR with nonsparse data sets, LL obtains high BSR high, and EN has higher BSR rate than L21. For dense data sets, LL, L1 SVM, and EN give the best result. In terms of execution time, EN performs better than other algorithms. The results of feature selection methods are different.

In reference [13], feature selection algorithms are embedded in SVM learning. Two algorithms, namely, L1 weight regularization and RFE extension, are proposed. These algorithms are used to classify the multiclass problems. The efficient optimization technique is verified on the basis of information gain. Reference [14] uses decision tress, neural network, and random forest to predict diabetes mellitus. The model is examined through fivefold cross-validation. A total of 68,994 healthy persons are selected as training data. To overcome the data unbalance, the original data are tested for five times, and average of the five experiments is taken as the final result. Principal component analysis (PCA) and minimum redundancy maximum relevance are used to reduce the dimensionality of the features. Fourteen attributes are used, and random forest obtains the best accuracy of 80% compared with others.

To identify the set of prognostic genes, reference [15] proposed a novel random forest algorithm called random survival forest. This proposed algorithm forms many binary trees that are constructed on the basis of deterministic techniques. It uses several split criteria, such as log rank, log-rank score, conserve, and random. In accordance with the predictor variable values, each observation is assigned as leaf node or terminal node. A gene selection based method is combined to multivariate correlations in microarray data set. This research work performs well in terms of simulation and real data.

Reference [16] used RFE and PCA as feature reduction technique and deep neural network and artificial neural network (ANN) as classifier to design an expert system for predicting diabetes. The proposed technique is compared with other existing machine learning algorithms in terms of accuracy, sensitivity, and specificity. The analysis concludes that RFE performs better in feature reduction and classifies data with high accuracy compared with ANN and deep neural network classify. Reference [17] conducted a survey about diabetes prediction by using feature selection methods and classification. The F score, GA, SVM, and ANN are analyzed, and the embedded feature selection method called f score outperforms other algorithms.

Reference [18] predicted diabetes patients on the basis of two steps. Weighting methods are used in the selecting the relevant attributes, and classification is performed by using AdaBoost, gradient boosting, and random forest algorithms. The experimental results show that stability selection and AdaBoost algorithms exhibit better accuracy. Reference [19] used Fisher’s score, RFE, and decision tree to select features and utilized random forest, regression, SVM, and multilayer perceptron to predict diabetes. The Pima Indians Diabetes (PIDD) data set is used in the experiment, the result with a high accuracy of 98% is obtained, and random forest is used as a classifier with 19 features. The features are reduced with feature selection algorithm to five as new data set. The proposed algorithm obtains the highest accuracy compared with others.

Reference [20] identified insulin resistance by using noninvasive approaches of machine learning techniques. The CALERIE data set with 18 parameters, such as age, gender, and height, is used in the experiment. The selected attributes of feature selection are used as input to the classification algorithms, such as logistic regression, CART, SVM, LDA, and KNN. The analysis results show that logistic regression and SVM obtain a high accuracy of 97% in identifying insulin resistance.

Reference [21] proposed an SVM–RFE model by modifying SVM. It ranks the genes of the data on the basis of discriminatory power, and the genes not participating are removed. A gene regulatory network that has the genes is formed, and these genes that are used to identify diabetes have the top rank. The proposed method is tested on type II diabetes. The genes involved in the study are the cause of the disease.

In reference [22], standard SVM with RFE is explored. In this work, correlation bias reduction (CBR) is combined with feature selection. Experiments are conducted on breath analysis data set. Comprehensive attributes are selected, and classification is performed. The proposed SVM–RFE with CBR performs better than the original SVM with RFE algorithms. An ensemble version of the proposed study is the suggestion of the next work to improve its stability.

3  Proposed Hybrid L2-RFE Methodology

Diabetes mellitus is a disease where the body cannot metabolize the glucose level. The number of diabetes patients will increase in the future. Many researchers propose predictive models to predict diabetes mellitus at the early stage. Finding a good predictive model with high accuracy in predicting diabetes is still in exploratory stage. Feature selection is an important preprocessing step to find the relevant features for classification. In this work, a wrapper based feature selection method called RFE is combined with ridge regression (L2) to form a hybrid L2 regulated feature selection algorithm to overcome the overfitting problem of data set. The features are selected by using the proposed method, and random forest classifier is used to classify the data on the basis of the selected features. The overall architecture of the proposed algorithm is shown in Fig. 2. Diabetes data are used as input. The proposed algorithm contains two parts, namely, feature selection using L2-regulated RFE and classification using random forest.

Figure 2: Overall architecture of the proposed work

3.1 L2 Regulated RFE

L2-regulated feature selection is an embedded feature selection method that uses wrapper-based ridge regression with RFE as a feature selection algorithm. Overfitting is a major problem in feature selection, where new data are unfit to the model because the training data are small. Ridge regression is mainly used to overcome the overfitting problem and is widely combined with linear feature selection to select the relevant features from the data set for further processing. RFE selects the features of the data set by recursively executing the process to select the smaller amount of features on the basis of the coefficient value or the importance of the features. Thus, the least important attributes are pruned from the data set. This process is repeatedly performed to prune the maximum amount of irrelevant data for producing the minimum amount of relevant data for classification. The steps involved in L2RFE are as follows:

(1)   Fitting the model by using ridge regression.

(2)   Ranking the important features.

(3)   Discarding the least important feature.

(4)   Refitting the model until the relevant features are found.

As shown in Eq. (3), L2-regulated feature selection model is formulated by adding the squared magnitude of coefficient as the penalty shown in Eq. (1) to the loss function Eq. (2).

p=⋋∑j=1d|wj|2, (1)

LF=∑i=1n(yi,j−∑j=1dwi,j∗Xi)2, (2)

L2RFE=∑i=1n(yi,j−∑j=1dwi,j∗Xi)2+=⋋∑j=1d|wi|2, (3)

where p = penalty,

⋋ = control variable

|wj| = coefficient of the jth feature sample

The proposed L2-regulated feature selection is applied on Diabetes data to select the relevant features. This technique is efficient to select the relevant and optimal features that have minimal weight. L2RFE uses ⋋ to control the features for selecting the number of important features in terms of the value. If the ⋋ value is small, then few features are selected, and if the ⋋ value is high, then larger number of features are selected. Choosing the value for ⋋ is important. High value of ⋋ increases the weight that causes underfitting. If the weight of the features is zero, then these features are considered to be irrelevant, and nonzero weight features are considered to be relevant. This algorithm enforces to select the minimum valued feature to have zero coefficient as the optimal features for further processing.

The main advantage of this ridge regression-based RFE is to overcome the overfitting problem. Solving the overfitting problem through feature scaling is an important step. Eq. (1) is used for feature scaling between 0 and 1. The transformed scale value of the features is expressed as

fnew=(Xi−μ)/σ, (4)

where

Xi = ith feature of the data set

μ = feature vector mean

σ = feature vector standard deviation

3.2 Proposed Hybrid Algorithm

The steps of the proposed L2-RFE algorithm are stated as follows. Low values of λ are reduced recursively until the optimum number of features are selected because RFE is backward selection. The algorithm steps are programmatically implemented in Scikit-learn machine learning in Python.

3.3 Proposed Workflow on Feature Selection

The workflow of the proposed L2-RFE-based feature selection to predict diabetes mellitus is shown in Fig. 3. The diabetes mellitus data are used as input to the algorithm. Each feature in the data set is fitted to the proposed L2RFE model for reducing the features with low importance. The selected relevant features are scaled down by using Eq. (4) to overcome the overfitting problem. The data set is divided into test set and training set. The scaled features are fitted in the random forest classifier to predict diabetes.

3.4 Random Forest Classifier

Random forest classifier is an unbiased classification model that consists of a group of decision trees with average noise. This model gives a high predictive accuracy in binary classification problems. The entire data set is divided into subdata sets, and each subdata set is trained in d number of decision trees, as shown in Fig. 4. Each decision tree is trained separately, and the result of the subdata set is predicted. The final prediction is based on the majority of the subset predictive results. The probability of each subset of a predictive class is expressed as Eq. (5).

prob(c|f)=p1+p2+…+pn∑i=1n(pi(c|f)), (5)

where

c = class

f = features

p1…pn = probability of each feature and class (c|f)

n = number of subdata sets

3.5 Algorithm 2-RF

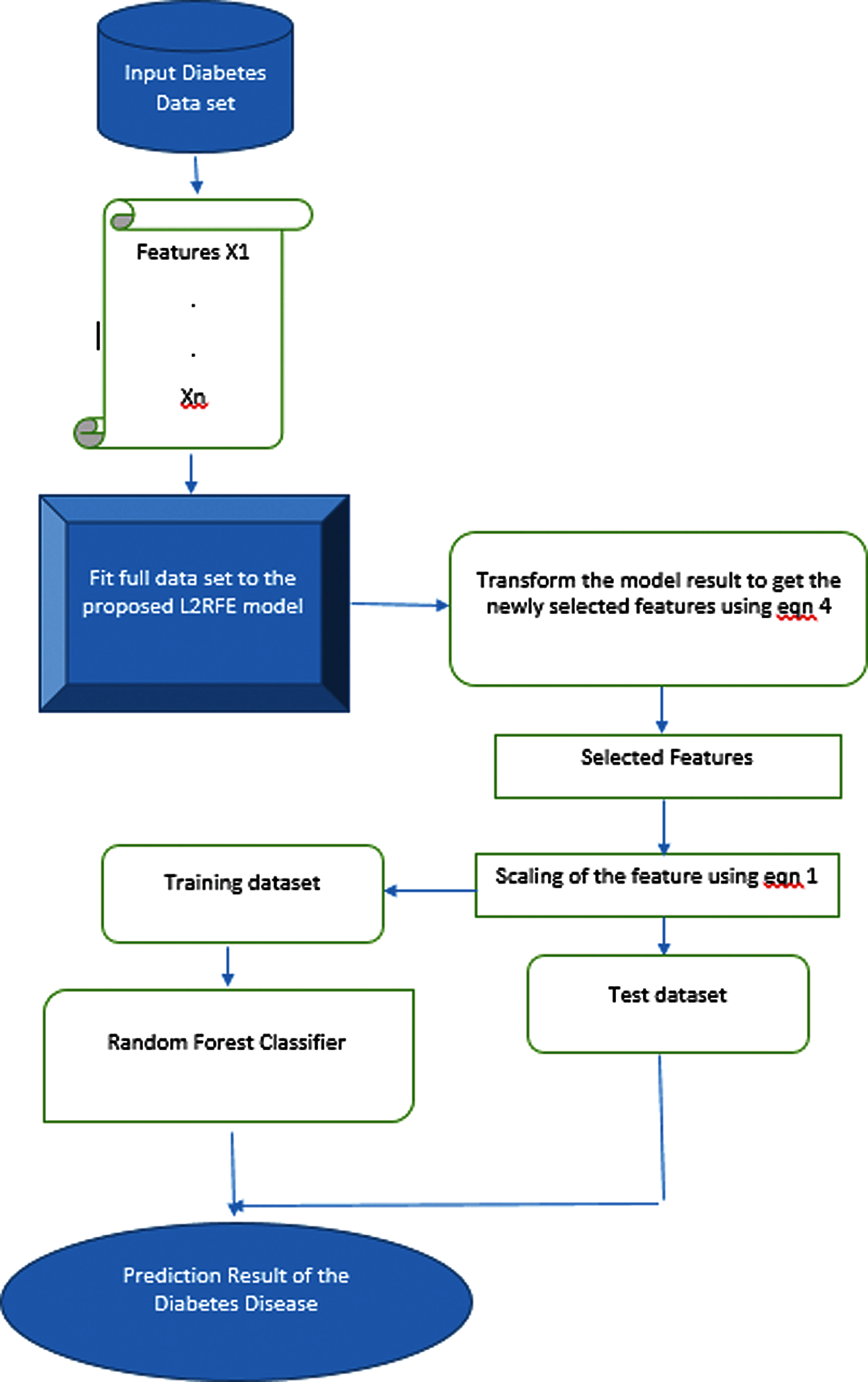
Figure 3: Workflow of the proposed algorithm

Figure 4: Workflow of random forest classifier

4  Experimental Results and Discussion

4.1 Data Set Evaluation

The proposed hybrid L2-regulated RFE-based feature selection on diabetes prediction using random forest classification is tested on the PIDD data set. This data set is open source and available in the UCI repository [12]. The data set consist of 768 samples, including one class attribute, to indicate the positive and negative diabetes. A total of 267 positive samples and 500 negative samples are found in the data set. The attributes are shown in Tab. 1.

The proposed algorithm is implemented by using Python machine learning library called Scikit-learn, and the experimental results are evaluated by using evaluation metrics called accuracy, sensitivity, specificity, F1 measure, recall, precision, Matthews correlation coefficient (MCC), and area under the curve (AUC). The result of our proposed algorithm is compared with existing algorithms, such as Naive Bayes, SVM, C4.5, branch and bound, kNN, simulated annealing, and randomized hill climb. The selected attributes of each algorithm are listed in Tab. 2.

4.2 Evaluation Criteria

The evaluation metrics are true positive, false negative, true negative, and false positive. The calculations for evaluation metrics are shown in Eqs. (6)–(13).

SN=TPTP+FN, (6)

SP=TNTN+FP, (7)

ACC=TN+TPTN+FN+TP+FP, (8)

MCC=(TP∗TN)−(FN∗FP)(TP+FN)∗(TN+FP)∗(TP+FP)∗(TN+FN), (9)

Precision=TPTP+FP, (10)

Recall=TPTP+FN, (11)

F−Measure=2∗Precison∗RecallPrecision+Recall, (12)

AUC=12(TPTP+FN+TNTN+FP). (13)

4.3 Experimental Results

The results of the proposed algorithm are shown in Tab. 3 in terms of the selected attributes. The proposed algorithm selects two attributes, namely, as DPF and blood glucose level. These attributes are compared by using the proposed method with one attribute called blood glucose level. The pictorial representation is shown in Fig. 5.

Figure 5: L2 RFE-RF result

The evaluated result of the proposed algorithm with two attributes exhibits higher accuracy compared with the proposed algorithm with one attribute. One attribute selection does not provide correct prediction compared with two attribute selection.

The decision tree based on the features of PIDD is shown in Fig. 6. The root node is blood glucose level. The next subtrees are generated with the respective root node. The next subtree root node is insulin level, and its class value is zero, which indicates negative. Each subtree is evaluated, and the majority of the class label of the sub trees gives the overall class prediction of the data set. For this sample, 50% of the samples is positive, and 50% is negative.

Figure 6: Features with class attribute of PIDD using L2-RFE-RF

The comparative result with existing algorithms is shown in Tab. 4. On the basis of the selected attributes of each algorithm, the results are compared in terms of the metrics. The resultant pictorial representation is shown in Fig. 7. In all the cases, our proposed algorithm obtains 100% sensitivity, 97% specificity, 100% accuracy, 86% MCC, 100% precision, 91% recall, 92% F measure, and 0.97 AUC. The next best method after our proposed algorithm is branch and bound with 96% accuracy.

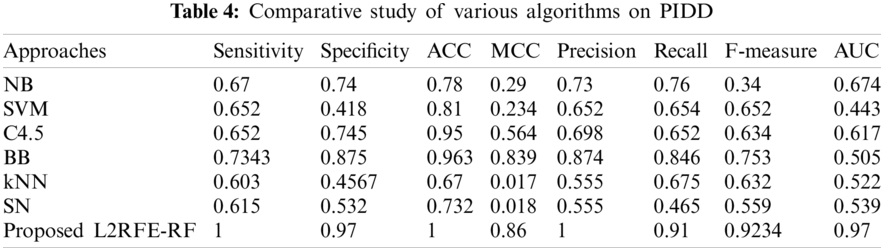
Figure 7: Comparative analysis of various algorithms with respect to the proposed L2RFE-RF

The ROC of the proposed algorithm with two and one attributes and the two methods with the best accuracy from Fig. 8 are compared. This condition shows the high-level accuracy with two attributes of our proposed algorithm.

Figure 8: ROC of the proposed algorithm

The experimental results and discussion show that our proposed algorithm called hybrid L2RFE with random forest is one of the best machine learning method to predict diabetes. Finding suitable attributes and classifiers are an important part in prediction. The proposed algorithm gives better prediction because it selects two relevant attributes, namely, DPF and glucose level, by using the proposed feature selection algorithm called ridge regression (L2)-based RFE. The selected suitable features are then classified by using random forest classifier for classification. Hence, our proposed algorithm utilizes the best suitable features with the best classification algorithm on the PIDD data set to predict diabetes.

5  Conclusions

Feature selection in big data and data mining is extremely challenging. Our proposed L2-RFE model produces higher accuracy compared with existing models, such as SVM and kNN. L1 regularization does not have analytical solution, whereas L2 processes have analytical calculation. RFE helps to eliminate the worst unfit data from the feature data. It loops until it finds the best solution and feature selection. Output features are further classified by using random forest classifier to obtain the best accuracy in feature selection. In the future, different machine learning algorithms can be implemented with L2 for accurate feature selection process.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  J. Carner, A. Mestres, E. Alarcón and A. Cabellos, “Machine learning-based network modeling: An artificial neural network model vs. a theoretical inspired model,” in Proc. ICUFN2017, Milan, Italy, IEEE, pp. 522–524, 2017. [Google Scholar]

 2.  H. Zhang, L. Zhang and Y. Jiang, “Overfitting sand underfitting analysis for deep learning based end-to-end communication systems,” in Proc. WCSP 2019, Xi’an, China. IEEE, pp. 1–6, 2019. [Google Scholar]

 3.  J. N. Zaech, D. Dai, M. Hahner and L. Van Gool, “Texture underfitting for domain adaptation,” in Proc. ITSC, Yokohama, Japan, IEEE, pp. 547–552, 2019. [Google Scholar]

 4.  M. Molinier and J. Kilpi, “Avoiding overfitting when applying spectral-spatial deep learning methods on hyperspectral images with limited labels,” in Proc. IGARSS, Yokohama, Japan, IEEE, pp. 5049–5052, 2019. [Google Scholar]

 5.  S. Maheswaran, M. Ramya, P. Priyadharshini and P. Sivaranjani, “A real time image processing based system to scaring the birds from the agricultural field,” Indian Journal of Science and Technology, vol. 9, no. 30, pp. 1–5, 2016. [Google Scholar]

 6.  K. Kavin Kumar, T. Meera Devi and S. Maheswaran, “An efficient method for brain tumor detection using texture features and SVM classifier in MR images,” Asian Pacific Journal of Cancer Prevention, vol. 19, no. 10, pp. 2789–2794, 2018. [Google Scholar]

 7.  I. Bilbao and J. Bilbao, “Overfitting problem and the over-training in the era of data: Particularly for artificial neural networks,” in Proc. ICICIS, Cairo, Egypt, IEEE, pp. 173–177, 2017. [Google Scholar]

 8.  R. Lomte, S. Dagale, S. Bhosale and S. Ghodake, “Survey of different feature selection algorithms for diabetes mellitus prediction,” in Proc. ICCUBEA, Pune, India, pp. 1–5, 2018. [Google Scholar]

 9.  S. Colaco, S. Kumar, A. Tamang and V. G. Biju, “A review on feature selection algorithms,” in Emerging Research in Computing, Information, Communication and Applications, 1st edition, Cham: Springer, pp. 133–153, 2019. [Google Scholar]

10. B. Shekar and G. Dagnew, “L1-Regulated feature selection in microarray cancer data and classification using random forest tree,” in Emerging Research in Computing, Information, Communication and Applications, 1st edition, Cham: Springer, pp. 65–87, 2019. [Google Scholar]

11. H. Lai, H. Huang, K. Keshavjee, A. Guergachi and X. Gao, “Predictive models for diabetes mellitus using machine learning techniques,” BMC Endocrine Disorders, vol. 19, no. 1, pp. 1–9, 2019. [Google Scholar]

12. N. Sharma, P. Verlekar, R. Ashary and S. Zhiquan, “Regularization and feature selection for large dimensional data,” arXiv preprint, arXiv:1712.01975, 2017. [Google Scholar]

13. O. Chapelle and S. S. Keerthi, “Multi-class feature selection with support vector machines,” American Statistical Association, vol. 58, no. 1, pp. 154–169, 2008. [Google Scholar]

14. Q. Zou, K. Qu, Y. Luo, D. Yin, Y. Ju et al., “Predicting diabetes mellitus with machine learning techniques,” Frontiers in Genetics, vol. 9, pp. 515, 2018. [Google Scholar]

15. H. Pang, S. L. George, K. Hui and T. Tong, “Gene selection using iterative feature elimination random forests for survival outcomes,” IEEE/ACM Transactions on Computational Biology and Bioinformatics, vol. 9, no. 5, pp. 1422–1431, 2012. [Google Scholar]

16. J. Vijayashree and J. Jayashree, “An expert system for the diagnosis of diabetic patients using deep neural networks and recursive feature elimination,” International Journal of Civil Engineering and Technology, vol. 8, no. 12, pp. 633–641, 2017. [Google Scholar]

17. K. K. Gandhi and N. B. Prajapati, “Diabetes prediction using feature selection and classification,” International Journal Of Advance Engineering and Research Development, vol. 1, no. 5, pp. 2348–4470, 2014. [Google Scholar]

18. K. Akyol and B. Şen, “Diabetes mellitus data classification by cascading of feature selection methods and ensemble learning algorithms,” International Journal of Modern Education & Computer Science, vol. 10, no. 6, pp. 10–16, 2018. [Google Scholar]

19. J. Hou, Y. Sang, Y. Liu and L. Lu, “Feature selection and prediction model for type2 diabetes in the chinese population with machine learning,” in Proc. CSAE, New York, NY, USA, pp. 1–7, 2020. [Google Scholar]

20. M. C. A. Aggarwal, “A machine learning based approach for the identification of insulin resistance with non-invasive parameters using homa-IR,” International Journal, vol. 8, no. 5, pp. 1–12, 2020. [Google Scholar]

21. A. Kumar, D. J. S. Sharmila and S. Singh, “SVMRFE based approach for prediction of most discriminatory gene target for type II diabetes,” Genomics Data, vol. 12, no. 6, pp. 28–37, 2017. [Google Scholar]

22. K. Yan and D. Zhang, “Feature selection and analysis on correlated gas sensor data with recursive feature elimination,” Sensors and Actuators B: Chemical, vol. 212, pp. 353–363, 2015. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.