Computers, Materials & Continua DOI:10.32604/cmc.2022.020432
Article

Chaos-Based Cryptographic Mechanism for Smart Healthcare IoT Systems

Muhammad Samiullah1, Waqar Aslam1, Arif Mehmood1, Muhammad Saeed Ahmad2, Shafiq Ahmad3, Adel M. Al-Shayea3 and Muhammad Shafiq4,*

1Department of Computer Science & IT, The Islamia University of Bahawalpur, Bahawalpur, 63100, Pakistan
2Department of Computer Science & IT, Government Sadiq College Women University, Bahawalpur, Pakistan
3Industrial Engineering Department, College of Engineering, King Saud University, P.O. Box 800, Riyadh, 11421, Saudi Arabia
4Department of Information and Communication Engineering, Yeungnam University, Gyeongsan, 38541, Korea
*Corresponding Author: Muhammad Shafiq. Email: shafiq@ynu.ac.kr
Received: 24 May 2021; Accepted: 30 August 2021

Abstract: Smart and interconnected devices can generate meaningful patient data and exchange it automatically without any human intervention in order to realize the Internet of Things (IoT) in healthcare (HIoT). Due to more and more online security and data hijacking attacks, the confidentiality, integrity and availability of data are considered serious issues in HIoT applications. In this regard, lightweight block ciphers (LBCs) are promising in resource-constrained environment where security is the primary consideration. The prevalent challenge while designing an LBC for the HIoT environment is how to ascertain platform performance, cost, and security. Most of the existing LBCs primarily focus on text data or grayscale images. The main focus of this paper is about securing color images in a cost-effective way. We emphasis high confidentiality of color images captured by cameras in resource-constrained smartphones, and high confidentiality of sensitive images transmitted by low-power sensors in IoT systems. In order to reduce computational complexity and simulation time, the proposed Lightweight Symmetric Block Cipher (LSBC) exploits chaos-based confusion-diffusion operations at the inter-block level using a single round. The strength of LSBC is assessed by cryptanalysis, while it is ranked by comparing it to other privacy-preserving schemes. Our results show that the proposed cipher produces promising results in terms of key sensitivity and differential attacks, which proves that our LSBC is a good candidate for image security in HIoT.

Keywords: IoT; healthcare; lightweight block cipher; symmetric block cipher

1  Introduction

Internet-of-Things (IoT)-based solutions and applications are facilitating medical service providers to nurture the patients with accurate, improved and timely treatment services. Hospitals can reduce system costs and errors through the timely intervention of doctors, accurate diagnosis and treatment, accurate data collection, and automated workflow of intelligent (Healthcare IoT) HIoT system. The patient's trust in the HIoT system is directly affected by the instant and secure availability of authorized users’ digital information. Sensitive data transmitted from IoT sensor nodes may be stolen by hackers and may be used to blackmail HIoT entities. This challenge can be minimized by deploying strong passwords suitable for IoT devices, which can be safely transmitted to the IoT cloud [1].

In resource-constrained IoT devices (limited battery power, low computability, and less memory), lightweight block ciphers have attracted the attention of researchers due to the enhanced security they provide. The lightweight cryptosystems for text data are provably efficient regarding memory usage and power consumption [2–7]. Traditional passwords (such as high-end passwords based on multiple chaotic systems combined with digital DNA sequences) have shown encouraging platform performance on desktop and server computers. The feasibility of these high-end passwords in resource-constrained environments is extremely challenging, leading to research gaps that span optimization and corresponding performance evaluation of adjacent problems. For this reason, the optimization of security, robustness, area, speed, and power consumption should be considered when designing a lightweight password. Lightweight passwords are mainly used for text data or grayscale images. These passwords rarely perform in-depth analysis of color image or video data.

The chaos-based ciphers have proven to be effective and reliable due to the sensitive dependence on initial conditions, ergodicity, and deterministic pseudo-randomness [8]. However, chaos and DNA-based color image cryptosystems face many problems, including the trade-off between cryptanalysis parameters and performance analysis parameters. Another problem with most public gray-scale cryptosystems is that when they are applied to color images, their performance will decrease, and when they are applied to larger size and higher dimensional color images, their performance will decrease. It is necessary to maintain a good balance between a reasonable security level and computational time complexity.

In this article, we aim to design a lightweight password with high security, which takes into account limited computing resources such as processor speed and power consumption. We use 2-dimensional (2D) logistic map because it proves to be more chaotic and random than 1D logistic map [8]. This type of method makes the password suitable for IoT devices [9]. The key contributions of this paper can be summarized as follows. We have made a 2D logistic map which includes pixel position permutation within image sub-blocks, random image generation, and dynamic DNA encodings with fewer formatting operations. We design the generation of three chaotic boxes one for each RGB components. Finally, we analyzed the performance of the proposed light password design on smartphone platform.

The structure of this article is as follows. Section 2 provides a summary of related work. Section 3 discusses system model. Section 4 presents our proposed cipher. Section 5 describes security analysis. Section 6 discusses the performance of the proposed cipher. The last section is our conclusion.

2  Literature Review

We provide a review of lightweight encryption schemes here. In most cases, cipher schemes occupy resources and have high computational complexity. Such ciphers are not feasible on resource-constrained devices. We can find a highly secure cryptographic system in [10], which is based on multiple chaotic systems having Secure Hash Algorithm (SHA), DNA and Linear Feedback Shift Register (LFSR). However, this cryptographic system is computationally intensive. In [11], a lightweight block cipher is proposed, which improves the cipher efficiency by 20%. However, this system loses its robustness to correlated power analysis (CPA). In [12], another system was proposed, which has a 128-block cipher that uses parallelism (1 bit to 64 bit parallel data path) to evaluate the trade-off in power, energy, throughput, and area. In [13], a block-level image cipher is designed based on two rounds of permutation, substitution, and chaining. In [14], another gray-scale image encryption scheme uses zigzag scanning for obfuscation, one-dimensional chaotic logic mapping for diffusion, and a 128-bit key. In [15], outer-inner structure is proposed to enhance the confusion and diffusion in the outer phase. However, this scheme resists the linear and differential cryptanalysis in the inner phase. In [16], an image encryption algorithm deploys a block permutation layer to randomize the order of all blocks in the image.

In [17], we can find a chaos-based image cipher design, which consists of a diffusion layer and a position permutation layer. The diffusion layer occupies a block of 32 bytes, processes it, and prepares data for the permutation layer. On the other hand, the permutation layer uses the modified 2D mapping to reorder the bit positions in the image. However, this system is not cost-effective due to increased energy consumption. In [18], another DNA-based hyperchaotic algorithm is proposed for cloud CCTV system. It uses a hyperchaotic map to generate a key sequence, which is further processed by the DNA encoding and diffusion process. In [19], symmetric block ciphers are designed to resist white box attacks. In [20], another block cipher based on Feistel network is proposed, which uses a 64-bit key size and an effective key update mechanism to ensure a medium-level security. In [21], another system combines generalized Feistel structure (GFS) with “AND”, “Rotation”, and “XOR” (ARX) operations. In [22], a hybrid encryption scheme with a 128-bit key is proposed, which encrypts and decrypts the data collected by the fog node. In [23], another system is proposed, which uses a method based on dynamic key alteration to report the results of encrypted text files. However, this system took 1.983 ms to encrypt a text file of 26.7 KB in size. In [24], a mathematical model is used to find the success probability of establishing a secure communication key between smart home devices without relying on a third party. However, the design of all these ciphers does not fully meet the requirements of lightweight ciphers in terms of reduced block size, smaller keys, reduced number of rounds, effective key scheduling, and corresponding implementations for security-hardened HIoT systems. In [25], a new set of attacks (point-based attacks, high-order differential attacks, and bit-based points-based attacks) were performed on a reduced PRINCE round to fill the gaps in actual directed attacks. The conclusion of applying these attacks is that 12 rounds have sufficient safety margin against these attacks.

3  System Model

We consider a smart hospital, which consists of independent nodes with different resources (such as cost, memory capacity, CPU, programmable components, power supply, anti-tampering function, etc.) that can communicate with each other automatically. In our system model, the HIoT smart hospital is divided into different entities, such as patients, doctors, pharmacists, ambulances, receptionists, pathologists, administrators, super administrators, radiologists, etc. These entities are connected to the main gateway server containing the collected encrypted data from different nodes. And only the registered entity can collect and decrypt data from the gateway for further necessary operations. According to the security level requirements, the nodes are divided into four categories (represented by N1, N2, N3, and N4). The N1 node does not require or requires very few resources to obtain very little security. For example, nodes are used to sense pressure, light, or temperature. N2 nodes have low-level security requirements for low-level resources. For example, the application-specific integrated circuit (IC) is implanted in a secure environment that can only be accessed by authorized personnel. N3 nodes have moderate to advanced security requirements, and the average resource depends on the importance of the data. The N4 node has high security and high resource requirements. N4 is only used for critical or sensitive data (such as medical color images). N4 nodes require a long list of resources, such as [26]: (a) physical device security, (b) trusted execution environment, (c) memory, (d) data flow, (e) clock and synchronization, (f) energy Management; (g) bootloader, (h) key management, (i) random number generator, (j) encryption mechanism, (k) message verification, (l) hash engine, (m) modulation/demodulation, (N) TRANSEC engine and (o) data logging.

4  Proposed Method

We propose a cryptographic system to ensure the confidentiality of medical images taken from smart cameras (N4 type nodes of HIoT). Our proposed chaotic-based block cipher (hereinafter referred to as lightweight symmetric chaos and DNA-based encryption (LSBC-encryption)) is applied to pure color images. We use 2D Logistic Map, DNA dynamic operation and Chaotic Box. The 2D Logistic Map [8] is as follows,

{x(i+1)=x(i)k1(1−x(i))+k3(y(i)2)y(i+1)=y(i)k2(1−y(i))+k4(x(i)2+x(i)y(i))(1)

where 2.75<k1≤3.4, 2.75<k2≤3.45, 0.15<k3≤0.21, 0.13<k4≤0.15, x(i), y(i)∈ [0,1] is considered in a chaotic state [8]. The coefficients  k1, k2, k3, k4, and the initial conditions of x(i) and y(i) are used as the secret keys for encryption and decryption with a precision of 10−15. Algorithm describes our block cipher using chaos and DNA. Decryption algorithm (LSBC-Decryption) corresponding to LSBC-Encryption takes an encrypted image (Ie) as input to generate the decrypted image (Id).

5  Security Analysis

The cryptanalysis of SCD encryption system is performed in this section. We compare the result with the existing symmetric image cipher various for images. We took these images from the database of the University of Southern California. Tab. 1 details the functional comparison between our method and contemporary works.

5.1 Histogram and Variance

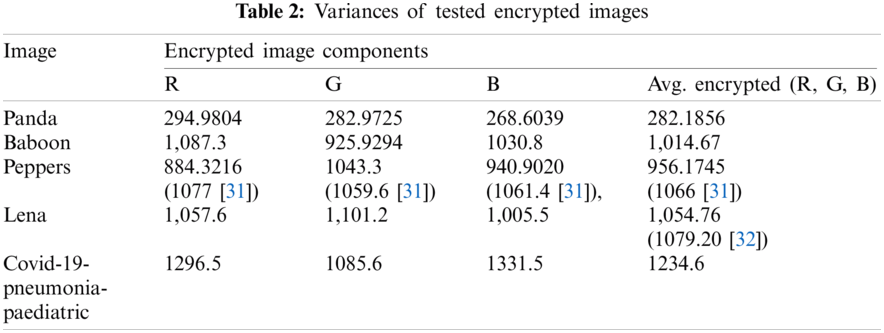
The low variance in the histogram of the encrypted image is a desired feature [29,30]. Compared with ordinary images, the histograms of synpic24310.jpg (acute appendicitis) and Covid-19-pneumonia-paediatric.jpg (lung) encrypted images are uniform. The flowchart of the LSBC-encryption algorithm is shown in Fig. 1. Similarly, the histogram variance of another group of ordinary images and encrypted images given in Tab. 2 clearly proves the effectiveness of SCD encryption against statistical attacks.

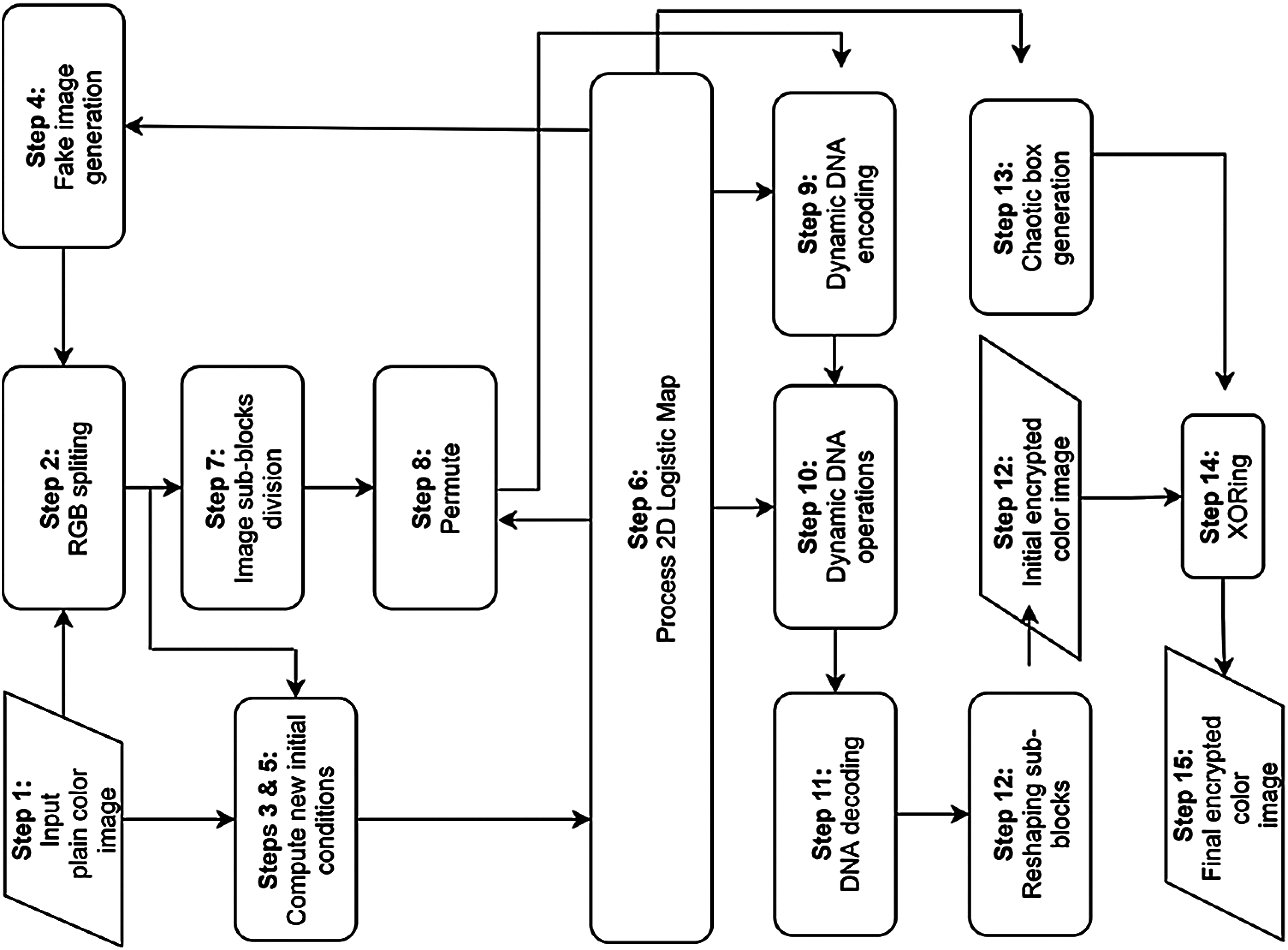
Figure 1: Flowchart of the LSBC-encryption

5.2 Correlation

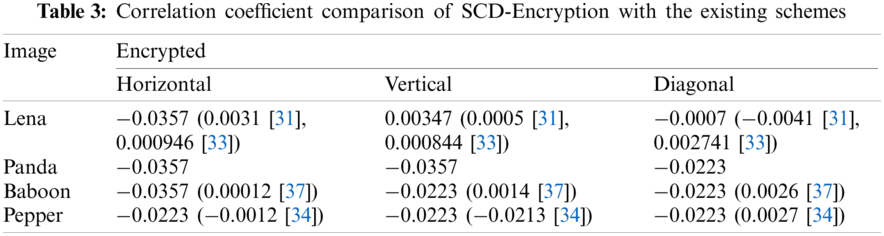
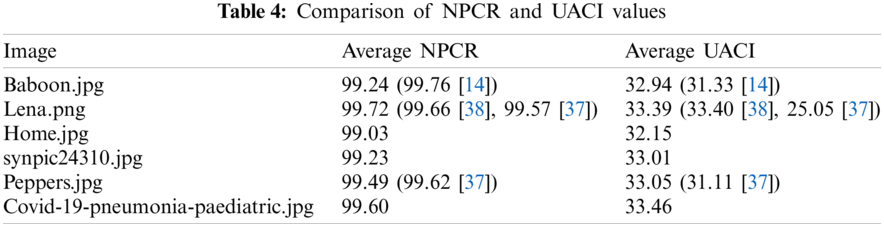
We calculate the correlation of the encrypted image between vertical, horizontal and diagonal pixels. The correlation graphs of the normal image and the encrypted image (Home and Lena) are shown in Fig. 2. Tab. 3 lists the correlation results of the four encrypted images (Lena, Panda, Baboon and Peppers). Therein, zero correlation or little correlation reflects the high security due to encryption [31]. Correlation values in Tab. 3 are mostly negative, which prove that SCD encryption effectively resists statistical attacks.

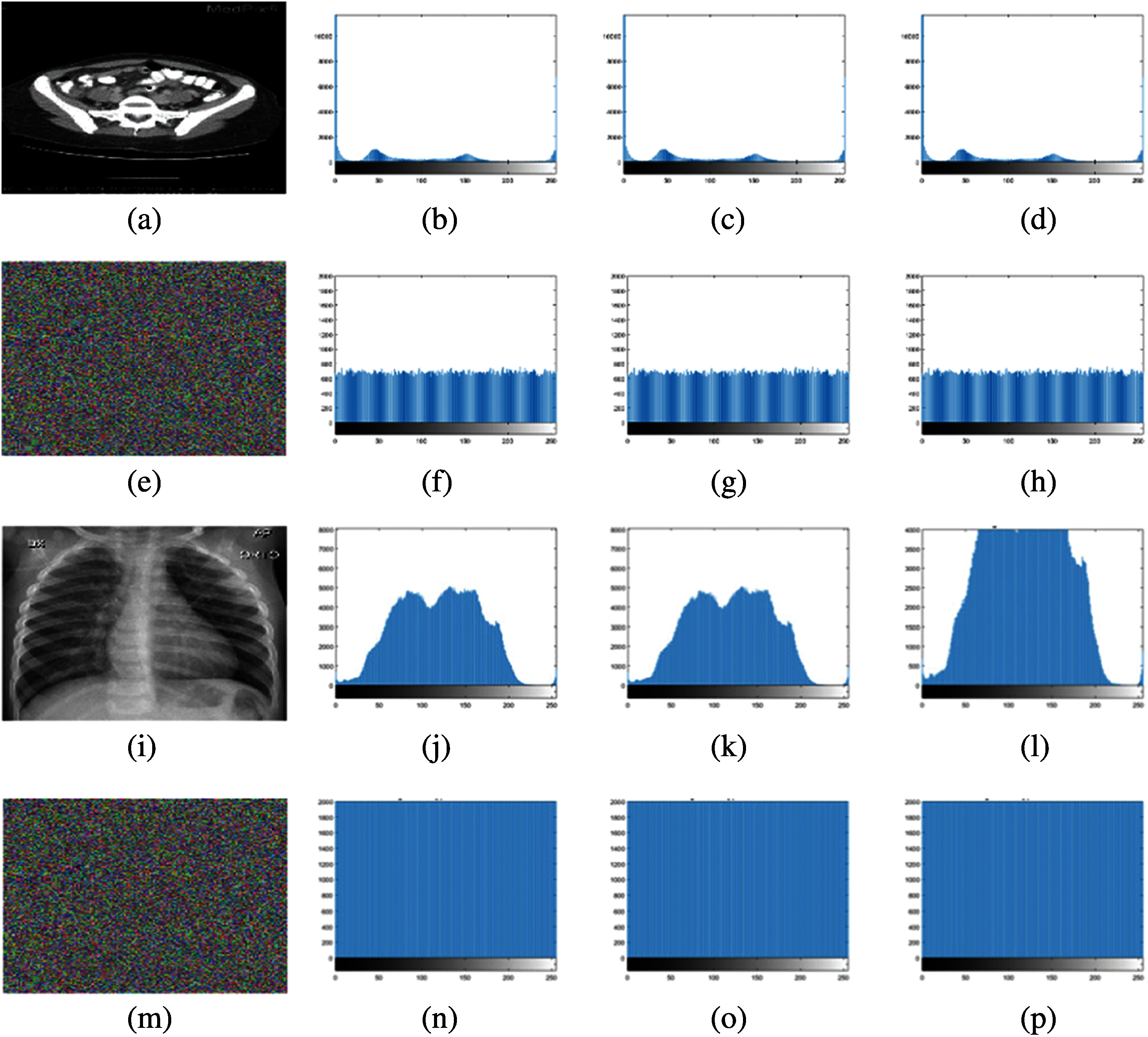
Figure 2: Histogram images: (a) plain image (acute appendicitis.jpg), (b)–(d) RGB histograms of (a), (e) encrypted image (acute appendicitis.jpg), (f)–(h) RGB histograms of (e), (i) Plain Image (Covid-19-pneumonia-paediatric.jpg), (j)–(l) RGB histograms of (i), (m) encrypted image (Covid-19-pneumonia-paediatric.jpg), (n)–(p) RGB histograms of (m)

5.3 Differential Attack Analysis

The differential attack is estimated by the pixel change rate (NPCR) and the uniform average change intensity (UACI) [32–35]. In order to estimate the effect of this attack, the normal image is encrypted before and after slight modification to generate two encrypted variants. The encrypted variants before and after slight modification are denoted by Ie and Ive respectively. A secure image encryption system strives for maximal NPCR and UACI. If NPCR is between 0% and 100%, and UACI is between 0% and 33%, we can then calculate their values by Eqs. (2) and (3) [36] as follows,

npcr(Ie,Ive)=∑1≤i≤m1≤j≤nd(i,j)m×n×100,(2)

where d(i,j)={0 ifIe(i, j)=Ive(i, j)1 ifIe(i, j)≠Ive(i, j), and

uaci(Ie,Ive)=1m×n[∑1≤i≤m1≤j≤n|Ie(i, j)−Ive(i, j)|255]×100(3)

We also juxtapose the NPCR and UACI values in Tab. 4.

5.4 Entropy Analysis

Entropy indicates the degree of randomness allowed by the cypher. For example, the ideal entropy value of an 8-bit encrypted image is 8. Eq. (4) denotes entropy which is expressed in pixel intensity values [38,39].

Entropy(Ie)=−∑i=02k−1⁡p(intensity(Iie)) log2 (p(intensity(Iie)))(4)

where intensity(Iie) is the ith intensity value of an encrypted image and p(⋅) is the probability density function. k=8 accounts for a gray level image. Tab. 5 shows the entropy results close to 8, which proves the high randomness in the encrypted image.

5.5 Keyspace and Key Sensitivity Analysis

The security encryption algorithm is also characterized by large keyspace and high sensitivity to keys. A keyspace of at least 2100 is sufficient to resist brute force attacks [40]. As in Eq. (1), the coefficients k1, k2, k3, k4 and the initial values of x(i) and y(i) of 2D Logistic Map are utilized as a secret key for encryption and decryption each with a precision of 10−15. The keyspace is computed as (1015)6=1090≅2300, which is hard enough to resist all sorts of brute force attacks [1,40]. The key sensitivity is estimated by the degree of change in the ciphertext after minor changes to the secret key. The key sensitivity of SCD-Encryption is estimated by encrypting the image Covid-19-pneumonia-paediatric.jpg and decrypting the result with slight modifications in the initial parameters. Fig. 3 demonstrates the absence of visual relationship between the decrypted image and the plain image. Denoting the plaintext by P, the keys by K1=k01, k11,…,kMN−11 and K2=k02, k12,…,kMN−12, and cipher images by C1=encrypt(P,K1) and C2=encrypt(P,K2), key sensitivity (kS) i.e., Eq. (5) is processed by the Hamming Distance [40]:

kS=1MN∑j=0MN−1⁡(cj1⊕cj2).(5)

K1 and K2 have n-bits difference. We illustrate the key sensitivity in Fig. 4. We tested several encryption variants of Covid-19-pneumonia-paediatric.jpg. These variants were created by changing bits 1, 2, 3, and 4. We noticed in Fig. 5 that the average kS value of 98.7% stayed in the range of [0.468–0.502], which is close to 0.5 because kS=0.5 specifies a secure cipher [41]. Hence, LSBC-encryption has high key sensitivity.

5.6 Gray-Level Co-Occurrence Matrix (GLCM)-Based Analysis

GLCM is formed by generating several gray-scale image variants. GLCM allows computational contrast analysis (CA), energy analysis (EA) and homogeneity analysis (HA). CA, EA and HA can be computed by the Eqs. (6)–(8) [42].

5.6.1 Contrast Analysis

Contrast analysis (CA), is computed in [43] as follows,

CA=∑i=0gt−1⁡∑j=0gt−1⁡|i−j|2×Gi,j2(6)

where Gi,j is the encrypted image GLCM at coordinates i,j and gt is the gray tone. CA results are listed in Tab. 6, in which large values of CA signify better security.

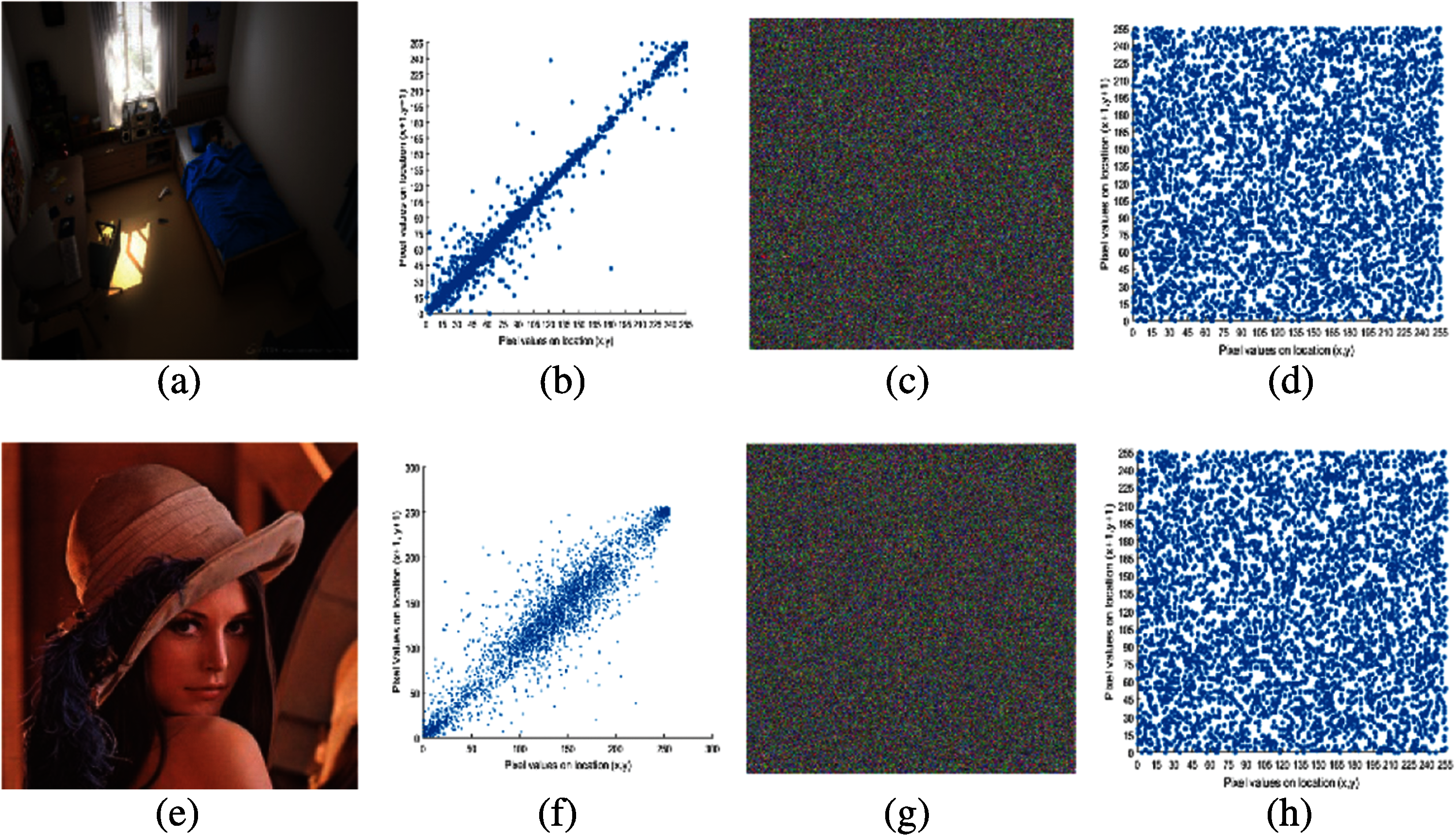
Figure 3: Correlation images: (a) plain image home, (b) correlation plot of (a), (c) encrypted image of (a), (d) correlation plot of (c), (e) plain image Lena, (f) correlation plot of (e), (g) encrypted image of (e), (h) correlation plot of (g)

Figure 4: Tests for key sensitivity: (a) plain image; (b) encrypted image; (c) decrypted image with minor modifications in the initial conditions; (d) decrypted image without modifications in the initial conditions

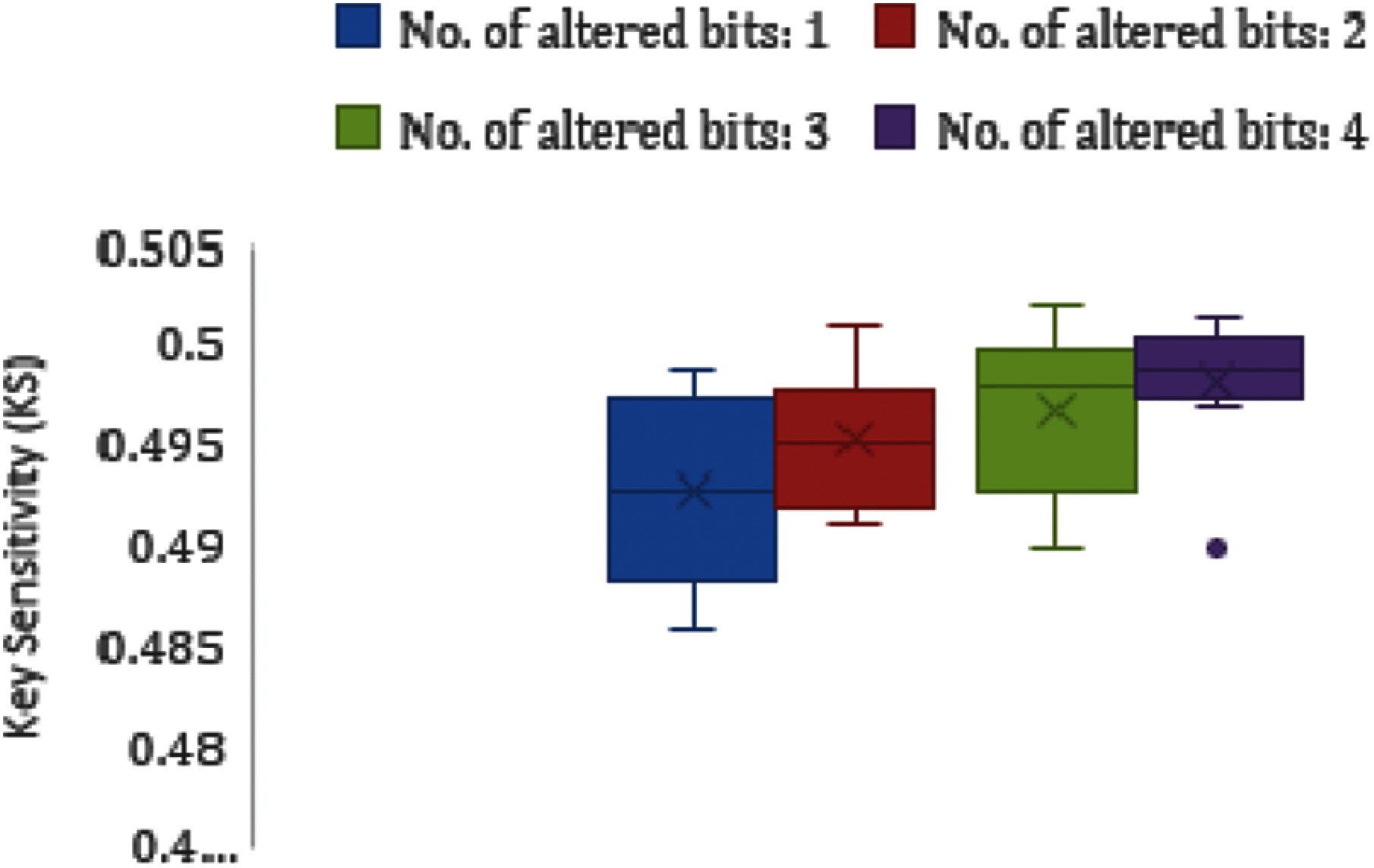
Figure 5: Boxplot analysis for key sensitivity for the image (Covid-19-pneumonia-paediatric.jpg)

5.6.2 Energy Analysis

Energy analysis (EA) is computed by the sum of the squared elements in GLCM in the following,

EA=∑i=0gt−1⁡∑j=0gt−1⁡Gi,j2(7)

where i,j represent the spatial coordinates. We have shown the EA results in Tab. 6. The lower the EA value, the better the encryption quality.

5.6.3 Homogeneity Analysis

Homogeneity measures the closeness of the element distribution in GLCM. We calculate the homogeneity analysis (HA), as follows,

HA=∑i=0gt−1⁡∑j=0gt−1⁡Gi,j1+|i−j|(8)

where i,j indicate the spatial coordinates. The lower the values of HA, the better the encryption quality is. HA values are shown in Tab. 6.

5.7 Mean Absolute Error (MAE)

MAE i.e., Eq. (9) reflects the difference between pure images and encrypted images, which is calculated as in [44],

mae(Ip,Ie)=∑1≤i≤m1≤j≤n|Ie(i,j)−Ip(i,j)|m×n(9)

The lower the value of MAE, the more secure the cryptographic system. Tab. 7 shows the comparison based on the MAE values. Our MAE values are comparable with recent existing works for the image Peppers while it exceeds in case of Lena, Baboon, and Boats images.

5.8 Robustness Against Noise and Occlusion Attack

In addition to occlusion attacks, various types of noise are used to test the robustness of SCD encryption. The PSNR between the original image and the decrypted image is used to quantify the quality of the decrypted image. We extract the decrypted image from the encrypted image caused by noise. PSNR can be computed by using the Eq. (10) in [45,46].

PSNR(Ip,Id)=10 log10(MAX2MSE(Ip,Id))(10)

where MSE(Ip,Id)=∑1≤i≤m1<j<n⁡[Ip(i, j)−Id(i, j)]2M×N is the mean square error. MAX represents the maximum pixel intensity in the plain image and M×N is height and width of the plain image.

We considered three types of noise to quantify the robustness of PSNR including salt and pepper noise (SPN), speckle noise (SN), and Gaussian noise (GN). The visual results are shown in Fig. 6. The high PSNR values in all three noise types indicate that the proposed approach has better robustness. Fig. 7 shows the occlusion attack on the encrypted image and its recovery. The image decrypted from the 60% occluded encrypted image can still be recognized.

Figure 6: Visual analysis of robustness against noise: (a) salt and pepper noise (density 5%); (b) decrypted image of (a) having PSNR = 64.20; (c) speckle noise (density 1%); (d) decrypted image of (c) having PSNR = 17.2837

6  Performance Analysis

With the improvement of trend setting innovations in cloud computing, designing the secure ciphers along with the consideration of encryption and decryption times and memory usage remains one of the key problems [37]. Therefore, along with security considerations, encryption and decryption time of an image cipher for a real life application must be considered. In this respect, the empirical and theoretical are the 2 ways for assessing the time complexity of a cipher. In empirical evaluation, algorithm is run on some platform and execution time is observed or measured through stopwatch or any other tool. Whereas, in theoretical assessment, asymptotic notation is commonly used to assess the computational complexity. In this research work, we are employing empirical assessments.

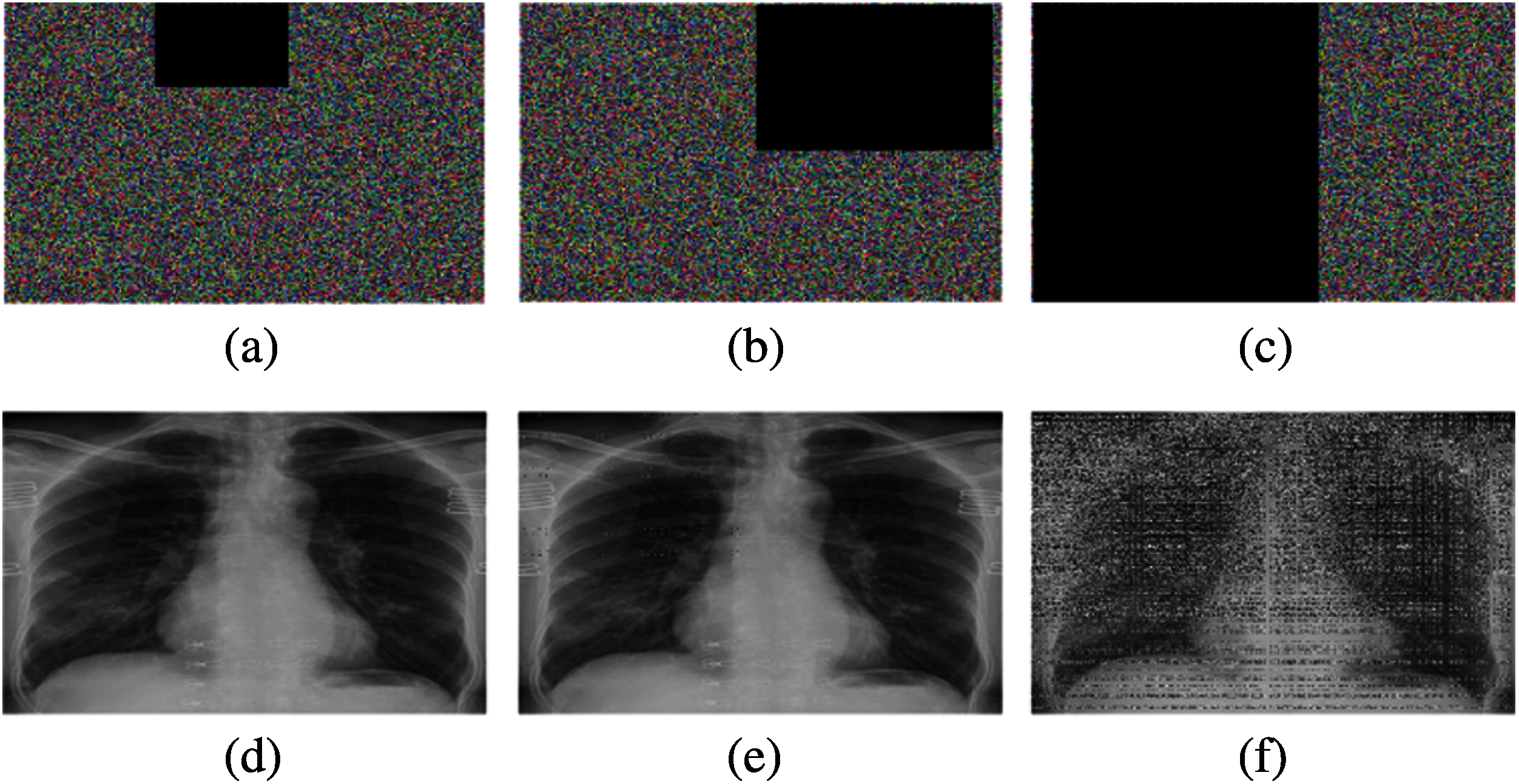
Figure 7: Visual analysis of occlusion attacks on the image Covid-19-pneumonia-paediatric.jpg: (a)–(c) different occlusion attacks, (d)–(f) recovered images

Most existing lightweight symmetric ciphers are only used for text data. We focus on the encryption of color images and use five indicators to evaluate platform performance including encryption time, memory consumption, battery consumption (mAh), power (mW) and energy consumption (mJ). Our experiments are carried out on two platforms, which includes Raspberry Pi 3 Model B+ connected with MatlabR2015a and Android smartphone HUAWEI Prime P7, (CPU HUAWEI Kirin 710F processor, Octa-core 4 x Cortex-A73 Based 2.2 GHz + 4 x Cortex-A53 Based 1.7 GHz) having 4 GB RAM, 64 GB internal storage, 4000mAh battery and operating at 5 V. These two platforms were chosen because we can use the results of existing works for comparison. The comparison of the results on Raspberry is shown in Tab. 8, (Results of proposed cipher are shown in bold, while the underlined results are derived using color images).

We use oscilloscope with Raspberry (1 GB RAM, CPU 900 MHz, Voltage = 5 V, resistance R of 1 Ohm) to measure the power consumption by =VI, where P is the power, V is the voltage and I is the current intensity. The current intensity (I) can be calculated by I=1T∫0T⁡V(t)dt, where V is the voltage and T is the time period of the curve that will be displayed on the screen of oscilloscope during the execution of cipher while encrypting standard Lena color image. The intensity I can be directly noted from the oscilloscope. Energy E=P×t, where P is the power consumption and t is the time measured while encrypting a standard Lena color image.

Our power consumption exceeds the rest of the work due to image data. However, the existing works use “plain text” data for experimentation, except for [2] using color images and [15] using gray images. We associate the difference in results with the choice of software platform. In our case, Matlab was chosen to easily encode portability and conduct experiment on other resource-constrained platforms. We optimized the number of rounds, which avoids time overhead. Additionally, the platform performance of HUAWEI Prime P7 is shown in Fig. 8. We notice the battery consumption value (mAh) of an application while encrypting using the battery/power consumption feature available in Android phones.

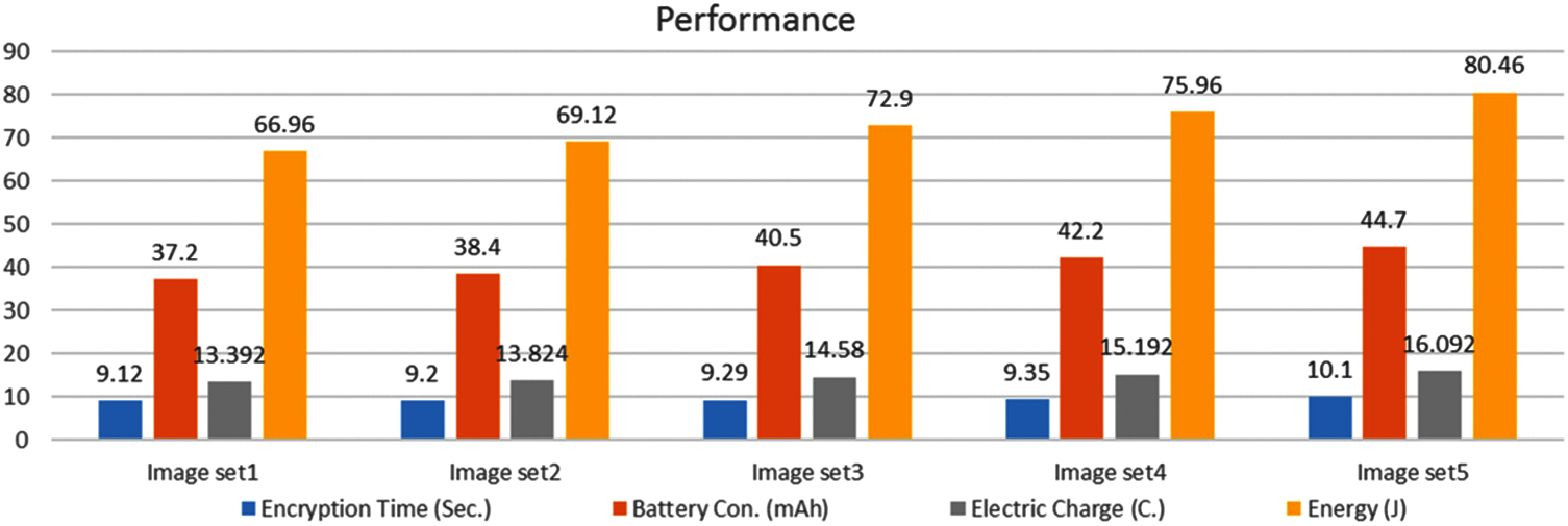
Figure 8: Individual results of five different image sets

We use the same phone camera to capture five sets of images. Each set contains 10 different color images. Set sizes are described as follows: set 1 (450 KB); set 2 (555 KB); set 3 (858 KB); set 4 (950 KB); and set 5 (1120 KB). Battery consumption in mAh is converted to joules using the energy formula, E = Q × V, where Q is the electric charge in coulombs (C), V is the voltage in volts (V) and Q can be calculated as (Q = I × t), I is the current in amperes (A) and t is the time in seconds (s). For instance, 1 mAh (0.001 A) is equal to 3.6C and when voltage is 5 V then 1 mAh will be equal to E = Q × V = 3.6C×5 V = 18 J.

7  Conclusion

In this article, we propose chaos-based and DNA-based lightweight cryptography for color images captured from smart cameras. The disadvantage of the existing method is its fragile security, that is, the performance problem in terms of non-scalability on color/gray images as the size increases. The proposed method performs well in terms of scalability, security, and platform resources (such as memory, battery consumption, and execution time). We provide visual and quantitative security evidence by running the algorithm on different platforms. We also proved that our proposed cipher is robust against the noise and occlusion attacks. In addition, our proposed cipher outperforms existing ciphers in terms of gray-level co-occurrence matrix evaluations and key sensitivity. Even if the size of the color image changes, our proposed cypher can be executed consistently. For future work, it will be interesting to extend battery life by improving the performance of password design and managing energy to deal with extravagant power attacks. In addition, the encryption of regions of interest (ROI) in medical images is also interesting, while keeping the algorithm lightweight.

Acknowledgement: The authors extend their appreciation to King Saud University for funding this work through Researchers Supporting Project Number (RSP–2021/387), King Saud University, Riyadh, Saudi Arabia.

Funding Statement: This work was supported by the King Saud University (in Riyadh, Saudi Arabia) through the Researcher Supporting Project Number (RSP–2021/387).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  F. Meneghello, M. Calore, D. Zucchetto, M. Polese and A. Zanella, “IoT: Internet of threats? A survey of practical security vulnerabilities in real IoT devices,” IEEE Internet Things Journal, vol. 6, no. 5, pp. 8182–8201, 2019. [Google Scholar]

 2.  A. Bogdanov, L. R. Knudsen, G. Leander, C. Paar and A. Poschmann, “PRESENT: An ultra-lightweight block cipher,” in Proc. CHES, Vienna, Austria, vol. 4727, pp. 450–466, 2007. [Google Scholar]

 3.  Y. Liu, K. Fu, W. Wang, L. Sun and M. Wang, “Linear cryptanalysis of reduced-round SPECK,” Information Processing Letters, vol. 116, no. 3, pp. 259–266, 2016. [Google Scholar]

 4.  W. Zhang, Z. Bao, D. Lin, V. Rijmen, B. Yang et al., “RECTANGLE: A bit-slice lightweight block cipher suitable for multiple platforms,” Science China Information Sciences, vol. 58, no. 12, pp. 1–15, 2015. [Google Scholar]

 5.  R. Beaulieu, D. Shors, J. Smith, S. Treatman-Clark, B. Weeks et al., “Simon and speck: Block ciphers for the internet of things,” in Proc. LCW, Gaithersburg, Maryland, pp. 1–15, 2015. [Google Scholar]

 6.  T. Suzaki, K. Minematsu, S. Morioka and E. Kobayashi, “TWINE: A lightweight block cipher for multiple platforms,” in Proc. SAC, Louvain-la-Neuve, Belgium, pp. 339–354, 2012. [Google Scholar]

 7.  Y. Yang, J. Lu, K. K. Choo and J. K. Liu, “On lightweight security enforcement in cyber-physical systems,” in Proc. IWLCSP, Bochum, Germany, pp. 97–112, 2015. [Google Scholar]

 8.  X. Y. Wang, Y. Q. Zhang and Y. Y. Zhao, “A novel image encryption scheme based on 2-D logistic map and DNA sequence operations,” Nonlinear Dynamics, vol. 82, no. 3, pp. 1269–1280, 2015. [Google Scholar]

 9.  N. M. Kerry, A. McKay, L. Bassham and M. S. Turan, “NISTIR 8114 report on lightweight cryptography,” in Proc. NIST, Gaithersburg, Maryland, 2017. [Google Scholar]

10. M. Samiullah, W. Aslam, H. Nazir, M. I. Lali, B. Shahzad et al., “An image encryption scheme based on DNA computing and multiple chaotic systems,” IEEE Access, vol. 8, pp. 25650–25663, 2020. [Google Scholar]

11. L. Dalmasso, F. Bruguier, P. Benoit and L. Torres, “Evaluation of SPN-based lightweight crypto-ciphers,” IEEE Access, vol. 7, pp. 10559–10567, 2019. [Google Scholar]

12. A. Singh, N. Chawla, J. H. Ko, M. Kar and S. Mukhopadhyay, “Energy efficient and side-channel secure cryptographic hardware for IoT-edge nodes,” IEEE Internet Things Journal, vol. 6, no. 1, pp. 421–434, 2019. [Google Scholar]

13. H. Noura, L. Sleem and M. Noura, “A new efficient lightweight and secure image cipher,” Multimedia Tools and Applications, vol. 77, pp. 15457–15484, 2018. [Google Scholar]

14. S. Janakiraman, K. Thenmozhi, J. B. B. Rayappan and R. Amirtharajan, “Lightweight chaotic image encryption algorithm for real-time embedded system: Implementation and analysis on 32-bit microcontroller,” Microprocessors and Microsystems, vol. 56, pp. 1–12, 2018. [Google Scholar]

15. T. Omrani, R. Rhouma and R. Becheikh, “LICID: A lightweight image cryptosystem for IoT devices,” Cryptologia, vol. 43, no. 4, pp. 313–343, 2019. [Google Scholar]

16. H. Noura, A. Chehab, M. Noura, R. Couturier and M. M. Mansour, “Lightweight, dynamic and efficient image encryption scheme,” Multimedia Tools and Applications, vol. 78, no. 12, pp. 16527–16561, 2019. [Google Scholar]

17. S. El and M. Farajallah, “A new chaos-based image encryption system,” Signal Processing: Image Communication, vol. 41, pp. 144–157, 2016. [Google Scholar]

18. T. Y. Wu, X. Fan, K. H. Wang, C. F. Lai, N. Xiong et al., “A DNA computation-based image encryption scheme for cloud CCTV systems,” IEEE Access, vol. 7, pp. 181434–181443, 2019. [Google Scholar]

19. M. Beunardeau, A. Connolly, R. Géraud and D. Naccache, “White-box cryptography: Security in an insecure environment,” IEEE Security & Privacy, vol. 14, no. 5, pp. 88–92, 2016. [Google Scholar]

20. Y. Shi, W. Wei, H. Fan, M. H. Au and X. Luo, “A light-weight white-box encryption scheme for securing distributed embedded devices,” IEEE Transactions on Computers, vol. 68, no. 10, pp. 1411–1427, 2019. [Google Scholar]

21. Y. Guo, L. Li and B. Liu, “Shadow: A lightweight block cipher for IoT nodes,” IEEE Internet Things Journal, vol. 8, no. 16, pp. 1, 2021. [Google Scholar]

22. O. A. Khashan, “Hybrid lightweight proxy re-encryption scheme for secure fog-to-things environment,” IEEE Access, vol. 8, pp. 66878–66887, 2020. [Google Scholar]

23. S. Rajesh, V. Paul, V. G. Menon and M. R. Khosravi, “A secure and efficient lightweight symmetric encryption scheme for transfer of text files between embedded IoT devices,” Symmetry, vol. 11, no. 2, pp. 1–21, 2019. [Google Scholar]

24. Y. Zhang, H. Zhao, Y. Xiang, X. Huang and X. Chen, “A key agreement scheme for smart homes using the secret mismatch problem,” IEEE Internet Things Journal, vol. 6, no. 6, pp. 10251–10260, 2019. [Google Scholar]

25. P. Morawiecki, “Practical attacks on the round-reduced PRINCE,” IET Information Security, vol. 11, no. 3, pp. 146–151, 2017. [Google Scholar]

26. J. M. Mcginthy and A. J. Michaels, “Secure industrial internet of things critical infrastructure node design,” IEEE Internet Things Journal, vol. 6, no. 5, pp. 8021–8037, 2019. [Google Scholar]

27. A. Alghafis, F. Firdousi, M. Khan, S. I. Batool and M. Amin, “An efficient image encryption scheme based on chaotic and deoxyribonucleic acid sequencing,” Mathematics and Computers in Simulation, vol. 177, pp. 441–466, 2020. [Google Scholar]

28. E. Z. Zefreh, “An image encryption scheme based on a hybrid model of DNA computing, chaotic systems and hash functions,” Multimedia Tools and Applications, vol. 79, pp. 24993–25022, 2020. [Google Scholar]

29. W. Wu and L. Zhang, “LBlock: A lightweight block cipher,” in Proc. ACNC, Nerja, Spain, pp. 327–344, 2011. [Google Scholar]

30. X. Wu, H. Kan and J. Kurths, “A new color image encryption scheme based on DNA sequences and multiple improved 1D chaotic maps,” Applied Soft Computing, vol. 37, pp. 24–39, 2015. [Google Scholar]

31. K. A. K. Patro and B. Acharya, “An efficient colour image encryption scheme based on 1-D chaotic maps,” Journal of Information Security and Applications, vol. 46, pp. 23–41, 2019. [Google Scholar]

32. X. Liao and M. Abbas, “Optik an efficient mixed inter-intra pixels substitution at 2bits-level for image encryption technique using DNA and chaos,” Optik-International Journal for Light and Electron Optics, vol. 153, pp. 117–134, 2018. [Google Scholar]

33. S. Kandar, D. Chaudhuri, A. Bhattacharjee and B. Chandra, “Image encryption using sequence generated by cyclic group,” Journal of Information Security and Applications, vol. 44, pp. 117–129, 2019. [Google Scholar]

34. Y. Luo, R. Zhou, J. Liu, S. Qiu and Y. Cao, “An efficient and self-adapting colour-image encryption algorithm based on chaos and interactions among multiple layers,” Multimedia Tools and Applications, vol. 77, no. 20, pp. 26191–26217, Oct. 2018. [Google Scholar]

35. X. Wu, J. Kurths and H. Kan, “A robust and lossless DNA encryption scheme for color images,” Multimedia Tools and Applications, vol. 77, no. 10, pp. 12349–12376, May 2018. [Google Scholar]

36. S. Sun, Y. Guo and R. Wu, “A novel image encryption scheme based on 7D hyperchaotic system and row-column simultaneous swapping,” IEEE Access, vol. 7, pp. 28539–28547, 2019. [Google Scholar]

37. F. Thabit, S. Alhomdy, S. Jagtap, “Security analysis and performance evaluation of a new lightweight cryptographic algorithm for cloud computing,” Global Transitions Proceedings, vol. 2, no. 1, pp. 100–110, 2021. [Google Scholar]

38. G. Bachira and N. Khan, “A New hybrid image encryption algorithm based on 2D-CA, FSM-DNA rule generator, and FSBI,” IEEE Access, vol. 7, pp. 81333–81350, 2019. [Google Scholar]

39. K. A. K. Patro and B. Acharya, “Secure multi level permutation operation based multiple colour image encryption,” Journal of Information Security and Applications, vol. 40, pp. 111–133, 2018. [Google Scholar]

40. S. Sun, “A novel hyperchaotic image encryption scheme based on DNA encoding, pixel-level scrambling and bit-level scrambling,” IEEE Photonics Journal, vol. 10, no. 2, pp. 1–14, 2018. [Google Scholar]

41. A. Belazi, M. Talha, S. Kharbech, W. E. I. Xiang and S. Member, “Novel medical image encryption scheme based on chaos and DNA encoding,” IEEE Access, vol. 7, pp. 36667–36681, 2019. [Google Scholar]

42. F. A. Khan, J. Ahmed, J. S. Khan, J. Ahmad and M. A. Khan, “A novel image encryption based on lorenz equation, gingerbreadman chaotic map and S8 permutation,” Journal of Intelligent & Fuzzy Systems, vol. 33, no. 6, pp. 3753–3765, 2017. [Google Scholar]

43. J. Sher and K. Jawad, “Chaos based efficient selective image encryption,” Multidimensional Systems and Signal Processing, vol. 30, no. 2, pp. 943–961, 2018. [Google Scholar]

44. H. Liu, B. Zhao and L. Huang, “Quantum image encryption scheme using arnold transform and S-box scrambling,” Entropy, vol. 21, no. 4, pp. 1–14, 2019. [Google Scholar]

45. G. Cheng, C. Wang and H. Chen, “A novel color image encryption algorithm based on hyperchaotic system and permutation-diffusion architecture,” International Journal of Bifurcation and Chaos, vol. 29, no. 9, pp. 1–17, 2019. [Google Scholar]

46. S. N. Lagmiri, J. Elalami, N. Sbiti and M. Amghar, “Hyperchaos for improving the security of medical data,” International Journal of Engineering & Technology, vol. 7, no. 3, pp. 1049–1055, 2018. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.