Computers, Materials & Continua DOI:10.32604/cmc.2022.018469
Article

Optimal Resource Allocation Method for Device-to-Device Communication in 5G Networks

Fahd N. Al-Wesabi1,2,*, Imran Khan3, Saleem Latteef Mohammed4, Huda Farooq Jameel4, Mohammad Alamgeer5, Ali M. Al-Sharafi6 and Byung Seo Kim7

1Department of Computer Science, King Khalid University, Muhayel Aseer, KSA
2Faculty of Computer and IT, Sana’a University, Yemen
3Department of Electrical Engineering, University of Engineering and Technology, Peshawar, Pakistan
4Department of Medical Instrumentation Techniques Engineering, Electrical Engineering Technical College, Middle Technical University, Baghdad, 10013, Iraq
5Department of Information Systems, King Khalid University, Mayahel Aseer, KSA
6Department of Computer Science, College of Computers and Information Technology, University of Bisha, KSA
7Department of Software and Communications Engineering, Hongik University, Korea
*Corresponding Author: Fahd N. Al-Wesabi. Email: falwesabi@kku.edu.sa
Received: 08 March 2021; Accepted: 09 April 2021

Abstract: With the rapid development of the next-generation mobile network, the number of terminal devices and applications is growing explosively. Therefore, how to obtain a higher data rate, wider network coverage and higher resource utilization in the limited spectrum resources has become the common research goal of scholars. Device-to-Device (D2D) communication technology and other frontier communication technologies have emerged. Device-to-Device communication technology is the technology that devices in proximity can communicate directly in cellular networks. It has become one of the key technologies of the fifth-generation mobile communications system(5G). D2D communication technology which is introduced into cellular networks can effectively improve spectrum utilization, enhance network coverage, reduce transmission delay and improve system throughput, but it would also bring complicated and various interferences due to reusing cellular resources at the same time. So resource management is one of the most challenging and importing issues to give full play to the advantages of D2D communication. Optimal resource allocation is an important factor that needs to be addressed in D2D communication. Therefore, this paper proposes an optimization method based on the game-matching concept. The main idea is to model the optimization problem of the quality-of-experience based on user fairness and solve it through game-matching theory. Simulation results show that the proposed algorithm effectively improved the resource allocation and utilization as compared with existing algorithms.

Keywords: D2D communication; resource allocation; optimization; networks

1  Introduction

In the past few decades, mobile communication has completely changed people’s lifestyles, but people’s pursuit of higher-performance mobile communication systems has never stopped. To adapt to the technical scenarios of the future 5G system with continuous wide-area coverage, high-capacity hotspots, large connections with low power consumption, and low latency and high reliability, driven by the development of the mobile Internet of Things and the Internet, the mobile communication system has entered a new stage of development, namely, the 5G mobile communication system stage [1–10].

When the mobile communication system responds to diversified service requirements and increasing speed requirements, spectrum resources, energy consumption and deployment costs have become the main constraints for the development of mobile communication systems. At the same time, the 5G mobile communication system has characteristics such as dynamic and heterogeneous, which all pose severe challenges to wireless resource management. Therefore, the issue of wireless resource management in the 5G environment has become a research hotspot in the current wireless communication field [11–18].

The problem of radio resource management essentially refers to the problem of matching between radio resources and the user’s business needs [19–25]. The matching algorithm of wireless resources can be divided into three levels: the first-level service-side optimization algorithm, that is, by reducing the user experience quality, adaptively optimizing the service transmission index requirements to achieve the matching of service requirements and given network resources, for example, [26] proposes a rate allocation scheme that adjusts the user’s rate according to the minimum demand of different users in the case of limited bandwidth and seeks to maximize the overall utility of the system. The second layer of network-side optimization algorithms refers to the realization of certain network performance goals (throughput, system transmission delay) through the optimal matching of network resources, to ensure the user’s business needs. At present, this type of matching is the focus of research as shown in the algorithm given in [27] as an example, the system throughput is used as the optimization index, and the alliance game algorithm is used to solve the uplink resource allocation problem of multiple D2D users and cellular users; the third layer network and service matching algorithm through joint optimization from the network side and the business side, the user’s service experience quality is guaranteed with the smallest amount of resources and the best allocation method. Reference [28] gives a timely adjustment of the transmission load according to the network status and then meets the case of transmission delay requirements, an algorithm that optimizes the overall utility of the system by optimizing the resource scheduling scheme.

The matching algorithm studied in this paper belongs to the second-layer network-side optimization algorithm. For the channel allocation problem in the 5G environment, the existing research mainly uses a convex optimization algorithm [29], a greedy algorithm [30], and an algorithm based on game theory [31–33]. Among them, algorithms based on game theory are widely used. For example, non-cooperative game theory is often used to solve the resource allocation problem in D2D communication in a distributed manner [32–36], but the Nash equilibrium obtained from this model is unilaterally unstable. of. In comparison, resource allocation based on matching game theory provides a distributed, self-organized bilateral stable matching. Matching game theory was originally used in the field of economics to solve bilateral matching problems such as marriage matching and university admissions [37]. With the development of matching game theory, more and more scholars use it in the field of wireless communication to solve the problem of wireless resource matching [38], breaking through many limitations of game theory.

Reference [39] proposed an algorithm based on matching game theory to allocate channels for cellular users in base stations. Reference [40] proposed an algorithm for joint allocation of spectrum and power using an iterative method in a D2D communication environment based on game theory, taking system energy consumption as an optimization index. In [41], a D2D user channel allocation algorithm based on the many-to-many matching game theory based on the throughput of the system as an optimization index is proposed. These algorithms all provide an easy-to-implement architecture to solve the NP-hard wireless resource allocation problem.

However, the algorithm proposed in the above reference does not consider the problem of assigning channels to both cellular users and D2D users in the 5G cellular-D2D hybrid scenario. At the same time, most of them are based on the throughput of the system is an optimization index, and the fairness of users is not considered. In the 5G environment, D2D communication technology, as one of the key technologies, not only improves system capacity and frequency utilization but also introduces interference to cellular users, which greatly increases the complexity of channel allocation for different users. At the same time, the 5G communication system is user-experience-oriented, and the blind pursuit of system throughput is no longer

Applicable, so this paper proposes a two-tier game matching algorithm for cellular-D2D hybrid scenarios, and establishes a fairness matching model based on the quality of experience (QoE).

2  System Model

In the 5G cellular-D2D user hybrid scenario, it is assumed that there are I cellular users (CU) and J D2D user pairs (DU) in a cell at the same time, that is, C={c1,c2,…,cI}, D={d1,d2,…,dJ}. Among them, the sending end and the receiving end in DU are represented by {dt1,dt2,…,dtJ} and {dr1,dr2,…,drJ} respectively. At the same time, there are L channels in the cell, that is, L = {1, 2,…, L} and the cellular users (CU) communicate on these channels. For CU ci, all channels allocated to it can be regarded as a resource block RBi, which corresponds to a user set. The set of resource blocks is expressed as RB={RB1,RB2,…,RBI}. The DU multiplexes the resource block RB of the CU to transmit messages. Each DU can use multiple CU resource blocks for communication, and each CU resource block can also be accessed by multiple DUs. The proposed system model is shown in Fig. 1.

When the channel response obeys the independent Gaussian distribution, the channel envelope can be regarded as Rayleigh fading. Therefore, the channel gain can be expressed as G=βd−η|h|2, where β is the system parameter and η is the index of path fading, and h is the parameter of the complex Gaussian channel, which follows h ~ CN (0, 1).

In the system, the transmission power of each CU ci is Qi, and γi is used to represent the signal-to-noise ratio (SINR) received at the user ci when transmitting on channel l which is expressed as γi=QiGB,i/∑jxi,jpjiGB,j+N0. Among them, GB,i, and GB,j refer to the gain from the base station to ci and dj, respectively, and N0 refers to the Gaussian noise at the receiving end. Based on Shannon’s formula, it can be obtained that the transmission rate of user ci on channel l is ri=Blog2⁡(1+γi). For DU, multiple DUs share the same resource block, and the same DU is also allowed to occupy multiple resource blocks. We use xi,j to indicate whether a resource block is allocated to a DU. Specifically, if a resource block RBi is allocated to DU Dj, then xi,j=1, otherwise xi,j=0. It is stipulated that the transmission power of each DU is fixed and is evenly allocated to the resource blocks occupied by it, namely pji=Pj/∑i=1Ixi,j, and Pj is the total transmission power of the DU dj transmitter. Similarly, when DU dj is transmitted on RBi, the SINR received by drj is γji=pjiGj/QiGi,j+∑j′≠jxi,j,pji,Gj,j′+N0. Among them, Gj, Gi,j and Gj,j are the channel gain between DU dtj and drj, the gain between RBi and DU drj, and the gain between drj and dtj, respectively. pji, is the transmission power of DU dtj. Therefore, the data rate of DU when transmitting on RBi is rji=Blog2⁡(1+γji).

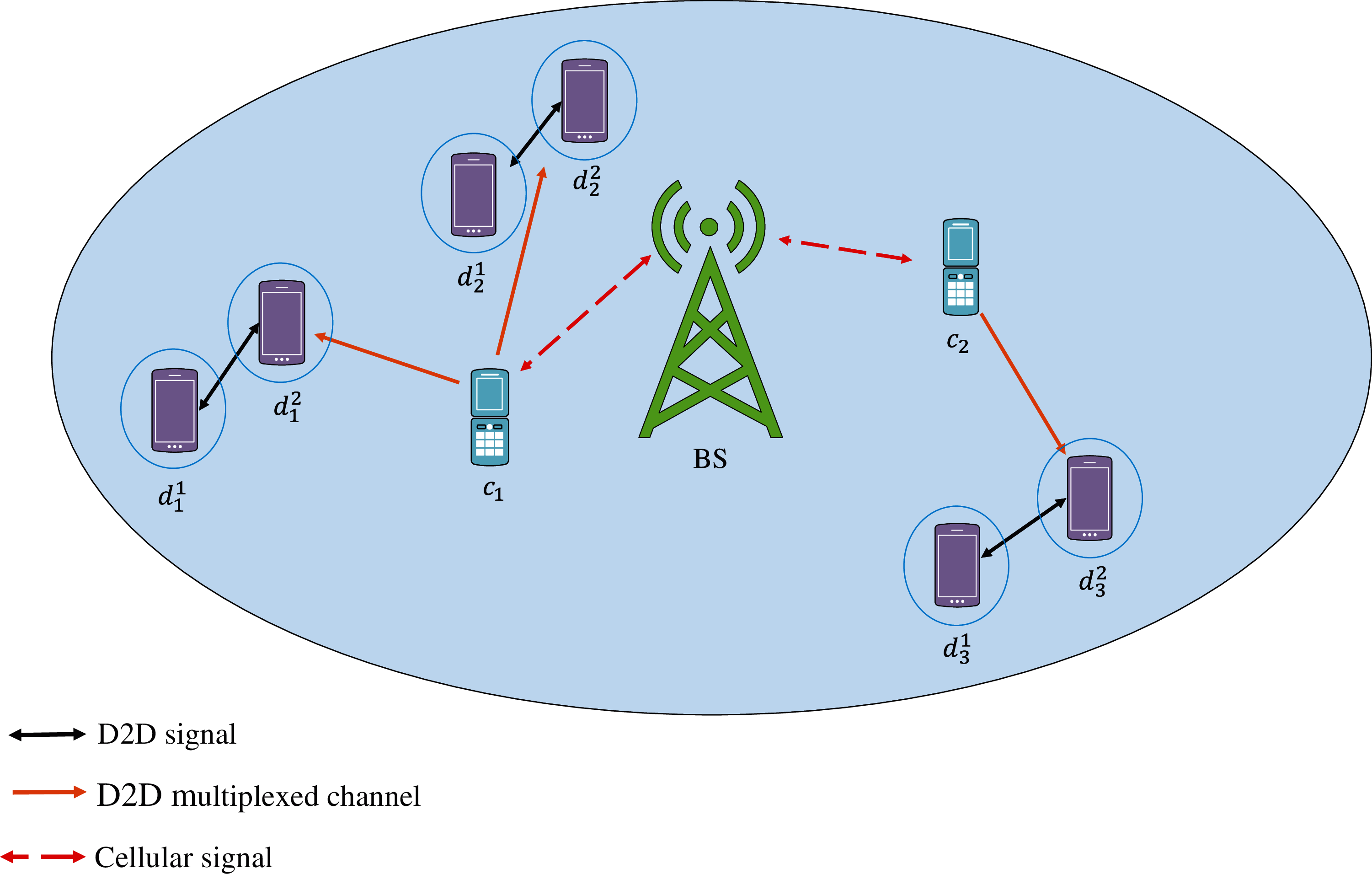
Figure 1: Proposed system model

Since the 5G system is user-experience-oriented, QoE is used as the optimization indicator in this model, and the satisfaction utility function is used to describe the QoE of users with different speed requirements, which is defined as follows:

u(r)=12(11+e−τ(r−rreq)+11+eτ[r+rreq−(rd+rs)]) (1)

Among them, r represents the throughput of a single user, rreq represents the user’s basic rate demand; rs represents the user’s saturation rate demand, rd represents the initial value of the rate corresponding to the decrease of user satisfaction, and τ is the slope parameter. For each user, rreq, rs, rd and τ may be different. It can be seen that the above definition can accurately describe the relationship between throughput and QoE.

Then, the overall utility value of the system is represented by U(X), which is the sum of the satisfaction utility of all CUs and DUs in the system. uci(Rci) and udi(Rdi) are calculated by Eq. (1). Therefore, the optimization model is constructed as follows:

maxU(X)=∑i∈Iuci(Rci)+∑j∈Judj(Rdj) (2)

Subject to:

C1:xi,jγij≥xi,jγjimin,∀i,j (2a)

C2:γi≥γimin,∀i (2b)

C3:xi,j∈{0,1},∀i,j∈{1,2,…,J} (2c)

C4:∑jxi,j≤qmax,∀i (2d)

C5:us≤usmin,∀s=ci,dj (2e)

Constraints C1 and C2 restrict CU and DU to meet their SINR requirements. C3 indicates that the value of xi,j can only be 0 or 1, and C4 indicates that each CU channel can be multiplexed by qmax DUs at most. This condition can limit Interference on the channel of each CU, while reducing the complexity of execution, C5 restricts the condition of taking into account the fairness of users, ensuring that the quality of experience obtained by each DU and CU can reach their minimum, in case there is a channel Severely uneven distribution.

3  Proposed Algorithm

In the cellular-D2D hybrid scenario in the 5G environment, there are two kinds of interference, namely the interference caused by the DU reused by the resource block of the CU on the CU and the interference caused by the DU reused by the same CU resource block. The matching results influence each other, which greatly increases the complexity of the channel allocation problem. Therefore, this paper proposes an easy-to-operate two-tier game matching algorithm, which reduces this complex channel allocation problem to a two-layer problem to solve, that is, the first layer: CU allocates channels, based on the many-to-one matching game theory, using cellular The user’s channel allocation algorithm is solved; the second layer: DU reuses the resource block of the CU, based on the many-to-many matching game theory, using the D2D user’s channel allocation algorithm to solve. Finally, an iterative method is used to solve the first layer and the second layer separately, that is, the two-layer game matching algorithm is used to solve the complicated channel allocation problem.

For the above-mentioned problems involving the interaction of multiple objects, matching game theory is an effective tool. Therefore, a many-to-one matching game theory based on the consideration of existing matches, in which the player is the CU and channel agent, and a many-to-many matching game theory based on the consideration of existing matches, in which the player is the DU and the channel coordinator, are established respectively. The structure of the entire two-tier game matching algorithm is shown in Fig. 2. Next, we will analyze the process of solving the above two-layer problem.

3.1 Channel Allocation Algorithm for Cellular Users

First, consider establishing a matching model between the CU and the channel. Assume that the channel set in the cell is Ḹ and the cell user is C. The many-to-one matching game theory is used to solve the small cell channel allocation problem. The two parties involved in the matching are the CU and the channel resource agent. From the matching game theory, we know that the individuals of the two parties involved in the match have a preference relationship with the individuals of the other party, which reflects the order in which the party chooses the other party’s individuals. The operations (matching request, acceptance/rejection) performed when the two parties are matched are all determined according to the preference list. The symbol ≻m is usually used to indicate the preference of individual m. For example, I′≻cil means that the user ci is more willing to access the channel I′ than the channel l.

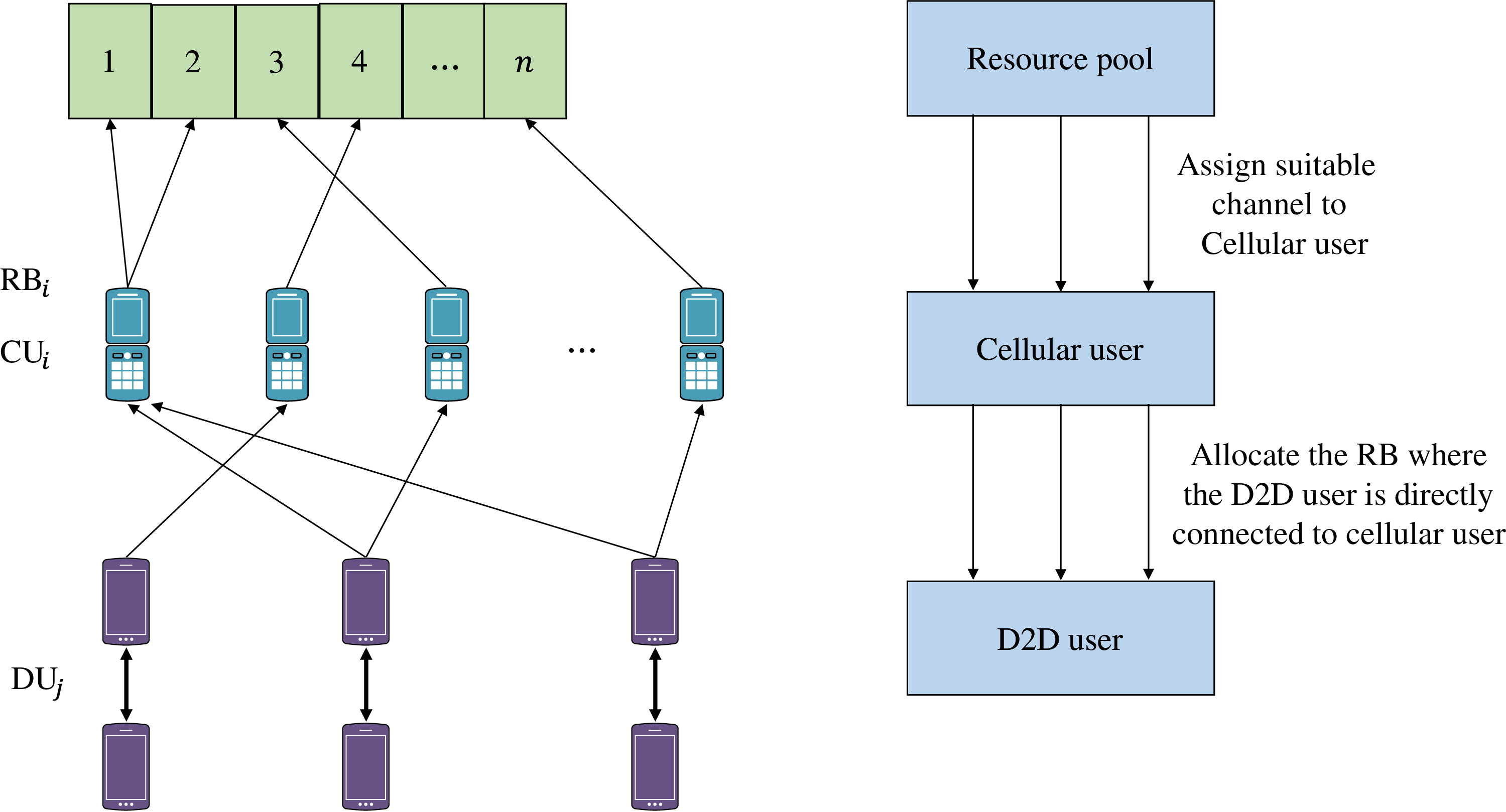
Figure 2: Proposed algorithm mechanism

Definition 1: Many-to-one matching μ [42] is a mapping from set C ∪ Ḹ to set C ∪ Ḹ, ∀l∈L¯, c∈C, we have:

(1) μ(l)=1, and if μ(l)≠C, then μ(l)=l;

(2) |μ(c)|= {1, 2,…, L}, and if μ(c) ∉ L, then μ(c)=c;

(3) If and only if μ(c)=l, μ(c)=c.

Therefore, the array {C, Ḹ, ≻c, ≻ Ḹ} is used to determine the cellular network channel allocation problem, where ≻c is the preference list of cellular users, and ≻ Ḹ is the preference list. To better describe the many-to-one matching μ, the preference list defined in the matching game is bilateral.

On the cellular user side, each CU ci can occupy multiple channels, seeking an access solution that maximizes its satisfaction function. Therefore, CU ci only requests access to channels that it does not occupy. Assume that each CU only requests its most preferred channel each time until the match reaches a stable level. Assuming that the current channel allocation plan is a={ac1,ac2,…,acI}, aci refers to the set of channels occupied by user ci. The satisfaction of CU ci can be rewritten as ui(aci)=uci(Rci).

Therefore, for a given channel l, the utility of CUci, ∈ci(l,aci) can be expressed by Eq. (3):

∈ci(l,aci)=ui(aci+l)−ui(aci) (3)

where ui(aci+l) refers to the satisfaction of ci after adding channel l under the condition that the original channel of ci remains unchanged, and Eq. (3) uses the increment of user satisfaction after channel l is allocated to express ci utility on channel l.

For CU ci, the preference relationship ≻ ci is defined as, for any two channels l, l′∈ Ḹ , and l≠l′. If and only if ∈ci(l,aci)>∈ci(l′,aci), l ≻ cil′.

Similarly, on the channel side, each channel seeks to make the greatest contribution to the satisfaction of access users. For a given user ci, the utility εl(ci) on channel l is expressed by Eq. (4):

εl(ci)={ui(aci+l)−ui(aci),l∉aciui(aci)−ui(aci−l),l∈aci (4)

Among them, ui(aci−l) refers to the satisfaction degree when CU ci leaves the channel l.

For channel l, the preference relation is defined as ≻ l for any two users, and i≠i′. If and only if εl(ci)>εl(ci′), ci ≻ ci′.

Definition 2: (Blocking individual) ∀ci∈C; ci ≻ ciμ(ci), ∀l∈ Ḹ, ∃l≻lμ(l), that is, relative to the current matching object, the individual would rather choose not to match.

Definition 3: (Blocking pair) ∃(ci,l)∈C∪ Ḹ, satisfying:

1.    l≻ciμ(ci)

2.    ci ≻ lμ(l)

Definition 4: (Stable) There are no blocking individuals and blocking pairs in the matching μ.

The steps of the CU channel allocation plan are as follows in Algorithm 1.

3.2 Channel Allocation Algorithm for D2D Users

Consider establishing a many-to-many matching model between D2D user pairs (DU) and resource blocks RB. In the network, CU and DU share spectrum resources to improve the utilization efficiency of spectrum and energy, but D2D communication will introduce new interference to the cell. Multiple DUs can multiplex the same channel, and one DU can multiplex multiple channels at the same time. Therefore, there is interference between DUs and CUs using the same channel, and there will also be interference between DUs using the same channel. The problem of DU channel allocation is solved based on the many-to-many matching game theory of existing matches.

Definition 5: Many-to-many matching [43] is a mapping from set D ∪ RB to set D ∪ RB. ∀di∈D, RBi∈RB has:

1.    |μ(dj)|≤I, and if μ(di) ∉ RB, then μ(di)=di;

2.    |μ(RBi)|=qmax, and if μ(RBi) ∉ D, then μ(RBi)=RBi;

3.    If and only if μ(RBi)=dj, μ(dj)=RBi

This type of matching is called a matching game algorithm that considers existing matches, that is, each individual has a dynamic preference list based on the other individual, which is different from the traditional matching algorithm in which individuals have a fixed preference list [44]. In this matching model, the preference list is established according to the utility values of DU and RB in a certain matching state μ.

In the matching state μ, the utility of DU dj on RBi is Uj(i,μ), that is, Uj(i,μ)=u(rji). The preference list of DU dj is arranged according to the descending order of Uj(i,μ) values. In the matching state μ, D2D user pairs using the same resource block RBi are represented by a set S. Define the utility of RBi as the sum of the utility of all DUs occupying it and the corresponding CU, namely Ui(S,μ)=u(ri)+∑j∈S(rji). The preference list is also arranged according to the utility value of RBi, that is, Ui(S,μ) in descending order.

Inspired by the housing allocation problem, a matching game algorithm that extends it to many-to-many is proposed. Different from the traditional delay acceptance algorithm, this algorithm allows two D2D user pairs to directly exchange their respective resource blocks. To better describe the interaction between the two parties’ preferences, the concept of exchange matching is defined as follows:

μiji′={μ{(j,μ(j)),(j′,μ(j′))}}∪{(j,{{μ(j){i}{j′}}),(j′,{{μ(j′){i′}}∪{i}})} (5)

where, i∈μ(j), i′∈μ(j′), i ∉ μ(j′) and i′ ∉ μ(j). In other words, swap matching allows D2D pair Dj and Dj′ to swap one of their matching RBs, while keeping the matching of other D2D pairs and RB unchanged. It should be noted that one of the DUs participating in the exchange can be an idle RB, which is represented by ????, so one DU is allowed to access a vacancy. In the same way, one of the RBs participating in the exchange can also be a hole.

Based on the concept of exchange matching, the exchange blocking pair is defined as follows.

Definition 6: (Exchange blocking pair) (Dj,Dj′) is an exchange blocking pair, if and only if:

1.    ∀x∈{i,i′,j,j′}, Ux(μiji′)≥Ux(μ);

2.    ∃x∈{i,i′,j,j′}, Ux(μiji′)>Ux(μ)

The exchange operation is carried out between the exchange-blocking pairs. Condition (1) indicates that after the exchange-blocking pair (Dj,Dj) performs the exchange operation, the utility of the individuals participating in the exchange, including the resource block and the D2D user pair, cannot be reduced. Condition (2) indicates that the utility of at least one individual will increase after the exchange. It is worth noting that the utility of holes and the individuals matching the holes do not need to consider these two conditions.

The specific steps of the DU channel allocation plan are as follows in Algorithm 2.

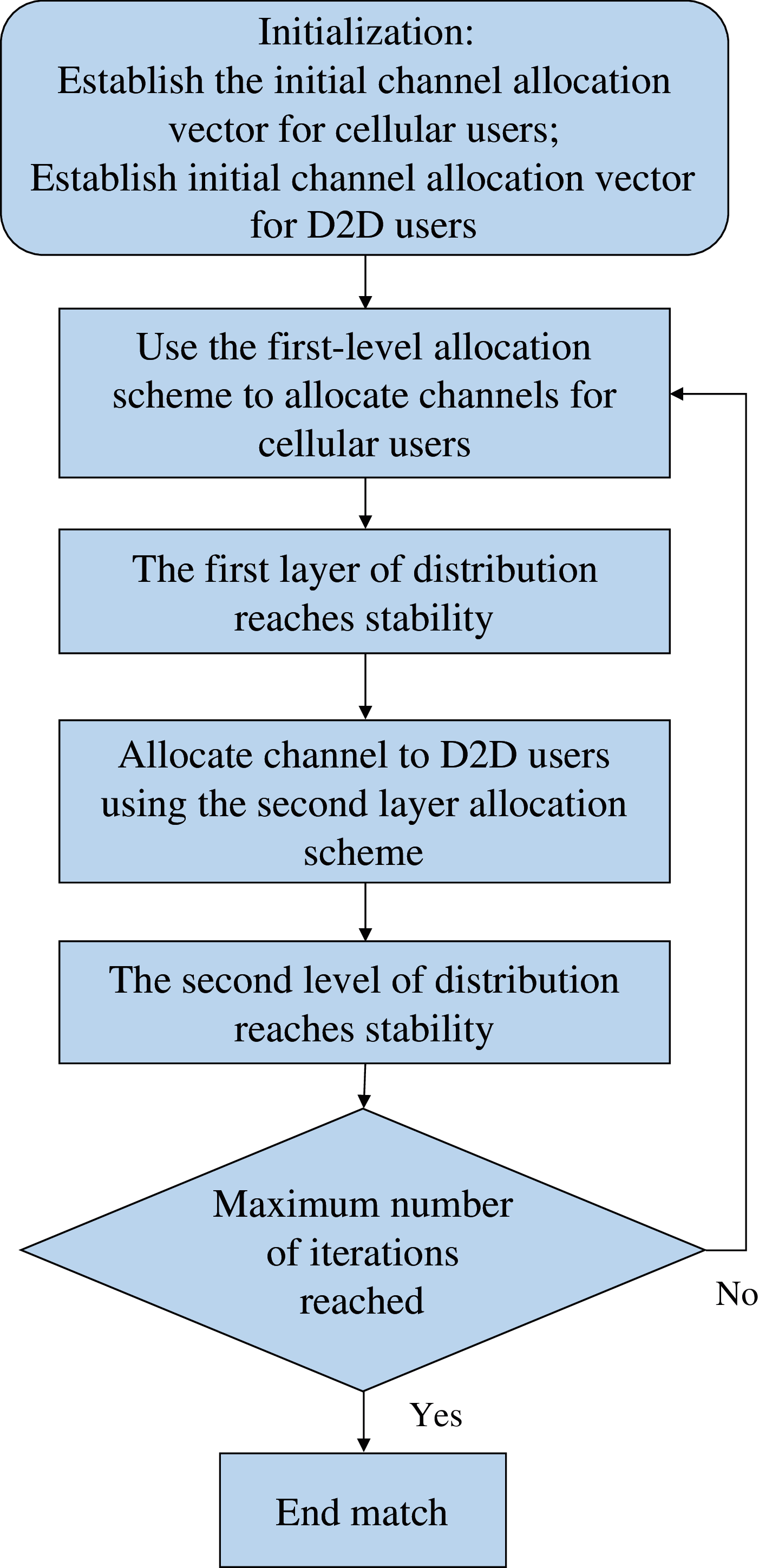
Figure 3: Proposed algorithm flowchart

3.3 Algorithm Flow

Combining the above CU and DU channel allocation schemes, the algorithm flow of double-layer game matching in a complete cellular-D2D hybrid environment is as follows.

Step 1: System initialization, establish initial CU channel matching vector a[0] and DU resource block matching vector b[0], input l∈ Ḹ, ci∈C, dj∈D.

Step 2: If the number of iterations is not greater than the maximum number of matching times, that is, when t≤tmax, go to step 3, otherwise go to step 4.

Step 3: Using the first-layer CU channel matching scheme, the allocation vector a is updated, and then RB is updated.

Step 4: According to the matching result in step 1, use the DU channel matching scheme to update the allocation vector b; return to step 2.

Step 5: Obtain stable matching results.

In summary, the matching process of the proposed algorithm proposed is shown in Fig. 3.

4  Simulation Results

To verify the effectiveness of the proposed algorithm, we used MATLAB software to simulate the results for evaluation. In this simulation model, the CUs and DUs are randomly distributed in a circular area with a radius of 50 m, and the maximum distance between the receiving end and the transmitting end of the DU is 20 m. Other system simulation parameters are as follows in Tab. 1.

Fig. 4a shows the variation curve of the overall system utility QoE with the number of CUs (Ncu), when the number of channels is 6 and the number of DUs is 2. It can be seen that as the number of cellular users increases, the overall utility of the system also increases. Fig. 4b shows the variation of the overall system utility QoE with the number of channels (Nchannel) when the number of CUs is 4 and the number of DUs is 3. It can be seen from this that as the number of channels increases, the overall utility of the system continues to increase. Moreover, it can be seen from Fig. 4 that the proposed algorithm finally stabilizes as the number of iterations increases.

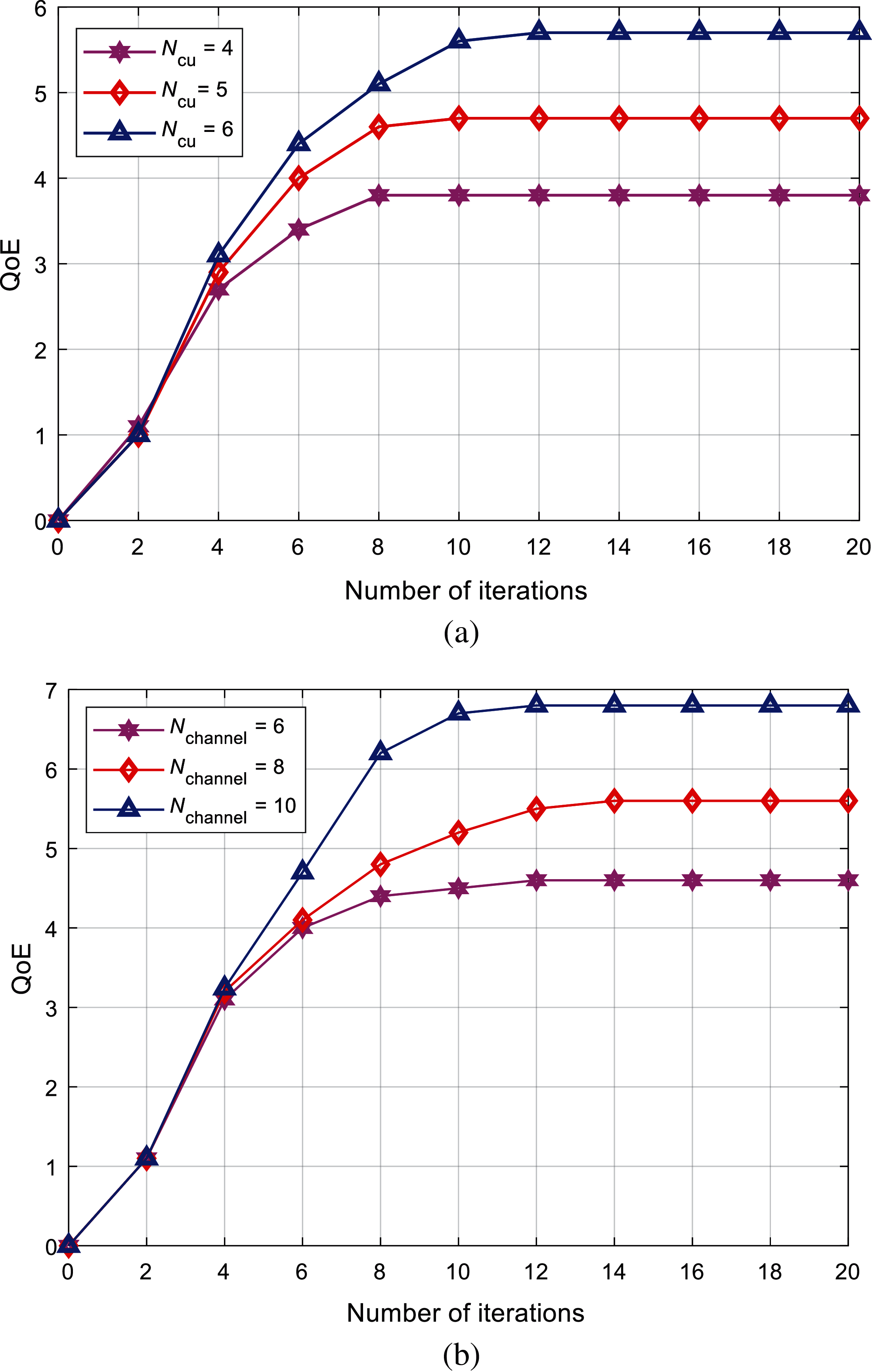
Figure 4: Comparison of the QoE of the proposed algorithm (a) QoE varies with the number of CUs (b) QoE varies with the number of channels

Next, the proposed algorithm, the random matching algorithm, and the optimal matching algorithm are compared from the aspects of effectiveness, stability, convergence, and complexity. The random matching algorithm uses Eq. (2) as the optimization model, and does not consider user fairness, and uses the pairwise random matching method to solve the corresponding model. The optimization matching algorithm constructs an optimization model with throughput as the optimization goal, and does not consider user fairness, and uses many-to-many matching game theory to solve the corresponding model [41]. The comparison indicators of the three algorithms all adopt the user QoE indicator defined in this article.

4.1 Effectiveness

The proposed algorithm is based on QoE as the index for matching optimization, and the algorithm is compared with random matching and optimal matching algorithms. In Fig. 5a, when the number of DUs is 2 and the number of channels is 10, compare the QoE utility value of each algorithm after the number of CUs changes. In Fig. 5b, when the number of CUs is 4 and the number of channels is 8, compare the QoE utility value of each algorithm after the number of DUs changes.

Since the optimal matching algorithm does not consider user fairness, the overall throughput can be maximized. In some cases, (when the QoE index is in an increasing relationship with the total throughput), the optimal matching algorithm has better performance (see the second point in Fig. 5a). But in most cases (the QoE index and total throughput are not a simple incremental relationship), and the two-tier game matching algorithm directly optimizes the QoE index, so the performance of the two-tier game matching algorithm will be better. From Figs. 5a and 5b, it can be seen that the performance of the proposed algorithm is better than the random matching algorithm and the optimal matching algorithm.

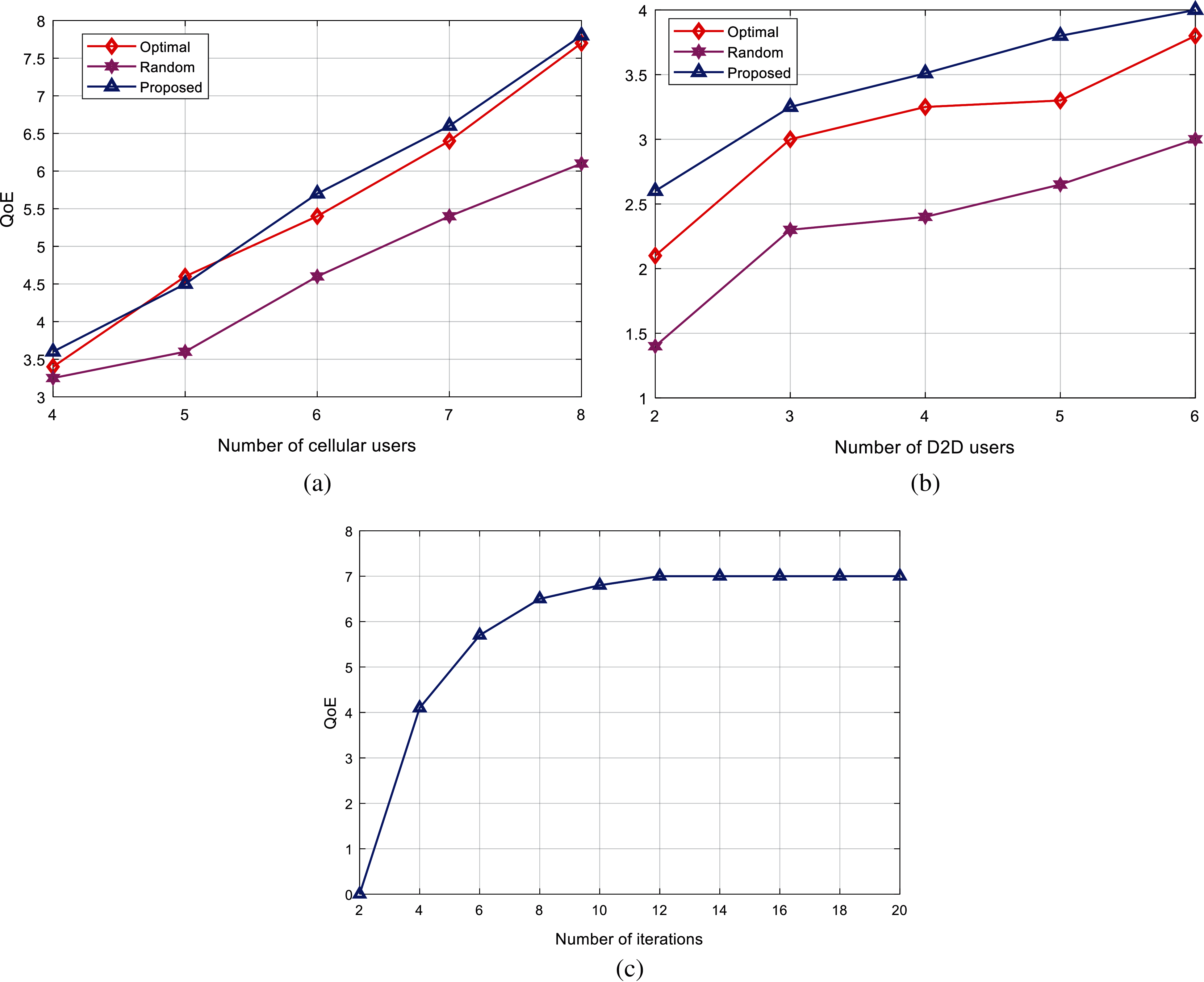
Figure 5: QoE performance comparison of the proposed and existing algorithms (a) Variation of QoE with CUs (b) Variation of QoE with D2D users (c) Variation of QoE with iterations

4.2 Convergence and Stability

The algorithm converges to a matching μ, which is a bilateral stable matching. In the double-layer game matching, if ∃[l,c], s.t. l≻c ∖O and c≻lμ(i), then the matching ends, indicating that the final matching result of the algorithm is stable. From Figs. 4a, 4b and 5c, it can be seen that the proposed algorithm has better convergence.

5  Conclusion

Based on the matching game theory and combined with the characteristics of the 5G environment, this paper proposes a QoE double-layer game matching algorithm, which divides the complex channel allocation problem into layers. First, the first layer of the cellular user channel allocation algorithm is established, and then the second layer of the D2D user channel allocation algorithm is established, thereby forming the entire algorithm to solve the problem of all user channel allocation. In this process, the fairness of users and the complex interference problems between users are fully considered, and the system optimization objective function, that is, the utility function, is improved. It is no longer a blind pursuit of high throughput. Instead, consider the quality of the user experience. The proposed algorithm is based on the matching game theory, so the matching result is bilaterally stable, and the algorithm is not centralized, but a distributed algorithm, which does not depend on the topological structure of the terminals and the system participating in the matching, and has good effect in terms of convergence and feasibility.

Acknowledgement: The author extends his appreciation to the Deanship of Scientific Research at King Khalid University for funding this work under Grant Number (RGP.2/25/42), Received by Fahd N. Al-Wesabi. https://www.kku.edu.sa.

Funding Statement: The corresponding author Byung Seo Kim is thankful to Hongik University for supporting this work.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  M. Waqas, Y. Niu, Y. Li, M. Ahmed, D. Jin et al., “A comprehensive survey on mobility-aware D2D communications: Principles, practice and challenges,” IEEE Communications Surveys & Tutorials, vol. 22, no. 3, pp. 1863–1886, 2020.

 2.  M. Ahmed, Y. Li, M. Waqas, M. Sheraz, D. Jin et al., “A survey on socially aware device-to-device communications,” IEEE Communications Surveys & Tutorials, vol. 20, no. 3, pp. 2169–2197, 2018.

 3.  F. S. Shaikh and R. Wismuller, “Routing in multi-hop cellular device-to-device (D2D) networks: A survey,” IEEE Communications Surveys & Tutorials, vol. 22, no. 3, pp. 2622–2657, 2018.

 4.  M. Haus, M. Waqas, A. Y. Ding, Y. Li, S. Tarkoma et al., “Security and privacy in device-to-device (D2D) communication: A review,” IEEE Communications Surveys & Tutorials, vol. 19, no. 2, pp. 1054–1079, 2017.

 5.  O. Hayat, R. Ngah, S. Z. M. Hashim, M. H. Dahri, R. F. Malik et al., “Device discovery in D2D communication: A survey,” IEEE Access, vol. 7, pp. 131114–131134, 2019.

 6.  A. Asadi, Q. Wang and V. Mancuso, “A survey on device-to-device communication in cellular networks,” IEEE Communications Surveys & Tutorials, vol. 16, no. 4, pp. 1801–1819, 2014.

 7.  B. M. Elhalawany, R. Ruby and K. Wu, “D2D communication for enabling internet-of-things: Outage probability,” IEEE Transactions on Vehicular Technology, vol. 68, no. 3, pp. 2332–2345, 2019.

 8.  I. Loannou, V. Vassiliou, C. Christophorou and A. Pitsillides, “Distributed artificial intelligence solution for D2D communication in 5G networks,” IEEE Systems Journal, vol. 14, no. 3, pp. 4232–4241, 2020.

 9.  P. Pawar, A. Trivedi and M. K. Mishra, “Outage and ASE analysis for power controlled D2D communication,” IEEE Systems Journal, vol. 14, no. 2, pp. 2269–2280, 2020.

10. F. Qamar, M. U. A. Siddiqui, M. H. D. Hinidia, R. Hassan and Q. N. Nguyen, “Issues, challenges, and research trends in spectrum management: A comprehensive overview and new vision for designing 6G networks,” Electronics, vol. 9, no. 9, pp. 1–124, 2019.

11. Y. R. B. Al-Mayouf, N. F. Abdullah, O. A. Mahdi, S. Khan, M. Ismail et al., “Real-time intersection-based segment aware routing algorithm for urban vehicular networks,” IEEE Transactions on Intelligent Transportation Systems, vol. 19, no. 7, pp. 2125–2141, 2018.

12. M. K. Hasan, M. M. Ahmad, A. H. A. Hashim, A. RAzzaque, S. Islam et al., “A novel artificial intelligence based timing synchronization scheme for smart grid applications,” Wireless Personal Communications, vol. 114, no. 2, pp. 1067–1087, 2019.

13. S. N. Makhadmeh, A. T. Khader, M. A. Al-Betar, S. Naim, A. K. Abasi et al., “A novel hybrid grey wolf optimizer with min-conflict algorithm for power scheduling problem in a smart home,” Swarm and Evolutionary Computation, vol. 60, no. 2, pp. 1–17, 2021.

14. N. Nurelmadina, M. K. Hasan, I. Memon, R. A. Saeed, K. A. Z. Ariffin et al., “A systematic review on cognitive radio in low power wide area network for industrial IoT applications,” Sustainability, vol. 13, no. 1, pp. 1–21, 2021.

15. S. Bashir, M. H. Alsharif, I. Khan, M. A. Albreem, A. Sali et al., “MIMO-Terahertz in 6G nano-communications: Channel modeling and analysis,” Computers, Materials & Continua, vol. 66, no. 1, pp. 263–274, 2020.

16. A. Amin, X. Liu, I. Khan, P. Uthansakul, M. Forsat et al., “A robust resource allocation scheme for device-to-device communications based on Q-learning,” Computers, Materials & Continua, vol. 65, no. 2, pp. 1487–1505, 2020.

17. S. Alemaishat, O. A. Saraereh, I. Khan, S. H. Affes, X. Li et al., “An efficient precoding scheme for millimeter-wave massive MIMO systems,” Electronics, vol. 8, no. 9, pp. 1–15, 2019.

18. A. Al-Nimrat, M. Smadi, O. A. Saraereh and I. Khan, “An efficient channel estimation scheme for mmwave massive MIMO systems,” in Proc. IEEE Int. Conf. on Communication, Networks and Satellite, Makassar, Indonesia, pp. 1–8, 2019.

19. I. Khan and D. Singh, “Efficient compressive sensing based sparse channel estimation for 5G massive MIMO systems,” AEU-International Journal of Electronics and Communications, vol. 89, no. 2, pp. 181–190, 2018.

20. A. Amin, X. H. Liu, M. A. Saleem, S. Henna, T. Islam et al., “Collaborative wireless power transfer in wireless rechargeable sensor networks,” Wireless Communications and Mobile Computing, vol. 9701531, pp. 1–13, 2020.

21. F. Jameel, T. Ristaniemi, I. Khan and B. M. Lee, “Simultaneous harvest-and-transmit ambient backscatter communications under Rayleigh fading,” EURASIP Journal on Wireless Communications and Networking, vol. 19, no. 1, pp. 1–9, 2019.

22. W. Shahjehan, S. Bashir, S. L. Mohammed, A. B. Fakhri, A. A. Isaiah et al., “Efficient modulation scheme for intermediate relay-aided IoT networks,” Applied Sciences, vol. 10, no. 6, pp. 1–12, 2020.

23. O. A. Saraereh, A. Alsaraira, I. Khan and B. J. Choi, “A hybrid energy harvesting design for on-body internet-of-things (IoT) networks,” Sensors, vol. 20, no. 2, pp. 1–14, 2020.

24. T. Jabeen, Z. Ali, W. U. Khan, F. Jameel, I. Khan et al., “Joint power allocation and link selection for multi-carrier buffer aided relay network,” Electronics, vol. 8, no. 6, pp. 1–15, 2019.

25. S. Alemaishat, O. A. Saraereh, I. Khan and B. J. Choi, “An efficient resource allocation algorithm for D2D communications based on noma,” IEEE Access, vol. 7, pp. 120238–120247, 2019.

26. L. Tan, Z. Zhu, F. Ge and N. Xiong, “Utility maximization resource allocation in wireless networks: Methods and algorithms,” IEEE Transactions on Systems, Man & Cybernetics Systems, vol. 45, no. 7, pp. 1018–1034, 2015.

27. Y. Li and D. Jin, “Coalitional games for resource allocation in the device-to-device uplink underlaying cellular networks,” IEEE Transactions on Communications, vol. 13, no. 7, pp. 3965–3977, 2014.

28. S. Zuo, I. H. Hou, T. Liu, A. Swami and P. Basu, “Joint rate control and scheduling for real-time wireless networks,” IEEE Transactions on Wireless Communications, vol. 16, no. 7, pp. 4562–4570, 2017.

29. Y. S. Liang, W. H. Chung, G. K. Ni, I. Y. Chen, H. Zhang et al., “Resource allocation with interference avoidance in OFDMA femtocell networks,” IEEE Transactions on Vehicular Technology, vol. 61, no. 5, pp. 2243–2255, 2012.

30. D. T. Ngo, S. Khakurel and T. L. Ngoc, “Joint subchannel assignment and power allocation for OFDMA femtocell networks,” IEEE Transactions on Wireless Communications, vol. 13, no. 1, pp. 342–355, 2014.

31. C. Wang, Y. Liu, M. Tao, Z. Han and D. I. Kim, “Stackelberg game for spectrum reuse in the two-tier LTE femtocell network,” in IEEE Wireless Communications and Networking Conf., Shanghai, China, pp. 1888–1892, 2013.

32. Y. Sun, J. Wang, F. Sung and J. Zhang, “Energy-aware joint user scheduling and power control for two-tier femtocell networks: A hierarchical game approach,” IEEE Systems Journal, vol. 12, no. 3, pp. 2533–2544, 2018.

33. Y. Sun, J. Wang, F. Sun and Z. Zhang, “Local altruistic coalition formation game for spectrum sharing and interference management in hyper-dense cloud-RANs,” IET Communications, vol. 10, no. 15, pp. 1914–1921, 2016.

34. S. Wen, X. Zhu, Z. Lin, X. Zhang and D. Yang, “Distributed resource management for device-to-device (D2D) communication underlay cellular networks,” in IEEE 24th Annual Int. Symp. on Personal, Indoor, and Mobile Radio Communications, London, UK, pp. 1624–1628, 2013.

35. J. Liu, N. Kato, J. Ma and N. Kadowaki, “Device-to-device communication in LTE-advanced networks: A survey,” IEEE Communications Surveys & Tutorials, vol. 17, no. 4, pp. 1923–1940, 2017.

36. Z. Zhou, M. Dong, K. Ota, R. Shi, Z. Liu et al., “Game-theoretic approach to energy-efficient resource allocation in device-to-device underlay communications,” IET Communications, vol. 9, no. 3, pp. 375–385, 2014.

37. D. Gale and L. S. Shapley, “College admission and the stability of marriage,” American Mathematical Monthly, vol. 120, no. 5, pp. 386–391, 2013.

38. Y. Gu, W. Saad, M. Bennis, M. Debbah and Z. Han, “Matching theory for future wireless networks: Fundamentals and applications,” IEEE Communications Magazine, vol. 53, no. 5, pp. 52–59, 2015.

39. A. M. Elhajj, Z. Dawy and W. Saad, “A stable matching game for joint uplink/downlink resource allocation in OFDMA wireless networks,” in IEEE Int. Conf. on Communications, Otlawa, Canada, pp. 5354–5359, 2012.

40. Z. Y. Zhou, G. Ma, M. Dong, K. Ota, C. Xu et al., “Iterative energy-efficient stable matching approach for context-aware resource allocation in D2D communications,” IEEE Access, vol. 4, pp. 6181–6196, 2016.

41. J. Zhao, Y. Liu, K. Chai, Y. Chen and M. Elkashlan, “Many-to-many matching with externalities for device-to-device communications,” IEEE Wireless Communications Letters, vol. 6, no. 1, pp. 3452–3458, 2016.

42. S. Kim, “Cognitive radio bandwidth sharing scheme based on the two-way matching game,” Wireless Personal Communications, vol. 68, no. 3, pp. 893–905, 2013.

43. B. Holfeld and E. Jorswieck, “On stable many-to-many matching for distributed medium access with reuse of spectral resources,” in Int. ITG Workshop on Smart Antennas, Munich, Germany, pp. 536–543, 2016.

44. Y. Gu, Y. Zhang and M. Pan, “Matching and cheating in device to device communication underlaying cellular networks,” IEEE Journal on Selected Areas in Communications, vol. 33, no. 10, pp. 2156–2166, 2015.

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.