Computers, Materials & Continua DOI:10.32604/cmc.2022.021657
Article

Estimating Fuel-Efficient Air Plane Trajectories Using Machine Learning

Jaiteg Singh1, Gaurav Goyal1, Farman Ali2, Babar Shah3 and Sangheon Pack4,*

1Chitkara University Institute of Engineering & Technology, Chitkara University, Punjab, 140401, India
2Department of Software, Sejong University, Seoul, 05006, Korea
3College of Technological Innovation, Zayed University, UAE
4School of Electrical Engineering, Korea University, Seoul, Korea
*Corresponding Author: Shangheon Pack. Email: shpack@korea.ac.kr
Received: 09 July 2021; Accepted: 23 August 2021

Abstract: Airline industry has witnessed a tremendous growth in the recent past. Percentage of people choosing air travel as first choice to commute is continuously increasing. Highly demanding and congested air routes are resulting in inadvertent delays, additional fuel consumption and high emission of greenhouse gases. Trajectory planning involves creation identification of cost-effective flight plans for optimal utilization of fuel and time. This situation warrants the need of an intelligent system for dynamic planning of optimized flight trajectories with least human intervention required. In this paper, an algorithm for dynamic planning of optimized flight trajectories has been proposed. The proposed algorithm divides the airspace into four dimensional cubes and calculate a dynamic score for each cube to cumulatively represent estimated weather, aerodynamic drag and air traffic within that virtual cube. There are several constraints like simultaneous flight separation rules, weather conditions like air temperature, pressure, humidity, wind speed and direction that pose a real challenge for calculating optimal flight trajectories. To validate the proposed methodology, a case analysis was undertaken within Indian airspace. The flight routes were simulated for four different air routes within Indian airspace. The experiment results observed a seven percent reduction in drag values on the predicted path, hence indicates reduction in carbon footprint and better fuel economy.

Keywords: Airplane trajectory; coefficient of drag; four-dimensional trajectory prediction; machine learning; route planning; stochastic processes

1  Introduction

Airline industry has witnessed a tremendous growth in the recent past. Percentage of people choosing air travel as first choice to commute is continuously increasing. This fact is supported by Deloitte’s recent report that states there is a 4.2 percent increase in global air traffic and passenger demand [1]. Technological enhancement and globalization are the apparent reasons for this unprecedented growth. With more passengers opting for air travel, airspace congestion has reached its peak. The air traffic control is managing a greater number of airplanes every hour than in past. Highly demanding and congested air routes are resulting in inadvertent delays, additional fuel consumption and high emission of greenhouse gases. Furthermore, congested airspaces have repercussions like passenger dissatisfaction, poor coordination amongst ground crew and disturbance in schedule of connected flights. Ever changing socio-political scenario further adds to existing challenges for air traffic scheduling and management. Tackling such challenges require long term planning by the international community. Optimization of flight trajectory planning paradigms may help deescalate contemporary problems of aerospace industry. Trajectory planning involves identification of cost-effective flight plans for optimal utilization of fuel and time. It is a scientific procedure, that considers a variety of parameters like regional and/or international air traffic, political air space, capacity of airports, weather data and aircraft performance to chart optimal flight path. These are the minimal parameters required to calculate and optimize any flight route [2]. Airlines do follow a set of standardized predefined routes and such routes are selected based on airline service network. As per existing practices, these calculations involve hours of human effort and still does not guarantee desired optimizations [3]. This situation warrants the need of an intelligent system for dynamic planning of optimized flight trajectories with least human intervention required. In this paper, an algorithm for dynamic planning of optimized flight trajectories has been proposed. The proposed algorithm divides the airspace into four dimensional cubes and calculate a dynamic score for each cube to cumulatively represent estimated weather, aerodynamic drag and air traffic within that virtual cube. This virtual cube comprises of four dimensions namely Latitude, Longitude, Altitude and Time (4D-T). An optimal flight path/ trajectory could be planned in reference to these four dimensions and is named four-dimensional trajectory planning (4D-TP). 4D-TP is a NP hard problem as it strives to optimize multiple objectives like minimal fuel consumption, minimal flight time and safety. There are several constraints like simultaneous flight separation rules, weather conditions like air temperature, pressure, humidity, wind speed and direction that pose a real challenge for calculating optimal 4D-TP. To predict an optimal 4D trajectory, future temporal position of an aircraft is to be estimated correctly [4]. Hence, there is a need of robust algorithms, which can take into consideration weather parameters, aerodynamic drag and air traffic to heuristically calculate optimal 4D-TP. Such heuristic calculations can also predict the estimated time of arrival (ETA) of any flight.

Rest of this manuscript is organized as follows, section two debriefs materials and methods, section three details problem statement, section four elaborates the adopted methodology and section five comprises of detailed case analysis. Section six concludes the study with a discussion on future scope of research.

2  Materials and Methods

Research publications related to airplane trajectory planning and optimization, which were published from year 2005 till 2019 were referred for designing methodology and experiment. Recently a calculation tool was proposed to plan accurate trajectory with respect to the one generated by on board flight management system. It was used to draw a logical conclusion for various cost index values affecting aircraft trajectory with given flight route and initial aircraft mass [5]. Trajectory optimization is an optimization problem, this was supported by a novel framework which investigated sustainable fixed wing aircraft trajectory mathematical optimization problem [6]. The impact of multicriteria optimized route trajectories recorded on air traffic flow management were analyzed and compared with a few validated scenarios. These validated scenarios had real trajectories during peak hours of Europe’s completer air traffic in the upper airspace [7]. An algorithm for optimization of global airplane traffic using stochastic techniques was also proposed. The algorithm was designed in a way that, the aircraft trajectory should avoid all threatful spaces, pass all waypoints, utilize all environments, minimize flight time or route distance, and satisfy all kinds of constraints [8]. A review focusing on Multi Objective Trajectory Optimization (MOTO) techniques deployable for aircraft flight operations was undertaken. The review typically focused upon recent advances introduced in the Communication, Navigation and Surveillance/Air Traffic Management (CNS/ATM) and Avionics (CNS+A) as research context. Later advancements of CNS+A included MOTO algorithm, which have a clear potential to enable real-time planning and re-planning. Re-planned routes are more environment friendly, more efficient and economically viable. These routes are optimal because, they addressed dynamic weather and air traffic conditions [9]. Random forest inspired machine learning techniques were also explored for enhanced aircraft ETA predictions. These experiments took into consideration generic information like flight, weather and air traffic for predicting trajectories. The results confirmed the possibility of enhancing ETA predictions by finetuning them using a model that studies statistical relationships between flight, air traffic and weather [10]. Further, methods were proposed to find out the nominal flight profile and revised airway meteorological forecasts. Dynamic space warping (DSW) algorithm was considered as an option to measure the distance between two flight altitude profiles. Meteorological forecast error from GRIdded Binary (GRIB) data, Cressman interpolation were referred to revise the original forecasts from GRIB data [11]. A trajectory planning function was later implemented and evaluated for trajectory prediction. This function is a critical component for tactical flight management. It introduced concepts, which increased resiliency and robustness of trajectory driven operations. This resulted in a paradigm shift which resulted in improved flight management system in close proximity with tactical operations [12]. Subsequent researchers worked on a stepwise regression model, which was trained using historic dataset. This historic dataset included information about type of aircraft, groundspeed of aircraft, altitude at the start of aerial route, surface wind and altitude winds etc., to make arrival time predictions [13]. A four-dimensional trajectory regression-based prediction model was proposed. This model made use of history and real-time radar data for predicting trajectory [14]. Later, accuracy of trajectory prediction was validated through comprehensive implementation for supporting validation methodologies. This implementation included parsing and checking of actual positional data of an aircraft, parsing trajectory predictions, comparison of actual and predicted aircraft trajectory through sampling and measuring, followed by analysis of results [15]. At an initial stage, algorithms for predicting take off aircraft trajectory were developed. These algorithms explored various configurations through a detailed model [16]. Intent based trajectory prediction (IBTP) algorithm that performs aircraft tracking, intent inference and trajectory prediction [17]. An error model based on linear error covariance analysis combined with linear control feedback explored the feasibility of curtailing uncertainty within trajectory predictions. This paper also discussed the development and implantation of the proposed model [18]. Pseudospectral integration scheme, built on Chebysev polynomial for optimization and control problem for 4D trajectories was also explored by researchers [19]. Newer studies are trying to optimize multiple problems like aircraft routing and crew pairing. Both of these factors have a high impact on operating costs of airlines. Later, the use of compact Integer Programming (IP) and Multiple Integer Programming (MIP) solvers was proposed to attain optimality. It was also used tried for crew pairing. Column generation pricing subproblem within a new resource constrained shortest path framework was also modelled [20]. Later, it was also suggested that to enable Air Traffic Controllers to control and supervise traffic with ease, flight traffic is carried out on set of predefined routes that have very low number of intersections. This has two significant consequences, firstly the ratio of used to unused airspace is low and not necessarily a shortest path is used for each flight. To eliminate this, the concept of free routing was proposed which enables an aircraft to use the direct connection between source and destination. It helped in generating a traffic distribution that enables use entire airspace optimally [20].

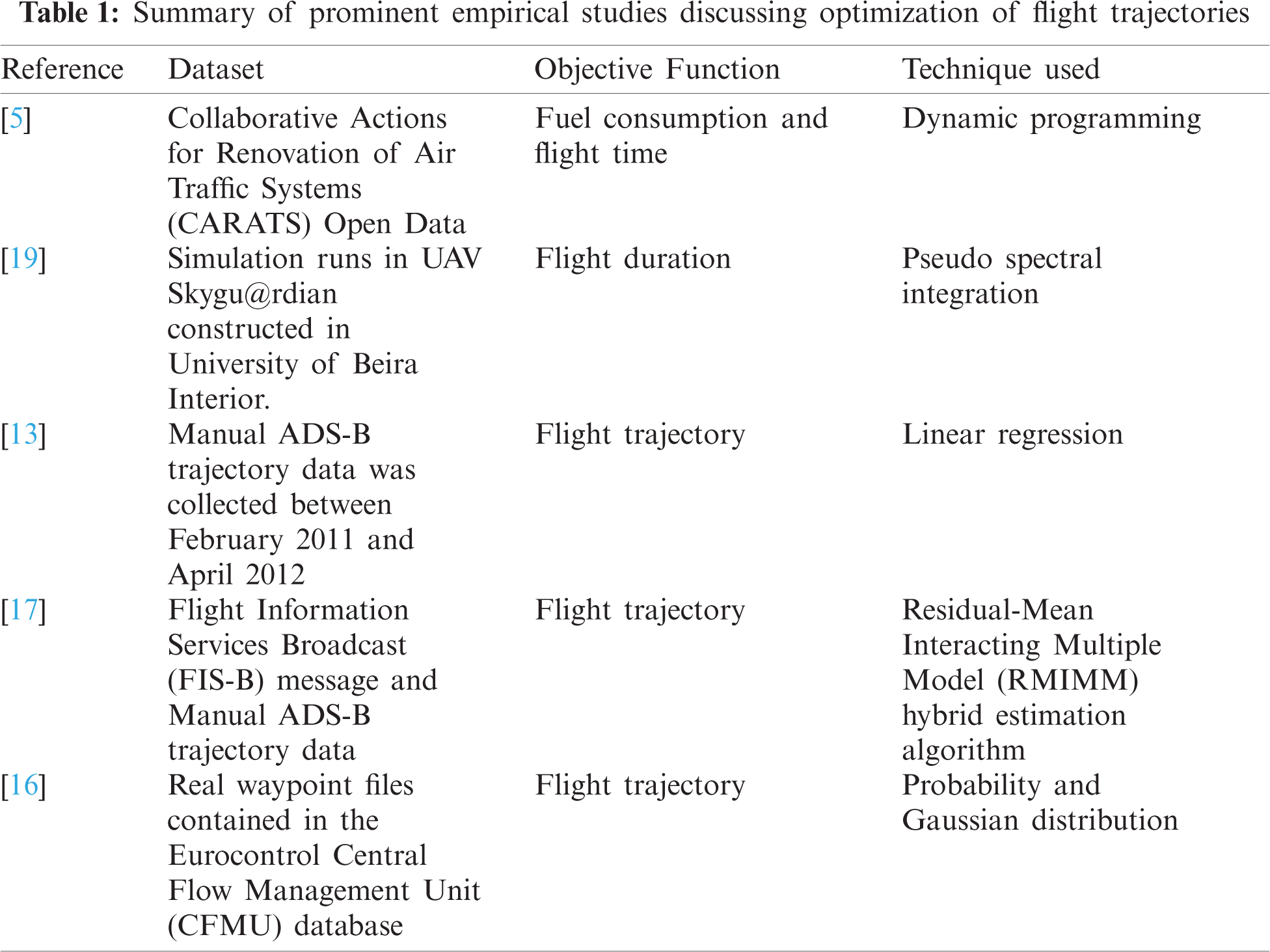
Few of the prominent empirical studies, which experimented with optimization of flight trajectories are summarized in Tab. 1.

Previous research has also touched upon “Flight retiming” methods which involves slightly modifying the scheduled departure time of flights. It intended to ensure better service at a lower cost. Mixed Integer Linear Programming model involving path variables, crew pairings, and arc variables representing the aircraft routes are used. Additionally, features like path/demands based on itinerary, variable flight times, schedule, recapture issues, and multiple class fare were also optimized using Linear Programming solution obtained within a column generation process [21]. Later, tail management was also included in flight scheduling. It involves assigning airplanes to flights as per given schedule. Researchers have worked upon an improved compact optimization model which involves a number of zero or one decision variables. Constrained polynomial in the problem size parameters were also used to minimize operational costs [22]. Fleet assignment, aircraft routing, and crew pairing are studied in the past as one combined problem. The objective function was aimed to minimize a weighted sum of the count of aircraft routes, pairings of crew members, and the waiting time consumed by crew within consecutive flights. Two mixed integer linear programming models were presented for the combined problem. The path-path model, uses path-based variables to describe both the aircraft routes and the crew pairings. The second model, called the arc-path model, is built on arc-based variables to describe the aircraft routes and path-based variables to represent the crew pairings [23]. Aircraft maintenance also has a huge role to play in the flight path optimization problems. The range and type of maintenance required, aircraft age, and utilization rates determines the demand for maintenance and it is different for every aircraft. Such considerations complicate the aircraft routing decisions. Researchers present a new approach that promises minimal maintenance and misalignment using an interactive mechanism connecting aircraft route planning and maintenance planning decisions [24]. Light propagation algorithm (LPA) based on wavefront propagation method that yields approximate geodesic solutions (minimal-in-time solutions) for the path planning to avoid air-traffic congestion was suggested by researchers [25].

From the literature reviewed, it was concluded that most of the published literature is restricted to optimization of fuel and flight time only. Further, optimized flight trajectories are predicted using one or at max two data sources of historical data. Most of the historical weather data comprises of windspeed and direction only. This traditional set of experimentation has virtually ignored many promising factors, which could potentially contribute towards safe trajectory planning like dynamic data generated by aircrafts and weather recording devices. Most studies have tried deploying Auto Regressive Integrated Moving Average (ARIMA) or Dynamic time wrapping time series approach for forecasting. Such techniques are found to be less accurate and have ample scope for refinement. Latest time series forecasting techniques like Long Short-term memory networks (LSTM) [26] have not been tried yet. Flight trajectory data is recorded using ADS-B [elaborate] devices present at ground stations. To facilitate mid-air decision support assistance for air traffic management, a dynamic four-dimensional trajectory prediction (4D-TP) method is proposed. The adopted methodology for experiment design and fundamental concepts associated with deployment of 4D-TP are detailed in the following sections.

3  Problem Formulation

Preparing a fuel, time & safety optimized flight plan requires an efficient division of airspace above us. This process is tricky because airspace is not uniform due to uncertain nature of multiple parameters like weather and air traffic etc. Hence it is of utmost importance to model the airspace into smaller sections with each section representing its state (Weather, Aerodynamic Drag & Traffic). As per the existing literature, state of art systems represents the airspace as three-dimensional cubes of fixed length, breadth & height. A novel technique of representing the airspace as Three-Dimensional Dynamic cubes (3DD), as shown in Fig. 6 has been introduced in this manuscript. This 3DD layout will establish a base for effective 4D-TP. 4D-TP requires a real time multidimensional coverage of the airspace conditions to be provided by 3DD cubes. These conditions include weather parameters, air traffic & aerodynamic drag etc. Every 3DD cube will have a representation vector, which would provide information about weather, traffic & aerodynamic drag within it. Flight planning requires us to forecast values of these parameters with respect to some constraints as given below:

3.1 Flight Dynamics

An aircraft needs to follow an Aircraft Dynamic Model (ADM). ADM enlists three degrees of freedom point mass model (PMM) with variable mass. PMM represents all the intricacies of an aircraft movement as shown in Eqs. (1)–(6).

La=VTAS∗sin⁡χcos⁡γ+w1 (1)

Lo=VTAS∗cos⁡χcos⁡γ+w2 (2)

h=VTAS∗sin⁡γ (3)

VTAS=Th−D/m−g sin⁡γ (4)

X=gtan⁡φ/VTAS (5)

m=η∗Th  (6)

where La, Lo, h, VTAS, Y, X, φ, m, w1, w2, D, Th, h, and g are Geodetic latitude, Geodetic longitude, Altitude, True Airspeed, Flight path angle, Heading angle, Bank angle, Mass of aircraft, East treading winds, North treading winds, Aerodynamic drag, Thrust, Thrust specific fuel consumption parameter and gravity respectively.

3.2 Path Constraints

A flight needs to conform to certain path constraints which arise due to military procedures and other socio-political constraints. There are specific no-fly zones declared globally. Such zones act as deterrent in fixing the optimal path. This deterrence is considered as a constraint in 4D-TP planning.

3.3 Flight Data Sources

Calculating the optimal 4D-TP require temporal flight trajectory data, flight plan data and weather data as inputs. Such data has been curated from following sources:

a) Automatic dependent surveillance-broadcast (ADSB) is the most prominent method for tracing flight trajectory of an aircraft. This surveillance technology broadcasts aircraft identification, technical and position information to nearby aircrafts and ground stations [27]. The data sources used for obtaining the flight trajectories are FlightRadar24 [28] & FlightAware [29]. Both use crowdsourced ADSB devices placed all over the globe to collect flight trajectory data. Flightradar24 is a global service for flight tracking and broadcasts real-time information about thousands of aircrafts flying across the world. Flightradar24 tracks 180,000+ flights, from 1,200+ airlines, flying to or from 4,000+ airports around the world in real time.

b) FlightAware is a digital aviation company and manages the world’s largest flight tracking data platform. It has global connectivity to every segment of aviation. FlightAware serves over 10,000 aircraft operators, service providers and more than 13,000,000 passengers with global flight tracking solutions. It also offers predictive technology, analytics, and decision-making tools. Flight trajectories from Delhi–Mumbai within Indian subcontinent and recorded using FlightRadar24 and FlightAware are shown in Fig. 1.

Figure 1: Different paths attained by New Delhi–Mumbai flight

3.4 Weather Data

The weather could be defined as an atmospheric condition, with respect to hot or cold, wet or dry, calm or stormy, clear or cloudy at any time. There are multiple agencies, which record and promulgate weather information. To enhance precision of anticipated 4D-TP, it is preferred to consider the weather data from multiple sources. Weather data from following agencies was considered while calculating optimal flight trajectories.

a) India Meteorological Department (IMD) is a subsidiary of the Ministry of Earth Sciences of the Government of India. It is primarily responsible for meteorological observations, weather forecasting and seismology.

b) MetGIS portal promulgates ultra-precise forecasts through a fusion of exact weather models and terrain data. MetGIS forecasts are considered the best in the world and provides a resolution of up to 30 m.

c) OpenWeather is a small IT company, established in 2014 by a group of engineers and experts in Big Data, data processing, and satellite imagery processing. Its headquarters is in the UK, has office in the US, and a development team in Latvia (EU).

d) METAR is maintained by Aviation Weather center and delivers consistent, timely and accurate weather information for the world airspace system.

e) World Weather Information Service (WWIS) is a centralized source on the Internet to access official weather information released by National Meteorological and Hydrological Services (NMHSs). The WWIS website is developed and maintained by the Hong Kong Observatory (HKO) of Hong Kong, China.

f) Weather web is maintained by University of Wyoming to provide precise and reliable weather information.

4  Methodology

The experiment methodology uses radar recordings, flight plan data and weather data as inputs. Input data is pre-processed to weed out potential outliers and discrepancies. Cleansed data is further added to a multidimensional database. Incoming live DataStream from aircraft is processed along with multidimensional database using machine learning techniques for predicting optimal 4D-TP and airline procedures. Fundamental experiment method is depicted in Fig. 2.

Figure 2: Proposed methodology for calculating 4D-TP

Flight tracking websites (FLightRadar24 & FlightAware) use crowdsourced ADS-B devices to track the position of an aircraft. ADS-B are special hardware located at various geographical locations that receive flight tracking info from transponders in aircraft. These devices are limited in number and hence we might not get complete tracking data of a flight. Furthermore, the frequency at which these devices send/receive data is low which makes tracking of airplanes prone to errors. The proposed method calculates 4D-TP based on recorded reference radar, weather and flight plan data. Researchers have prominently used time series techniques like ARIMA, for time series-based forecasting. The proposed 4D-TP technique made use of LSTM [30] for anticipating weather and traffic conditions [31,32]. A typical LSTM calculation logic is given in Fig. 3.

Figure 3: Structure of proposed LSTM to calculate optimized 4D-TP

Weather information pertaining to cloud cover, anticipated thunderstorms and precipitation probability are jointly processed as cumulative weather index. Further, inclusion of aerodynamic drag along with weather and time series data, make this experiment unique amongst available literature. Aerodynamic drag can be defined as the resistance offered by the air in opposite direction to the movement of the aircraft. Each aircraft has its own coefficient of drag which helps in estimating the drag value. During data analysis of 126 Delhi–Bengaluru Flights flown between June 2018–August 2019 from, it was observed that different air routes offer different drags as shown in Fig. 4.

Figure 4: Different aerodynamic drag on different air routes between New Delhi–Bengaluru flights

The procedure to calculate aerodynamic drag and cumulative traffic index is given as under:

a) Coefficient of Drag: CD

Config: Aircraft either in take-off, climb, cruise, approach or landing phase.

Lift coefficient: CL

CL=2*m*g*cosγVTAS2*cos∅*S (7)

CD=CD0,config+CD2,config*CL2 (8)

Density: δ

Surface area: S

Cumulative Aerodynamic Drag Index=12∗CD∗δ*S* VTAS2

To better access the drag conditions we have divided values of drags into different levels of favorability [32].

Least Favorable: >60000

Average/Moderately Favorable: ≤60000 and >20000

Highly Favorable: ≤20000

b) Cumulative Traffic Index: During experiment design, the air traffic was modelled into following subcategories:

i Airport Congestion

Scheduled arrivals: Sa

Scheduled departures: Sd

Average actual departures: AvgD

Average Actual Arrivals: AvgA

Flight no: fn

Airport congestion rate = (Sa + Sd)/ (AvgD + AvgA)

ii Sector Congestion

Sector size: S

Scheduled flights at time t in sector s: Ss

Total time take to cross S: t

Sector congestion rate: Ss/t

Once cumulative traffic index and coefficient of drag have been calculated for all the data points, a scoring mechanism would suggest an optimal 4D-TP as shown in Fig. 5.

Figure 5: LSTM memory network driven scoring mechanism to suggest optimal air trajectory

Score of one 3DD cube=α(Cumulative weather index)+β(Cumulative Drag Index)+γ(Cumulative Traffic Index) (9)

5  Case Analysis

To validate the proposed methodology, a case analysis was undertaken within Indian airspace. Following are the dimensions included during case analysis. Route information is shown in Tab. 2 and 3DD division of Indian airspace is shown in Fig. 6:

Airspace Considered: India

Area Covered: North to South – 4000 km, East to West 4000 km

Vertical height: 100 ft–50000 ft which is approximately 16 km

Total volume of airspace considered: 4000 * 4000 * 16 = 256,000,000 km3

3D cube size: 2 km * 2 km * 2 km

Total Cubes: 32,000,000

Weather data: Weather timeline between June 2016–September 2019 was considered to forecast weather conditions.

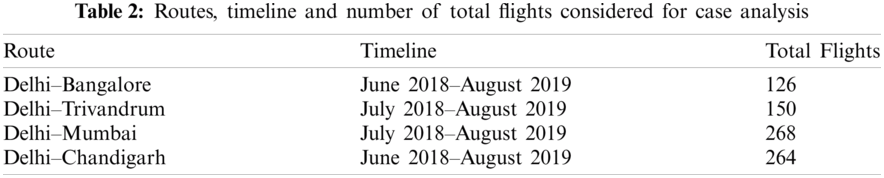
Figure 6: 3DD division of 256,000,000 km3 volume of Indian airspace

6  Results

The result section is divided into two subsections. First part entails the results for forecasting accuracy on weather & traffic data. While the second one entails the validity of airspace division by proving lower drag offering on new routes. The performance of aircraft was calculated based upon fuel consumed which was further calculated using Thrust produced by the engine which was further calculated by Drag indicted on the aircraft by the path followed. While there exists a direct proportionality between Fuel Consumed & Thrust produced by an engine. Thrust & Drag relation is given below.

(Thr−D)∗VTAS=dhdt∗mg0+dVTASdt∗VTAS∗m (10)

where Thr, D, VTAS, h, g0, dVTAS, d/dt are thrust acting parallel to the aircraft velocity vector, Aerodynamic Drag, Aircraft Mass, Geodectic Altitude, Gravitational Acceleration, True Airspeed and Time Derivative respectively.

6.1 Forecasting Accuracy

From the weather timeline of June 2016–September 2019, we have considered June 2016–April 2019 as training information for our LSTM and June 2019– September 2019 as our test data. We used one day ahead method to forecast the weather conditions. Mean Absolute Error (MAE) is used to estimate the accuracy of our LSTM.

MAE=1n∑i=1n|xi−x| (11)

where n, ∑ and |xi−x| are the number of errors, summation and the absolute errors respectively.

Fig. 7 represents the actual vs. predicted temperature values for Latitude = 28.571297, Longitude = 77.067101 & Altitude = 4275 ft for 15th June 2019 (8 AM–10 AM) a total of 200 values (1 value per minute is represented).

Figure 7: Actual vs predicted temperature values for any given latitude, longitude and altitude

To calculate the effectiveness of the airspace division & scoring we simulated past flights on two different routes. First was the actual route followed by aircraft in the past and second route was through new divided airspace.

6.2 Thrust Drag Relation

We can use the cumulative drag index value from above equations to calculate Thrust which would provide us an estimated value of Fuel consumed. Fig. 8 below represents the change in air density value for a Delhi–Mumbai Flight on 13 June 2018 (Time 17:20:37–19:05:34 & distance Covered: 1133 km). Fig. 9 represents the change in temperature, pressure & humidity values for a 3D cube at Latitude = 28.571297, Longitude = 77.067101 & Altitude = 4275 ft on 3rd March 2018. Drag offered on Simulated Route for a Delhi–Mumbai Flight on 13th June 2018 (Time 17:20:37–19:05:34 & distance Covered: 1133 km) is shown in Fig. 10.

Figure 8: Actual vs predicted temperature values for any given latitude, longitude and altitude

Figure 9: Recorded variations in temperature, pressure and humidity values for a 3D cube at given latitude, longitude and altitude

Figure 10: Calculated drag values for actual and simulated route for Delhi–Mumbai flight

There was approximately seven percent less drag recorded on the simulated route against the actual route for this Delhi–Mumbai sample flight. The experiment was repeated on Delhi–Bengaluru, Delhi–Trivandrum, Delhi–Chandigarh routes were calculated and are shown in Tab. 3.

7  Conclusions and Future Scope

The study concludes the fact that LSTM offers higher accuracy in forecasting weather conditions like temperature, pressure and humidity etc. Further, a direct association was observed between weather conditions, aerodynamic drag, air traffic congestion and economies of scale associated with an air route. Division of airspace in three dimensional cubes may help better prediction of environmental variables for optimal route planning and minimal drag values. Division of airspace also gives better control over entire airspace for flight path planning as it eventually helps in reducing drag values. As coefficient of drag is inversely proportionate to fuel consumption, hence planning a flightpath with minimal drag values would result in higher fuel savings. The experiment results observed a seven percent reduction in drag values on the predicted path, hence indicates reduction in carbon footprint and better fuel economy. This experiment was restricted to national flights only. For international flights, calculation of drag coefficient would be a real challenge as there is little or no data available for any flight flying from over the oceans. Generative adversarial networks could be used to generate missing trajectories over the oceans to evaluate the performance of 4D-TP for longer duration international flights. The future scope of this work lies with prediction of aircraft flight trajectories over the oceans and calculating coefficient of drag on such routes for better route planning and fuel economies. This work can further be extended to predict trajectories with minimal risk of avoid midair collisions using image segmentation techniques [33]. The proposed technique can be deployed to deal with extreme weather like uncertain winds, thunderstorms or other uncertain convective environments. Furthermore, it could help in planning of safe flight trajectories in case of loss of thrust emergencies.

Author Contributions: Jaiteg Singh and Farman Ali were primarily involved in conceptualization, methodology, experiment design, result analysis and drafting the manuscript Gaurav Goyal developed code, executed experiment, performed testing, editing and contributed in interpretation of results. Sangheon Pack reviewed the experiment and arranged funds. Baber Shah helped in proofreading.

Funding Statement: This work was supported by the MSIT (Ministry of Science & ICT), Korea, under the ITRC support program (IITP-2021-2017-0-01633). This research work was also supported by the Research Incentive Grant R20129 of Zayed University, UAE.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  R. Lineberger, “Global aerospace and defense industry outlook,” Deloitte, vol. 2019, pp. 12, 2019. [Google Scholar]

 2.  S. Wang, X. Cao, H. Li, Q. Li, X. Hang et al., “Air route network optimization in fragmented airspace based on cellular automata,” Chinese Journal of Aeronautics, vol. 30, no. 3, pp. 1184–1195, 2017. [Google Scholar]

 3.  M. Hrastovec and F. Solina, “Prediction of aircraft performances based on data collected by air traffic control centers,” Transportation Research Part C: Emerging Technologies, vol. 73, no. 2, pp. 167–182, 2016. [Google Scholar]

 4.  X. Zhang, X. Guan, Y. Zhu and J. Lei, “Strategic flight assignment approach based on multi-objective parallel evolution algorithm with dynamic migration interval,” Chinese Journal of Aeronautics, vol. 28, no. 2, pp. 556–563, 2015. [Google Scholar]

 5.  A. Harada, N. Takeichi and K. Oka, “An optimal trajectory-based trajectory prediction method for automated traffic flow management,” American Institute of Aeronautics and Astronautics Science and Technology 2019 Forum, pp. 1360–1373, 2019. [Google Scholar]

 6.  A. W. A. Hammad, D. Rey, A. Bu-Qammaz, H. Grzybowska and A. Akbarnezhad, “Mathematical optimization in enhancing the sustainability of aircraft trajectory: A review,” International Journal of Sustainable Transportation, vol. 14, no. 6, pp. 1–24, 2019. [Google Scholar]

 7.  J. Rosenow, H. Fricke, T. Luchkova and M. Schultz, “Impact of optimised trajectories on air traffic flow management,” Aeronautical Journal, vol. 123, no. 1260, pp. 157–173, 2019. [Google Scholar]

 8.  Y. Yang, Y. Nan and H. Chen, “Trajectory optimization in stochastic environment based on original natural computation,” in Proc. of 30th Chinese Control Decision Conf. CCDC, Shenyang, China, pp. 6027–6031, 2018. [Google Scholar]

 9.  A. Gardi, R. Sabatini and S. Ramasamy, “Multi-objective optimisation of aircraft flight trajectories in the ATM and avionics context,” Progress in Aerospace Sciences, vol. 83, no. 5, pp. 1–36, 2016. [Google Scholar]

10. C. S. Kern, I. P. De Medeiros and T. Yoneyama, “Data-driven aircraft estimated time of arrival prediction,” in 9th Annual IEEE Int. Systems Conf., SysCon 2015—Proc., Vancouver, BC, Canada, pp. 727–733, 2015. [Google Scholar]

11. X. Tang, P. Chen and Y. Zhang, “4D trajectory estimation based on nominal flight profile extraction and airway meteorological forecast revision,” Aerospace Science and Technology, vol. 45, pp. 387–397, 2015. [Google Scholar]

12. J. Kaneshige, J. Benavides, S. Sharma, L. Martin, R. Panda et al., “Implementation of a trajectory prediction function for trajectory based operations,” in American Institute of Aeronautics and Astronautics Atmospheric Flight Mechanics Conf., Atlanta, GA, pp. 1–14, 2014. [Google Scholar]

13. A. D. Leege, M. V. Paassen and M. Mulder, “A machine learning approach to trajectory prediction,” in American Institute of Aeronautics and Astronautics Guidance, Navigation, and Control (GNC) Conf., Boston, MA, pp. 4782–4794, 2013. [Google Scholar]

14. W. Kun and P. Wei, “A 4-D trajectory prediction model based on radar data,” in Proc. of 27th Chinese Control Conf. CCC, Kunming, China, pp. 591–594, 2008. [Google Scholar]

15. M. M. Paglione and R. D. Oaks, “Implementation and metrics for a trajectory prediction validation methodology,” in American Institute of Aeronautics and Astronautics Guidance, Navigation and Control Conf. 2007, Hilton Head, South Carolina, pp. 1912–1929, 2007. [Google Scholar]

16. I. Lymperopoulos, J. Lygeros and A. Lecchini, “Model based aircraft trajectory prediction during takeoff,” in American Institute of Aeronautics and Astronautics Guidance, Navigation, and Control Conf. 2006, Keystone, Colorado, pp. 6098–6109, 2006. [Google Scholar]

17. J. L. Yepes, I. Hwang and M. Rotea, “An intent based trajectory prediction algorithm for air traffic control,” in American Institute of Aeronautics and Astronautics Guidance, Navigation, and Control Conf., San Francisco, California, pp. 5824–5841, 2005. [Google Scholar]

18. J. L. Yepes, I. Hwang and M. Rotea, “New algorithms for aircraft intent inference and trajectory prediction,” Journal of Guidance, Control, and Dynamics, vol. 30, no. 2, pp. 370–382, 2007. [Google Scholar]

19. K. Bousson and P. Machado, “4D Flight trajectory optimization based on pseudospectral methods,” World Academy of Science Engineering and Technology, vol. 70, pp. 551–557, 2010. [Google Scholar]

20. A. Parmentier and F. Meunier, “Aircraft routing and crew pairing: Updated algorithms at Air France,” Omega, vol. 93, no. 1, pp. 102073–102108, 2020. [Google Scholar]

21. I. Gerdes, A. Temme and M. Schultz, “From free-route air traffic to an adapted dynamic main-flow system,” Transportation Research Part C: Emerging Technologies, vol. 115, no. 4, pp. 102633–102658, 2020. [Google Scholar]

22. V. Cacchiani and J. J. Salazar-González, “Heuristic approaches for flight retiming in an integrated airline scheduling problem of a regional carrier,” Omega, vol. 91, no. 2, pp. 102028–102045, 2020. [Google Scholar]

23. O. Khaled, M. Minoux, V. Mousseau, S. Michel and X. Ceugniet, “A compact optimization model for the tail assignment problem,” European Journal of Operational Research, vol. 264, no. 2, pp. 548–557, 2018. [Google Scholar]

24. V. Cacchiani and J. J. Salazar-González, “Optimal solutions to a real-world integrated airline scheduling problem,” Transportation Science, vol. 51, no. 1, pp. 250–268, 2017. [Google Scholar]

25. N. Safaei and A. K. S. Jardine, “Aircraft routing with generalized maintenance constraints,” Omega, vol. 80, no. 1, pp. 111–122, 2018. [Google Scholar]

26. N. Dougui, D. Delahaye, S. Puechmorel and M. Mongeau, “A light-propagation model for aircraft trajectory planning,” Journal of Global Optimization, vol. 56, no. 3, pp. 873–895, 2013. [Google Scholar]

27. de Santos Júnior D. S. O., de Oliveira J. F. L. and de Mattos Neto P. S. G., “An intelligent hybridization of ARIMA with machine learning models for time series forecasting,” Knowledge-Based Systems, vol. 175, no. 1, pp. 72–86, 2019. [Google Scholar]

28. S. Farouq, “Investigating discourse markers in the annexes of the International Civil Aviation Organization,” Southern African Linguistics and Applied Language Studies, vol. 37, no. 1, pp. 77–90, 2019. [Google Scholar]

29. A. Aljubairy, W. E. Zhang, A. Shemshadi, A. Mahmood and Q. Z. Sheng, “A system for effectively predicting flight delays based on IoT data,” Computing, vol. 102, no. 9, pp. 2025–2048, 2020. [Google Scholar]

30. S. B. Panuntun and S. Pramana, “Development of automated flight data collection system for air transportation statistics,” Journal of Physics: Conference Series, vol. 1863, no. 1, pp. 012020–012030, 2021. [Google Scholar]

31. S. Hochreiter, “Long short-term memory,” Neural Computation, vol. 1780, no. 8, pp. 1735–1780, 1997. [Google Scholar]

32. S. Balachander, K. Liu and M. Lakhote, “Self-induced velocity correction for improved drag estimation in Euler-Lagrange point-particle simulations,” Journal of Computational Physics, vol. 376, no. 1, pp. 160–185, 2019. [Google Scholar]

33. R. A. Naqvi, D. Hussain and W. Loh, “Artificial intelligence-based semantic segmentation of ocular regions for biometrics and healthcare applications,” Computers Materials & Continua, vol. 66, no. 1, pp. 715–732, 2021. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.