DOI:10.32604/cmc.2022.021483

| Computers, Materials & Continua DOI:10.32604/cmc.2022.021483 |  |
| Article |
Improved Software Implementation for Montgomery Elliptic Curve Cryptosystem
Computer Science Department, College of Computer and Information Sciences, Imam Mohammad Ibn Saud Islamic University (IMSIU), Riyadh, Saudi Arabia
*Corresponding Author: Mohammad Al-Khatib. Email: mohkhatib83@gmail.com
Received: 03 July 2021; Accepted: 04 August 2021
Abstract: The last decade witnessed rapid increase in multimedia and other applications that require transmitting and protecting huge amount of data streams simultaneously. For such applications, a high-performance cryptosystem is compulsory to provide necessary security services. Elliptic curve cryptosystem (ECC) has been introduced as a considerable option. However, the usual sequential implementation of ECC and the standard elliptic curve (EC) form cannot achieve required performance level. Moreover, the widely used Hardware implementation of ECC is costly option and may be not affordable. This research aims to develop a high-performance parallel software implementation for ECC. To achieve this, many experiments were performed to examine several factors affecting ECC performance including the projective coordinates, the scalar multiplication algorithm, the elliptic curve (EC) form, and the parallel implementation. The ECC performance was analyzed using the different factors to tune-up them and select the best choices to increase the speed of the cryptosystem. Experimental results illustrated that parallel Montgomery ECC implementation using homogenous projection achieves the highest performance level, since it scored the shortest time delay for ECC computations. In addition, results showed that NAF algorithm consumes less time to perform encryption and scalar multiplication operations in comparison with Montgomery ladder and binary methods. Java multi-threading technique was adopted to implement ECC computations in parallel. The proposed multithreaded Montgomery ECC implementation significantly improves the performance level compared to previously presented parallel and sequential implementations.
Keywords: Elliptic curve cryptosystem; parallel software implementation; multi-threading; scalar multiplication algorithms; modular arithmetic
Elliptic Curve cryptosystem (ECC) is a next-generation approach to public key cryptosystems that uses relatively small keys to provide the same or greater level of security compared to the other public-key cryptosystems [1]. The use of smaller key sizes led to a considerable improvement on the speed of the cryptosystem [2]. Therefore, ECC received increasing interest in last decade, especially for security applications that demand high-performance cryptosystem, such as multimedia and military applications. Recently, the dramatic increase in the amount of data being processed by those applications, and the need to provide higher security levels make it compulsory to improve the performance of ECC to satisfy these requirements.
The performance of ECC is affected by the choices of implementation environment; software and hardware implementations, and the domain parameters such as field representation, Elliptic curve (EC) form, algorithm for scalar multiplication, and the coordinates system. Every one of the aforementioned parameters plays important role in the ECC performance [3].
The current research investigates the ECC performance using the different parameters, and selects the best possible parameters’ choices and scalar multiplication algorithms to optimize the cryptosystem's performance. This study considers software implementation of ECC since it is cost-effective and consumes less resources in comparison with hardware implementation. The rest of this article is organized as follows: Section 2 mathematical background, Section 3 related works, Section 4 proposed cryptosystem design, Section 5 results and discussion, and finally the conclusion in Section 6.
ECC is a type of public key cryptography that depends on the discrete logarithm problem for EC. ECC has two levels of computations; upper and lower levels of computations. The main operation in the upper level is the scalar multiplication, which consists of two operations; point doubling and point addition (called point operations). The lower level, on the other hand, includes finite field (called Galois field GF) computations, which are modular addition, subtraction, multiplication, and division operations. The latter is the most time consuming operation because it requires finding the multiplicative inverse [4].
The scalar multiplication algorithm performs either one or both of point operations in each iteration. The point addition operation adds two different points G and Q on the EC to obtain another EC point R. The point addition can be calculated via computing the coordinates (x3, y3) of the resulting point, as follows:
G(
Alternatively, the point doubling operation adds the point to itself (Q = G) and can be calculated as follows:
It worth mentioning that the EC form does not affect the point addition calculations, hence it relies only on the two points on the curve. On the contrary, point doubling calculation changes according to the EC form and the use of coordinate systems, since it requires to derive the slope equation from the elliptic curve equation.
There are two common types of finite fields in which ECC computations are applied; the prime field GF(P) and the binary field GF(
Several elliptic curve forms over GF(P) were presented previously. Among the most important forms is the Montgomery curve since it has less computational complexity, which makes it appropriate for security applications that need high speed ECC.
The Montgomery curve equation is defined as follows: E:
To find all points on the Montgomery curve over GF(P), substitute the value of x = 0, 1,…P in the Montgomery curve equation then take the square roots to find the value of y. The EC is distinguished from other curves since it is symmetric about the x-axis; every point on the elliptic curve has a mirrored point on the other side of the x-axis. For any non-vertical line drawn through the elliptic curve, it will intersect exactly at three points. The EC has a point Ɵ called point at infinity [5].
Points on a curve can be represented using different types of coordinates systems. The standard coordinates is affine coordinates P(x, y). Alternatively, the use of projective coordinates introduced to improve the performance of elliptic curve computations due to its ability to avoid the time-consuming inversion operation. In projective coordinates a point
The main operation in ECC encryption is the scalar multiplication, which is usually used to judge the cryptosystem performance. Three main algorithms were used to perform scalar multiplication, which are the Montgomery ladder, NAF, and Binary left to right (LTR). The scalar multiplication algorithms vary in terms of speed and security levels [7]. Their characteristics will be studied in this research to determine the most efficient algorithm for developing high-speed ECC.
There has been an intense amount of researches done in the field of ECC since it was introduced in 1985. The majority of previous studies investigated possible factors to improve ECC performance such as the use of certain EC form, the use of projective coordinates, the parallel and concurrent execution of elliptic curve computations, and the use of efficient scalar multiplication algorithms. Again, all these factors affect the ECC performance and should be considered when designing high-speed cryptosystem. Other research works focused on safeguarding ECC against certain types of attacks such as simple time attack (STA). This section surveys the most important research works that studied the possible improvements on the performance and security of ECC.
EC point operations (point doubling (ECDBL) and point addition (ECADD)) include the time expensive modular Inversion when using affine coordinates. Many researchers proposed using projective coordinates systems to eliminate the modular Inversion [8]. The studies presented in [9,10] proposed several parallel hardware designs for ECC point addition and point doubling respectively using the standard EC over GF(P). Both studies investigated the use of three known projective coordinates to eliminate the modular inversion operation. Researchers also used parallel hardware implementation to utilize the inherent parallelism in ECC computations and hence improve the speed of ECC encryption. Authors of [11] proposed parallel data flows for EC computations over GF(P) using several projective coordinates. The mathematical equations of Montgomery curve point operations were developed and then transformed into the best parallel data flow that exploits the maximum parallelism degree. It has been suggested by this study that Montgomery curve represents efficient choice for developing a high-speed EC crypto-processor. It achieved better performance results compared to the standard EC form.
There is a plenty of studies that examined the hardware implementation of ECC forms. Some of them used sequential implementation [12,13], where others investigated potential enhancements that could be obtained using parallel hardware implementations [14–16].
However, the major disadvantage of hardware implementations is that they require a dedicated crypto-processor and hardware components, entailing significant increase in the cost of designing and implementing the cryptosystem. This makes hardware implementation of ECC not affordable and complicated choice for many security applications, especially those applications with limited resources. Software implementations for ECC, on the other hand, have low development costs, easy to upgrade, and more flexible [17]. In addition, the majority of previous studies examined the cryptosystem performance with only one scalar multiplication algorithm. This research uses the software approach instead of hardware implementation, and investigates the cryptosystem performance with three different and efficient scalar multiplication algorithms. Both sequential and parallel software implementations will be studied in this research.
Authors of [18,19] surveyed the scalar multiplication algorithms that are common in EC cryptography field. These algorithms were compared in terms of the execution time, the hamming weight of the scalar k, the number of doubling operations, and the required precomputations. Both studies stated that the addition and subtraction algorithm is more efficient than the binary scalar algorithm because it uses signed binary representation of the scalar called Non Adjacent Form (NAF), which is proven to have less hamming weight. The window method is suitable for less constrained memory since it uses a table of pre-computed points. Another study [20] conducted a performance analysis on five different scalar multiplication algorithms using the Weierstrass curve over the two finite fields. The study stated that the NAF Algorithm was shown to have the least execution time GF(P) compared to other algorithms. Moreover, the results confirmed that the prime field is more efficient for software implementations; the scalar multiplication over the prime field is faster than the binary field.
In [21], researchers conducted a performance analysis on Java implementations of EC operations over both standard finite fields. The study suggested that the java BigInteger class is more efficient for the software implementations of EC operations in the prime field more than the binary field. The research work published in [22] presented a description for the software implementation of ElGamal ECC over GF(P). In addition, the study provided detailed description about the main steps of ElGamal ECC. The author used the general Weierstrass EC equation, and the affine coordinates for point representation, in addition to the NAF algorithm to perform the scalar multiplication. Authors in [23] proposed a new ECC that eliminates the need for the mapping operation that has been used in previous studies, which contributes in increasing the speed of the encryption process. This was achieved by using the ASCII values for each character rather than a dedicated algorithm for implementing the mapping procedure. The study presented in [24] provided implementation details for the proposed software ECC that is able to encrypt/decrypt text and images.
Authors of [25] proposed ECC software implementations using a new scalar multiplication algorithm. In particular, the binary trees were used to carry out the results of point multiplication. The proposed technique was based on adding the point to itself repeatedly and the divide and conquer approach. The research work [26] introduced an EC cryptosystem that runs in a multi-threading environment. The proposed parallel cryptosystem runs different mathematical algorithms for point multiplication on the standard Weierstrass curve. The point multiplication algorithms used are Karatsuba and Montgomery algorithms. Again, the results showed that the prime field is faster than the binary field, which makes it appropriate choice for software applications.
The study presented in [27] provided an explanation on how to implement a java EC cryptosystem over the prime and binary fields. The paper implemented the key pairs generation, keys exchange, and ECDSA using SunEC provider. Another study [28] implemented the EC Digital Signature Algorithm using the Java Development Kit (JDK) version 1.2. The developed system was tested using the following key sizes 192,239, and 256 bits. The experimental results showed that key pair generation using 256-bits takes 13.6 ms, and the signing process takes 13.7 ms, and the verifying takes 13.7 ms.
It has been noticed that majority of previous research works did not conduct performance testing on their software implementations of ECC to highlight the efficiency of their proposed cryptosystems. In addition, previous studies focused on the sequential software implementation for ECC computations and considered one scalar multiplication algorithm per each proposed ECC implementation.
Furthermore, the reviewed research works that studied the software implementation of ECC focused on the standard EC form and did not investigate the use of newly introduced EC representations such as Montgomery, and tripling oriented curves. Another issue in previous works is that they are predominately use the affine coordinates system to represent the EC points, which leads to a significant drawback in ECC performance. This is because the use of affine coordinates requires finding the multiplicative inverse to perform the modular division operation. Computing the inverse is the most time consuming operation in EC cryptography.
Although, the projective coordinates were used in some studies, those researches did not benefit from the parallel and concurrent execution of ECC computations with projective coordinates. Instead, the vast majority of reviewed researches used the sequential implementation of ECC, in which only one finite field operation can be performed in each level of computations. Again, this increases the time delay of ECC operations and exposes the cryptosystem to the risk of side channel attacks. The sequential software implementation of ECC in not efficient for security applications that require high-speed cryptosystems such as multimedia and military applications.
This research seeks to develop improved software implementation for ECC. To this end, the different factors affecting the ECC performance will be investigated, which are the use of projective coordinates, the use of EC forms with less computations complexity, the scalar multiplication algorithm, and the use of parallel software implementation to perform ECC computations. In the proposed ECC's implementations, the different factors are tuned up and combined to reduce the time delay. The ECC performance is evaluated and analyzed to find the best combination of these factors that achieves the optimum performance level. This aims to develop a high-performance and efficient ECC. To our knowledge, this combination of factors and optimization of the software implementation of ECC have never been proposed and studied previously.
4 Proposed Cryptosystem Design
This section presents the equations and methods used to implement ECC computations. The parallel computational schemes, which are required for parallel software implementations, are designed in this section. Eventually, this section introduces the enhanced software implementation of ECC.
This research uses the recently introduced form of EC called Montgomery curve, which was presented in Section 2. The Montgomery EC is selected since it has relatively low computational complexity. EC points are represented using projective coordinates instead of usual affine form to avoid the modular division operation. Three types of projective coordinates (Homogenous, Lopez Dahab, and Jacobian) were tested in this research to find the one that gives the best performance.
The computations of point doubling and addition operations were implemented in parallel manner via utilizing the inherent parallelism in ECC computations. Different parallelization levels were tested to find out the best level that achieves the least time delay.
The major scalar multiplication algorithms were examined in this research. In particular, we evaluated the performance of ECC using the Binary method, the NAF algorithm, and the Montgomery scalar algorithm. Proposed ECC implementations are evaluated and compared in terms of time consumption of the scalar multiplication operation. The Java programming language is used to implement the proposed ECC and perform encryption and decryption operations. The following section presents the underlying computations for Montgomery point operations using the three coordinates systems.
In this section, the ECC point computations using projective coordinates are illustrated. The main EC point operations are point doubling and point addition. Each one of them requires performing a number of finite filed computations; multiplication, addition, and subtraction. The projective coordinates use three dimensions (x, y, and z) to represent an EC point instead of two dimensions. The point addition operation adds two different EC points to find a third point, while the point doubling operation duplicates an EC point to find another point. Equations of point doubling and addition are presented in Section 2.
4.1.1 Homogeneous Projection System
The Homogeneous coordinates were used to represent the points on the Montgomery curve. The point doubling operation computes the third point represented by the coordinates X3, Y3, and Z3. This can be done using the following equations:
4.1.2 Lopez-Dahap Projection System
In the Lopez-Dahap coordinates, the EC point is represented using the coordinates system. The equations used to compute the result of Montgomery point doubling using Lopez-Dahap coordinates are as follows:
4.1.3 Jacobean Projection System
The Jacobean coordinates system uses the following equations to find the result of the Montgomery point doubling operation:
The point addition computations, on the other hand, are similar for all ECs over GF(P) and are not affected by the change in EC equation. The point addition computations are presented in great details in [3]. The following section introduces the computational scheme designs that are used to implement ECC computations in parallel manner.
4.2 Computational Scheme Designs
In this section, the ECC computational schemes to implement finite field arithmetic are designed. All possible design choices to perform ECC points computations were investigated; starting from the sequential design tell reaching the design with maximum parallel operations. The rationale behind parallelizing ECC computations is to reduce the time delay as much as possible and hence improving the cryptosystem performance. This study focused on the parallel ECC design that achieves the shortest time delay. The main disadvantage of sequential implementation of ECC is that it consumes longer time to implement the cryptosystem's computations and wastes the CPU capability by executing only one modular operation per each step.
The current study aims to improve the speed of ECC through utilizing the CPU's capability to allow the concurrent execution of multiple modular operations simultaneously. In this section we present the data flows from inputs to outputs of the Montgomery ECC point Doubling over GF(P). These designs created by mapping the computational operation to a parallel software designs. Figs. 1–3 show the computational schemes for point doubling computations using homogeneous, Lopez-Dahab, and Jacobian projections respectively.
The proposed designs use four parallel multiplications (4-PM) and two parallel additions (2-PA), since it is considered the best parallelization level that yields the highest performance for point doubling. In each level of computations, either addition or multiplication operations are performed. The operations in each level are executed in a parallel manner. This was achieved through using the multi-threading technique in software implementation as will be clarified in Section 4.3.
Note that the modular operations within each sequential level cannot begin unless the operations from the previous level are fully executed.

Figure 1: Computational design for Montogomery point doubling using homogenous projection

Figure 2: Computational design for Montogomery point doubling using Lopez-Dahap projection
Unlike the sequential design, the proposed ECC designs exploit the inherited parallelism in EC commutations by allowing the concurrent executions of multiple modular operations within each level.
It can be noticed from Fig. 3 that applying Montgomery ECC computations using Jacobian projection requires the least number of multiplication operations. Thus, it is efficient choice for sequential ECC implementations. On the other hand, applying the cryptosystem computations using Homogenous projection presented in Fig. 3 requires less number of parallel multiplication levels, which yields the shortest time delay for points operations. Therefore, it is considered the most efficient coordinates system when using parallel implementation for Montgomery ECC.
This section elaborates on the software implementation of proposed parallel and high-speed GF(P) ECC using Montgomery curve. First, we illustrate the implementation of modular arithmetic; multiplication, addition, subtraction, and inversion operations. Then, the parallel multi-threaded implementation of point doubling and addition operations is presented. The software implementation of the scalar multiplication using the Montgomery ladder, the NAF, and the Binary algorithms is shown in this section. Finally, an ECC encryption and decryption experiments are performed to verify the cryptosystem efficiency and evaluate its performance level.
For Modular arithmetic operations, the java BigInteger class is used to allow very large integer (typically 256-bit) calculations beyond the limits of all primitive data types, which cannot handle values greater than 64 bits. In addition, the java BigInteger class provides a set of methods to support the execution of modular addition, modular subtraction, modular multiplication and modular inversion. All of these operations are implemented using built-in methods in the BigInteger class. For example, the modular multiplication is implemented by using the multiply and mod methods of BigInteger class. The following code segment shows an example for the modular multiplication operation used in the proposed cryptosystem.
BigInteger A = new BigInteger(“587995594274”);
BigInteger B = new BigInteger(“2000000000000”);
BigInteger P = new BigInteger (“504842927415879955942747”);
BigInteger C = A.multiply(B).mod(P);
System.out.println(“The result of A * B mod P is “+C);
In this research, we examined all possible design choices for Montgomery ECC using the three main projections. The next section presents the software implementations for the most efficient design choices used to perform ECC points operations.
To facilitate the points operations on an elliptic curve, we implemented Point and EllipticCurve Classes. The Point Class has three private members, representing the X and Y and Z coordinates of a point. These members are objects of the BigInteger class.
The EllipticCurve class handles the domain parameters and have public functions pointAddition() and PointDoubling () and scalarMultplication(). The pointAddition() and PointDoubling () methods have sequential and multithreaded java implementations for each of the three coordinates systems.
While the sequential implementation of point operations is straightforward and performs one operation per each level, the parallel implementation of point operations reflects the parallel designs presented in Section 4.2 and exploit the inherited parallelism in ECC computations. To achieve this, the multi-threading technique in java was used to allow the parallel execution of ECC computations. The Java threads are independent and save time; multiple operations can be performed simultaneously and separately. Three main methods from the Java Thread class were used in the proposed implementation, as follows:
• Run (): It is used to do an action for a thread.
• start (): It is used to trigger the execution of the finite field operation within the thread.
• join (): It is used to wait for the results of the finite field operation within a specific thread. This method can be used for the caller thread to wait for the completion of called thread.
At each level, multiple threads are created; one thread for each finite field operation within the level. Within the bracket of the Run method, any segment of Java code can be placed. In our implementation, a prime finite field operation using BigInteger Class's object and procedures is used. For the purpose of controlling the order of the executions of the levels within the parallel design, the join () method used, to make the main thread waits for the completion of all called threads that perform the field operations within a particular level. The code segment below showcases the creation and start of a Java thread used in the parallel Implementations of ECC.
Thread thread1 = new Thread(new Runnable() {
Public void run() { } };
thread1.start();
Within the bracket of the Run method, any segment of Java code can be placed. In our implementation, a prime finite field operation using BigInteger Class's object and procedures is used. And for the purpose of controlling the order of the executions of the levels within the parallel design, the join () method used, to make the main thread waits for the completion of all called threads that performs the finite field operations within the same level. For instance, in the code of the parallel implementation for Montgomery Point Doubling using Homogeneous projection, four thread objects were created at the first multiplication level and named thread1, thread2, thread3, and thread4. In this level, each thread responsible for carrying out the result of modular multiplication assigned to it within the design presented in Fig. 3. After each thread creation, the thread immediately started using the start method. The following code segment presents the parallel implementation of the first level of multiplications for Montgomery ECC point doubling.
At the end of a particular level of computations, each thread was created in this level will call the join method to ensure that each thread completes its calculations before starting the next level. Other levels of computations for ECC points are implemented in parallel using similar mechanism. Sixteen java threads were created to implement the Montgomery point doubling using Homogeneous Projective system.
Thread thread1 = new Thread(new Runnable() {
public void run() {
M1 = G.getX().multiply(G.getX()); } };
thread1.start();
Thread thread2 = new Thread(new Runnable() {
public void run() {
M2 = G.getY().multiply(G.getY()); } };
thread2.start();
Thread thread3 = new Thread(new Runnable() {
public void run() {
M3 = G.getZ().multiply(G.getZ()); } };
thread3.start();
Thread thread4 = new Thread(new Runnable() {
public void run() {
M4 = G.getX().multiply(G.getZ()); } };
thread4.start(); thread1.join(); thread2.join(); thread3.join(); thread4.join();
4.3.3 Implementation of Scalar Multiplication Algorithms
The scalar multiplication is the most critical operation in ECC. The current research investigates the three main algorithms used for performing the scalar multiplication, which are the Montgomery Ladder, the NAF, and the Binary algorithms. This aims to determine the fastest algorithm that provides best performance level for ECC encryption/decryption processes. Experimental results showed that the NAF algorithm is faster than the Montgomery ladder and the Binary Left-to-Right method, because it requires less number of point addition operations. The following code segment is used to implement the NAF algorithm after computing the signed binary representation (NAF) of the scalar K through the function (computeNAF(k)).
public Point scalarMultplication(BigInteger k , Point G) {// The NAF Algorithm
Point R = new Point (new BigInteger (“0”), new BigInteger(“0”), new BigInteger(“0”) );
BigInteger [] s = {computeNAF}(k); // compute the NAF representation
R = G; //The result point R initialized to the input point G
for (int i = s.length-2; i >= 0; i--) { //traverse through each NAF digit
R = PointDoubling(R); // During each iteration perform a point doubling
if (s[i].compareTo(BigInteger.ONE) == 0)
R = PointAddition(R,G); // if value = 1, perform a point addition R = R + G
else if (s[i].compareTo(new BigInteger(“−1”)) == 0)
{Point inverseG = new Point (G.getX(), P.subtract(G.getY()));
R = PointAddition(R, inverseG); // If value = −1 perform a point subtraction
} }
return R; }
4.3.4 ECC Encryption and Decryption Experiments
In order to test the proposed cryptosystem, and verify its functionality, a number of encryption and decryption experiments were conducted. Moreover, this contributes in evaluating the ECC performance more precisely, and assists developers to build high-speed and efficient cryptosystems.
For multithreaded implementations of point operations. all of the tests are run on a Dell PC (Intel(R) Core(TM) i7–4770 CPU @ 3.40 GHz, 4GB RAM), running the Windows 7 operating system. The code was compiled and run with Java version 1.8 using the Eclipse IDE tool. The M-221 curve used for the implementation and testing of the cryptosystems.

Figure 3: Computational design for Montogomery point doubling using Jacobean projection
The process of implementing the ECC encryption and decryption went through the following phases:
1) Cryptosystem setup:
To set up an ECC, both senders and receivers are required to select and agree upon the same EC domain parameters, i.e., the underlying finite field
2) Key generation and exchange:
Each side selects a random integer as its private keys and then computes its public key. The selectPrivatekey, getRandomNumber, and computePublic_key methods were used for the key generation purposes.
3) Message encoding:
In this phase, each char in the message is mapped to its corresponding point in the lookup table that the senders and receivers have agreed upon. The encoding method takes an array of char types and returns an array of Point types. The method loop the input array to map each char element with its EC Point using the ASCII value of the char, and then this value is used as an index for the point representing this char.
4) ECC Encryption
In this phase, the cryptosystem encrypts the point array representing the message after encoding to produce a cipher array. The encryption function is a part of the EllipticCurve class, and takes as an input; the Private Key, the message points, and the other Party's Public Key. This method returns a cipher array of points for each char in the message after encryption. The encryption process is implemented through the following code segment:
Point [] cipher = new Point [messagetoPoints.length];
cipher = ec.Encryption(Private_Key, messagetoPoints, other_Party_Public_Key);
Point[] Encryption (BigInteger Private_Key, Point[] M , Point otherPartyPublicKey)
for (int n = 0; n < M.length; n++) {
Ciphers[n] = PointAddition(M[n], scalarMultplication(Private_Key, otherPartyPublicKey));
return Ciphers; }
5) Decryption
In the decryption phase, the cryptosystem decrypts the ciphertext using a member method of the EllipticCurve Class. The Decryption method takes the cipher array of points as an input and returns the message mapped points back. The decryption process inverses the encryption to restore the plaintext.
6) Message Decoding
In the message decoding phase, each elliptic curve Point in the cipher array is mapped back to its corresponding char using the lookup table that both sender and receiver have agreed upon at the setup phase. The decoding method takes an array of Point types and returns an array of Char types representing the plaintext.
The following section presents the experimental results for the proposed ECC, and discussion about the performance evaluation.
Tab. 1 shows the average execution time for the finite field operations. The experimental results confirmed that modular inversion is the most expensive in terms of time delay. The results also showed that modular multiplication and addition operations are the second and third time-consuming operations respectively. To calculate the running time for proposed ECC implementations precisely, the java command System.nanoTime was used to get the current time at the beginning (startTime) and the end (endTime) of the encryption process. Then, the actual time consumption is calculated by subtracting the start time from the end time
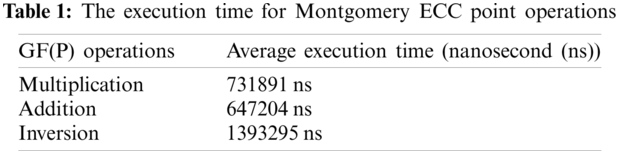
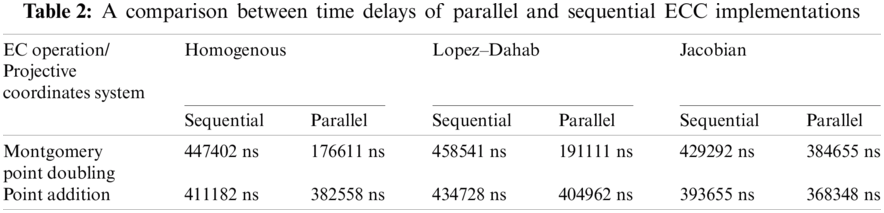
Tab. 2 presents a comparison in terms of time consumption for ECC point operations when implemented using sequential and parallel designs. The implementation results also highlight the time delay for each projective coordinates system used to apply EC computations.
In order to highlight the improvement on the performance achieved by using the proposed parallel implementation, Tab. 3 shows an estimated Speed-up Percentage for each parallel ECC operation with each projection. The Speedup Percentage for the parallel designs can be computed as follows:
It can be observed from the results presented in Tabs. 1–3 that parallel implementation significantly improves the ECC performance compared to the sequential implementation. The best reported improvement percentage is 253% and was achieved using the Homogenous projection. Moreover, this projection achieved the shortest time delay (191111 ns) for the parallel (multi-threaded) implementation of point doubling operation. For sequential ECC implementation, Jacobian coordinates system achieved the shortest time delay. This was expected since Jacobian projection requires less number of modular multiplications.

The scalar multiplication is the main operation in ECC encryption, and usually used to evaluate the cryptosystem performance. Tab. 4 presents a performance (time consumption in millisecond (ms)) comparison between the sequential and parallel ECC implementations using three known algorithms; Montgomery ladder, NAF, and Binary (LRT) method.
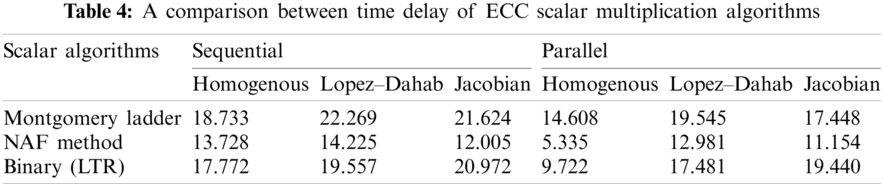
It can be noticed from Tab. 4 that NAF algorithm achieved the least time consumption results (5.335 ms) for Montgomery ECC encryption when applied using the parallel (multi-threaded) design and Homogenous projection. For sequential ECC implementation, NAF algorithm also achieved the shortest time delay (12.005 ms) when used with Jacobian coordinates. The low humming wait of the NAF algorithm might be the main reason for its good performance levels. The Binary (LTR) and Montgomery ladder algorithms achieved the second and third place respectively in respect to the performance level.
Fig. 4 shows the results of the running time of all scalar multiplication algorithms on Montgomery Curve using sequential and parallel implementations. The results clearly show that NAF with the parallel implementation and the use of homologous projection takes the least time compared to the other implementations. On the other side, the sequential ECC implementation using Montgomery ladder and Lopez_Dahab projection consumes the longest (worst) time delay.
Tab. 5 presents a comparison with ECC implementations presented in previous research works. It can be noticed that proposed parallel ECC implementation overcomes others in terms of performance for the main EC operations; including Encryption, scalar multiplication (ECSM), point addition (ECADD), and point doubling (ECDBL).

Figure 4: The time-delay (in Millisecond) of ECSM algorithms on Montgomery ECC

The explosive increase in the amount of data being transmitted over communication networks makes it necessary to develop a high-speed cryptosystem. Elliptic curve cryptosystem (ECC) has been proposed as an efficient public key cryptosystem since it can provide comparable security level to other systems with using shorter key length. However, ECC using its usual sequential implementation and affine coordinates cannot achieve adequate performance level to protect the huge amount data processes by modern applications such as multimedia and military. Moreover, the majority of previous studies investigated the hardware implementation of ECC, which is costly option, and used only one standard curve.
In this article, a high-speed parallel software implementation for ECC is developed. It studied and tuned-up the main factors playing significant role in improving ECC performance. A newly introduced form called Montgomery curve is studied in this research because it has lower computational complexity, and hence requires less field operations. This research studied the performance level of sequential and parallel implementation of Montgomery ECC. The parallel implementation was done using Java multithreading techniques. Three projective coordinates were implemented and examined due to their ability to avoid the long time inversion operation. It has been shown the proposed multi-threaded ECC implementation using Homogenous projection achieved the best performance results. Such implementation is efficient choice for applications that need fast encryption process. For sequential Montgomery ECC, Jacobian projection obtained the shortest time delay. As a future research, other forms of EC and extensions of projective coordinates can be studied, since it may reduce the time complexity. Parallelizing the upper level of computations for ECC could be considered to increase the speed of encryption process as well.
Acknowledgement: Authors Acknowledge the support from Imam Mohammad Ibn Saud Islamic University for this research.
Funding Statement: Authors extend their appreciation to the Deanship of Scientific Research at Imam Mohammad Ibn Saud Islamic University for funding and supporting this work through Graduate Student Research Support Program.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. W. Trappe and L. Washington, “Elliptic curves,” in Introduction to Cryptography: With Coding Theory, 3rd ed., New Jersey, USA: Pearson Prentice Hall, 2020. [Google Scholar]
2. V. Miller, “Uses of elliptic curves in cryptography,” Lecture Notes in Computer Science, vol. 218, pp. 417–426, 1986. [Google Scholar]
3. G. Dormale and J. Quisquater, “High-speed hardware implementations of elliptic curve cryptography: A survey,” Journal of Systems Architecture, vol. 53, pp. 72–84, 2007. [Google Scholar]
4. N. Koblitz, “Elliptic curve cryptosystem,” Mathematics of Computation, vol. 48, pp. 203–209, 1987. [Google Scholar]
5. C. Paar and J. Pelzl, “Elliptic curve cryptosystem,” in Understanding Cryptography: A Textbook for Students and Practitioners, 2nd ed., Berlin, Germany: Springer Science & Business Media, 2010. [Google Scholar]
6. Q. Al-Haija and M. Al-Khatib, “Parallel hardware algorithms & designs for elliptic curves cryptography to improve point operations computations using new projective coordinates,” Journal of Information Assurance and Security (JIAS), vol. 4, no. 1, pp. 588–594, 2010. [Google Scholar]
7. E. Karthikeyan, “Survey of elliptic curve scalar multiplication algorithms,” International Journal of Advanced Networking and Applications, vol. 4, no. 2, pp. 1581–1590, 2012. [Google Scholar]
8. A. Gutub, A. Tabakh, A. Al-Qahtani and A. Amin, “Serial vs. parallel elliptic curve crypto processor designs,” in IADIS Int. Conf.: Applied Computing, Fort Worth, Texas, pp. 67–74, 2013. [Google Scholar]
9. M. Al-khatib, Q. Al-Haijaa and A. Jaafar, “Hardware architecture & designs for projective elliptic curves point addition operation using variable levels of parallelism,” International Review on Computers and Software, vol. 6, no. 2, pp. 237–243, 2011. [Google Scholar]
10. M. Al-khatib, A. Jaafar and Q. Al-Haija, “Choices on designing GF (p) elliptic curve coprocessor benefiting from mapping homogeneous curves in parallel multiplications,” International Journal on Computer Science and Engineering, vol. 3, no. 2, pp. 467–480, 2011. [Google Scholar]
11. M. Al-khatib, “High-speed and secure elliptic curve cryptosystem for multimedia applications,” International Journal of Advanced Computer Science and Applications, vol. 11, no. 9, pp. 117–129, 2020. [Google Scholar]
12. A. Satoh and K. Takano, “A scalable dual-field elliptic curve cryptographic processor,” IEEE Transactions Computers, vol. 52, no. 4, pp. 449–460, 2003. [Google Scholar]
13. G. Orlando and C. Paar, “A scalable GF (p) elliptic curve processor architecture for programmable hardware,” in Proc. Cryptographic Hardware and Embedded Systems-CHES 2001, Paris, France, 2001. [Google Scholar]
14. M. Al-khatib, A. Jaafar, Z. Zukarnain and M. Rushdan, “On the design of projective binary edwards elliptic curves over GF (p) benefiting from mapping elliptic curves computations to variable degree of parallel design,” International Journal on Computer Science and Engineering, vol. 3, no. 4, pp. 1697–1712, 2011. [Google Scholar]
15. T. Al-Somani, “Performance evaluation of elliptic curve projective coordinates with parallel GF (p) field operations and side-channel atomicity,” Journal of Computers, vol. 5, no. 1, pp. 99–109, 2010. [Google Scholar]
16. M. Al-khatib and A. Al-Salem, “Efficient hardware implementations for tripling oriented elliptic curve crypto-system,” International Review on Computers and Software, vol. 9, no. 4, pp. 609–617, 2014. [Google Scholar]
17. L. Singh, “Implementation of text encryption using elliptic curve cryptography,” in Proc. Eleventh Int. Multi-Conf. on Information Processing, India, pp. 73–82, 2015. [Google Scholar]
18. A. Reyes and A. Castillo, “A performance comparison of elliptic curve scalar multiplication algorithms on smartphones,” in Proc. 23rd Int. Conf. on Electronics, Communications and Computing, Puebla, Mexico, pp. 114–119, 2013. [Google Scholar]
19. A. Kaur, V. Goyal and P. Luthra, “Java implementation and arithmetic performance evaluation of elliptic curve cryptography using MATLAB,” International Journal of Engineering Research & Technology (IJERT), pp. 2695–2699, 2013. [Google Scholar]
20. A. Bose, “Elliptic curve cryptosystem,” Review of Computer Engineering Studies, vol. 4, no. 2, pp. 67–69, 2017. [Google Scholar]
21. A. Kumar, “Implementation of elliptical curve cryptography,” International Journal of Computer Science Issues, vol. 8, no. 4, pp. 544–549, 2011. [Google Scholar]
22. A. Mitra, S. Chakrabarty and P. Mitra, “Elliptic curve cryptosystem for email encryption,” International Journal of Computer and Communication Technology, vol. 1, no. 4, pp. 230–235, 2010. [Google Scholar]
23. T. M. Aung and N. N. Hla, “Implementation of elliptic curve arithmetic operations for prime field and binary field using java bigInteger class,” International Journal of Engineering Research & Technology (IJERT), vol. 6, no. 8, pp. 454–459, 2018. [Google Scholar]
24. M. Ahmed, W. Kadir and M. Namiq, “A new cryptosystem for encryption and decryption using ellipitic curves in cryptography over finite fields,” Journal of Theoretical and Applied Information Technology, vol. 96, no. 1, pp. 182–188, 2018. [Google Scholar]
25. I. Setiadi, A. Kistijantoro and A. Miyaji, “Elliptic curve cryptography: Algorithms and implementation analysis over coordinate systems,” in Proc. 2nd Int. Conf. on Advanced Informatics: Concepts, Theory and Applications (ICAICTAChonburi, Thailand, pp. 1–6, 2015. [Google Scholar]
26. A. Samsudin, “Multi-threading elliptic curve cryptosystems,” in IEEE Int. Conf. on Telecommunications and Malaysia Int. Conf. on Communications, penang, Malaysia, pp. 143–139, 2007. [Google Scholar]
27. G. Encinas, “Implementing ECC with java standard edition 7,” International Journal of Computer Science and Artificial Intelligence, vol. 3, no. 4, pp. 134–142, 2013. [Google Scholar]
28. Y. Kortesniemi, “Implementing elliptic curve cryptosystems in Java 1.2,” in Nordsec'98, The Third Nordic Workshop on Secure IT Systems, Trondheim, Norway, pp. 145–154, 1998. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |