DOI:10.32604/cmc.2022.020682

| Computers, Materials & Continua DOI:10.32604/cmc.2022.020682 |  |
| Article |
A Novel Binary Emperor Penguin Optimizer for Feature Selection Tasks
1Computer Science Department, Government College Bahadurgarh, Bahadurgarh, 124507, India
2CSE Department, National Institute of Technology Hamirpur, 177005, India
3School of Engineering and Applied Sciences, Bennett University, Greater Noida, 201310, India
4College of Industrial Engineering, King Khalid University, Abha, Saudi Arabia
5Department of Electrical and Electronics Engineering, Amasya University, Amasya, Turkey
6Faculty of Computers and Information, South Valley University, Qena, 83523, Egypt
*Corresponding Author: Hammam Alshazly. Email: hammam.alshazly@sci.svu.edu.eg
Received: 03 June 2021; Accepted: 23 August 2021
Abstract: Nowadays, due to the increase in information resources, the number of parameters and complexity of feature vectors increases. Optimization methods offer more practical solutions instead of exact solutions for the solution of this problem. The Emperor Penguin Optimizer (EPO) is one of the highest performing meta-heuristic algorithms of recent times that imposed the gathering behavior of emperor penguins. It shows the superiority of its performance over a wide range of optimization problems thanks to its equal chance to each penguin and its fast convergence features. Although traditional EPO overcomes the optimization problems in continuous search space, many problems today shift to the binary search space. Therefore, in this study, using the power of traditional EPO, binary EPO (BEPO) is presented for the effective solution of binary-nature problems. BEPO algorithm uses binary search space instead of searching solutions like conventional EPO algorithm in continuous search space. For this purpose, the sigmoidal functions are preferred in determining the emperor positions. In addition, the boundaries of the search space remain constant by choosing binary operators. BEPO's performance is evaluated over twenty-nine benchmarking functions. Statistical evaluations are made to reveal the superiority of the BEPO algorithm. In addition, the performance of the BEPO algorithm was evaluated for the binary feature selection problem. The experimental results reveal that the BEPO algorithm outperforms the existing binary meta-heuristic algorithms in both tasks.
Keywords: Metaheuristics; optimization algorithms; emperor penguin optimizer; intensification; diversification; feature selection
Technological developments enable information to increase and spread easily. This situation makes it challenging to choose the relevant information among all the information. The increase in the number of information is often confusing as irrelevant knowledge is involved. It is misleading to think of this information as just literature. In real-world applications, the information obtained from the devices is increasing. The reason for this is the data provided by the technological devices added to the traditional production process. These data present all the details regarding the functioning of the system in almost every field from the production process to the health system. The reason for collecting such data is usually the control of the production process, classification, or making a decision [1]. Today, developments in artificial intelligence (AI) methods allow the mentioned processes to be performed automatically. However, the decision-making processes of AI algorithms depend on the quality of the information produced by these devices. The large size of the data obtained in real-world applications is not beneficial for automatic decision-making systems (curse of dimensionality) [2]. Therefore, optimization of feature vectors emerges as an essential task. In the literature, feature selection or feature dimensionality reduction approaches are generally preferred using optimization approaches [3]. In this way, the performance of AI methods is increased by eliminating unrelated features. In the past, the effect of optimization could be seen on the performance in these tasks performed using hand-crafted methods. Today, these tasks are usually performed using automated methods. The adaptation of optimization algorithms to these techniques has a significant share in the realization of automatic methods. Nowadays, optimization studies of deep automatic architectures using external optimization algorithms are available in the literature.
The usage areas of optimization algorithms are not limited to a specific framework, it is obvious that optimization is required in almost every field today. As technological advances increase and automation becomes widespread, many complex problems arise that need to be considered. Optimization algorithms, which provide great support to the solutions of the mentioned problems, have been recommended since the past and still continue to be recommended. As the accumulation of knowledge increases and problems arise, drawbacks in current optimization techniques emerge. The historical development of optimization techniques is a very comprehensive topic and can be studied in detailed literature research [4]. Nearly all of the metaheuristic techniques are developed for solving real-life problems. These are widely used for the past few years for solving complex problems. Some of them may not provide the exact solution to specific problems. They provide the optimal solution in a cost-effective manner. These algorithms are generally categorized into five main classes namely evolutionary, physics, bio-inspired, swarm, and nature-inspired based metaheuristics. Fig. 1 shows the categorization of metaheuristics optimization techniques.

Figure 1: Categorization of metaheuristic algorithms
Compared with exact search approaches, metaheuristic optimization approaches are more successful in terms of performance (also, they are less time-consuming). One of the most important reasons for this is that they do not have to analyze the entire search space during the research process. High computational complexity is an undesirable feature today, although exact search approaches guarantee to find the best solution when they have sufficient time and hardware power. Metaheuristic approaches are a kind of random search engine. But randomness here is usually in a directed form. Thanks to this manageability, they can determine the most suitable solution in a short time. The evolutionary-based algorithms are motivated by biological evolution. Some of these are Genetic Algorithm (GA) [5], Genetic Programming (GP) [6], and Evolution Strategy (ES) [7]. The second category algorithms mimic the concepts drawn from Physics. The well-known algorithms are Gravitational Search Algorithm (GSA) [8], Simulated Annealing (SE) [9], Big Bang Big Crunch (BBBC) [10–14], Galaxy-Based Search Algorithm (GBSA) [15]. Swarm algorithms are influenced by the cooperative behavior of swarms present in nature. Some of the algorithms included in this category are Spotted Hyena Optimizer (SHO) [16], Grey Wolf Optimizer (GWO) [17], Particle Swarm Optimization (PSO) [18], Bat Algorithm (BA) [19], Ant Colony Optimization (ACO) [20], Bee collecting pollen algorithm [21], Wolf Pack Search Algorithm [22], Moth-flame Optimization Algorithm (MFO) [23,24], Seagull Optimization Algorithm (SOA) [25], Emperor Penguins Optimizer (EPO) [26]. All these suggested approaches aim to find the most appropriate solution to specific problems with the least effort. In this process, they are inspired by some systems in nature.
The above-mentioned optimization algorithms can be applied to the feature selection problem [27]. A feature selection process is an approach used to determine and select the most convenient features in a feature vector. Feature selection is a way to distinguish the relevant feature from the irrelevant ones and retrieving only substantial features. The main objective of the feature selection problem is to improve prediction performance and reduce data dimensionality. By relieving problems such as the curse of dimensionality, it increases the performance of the main decision-making algorithm. Decision-making main algorithms generally perform tasks such as classification, segmentation, tracking, feature selection, feature reduction and produce a meaningful result. The beginning of feature selection studies is very old, and detailed literature analysis can be reached [28]. In this study, the effects and contributions of remarkable optimization algorithms are examined in the literature analysis. Binary GWO (BGWO) is a type of GWO that includes the conversion of continuous numbers to binary [29]. After the high performance of the BGWO algorithm, various variants of this algorithm are suggested in the literature. Quantum GWO (QI-GWO) is one of the most popular of these [30]. On the other hand, binary PSO is one of the most frequently used algorithms in solving binary optimization problems [31]. There are also various variants of BPSO algorithms, which is almost one of the leading binary optimization algorithms [32]. The BPSO algorithm also has similar problems with traditional PSO. On the other hand, the binary GSA (BGSA) is frequently encountered in the literature to relieve feature selection problems [33]. Binary BA (BBA) performs feature selection task by separating the search space by n-cube [34]. Binary SOA (BSOA) was recently introduced and validated for the feature selection problem [35].
Binary versions of almost all meta-heuristic optimization algorithms are available in the literature. Our analysis on these algorithms clearly shows that it carries the problems that continuous optimization versions have. The proposed BEPO algorithm is proposed to eliminate current problems in the literature and for a better solution. The main difference between the original EPO and the proposed BEPO is that EPO works well in continuous search space. In contrast, BEPO works in discrete search space. For this, BEPO utilizes a sigmoidal transfer function that can change the positions of search agents between the values 0 and 1. Performance indicators of the proposed BEPO algorithms are calculated according to 29 benchmark test functions. Then they are compared with the existing binary metaheuristic algorithms in the literature. Furthermore, the feature selection problem is solved through BEPO. The main contributions of this paper can be concluded as follows.
• The binary version of EPO and search space range values are proposed and analyzed deeply.
• The sigmoidal binarization function is proposed to convert search agent values to 0 and~1.
• The performance of the proposed BEPO algorithm is analyzed in detail using many benchmark test functions and benchmark datasets.
• Extensive feature selection experiments are concluded based on BEPO.
The remainder of this paper is organized as follows. First, the preliminary concepts of EPO are mentioned in Section 2. Then, the binary variant of the emperor penguin optimizer algorithm is presented in Section 3. Results and discussions are depicted in Section 4. Section 5 illustrates the application of the proposed algorithm on the feature selection problem. Finally, concluding remarks are explained in Section 6.
2 Continuous Emperor Penguin Optimizer
Aptenodytes forsteri is the scientific name of the Emperor penguin. As compared to all different types of penguins, they are the largest ones. With respect to the size, all the males and females are very much alike. They have a blackhead, white stomach, wings, and tail and live in Antarctica. In order to survive in the winters of Antarctica, they huddle together to keep themselves warm and protect themselves from cold wind. The huddling mechanism of penguins is emphasized into four main phases: creating a huddling boundary, evaluating the temperature profile, calculating the distance among emperor penguins, and relocating mover [26].
The above-mentioned four phases of emperor penguins are mathematically modeled. The foremost motivation behind this algorithm is to find the efficient mover and update the position of emperor penguins.
Penguins create a huddle boundary of polygon shape. The wind flow is also considered during the generation of huddle boundaries. The complex variable is used to illustrate the behavior of huddle boundary creation. Let us assume that the velocity of wind and its gradient are denoted by
Based on Eq. (1), the mathematical formulation of potential function (
where
The penguins create a huddle to maintain the high temperature inside the huddle for survival in winter. It is assumed that when the radius of the polygon (
where t is temperature profile and x is current iteration.
The best-fit emperor penguin plays the most critical role in determining the location of other emperor penguins. The locations of all other emperor penguins are updated accordingly. During the huddle boundary creation, the distance among the emperor penguins is calculated. The mathematical formulation of distance computation is given below.
where
where N represents the movement parameter for maintaining the gap among penguins, and its value is set to 2.
The mathematical formulation of
where e is expression function, g and l are control parameters whose value lies in the range of [2,3] and [1.5, 2], respectively.
According to the mover (i.e., best-fit emperor penguin), the positions of emperor penguins are updated. The mover is used to vacate the current position of penguins and change the positions of other penguins. The position update function is given below.
where

3 Proposed Binary Emperor Penguin Optimizer
Many of the optimization problems we encounter in real life require the discrete/binary search field. For this, problems having continuous variables can be transformed into binary variables. The binary metaheuristic algorithms help in solving the discrete problems that are feature selection [36], unit commitment problem [37], and dimensionality reduction [38]. However, the existing algorithms are still far from producing optimal solutions [39–43]. Hence, a novel binary metaheuristic is needed to resolve this problem.
EPO is easy to understand and apply in a real-life scenario. Due to these advantages, a novel binary variant of EPO (BEPO) is developed. In the proposed algorithm, the position updating mechanism has been modified. As per the knowledge of the authors, there is no such algorithm present so far.
3.2 Mathematical Implementation
The proposed algorithm uses discrete search space instead of uninterrupted search space. The discrete search space can be deliberated as hyperspace. The penguins of BEPO are either moved to closer or extreme corners of the hypercube by switching the binary bits. In BEPO, the position updating mechanism has been modified.
The Original EPO algorithm is designed to allow penguins to move in continuous search space. However, BEPO uses discrete search space to solve binary problems. For this purpose, updating the position updating mechanism ensures that only 0 and 1 are produced. The sigmoidal transfer function is used to perform this process. The mathematical formulation of the sigmoidal transfer function is given below:
where
It forces penguins to transfer in binary space. It should be lying in the range of
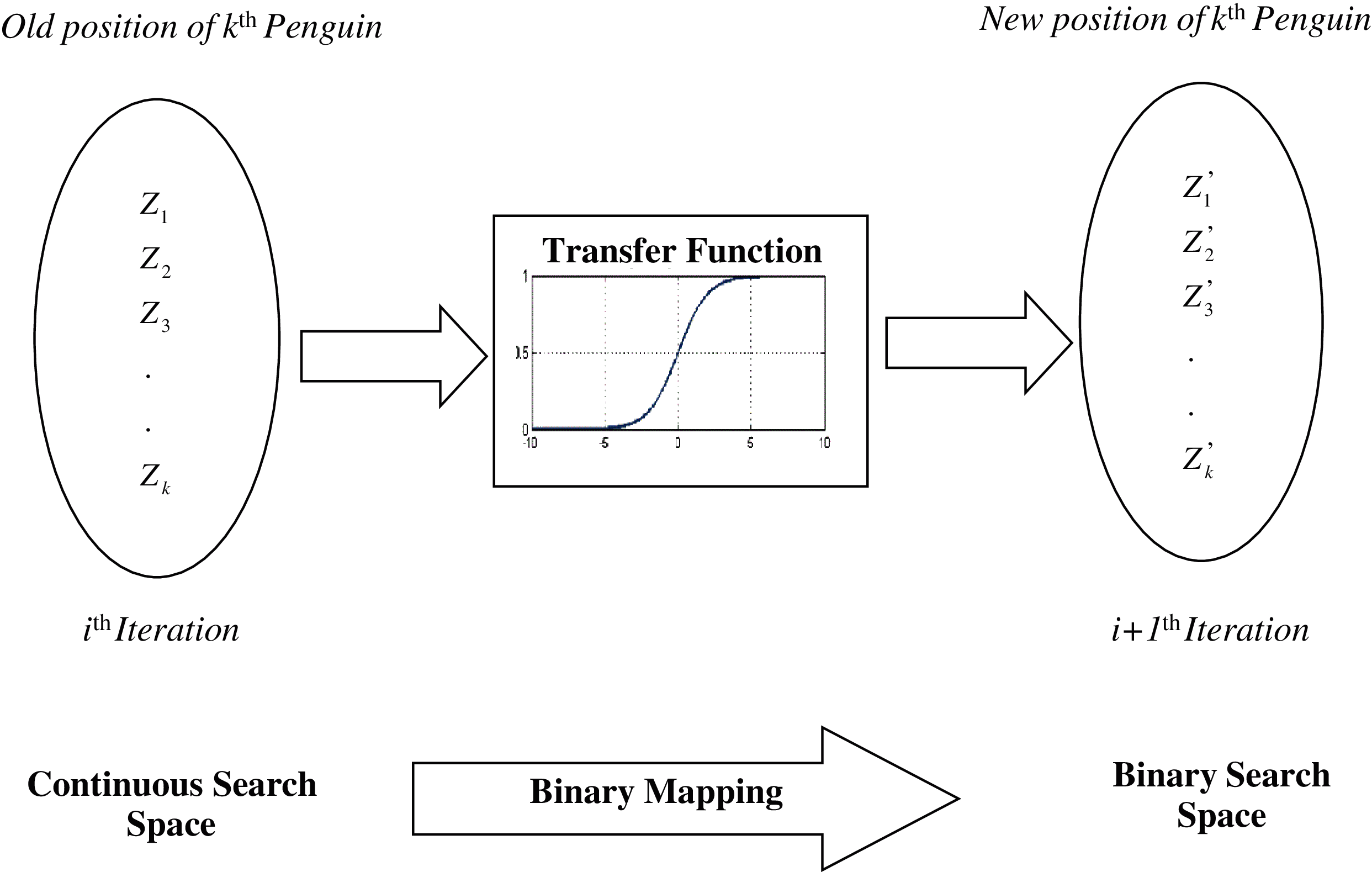
Figure 2: The transition from continuous space to discrete space
In order to show the superior performance of the proposed BEPO algorithm fairly, comparisons are made with recently developed binary metaheuristic algorithms. In this process, benchmarking standard test functions are used. In addition, 29 independent simulations are performed for each metaheuristic algorithm. Among these independent experiments, the best mean and standard deviation parameters for each method are selected. Finally, comparison tables are created according to this approach.
BEPO is validated on twenty-nine benchmark functions such as unimodal (F1-F7) [44], multimodal (F8-F13) [45], fixed dimensional multimodal (F14-F23) [45] and composite functions (F24-F29) [46]. The intensification capability of BEPO is established through unimodal functions (F1-F7). Multimodal functions (F8-F13) are used to validate the diversification ability of BEPO. The appropriate stability between intensification and diversification of BEPO is tested through F14-F29 test functions. Parametric values are kept the same to have fair comparison results in experiments using all these test functions.
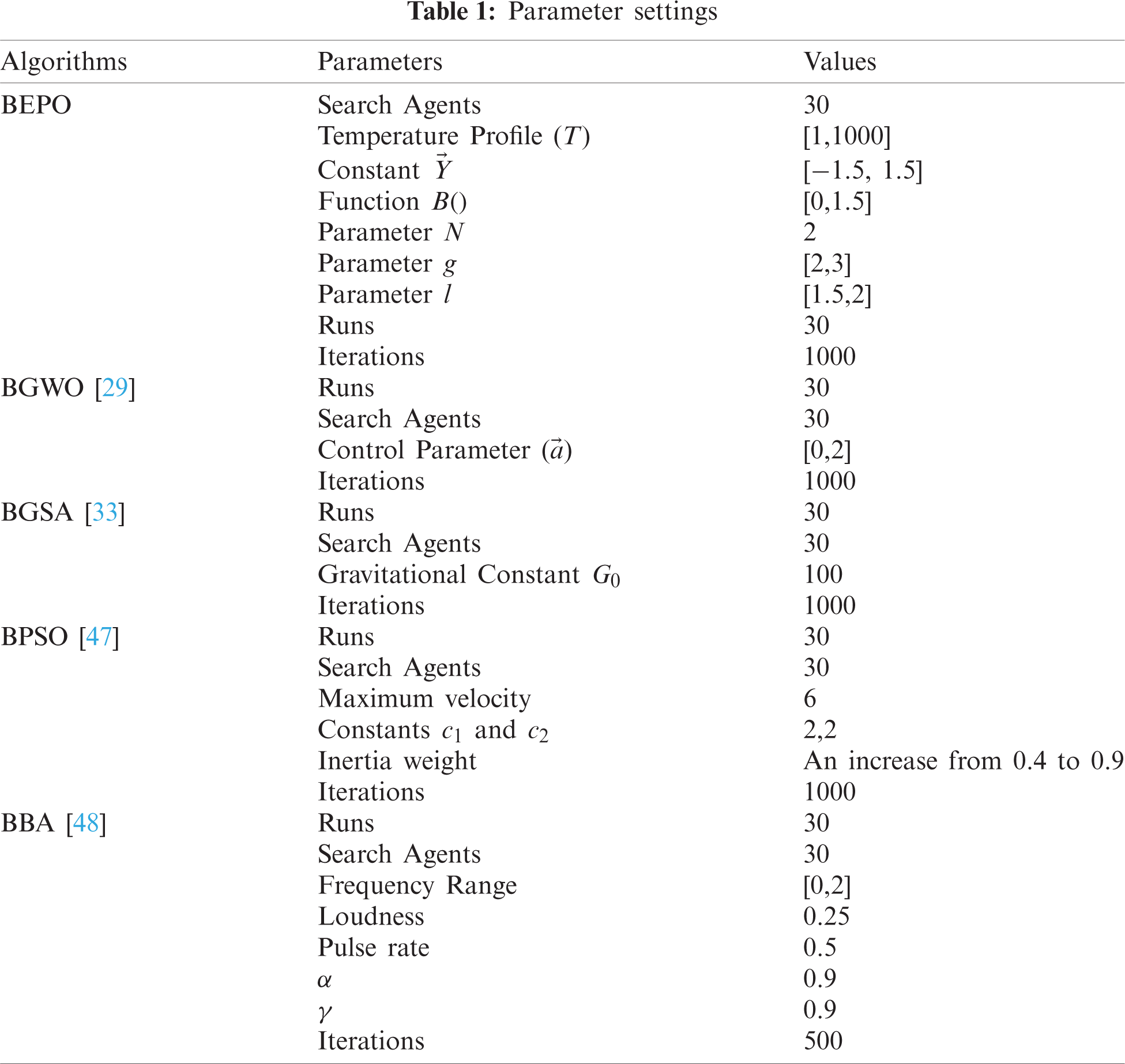
The BEPO algorithm is evaluated on the above-mentioned test functions in Section 4.1 and compared with four binary metaheuristic algorithms, namely Binary Grey Wolf Optimizer (BGWO) [29], Binary Gravitational Search Algorithm (BGSA) [33], Binary Particle Swarm Optimization (BPSO) [47], and Binary Bat Algorithm (BBA) [48]. The parameter settings of these algorithms are set as mentioned in their original papers.
Tab. 1 depicts the parameters settings of these algorithms. Two criteria are prioritized while selecting the parameters of the algorithms specified in Tab. 1. First, it is essential to preserve the parameters of the original algorithm. The second is that they are compatible with the general presentation in this study. These algorithms are implemented on MATLAB R2018a on Windows 7 with 4 GB RAM. These algorithms have run 30 independent times, and each run consists of 1000 iterations. The standard deviation (Std) and average (Avg) are calculated for the best solution obtained from each run and tabulated in tables.
BEPO is evaluated on test functions that are mentioned in Section 4.1. In addition, the convergence analysis of BEPO and other metaheuristics are also compared.
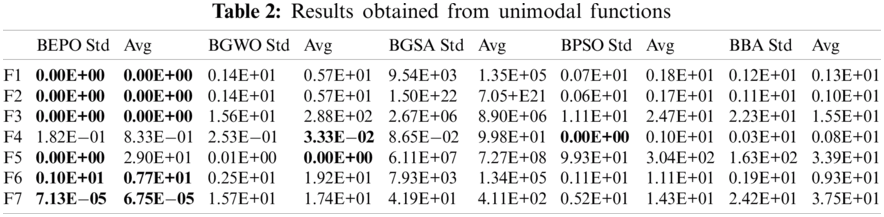
Tab. 2 depicts the unimodal test results obtained from BEPO and the existing binary metaheuristic techniques. For F1, F2, F3, F5, F6, and F7 test functions, BEPO suggests better results than the existing metaheuristics in terms of fitness value. BPSO is the subsequent best algorithm for F1, F2, F3, and F7 test functions. For the F5 function, BGWO is the succeeding algorithm. BBA is the following best algorithm for the F6 function. For the F4 function, BPSO performs better than the other state-of-the-art (SOTA) algorithms. Obtained results show that BEPO has a better intensification ability than the others. This is due to the adaptive nature of the proposed BEPO algorithm. In addition, keeping the original EPO properties of the BEPO algorithm is one of the main reasons for the high performance.
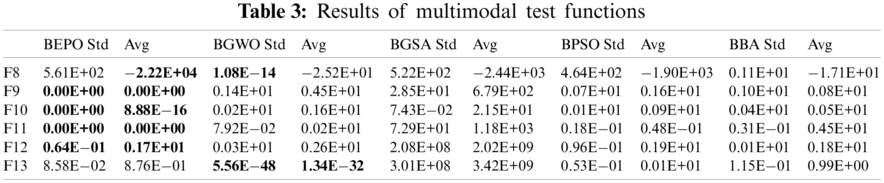
The results obtained from BEPO and other binary metaheuristic techniques on multimodal test functions are depicted in Tab. 3. For F8-F12 test functions, BEPO outperforms the existing binary metaheuristic techniques. For F8 and F11 test functions, BGSA and BPSO are the succeeding algorithms, respectively. For F9, F10, and F12 test functions, BBA is the subsequent best algorithm. When the performance indicators of the F13 function are examined, it is seen that the BGWO algorithm produces higher performance than other methods. BEPO is the succeeding technique for this test function. It can be seen from results that BEPO has better diversification capability than the existing binary metaheuristics. The sigmoidal transfer function and adaptive nature of BEPO are responsible for diversification.
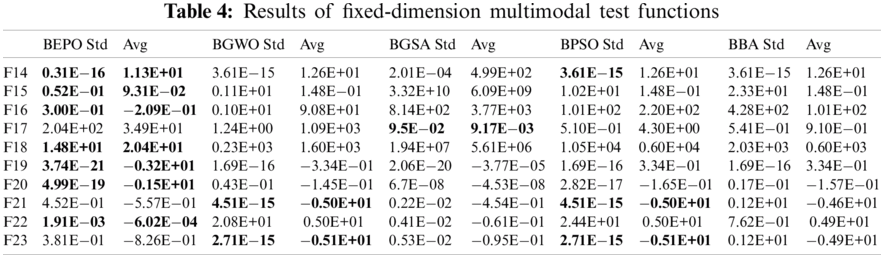
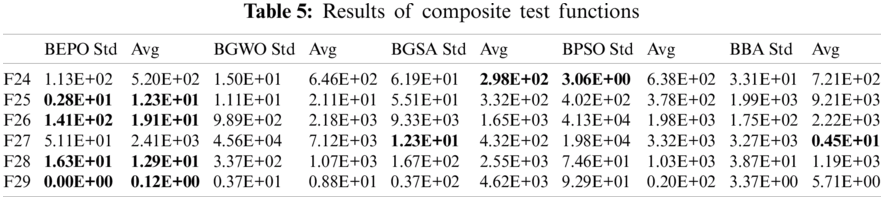
Tab. 4 illustrates the results obtained from BEPO and the above-mentioned algorithms on fixed dimensional multimodal test functions. BEPO offers better results than the existing metaheuristics for F14-F22 test functions except for F17 and F21. For the F17 function, BGSA outperforms the other SOTA techniques in terms of the fitness function. Furthermore, BGWO and BPSO perform better results than the binary metaheuristic techniques for F21 and F23 functions. The results divulge that BEPO can explore the global optimal solution. The results obtained from BEPO and binary metaheuristics on composite test functions are shown in Tab. 5. BGSA offers the optimal solution for the F24 test function. For this function, BEPO is the subsequent best algorithm. BEPO outperforms the binary metaheuristics for F25-F29 functions except for F27. For the F27 function, BBA gives an optimal solution. BEPO is the succeeding algorithm.
The proposed BEPO algorithm has better diversification and intensification than the existing algorithms. This is due to the adaptive nature of the proposed BEPO algorithm. Fig. 3 illustrates the convergence curves obtained from BEPO and the existing binary metaheuristics on F7, F9, F14, and F27 functions. It is observed from this figure that BEPO has better convergence than the existing algorithms.
5 Performance Evaluation of BEPO for Feature Selection Tasks
In this section the performance of the BEPO algorithm is analyzed in detail on the feature selection problem. Feature selection is a well-known optimization problem that uses discrete search space. The main purpose of feature selection techniques in the literature is to increase prediction performance. In order to demonstrate the performance of BEPO in the feature selection problems, it is compared with the well-known existing binary metaheuristics.
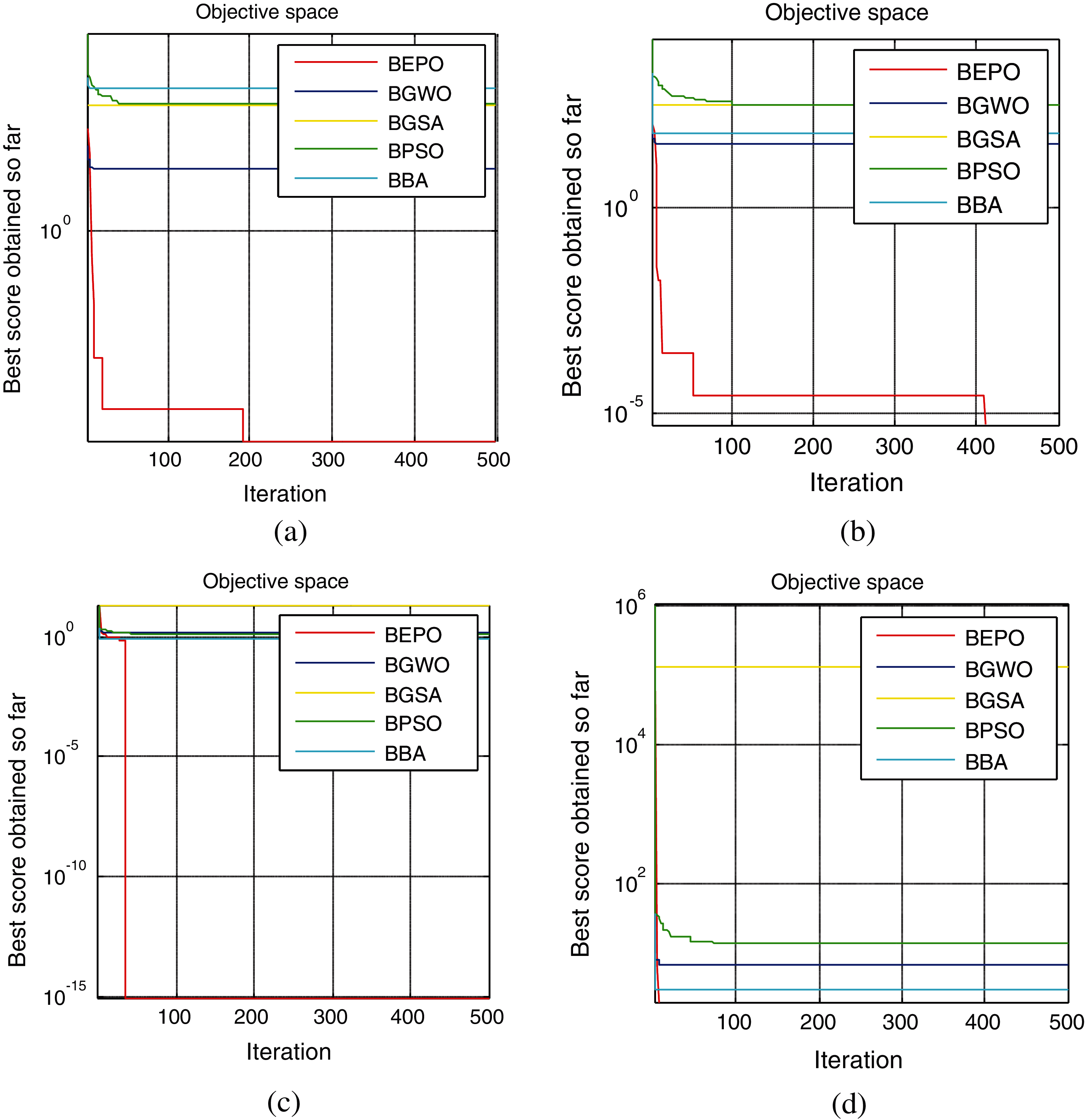
Figure 3: Convergence analysis of BEPO and other metaheuristics on benchmark functions (a) F7, (b) F9, (c) F14, and (d) F27
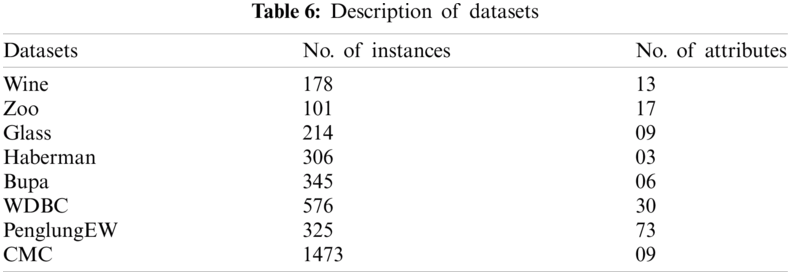
5.1 Datasets Used and Experimental Setup
The eight UCI datasets [49] have been used to validate the performance of BEPO. The detailed description of these datasets is mentioned in Tab. 6. BEPO is compared with the recently developed binary metaheuristics that were mentioned in Section 4.2 using the same parameter settings. The following fitness function is used to evaluate the feature selection performance of the proposed BEPO algorithm and compare it with current SOTA techniques.
where
The performance of the proposed BEPO algorithm is compared with the current binary metaheuristic algorithms in Tabs. 2, 3, 4, and 5. In all tables, the BEPO algorithm mostly produces higher performances compared to other algorithms. However, for some test functions, it produces similar results or lower performance compared with other algorithms. This situation is naturally met because all proposed algorithms are nature-inspired. In functions where the best solution is not produced by BEPO, BEPO is generally among the top three best solutions. From this point of view, BEPO can be considered as the most suitable algorithm for real-life problems. Fig. 3 provides information about the speed at which the binary algorithms reach the solution. According to Fig. 3, the BEPO algorithm can reach the most appropriate solution quite quickly compared to other algorithms. When all these binary SOTA approaches are evaluated in terms of speed, the proposed BEPO algorithm stands out for real-life applications.
Tab. 7 presents the results of comparing the BEPO algorithm with other binary metaheuristic methods for feature selection tasks. Accordingly, experiments of all mentioned binary optimization algorithms are carried out using eight benchmark datasets. The resulting performances show that BEPO produces higher performances in all datasets for feature selection tasks than other algorithms according to the average best fitness value. In Tab. 7, the average best fitness values produced by BGWO and BGSA algorithms are quite striking compared to the others. Fig. 4 compares the learning speed of the proposed BEPO algorithm and other algorithms. It is observed from the figure that BEPO has better convergence than the other algorithms. In the feature selection task, it is seen that the difference between the number of iterations decreases. However, it turns out that the proposed BEPO algorithm is more suitable for the solution of real-life feature selection problems in terms of both performance and speed. In some large dimensional datasets, BEPO may have slow computational speed due to the utilization of transfer functions.
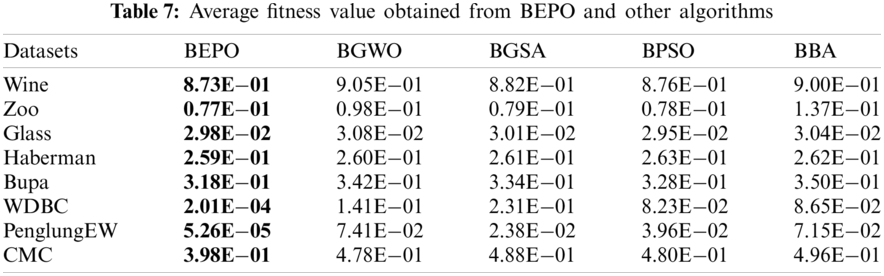
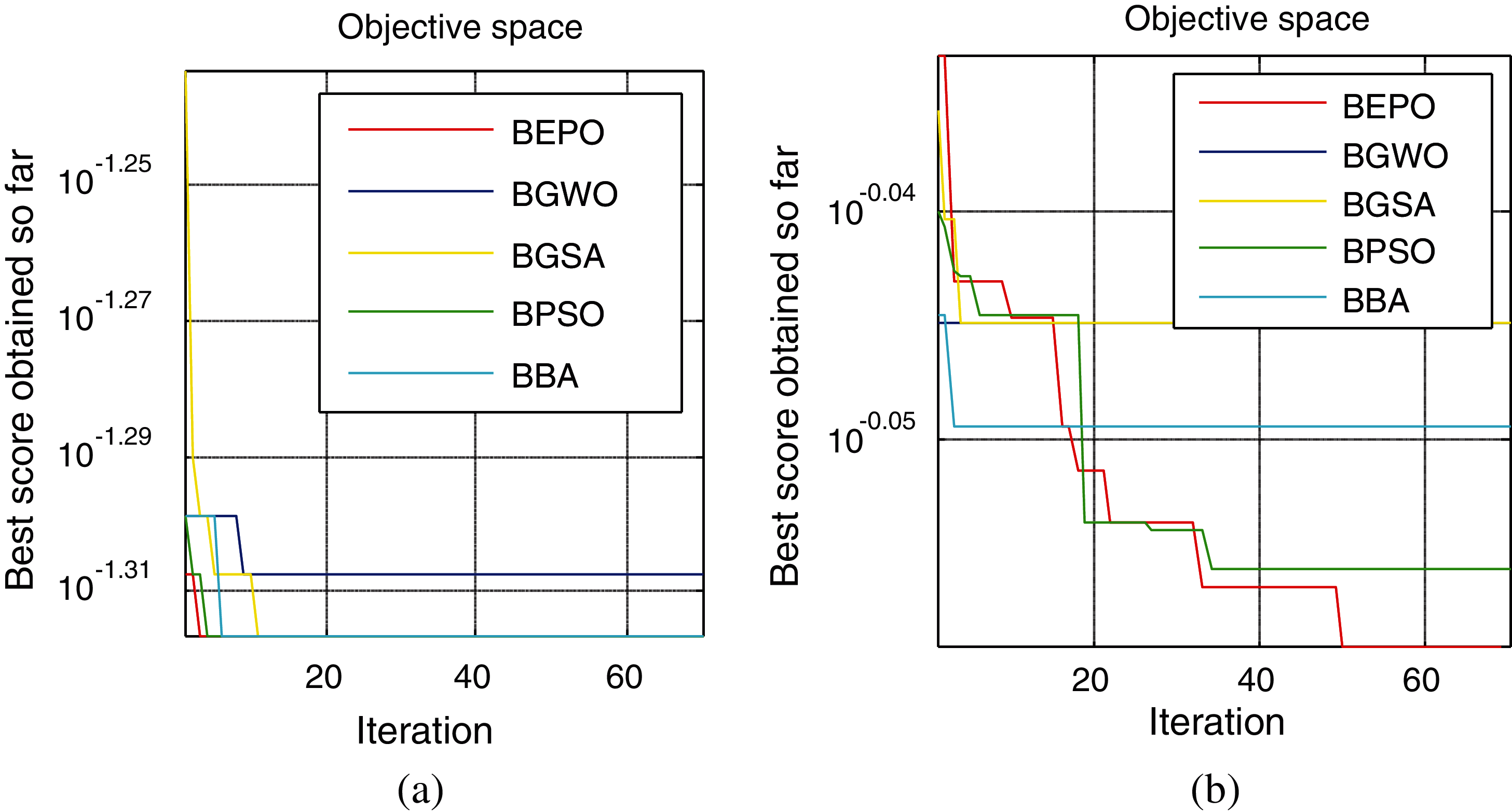
Figure 4: Convergence analysis of BEPO and binary metaheuristics on (a) Glass, (b) Wine datasets
Nowadays, optimization solutions that enable us to reach the most suitable solutions in almost every field in the shortest time are mostly offered in the continuous search space. However, studies in the literature show that many real-life problems are more appropriate in binary search space and in a discrete way. For this purpose, binary versions of existing optimization algorithms are being studied extensively. In this study, the binary version of the well-known EPO algorithm, which is dubbed BEPO, is proposed to solve binary problems in the binary search space. The position updating mechanism of the original EPO is modified to switch to the binary search space. For this purpose, binarization is performed using the sigmoidal transfer function. The performance of the proposed BEPO algorithm is tested for general optimization and feature selection problems in two separate sections. First, the performance of the proposed BEPO algorithm is evaluated using 29 benchmark test functions. Experimental results reveal that BEPO outperforms the existing binary metaheuristics. The superior results of the proposed method are presented according to different evaluation criteria and compared with SOTA methods. The statistical significance of the proposed algorithm is analyzed through ANOVA. In the second stage of the experiments, the effects of BEPO algorithm on the solution of the feature selection problem are analyzed. The results obtained show that BEPO can be used effectively in feature selection tasks with high performance. The detailed analysis performed in this study reveals that the proposed BEPO algorithm is the most suitable method for both real-life general optimization and real-life feature selection problems. In future studies, the use of BEPO algorithm with hybrid structures will be studied. Effects of the BEPO algorithm hybridization on performance will be investigated in detail. Also, BEPO variants will be studied to solve different real-world problems.
Acknowledgement: The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work.
Funding Statement: This work was supported by the Deanship of Scientific Research at King Khalid University through the Research Groups Program under Grant Number RGP.1/95/42.
Conflicts of Interest: The authors declare that they have no conflicts of interest.
1. A. G. Hussien, E. H. Houssein and A. E. Hassanien, “A binary whale optimization algorithm with hyperbolic tangent fitness function for feature selection,” in Proc. of the 8th Int. Conf. on Intelligent Computing and Information Systems (ICICISCairo, Egypt, pp. 166–172, 2017. [Google Scholar]
2. A. Kumar, A. Levine, T. Goldstein and S. Feizi, “Curse of dimensionality on randomized smoothing for certifiable robustness,” in Proc. of the Int. Conf. on Machine Learning, Vienna, Austria, pp. 5458–5467, 2020. [Google Scholar]
3. A. G. Hussien, D. Oliva, E. H. Houssein, A. A. Juan and X. Yu, “Binary whale optimization algorithm for dimensionality reduction,” Mathematics, vol. 8, no. 10, pp. 1821, 2020. [Google Scholar]
4. A. H. Halim, I. Ismail and S. Das, “Performance assessment of the metaheuristic optimization algorithms: An exhaustive review,” Artificial Intelligence Review, vol. 54, pp. 2323–2409, 2021. [Google Scholar]
5. E. Bonabeau, M. Dorigo and G. Théraulaz, “Swarm Intelligence: From Natural to Artificial Systems,” Oxford, United Kingdom: Oxford University Press, 1999. [Google Scholar]
6. J. R. Koza and R. Poli, “Genetic Programming: On the Programming of Computers by Means of Natural Selection,” Cambridge, Massachusetts, United States: MIT Press, 1992. [Google Scholar]
7. H. G. Beyer and H. P. Schwefel, “Evolution strategies –a comprehensive introduction,” Natural Computing, vol. 1, no. 1, pp. 3–52, 2002. [Google Scholar]
8. E. Rashedi and H. Nezamabadi-pour, “GSA: A gravitational search algorithm,” Information Sciences, vol. 179, no. 13, pp. 2232–2248, 2009. [Google Scholar]
9. S. Kirkpatrick, C. D. Gelatt and M. P. Vecchi, “Optimization by simulated annealing,” Science, vol. 220, no. 4598, pp. 671–680, 1983. [Google Scholar]
10. O. K. Erol and I. Eksin, “A new optimization method: Big bang-big crunch,” Advances in Engineering Software, vol. 37, no. 2, pp. 106–111, 2006. [Google Scholar]
11. H. Du, X. Wu and J. Zhuang, “Small-world optimization algorithm for function optimization,” in Int. Conf. on Natural Computation, Xi'an, China, pp. 264–73, 2006. [Google Scholar]
12. A. Hatamlou, “Black hole: A new heuristic optimization approach for data clustering,” Information Sciences, vol. 222, pp. 175–184, 2013. [Google Scholar]
13. R. A. Formato, “Central force optimization: A new deterministic gradient- like optimization metaheuristic,” Opsearch, vol. 46, no. 1, pp. 25–51, 2009. [Google Scholar]
14. B. Alatas, “ACROA: Artificial chemical reaction optimization algorithm for global optimization,” Expert Systems with Applications, vol. 38, no. 10, pp. 13170–13180, 2011. [Google Scholar]
15. H. S. Hosseini, “Principal components analysis by the galaxy-based search algorithm: A novel metaheuristic for continuous optimization,” International Journal of Computational Science and Engineering, vol. 6, no. 10, pp. 132–140, 2011. [Google Scholar]
16. G. Dhiman and V. Kumar, “Spotted hyena optimizer: A novel bio-inspired based metaheuristic technique for engineering applications,” Advances in Engineering Software, vol. 114, pp. 48–70, 2017. [Google Scholar]
17. S. Mirjalili, S. M. Mirjalili and A. Lewis, “Grey wolf optimizer,” Advances in Engineering Software, vol. 69, no. 1, pp. 46–61, 2014. [Google Scholar]
18. J. Kennedy and R. C. Eberhart, “Particle swarm optimization,” in Proc. of the IEEE Int. Conf. on Neural Networks, Perth, WA, Australia, pp. 1942–1948, 1995. [Google Scholar]
19. X. S. Yang, “A new metaheuristic bat-inspired algorithm,” Studies in Computational Intelligence, vol. 284, pp. 65–74, 2010. [Google Scholar]
20. M. Dorigo, M. Birattari and T. Stutzle, “Ant colony optimization - artificial ants as a computational intelligence technique,” IEEE Computational Intelligence Magazine, vol. 1, pp. 28–39, 2006. [Google Scholar]
21. X. Lu and Y. Zhou, “A novel global convergence algorithm: bee collecting pollen algorithm,” in Proc. of the 4th Int. Conf. on Intelligent Computing, Shangai, China, pp. 518–525, 2008. [Google Scholar]
22. C. Yang and J. Chen, “Algorithm of marriage in honey bees optimization based on the wolf pack search,” in Proc. of the Int. Conf. on Intelligent Pervasive Computing, Jeju, South Korea, pp. 462–467, 2007. [Google Scholar]
23. S. Mirjalili, “Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm,” Knowledge-Based Systems, vol. 89, pp. 228–249, 2015. [Google Scholar]
24. T. Singh, N. Saxena, M. Khurana, D. Singh, M. Abdalla et al., “Data clustering using moth-flame optimization algorithm,” Sensors, vol. 21, no. 12, pp. 4086, 2021. [Google Scholar]
25. G. Dhiman and V. Kumar, “Seagull optimization algorithm: Theory and its applications for large-scale industrial engineering problems,” Knowledge-Based Systems, vol. 165, pp. 169–196, 2019. [Google Scholar]
26. G. Dhiman and V. Kumar, “Emperor penguin optimizer: A bio-inspired algorithm for engineering problems,” Knowledge-Based Systems, vol. 159, pp. 20–50, 2018. [Google Scholar]
27. B. Chizi, L. Rokach and O. Maimon, “A survey of feature selection techniques,” Encyclopedia of Data Warehousing and Mining, pp. 1888–1895, 2009. [Google Scholar]
28. Y. Xue, B. Xue and M. Zhang, “Self-adaptive particle swarm optimization for large-scale feature selection in classification,” ACM Transactions on Knowledge Discovery from Data, vol. 13, no. 5, pp. 1–27, 2019. [Google Scholar]
29. E. Emary, H. M. Zawbaa and A. E. Hassanien, “Binary grey wolf optimization approaches for feature selection,” Neurocomputing, vol. 172, pp. 371–381, 2016. [Google Scholar]
30. K. Srikanth, L. K. Panwa, B. K. Panigrahi, E. H. Viedma, A. K. Sangaiah et al., “Meta-heuristic framework: Quantum inspired binary grey wolf optimizer for unit commitment problem,” Computers & Electrical Engineering, vol. 70, pp. 243–260, 2018. [Google Scholar]
31. M. A. Khanesar, M. Teshnehlab and M. A. Shoorehdeli, “A novel binary particle swarm optimization,” in in Proc. of Mediterranean Conf. on Control & Automation, Athens, Greece, pp. 1–6, 2007. [Google Scholar]
32. S. Lee, S. Soak, S. Oh, W. Pedrycz and M. Jeon, “Modified binary particle swarm optimization,” Progress in Natural Science, vol. 18, no. 9, pp. 1161–1166, 2008. [Google Scholar]
33. E. Rashedi, H. Nezamabadi-pour and S. Saryazdi, “BGSA: Binary gravitational search algorithm,” Natural Computing, vol. 9, no. 3, pp. 727–745, 2010. [Google Scholar]
34. S. Mirjalili, S. M. Mirjalili and X. S. Yang, “Binary bat algorithm. neural computing and applications,” Neural Computing and Applications, vol. 25, no. 3, pp. 663–681, 2014. [Google Scholar]
35. V. Kumar, D. Kumar, M. Kaur, D. Singh, S. A. Idris et al., “A novel binary seagull optimizer and its application to feature selection problem,” IEEE Access, vol. 9, pp. 103481–103496, 2021. [Google Scholar]
36. X. Wang, J. Yang, X. Teng, W. Xia and R. Jensen, “Feature selection based on rough sets and particle swarm optimization,” Pattern Recognition Letters, vol. 28, no. 4, pp. 459–471, 2007. [Google Scholar]
37. X. Yuan, H. Nie, A. Su, L. Wang and Y. Yuan, “An improved binary particle swarm optimization for unit commitment problem,” Expert Systems with Applications, vol. 36, no. 4, pp. 8049–8055, 2009. [Google Scholar]
38. G. Chandrashekar and F. Sahin, “A survey on feature selection methods,” Computers and Electrical Engineering, vol. 40, no. 1, pp. 16–28, 2014. [Google Scholar]
39. Y. Xue, T. Tang, W. Pang and A. X. Liu, “Self-adaptive parameter and strategy based particle swarm optimization for large-scale feature selection problems with multiple classifiers,” Applied Soft Computing, vol. 88, pp. 106031, 2020. [Google Scholar]
40. B. Xue, M. Zhang, W. N. Browne and X. Yao, “A survey on evolutionary computation approaches to feature selection,” IEEE Transactions on Evolutionary Computation, vol. 20, no. 4, pp. 606–626, 2016. [Google Scholar]
41. Y. Zhang, D. W. Gong and J. Cheng, “Multi-objective particle swarm optimization approach for cost-based feature selection in classification,” IEEE/ACM Transactions on Computational Biology and Bioinformatics, vol. 14, no. 1, pp. 64–75, 2017. [Google Scholar]
42. Y. Zhang, D. W. Gong, X. Z. Gao, T. Titan and X. Y. Sun, “Binary differential evolution with self-learning for multi-objective feature selection,” Information Sciences, vol. 507, pp. 67–85, 2020. [Google Scholar]
43. Y. Zhang, S. Cheng, Y. Shi, D. W. Gong and X. Zhao, “Cost-sensitive feature selection using two-archive multi-objective artificial bee colony algorithm,” Expert Systems with Applications, vol. 137, pp. 46–58, 2019. [Google Scholar]
44. J. Digalakis and K. Margaritis, “On benchmarking functions for genetic algorithms,” International Journal of Computer Mathematics, vol. 77, no. 4, pp. 481–506, 2001. [Google Scholar]
45. X. S. Yang, “Firefly algorithm, stochastic test functions and design optimization,” International Journal of Bio-Inspired Computation, vol. 2, no. 2, pp. 78–84, 2010. [Google Scholar]
46. V. Kumar and A. Kaur, “Binary spotted hyena optimizer and its application to feature selection,” Journal of Ambient Intelligence and Humanized Computing, vol. 11, pp. 2625–2645, 2020. [Google Scholar]
47. H. Nezamabadi-pour, M. Rostami-shahrbabaki and M. M. Farsangi, “Binary particle swarm optimization: Challenges and new solutions,” CSI on Computer Science and Engineering, vol. 6, no. 1, pp. 21–32, 2008. [Google Scholar]
48. R. Y. M. Nakamura, L. A. M. Pereira, K. A. Costa, D. Rodrigues, J. P. Papa et al., “BBA: A binary bat algorithm for feature selection,” in 25th SIBGRAPI Conference on Graphics, Patterns and Images, pp. 291–297, 2012. [Google Scholar]
49. A. Frank and A. Asuncion, In UCI Machine Learning Repository, 2021. [Online]. Available: https://archive.ics.uci.edu/ml/index.php. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |