DOI:10.32604/cmc.2022.020449

| Computers, Materials & Continua DOI:10.32604/cmc.2022.020449 |  |
| Article |
Training Multi-Layer Perceptron with Enhanced Brain Storm Optimization Metaheuristics
1Singidunum University, Danijelova, 11000, Belgrade, Serbia
2National Center for Robotics and IoT, Communication and Information Technology Research Institute, King Abdulaziz City for Science and Technology (KACST), Riyadh, 12371, Saudi Arabia
3Department of Computer Science and Engineering, CHRIST (Deemed to be University), Bangalore, 560074, India
4Prince Sattam Bin Abdulaziz University, College of Computer Engineering and Sciences, Alkharj, 11942, Saudi Arabia
*Corresponding Author: Khaled Alhazmi. Email: khazmi@kacst.edu.sa
Received: 24 May 2021; Accepted: 07 July 2021
Abstract: In the domain of artificial neural networks, the learning process represents one of the most challenging tasks. Since the classification accuracy highly depends on the weights and biases, it is crucial to find its optimal or suboptimal values for the problem at hand. However, to a very large search space, it is very difficult to find the proper values of connection weights and biases. Employing traditional optimization algorithms for this issue leads to slow convergence and it is prone to get stuck in the local optima. Most commonly, back-propagation is used for multi-layer-perceptron training and it can lead to vanishing gradient issue. As an alternative approach, stochastic optimization algorithms, such as nature-inspired metaheuristics are more reliable for complex optimization tax, such as finding the proper values of weights and biases for neural network training. In this work, we propose an enhanced brain storm optimization-based algorithm for training neural networks. In the simulations, ten binary classification benchmark datasets with different difficulty levels are used to evaluate the efficiency of the proposed enhanced brain storm optimization algorithm. The results show that the proposed approach is very promising in this domain and it achieved better results than other state-of-the-art approaches on the majority of datasets in terms of classification accuracy and convergence speed, due to the capability of balancing the intensification and diversification and avoiding the local minima. The proposed approach obtained the best accuracy on eight out of ten observed dataset, outperforming all other algorithms by 1–2% on average. When mean accuracy is observed, the proposed algorithm dominated on nine out of ten datasets.
Keywords: Artificial neural network; optimization; metaheuristics; algorithm hybridization; brain storm optimization
Machine learning (ML) belongs to the group of technologies that have recently become a major part of our lives. The main objective of ML can be summed up as the process of enabling computers and various computer systems to learn independently of humans. Deep learning is the part of ML that focuses on the application of algorithms that mimic the human brain structure (neurons and connections between them) and its functionality, also known as artificial neural networks (ANNs). ANNs consist of processing nodes (known under the same name as their counterparts in the human brain—neurons) that are inter-connected. The ANNs goal is to transform the set of input values to the set of output values, based on the characteristics of the processing neurons and the weights assigned to the connections between them.
ANNs must be adapted for each specific problem, as there is no single solution that fits all possible applications. This is done by changing the connections among the neurons in the network. The learning process of an ANN typically consists of the optimization of the network parameters (the weights of the connections and the biases). During the learning process, the network is fed with a set of input data that passes through the network in order to get the output prediction values. The obtained output values are then compared to the expected values to calculate the classification error rate measured with the loss function. The process continues with updating the weights and biases of ANN to reduce the total loss, therefore obtaining a better model. While the loss is being reduced, the network will slowly start to give the desired output for a specified problem.
Two major tasks must be addressed for any neural network before applying it to a specific problem. The first task is to determine the adequate structure of the neural network—the problem known as hyperparameter optimization. The second task is to train the network for a given problem. The ANNs are commonly trained by the standard optimizers, that are based on both deterministic and stochastic approaches. ANN training was until recently performed mostly by gradient descent and backpropagation. After calculating the loss, it needs to be propagated backward, starting by the output layer of the ANN, to the neurons positioned in the hidden layer that are producing the output. As every single neuron in the hidden layer contributes partially to the final output of the network, it will receive just a fraction of the overall loss, relative to its contribution. After propagating the loss information backward throughout the complete network, it is possible to adjust the connections’ weights, with an objective to make the loss close to zero for the next usage of the network. The gradient descent and back-propagation belong to the deterministic methods, with several clear drawbacks, such as stagnating in the local optima, vanishing gradient issue, and very slow speed of convergence, that can tamper the network training process.
The above-mentioned ANN challenges, namely the hyperparameter optimization and the network training, both belong to the group of NP-hard problems. To solve them, stochastic methods must be used, such as metaheuristics approaches. The nature-inspired algorithms are an appropriate choice as they can improve the ANN's training search capabilities by reducing the classification error at a faster rate than the gradient descent approach.
The main motivation behind the research presented in this paper is defined by the following research questions: How to implement a neural network training method that will improve the accuracy and speed of the training process? How to implement an efficient nature-inspired metaheuristics approach for the purpose of neural network training? The main objective of this research is to provide answers to those research questions in the following way.
• Implement an improved hybrid brain storm optimization (BSO) metaheuristic that outperforms the original BSO and its known variants both in terms of converging speed and quality of solutions and
• Use the proposed BSO method to optimize the connection weight and biases in the neural network, which will improve the accuracy and execute faster than other already existing approaches.
The remainder of the paper is structured in the following way: Section 2 gives the background and extensive survey about the related work. Then, Section 3 describes the artificial neural networks together with their optimization. Section 4 presents the basic BSO algorithm, highlights its drawbacks, and introduces the proposed method. Section 5 consists of the unconstrained simulations, followed by the experiment of artificial neural network training optimization and hidden unit optimization. In the end, Section 6 concludes the paper.
NP-hardness defines a class of problems that have a significant impact on modern computer science. A number of practical challenges from different application domains such as scheduling, routing, wireless sensor, and ad hoc networks localization, network lifetime maximization, and cryptography belong to this group. Neural network training and optimization of hyperparameters belong to this group as well. NP-hard problems are challenging because they cannot be solved by applying traditional deterministic methods within an acceptable time frame. Instead, these problems must be tackled by stochastic methods that typically focus on finding a solution that is good enough and acceptable for a given problem, although not guaranteed to be the best, in a much shorter time frame [1].
The swarm intelligence (SI) metaheuristics belong to the nature-inspired approaches. They are inspired by collective behavior and social activities found in large groups of simple insects and animals. A large number of SI approaches exist nowadays, both in original implementations and in hybrid/enhanced variations, that were proven to be efficient, including the cuckoo search (CS) [2,3], the firefly algorithm (FA) [4], the whale optimization algorithm [5] and the bat algorithm [6].
The variety of application domains where SI methods have been successfully used is wide, and in several cases, the obtained results can be considered to be world-class. The most successful SI applications include the COVID-19 cases prediction [7] the cloud systems and the scheduling problem [8]. WSN localization and energy-efficient operation and numerous others applications [9].
The ANN learning task is the most difficult problem that belongs to the group of NP-hard challenges, and it has been addressed by numerous SI approaches. The paper [10] proposed the whale optimization algorithm (WOA) for intrusion detection task ANN's training. The proposed ANN is capable to perform the classification of different classes of cyber-attacks, and also power-based incidents. Research presented in [11] used the grasshopper optimization algorithm (GOA) in a hybrid approach to train the multilayer perceptron (MLP). The research published in [12] proposed an enhanced PSO method that utilized the gradient penalties for optimal CNN structure generation and validated it on a set of EEG signals with three emotional states of the participants in the experiment. Another problem that neural networks face is over-fitting. It was also tackled with the SI-based approach in [13], where the researchers have developed and tested four SI metaheuristics (FA, BA, CS, and PSO) and used them to determine the appropriate selection of the regularization parameter dropout. Another recent paper used the enhanced firefly algorithm (FA) to optimize the feature selection process, with promising results [14]. GA was also recently used in a hybrid machine learning approach to predict the number of COVID-19 cases [15]. Another GA approach with ranked mutation was used for discovery of high utility itemsets in [16]. Stellar mass black hole optimization was used for utility mining in [17]. There were also numerous recent published papers dealing with different applications of the machine learning and deep learning approaches, ranging from the sentiment analysis [18], flood prediction [19], the Dengue disease prediction [20], other medical diagnostics [21–23], all the way to eHealth and IoT [24–26].
3 ANN Training Process and Hyper-Parameter Optimization
The training process of the ANNs represents a crucial task that is required to build a model that will be able to achieve better results. The main objective of the network training process is to optimize the loss function, which takes place in the weight learning phase. Another challenge during the training process of the ANNs is the overfitting problem, which arises when a large difference exists in the training and the test accuracy. The ANN's main purpose is to achieve the appropriate final model that will have good performances on both training data and the new data that is later fed to it. In this paper, multilayer perceptron (MLP) is considered, with an objective to perform the optimization of the hidden unit number in the hidden layer. Additionally, the optimization of the connection weights and biases has been conducted.
The typical structure of the MLP with one hidden layer is depicted in Fig. 1. The neurons between layers are connected, while each connection has the assigned weight. Each individual neural node can perform two fundamental operations: summation and activation. The summation operation is executed by utilizing the product of the inputs, weights, and bias, as defined by the Eq. (1):
where, n marks the number of inputs, Ii denotes the i-th input value, ωij represents the connection weight, and lastly, βj represents the bias.
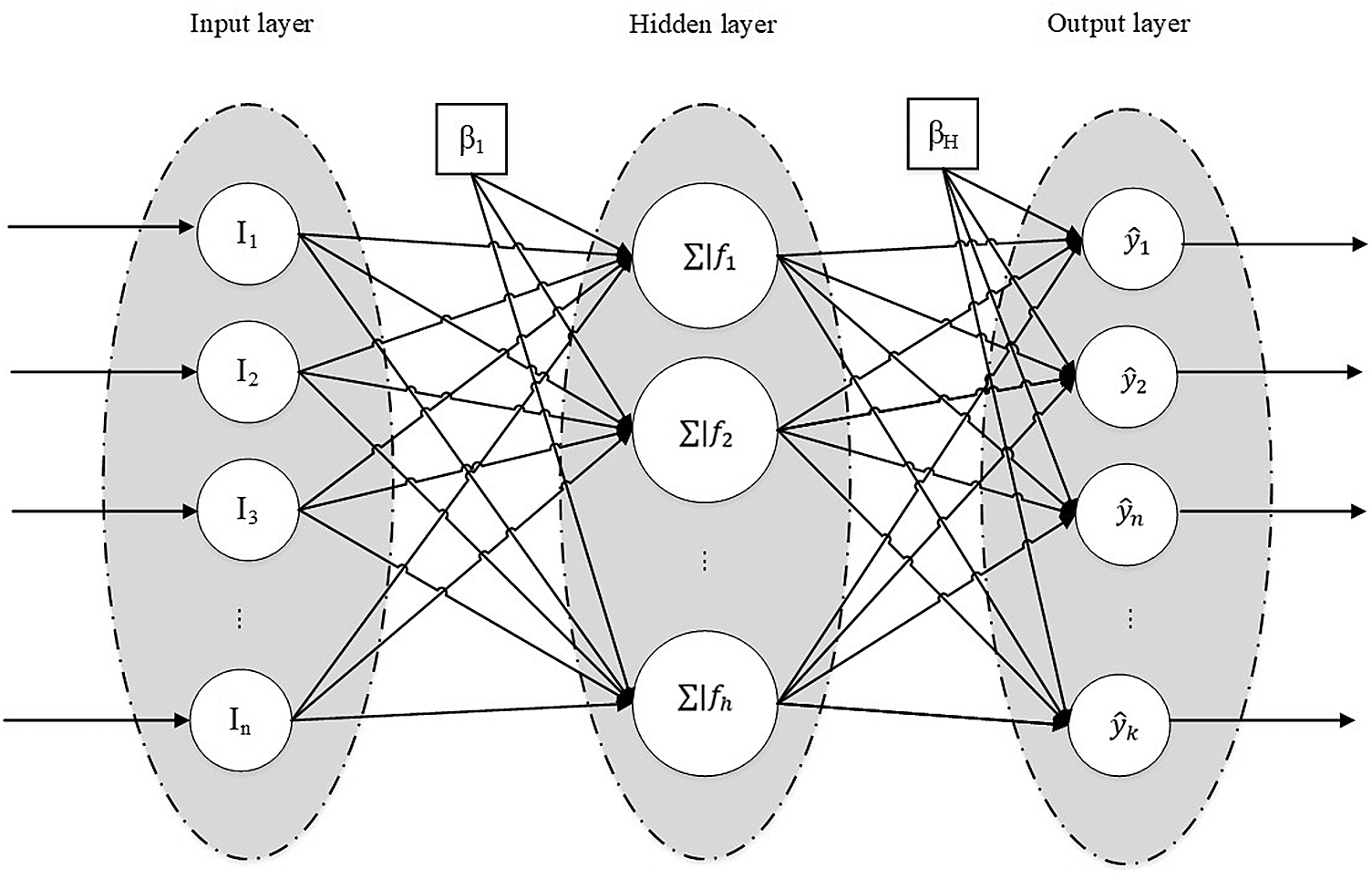
Figure 1: MLP architecture with one hidden layer
The activation functionality is performed over the result of the Eq. (1). Various activation functions exist, one common approach is to use the S-shaped curved sigmoid function, defined by the Eq. (2):
The measurement of the ANN's performance is determined by the loss function. The common approach is the utilization of the mean squared error (MSE) as the loss function. The MSE measures the sum of the squared differences between the actual and predicted values as given by the Eq. (3):
In the end, if the observed data contains for instance two features, that correspond to three nodes in the input layer, and if the hidden layer contains three hidden units, such NN can be mathematically denoted as:
The BSO algorithm belongs to the SI group of algorithms and it was introduced by [27]. The BSO approach differs from other SI methods as it is inspired by humans and simulates the brainstorming process that is performed to generate new ideas. This method has already been used to solve different problems recently, including solving multi-objective optimization challenges and many practical problems.
4.1 Original BSO Metaheuristics
The original BSO algorithm mimics the human process of generating new ideas, known as brainstorming. The generated ideas are in the ideal case as diverse as possible. The generation of the individual solution can be mathematically expressed as given in Eq. (4):
here, xdselected denotes the d-th dimension of the population component that generates a new component,
where logsig() represents the logarithmic sigmoid function, the maximum number of rounds is limited by the maxIter, while the current iteration is marked as t, the slope of the logsig() function is defined by K, and finally, r() denotes a random number ∈ [0, 1]. Additional details regarding the original BSO are available.
4.2 Observed Deficiencies of Basic BSO and Proposed Enhanced Metaheuristics
The original BSO algorithm was tested on standard unconstrained instances retrieved from Congress on Evolutionary Computation (CEC) test suite. By analyzing achieved performance metrics, it is concluded that the exploitation process and also the balance between exploration and intensification can be better adjusted. First, the proposed improved BSO approach incorporates chaotic local search (CLS) in the initialization phase, similar to the method used in [28]. The search process has been modified by introducing the CLS approach, which helps to improve the performances of BSO in achieving the global optimum. The proposed approach is able to accelerate the search process by forcing it to proceed to the region where the optimal solution is more likely to be found, therefore it improves the exploitation process. The CLS completes when either a better solution is found or a local search termination condition is fulfilled.
The CLS is a common optimizer that helps to escape the local optimal values. For example, it was used in [29] in combination with artificial algae algorithm (AAA) to help training the MLP. In this paper, ten chaotic maps were utilized to generate the corresponding chaos sets, as shown in Tab. 1. The chaotic maps can be initialized by a number between 0 and 1. The value used for the initialization in this paper was set to 0.7.
Second, followed another common way to improve metaheuristics by hybridization with another optimization algorithm, search equation from the FA metaheuristics is introduced in the original BSO. As stated in various other research including [30]. it can be concluded that the search procedure of the FA [31], shown in Eq. (6), expresses strong exploitation in the local neighborhood of the current solutions by using the parameters α, β0, and γ, that represent randomization, attractiveness at distance r = 0 and light absorption, respectively.
where the pseudo-random value from uniform or Gaussian distribution is marked as kappa, the distance between solutions xti and xji at iteration t is represented as ri,j and
The proposed algorithm incorporates both CLS and FA search processes, to address the drawbacks of getting stuck in the local optimum and slow convergence. The CLS adds the property of not repeatedly traversing the search space, while the FA search helps the algorithm getting closer to the global optimum. As the result, the performances and converging speed of the proposed algorithm will be improved when compared to the original BSO.
In each iteration, search is conducted either by using standard BSO procedure, either FA's search expression. To control this, an additional control parameter, called search adjustment (SA) is introduced. Parameters α, β0, and γ are standard FA's parameters, where α is used as the randomization factor, β0 denotes the attractiveness of the firefly at zero distance, and γ is the air light absorption coefficient that controls the visibility of the fireflies, respectively. The proposed method was named enhanced BSO (eBSO) and its pseudo-code is given in Algorithm 1.

This section is divided into two subsections, the first subsection describes the simulation setup along with the dataset used in the experiment, the second subsection presents the measures which are used for the model evaluation, and the obtained simulation results, as well as the comparative analysis.

Due to the fact that the basic BSO was not tested on datasets used in this paper, for the purpose of this research, along with proposed eBSO, original BSO was also implemented and tested.
In the proposed eBSO algorithm, the population consists of N solutions, and each candidate solution encodes the connection weights and biases. The population can be represented as follows:
where the population is denoted by P, D refers to the dimension of a solution and N indicates the number of candidate solutions in the entire population.
The dimension of a solution is obtained by the sum of the total number of weights and biases:
where D indicates the dimension, W denotes the number of connection weights and B indicates the number of biases.
The number of connection weights is calculated as:
I denotes the number of units in the input layer, that corresponds to the number of features in a given dataset, H refers to the number of units in the hidden layer, while O indicates the number of units in the output layer, that matches the number of classes.
In this experiment, the unit number in the hidden layer is determined by the following formula:
The number of biases is obtained by the sum of the hidden unit number and output unit number, since each unit has only one bias term, and it is calculated as:
where B denotes the number of biases, H indicates the number of hidden units, and O is the number of output units.
Fig. 2 depicts the solution representation and the assignment of the solution to the MLP.
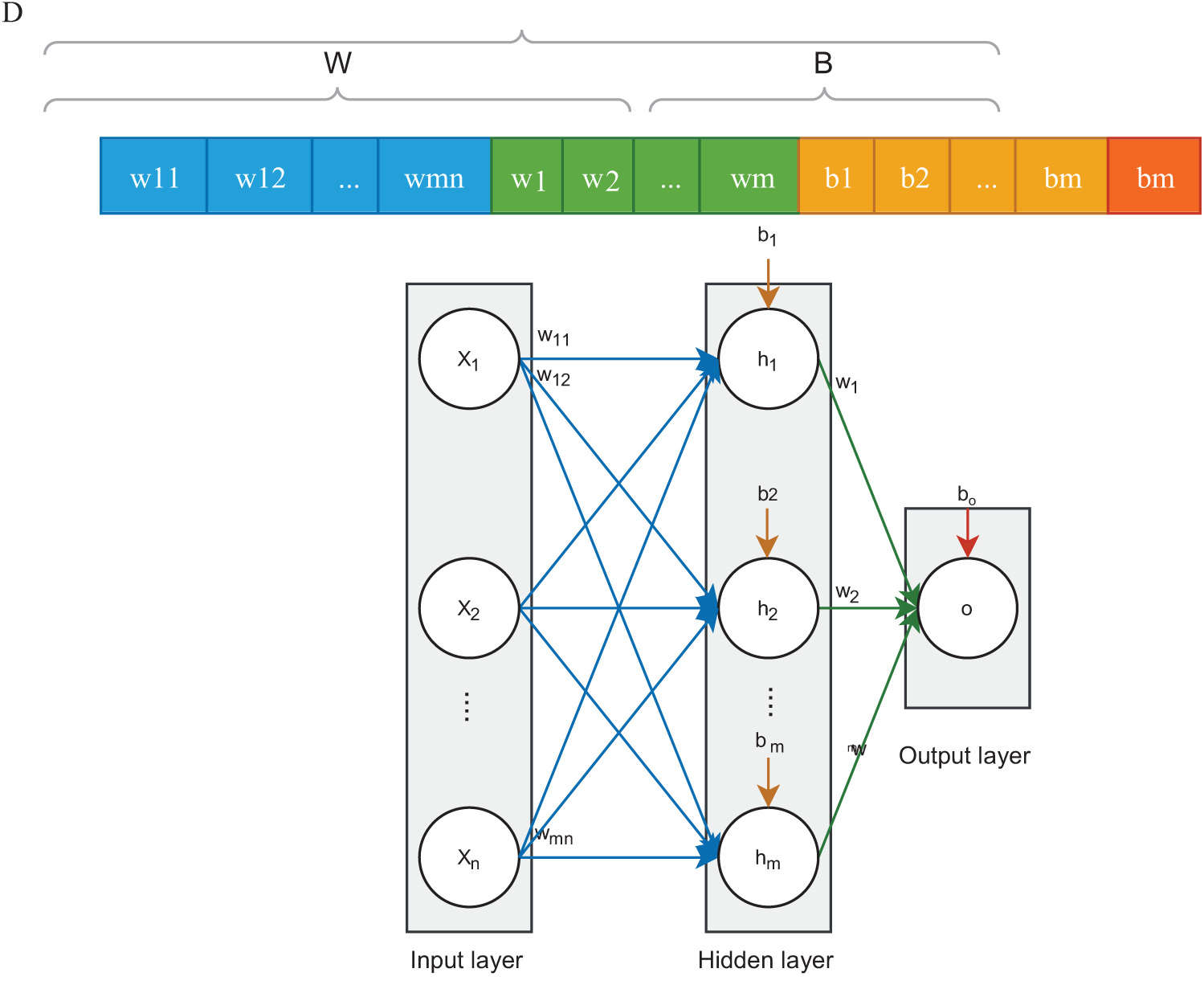
Figure 2: Solution representation and its assignment to MLP
The fitness function value determines the quality of the solutions. For the fitness evaluation, the Mean Square Error (MSE) is utilized, which calculates the squares of errors between the actual value and the predicted value and averages it for all data. The MSE is formulated as:
where the actual output is denoted by y, while


Each dataset in the experiment is normalized to speed up the process of learning, the values are scaled into the range between 0 and 1 as follows:
where xnormalized denotes the normalized data, xi is the original value, xmin, xmax denote the minimum value in a feature, and the maximum value in a feature, respectively.
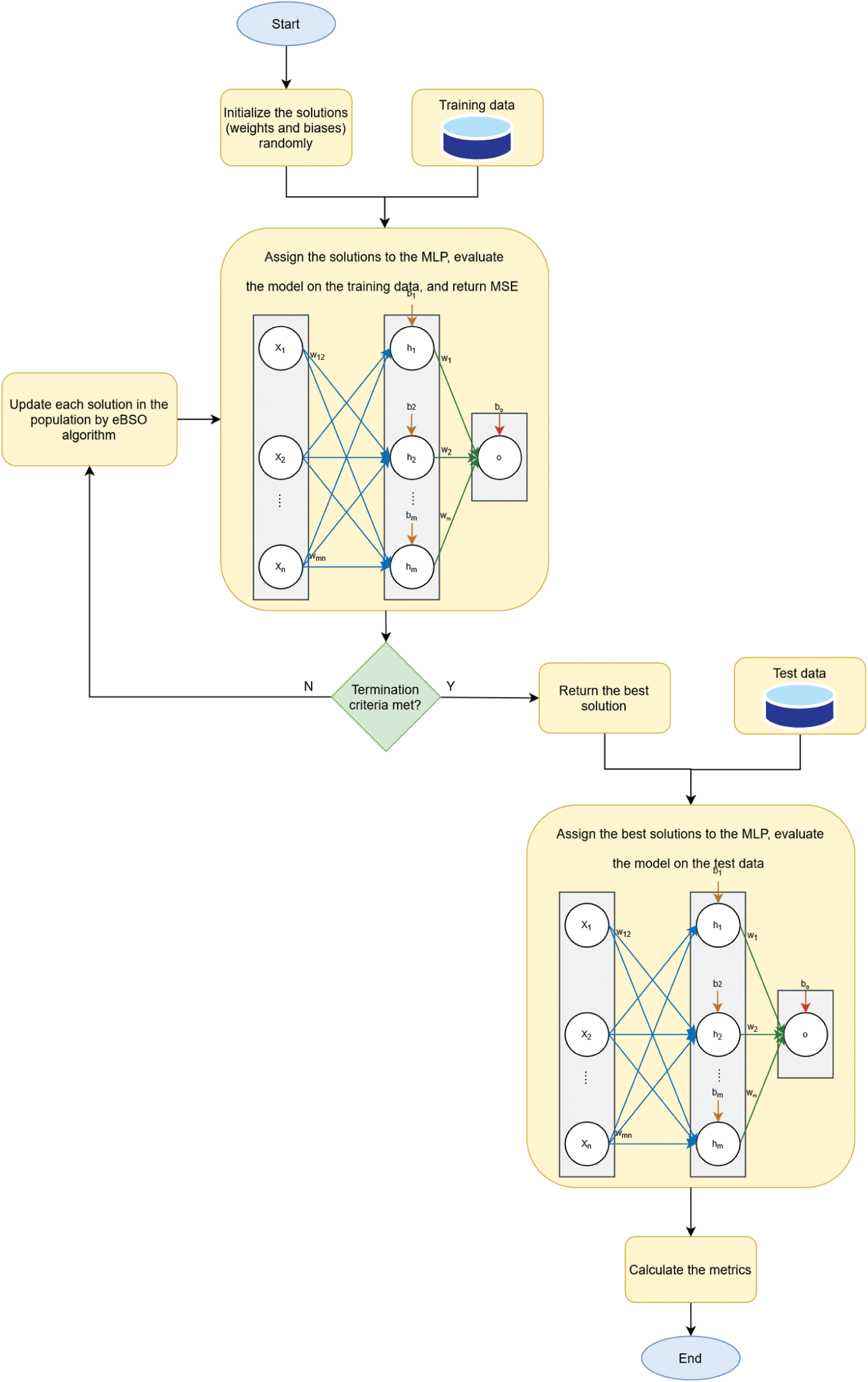
Figure 3: Representation of the eBSO based MLP training

In the simulations, 2/3 of the dataset is used for training purposes, while the remaining 1/3 is used as a test dataset. Initially, the solutions are randomly generated between −1 and 1. In the next step, the solution vector is assigned to the MLP, and the fitness value is evaluated for each solution. The solutions are updated by the proposed eBSO algorithm while the termination criteria are not reached. The algorithm returns the best solution which is applied to the test dataset. The experiment is executed in 30 independent runs, the termination criteria in each run are based on the fitness function evaluation (FFE), and it is set to 10,000. The population in the experiment consists of 40 solutions. Parameters of the original BSO, as well as the proposed eBSO are shown in Tab. 3. The flowchart of the proposed model is presented in Fig. 3.
5.2 Simulation Results and Discussion
To measure the performance of the proposed eBSO method, multiple metrics are used: mean accuracy, best accuracy, and standard deviation of the 30 independent runs. The experimental results of the eBSO are compared to the original BSO algorithm, back-propagation, and seven other state-of the-art metaheuristic-based approaches: artificial algae algorithm (AAA), particle swarm optimization (PSO), whale optimization algorithm (WOA), cuckoo search (CS), grey wolf optimizer (GWO), bat algorithm (BAT) and firefly algorithm (FFA). The experimental setup is done likewise in [29]. Tab. 4 presents the obtained results of eBSO, and the comparison with other approaches, where the results of AAA, PSO, WOA, CS, GWO, BAT, FFA, and BP are taken from [29] In Tab. 4 the boldface indicates the best results, and at the end of the table the best results are summarized for each approach.
Fig. 4 depicts the side-by-side comparison of the best classification accuracy over the proposed method and all other compared approaches.
Based on the obtained results and comparative analysis, the proposed eBSO shows superiority over other approaches on the majority of datasets. The proposed eBSO achieved the best accuracy on 8 datasets. Only GWO resulted in the best accuracy on the Chess dataset. In the case of average accuracy, GWO has the best performance on Chess datasets, while on all other datasets, eBSO achieved the highest average classification accuracy. Overall, eBSO has the best performance, the second-best method is BSO, and the third is AAA. Fig. 5 shows the convergence curve of the eBSO and BSO over the ten benchmark datasets.
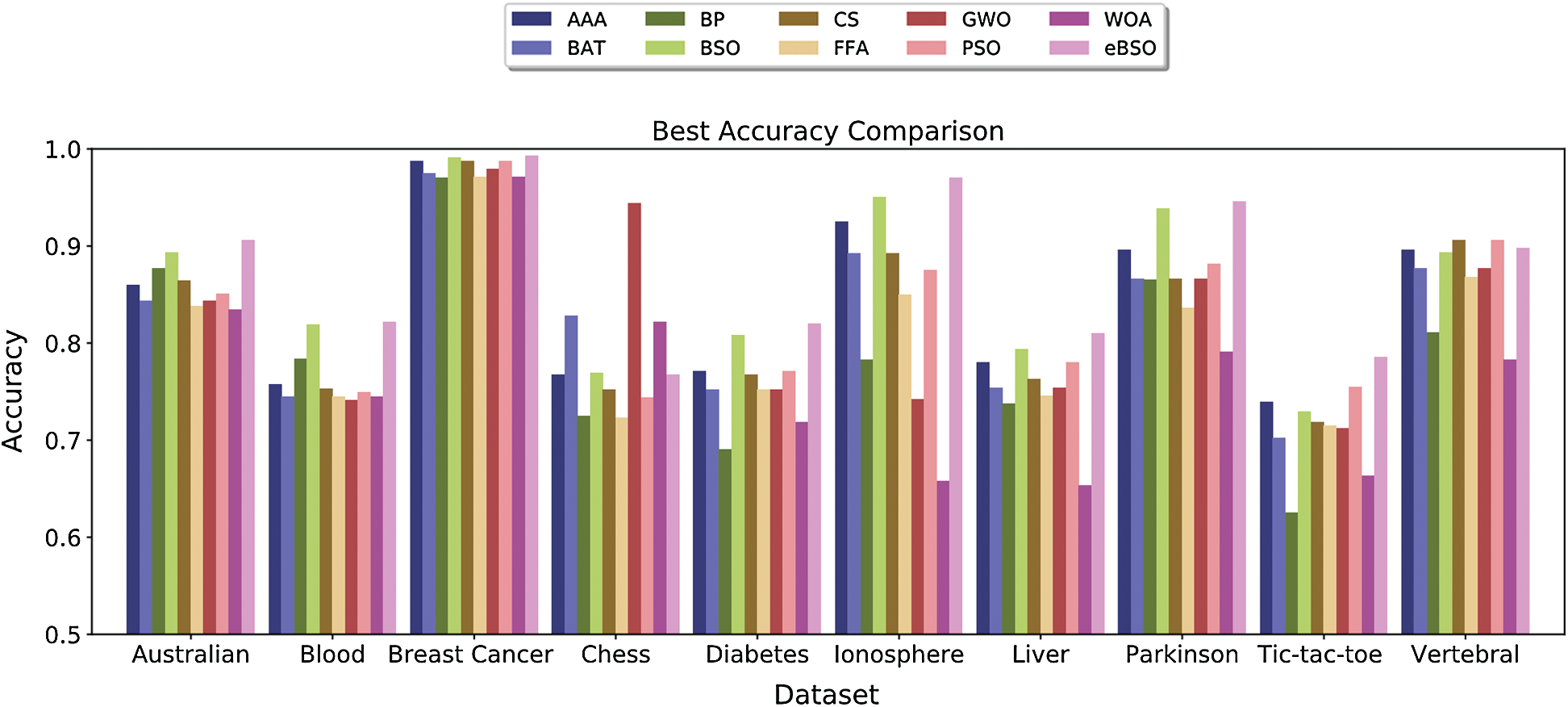
Figure 4: Comparison of the best classification accuracy
Based on the observation and analysis of the convergence graph, it is visible that the proposed enhancement on the BSO algorithm results in faster convergence. Finally, it is worth mentioning that we have also tested the proposed eBSO approach on other UCI and Keggle datasets as well, and compared the results to several other recent research papers published in the state-of-the-art journals that used the same datasets, including [32,33]. The obtained results are encouraging and indicate that the eBSO method could prove to be the superior optimizer for the feature selection problem.

Figure 5: Convergence graph of eBSO and BSO
In this research, we propose an enhanced Brain Storm Optimization algorithm for optimizing the values of connection weights and biases and to train multi-layer perceptron. The experiments are conducted on ten benchmark datasets from the UCI machine learning repository, which are Australian, Blood, Breast Cancer, Chess, Diabetes, Ionosphere, Liver, Parkinson, Tic-tac-toe, and Vertebral. The obtained results of eBSO are compared with the original BSO algorithm, BP, and seven metaheuristic-based approaches, namely, AAA, PSO, WOA, CS, GWO, and FFA. Based on the simulation results, we can conclude that eBSO is very efficient for MLP training, it is capable to find the proper set of connection weights and biases which leads to better classification accuracy. Besides the high classification accuracy, the algorithm converges fast and avoids the local optima issue.
Future research could include other parameters into the optimization process, such as the number of hidden layers, number of units. Additionally, we plan to test the proposed method on other datasets as well, to verify the performances of the eBSO even further. Moreover, we will include other nature-inspired algorithms for MLP training and improve it with different mechanisms. At the end, eBSO approach can be tested in other application domains, including cloud computing and wireless sensor networks lifetime optimization.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare no conflicts of interest to report.
1. I. Strumberger, N. Bacanin and M. Tuba, “Enhanced firefly algorithm for constrained numerical optimization, IEEE congress on evolutionary computation,” in Proc. San Sebastián, Spain, pp. 2120–2127, 2017. [Google Scholar]
2. X. S. Yang, “Firefly algorithms for multimodal optimization,” in Stochastic Algorithms: Foundations and Applications, Berlin, Heidelberg: Springer, pp. 169–178, 2009. [Google Scholar]
3. N. Bacanin, “Implementation and performance of an object-oriented software system for cuckoo search algorithm,” International Journal of Mathematics and Computers in Simulation, vol. 6, no. 1, pp. 185–193, 2012. [Google Scholar]
4. M. Zivkovic, N. Bacanin, I. Strumberger, I. Bezdan and E. Tuba, “Wireless sensor networks life time optimization based on the improved firefly algorithm,” in Proc. IWCMC, Limassol, Cyprus, pp. 1176–1181, 2020. [Google Scholar]
5. I. Strumberger, N. Bacanin, M. Tuba and E. Tuba, “Resource scheduling in cloud computing based on a hybridized whale optimization algorithm,” Applied Sciences, vol. 9, pp. 4893, 2017. [Google Scholar]
6. T. Bezdan, M. Zivkovic, E. Tuba, I. Strumberger, N. Bacanin et al., “Multi-objective task scheduling in cloud computing environment by hybridized bat algorithm,” in Proc. INFUS, Istanbul, Turkey, vol. 1197, pp. 718–725, 2020. [Google Scholar]
7. M. Zivkovic, N. Bacanin, K. Venkatachalam, A. Nayyar, A. Djordjevic et al., “Covid-19 cases prediction by using hybrid machine learning and beetle antennae search approach,” Sustainable Cities and Society, vol. 66, pp. 102669, 2021. [Google Scholar]
8. I. Strumberger, E. Tuba, M. Zivkovic, N. Bacanin, M. Beko et al., “Dynamic search tree growth algorithm for global optimization,” Technological Innovation for Industry and Service Systems, vol. 553. Springer, Cham, pp. 143–153, 2019. [Google Scholar]
9. N. Bacanin, E. Tuba, T. Bezdan, I. Strumberger and M. Tuba, “Artificial flora optimization algorithm for task scheduling in cloud computing environment,” in Proc. IDEAL, Berlin, Heidelberg: Springer, vol. 11871, pp. 437–445, 2019. [Google Scholar]
10. L. Haghnegahdar and Y. Wang, “A whale optimization algorithmtrained artificial neural network for smart grid cyber intrusion detection,” Neural Computing and Applications, vol. 32, pp. 9427–9441, 2020. [Google Scholar]
11. A. A. Heidari, H. Faris, I. Aljarah and S. Mirjalili, “An efficient hybrid multilayer perceptron neural network with grasshopper optimization,” Soft Computing, vol. 23, pp. 7941–7958, 2019. [Google Scholar]
12. Z. Gao, Y. Li, Y. Yang, X. Wang, N. Dong et al., “A gpso-optimized convolutional neural networks for eeg-based emotion recognition,” Neurocomputing, vol. 380, pp. 225–235, 2020. [Google Scholar]
13. G. H. Rosa, J. P. Papa and X. S. Yang, “Handling dropout probability estimation in convolution neural networks using meta-heuristics,” Soft Computing, vol. 22, pp. 6147–6156, 2018. [Google Scholar]
14. T. Bezdan, D. Cvetnic, L. Gajic, M. Zivkovic, I. Strumberger et al., “Feature selection by firefly algorithm with improved initialization strategy,” in Proc. CECGS, Novi Sad, Republic of Serbia, pp. 1–8, 2021. [Google Scholar]
15. M. Zivkovic, K. Venkatachalam, N. Bacanin, A. Djordjevic, M. Antonijevic et al., “Hybrid genetic algorithm and machine learning method for COVID-19 cases prediction,” in Proc. ICSES, Nepal, vol. 176, 2021. [Google Scholar]
16. S. Kannimuthu and K. Premalatha, “Discovery of high utility itemsets using genetic algorithm with ranked mutation,” Applied Artificial Intelligence, vol. 28, no. 4, pp. 337–359, 2014. [Google Scholar]
17. S. Kannimuthu and K. Premalatha, “Stellar mass black hole optimization for utility mining,” International Journal of Data Analysis Techniques and Strategies, vol. 11, no. 3, pp. 222–245, 2019. [Google Scholar]
18. P. D. Mahendhiran and S. Kannimuthu, “Deep learning techniques for polarity classification in multimodal sentiment analysis,” International Journal of Information Technology, vol. 17, no. 3, pp. 883–910, 2018. [Google Scholar]
19. C. Priyadharsini and S. Kannimuthu, “An intillegent decision making system for flood prediction,” Asian Journal of Research in Social Sciences and Humanities, vol. 7, no. 2, pp. 195–207, 2017. [Google Scholar]
20. S. Kannimuthu, D. Bhanu and K. S. Bhuvaneshwari, “Performance analysis of machine learning algorithms for dengue disease prediction,” Journal of Computational and Theoretical Nanoscience, vol. 16, no. 12, pp. 5105–5110, 2020. [Google Scholar]
21. K. A. Bhavsar, A. Abugabah, J. Singla, A. A. AlZubi, A. K. Bashir et al., “A comprehensive review on medical diagnosis using machine learning,” Computers, Materials & Continua, vol. 67, no. 2, pp. 1997–2014, 2021. [Google Scholar]
22. K. A. Bhavsar, A. Abugabah, J. Singla, A. A. AlZubi, A. K. Bashir et al., “A comprehensive review on medical diagnosis computers,” Computers, Materials & Continua, vol. 67, pp. 1997–2014, 2021. [Google Scholar]
23. K. A. Bhavsar, J. Singla, Y. D. Al Otaibi, O. Y. Song, Y. B. Zikriya et al., “Medical diagnosis using machine learning: A statistical review,” Computers, Materials & Continua, vol. 67, no. 1, pp. 107–125, 2021. [Google Scholar]
24. S. Kutia, S. H. Chauhdary, C. Iwendi, L. Liu and W. Yong, “Socio technological factors affecting user's adoption of e-health functionalities: A case study of China and Ukraine ehealth systems,” IEEE Access, vol. 7, pp. 90777–90788, 2019. [Google Scholar]
25. O. Irshad, M. U. G. Khan, R. Iqbal, S. Bashir and A. K. Bashir, “Performance optimization of IoT based biological systems using deep learning,” Computer Communication, vol. 155, pp. 24–31, 2020. [Google Scholar]
26. H. H. Attar, A. A. Solyman, A. F. Mohamed, M. R. Khosravi, V. G. Menon et al., “Efficient equalizers for OFDM and DFrFT-OCDM multicarrier systems in mobile E-health video broadcasting with machine learning perspectives,” Physical Communication, vol. 42, pp. 101173, 2020. [Google Scholar]
27. J. Xue, Y. Wu, Y. Shi and S. Cheng, “Brain storm optimization algorithm for multi-objective optimization problems,” in Proc. Chiang Mai, Thialand, pp. 513–519, 2012. [Google Scholar]
28. X. Zhao, F. Yang, Y. Han and Y. Cui, “An opposition-based chaotic salp swarm algorithm for global optimization,” IEEE Access, vol. 8, pp. 36485–3650, 2020. [Google Scholar]
29. B. Turkoglu and E. Kaya, “Training multi-layer perceptron with artificial algae algorithm,” Engineering Science and Technology, An International Journal, vol. 23, pp. 1342–1350, 2020. [Google Scholar]
30. M. Tuba and N. Bacanin, “Improved seeker optimization algorithm hybridized with firefly algorithm for constrained optimization problems. Neurocomputing, vol. 143, pp. 197–207, 2014. [Google Scholar]
31. X. S. Yang, “Firefly algorithms for multimodal optimization,” in Stochastic Algorithms: Foundations and Applications, Berlin, Heidelberg: Springer, pp. 169–178, 2009. [Google Scholar]
32. D. Zouache and F. B. Abdelaziz, “A cooperative swarm intelligence algorithm based on quantum-inspired and rough sets for feature selection,” Computers & Industrial Engineering, vol. 115, pp. 26–36, 2018. [Google Scholar]
33. R. A. Ibrahim, A. A. Ewees, D. Oliva, M. Abd Elaziz and S. Lu, “Improved salp swarm algorithm based on particle swarm optimization for feature selection,” Journal of Ambient Intelligence and Humanized Computing, vol. 10, no. 8, pp. 3155–3169, 2019. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |