[BACK]
Computers, Materials & Continua
DOI:10.32604/cmc.2022.020384		 images
Article

A Study of Cellular Neural Networks with Vertex-Edge Topological Descriptors

Sadia Husain1, Muhammad Imran2,*, Ali Ahmad1, Yasir Ahmad1 and Kashif Elahi3

1Country College of Computer Science & Information Technology, Jazan University, Jazan, Saudi Arabia
2Department of Mathematical Sciences, United Arab Emirates University, Al Ain, United Arab Emirates
3Deanship of E-learning and Information Technology, Jazan University, Jazan, Saudi Arabia
*Corresponding Author: Muhammad Imran. Email: imrandhab@gmail.com
Received: 22 May 2021; Accepted: 23 June 2021

Abstract: The Cellular Neural Network (CNN) has various parallel processing applications, image processing, non-linear processing, geometric maps, high-speed computations. It is an analog paradigm, consists of an array of cells that are interconnected locally. Cells can be arranged in different configurations. Each cell has an input, a state, and an output. The cellular neural network allows cells to communicate with the neighbor cells only. It can be represented graphically; cells will represent by vertices and their interconnections will represent by edges. In chemical graph theory, topological descriptors are used to study graph structure and their biological activities. It is a single value that characterizes the whole graph. In this article, the vertex-edge topological descriptors have been calculated for cellular neural network. Results can be used for cellular neural network of any size. This will enhance the applications of cellular neural network in image processing, solving partial differential equations, analyzing 3D surfaces, sensory-motor organs, and modeling biological vision.

Keywords: Cellular neural networks; degree; topological indices

1  Introduction

Graph theory is a vast field and is used to solve real problems and natural phenomena. That’s why it has applications in molecular chemistry, robotics, physics, networks, computer science, statistics, biological activities, and data science. It represents real scenarios in the graph based on vertices and edges.

A topological descriptor is a single value that characterizes the whole graph [1–3]. In chemical graph theory, they are used to estimate biological activities and atomic movements [4–6]. The first topological descriptor Wiener index was introduced by Wiener in 1947 [7]. Hosoya polynomial, Schultz index, atom bond connectivity, geometric-arithmetic index are other famous topological descriptors [4,8,9]. Topological descriptors can be categorized on the basis of the mechanism of calculation involved [10–17]. Nowadays vertex-edge topological descriptors are gaining importance in applied sciences [18].

Let G be a simple connected graph with vertex sets V(G) and edge sets E(G). The degree of a vertex ϵ, denoted by d(ϵ), is the number of edges that are incident to the ϵ. The open neighbourhood of ϵ is defined as N(ϵ)={ε∈V(G):ϵε∈E(G)} and closed neighbourhood N[ϵ]=N(ϵ)∪{ϵ} [19]. The ve-degree, denoted by dve(ϵ), of any vertex ϵ∈V is the number of different edges that are incident to any vertex from the N[ϵ]. In [20] defined the ev-degree of the edge e=ϵε∈E, denoted by dev(e), the number of vertices of the union of the closed neighborhoods of ϵ and ε. For details see [21–27].

The ve-degree and ev-degree topological indices are defined as: ∑e∈E(G) (dev(e))2, ∑ϵ∈V dve(ϵ)2,∑ϵε∈E (dve(ϵ)+dve(ε)), ∑ϵε∈E (dve(ϵ)×dve(ε)), ∑ϵε∈E (dve(ϵ)×dve(ϵ))−12, ∑e1E dve(e1)−12, ∑ϵε∈E (dve(ϵ)+dve(ε)−2dve(ϵ)×dve(ε))12, ∑ϵε∈E 2(dve(ϵ)×dve(ε))12dve(ϵ)+dve(ε), ∑ϵε∈E 2dve(ϵ)+dve(ε) and ∑ϵε∈E (dve(ϵ)+dve(ε))−12 are named as: ev-degree Zagreb (Mev) index, the first ve-degree Zagreb α (Mαve1) index, the first ve-degree Zagreb β (Mβve1) index, the second ve-degree Zagreb (Mve2) index, ve-degree Randic (Rve) index, the ev-degree Randic (Rev) index, the ve-degree atom-bond connectivity (ABCve) index, the ve-degree geometric-arithmetic (GAve) index, the ve-degree harmonic (Hve) index and the ve-degree sum-connectivity (χve) index, respectively.

2  Applications and Importance

The Cellular Neural Network (CNN) is an array of cells that are interconnected locally. It is an analog paradigm with various applications including image processing, parallel processing, and high-speed computations. Each cell has an input, an output, and its state. A cell can interact with neighbor cells only. A neighbor cell of a cell is in its radius. A neighborhood includes the cell itself and its eight neighboring cells [28,29]. Fig. 1, consists of two diagrams (a) and (b). Diagram (a), is a graph of two-dimensional CNN, in which a neighborhood is representing red and blue colors. Diagram (b), is the internal structure of the red cell of diagram (a), this cell can interact with all blue cells in this neighborhood. In this article, vertex-edge topological descriptors have been calculated for CNN. The results are generalized and can be used for CNN of any structure and size. This will enhance the applications of CNN in image processing, parallel processing, image processing, non-linear processing, geometric maps, high-speed computations, solving partial differential equations, analyzing 3D surfaces, sensory-motor organs, and modeling biological vision [30].

In 2018, new degree-based topological indices are considered and the analytical sharp bounds has been derived for neural networks in [31]. In 2019, Imran et al. [32] has been calculated the degree based topological indices of cellular neural network. Topology optimization and Zagreb connection indices for cellular neural network are studied in [30,33]. Recently in 2021, the comparison and analysis between the dominating topological indices are determined for the cellular neural network [34]. Some topological indices have been calculated for cellular neural network, and are prominence their importance, but still many topological indices have not been calculated. Their calculation will provide an analytical study of cellular neural network in different applications. The cellular neural network is also known as the strong product of two paths, which has applications in different area of research, see [35,36].

images

Figure 1: Graph of cellular neural networks. (a) Two-dimensional CNN graph, (b) red cell internal structure of (a)

3  The Graph of Cellular Neural Networks

The Figs. 2 and 3 show cellular neural network for different values of p and q.

images

Figure 2: Graph representing cellular neural networks p = 5 (rows) and q = 4 (columns)

The cellular neural network can be arranged either linearly or in a sheet form. A cellular neural network of p rows and q columns, contains pq vertices and 4pq−3p−3q+2 edges, which are shown in Tab. 1. The number of vertices corresponding to their degrees of CNN are shown in Tab. 2 and the edge partition based on degree of end vertices of each edge is shown in the Tab. 3.

images

Figure 3: This is an example of cellular neural networks graph for p = 7 and q = 7 along with sum of degrees of neighborhood vertices

images

images

images

We partitioned the edges of CNN, based on ev-degree in Tab. 4.

images

In Tab. 5, we partitioned the vertices of CNN, based on ev-degree.

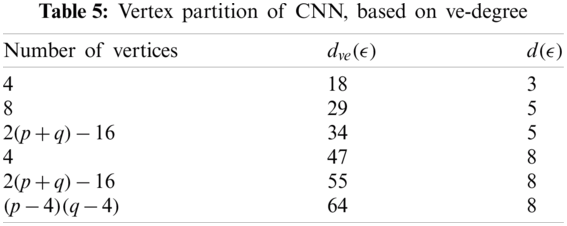
images

We partitioned the edge of CNN with respect to ve-degrees.

Now we calculated ev-degree and ve-degree based indices such as Mev index, Mαve1 index, Mβve1 index, Mve2 index, Rve index, Rev index, ABCve index, GAve index, Hve index and χve index for~CNN.

3.1 The ev-Degree Zagreb Index

The values of ev-degree of each edge is calculated by the sum of degree of its end vertices. The edge partition according to ev-degree for cellular neural network (CNN) is shown in Tab. 4. By using ev-degree of CNN from Tab. 4, we compute the ev-degree based Zagreb index:

Mev(CNN)=∑e∈E(CNN) (dev(e))2=8×82+4×112+(2p+2q−8)×102+(6p+6q−32)×132+(4pq−11p−11q+30)×162=1024pq−1602p−1602q+2468.

3.2 The First ve-Degree Zagreb α Index

The ve-degree of each vertex is obtained by the sum of all degrees of its neighboring vertices. We partitioned the vertices of cellular neural network (CNN) according to its ve-degree that is shown in Tab. 5. Using Tab. 5 we compute the first ve-degree Zagreb α index:

Mαve1(CNN)=∑ϵ∈V dve(ϵ)2 Mαve1(CNN)=4×182+8×292+(2q+2p−16)×342+4×472+(2q+2p−16)×552+(pq−4q−4p+16)×642=4096pq−8022(p+q)+15500.

3.3 The First ve-Degree Zagreb β Index

The edge partition of cellular neural network (CNN) with respect to ve-degree is shown in Tab. 6. Using Tab. 6 we compute the first ve-degree Zagreb β index:

Mβve1(CNN)=∑ϵε∈E (dve(ϵ)+dve(ε)) Mβve1(CNN)=8×(18+29)+4×(18+47)+4×(29+29)+8×(29+34)+(2p+2q−20)×(34+34)+8×(29+47)+8×(29+55)+8×(34+47)+(6p+6q−56)×(34+55)+8×(47+55)+4×(47+64)+(2p+2q−16)×(55+55)+(6p+6q−56)×(55+64)+(2pq−8p−8q+32)×(64+64)=256pq+580(p+q)−6112.

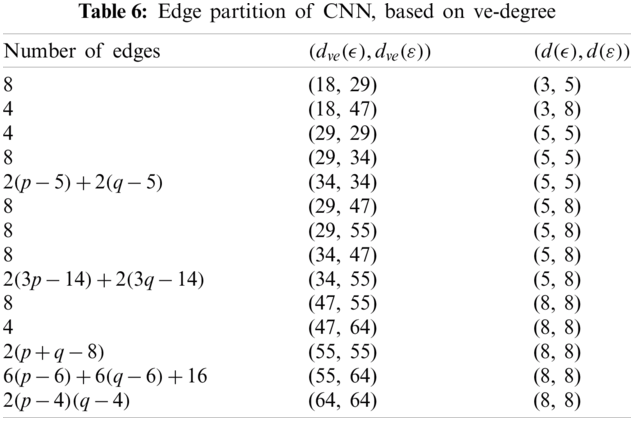
images

3.4 The Second ve-Degree Zagreb Index

Using Tab. 6 we compute the second ve-degree Zagreb index:

Mve2(CNN)=∑ϵε∈E (dve(ϵ)×dve(ε)) Mve2(CNN)=8×(18×29)+4×(18×47)+4×(29×29)+8×(29×34)+(2p+2q−20)×(34×34)+8×(29×47)+8×(29×55)+8×(34×47)+(6p+6q−56)×(34×55)+8×(47×55)+4×(47×64)+(2p+2q−16)×(55×55)+(6p+6q−56)×(55×64)+(2pq−8p−8q+32)×(64×64)=8192pq+7934(p+q)−154316.

3.5 The ve-Degree Randic Index

Using Tab. 6 we compute the ve-degree Randic index:

Rve(CNN)=∑ϵε∈E (dve(ϵ)×dve(ϵ))−12 Rve(CNN)=8×(18×29)−12+4×(18×47)−12+4×(29×29)−12+8×(29×34)−12+(2p+2q−20)×(34×34)−12+8×(29×47)−12+8×(29×55)−12+8×(34×47)−12+(6p+6q−56)×(34×55)−12+8×(47×55)−12+4×(47×64)−12+(2p+2q−16)×(55×55)−12+(6p+6q−56)×(55×64)−12+(2pq−8p−8q+32)×(64×64)−12=48758+214194−1308154230+4493986−2237480p−2237480q+813631363+815951595+47991598+11870(6p+6q−56)1870+825852585+19447+1440(6p+6q−56)55+132pq=132pq+(39351870−2237480+322055)(p+q)+48758+214194−1308154230+4493986+47991598−289351870+813631363+815951595+19447+825852585−75555.

3.6 The ev-Degree Randic Index

Using Tab. 4 we compute the ev-degree Randic index:

Rev(CNN)=∑e1E dev(e1)−12 Rev(CNN)=8×(8)−12+4×(11)−12+(2p+2q−8)×(10)−12+(6p+6q−32)×(13)−12+(4pq−11p−11q+30)×(16)−12=22+41111+110(2p+2q−8)10+113(6p+6q−32)13+pq−114p−114q+152=pq+(1510−114+61313)(p+q)+22+41111−4510−321313+152.

3.7 The ve-Degree Atom-Bond Connectivity Index

Using Tab. 6 we compute the ve-degree atom-bond connectivity index:

ABCve(CNN)=∑ϵε∈E (dve(ϵ)+dve(ε)−2dve(ϵ)×dve(ε))12 ABCve(CNN)=8×45522+4×63846+4×56841+8×61986+(2p+2q−20)×661156+8×741363+8×821595+8×791598+(6p+6q−56)×871870+8×1002585+4×1093008+(2p+2q−16)×1083025+(6p+6q−56)×1173520+(2pq−8p−8q+32)×1264096=33214pq+(3935162690+12553+9220715+11766−3814)(p+q)+429290+247658+1035814+449360146−101766+81595130790−28935162690−96553+81363100862+165172585+4799126242−2155715+1945123.

3.8 The ve-Degree Geometric-Arithmetic Index

Using Tab. 6 we compute the ve-degree geometric-arithmetic index:

GAve(CNN)=∑ϵε∈E 2(dve(ϵ)×dve(ε))12dve(ϵ)+dve(ε) GAve(CNN)=1652247+884665+884158+1698663+2(2p+2q−20)115668+16136376+16159584+16159881+2(6p+6q−56)187089+162585102+83008111+2(2p+2q−16)3025110+2(6p+6q−56)3520119+2(2pq−8p−8q+32)4096128=2pq+(12891870−4+9611955)(p+q)+484758+246594+1663986+16811598−112891870+4191363+4211595+6411147+8512585−1281755.

3.9 The ve-Degree Harmonic Index

Using Tab. 6 we compute the ve-degree harmonic index:

Hve(CNN)=∑ϵε∈E 2dve(ϵ)+dve(ε) Hve(CNN)=1647+865+858+1663+2(2p+2q−20)68+1676+1684+1681+2(6p+6q−56)89+16102+8111+2(2p+2q−16)110+2(6p+6q−56)119+2(2pq−8p−8q+32)128=132pq+9593114660040p+9593114660040q−3008776855924133584675843862.

3.10 The ve-Degree Sum-Connectivity Index

Using Tab. 6 we compute the ve-degree sum-connectivity index:

χve(CNN)=∑ϵε∈E (dve(ϵ)+dve(ε))−12 χve(CNN)=8(47)−12+4(65)−12+4(58)−12+8(63)−12+(2p+2q−20)(68)−12+8(76)−12+8(84)−12+8(81)−12+(6p+6q−56)(89)−12+8(102)−12+4(111)−12+(2p+2q−16)(110)−12+(6p+6q−56)(119)−12+(2pq−8p−8q+32)(128)−12=28pq+(68989+155110+6119119+1/1717)−1/22)(p+q)+84747+46565+22958+8217−101717+42121−568989−855110+41919+451102+89∗+22−817119+4111111.

4  Numerical and Graphical Representation

In this section, we determine the numerical values of the Mαve1,Mβve1,Mve2,Rev,ABCve,GAve,Rve,Hve,χve, in Tabs. 7–9. We represented these results graphically in Figs. 4–6.

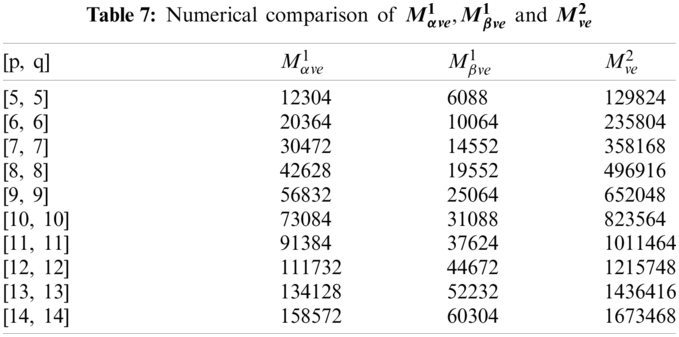
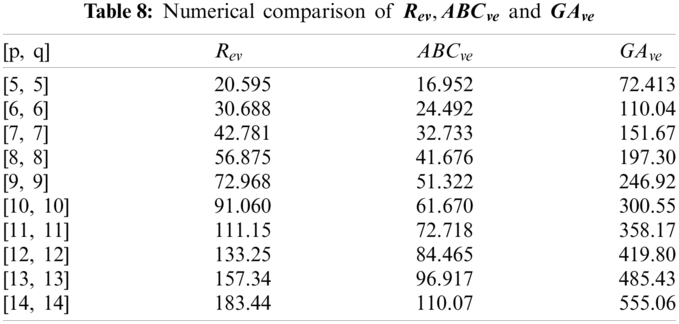
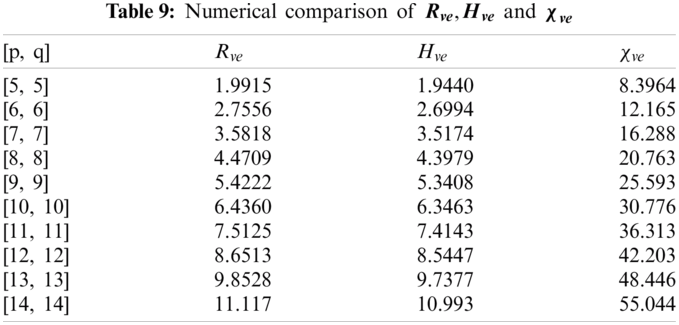
images

images

images

images

Figure 4: Graphical comparison of Mαve1,Mβve1 and Mve2 for CNN

images

Figure 5: Graphical comparison of Rev,ABCve and GAve for CNN

images

Figure 6: Graphical comparison of Rve,Hve and χve for CNN

5  Advantages and Limitations

5.1 Advantages

As a machine learning algorithm, CNN can take image as an input, highlight image key features, and differentiate one image from the other [37]. CNN has powerful function-fitting capabilities and has great potential to study partial differential equations [38,39]. CNN has been widely used in analyzing 3D surfaces and facial images applications [40]. The design components underlying the implementation of the physiologically faithful retina and other topographic sensory organ models on CNN universal chips. The results obtained through the proposed technique can better understand the features and characteristics of CNN. It can enhance image processing applications, solve partial differential equations, analyze 3D surfaces, sensory-motor organs, and model biological vision. Combinations of CNN and artificial intelligence provide enhanced human-level performance to computer architectures [41]. This article is vital in the implementation of Human-level visual recognition.

5.2 Limitations

The calculation of vertex-edge topological descriptors carried out in this research are specifically derived for cellular neural networks. However, with some modifications they can be applied in other fields like image processing, biological modelling, 3D surface analyzing, and complex imaging. The applicability of this research still needs to be validated for these fields to identify the full potential of this research. These open problems can be further studied to get full benefit of this research.

6  Conclusion

A cell in Cellular Neural Network (CNN), can communicate with neighbor cells only. Due to its architecture, it is used to manage hierarchical levels, and it has variety of applications. In applied sciences, graph theory provides different tools and methods to remedy real-world problems. To solve these problems, it represents them in the form of graphs. Topological descriptors in graph theory are used to study and characterize biological activities in the form of graphs. In this article, the vertex-edge topological descriptors have been calculated for the graphic representation of CNN. Results can be used for the CNN of any size. The proposed technique can enhance the CNN’s applications in image processing, parallel processing, non-linear processing, geometric maps representations, high-speed computations, solving partial differential equations, analyzing 3D surfaces, sensory-motor organs, and modeling biological vision.

Funding Statement: This research is supported by the University program of Advanced Research (UPAR) and UAEU-AUA grants of United Arab Emirates University (UAEU) via Grant No. G00003271 and Grant No. G00003461.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  A. Ahmad, “On the degree based topological indices of benzene ring embedded in P-type-surface in 2D network,” Hacettepe Journal of Mathematics and Statistics, vol. 47, no. 1, pp. 9–18, 2018. [Google Scholar]

 2.  M. Karelson, Molecular Descriptors in QSAR/QSPR. New York: Wiley, 2000. [Google Scholar]

 3.  R. Todeschini and V. Consonni, Handbook of Molecular Descriptors. Weinheim: Wiley-VCH, 2000. [Google Scholar]

 4.  A. Ahmad, “Computation of certain topological properties of honeycomb networks and graphene,” Discrete Mathematics, Algorithms and Applications, vol. 9, no. 5, pp. 1750064, 2017. https://doi.org/10.1142/S1793830917500641. [Google Scholar]

 5.  Ahmad, K. Elahi, R. Hasni and M. F. Nadeem, “Computing the degree based topological indices of line graph of benzene ring embedded in P-type-surface in 2D network,” Journal of Information and Optimization Sciences, vol. 40, no. 7, pp. 1511–1528, 2019. [Google Scholar]

 6.  M. Bača, J. Horváthová, M. Mokrišová, A. Semaničová-Feňovčíková and A. Suhányiová, “On topological indices of carbon nanotube network,” Canadian Journal of Chemistry, vol. 93, no. 10, pp. 1157–1160, 2015. [Google Scholar]

 7.  H. Wiener, “Structural determination of paraffin boiling points,” Journal of the American Chemical Society, vol. 69, no. 1, pp. 17–20, 1947. [Google Scholar]

 8.  M. Bača, J. Horváthová, M. Mokrišová and A. Suhányiová, “On topological indices of fullerenes,” Applied Mathematics and Computation, vol. 251, pp. 154–161, 2015. [Google Scholar]

 9.  G. Hong, Z. Gu, M. Javaid, H. M. Awais and M. K. Siddiqui, “Degree-based topological invariants of metal-organic networks,” IEEE Access, vol. 8, pp. 68288–68300, 2020. [Google Scholar]

10. A. Ahmad, “Topological properties of sodium chloride,” Scientific Bulletin-University Politehnica of Bucharest, Series B, vol. 82, no. 1, pp. 35–46, 2020. [Google Scholar]

11. Gutman, J. Tošović, S. Radenković and S. Marković, “On atom-bond connectivity index and its chemical applicability,” Indian Journal of Chemistry, vol. 51, pp. 690–694, 2012. [Google Scholar]

12. M. Javaid, J.-B. Liu, M. A. Rehman and S. Wang, “On the certain topological indices of titania nanotube TiO2[m, n],” Zeitschrift fur Naturforschung A, vol. 72, no. 7, pp. 647–654, 2017. [Google Scholar]

13. S. Zaman, F. A. Abolaban, A. Ahmad and M. A. Asim, “Maximum H-index of bipartite network with some given parameters,” AIMS Mathematics, vol. 6, no. 5, pp. 5165–5175, 2021. [Google Scholar]

14. S. Hayat and M. Imran, “Computation of topological indices of certain networks,” Applied Mathematics and Computation, vol. 240, pp. 213–228, 2014. [Google Scholar]

15. Ali, N. A. Koam and A. Ahmad, “Polynomials of degree-based indices for three-dimensional mesh network,” Computers, Materials and Continua, vol. 65, no. 2, pp. 1271–1282, 2020. [Google Scholar]

16. Ali, N. A. Koam, A. Ahmad and M. F. Nadeem, “Comparative study of valency-based topological descriptor for hexagon star network,” Computer Systems Science and Engineering, vol. 36, no. 2, pp. 293–306, 2021. [Google Scholar]

17. A. Ahmad, R. Hasni, K. Elahi and M. A. Asim, “Polynomials of degree-based indices for swapped networks modeled by optical transpose interconnection system,” IEEE Access, vol. 8, pp. 214293–214299, 2020. [Google Scholar]

18. T. Došlić, B. Furtula, A. Graovac, I. Gutmanb, S. Moradid et al., “On vertex-degree-based molecular structure descriptors,” MATCH Communications in Mathematical and in Computer Chemistry, vol. 66, pp. 613–626, 2011. [Google Scholar]

19. M. Chellali, T. W. Haynes, S. T. Hedetniemi and T. M. Lewis, “On ve-degrees and ev-degrees in graphs,” Discrete Mathematics, vol. 340, no. 2, pp. 31–38, 2017. [Google Scholar]

20. M. Cancan, “On ev-degree and ve-degree topological properties of tickysim spiking neural network,” Computational Intelligence and Neuroscience, vol. 2019, pp. 1–7, 2019. [Google Scholar]

21. A. Ahmad, “Comparative study of ve-degree and ev-degree topological descriptors for benzene ring embedded in P-type-surface in 2D network,” Polycyclic Aromatic Compounds. https://doi.org/10.1080/10406638.2020.1834415. [Google Scholar]

22. S. Ediz, “A new tool for QSPR researches: ev-degree Randic index,” Celal Bayar Universitesi Fen Bilimleri Dergisi, vol. 13, no. 3, pp. 615–618, 2017. [Google Scholar]

23. S. Ediz, “On ve-degree molecular topological properties of silicate and oxygen networks,” International Journal of Computer Science Mathematics, vol. 9, no. 1, pp. 1–12, 2018. [Google Scholar]

24. Horoldagva, K. C. Das and T. A. Selenge, “On ve-degree and ev-degree of graphs,” Discrete Optimization, vol. 31, pp. 1–7, 2019. [Google Scholar]

25. B. Sahin and S. Ediz, “On ev-degree and ve-degree topological indices,” Iranian Journal of Mathematical Chemistry, vol. 9, no. 4, pp. 263–277, 2018. [Google Scholar]

26. J. Zhang, M. K. Siddiqui, A. Rauf and M. Ishtiaq, “On ve-degree and ev-degree based topological properties of single walled titanium dioxide nanotube,” Journal of Cluster Science, 2020. [Online]. Available: https://dx.doi.org/10.1007/s10876-020-01842-3. [Google Scholar]

27. N. Zahra, M. Ibrahim and M. K. Siddiqui, “On topological indices for swapped networks modeled by optical transpose interconnection system,” IEEE Access, vol. 8, pp. 200091–200099, 2020. [Google Scholar]

28. R. Tetzlaff, Cellular Neural Networks and their Applications. Singapore: World Scientific, 2002. [Google Scholar]

29. L. O. Chua and L. Yang, “Cellular neural networks: Theory,” IEEE Transactions on Circuits and Systems, vol. 35, no. 10, pp. 1257–1272, 1988. [Google Scholar]

30. J. B. Liu, Z. Raza and M. Javaid, “Zagreb connection numbers for cellular neural networks,” Discrete Dynamics in Nature and Society, vol. 2020, pp. 8, 2020. [Google Scholar]

31. J.-B. Liu, Z. Jing, W. Shaohui, M. Javaid and C. Jinde, “On the topological properties of the certain neural networks,” Journal of Artificial Intelligence and Soft Computing Research, vol. 8, no. 4, pp. 257–268, 2018. [Google Scholar]

32. M. Imran, M. K. Siddiqui, A. Q. Baig and W. Khalid, “Topological properties of cellular neural networks,” Journal of Intelligent & Fuzzy Systems, vol. 37, no. 3, pp. 3605–3614, 2019. [Google Scholar]

33. V. Bhambhani and H. G. Tanner, “Topology optimization in cellular neural networks,” in 49th IEEE Conf. on Decision and Control, Atlanta, GA, USA, IEEE, 2010. [Google Scholar]

34. F. Ejaz, M. Hussain, H. Almohamedh, K. M. Alhamed, R. Alabdan et al., “Dominating topological analysis and comparison of the cellular neural network,” Mathematical Problems in Engineering, vol. 2021, Article ID 6613433, 9 pages, 2021. https://doi.org/10.1155/2021/6613433. [Google Scholar]

35. A. Ahmad, M. Bača, Y. Bashir and M. K. Siddiqui, “Total edge irregularity strength of strong product of two paths,” ARS Combinatoria, vol. 106, pp. 449–459, 2012. [Google Scholar]

36. D. Ma, “The crossing number of the strong product of two paths,” Australasian Journal of Combinatorics, vol. 68, no. 1, pp. 35–47, 2017. [Google Scholar]

37. A. K. Rizhevsky, I. Sutskever and G. E. Hinton, “Image net classification with deep convolutional neural networks,” Advances in Neural Information Processing Systems, vol. 2, pp. 1097–1105, 2012. [Google Scholar]

38. G. Yanan, C. Xiaoqun, L. Bainian and G. Mei, “Solving partial differential equations using deep learning and physical constraints,” Applied Sciences, vol. 10, pp. 2076–3417, 2020. [Google Scholar]

39. J. Sirignano and K. Spiliopoulos, “A deep learning algorithm for solving partial differential equations,” Journal of Computational Physics, vol. 375, no. 3, pp. 1339–1364, 2018. [Google Scholar]

40. H. Jin, Y. Lian and J. Hua, “Learning facial expressions with 3D mesh convolutional neural network,” ACM Transactions on Intelligent Systems and Technology, vol. 7, pp. 2157–6904, 2018. [Google Scholar]

41. N. Kriegeskorte, “Deep neural networks: A new framework for modeling biological vision and brain information processing,” Annual Review of Vision Science, vol. 1, no. 1, pp. 417–446, 2015. [Google Scholar]

images This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.