DOI:10.32604/cmc.2022.020222

| Computers, Materials & Continua DOI:10.32604/cmc.2022.020222 |  |
| Article |
Flow-Shop Scheduling with Transportation Capacity and Time Consideration
1Department of Industrial Engineering and Management, National Kaohsiung University of Science and Technology, Kaohsiung, 80778, Taiwan
2College of Engineering, National Kaohsiung University of Science and Technology, Kaohsiung, 80778, Taiwan
3Department of Mechanical Engineering, National Kaohsiung University of Science and Technology, Kaohsiung, 80778, Taiwan
4Faculty of Commerce, Van Lang University, Ho Chi Minh City, 70000, Vietnam
*Corresponding Author: Ching-Chien Huang. Email: huangcc@nkust.edu.tw
Received: 15 May 2021; Accepted: 29 June 2021
Abstract: Planning and scheduling is one of the most important activity in supply chain operation management. Over the years, there have been multiple researches regarding planning and scheduling which are applied to improve a variety of supply chains. This includes two commonly used methods which are mathematical programming models and heuristics algorithms. Flowshop manufacturing systems are seen normally in industrial environments but few have considered certain constraints such as transportation capacity and transportation time within their supply chain. A two-stage flowshop of a single processing machine and a batch processing machine are considered with their capacity and transportation time between two machines. The objectives of this research are to build a suitable mathematical model capable of minimizing the maximum completion time, to propose a heuristic optimization algorithm to solve the problem, and to develop an applicable program of the heuristics algorithm. A Mixed Integer Programming (MIP) model and a heuristics optimization algorithm was developed and tested using a randomly generated data set for feasibility. The overall results and performance of each approach was compared between the two methods that would assist the decision maker in choosing a suitable solution for their manufacturing line.
Keywords: Scheduling; two-stage flowshop; supply chain management; transportation; batch processing machine; heuristic
Flowshop scheduling was derived since 1959 by Johnson [1] and since then has been extensively researched and developed. It is considered to have opened a new horizon for advanced development of the industrial environment and especially scheduling field. In its early years, researches only mentioned about scheduling flowshop for single processing machine. Then, in the late of 1990's, a new flowshop scheduling problem emerged in the manufacturing of custom-built very large-scale integrated circuits (IC) concerning two-stage machine where one is a single processing machine and the other is batch processing machine. Afterwards, the same problem then considered the transportation and deterioration between batch and single processing machine that arose in the steel industry, specifically the steel ingot teeming, heating and rolling processes in the steel plant.
In particular manufacturing and distribution systems, semi-finished jobs are transported from one facility to another for further processing by material handling systems such as automated guided vehicles (AGVs) and conveyors whereas finished jobs are delivered to the customers or warehouses by vehicles such as trucks. Numerous researches have been carried out to investigate this problem. Nevertheless, most of them presume that either there are an infinite number of transporters or unlimited capacity to deliver the tasks whenever the jobs are finished or jobs that are transported immediately from one location the another without transportation time involved, neglecting transportation time.
Scheduling problems that address the optimal coordination of machine scheduling along with job transportation are more practical to those that do not consider these factors. It is apparent that different operations in manufacturing and distribution systems must be coordinated carefully in order to achieve an optimal overall system performance. The recent enormous expansion of supply chain management in both academic and industrial communities has demonstrated the importance of such coordination.
In steel industry, there are processes, referred as the two-stage flowshop scheduling problems, considers transportation as a constraint, specifically from the steel ingot teeming, heating and rolling process shown in Figs. 1 and 2. Teeming is the process where molten steel in the ladle is poured into molds to produce steel ingots. After the ingots are stripped from the molds, they are appropriately segregated into batches and transported to the soaking pit by a vehicle inside the manufacturing plant. The soaking pit can be considered as a batch processor as it reheats the ingots to a desirably high temperature. The reheated ingots are again transported to a rough mill. The ingots are later rolled to a usable from of steel, such as the slabs and the blooms, on the rough mill where its temperature drops gradually as waiting time passes. If the temperature drops considerably low, the ingots are required to add more heating time to reach the rolling temperature. Consequently, the rolling time of the ingots is prolonged.

Figure 1: The process of ingot teeming and heating

Figure 2: The process of ingot heating and rolling
As shown in Figs. 1 and 2 respectively, the process of teeming and heating is commonly referred to as the two-machine flowshop problem where a single processor is followed by a batch processor whereas the heating and rolling refer to the problem where a batch processor followed by a single processor, both with transportation time considered.
Motivated from the procedure above and developed from former papers, this research considers a two-machine flowshop scheduling problem comprising of a discrete processing machine and a batch processing machine. Specifically, there are two scheduling models are considered:
(1) Single processing machine followed by batch processing machine.
(2) Batch processing machine followed by single processing machine.
In the first model, each job that is completed on the single processing machine are transported to the batch processing machine by a vehicle. On the other hand, jobs in the second model are transported to the single processing machine also by a vehicle after processed on the batch machine. The transportation time is a given constant, and the transportation capacity is equal to the batch size. The batch processing machine processes a number of jobs in a batch so that all jobs in each batch start together, and also finish their processing at the same time. For the situation where the processing time of each batch is job-dependent, i.e., the maximum processing time of jobs assigned to the batch, the proposed problem is to find the optimal schedule which minimizes the maximum completion time.
The burn-in operation in semiconductor manufacturing with their objectives are to minimize the maximum completion time (makespan). There are a lot of research concerning these problems and extensive surveys of different mathematical models and problems that have been conducted by Webster et al. [2] and Potts et al. [3].
As the reported pattern of the batch processing time, this research can be divided into two categories. In the first category, the processing time of each batch is fixed and independent from the jobs listed in the batch. Ikura et al. [4] were seemingly the first to study the batching scheduling problems with a constant batch processing time in which they introduce the First-Only-Empty (FOE) algorithm and Greedy-Adjusted-Bunching (GAB) algorithm to minimize the completion time. Ahmadi et al. [5] examined a 2-stage flowshop scheduling in which one or both stages may consist of a batch processor. They analyze the complexity for the two problems with the objectives of minimizing the makespan and minimizing the total completion times. Sung et al. [6] further studied the extension of one of the models of Ahmadi et al. [5]. They investigate a scheduling problem for a two-machine flowshop with a discrete processing machine followed by a batch processing machine to minimize makespan where dynamic job arrivals are allowed.
On the other hand, the second category consider the batch processing time that is dependent of the jobs assigned to the batch, i.e., the processing time of a batch is given by the maximum processing time of all jobs in the batch. Damodaran et al. [7] proposed a mixed integer programming approach for the flowshop problem in case the buffer space is unlimited or zero. Numerical examples are presented to demonstrate the application of the model. Lee et al. [8] considered the problem of minimizing the makespan on a single batch processing machine in the presence of dynamic job arrivals. Chandru et al. [9] studied the problem of minimizing total completion time on single and parallel batch processing machines where the processing time of a batch is equal to the longest processing time among all jobs in the batch. They propose a branch-and-bound algorithm and several heuristic algorithms for the problem of minimizing the total completion time on a burn-in oven, and also a heuristic algorithm for a parallel oven system. The authors also propose an optimal dynamic programming approach for a problem of minimizing the total completion time on a burn-in oven with fixed number of job families. Sung et al. [10] investigated a scheduling problem of a single batch processing machine. They propose a branch-and-bound algorithm and several heuristic algorithms and derived the worst-case error bounds of their heuristic algorithms to minimize the makespan on a single burn-in oven with dynamic job arrivals allowed. Uzsoy [11] examined a problem of scheduling jobs with non-identical size on a single burn-in oven to minimize the total completion time and the makespan.
The second category also consider the total processing time of the jobs assigned to the batch as the batch processing time. Cheng et al. [12] consider the two-machine flowshop in which one is a discrete processor and the other is a batch processor. They prove the NP-hardness of the problem and propose efficient algorithms for some polynomial solvable cases. Cheng et al. [13] present the same configuration except that both machines process the jobs in batches. They provide strong NP-hardness proofs and propose properties and polynomial algorithms for some special cases. They also propose heuristic algorithms to deal with the general problem.
This scheduling problem with the consideration of transportation involving batch processing machine arises from the ingot teeming and heating process in the steel plant. Their objectives are, likewise, to minimize the maximum completion time (makespan). By Lee et al. [14], this problem can be categorized into two types. The first type is intermediate transportation where semi-finished jobs are transported from one machine to another for further processing. Type two is the transportation of finished jobs to the customers. A variety of scheduling problems involving these two types of transportation is considered with transporter capacity and transportation time taken into account.
Maggu et al. [15] is probably the first to explicitly consider the transportation factor. They consider a two-machine flowshop scheduling problem with unlimited buffer spaces on both machines, i.e., there are a sufficient number of transporters so that whenever a job is completed on the first machine it can be transferred immediately to the second machine. The transportation time is job-dependent. They generalize the well-known Johnson's rule to solve their problem. Kise [16] investigates a similar problem but with only one transporter with a capacity of one, i.e., it can transport only one job at a time. He proves that this problem is NP-hard even with job-independent transportation times. As opposed to the above studies, Stern et al. [17] have investigated two-machine flowshop problems where a transporter only with a capacity of one such as AGV travelling back and forth between machines and job-independent transportation times in which there is not any intermediate buffer space. They formulate the problem as an asymmetric traveling salesman problem and give a polynomial-time heuristic. Ganesharajah et al. [18] later on point out that this problem is strongly NP-hard. Langston [19] analyses some heuristics for a k-station flowshop problem where each station has a number of machines that can be used to process jobs, and there is only one transporter with a capacity of one to transfer jobs with transportation times dependent on the physical locations of the origin and destination machines. Tang et al. [20] study the two-machine flowshop scheduling problems where a single machine is followed by a batching machine. The processing time of a batch is a constant. They also consider a transporter to carry the jobs between two machines and deteriorating jobs to be processed on the single machine. They prove that this problem is strongly NP-hard and propose a mixed integer programming to formulate the problem. Behnamian et al. [21] approached the two-stage flowshop manufacturing scheduling problem under transportation capacity and time constrains with the mixed integer mathematic programming method. The objective of the proposed model is to find the optimal makespan.
To take a look at more modern problems of this flowshop problem, a number of recent researched have also addressed to this problem. Cai et al. [22] investigated a distributed permutation flow shop scheduling problem (DPFSSP) with transportation and elibility constraints using the Nondominated Sorting Genetic Algorithm II (NSGA-II) methodology due to multi-objective nature of DPFSSP. The findings showed optimistic Pareto solutions that minimized the overall makespan of the process. Kumar et al. [23] researched into another flow shop scheduling problem that considered breakdown intervals, transportation time and weights of jobs and proposed a Genetic Algorithm (GA) approach into solving. The method showed suitable results through a variety of different problem sizes. Qin et al. [24], on the other hand, considered a hybrid flow shop problem at a seaport and was able to utilize the mixed integer programming combined with constraint programming to model the activities happening in the port. The study was able to improve the activity of the port by 3.31% from a feasible solution time of 2 min operating. Finally, Gheisariha et al. [25] proposed a different methodology into solving a flexible flow shop scheduling problem of simulation-optimization. The algorithm considered in the enhanced multi-objective harmony search with a Gaussian mutation in order to incorporate the data together with objectives of minimizing completion time and minimizing mean tardiness between the jobs and machine.
While flowshop scheduling problem has been studied extendedly in past studies, few have look into the flowshop scheduling problem under transportation capacity and time constrains. In this study, two approaches to the flowshop scheduling problem under transportation and capacity and time constrains are developed: a Mixed Integer Programming (MIP) Model and a Heuristics Model. Both approaches are then applied to a numerical examples to demonstrate their performance and feasibility.
Consider a set J of n independent and non-preemptive jobs J = {1, 2,…, n} to be processed at a two-machine flowshop, where one processes one job at a time—single processing machine—and one processes jobs as a batch simultaneously—batch processing machine. Each batch has the capacity of c jobs (c ≤ n), i.e., up to c jobs can be assigned to one batch and processed simultaneously, where all the jobs have different processing times. The processing times of job j on machine 1 and machine 2 are denoted by p1j and p2j. The processing time of a batch is equivalent to the longest processing time of a job among all jobs in a batch. Once the batch process machine is initiated, no job can be entered or released from the machine until the entire batch is completed. Also consider a transporter which transports the semi-finished jobs from machine 1 to machine 2 and returns from machine 2 to machine 1 and so on. The capacity of the transporter is equal to the batch capacity c of the batch processing machine, i.e., it can carry up to c jobs in one shipment. Assume that a round trip time of the transporter is a constant T unit of time and as two halves of the trip are identical, each takes T/2 units of time, where T ≥ P to emphasize the significance of transportation. Let Cj denote the completion time of job j, and the objective function is to minimize the makespan Cmax = max1 ≤ j ≤ n{Cj}.
As aforementioned, we are considering two scheduling models:
(1) Single processing machine followed by batch processing machine.
(2) Batch processing machine followed by single processing machine.
In order for further clear explanation, we adopt the three-field notation ψ1ψ2ψ3 of Graham et al. to denote the two scheduling models.
The first model can be denoted as F2 | b1 = 1, b2 = c, M2k = max{P2j}, tk = T | Cmax, where F2 indicates two-machine flowshop, b1 = 1 and b2 = c indicate that the first machine is a single processing machine and the second is a batch processing machine with capacity c, M2k denotes the processing time of kth batch on batch processing machine and is equal to the longest processing time of a job among all jobs in batch k. tk is the transportation time of batch k and equals to a constant T and lastly minimizing the makespan Cmax.
On the other hand, the second model is denoted as F2 | b1 = c, b2 = 1, M1k = max{P1j}, tk = T | Cmax. The notations indicate in the same way as the first model except for the order of processing machines whereby the batch machine is followed by a single machine. Thus, M1k denotes the processing time of kth batch on batch processing machine equally to the maximum of processing times of jobs assigned to the kth batch.
3.1 The First Model (F2 | b1 = 1, b2 = c, M2k = max{P2j}, tk = t | Cmax)
• Parameters
J Set of all jobs, J = {1, 2,…, N}; where N is the total number of jobs
• c Capacity of the transporter and batch processing machine
• T Round trip time of transporter
• P1j Processing time of job j on the single processing machine; j = 1, 2,…, N
• P2j Processing time of job j on the batch processing machine; j = 1, 2,…, N
Decision variables
xjk 1, if job j belongs to the kth batch; 0, otherwise
Ck The completion time of kth batch; k = 1, 2,…, B
Rk Departure time of transporter which contains kth batch; k = 1, 2,…, B
M1k Processing time of kth batch on single processing machine; k = 1, 2,…, B
M2k Processing time of kth batch on batch processing machine; k = 1, 2,…, B
B Number of batches; B = [N/c]
3.1.2 Mixed Integer Programming Model
Subject to:
The objective function (1) is to minimize the makespan, Cmax = max1 ≤ j ≤ n{Cj}, where Cj denotes the completion time of job j. Constraint (2) ensures that each job is assigned to one and only one batch, i.e., it is scheduled particularly once. Constraint (3) guarantees that the number of jobs contained in each batch cannot exceed capacity c. Constraint (4) defines the processing times of kth batch on single processing machine as sum of processing times of jobs assigned to the kth batch on single processing machine. Constraint (5) indicates the batch processing time as the maximum processing time of jobs assigned to each batch. Constraint (6) determines the departure time of transporter containing first batch upon the completion of its on single processing machine. Constraint (7) ensures that the transporter transfers the jobs in kth batch only when all jobs have been completely processed in single machine. Constraint (8) guarantees that the transporter departs from single to batch machine only after it has returned to origin point. Constraint (9) indicates the completion time of the first batch. Constraint (10) defines that the batch processing machine only starts to process when the batch have arrived. Constraint (11) ensures that the batch is processed until the preceeding batch has been finished. Constraint (12) defines the characteristics of the completion time of batch k. Constraint (13) and (14) illustrate the range of the namely variables.
Since there is hardly any specific and accurate method to solve an MIP model, a heuristic algorithm is necessary in order to yield near-optimal solutions. The heuristic algorithm introduced consists of three phases namely job sequencing, job batching and processing. Job sequencing phase is based on Johnson's rule for two machines whereas job batching and processing are done heuristically.
• Phase 1: Job Sequencing
The Johnson's interactive procedure for determining the optimal sequence for an n-jobs 2 machines can be outlined as follows:
Step 1: Find the shortest processing time among the jobs not yet scheduled. If two or more jobs are tied, choose one job arbitrarily.
Step 2: If the shortest processing time is on machine 1, schedule the corresponding job as early as possible. If the shortest processing time is on machine 2, schedule the corresponding job as late as possible
Step 3: Eliminate the last job scheduled from further consideration.
Step 4: Repeat step 1 and 2 until all jobs have been scheduled.
• Phase 2: Job Batching
Given the Job Sequence from phase 1, the phase 2 can start. Each and every job j to L batches is assigned until all batches are full or there are no jobs left to assign. Simultaneously, assigning jobs to the 1st batch and the last batch with full capacity are prioritized.
• Phase 3: Processing
Upon the completion of Job Batching, each job is processed on the single machine and then transferred by transporter to process on batch machine, where completion time of single machine, departure time and completion time of batch machine are determined as followed:
3.2 The Second Model (F2 | b1 = c, b2 = 1, M1k = max{P1j}, tk = t | Cmax)
As this problem is explicitly opposite of the above problem, all the parameters and variables remain the same except:
• Parameters
P1j Processing time of job j on the batch processing machine; j = 1, 2,…, N
• P2j Processing time of job j on the single processing machine; j = 1, 2,…, N
Decision variables
M1k Processing time of kth batch on batch processing machine; k = 1, 2,…, B
M2k Processing time of kth batch on single processing machine; k = 1, 2,…, B
3.2.2 Mixed Integer Programming Model
Likewise, the MIP model does not change much except for constraint (21) and (22). Contraint (21) in this problem indicates the batch processing time as the maximum processing time of jobs assigned to each batch. Constraint (22) defines the processing times of kth batch on single processing machine as sum of processing times of jobs assigned to the kth batch on single processing machine.
In this problem, we modify the above heuristic algorithm in which phase 1 is similarly methods for job sequencing and phase 2 is methods for job batching.
• Phase 1: Job Sequencing
The sequence of jobs in problem 2 is sorted exactly the same as problem 1. Hence, the Johnson's interactive procedure for determining the optimal sequence for an n-jobs 2 machines can be outlined as follows:
Step 1: Find the shortest processing time among the jobs not yet scheduled. If two or more jobs are tied, choose one job arbitrarily.
Step 2: If the shortest processing time is on machine 1, schedule the corresponding job as early as possible. If the shortest processing time is on machine 2, schedule the corresponding job as late as possible
Step 3: Eliminate the last job scheduled from further consideration.
Step 4: Repeat step 1 and 2 until all jobs have been scheduled.
These steps are shown in Fig. 3.

Figure 3: Flowchart of sorting algorithm
• Phase 2: Job Batching
Given the Job sequence from phase 1, we begin phase 2 which is presented in Fig. 4. We assign each and every job j to L batches until the all batches are full or there are no jobs left to assign. Simultaneously, we prioritize assigning jobs to the 1st batch and the last batch with full capacity.

Figure 4: Flowchart of batching algorithm
• Phase 3: Processing
Upon the completion of Job Batching, each job is processed on the single machine and then transferred by transporter to process on batch machine, where completion time of single machine, departure time and completion time of batch machine are determined as followed:
The numerical example below is taken to test the program (Tab. 1):

In addition, we consider c = 4 and T = 13.
In order to analyze the performance of the MIP model vs. the proposed heuristic algorithms, computational experiments are conducted using both CPLEX and Python. Some data sets in which the jobs processing times of single processing machine and batch processing machine are randomly generated from the discrete uniform distribution within the range of [1, 30]. The transporter's capacity/batch size c and transportation time T is taken as 4 and 55 respectively. The input data are shown from Tabs. 2–6.





The result of the problem F2 | b1 = 1, b2 = c, M2k = max{P2j}, tk = T | Cmax is shown in Tab. 7.
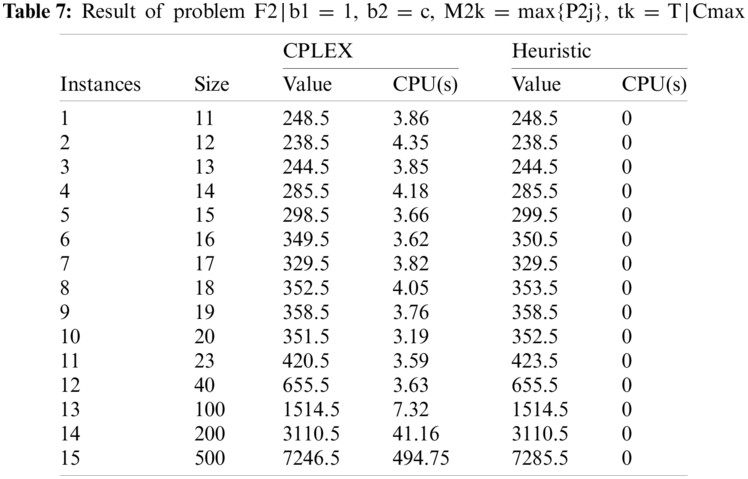
As shown in Tab. 8, p-value is greater than 0.05. Therefore, it can be concluded that both CPLEX and heuristic algorithm significantly give the same results.
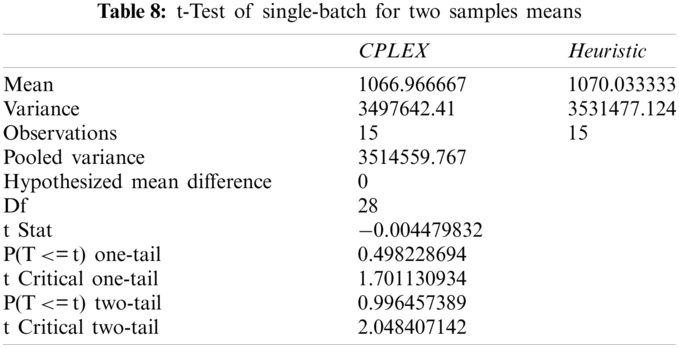
The result of the problem F2 | b1 = c, b2 = 1, M1k = max{P1j}, tk = T | Cmax is shown in Tab. 9.
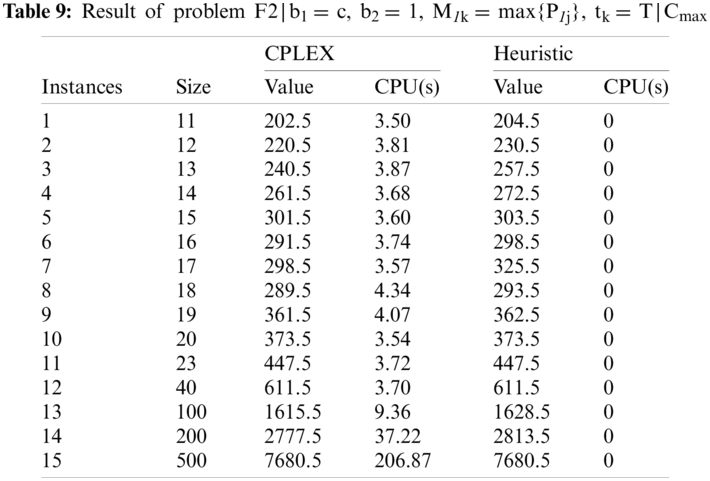
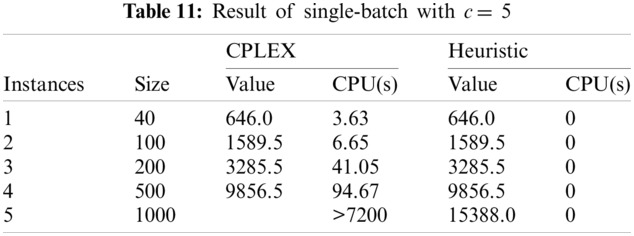
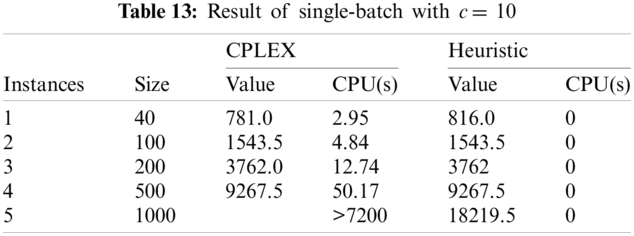
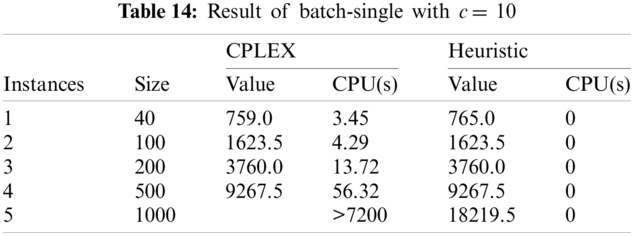
As shown in Tab. 10, p-value is greater than 0.05. Therefore, it can be concluded that both CPLEX and heuristic algorithm in this problem also significantly give the same results. The cases where c and T are changed are also experimented, the results are shown from Tabs. 11–16.
• c =5, T = [minimum processing time * c, maximum processing time * c]

• c =10, T = [minimum processing time * c, maximum processing time * c]
• c = 15, T = [minimum processing time * c, maximum processing time * c]
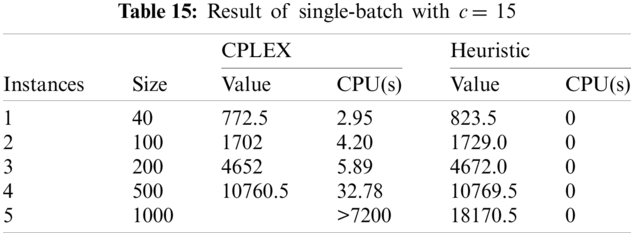
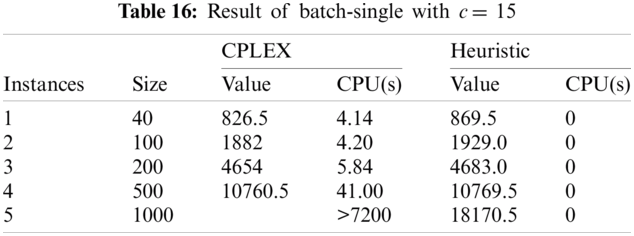
As seen in from Tabs. 11–16, the proposed heuristic solves the problem much faster than CPLEX such that it takes so small amount of time (almost 0) that it can be negligible for all given cases. Simultaneously, the objectives found by using the heuristic are close to the MIP model for sample size 40, 100, 200, and 500. However, with the increasing in the sample size, the time required for the MIP model to solve would scale up exponentially, i.e., it takes excessively more time to solve a large-scale problem: for a sample size of 1000, the MIP model failed to provide result in a suitable time frame (under 120 min). With the heuristic algorithm, the results remain close to the optimal results from the MIP model without scaling up the solving time. The heuristics model also have significant shorter runtime compared to the MIP model, with all problems solved instantaneously regardless of sample size. The results suggest that the MIP model should be used with small to medium size problems (500 and under) while the heuristics model should be used with large size problems (more than 500) and provide adequate result.
This research focuses on solving a scheduling problem concerning two-stage flowshop of a single processing machine and a batch processing machine with transportation between the two machines taken into account. Both capacity of the vehicle and transportation time are particularly regarded.
With the aim to minimize the completion time makespan of all jobs assigned, a mathematical model capable of minimizing the maximum completion time Cmax (makespan) is built to describe the problem. As aforementioned, we considered two scheduling models: single-batch model in which single processing machine followed by batch processing machine while batch-single model contains batch processing machine followed by single processing machine. Then, a heuristic algorithm is proposed to solve the problem efficiently with the numerical example given showing that the heuristic is practically effective. Finally, an applicable program of the heuristic algorithm is developed to solve the problem automatically and almost instantly. The output of the developed program turns out to be an optimal sequential jobs scheduling suggestion as well as the expected minimum completion time.
However, some drawbacks are that the transportation time is a constant which is not practical. In addition, unlimited buffer space is assumed for the two machines. Therefore, future research are to study the problem in the case that buffer space is limited and also, the transportation time data is collected. There may be additional factors to be considered in the model such as release time, due time of the job and set up time of the machines.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. S. M. Johnson, “Discussion: Sequencing n jobs on Two machines with arbitrary time lags,” Management Science, vol. 5, no. 3, pp. 299–303, 1959. [Google Scholar]
2. S. Webster and K. R. Baker, “Scheduling groups of jobs on a single machine,” Operations Research, vol. 43, no. 4, pp. 692–703, 1995. [Google Scholar]
3. C. N. Potts and M. Y. Kovalyov, “Scheduling with batching: A review,” European Journal of Operational Research, vol. 120, no. 2, pp. 228–249, 2000. [Google Scholar]
4. Y. Ikura and M. Gimple, “Efficient scheduling algorithms for a single batch processing machine,” Operations Research Letters, vol. 5, no. 2, pp. 61–65, 1986. [Google Scholar]
5. J. H. Ahmadi, R. H. Ahmadi, S. Dasu and C. S. Tang, “Batching and scheduling jobs on batch and discrete processors,” Operations Research, vol. 39, no. 4, pp. 750–763, 1992. [Google Scholar]
6. C. S. Sung and Y. H. Kim, “Minimizing makespan in a two-machine flowshop with dynamic arrivals allowed,” Computers and Operations Research, vol. 29, no. 3, pp. 275–294, 2002. [Google Scholar]
7. P. Damodaran and K. Srihari, “Mixed integer formulation to minimize makespan in a flowshop with batch processing machines,” Mathematical and Computer Modelling, vol. 40, no. 13, pp. 1465–1472, 2004. [Google Scholar]
8. C. Y. Lee and R. Uzsoy, “Minimizing makespan on a single batch processing machine with dynamic job arrivals,” International Journal of Production Research, vol. 37, no. 1, pp. 219–236, 1999. [Google Scholar]
9. V. Chandru, C. Y. Lee and R. Uzsoy, “Minimizing total completion time on batch processing machines,” International Journal of Production Research, vol. 3, no. 9, pp. 2097–2121, 1993. [Google Scholar]
10. C. S. Sung and Y. I. Choung, “Minimizing makespan on a single burn-in oven in semiconductor manufacturing,” European Journal of Operational Research, vol. 120, no. 3, pp. 559–574, 2000. [Google Scholar]
11. R. Uzsoy, “Scheduling a single batch processing machine with non-identical job sizes,” International Journal of Production Research, vol. 32, no. 7, pp. 1615–1635, 1994. [Google Scholar]
12. T. Cheng and G. Wang, “Batching and scheduling to minimize the makespan in the two-machine flowshop,” IIE Transactions, vol. 30, no. 5, pp. 447–453, 1998. [Google Scholar]
13. T. Cheng, B. M. T. Lin and A. Toker, “Makespan minimization in the two-machine flowshop batch scheduling problem,” Naval Research Logistics, vol. 47, no. 2, pp. 128–144, 2000. [Google Scholar]
14. C. Lee and Z. Chen, “Machine scheduling with transportation considerations,” Journal of Scheduling, vol. 4, no. 1, pp. 3–24, 2001. [Google Scholar]
15. P. L. Maggu and G. Das, “On 2*n sequencing problem with transportation times of jobs,” Int. J. Pure and Applied Mathematika Sciences, vol. 12, pp. 1–6, 1980. [Google Scholar]
16. H. Kise, “On an automated two-machine flowshop scheduling problem with infinite buffer,” Journal of the Operations Research Society of Japan, vol. 34, no. 3, pp. 354–361, 1991. [Google Scholar]
17. H. Stern and G. Vitner, “Scheduling parts in a combined production-transportation work cell,” Journal of the Operational Research Society, vol. 41, no. 7, pp. 625–632, 1990. [Google Scholar]
18. T. Ganesharajah, N. Hall and C. Sriskandarajah, “Design and operational issues in AGV-served manufacturing systems,” Annals of Operations Research, vol. 76, pp. 109–154, 1998. [Google Scholar]
19. M. Langston, “Interstage transportation planning in the deterministic flow-shop environment,” Operations Research, vol. 35, no. 4, pp. 556–564, 1987. [Google Scholar]
20. L. Tang and P. Liu, “Two-machine flowshop scheduling problems involving a batching machine with transportation or deterioration consideration,” Applied Mathematical Modelling, vol. 33, no. 2, pp. 1187–1199, 2009. [Google Scholar]
21. J. Behnamian, S. Fatemi Ghomi, F. Jolai and O. Amirtaheri, “Realistic two-stage flowshop batch scheduling problems with transportation capacity and times,” Applied Mathematical Modelling, vol. 36, no. 2, pp. 723–735, 2012. [Google Scholar]
22. S. Cai, K. Yang and K. Liu, “Multi-objective optimization of the distributed permutation flow shop scheduling problem with transportation and eligibility constraints,” Journal of the Operations Research Society of China, vol. 6, no. 3, pp. 391–416, 2017. [Google Scholar]
23. H. Kumar, P. Kumar and M. Sharma, “A genetic algorithm for a flow shop scheduling problem with breakdown interval, transportation time and weights of jobs,” International Journal of Operational Research, vol. 35, no. 4, pp. 470, 2019. [Google Scholar]
24. T. Qin, Y. Du, J. Chen and M. Sha, “Combining mixed integer programming and constraint programming to solve the integrated scheduling problem of container handling operations of a single vessel,” European Journal of Operational Research, vol. 285, no. 3, pp. 884–901, 2020. [Google Scholar]
25. E. Gheisariha, M. Tavana, F. Jolai and M. Rabiee, “A simulation–optimization model for solving flexible flow shop scheduling problems with rework and transportation,” Mathematics and Computers in Simulation, vol. 180, pp. 152–178, 2021. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |