Computers, Materials & Continua DOI:10.32604/cmc.2022.020160
Article

An Efficient Reference Free Adaptive Learning Process for Speech Enhancement Applications

Girika Jyoshna1,*, Md. Zia Ur Rahman1 and L. Koteswararao2

1Deptartment of Electronics and Communication Engineering, Koneru Lakshmaiah Education Foundation, KL University, Vaddeswaram, Guntur, Andhra Pradesh, India
2Department of Electronics and Communication Engineering, Koneru Lakshmaiah Education Foundation, KL University, Hyderabad, Telangana, India
*Corresponding Author: Girika Jyoshna. Email: girikajyoshna1986@gmail.com
Received: 12 May 2021; Accepted: 21 June 2021

Abstract: In issues like hearing impairment, speech therapy and hearing aids play a major role in reducing the impairment. Removal of noise signals from speech signals is a key task in hearing aids as well as in speech therapy. During the transmission of speech signals, several noise components contaminate the actual speech components. This paper addresses a new adaptive speech enhancement (ASE) method based on a modified version of singular spectrum analysis (MSSA). The MSSA generates a reference signal for ASE and makes the ASE is free from feeding reference component. The MSSA adopts three key steps for generating the reference from the contaminated speech only. These are decomposition, grouping and reconstruction. The generated reference is taken as a reference for variable size adaptive learning algorithms. In this work two categories of adaptive learning algorithms are used. They are step variable adaptive learning (SVAL) algorithm and time variable step size adaptive learning (TVAL). Further, sign regressor function is applied to adaptive learning algorithms to reduce the computational complexity of the proposed adaptive learning algorithms. The performance measures of the proposed schemes are calculated in terms of signal to noise ratio improvement (SNRI), excess mean square error (EMSE) and misadjustment (MSD). For cockpit noise these measures are found to be 29.2850, –27.6060 and 0.0758 dB respectively during the experiments using SVAL algorithm. By considering the reduced number of multiplications the sign regressor version of SVAL based ASE method is found to better then the counter parts.

Keywords: Adaptive algorithm; speech enhancement; singular spectrum analysis; reference free noise canceller; variable step size

1  Introduction

Adaptive speech enhancement plays a key role in speech therapy as well as in hearing aids. In speech therapy the presence of noise degrades the quality of the speech and hence the therapy may not be faithful. Further, ambiguities due to noise leads improper identification of audio signals and lead to unsatisfactory results in speech recognition. Hence, facilitating a high-resolution speech signal is highly desirable in speech therapy applications. In the literature several contributions are made in this aspect. In Laufer et al. [1], Bayesian hierarchical model approach is used for speech enhancement. This method relies on the Gaussian prior of the speech signal and gamma hyper. Spectra mapping [2] is used in throat microphone to avoid acoustic noises. Low band and high band spectral structures between acoustic microphone and throat microphone speech are considered in this analysis. A dynamic filter structure is proposed for speech enhancement, it performs instantaneously based on noisy speech signal. Enhancement of speech signal is done by using two gain functions, i.e., estimation of noise power spectrum and estimation of noisy speech spectrum signal. Variances of this power estimation signal degrades quality of speech signal, so the proposed method estimates noisy power spectrum signals based on adaptive time segmentation. Further demonstration of adaptive segmentation was done based on decision-based speech enhancement and maximum likelihood are proposed in [3,4]. Convolution neural networks (CNN) are used for speech enhancement by utilizing data from various modules. Audio visual deep CNN [5] network is proposed for speech enhancement by utilizing audio and visual stream frame networks. The reconstruction of audio and visual signals is done at the output of the system. Compressive sensing [6] is used for speech enhancement and is performed in frequency domain. A new adaptive beam-forming algorithm was suggested to avoid noisy car environments to improve speech recognition. It contains speech and noise signals in constrained sections as noise adaptive beam-former and speech adaptive beam-former. Later performance investigation was done using delay and sum beam-forming to decrease the word error rate in identification of speech signal. Also auto regression-based gaussian distribution and Laplacian distribution is used for enhancing speech signal are described in [7–12]. The proposed Laplacian prior estimators minimize unnecessary noise signals in desired speech signals. By deriving minimum mean square error and reducing distortion in speech signals with the use of linear bilateral Laplacian gain estimator and non-linear bilateral gain estimators. Main aim of speech enhancement algorithm [13] is to improve intelligibility and quality of noisy speech signal by using spectral or temporal modifications. Maximum speech signal enhancement is done using magnitude spectrum. In Mowlaee et al. [14], magnitude and phase spectra are changed in order to enhance noisy speech signals using multi-level speech enhancement algorithm. Double spectrum consists of modulation transforms further pitch synchronization is used for enhancement of single channel speech signal [15]. Frame wise context modeling is also considered with adaptive filter coefficient frame wise tracking, so that robust performance is obtained in non-stationary noisy condition of speech signals [16]. For speech enhancement, semi supervised multi channels with non-negative matrix factorization [17–19] is used to reduce noisy signals along with constraint variants called as independent low matrix analysis. Unsupervised speech enhancement low power spectral densities are considered in Ming et al. [20]. Various adaptive learning algorithms are presented in [21–25]. Adaptive low rank matrix decomposition is often used for signal enhancement and enhanced efficiency in terms of speech quality. In these contributions mainly two aspects are not addressed. They are reference generation from the noisy speech signal and reduction of computational complexity of the speech enhancement algorithm.

In order to address this limitation, in this manuscript both the aspects of reference generation form the noisy speech and reduction of computational complexity are considered. These two are key entities for the development of system on chip realizations. A modified singular spectrum analysis (MSSA) with modified grouping step is used for reference generation from the noisy speech signal. This is fed to ASE module, which is driven by an adaptive learning algorithm. In our experiments we have used SVAL and TVAL methods. These algorithms are combined with sign regressor function. This function minimizes the computational complexity of the algorithm by an amount equal to the tap length of the filter. The methodology of MSSA for reference generation and adaptive learning algorithms for speech enhancement process are discussed in Section 2. The experimental results are illustrated and presented in Section 3.

2  Hybrid Adaptive Algorithm for Speech Enhancement

In real time applications, removal of noise from the desired signal is considered as inverse problem. It means artifacts are removed from contaminated signal. In this work, it is proposed to eliminate the noise signal from the contaminated speech waves. For this a modified SSA (MSSA) algorithm is used for the generation of reference signal. In an adaptive speech enhancer reference signal is a key element. The reference generated from MSSA is fed to the adaptive learning algorithm. The learning algorithm trains the weight coefficients and trains the weight coefficients, in such a way the reference and contamination in the actual speech signal are correlates with each other. Then both the correlated components get cancel with each other. The MSSA extracts an embedded feature matrix from the speech signal. This matrix is a delayed version and the matrix elements are grouped by using k-means algorithm. Then for each cluster group, Eigen values and eigen vectors are computed using singular value decomposition. For estimating noise components in speech signal, minimum description length concept is considered. It will give dimension length of each eigen vector for estimating speech signal. But to estimate dimension length of each eigen vector, magnitude difference between eigen values is maintained for representing enhanced speech signal and noise signal. As Magnitude of noisy speech signal is high, MSSA has better performance in removing noisy speech signal efficiently. These four steps are followed in MSSA [26]: they are Embedding, Decomposition, Grouping and Reconstruction. Let us consider contaminated speech signal and it is represented as

r(i)=s(i)+n(i) (1)

where ‘s’ is a desired signal, ‘n’ is noise component signal, ‘i’ is number of samples. In first step, sampled data vector of single channel ‘i’, r=[r(1),r(2),…,r(I)] maps to multivariate matrix R as

R=[r(1)r(2)…r(T)r(2)r(3)…r(T+1)⋮r(K)⋮r(K+1)⋮r(I)] (2)

where ‘K’ is window length T = I–K + 1, window length ‘K’ is selected based on criteria K > fs/f, here f and fs are signal frequency and sample frequency of a signal of interest respectively. Trajectory matrices of desired speech signal are s(i) and n(i) respectively, then measured signal trajectory matrix r(i)=s(i)+n(i) is represented as R = S + N, where matrix ‘N’ is estimated by using trajectory matrix ‘R’. In next step, singular value decomposition is performed on trajectory matrix R=V∑W, where V and W are left and right orthogonal matrices respectively and its column elements contains eigen vectors of matrix D, ∑ is a rectangular diagonal matrix, its elements are eigen values with squared roots. Golub and Reinsh algorithms generally perform singular value decomposition on rectangular matrix with K × T dimension and it involves o(K2T+KT2+T3). By using eigen value decomposition and covariance matrix, singular value decomposition is performed on trajectory matrix as H=BBT, then the covariance matrix ‘H’, eigen values and eigen vectors are represented as ð1,ð2,…,ðKandθ1,θ2,…,θK≥0, so that right orthogonal matrix W of tth eigen vector is represented as

wk=BTσtðt (3)

where, t = 1,2, …, K. Measured signal R for tth component trajectory matrix is expressed as

Bt=ðtσtσtT (4)

By substituting Eq. (3) in Eq. (4), tth trajectory matrix Bt is represents as

Bt=σtσtTB (5)

σtσtT term in Eq. (5) forms a tth component subspace element in single vector B, then Eq. (2) trajectory matrix is decomposing into K elements so that R=R1+R2+…RK was obtained. In grouping step, basic SSAs trajectory matrix Bt with elements t = {1, 2, …, K} splits into ‘J’ groups, here J value is considered as two because in measuring speech signal enhanced speech signal is obtained from combination of desired signal and artifact signal. But in general, SSA grouping step is performed based on eigen value magnitudes of trajectory matrix. For example, initially in grouping trajectory matrices high energy signal magnitudes with large own values are considered, then corresponding trajectory matrices with recognized arguments are added to get a trajectory matrix of high energy signal. For trajectory matrix automatic grouping and minimum description length is considered to get desired signal. In case of noisy speech signal reduction this grouping criterion does not work well as artifact signal varies with time signal. So, a new grouping criterion is considered, based on eigen vectors local mobility. For given signal, eigen vectors are represented with frequency components then in grouping step local mobility of every eigen vector is exploited. To define tth eigen vector local mobility σt=[σt(1),σt(2),…,σt(K)], defined difference signal d(i) as d(i)=σt(i)−σt(i−1),i=1,2,…,K. Then for eigen vector σt, local mobility mk is represented as

mk=F1F0 (6)

where F1=∑i=1K−1d(i)K−1,F0=∑i=1Kσt(i)K, here F1 represents average of difference signal and it increases as σt frequency increases. To determine threshold value, investigated local mobility for sinusoidal frequency then its maximum frequency component and local mobility value is also fixed. By projecting data matrix R, estimated trajectory matrix with eigen vectors σt is obtained as N^=σ1σ1TR. Finally, reconstruction step for MSSA is obtained by estimating trajectory matrix with signal of interest as N^ and it maps to single channel signal. Now for example, trajectory matrix a^tg with ‘t’ rows and ‘g’ columns then reconstruction step for single channel noisy signal n^(i) is mathematically expressed from estimated trajectory matrix N^ as

n^(i)={1i∑t=1in^t,i−t+1for 1≥i<K1K∑t=1Kn^t,i−t+1for K≥i≤T1I−i+1∑t=i−T+1I−T+1n^t,i−t+1for T<i≤I (7)

Step Variable Size Adaptive Learning Algorithm with Modified Singular Spectrum Analysis Based Reference Generation

Once the reference signal is generated by the MSSA based decomposition it is fed to the noise canceller. The learning algorithm trains the weight coefficients, such that the reference and noise component present in the actual speech correlates with each other and there by cancel with each other [27]. The block diagram of proposed MSSA based adaptive speech enhancer is shown in Fig. 1. Based on steepest descent algorithm, least mean square (LMS) algorithm weight update equation is estimated to get error free speech signal.

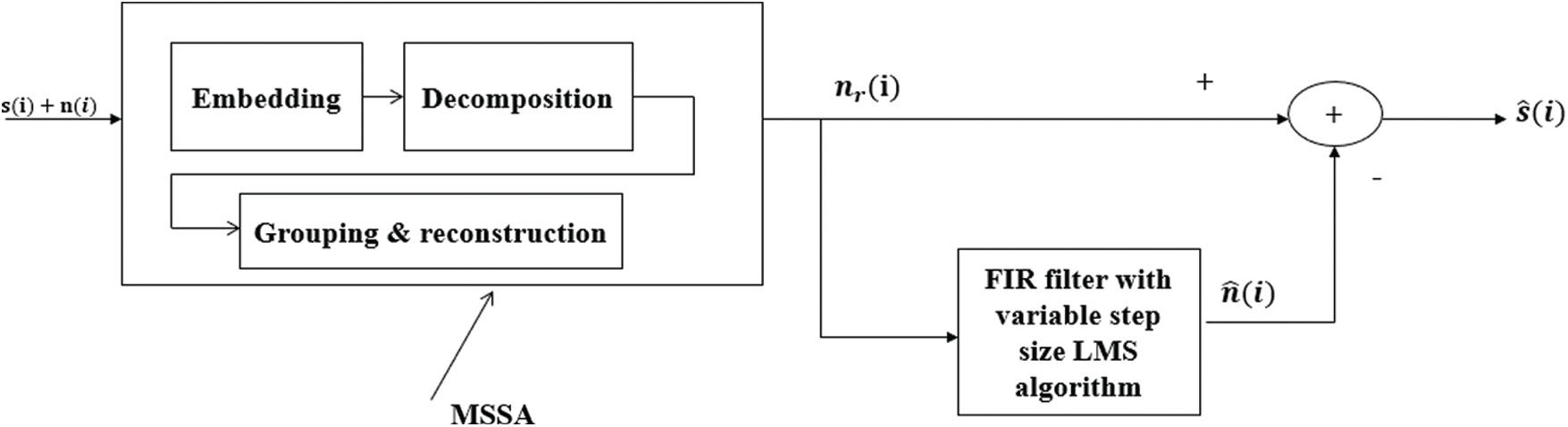
Figure 1: Block diagram of adaptive noise canceller using MSSA based reference generation

Output of FIR filter is

r(i)=aT(i)c(i) (8)

Error n(i) is defined as difference between desired response and actual response

n(i)=s(i)−r(i) (9)

Then the weight update equation becomes

a(i+1)=a(i)+ωn(i)c(i) (10)

where n(i) is error in adaptive filter, s(i) is desired output, c(i) is filter input and ω is step size for updating weight vector.

Normalized adaptive algorithm weight update equation is given as

a(i+1)=a(i)+ωK+c2(i)ωn(i)c(i) (11)

Here ‘K’ is constant

In non-stationary environment, estimating variability and convergence time are main parameters, they are controlled by minimum cost function and vary with time and step size parameter. If the step size is smaller, a lot of iterations are required and there will be less residual noise. Hence, an optimized step value has to be chosen [27]. Similar to constant step size adaptive learning algorithm, in Ram et al. [28] an adaptive step size algorithm is proposed. Flowchart for speech enhancement process using SVAL algorithm with MSSA based reference generation is shown in Fig. 2.

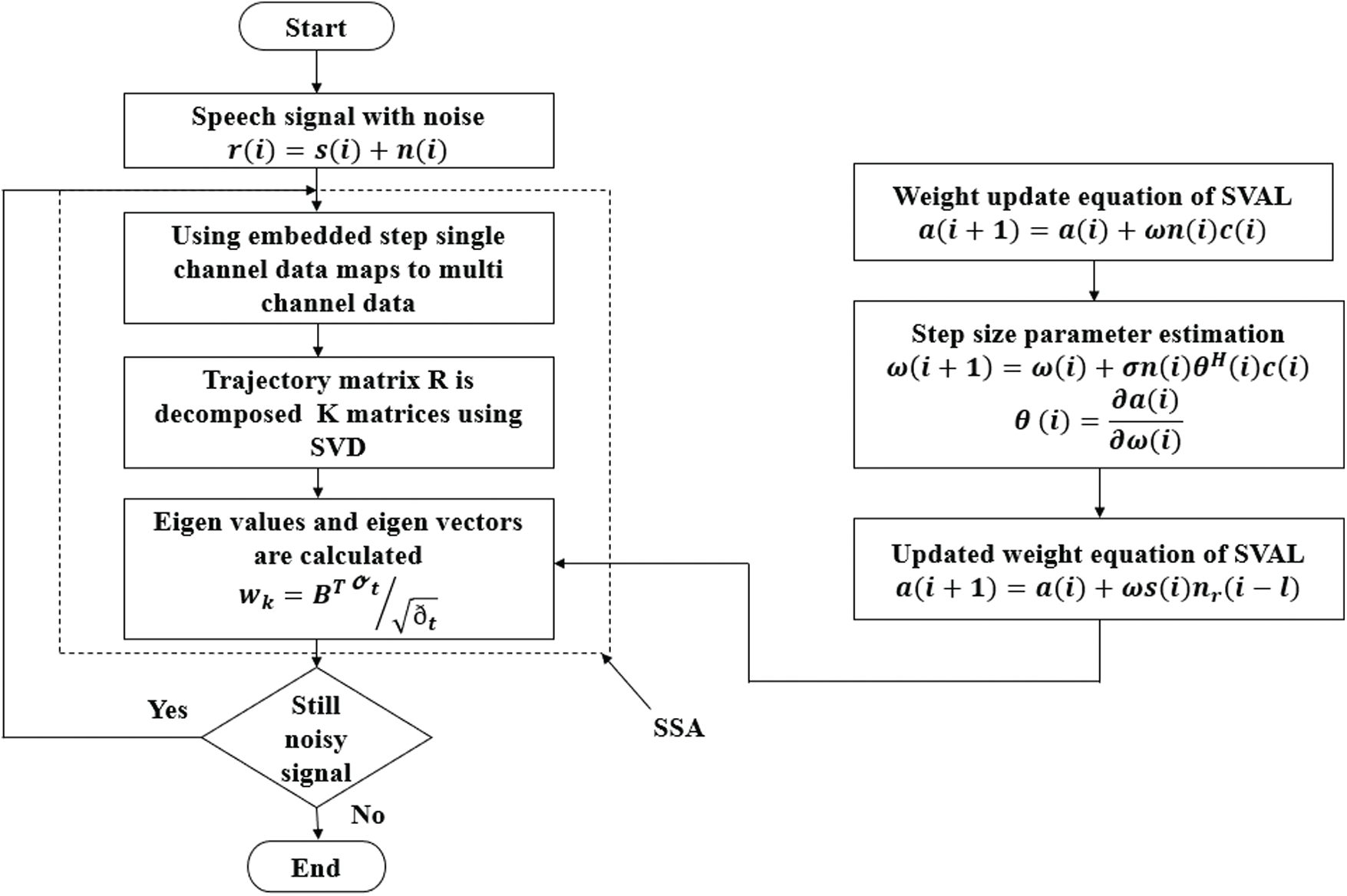
Figure 2: Flowchart of adaptive speech enhancement using modified singular spectrum analysis-based reference generation

For this a Step size ω is updated with the following equation and it is expressed as

ω(i+1)=ω(i)+σn(i)θH(i)c(i) (12)

θH is a gradient vector and it is defined as ratio of partial derivative of weight update vector at each sample with respect to step size at each sample.

θH(i)=∂a(i)∂ω(i) (13)

Here σ is a small positive constant and it will control step size parameter updating. In practice, LMS is exponentially convergent, whereas sign algorithms are linearly convergence. Therefore, signed algorithms makes convergence slower when initial weight updating equation is far from optimum [29]. For minimizing computational complexity, the variable step algorithms are combined with signum function. The resultant mathematical recursions are written as,

a(i+1)=a(i)+ωn(i)signc(i) (14)

a(i+1)=a(i)+ωK+c2(i)ωn(i)signc(i) (15)

Finally, exact speech signal s^(i) is extracted by subtracting estimated noisy signal from the calculated speech signal r(i) and it is expressed as

s^(i)=r(i)−n^(i)=s(i)+n(i)−n^(i) (16)

a(i+1)=a(i)+ωs(i)nr(i−l) (17)

Here nr noise reference signal, it is obtained by passing through reference generator, ‘J’ is filter order with length l = 0, 1, 2, …, J.

3  Experimental Results and Analysis

In our experiments, noise cancellation from speech signals is done using modified singular spectrum analysis with adaptive step size algorithm. Singular spectrum analysis is a technique to extract the reference signal from the contaminated speech signal. As a result, the enhancement process does not require any prior knowledge on types of speech and noise signal. In order to circumvent these issues adaptive algorithm is recommended for speech enhancement along with singular spectrum analysis. It uses prior information about noise and speech types, then it will map to functions of clear speech and noise type features. For this entire process, the reference signal generated by the MSSA is taken in to consideration. By the proposed method, speech intelligibility is enhanced when it trains to specific scenarios. Performance of MSSA based adaptive algorithms is investigated in terms of intelligibility and objective measures. General SSA method shows improvement in objective measures, but it has failed in intelligibility test of speech signals across SNR regions. The MSSA with adaptive step size learning algorithm can overcome this drawback. Auto regressor coefficients of speech and noise signals parameters are considerably less when compared to the proposed algorithm. If weight parameters are trained smaller then it is possible to train these parameters for enhancement process. This results improvement in single channel intelligibility test signals. Diverse type of real noises is considered in our experiment’s namely: cockpit noise, elevator noise, random noise and high voltage murmuring. As described in Section 2, the enhancement process is carried in two steps. First one is reference generation using MSSA and noise removal using adaptive learning algorithm.

The computational complexity is reduced in the proposed algorithm by applying sign regressor function to weight update equation. For the comparison of performance measures, adaptive noise cancellation due to LMS, TVAL, SRTVAL, SVAL and SRSVAL algorithms are considered. Performance measures are calculated in terms of signal to noise ratio improvement (SNRI), misadjustement (MSD) and excess mean square error (EMSE). The speech enhancement experiments are performed for ten times and average values are tabulated in Tabs. 1–3. Simulations are carried using MATLAB tool, window size of adaptive filter is considered as ten, step size is 0.01. Elimination of the noise process initially done by adding additive Gaussian noise, then simulations of polluted speech signals are performed by the proposed procedure, with zero mean and variance of 0.02 in white Gaussian noise. Real noises and synthetic noises are considered in the experiments. Random noise was shaped in accordance with threshold value estimations using spectral masking. The five speech samples labeled as Wave-1, Wave-2, Wave-3, Wave-4, Wave-5 and are contaminated with different types of noises. By using estimated thresholds and adaptive learning process, noise components are removed. The enhancement results of wave 1 contaminated with cockpit noise are shown in Fig. 3, due to space constraint only one signal is shown, the performance measures of all signals are tabulated. After achieving constant impulse response output, impulse response is considered for the next half of the samples and the results are observed. On observation, the before and after results in variations of impulse response feedback path exhibit faster convergence for proposed MSSA based SRSVAL algorithm as sign regressor function is used in comparison to MSSA-SVAL algorithm. Comparisons of various performance measures are also graphically shown in Figs. 4–6. The key benefit of the proposed implementation is that the reference produced from the noisy speech signal itself is the MSSA mechanism. The adaptive algorithm-related sign regressor operation minimizes the number of multiplications required for the filtering operation to be performed. The SVAL algorithm filters the speech signal with better convergence and filtering ability. It’s been observed in our work that the proposed MSSA based sign regressor version of SVAL is found to be a better candidate for speech enhancement applications and suitable for immediate applications like mobile communications, speech, hearing aids and noise cancelers in defense, space applications.

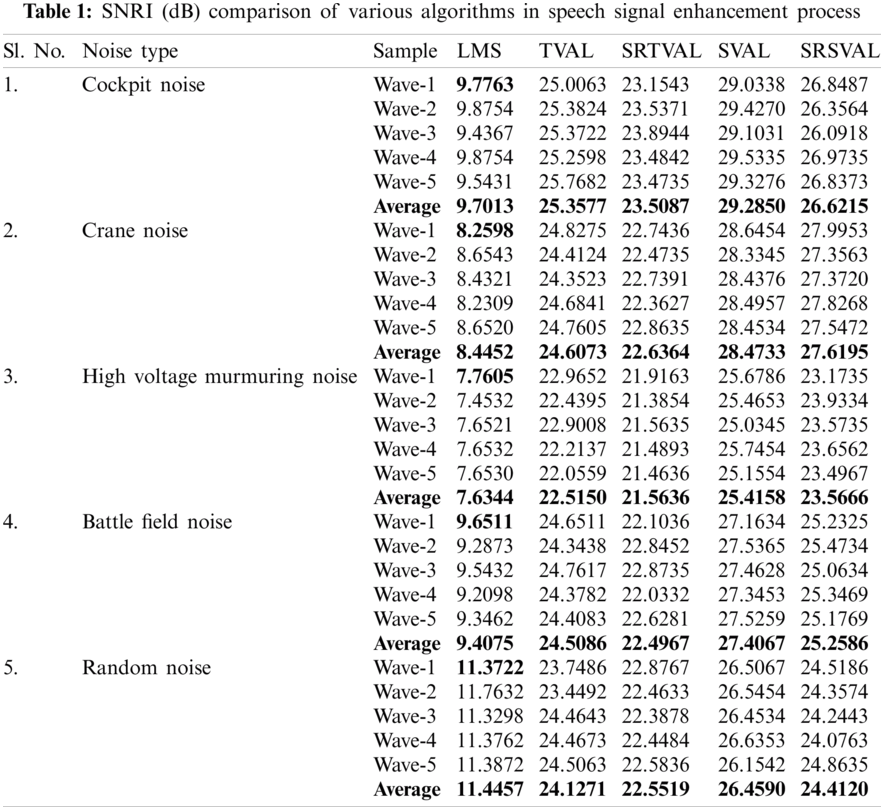
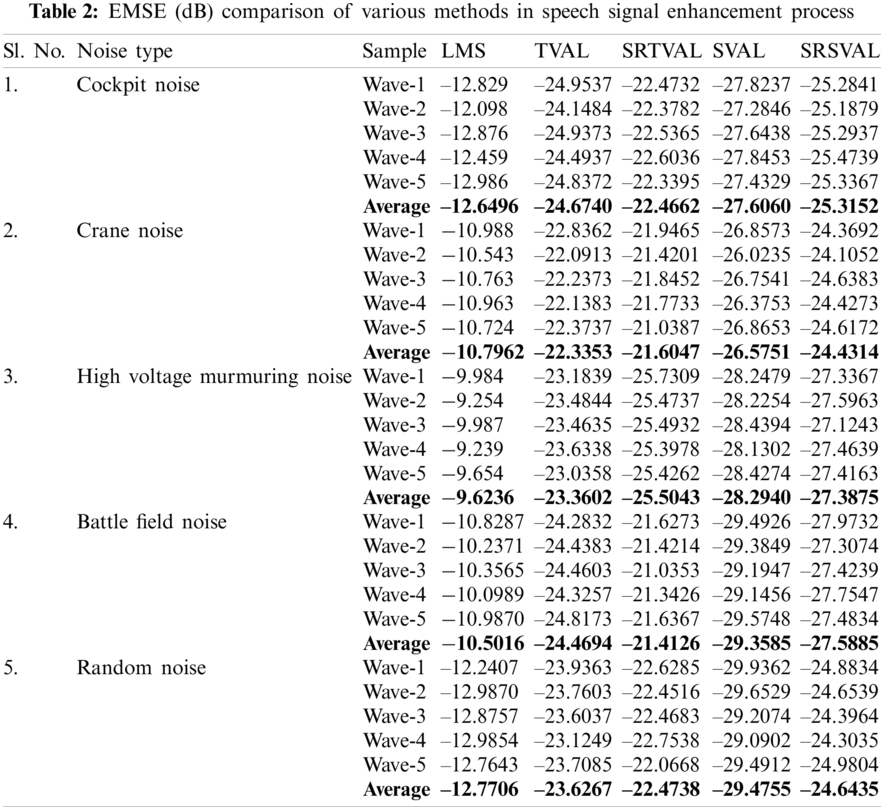
Figure 3: Speech enhancement using modified SSA based reference free ANC, (a). Speech signal contaminated with cockpit noise corresponds to the wave “adaptive noise cancellation”, (b). Enhanced signal with TVLAL ANC, (c). Enhanced signal with SRTVAL ANC, (d). Enhanced signal with SVAL ANC, (e). Enhanced signal with SRSVAL ANC. (X-axis number of samples, Y-axis amplitude of the signal)

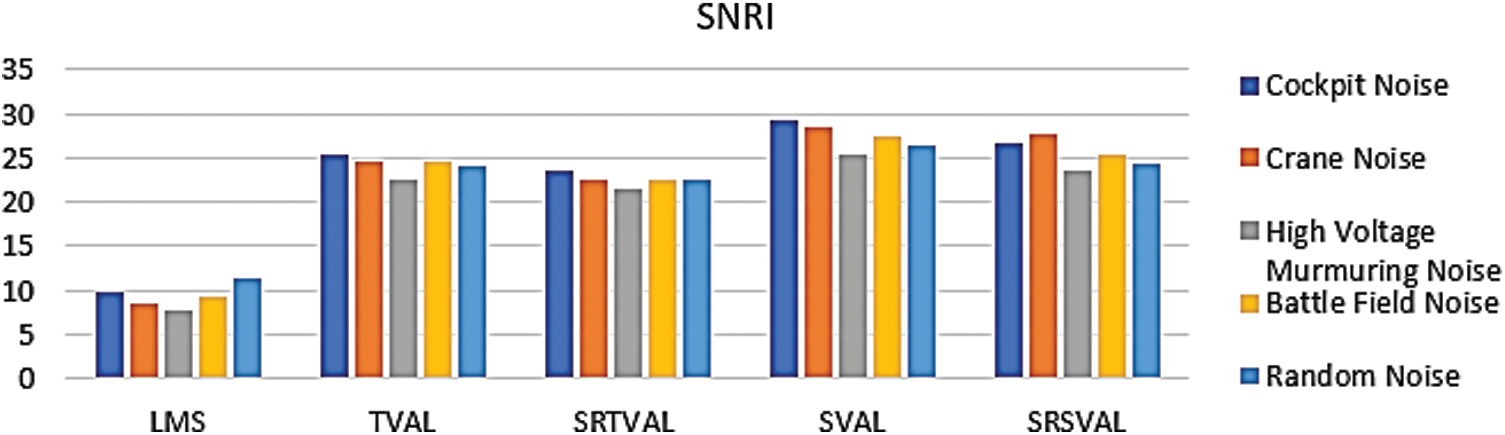
Figure 4: Performance measure comparison of SNRI (dB) for various adaptive algorithms

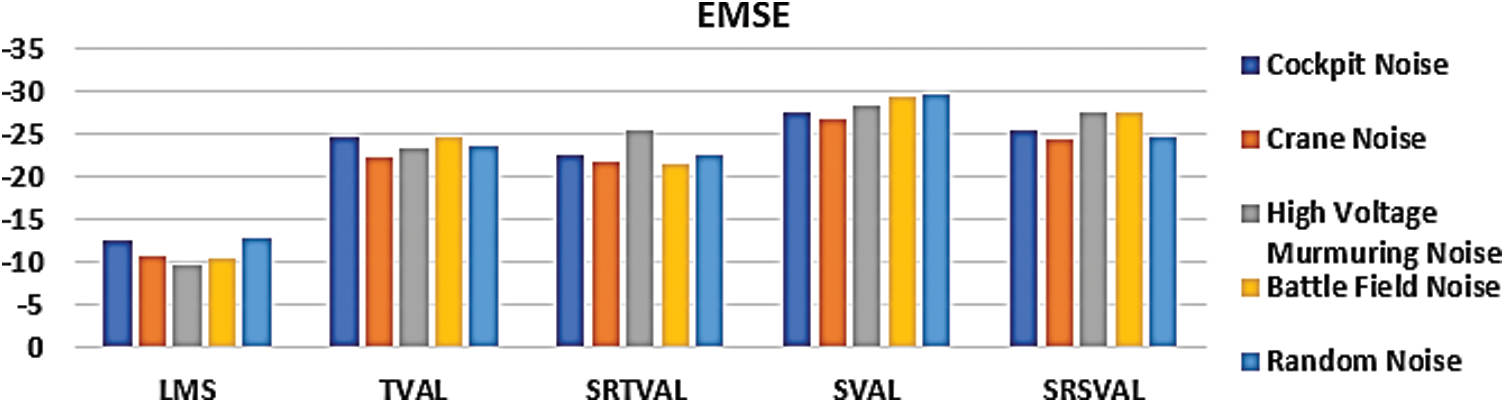
Figure 5: Performance measure comparison of EMSE (dB) for various adaptive algorithm

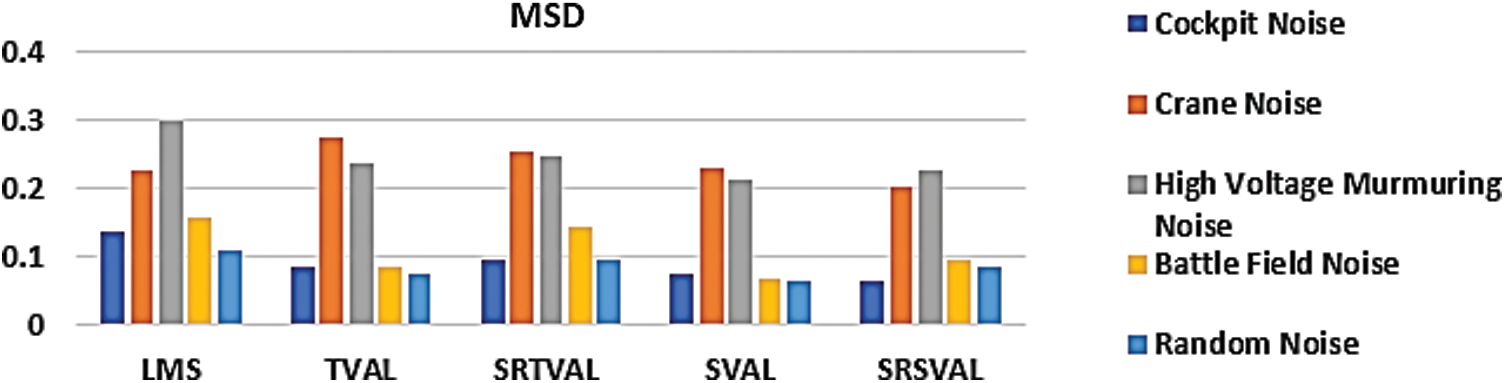
Figure 6: Performance measure comparison of MSD (no units) for various adaptive algorithms

4  Conclusion

In general, speech signals are contaminated with the background noise and results ambiguities in speech recognition. In order to avoid those noises, a modified SSA based variable step size driven adaptive learning algorithms are proposed. The new grouping technique improves the performance of MSSA in the process of reference generation. The step variable adaptive learning process eliminates the noise components very effectively. The combination of sign regressor function reduces the number of multiplications involved in the process of noise cancellation. The performance measures are calculated, averaged for ten experiments and are tabulated in Tabs. 1–3. Several real time noises like cockpit noise, crane noise, high voltage murmuring noise, battle field noise and random noise are considered in the experiments. Between TVAL and SVAL, the performance of SVAL is found to be better than the counterpart. By considering the performance measures like SNRI, EMSE, MSD and computational complexity, it is found that sign regressor version of SVAL is better than the other learning methods. Hence, SRSVAL based adaptive speech enhancement unit is well suited for real time realization as system on chip or lab on chip.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Y. Laufer and S. Gannot, “A Bayesian hierarchical model for speech enhancement with time-varying audio channel,” IEEE/ACM Transactions on Audio, Speech, and Language Processing, vol. 27, no. 1, pp. 225–239, 2019. [Google Scholar]

 2.  C. Zheng, J. Yang, X. Zhang, M. Sun and T. Cao, “A spectra-based equalization-generation combined framework for throat microphone speech enhancement,” IEEE Access, vol. 6, pp. 71455–71463, 2018. [Google Scholar]

 3.  M. P. A. Jeeva, T. Nagarajan and P. Vijayalakshmi, “Adaptive multi-band filter structure-based far-end speech enhancement,” IET Signal Processing, vol. 14, no. 5, pp. 288–299, 2020. [Google Scholar]

 4.  R. C. Hendriks, R. Heusdens and J. Jensen, “Adaptive time segmentation for improved speech enhancement,” IEEE Transactions on Audio, Speech, and Language Processing, vol. 14, no. 6, pp. 2064–2074, 2006. [Google Scholar]

 5.  J. Hou, S. Wang, Y. Lai, Y. Tsao, H. Chang et al., “Audio-visual speech enhancement using multimodal deep convolutional neural networks,” IEEE Transactions on Emerging Topics in Computational Intelligence, vol. 2, no. 2, pp. 117–128, 2018. [Google Scholar]

 6.  J. Wang, Y. Lee, C. Lin, S. Wang, C. Shih et al., “Compressive sensing-based speech enhancement,” IEEE/ACM Transactions on Audio, Speech, and Language Processing, vol. 24, no. 11, pp. 2122–2131, 2016. [Google Scholar]

 7.  R. Martinek, R. Jaros, J. Baros, L. Danys, A. Kawala-Sterniuk et al., “Noise reduction in industry based on virtual instrumentation,” Computers, Materials & Continua, vol. 69, no. 1, pp. 1073–1096, 2021. [Google Scholar]

 8.  O. M. A. Zaid, M. A. Tawfeek and S. Alanazi, “Applying and comparison of chaotic-based permutation algorithms for audio encryption,” Computers, Materials & Continua, vol. 67, no. 3, pp. 3161–3176, 2021. [Google Scholar]

 9.  Y. Li and S. Kang, “Deep neural network-based linear predictive parameter estimations for speech enhancement,” IET Signal Processing, vol. 11, no. 4, pp. 469–476, 2017. [Google Scholar]

10. A. Aroudi, H. Veisi and H. Sameti, “Hidden Markov model-based speech enhancement using multivariate Laplace and Gaussian distributions,” IET Signal Processing, vol. 9, no. 2, pp. 177–185, 2015. [Google Scholar]

11. H. Taherian, W. Zhong-Qiu, J. Chang and W. DeLiang, “Robust speaker recognition based on single-channel and multi-channel speech enhancement,” IEEE/ACM Transactions on Audio, Speech, and Language Processing, vol. 28, pp. 1293–1302, 2020. [Google Scholar]

12. B. M. Mahmmod, A. R. Ramli, S. H. Abdulhussian, S. A. R. Al-Haddad and W. A. Jassim, “Low-distortion MMSE speech enhancement estimator based on Laplacian prior,” IEEE Access, vol. 5, pp. 9866–9881, 2017. [Google Scholar]

13. T. Lavanya, T. Nagarajan and P. Vijayalakshmi, “Multi-level single-channel speech enhancement using a unified framework for estimating magnitude and phase spectra,” IEEE/ACM Transactions on Audio, Speech, and Language Processing, vol. 28, pp. 1315–1327, 2020. [Google Scholar]

14. P. Mowlaee, M. Blass and W. B. Kleijn, “New results in modulation-domain single-channel speech enhancement,” IEEE/ACM Transactions on Audio, Speech, and Language Processing, vol. 25, no. 11, pp. 2125–2137, 2017. [Google Scholar]

15. P. C. Bhattacharya, N. Tangsangiumvisai and A. Worapishet, “Performance improvement of adaptive wavelet thresholding for speech enhancement using generalized Gaussian priors and frame-wise context modeling,” IEEE Access, vol. 8, pp. 168361–168380, 2020. [Google Scholar]

16. G. Shi, P. Aarabi and H. Jiang, “Phase-based dual-microphone speech enhancement using a prior speech model,” IEEE Transactions on Audio, Speech, and Language Processing, vol. 15, no. 1, pp. 109–118, 2007. [Google Scholar]

17. K. Sekiguchi, Y. Bando, A. A. Nugraha, K. Yoshii and T. Kawahara, “Semi-supervised multichannel speech enhancement with a deep speech prior,” IEEE/ACM Transactions on Audio, Speech, and Language Processing, vol. 27, no. 12, pp. 2197–2212, 2019. [Google Scholar]

18. C. Li, T. Jiang, S. Wu and J. Xie, “Single-channel speech enhancement based on adaptive low-rank matrix decomposition,” IEEE Access, vol. 8, pp. 37066–37076, 2020. [Google Scholar]

19. Y. Bando, K. Itoyama, M. Konyo, S. Tadokoro, K. Nakadai et al., “Speech enhancement based on Bayesian low-rank and sparse decomposition of multichannel magnitude spectrograms,” IEEE/ACM Transactions on Audio, Speech, and Language Processing, vol. 26, no. 2, pp. 215–230, 2018. [Google Scholar]

20. J. Ming and D. Crookes, “Speech enhancement based on full-sentence correlation and clean speech recognition,” IEEE/ACM Transactions on Audio, Speech, and Language Processing, vol. 25, no. 3, pp. 531–543, 2017. [Google Scholar]

21. M. N. Salman, P. Trinatha Rao and M. Z. Ur Rahman, “Adaptive noise cancellers for cardiac signal enhancement for IOT based health care systems,” Journal of Theoretical and Applied Information Technology, vol. 95, no. 10, pp. 2206–2213, 2017. [Google Scholar]

22. A. Sulthana and M. Z. Ur Rahman, “Efficient adaptive noise cancellation techniques in an IOT enabled telecardiology system,” International Journal of Engineering and Technology (UAE), vol. 7, no. 2, pp. 74–78, 2018. [Google Scholar]

23. P. Srinivasareddy and M. Z. Ur Rahman, “Novel simplified logarithmic adaptive exon prediction for DNA analysis,” vol. 10, pp. 1422–1432, 2018. [Google Scholar]

24. M. N. Salman, P. Trinatha Rao and M. Z. U. Rahman, “Novel logarithmic reference free adaptive signal enhancers for ECG analysis of wireless cardiac care monitoring systems,” IEEE Access, vol. 6, pp. 46382–46395, 2018. [Google Scholar]

25. P. Srinivasareddy, M. Z. Ur Rahman and S. Y. Fathima, “Cloud-based adaptive exon prediction for DNA analysis,” Healthcare Technology Letters, vol. 5, no. 1, pp. 25–30, 2018. [Google Scholar]

26. M. Ajay Kumar and S. Rafi Ahamed, “Motion artifact removal from single channel electroencephalogram signals using singular spectrum analysis,” Biomedical Signal Processing and Control, vol. 30, no. 6, pp. 79–85, 2016. [Google Scholar]

27. S. S. Haykin, Adaptive Filter Theory. Eaglewood Cliffs, NJ, USA: Prentice-Hall, 2007. [Google Scholar]

28. M. R. Ram, K. V. Madhav, E. H. Krishna, N. R. Komalla and K. A. Reddy, “A novel approach for motion artifact reduction in PPG signals based on AS-LMS adaptive filter,” IEEE Transactions on Instrumentation and Measurement, vol. 61, no. 5, pp. 1445–1457, 2012. [Google Scholar]

29. A. Sulthana, M. Z. U. Rahman and S. S. Mirza, “An efficient Kalman noise canceller for cardiac signal analysis in modern telecardiology systems,” IEEE Access, vol. 6, pp. 34616–34630, 2018. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.