Computers, Materials & Continua DOI:10.32604/cmc.2022.020066
Article

Optimal Deep Reinforcement Learning for Intrusion Detection in UAVs

V. Praveena1, A. Vijayaraj2, P. Chinnasamy3, Ihsan Ali4,*, Roobaea Alroobaea5, Saleh Yahya Alyahyan6 and Muhammad Ahsan Raza7

1Department of Computer Science and Engineering, Dr. N. G. P Institute of Technology, Coimbatore, 641048, India
2Department of Information Technology, Vignan’s Foundation for Science, Technology & Research, Guntur, 522213, India
3Department of Information Technology, Sri Shakthi Institute of Engineering and Technology, Coimbatore, 641062, India
4Department of Computer System and Technology, Faculty of Computer Science and Information Technology, University of Malaya, Kuala Lumpur, 50603, Malaysia
5Department of Computer Science, College of Computers and Information Technology, Taif University, Taif, 21944, Saudi Arabia
6Department of Computer Science, Community College in Dwadmi, Shaqra University, 11961, Saudi Arabia
7Department of Information Technology, Bahauddin Zakariya University, Multan, 60000, Pakistan
*Corresponding Author: Ihsan Ali. Email: ihsanali@ieee.org
Received: 07 May 2021; Accepted: 15 June 2021

Abstract: In recent years, progressive developments have been observed in recent technologies and the production cost has been continuously decreasing. In such scenario, Internet of Things (IoT) network which is comprised of a set of Unmanned Aerial Vehicles (UAV), has received more attention from civilian to military applications. But network security poses a serious challenge to UAV networks whereas the intrusion detection system (IDS) is found to be an effective process to secure the UAV networks. Classical IDSs are not adequate to handle the latest computer networks that possess maximum bandwidth and data traffic. In order to improve the detection performance and reduce the false alarms generated by IDS, several researchers have employed Machine Learning (ML) and Deep Learning (DL) algorithms to address the intrusion detection problem. In this view, the current research article presents a deep reinforcement learning technique, optimized by Black Widow Optimization (DRL-BWO) algorithm, for UAV networks. In addition, DRL involves an improved reinforcement learning-based Deep Belief Network (DBN) for intrusion detection. For parameter optimization of DRL technique, BWO algorithm is applied. It helps in improving the intrusion detection performance of UAV networks. An extensive set of experimental analysis was performed to highlight the supremacy of the proposed model. From the simulation values, it is evident that the proposed method is appropriate as it attained high precision, recall, F-measure, and accuracy values such as 0.985, 0.993, 0.988, and 0.989 respectively.

Keywords: Intrusion detection; UAV networks; reinforcement learning; deep learning; parameter optimization

1  Introduction

The exponential developments in the fields of cloud computing and artificial intelligence technologies have drastically improved the design of Internet of Things (IoT) technologies. Various smart devices have the ability to generate and receive massive quantities of data through communication and interconnectivity. The familiarity of IoT technologies and the smartness of gadgets have provided a comfy lifestyle to its users. Nevertheless, the utilization of latest technologies and intelligent gadgets paved the way for new security and privacy issues [1]. IoT network is deemed to be a significant target for hackers since the IoT devices gather and archive massive quantities of private data of clients. At this moment, the protection of user’s private data and security are highly essential [2]. Due to the progression of technologies and constant reduction in production cost, there is an increasing penetration of IoT network that comprises of Unmanned Aerial Vehicles (UAVs) right starting from manufacturing & production to daily lives of the people in terms of border surveillance. At present, UAVs are extensively utilized in movie and television shooting, smart farming, climate observation, forest fire recognition, disaster management, etc. But UAVs brought distinct accessibilities to life and increased productivity whereas the network security issues are occurring in parallel [3,4].

If a number of UAVs collaboratively carry out its functions, it is essential to design a data connection channel among themselves so as to develop a mobile self-organized network of UAVs. UAV system allows the real-time distribution of data using mobile networks that do not require transmission from ground station. It increases the survival and combating abilities of UAV network in an efficient manner. Since UAV network is a sub kind in Mobile Ad hoc Network (MANET), a typical attack in MANET affects the UAV network too. Due to the existence of different network accessing techniques and openness of networks, UAV networks suffer from unavoidable security challenges. The defensive operations of classical network security technologies are frequently passive and it is challenging to resist the network attacks using such unstable technologies.

When it comes to dynamic defensive network security technologies, Intrusion Detection System (IDS) has limitations of conventional security technologies. However, intrusion detection systems have received considerable interest on client end though quite a few difficulties have to be overcome in real-time applications. Classical IDS usually experiences inadequate efficiency and ineffectiveness, particularly when handling recent computer networks that work with high bandwidth and enormous data traffic. Since the attacks are highly complicated, automatic, and distributed, the classical IDS does not fulfil the requirements of recent network security challenges. This scenario enhances the Detection Rate (DR) and diminish the false alarm frequency of IDSs. Various studies have presented Machine Learning (ML) techniques in the domain of intrusion detection.

Evolutionary Algorithms (EAs) are simulated from the concept of natural evolution yet with few variations theoretically. The variations exist because of the nature that every algorithm follows a different creature or that the behavior of individuals grow and create new solutions. In EA, a population of possible solutions attempts at survival based on the validation of fitness in a particular platform. They arbitrarily accomplish the optimization procedure. The initial population of optimization process is generated arbitrarily and it alters the fixed functions over a particular number of iterations or rounds. Different processes of reproduction, migration, and solution designing over optimization makes each one different from another.

Many population-oriented algorithms do not follow any structure. It depicts an identical feature during searching process based on exploration and exploitation stages which forms the major characteristics of algorithm. To obtain the maximum performance, metaheuristic techniques maintain a tradeoff between exploration and exploitation levels in searching area. The exploration level provides a chance to observe different & significant regions in a search space and generate new solutions to escape from the local optima issue. The exploitation stage denotes the convergence ability of the algorithm and obtains predictable solutions during exploration process. So, a better outcome between the exploration and exploitation stages ensures the avoidance of local optimization problems and achievement of better convergence speed. Besides, proper management of these two phases can reach the global optima.

Though several metaheuristic algorithms are available in the literature, the current research article utilizes Black Widow Optimization (BWO) algorithm. This BWO algorithm is framed on the basis of interesting nature of Black Widow (BW) spiders. It encompasses an important process of cannibalism. In this process, spiders without fitness are discarded from the region which results in earlier convergence. It significantly varies from other population-based optimization algorithms. BWO algorithm provides effective outcomes on exploitation and exploration levels. Besides, it provides rapid convergence and eliminates the local optimum issue. It is also noted that the BWO algorithm has the ability to investigate maximum search space to reach the global best solutions. Therefore, BWO algorithm can be utilized to solve the hyperparameter optimization problem.

The current research work presents a Deep Reinforcement Learning technique optimized by Black Widow Optimization (DRL-BWO) algorithm for UAV networks. In addition, DRL involves improved reinforcement learning-based Deep Belief Network (DBN) for intrusion detection. For parameter optimization of DRL technique, BWO algorithm is applied which helps in improving the intrusion detection performance among UAV networks. An extensive set of experimental analyses was conducted to highlight the supremacy of the proposed model. The contribution of this research article is summarized herewith.

•   DRL-BWO algorithm is proposed for intrusion detection in UAV networks

•   An improved reinforcement learning-based DBN model is employed with softmax layer for the detection of intrusions in UAV networks

•   For hyperparameter optimization of reinforced DBN model, BWO algorithm is utilized through which DR is enhanced

•   The intrusion detection performance of the DRL-BWO algorithm was validated against NSL-KDD Cup dataset

Rest of the sections in the paper are arranged as follows. Section 2 offers the works related to the domain and Section 3 introduces the presented DRL-BWO technique for UAV networks. Further, Section 4 validates the performance of the proposed DRL-BWO algorithm. Finally, Section 5 concludes the work.

2  Related Works

Shah et al. [5] studied the efficiency of two open source IDSs named Snort as well as Surcata. The outcome illustrated that an improved DR can be achieved when utilizing optimum Support Vector Machine (SVM) and firefly (FF) techniques. Kabir et al. [6] developed a novel model based on least squares SVM (LS-SVM) for IDS. Wang et al. [7] designed an IDS using SVM through feature augmentation process. With the conversion of logarithmic marginal density ratio for generating actual features, the novel efficient change features are achieved that considerably enhances the detection capability of a technique. Ahmed et al. [8] introduced a learning technique for IDS with the help of Neural Network (NN) that has better output in terms of convergence rate and learning time.

Hu et al. [9] developed a distributed IDS in which a local parameterized detection method is built for every individual node using an online Adaboost technique. Ma et al. [10] introduced a new method named SCDNN that associates Spectral Clustering (SC) and Deep NN (DNN) techniques. The simulation outcome depicted that the SCDNN classification model works efficiently over Back Propagation Neural Network (BPNN) and SVM models. But Deep Learning (DL) models have been extensively applied, thanks to its better efficiency in big data analytics and its feasibility in resolving intrusion detection issues of enormous, highly dimension, and non-linear data. With the construction of a nonlinear network along with multiple hidden layers, the low dimension features that are simple to categorize the data could be attained, and intrusion detection performance can be enhanced.

Hinton et al. [11] introduced a DL technique named Deep Belief Network (DBN) which sparked widespread interest among researchers. This technique converts high dimension and non-linear data features into abstracts that are appropriate for pattern classification using layer-wise feature extraction. Qu et al. [12] presented an IDS using DBN which is efficiently enhanced to find the abnormalities. Liang et al. [13] developed an IDS depending on DBN and ELM (Extreme Learning Machine) that increases the DR and effectiveness of algorithmic operations. The number of hidden layer node counts can be optimally found using Particle Swarm Optimization (PSO) technique.

In the literature [14], the researchers developed an effective technique to find indoor and open-air three-dimensional (3D) areas of nodes by determining the signal strength. The mathematical formulation is performed based on path-loss model and decision tree. The study conducted earlier [15] presented an IDS which is designed to be included in network gateway so that it can determine the attacks and filter the over length packets. IDS is executed based on integer optimization issue by the minimization of false alarm probability, while it maintains the missed detection probability below a desired level.

Few intelligent search algorithms proposed so far are Simulated Annealing (SA), ant colony algorithm, Genetic Algorithm (GA), and PSO. In ant colony technique, the time taken for resolution is high and is prone to premature. The original outcome of SA technique is considerably influenced by the variables such as global optimization and computation efficiency. On the other hand, Bayesian optimization techniques are frequently employed in the optimization of hyper parameters. Though it has the benefit of low number of iterations, it falls easily into local optima. Therefore, BWO algorithm can be utilized in resolving the hyperparameter optimization problem.

3  The Proposed DRL-BWO Based Intrusion Detection in UAV Networks

The working procedure involved in the proposed DRL-BWO algorithm is shown in Fig. 1. From the figure, it is apparent that the networking data, fed as input, undergoes preprocessing to remove the unwanted data and transform it into a compatible format. Then, DBN model is applied to determine the existence of intrusions in UAV networks. Finally, BWO algorithm is employed to determine the optimal hyperparameter values involved in the presented model.

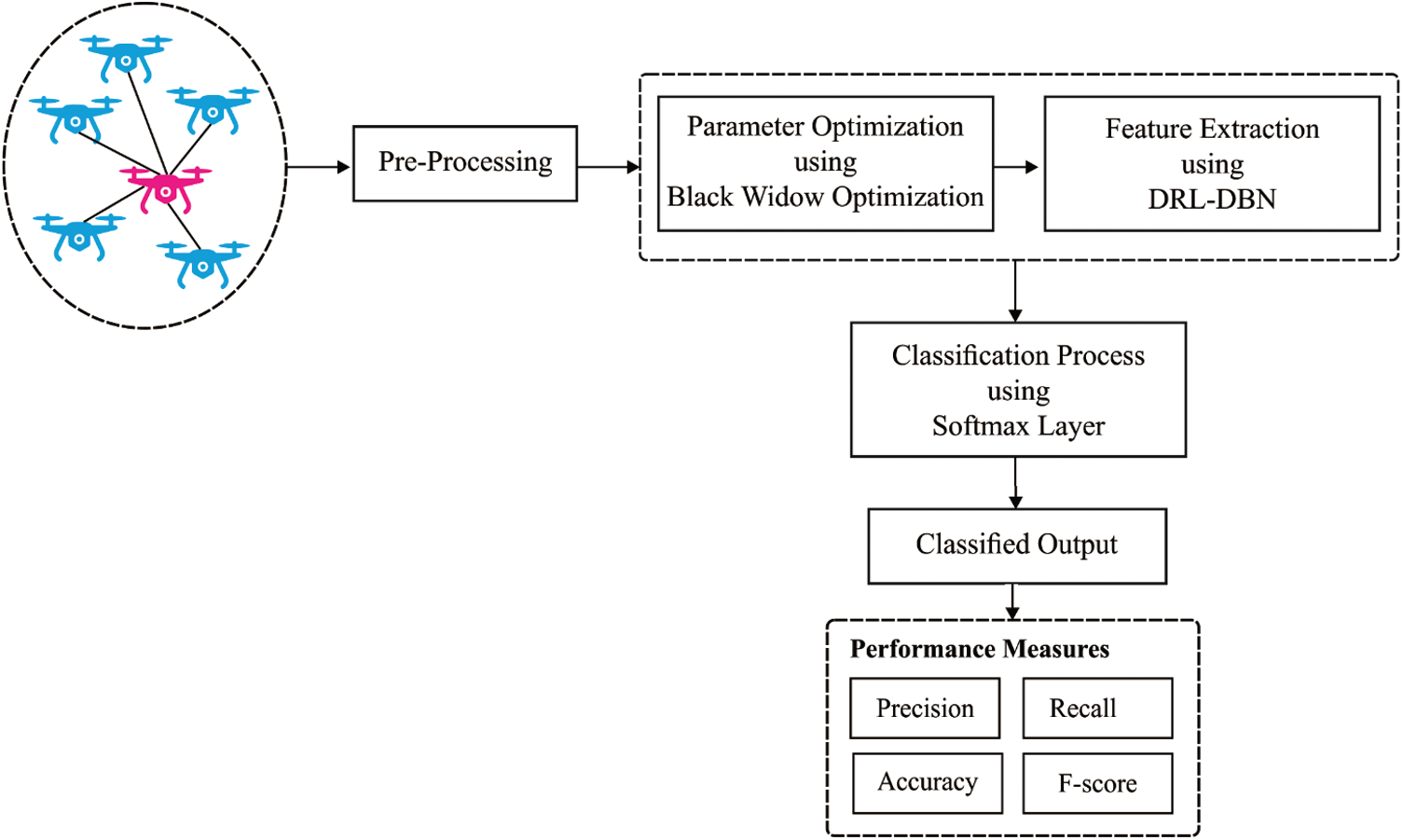
Figure 1: The working process of DRL-BWO model

3.1 Reinforcement Learning

DRL is integrated with RL and DNN. This combination allows the RL agents to improve if the provided conditions are separately explored. When a RL agent is a learning task, the situation provides the required data to agent based on its performance i.e., either best or worst. With this data, the agent should separately perform the task which results in the optimal execution of task purposes. The purposes can be illustrated by reward function which allocates the numerical value for all the performed actions in the provided state. Besides, an agent attains a novel state in the event of an action accomplishment. So, the agent connects the states with performances so as to maximize r0+γ⋅r1+γ2⋅r2+…. Here ri refers to the achieved reward in i-th episode and γ implies a discount factor measure which refers to how effective the future performances will be.

An essential part of RL model is Markov Decision Process (MDP) in which the upcoming moves as well as rewards are distributed only with the present state and chosen performance. Thus, when the Markovian assets exists in a state, such states possess all the data required for dynamic tasks. For sample, chess is a common instance of Markovian asset. During this game, the historical decisions have no say in decision making process for further proceedings [16]. Each data is already explained in present sharing of pieces over the board. Conversely, when the present state is identified, the earlier transitions which directed the agent to that condition develop in an unrelated manner in terms of decision-making process.

MDP is appropriately determined by 4-tuple <S, A, δ, r> where:

S refers to limited group of system states, s∈S;

A denotes a limited group of actions, a∈A, and Ast∈A indicate a limited group of actions that are accessible in st∈S at time t;

δ implies the transition process δ:S×A→S;

r signifies a direct reward (or reinforcement) function r: S×A→R.

During the timestep t, an agent observes the present state st∈S and selects their action i.e., at∈A to be performed. A situation provides a reward rt=r(st,at) and the agent goes to a state st+1=δ(st,at). The functions r and δ are decided based on the present state st and action at only. Hence, it cannot be considered as a memory procedure. In addition, an agent goes to study the policy π : S→A since the state st produces a maximum value or discounted reward as represented in Eq. (1):

Qπ(st,at)=rt+γ⋅rt+1+γ2⋅rt+2+…=∑i=0∞γi⋅rt+1 (1)

where Qπ(st,at) is the action-value function succeeding the procedure π (e.g., selecting action at) in a provided state st.

The end purpose of RL is to determine the best procedure (π∗) that maps the states to actions in order to maximize the future reward (r) over time (t) by rate of discount (γ∈[0,1]), as illustrated in Eq. (2). In this formula, Eπ[] indicates the estimated value provided that the agent follows a procedure π and Q∗(st,at) implies a better action-value function. In DRL, an estimate function, executed by DNN, permits an agent to work i th highly-dimensional spaces like pixels of an image:

Q∗(st,at)=max(Eπ[rt+γrt+1+γ2rt+2+⋯∣st=s,at=a,π]) (2)

Interactive feedback is the model which enhances the learning time of RL agent. During this technique, an external trainer is directed at an agent’s apprenticeship to explore further promising regions at initial learning phase. External trainer is an agent who might be a human, robot, or other artificial agent too.

3.2 DRL Based DBN Model

Restricted Boltzmann Machine (RBM) refers to a stochastic physics-oriented computation technique which can learn the intrinsic patterns of data distribution scenarios. It can be defined as a bipartite graph in which the data comprises of a visible input called layer v, whereas hidden n-dimensional vector h contains a number of hidden neurons. The training process of the model aims at minimizing the energy of model, as defined below.

E(v,h)=−∑i=1mbivi−∑j=1ncjhj−∑i=1m∑j=1nwijvihj, (3)

where m and n refer to the dimensions of visible as well as hidden layers, b and c are the corresponding bias vectors, additional W signifies the weight matrix that link these two layers, and wij denotes the link between the visible and hidden units of i and j respectively. It is noted that the RBM is limited inferring that none of the connections are enabled amongst the neurons of identical layer. It is considered to be resolved through the determination of joint probability of visible and hidden neurons. But, this method is intractable as it needs a partition function computation, i.e., computation of all probable configurations of the network. So, Hinton presented Contrastive Divergence (CD) to estimate the conditional probability of visible as well as hidden neurons that utilize Gibbs sampling over Monte Carlo Markov Chain (MCMC) method. Henceforth, a probability of input as well as hidden units are determined here:

p(hj=1∣v)=σ(cj+∑i=1mwijvi) (4)

and

p(vi=1∣h)=σ(bi+∑j=1nwijhj) (5)

where σ denotes the logistic sigmoid function.

Being a graph-based generative model, DBN is comprised of visible and hidden layers that are linked via weight matrices. Further, there are no connections exist among the neurons in an identical layer. Practically, DBN method holds a collection of stacked RBMs where the hidden layers insatiably feed the succeeding visible layer of the RBM. At last, a Softmax layer is used and the weights are tuned with the help of BWO algorithm. It is noticed that W(l), l∈[1,L], denotes the weight matrix at layer l, where L represents the hidden layer count. In addition, v and h(l) denote the visible and hidden layer respectively. Fig. 2 shows the architecture of RL-DBN.

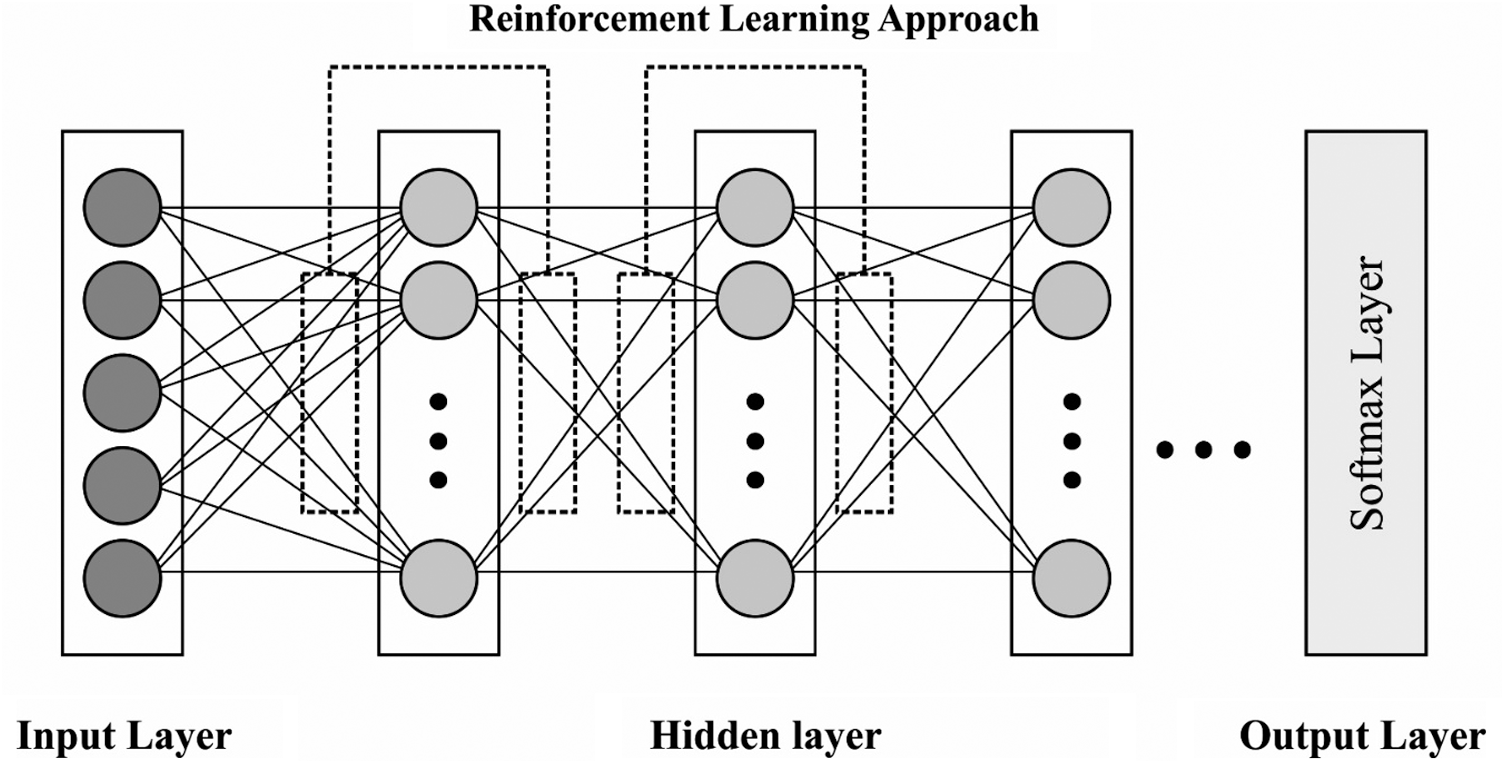
Figure 2: The architecture of RL-DBN

Here, the author presents a residual reinforcement layer-by-layer in DBN model called RL-DBN. It is a hybridization of sigmoid belief networks and binary RBMs [17] and is significant to highpoint few ‘tricks’ to utilize the data given in layer-by-layer. DBN is treated as a hybridized network which models the prior distribution of data in a layer-by-layer manner so as to improve the lower bound from model distribution. It is inspired to utilize the data learned at all the stacks of RBM for reinforcement since the pretraining of greedy layer activates the latent binary variable as the input of subsequent visible layer. The activation function is represented in Eq. (2), and the corresponding preactivation vector, a(l), is given below:

aj(l)=cj(l)+∑i=1mwij(l)xi(l−1) (6)

where, cj(l) denotes the bias in hidden layer l, m is the unit count that exists in the earlier layer, wij(l) denotes the weight matrix for layer l, and xi(l−1) indicates the input data from layer l−1, where xi0=vi.

Consequently, it is probable to utilize the ‘reinforcement preactivation’ vector, represented by â(l), from layer l, ∀l> 1. Since the classical RBM outcome of post activation lies in [0, 1] interval, it is essential to restrict the reinforcement element of the presented method as given herewith.

a^(l)=δ(a(l−1))max{δ(aj(l−1))} (7)

where, δ denotes the rectifier function and max offers the maximal value from δ output vector to normalize it. Afterwards, novel input data and the data aggregated at layer l are represented by the addition of values achieved in Eq. (5) for post-activation, i.e., implementation of σ(a(l−1)):

xi(l−1)=σ(aj(l−1))+a^j(l) (8)

where xi(l−1) denotes the new input data for layer l, ∀l>1 whereas the normalized and vectorized forms are provided herewith.

x(l−1)=x(l−1)max{xi(l−1)} (9)

3.3 Parameter Optimization Process

In order to tune the parameters of DBN model, BWO algorithm is employed. BWO algorithm imitates the routine development of BW spiders. In general, female BW spiders construct the net at night time and deposit few pheromones in nearby places in the net to attract the male black spiders for matting [18]. Male BW spiders get attracted towards the pheromone and enter the web. Female BW spider consumes the male BW spider after mating process is over. Next to mating, female BWs lay the egg sock on net. After 11 days of incubation, young spider lings get hatched out of eggs and involve in sibling cannibalism. It stays back in the net where it got hatched for a shorter duration while in some cases, they are consumed by their mother too. Rest of the young spiders are treated as fit spiders. Fig. 3 illustrates the lifecycle of a black widow. BWO algorithm follows the concept discussed herewith.

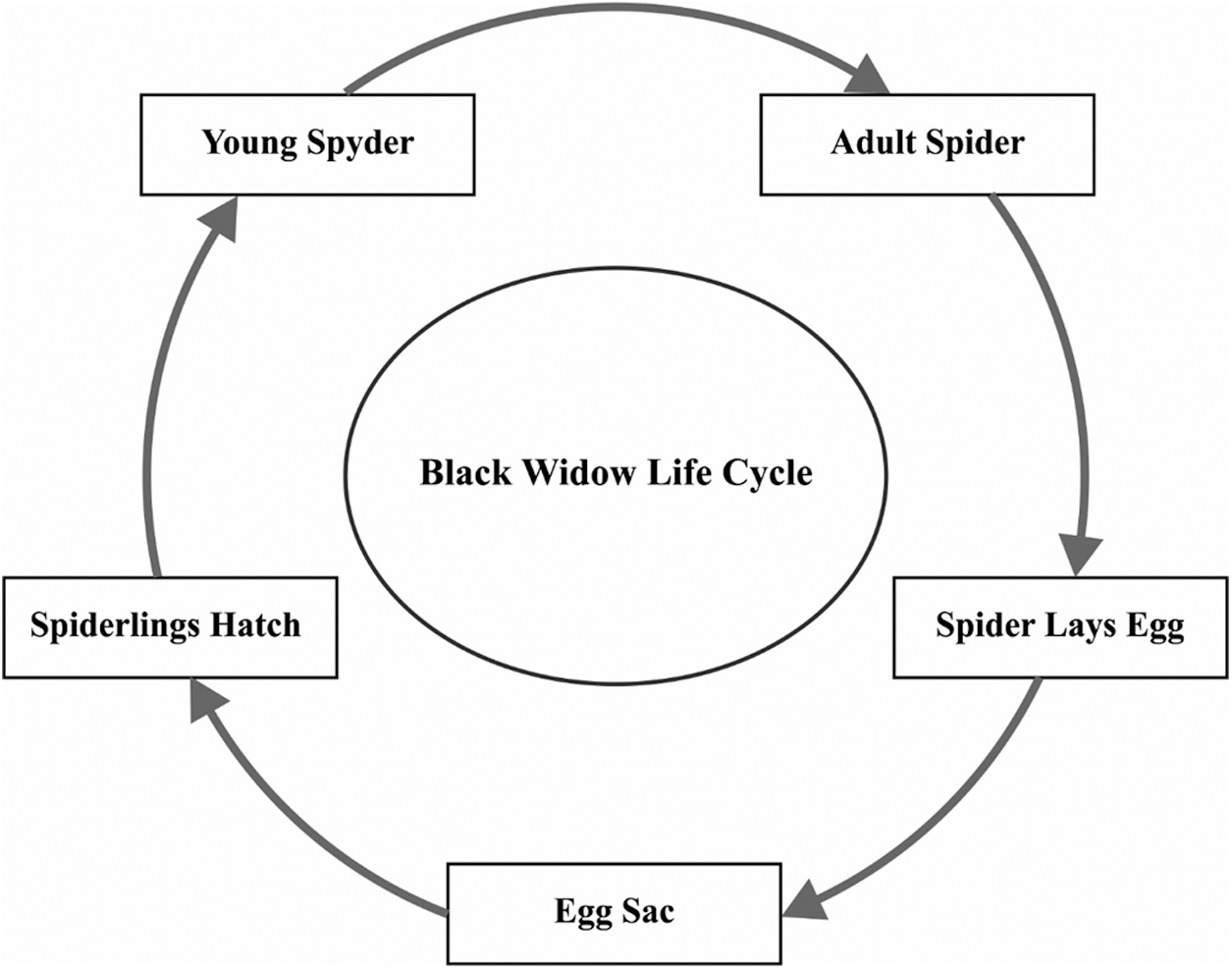
Figure 3: The lifecycle of black widow

BWO algorithm begins with an arbitrary initial BW spider population which includes both male and female BW spiders to generate offspring for subsequent life cycle. The initial population of BW spiders is defined in Eq. (8).

XN,d=[x1,1x1,2x1,3⋯x1,d⋮xN,1xN,2xN,3⋯xN,d] (10)

where XN,d denotes the number of BW spiders, d indicates the decision variable count, N represents the population, lb and ub indicate the lower and upper bounds of population. A significant solution population (XN,d) is used for minimizing or maximizing the objective function as defined below.

Objective function=f(XN,d) (11)

The subsequent process in BWO algorithm is the reproduction of young spider from mating process. During or after the mating process is over, the female BW eats the male BW. An arbitrary election procedure is employed to choose a pair of spiders to perform mating procedure so as to lay eggs that get hatched into young spiders. Then, the reproduction task of BWO algorithm is defined below:

Yi,d=β×Xi,d+(1−β)×Xj,d (12)

where Yi,d, and Yj,d are the young spiders in reproduction, i and j denote the arbitrary numbers in the range of 1 to N and β is the arbitrary number in the range of 0 to 1. To avoid the arbitrary duplicative election of pairs, the reproduction procedure takes place for d/2 times.

Next to reproduction, the population of mother and young spiders are arranged based on fitness value and the rate of cannibalism. At the time of optimization model, three cannibalism processes are considered. Sexual cannibalism is the primary one in which the female BW eats the male BW during or after the mating process. It is employed as fitness value of the female as well as male spider population. In sibling cannibalism, a strong young spider eats the weaker ones and is employed using the cannibalism rate. Finally, the mother BW gets eaten by their young ones. This mechanism makes use of fitness value of mothers as well as young spiders. Mutation is a subsequent procedure in BWO algorithm. A young spider is selected based on mutation rate and minor arbitrary value with the chosen young spiders for mutation; and this procedure is defined below.

Zk,d=Yk,d+α (13)

where Zk,d refers to the mutated spider population, Yk,d denotes the arbitrarily-elected young spider, k implies the arbitrary number, and α represents the arbitrary mutation value. Fig. 4 illustrates the flowchart of BWO technique. BWO algorithm relies on three distinct variables such as reproduction rate (RP), cannibalism rate (CP), and mutation rate (MR). Here, RP is used to control the production of young spiders and offers chances to explore the search space so as to determine the optimal solution. CP is applied in controlling the weaker fitness population and the fittest one is enabled to go to the subsequent round. Finally, MR is employed in the management of diversity in present to subsequent rounds.

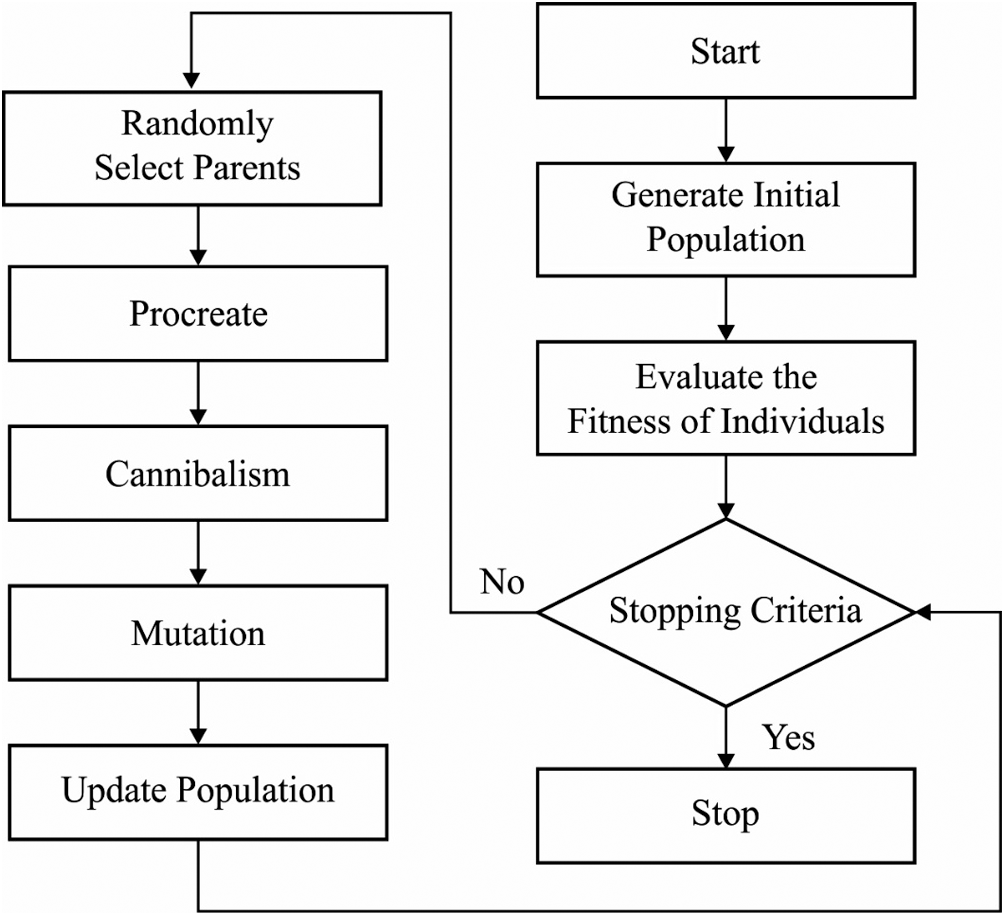
Figure 4: The flowchart of BWO algorithm

4  Experimental Validation

The presented DRL-BWO model was experimentally validated using NSL-KDD dataset [19]. It includes a total of 45927 instances under DoS attack, 995 instances under R2l attack, 11656 instances under Probe attack, 52 instances under U2r attack, and 67343 instances under Normal class as shown in Tab. 1. The parameter setting is given herewith; batch size: 128, learning rate: 0.001, epoch count: 500, and momentum: 0.2. Besides, the study made use of a 10-fold cross validation to split the dataset into training and testing datasets.

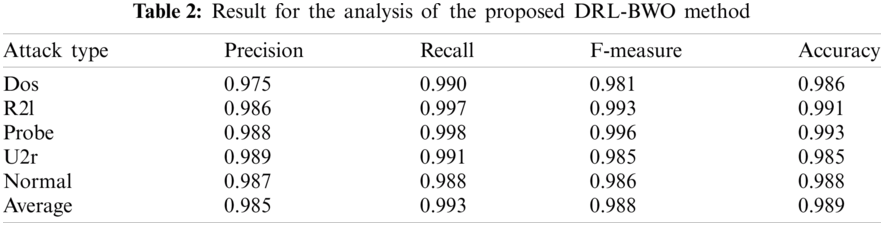
Tab. 2 and Fig. 5 shows the results of detection analysis of DRL-BWO model in terms of distinct measures. The experimental values showcase that the DRL-BWO method has effectively detected different types of attacks in UAV networks. For instance, the samples under ‘DoS’ attack type were detected at a precision of 0.975, recall of 0.990, F-measure of 0.981, and accuracy of 0.986. Eventually, the instances under ‘R21’ attack type got detected at a precision of 0.986, recall of 0.997, F-measure of 0.993, and accuracy of 0.991. Concurrently, the examples under ‘Probe’ attack type were detected at a precision of 0.988, recall of 0.998, F-measure of 0.996, and accuracy of 0.993. Simultaneously, the samples under ‘U2r’ attack type got detected at a precision of 0.989, recall of 0.991, F-measure of 0.985, and accuracy of 0.985. In line with these, the instances under ‘Normal’ attack type were detected at a precision of 0.987, recall of 0.988, F-measure of 0.986, and accuracy of 0.988.

Tab. 3 compares the results of the detection analysis attained by DRL-BWO model against existing methods in terms of distinct measures [20–25]. Fig. 6 shows the results of precision and recall analysis of DRL-BWO against existing techniques. The figure portrays that the detection performance of IDBN model got reduced since it achieved a minimal precision of 0.904 and recall of 0.92. Besides, the AK-NN model showcased a slightly higher detection outcome and it achieved a precision of 0.922 and recall of 0.938. Followed by, the DL model accomplished an even-more increased performance and accomplished a precision of 0.935 and recall of 0.949. Moreover, the DPC-DBN model depicted a moderate outcome with a precision of 0.951 and recall of 0.95. Furthermore, the DT model attempted to exhibit reasonable results with a precision of 0.966 and recall of 0.928. In line with these, the Adaboost method showcased somewhat acceptable outcome with a precision of 0.974 and recall of 0.932. Simultaneously, the T-SID model obtained a closer precision of 0.975 and recall of 0.952.

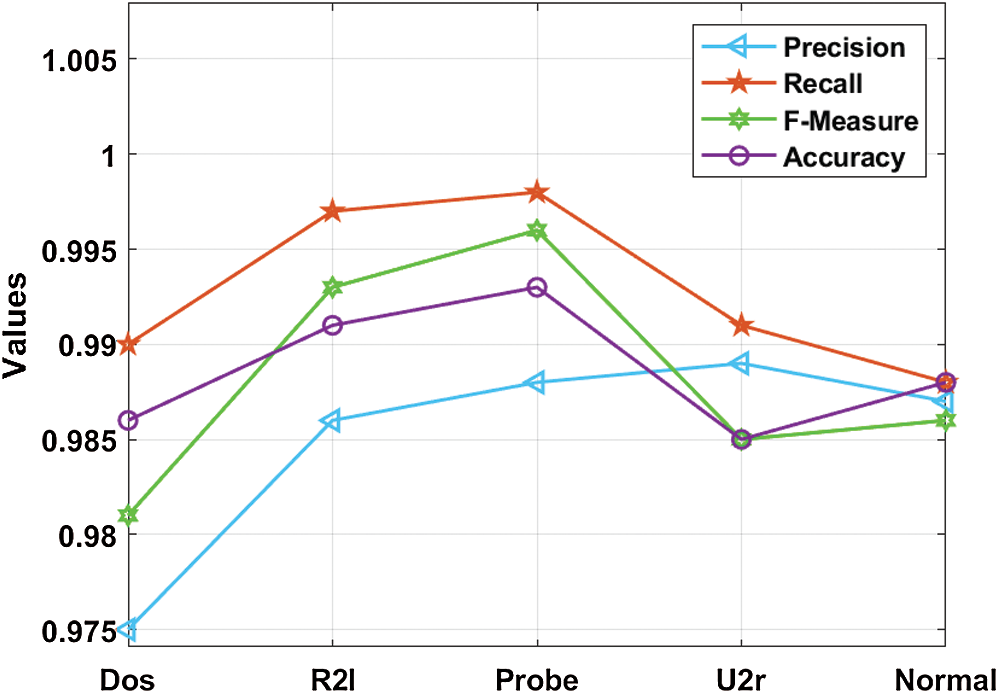
Figure 5: Intrusion detection results analysis of the DRL-BWO model

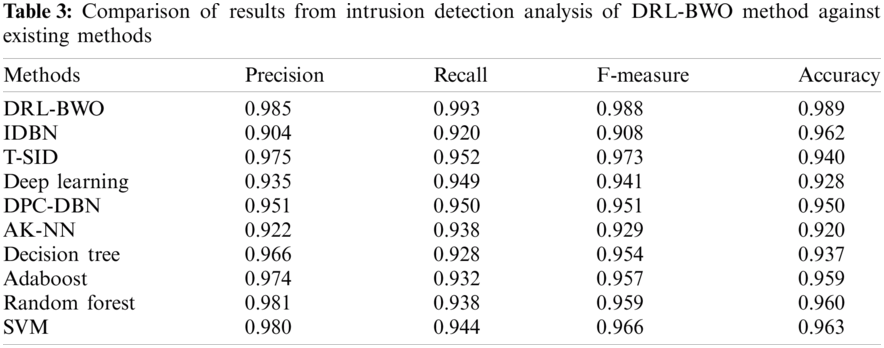
Concurrently, the SVM model demonstrated a certainly satisfactory outcome with a precision of 0.98 and recall of 0.944. Although the RF model attained a near optimum precision of 0.981 and recall of 0.938, the presented DRL-BWO model outperformed all the existing methods by accomplishing a maximum precision of 0.985 and recall of 0.993.

Fig. 7 examines the results of F-measure and accuracy analysis of DRL-BWO against existing methods. The figure portrays that the detection performance of IDBN technique got reduced as it offered a low F-measure of 0.908 and accuracy of 0.962. In line with this, the AK-NN approach demonstrated somewhat higher detection result as it yielded an F-measure of 0.929 and accuracy of 0.92. Along with that, the DL algorithm accomplished superior performance by obtaining an F-measure of 0.941 and accuracy of 0.928. In addition, the DPC-DBN model exhibited moderate results with an F-measure of 0.951 and accuracy of 0.95. Additionally, the DT model attempted to demonstrate reasonable outcomes with an F-measure of 0.954 and accuracy of 0.937.

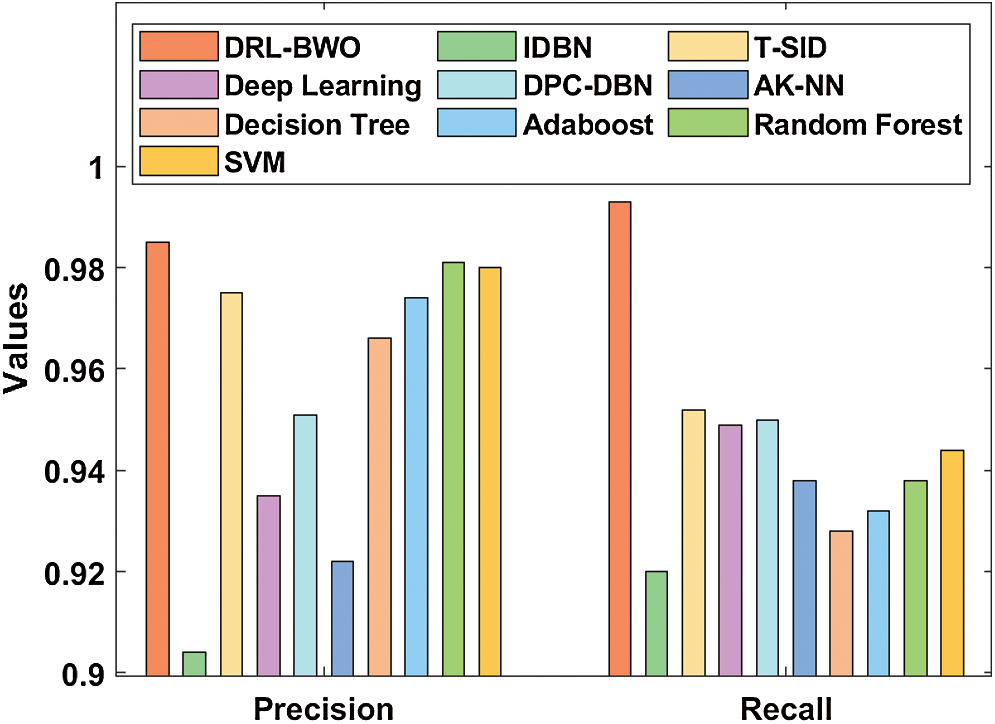
Figure 6: Comparative analysis of DRL-BWO model in terms of precision and recall

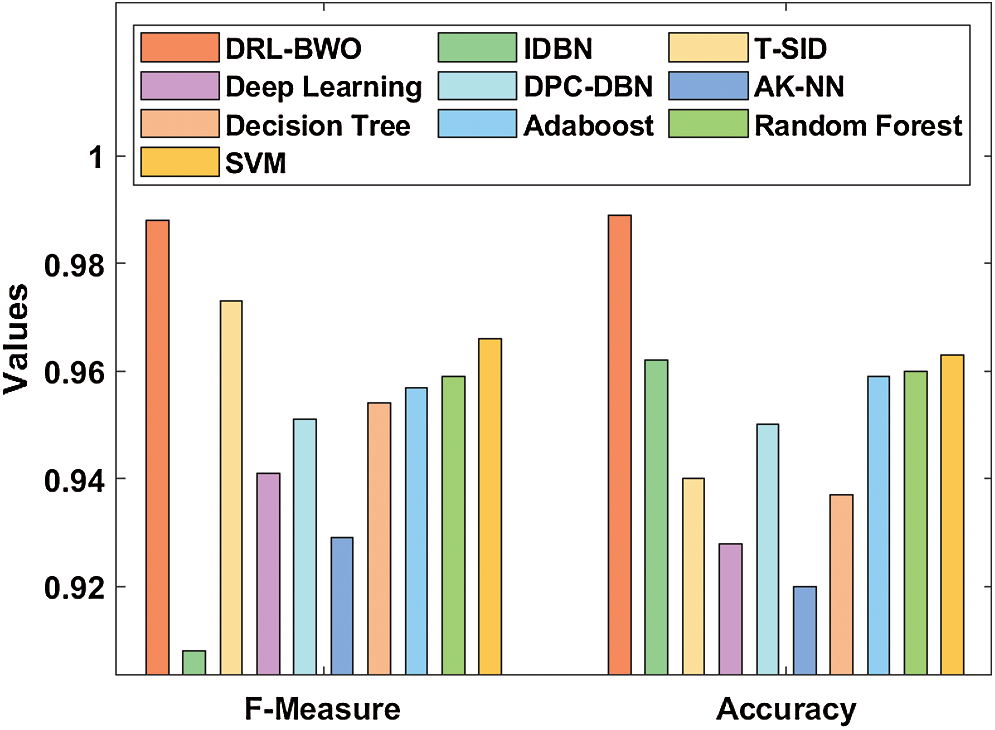
Figure 7: Comparative analysis of DRL-BWO model in terms of F-measure and accuracy

Similarly, the Adaboost method also outperformed with slightly acceptable outcome through an F-measure of 0.957 and accuracy of 0.959. At the same time, the RF technique attained a closer F-measure of 0.959 and an accuracy of 0.96. Further, the SVM technique portrayed a certainly satisfactory outcome with an F-measure of 0.966 and accuracy of 0.963. However, the T-SID method achieved a near optimum F-measure of 0.973 and accuracy of 0.940. In this scenario, the proposed DRL-BWO methodology outperformed the existing techniques and accomplished a superior F-measure of 0.988 and accuracy of 0.989. From the above discussed results of the analysis, it is apparent that the DRL-BWO algorithm is an efficient tool for UAV networks as it achieved improved outcomes. The DRL-BWO algorithm produced higher precision, recall, F-measure, and accuracy values such as 0.985, 0.993, 0.988, and 0.989 respectively.

5  Conclusion

The current research article developed a DRL-BWO algorithm for intrusion detection in UAV networks. Primarily, the networking data, fed as input, undergoes preprocessing to remove the unwanted data and transform it into a compatible format. Besides, the DRL involves improved reinforcement learning-based DBN for intrusion detection. Then, the DBN model is applied in the determination of existence of intrusions in UAV networks. At last, BWO algorithm is employed to determine the optimal hyperparameter values involved in the presented model. A comprehensive set of experimental analyses was conducted to highlight the supremacy of the proposed model. From the simulation values, it is evident that the proposed method is an appropriate method as it obtained high precision, recall, F-measure, and accuracy values such as 0.985, 0.993, 0.988, and 0.989 respectively. The model is found to be fit for information extraction tasks in high dimensional space. In addition, the application of BWO algorithm helps in fine tuning the classification performance of DBN model. In future, intrusion detection performance can be further improved using feature selection algorithms.

Funding Statement: This work is also supported by the Faculty of Computer Science and Information Technology, University of Malaya under Postgraduate Research Grant (PG035-2016A).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  F. Al-Turjman, H. Zahmatkesh and R. Shahroze, “An overview of security and privacy in smart cities’ IoT communications,” Transactions on Emerging Telecommunications Technologies, pp. 1–20, 2019. [Online]. Available: https://doi.org/10.1002/ett.3677. [Google Scholar]

 2.  Y. Zhang, P. Li and X. Wang, “Intrusion detection for IoT based on improved genetic algorithm and deep belief network,” IEEE Access, vol. 7, pp. 31711–31722, 2019. [Google Scholar]

 3.  X. Sun, D. W. K. Ng, Z. Ding, Y. Xu and Z. Zhong, “Physical layer security in UAV systems: Challenges and opportunities,” IEEE Wireless Communications, vol. 26, no. 5, pp. 40–47, 2019. [Google Scholar]

 4.  K. Lei, Q. Zhang, J. Lou, B. Bai and K. Xu, “Securing ICN-based UAV ad hoc networks with blockchain,” IEEE Communications Magazine, vol. 57, no. 6, pp. 26–32, 2019. [Google Scholar]

 5.  S. A. R. Shah and B. Issac, “Performance comparison of intrusion detection systems and application of machine learning to Snort system,” Future Generation Computer Systems, vol. 80, no. 3, pp. 157–170, 2018. [Google Scholar]

 6.  E. Kabir, J. Hu, H. Wang and G. Zhuo, “A novel statistical technique for intrusion detection systems,” Future Generation Computer Systems, vol. 79, no. 3, pp. 303–318, 2018. [Google Scholar]

 7.  H. Wang, J. Gu and S. Wang, “An effective intrusion detection framework based on SVM with feature augmentation,” Knowledge-Based Systems, vol. 136, no. 1, pp. 130–139, 2017. [Google Scholar]

 8.  H. I. Ahmed, N. A. Elfeshawy, S. F. Elzoghdy, H. S. El-sayed and O. S. Faragallah, “A neural network-based learning algorithm for intrusion detection systems,” Wireless Personal Communications, vol. 97, no. 2, pp. 3097–3112, 2017. [Google Scholar]

 9.  W. Hu, J. Gao, Y. Wang, O. Wu and S. Maybank, “Online adaboost-based parameterized methods for dynamic distributed network intrusion detection,” IEEE Transactions on Cybernetics, vol. 44, no. 1, pp. 66–82, 2014. [Google Scholar]

10. T. Ma, F. Wang, J. Cheng, Y. Yu and X. Chen, “A hybrid spectral clustering and deep neural network ensemble algorithm for intrusion detection in sensor networks,” Sensors, vol. 16, no. 10, pp. 1701, 2016. [Google Scholar]

11. G. E. Hinton, S. Osindero and Y.-W. Teh, “A fast learning algorithm for deep belief nets,” Neural Computation, vol. 18, no. 7, pp. 1527–1554, 2006. [Google Scholar]

12. F. Qu, J. Zhang, Z. Shao and S. Qi, “An intrusion detection model based on deep belief network,” in Proc. of the 2017 VI Int. Conf. on Network, Communication and Computing, Kunming, China, pp. 97–101, 2017. [Google Scholar]

13. D. Liang and P. Pan, “Research on intrusion detection system based on DBN-EL,” in 2019 Int. Conf. on Communications, Information System and Computer Engineering, Haikou, China, IEEE, pp. 495–499, 2019. [Google Scholar]

14. A. Israr, G. E. M. Abro, M. Sadiq Ali Khan, M. Farhan and S. U. A. Bin Mohd Zulkifli, “Internet of things (IoT)-enabled unmanned aerial vehicles for the inspection of construction sites: A vision and future directions,” Mathematical Problems in Engineering, vol. 2021, pp. 1–15, 2021. [Google Scholar]

15. A. Abdollahi and M. Fathi, “An intrusion detection system on ping of death attacks in IoT networks,” Wireless Personal Communications, vol. 112, no. 4, pp. 2057–2070, 2020. [Google Scholar]

16. M. Roder, L. A. Passos, L. C. F. Ribeiro, C. Pereira and J. P. Papa, “A layer-wise information reinforcement approach to improve learning in deep belief networks,” in Artificial Intelligence and Soft Computing, Proc.: Lecture Notes in Computer Science Book Series, New York City, NY, USA, vol. 12415, pp. 231–241, 2020. [Google Scholar]

17. K. Premkumar, M. Vishnupriya, T. S. Babu, B. V. Manikandan and T. Thamizhselvan, “Black widow optimization-based optimal pi-controlled wind turbine emulator,” Sustainability, vol. 12, no. 24, pp. 10357, 2020. [Google Scholar]

18. J. Li, Z. Zhao, R. Li and H. Zhang, “AI-based two-stage intrusion detection for software defined IoT networks,” IEEE Internet of Things Journal, vol. 6, no. 2, pp. 2093–2102, 2019. [Google Scholar]

19. A. A. Diro and N. Chilamkurti, “Distributed attack detection scheme using deep learning approach for internet of things,” Future Generation Computer Systems, vol. 82, no. 6, pp. 761–768, 2018. [Google Scholar]

20. [Online]. Available: https://www.unb.ca/cic/datasets/nsl.html. [Google Scholar]

21. Y. Yang, K. Zheng, C. Wu, X. Niu and Y. Yang, “Building an effective intrusion detection system using the modified density peak clustering algorithm and deep belief networks,” Applied Sciences, vol. 9, no. 2, pp. 238, 2019. [Google Scholar]

22. Y. Djenouri, A. Belhadi, J. C.-W. Lin and A. Cano, “Adapted k-nearest neighbors for detecting anomalies on spatio-temporal traffic flow,” IEEE Access, vol. 7, pp. 10015–10027, 2019. [Google Scholar]

23. Aroosa, S. S. Ullah, S. Hussain, R. Alroobaea and I. Ali, “Securing NDN-based internet of health things through cost-effective signcryption scheme,” Wireless Communications and Mobile Computing, vol. 2021, pp. 1–13, 2021. [Google Scholar]

24. A. Abbas, M. Krichen, R. Alroobaea, S. Malebary, U. Tariq et al., “An opportunistic data dissemination for autonomous vehicles communication,” Soft Computing, Feb, vol. 76, no. 4, pp. 2665, 2021. [Google Scholar]

25. W. Alhakami, A. ALharbi, S. Bourouis, R. Alroobaea and N. Bouguila, “Network anomaly intrusion detection using a nonparametric bayesian approach and feature selection,” IEEE Access, vol. 7, pp. 52181–52190, 2019. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.