DOI:10.32604/cmc.2022.020048

| Computers, Materials & Continua DOI:10.32604/cmc.2022.020048 |  |
| Article |
Efficient Model for Emergency Departments: Real Case Study
1Faculty of Computers and Informatics, Zagazig University, Zagazig, 44519, Egypt
2Department of Mathematics, Faculty of Science, Mansoura University, Mansoura, 35516, Egypt
3Department of Computational Mathematics, Science, and Engineering (CMSE), Michigan State University, East Lansing, MI, 48824, USA
4School of Mathematics, Unaizah College of Sciences and Arts, Qassim University, 51452, Saudi Arabia
*Corresponding Author: Mohamed Abouhawwash. Email: abouhaww@msu.edu
Received: 07 May 2021; Accepted: 13 July 2021
Abstract: There are several challenges that hospitals are facing according to the emergency department (ED). The main two issues are department capacity and lead time. However, the lack of consensus on performance criteria to evaluate ED increases the complication of this process. Thus, this study aims to evaluate the efficiency of the emergency department in 20 Egyptian hospitals (12 private and 8 general hospitals) based on 13 performance metrics. This research suggests an integrated evaluation model assess ED under a framework of plithogenic theory. The proposed framework addressed uncertainty and ambiguity in information with an efficient manner via presenting the evaluation expression by plithogenic numbers. Data Envelopment Analysis (DEA) technique is used in order to measure the efficiency of the emergency department of 20 hospitals according to the number of treated patients and effect on patient's life quality based on 11 factors. Using the Analytic Hierarchy Process (AHP), the weight of efficiency factors will be measured based on neutrosophic linguistic scale pairwise comparison. Plithogenic operations provide more accurate aggregation result according to contradiction degree between criteria values. The results show that ten of the hospitals are providing efficient service in their emergency department, while the other ten are less efficient. The analysis of the results shows that 58% of private hospitals emergency department is operating efficiently, while the efficient general hospitals represent 38%.
Keywords: Emergency department; plithogenic set; data envelopment analysis; analytic hierarchy process
Healthcare institutions play a vital role to enhance human life quality and maintain the required health level [1]. Hospitals are considered as the core of the healthcare system that keeps it running efficiently. One of the main parts that measure the operating performance of any hospital or medical centre is the emergency department. ED is considered as the most critical department that bears the highest load of concentration in comparison to other sections of the hospital. In order to minimize the health risks, treat as many patients as possible, enhance the quality of care, and other efficiency factors, evaluation of the emergency department performance became more serious. Usually, ED suffering from a situation in which the number of patients exceeds its capacity (in terms of equipment or staff) at a certain time. And such an issue may cause a threat to human safety through serious medical errors [2].
DEA is one of the most efficient methods proposed to evaluate the performance of Decision-Making Units (DMU) such as hospitals. This method considers multi-input and multi-output that applicable to variant decision-making environments [3]. For a long time, DEA reviewed great results in the efficiency evaluation of healthcare institutions. Cavalieri et al. [4] combined DEA with the game theory to measure the performance of hospitals in Iran. Kohl et al. [5] reviewed applied DEA in the healthcare sector and focused on the evaluation of hospitals’ performance. Ji et al. [6] proposed a nonlinear fuzzy classification model based on DEA for healthcare management systems.
Another most popular Multi-Criteria Decision-Making (MCDM) method to determine the weight of the criteria that measure the emergency department and any other healthcare institution is the AHP. AHP is based on a pairwise comparison among a set of evaluation criteria. Singh et al. [7] measured four hospitals in India based on the fuzzy-AHP method. Also, AHP was applied to evaluate the importance of error factors in the emergency department in Taiwan [8].
According to decision-making problems, most of the evaluations have uncertain factors that make the evaluation more complex and extended to various aspects, especially in the emergency department, which is differentiated by persistent fluctuations throughout the day, increasing the prospect of uncertainty in decision-making. Divergent views of decision-makers in assessing the efficiency criteria of healthcare institutions also increase instability in the decision-making process. To evaluate such a vagueness environment, the use of plithogenic set increases the accuracy and efficiency of decision making. Plithogeny is a generalization of neutrosophy introduced by Smarandache [9]. Plithogenic set is a group of elements categorized by attribute values v that has a corresponding contradiction degree c(x, v) and appurtenance degree d(x, v) of element x [9]. Thus, the features of the plithogenic set lessen the problem of ambiguity efficiently and take into account the different opinions of decision-makers, which helps to choose the optimal decision and obtain the best assessment.
This study aims to evaluate the efficiency of 20 hospitals in Egypt in both private and general sectors based on some criteria that may affect their performance. The evaluation of the criteria is considered in the plithogeny environment to consider truth membership, indeterminacy membership, and falsity membership. DEA will be used to evaluate the efficiency of hospitals based on multi-input and multi-outputs. In comparison, the AHP method will be applied to find the weight of the inputs and outputs. The applied DEA method is based on the Constant Returns to Scale (CRS) model.
The main contributions of this paper are as follows:
• An evaluation approach is suggested for the emergency department based on triangular neutrosophic numbers (TNNs), which can handle the vagueness well.
• Plithogenic set and neutrosophic set theories are applied with the combination of MCDM techniques (AHP-DEA) to add to the field of evaluation of the hospital emergency department literature.
• This is the first paper to develop a plithogenic MCDM approach that combines AHP and DEA methods for evaluating the emergency department.
• A case study was presented to prove the applicability of the proposed approach.
The remainder of the paper is organized as follows. In Section 2 a literature review of emergency department evaluation, DEA and MCDM techniques in healthcare institutions evaluation. Section 3 presents some definitions related to the neutrosophic set and plithogenic set. Section 4 presents the proposed framework background. Section 5 presents the application of the proposed framework to evaluate the performance of 20 hospitals in Egypt. Finally, Section 6 is the summarization of the work.
2.1 Performance Evaluation of Healthcare Institutions and ED
There are several studies in the evaluation of healthcare institutions according to different standards and methods. For instance, Glonek et al. [10] evaluated the patients’ quality of life with Chronic Obstructive Pulmonary Disease (COPD) in selected healthcare institutions in South Poland. In the same sector of quality-of-life evaluation, Lupo [11] proposed a novel fuzzy evaluation framework based on the ServQual disconfirmation paradigm and incorporates the Analytic Hierarchy Process (AHP) method with high consideration of uncertainty. His framework studied nine public hospitals in Italy to evaluate the public healthcare service in the region according to 15 fundamental service items [11]. On the other side, researchers considered an assessment of Lean Thinking (LT) in healthcare institutions. In this regard, Narayanamurthy et al. [12] proposed a mathematical model for assessing the implementation of LT in Indian hospitals.
By focusing on the emergency department of healthcare institutions, researchers have come a long way in solving many problems. One of the most popular problems in the ED is crowding. Chiu et al. [13] evaluated the importance of physicians’ decision-making time and the other factors that may lead more patients to stay in ED and cause crowding problems. Laker et al. [14] discussed the impacts of electronic health records and other clinical information systems on emergency department physicians’ quality in evaluations and their efficiency in decision making. Yazdanparast et al. [15] suggested a multi-response optimization methodology to optimize the resource allocation problem in an ED by composing Artificial Neural Network (ANN), Design of Experiment (DOE) and fuzzy DEA in an integrated algorithm. Yousefi et al. [16] discussed the problem of long Length of Stay (LOS) in ED that may cause crowding. They suggested a Genetic Algorithm (GA) based optimization approach, and the results showed a decrease of 14% in average LOS in the ED of this case study. Daldoul et al. [17] proposed a mixed-integer programming model to optimize the human and material resources to minimize the average total patient waiting time in ED.
Several challenges affect decision-making in the emergency department and make it more critical. Most of the research agreed that overcrowding is the main problem that EDs are suffering from, influencing the medical center's overall performance. Crilly et al. [18] proved that using a patient admission prediction tool may handle this issue by maintaining the patient access level stable enough, even if there is increasing in incoming patients. Helm et al. [19] suggested a mixed-integer programming model to solve hospital admission scheduling and control problems to improve the hospital census. Gharahi et al. [20] suggested an approach that depends on discrete event simulation and integrated AHP and Preference Ranking Organization Method for Enrichment Evaluations (PROMETHEE) methods to decrease long waiting times and increase patient satisfaction.
2.2 Neutrosophic Set and Plithogenic Set
Uncertainty and incomplete information are usually the main problems in decision-making evaluation. As a generalization of fuzzy set and intuitionistic fuzzy set, Smarandache [21] introduced neutrosophy. In healthcare sector evaluations, several studies improved great results using neutrosophic in the evaluation process. Abdel-Basset et al. [22] proposed a novel neutrosophic framework for early detection and evaluated the disease's symptoms. Characterizations of the neutrosophic set are clearly detailed in this subsection.
Also, plithogeny is a generalization of neutrosophy introduced by Smarandache [23], which refers to the genesis, construction, development, and progression of new entities from syntheses of contradictory or non-contradictory multiple old entities. Abdel-Basset et al. [24] proposed an evaluation model for assessing medical care systems in hospital based on plithogenic set. The proposed model was applied to measure hospitals In Zagazig, according to the VIKOR method (which stands for ‘Vlse Kriterijumska Optimizacija I Kompromisno Resenje,’ meaning multi-criteria optimization and compromise solution) based on 11 evaluation standards, where another application of plithogenic set was applied in supply chain sustainability evaluation based on Quality Function Deployment (QFD) [25].
2.3 Multi-Criteria Decision-Making
MCDM methods demonstrated efficient outputs in the valuation process, especially in healthcare institutions problems that may cause confusion in decision-making. Chang et al. [26] applied the Decision-making trial and evaluation laboratory (DEMATEL) method to measure the sustainability of healthcare institutions in Taiwan under the national health insurance system. Anas et al. [27] used the AHP method to evaluate the hospitals’ supply chain under a fuzzy environment. Also, Oliveira et al. [28] applied the AHP method to manage the life cycle of medical devices in different healthcare institutions. According to their information systems, Esfahani et al. [29] evaluated Iranian public hospitals using the DEMATEL method.
Moreover, there are several MCDM types of researches that focused their evaluation on emergency department problems. Hospital department layout problems are evaluated using multi-objective tabu search, and the solutions that produced may save about 5%-15% of patients’ time in the emergency department [30]. Also, Yousefi et al. [31] proposed a study that optimizes human resource allocation in ED in Brazil using three different machine-learning approaches. Qi et al. [32] evaluated another aspect is the emergency response capacity in ED using the AHP technique under a fuzzy environment.
2.4 Analytic Hierarchy Process and Healthcare Institutions Evaluation
In most multi-criteria decision-making evaluation problems, AHP is a sufficient method introduced by [33]. AHP has the ability to expound complex problems into simple sub-problems that make the problems easier to solve [34]. Thus, traditional AHP doesn't deal with uncertainty. By applying the AHP method to a neutrosophic environment that considers truth, falsity, and indeterminacy degrees, the evaluation results will be more accurate with respect to the decision-makers’ insight. Many studies applied the AHP method in the evaluation of healthcare institutions. For instance, Singh et al. applied AHP in order to define the priority of healthcare service quality to evaluate hospitals in India under a fuzzy environment. Moallem et al. [35] evaluated the risks related to patient care activities using AHP in order to obtain the importance of 12 objectives depending on identified risks as a real-world case study in Tunisian hospitals. Many other MCDM techniques were used in the evaluation of the healthcare and medical industry, but Mardani et al. [36] evaluated 202 published studies related to the evaluation of the healthcare industry. The results show that AHP is the most frequently implemented technique in the healthcare field multi-criteria problems.
2.5 Data Envelopment Analysis (DEA) and Healthcare Institutions Evaluation
DEA is an optimization procedure that can be adopted to improve the performance of multiple Decision-Making Units (DMUs). It's a linear programming methodology that evaluates the efficiency of DMUs according to multiple-inputs and multiple-outputs.
Traditional DEA categorizes DMUs into efficient and inefficient classification by evaluating their corresponding inputs and outputs; thus, it does not order them. The drawback of that is the confusion of the decision-maker to select one of the DMUs if the result shows more than one efficient DMU [37]. However, traditional DEA doesn't consider the uncertainty of information, which is most commonly in different evaluation problems. That's why, in this study, the evaluation of inputs and outputs are based on plithogenic set that considers the uncertain evaluation of decision-makers. The most frequently used models of DEA is Constant Return to Scale (CRS-DEA) and Variable Return to Scale (VRS-DEA). The first model scale of economies doesn't change as the size of DMU's increases, while the second model scale of economies changes according to DMU's size.
The literature presented several types of research on efficiency estimating healthcare institutions [38]. Using different DEA models, overall efficiency in hospitals was evaluated, but there are few studies that focused on specific departments. Akkan et al. [39] applied DEA models to analyze the efficiency of seven general hospitals in Turkey to handle the problem of overcrowding in the emergency department. They recognized the total number of emergency patients as the output variable while the ED level category and the number of beds as inputs. Also, there are many other studies that used DEA to evaluate the efficiency of healthcare institutions from different perspectives. For instance, Kazley et al. [40] evaluated the efficiency of hospitals’ electronic medical records (EMR) using DEA, and they consider equipment and medical staff as inputs while discharges and staff training as outputs. Mitropoulos et al. [41] evaluated the overall technical performance of Greek public hospitals using DEA, and they consider the number of medical staff also as input while transfers and laboratory tests as outputs. Chowdhury et al. [42] analyzed the production performance of hospital services in Canada by applying the DEA technique. Also, Khushalani et al. [43] examined the efficiency of production quality in hospitals using the Dynamic Network DEA.
In this section, we mention some concepts and definitions of neutrosophic set and plithogenic set.
Definition 1. Abdel-Basset et al. [44] Let X be a universe of discourse. A single neutrosophic set N over X is an object with a form of
Definition 2. Abdel-Basset et al. [45] Let
• Addition of two TNN:
• Subtraction of two TNN:
• Inverse of two TNN:
• Multiplication of two TNN:
• Division of two TNN:
Plithogenic set is providing high consideration of uncertainty to improve more accurate results and that due to its two main features contradiction degree and appurtenance degree. Contradiction (dissimilarity) degree function c(v,D) distinguishes between each attribute value and the dominant (most preferred) attribute value. The attribute value contradiction degree function c(v1, v2) is c: V × V → [0,1], and satisfying the following axioms:
• c(v1, v1) = 0, contradiction degree between the attribute values and itself is zero.
• c(v1, v2) = c(v2, v1), representing the dissimilarity between two attribute values v1 and v2.
Plithogenic set operations are intersection ∧p, union ∨p, complement ¬p, inclusion, and equality ↔.
Definition 3. Let
— Plithogenic intersection:
— Plithogenic union:
where
where, tnorm = ∧Fb = ab, tconorm a∨Fb = a + b − ab
— Plithogenic complement (negation):
The appurtenance degree d(x, v) of attribute value v is: ∀ x∈ P, d: P × V→ P ([0, 1]z), so d(x, v) is a subset of [0, 1]z, and P([0, 1]z) is the power set of [0, 1]z, where z = 1, 2, 3, for fuzzy, intuitionistic fuzzy, and neutrosophic degrees of appurtenance respectively.
This research proposed an integrated framework to evaluate emergency department using AHP and DEA based on plithogenic set. A group of useful MCDM methods is used in this model with the intention of evaluating the performance efficiently by considering different aspects of decision making. The main steps of this framework are discussed and illustrated in Fig. 1.
Step 1. Obtain evaluation information by integrating a committee of decision-makers who have experience in the healthcare field
Step 2. Divide the problem into sub-problems in order to build the problem hierarchy. The top-level is the main problem, the second level is the set of standards that the problem will be evaluated based on them, and the last level is the set of alternatives that will be evaluated.
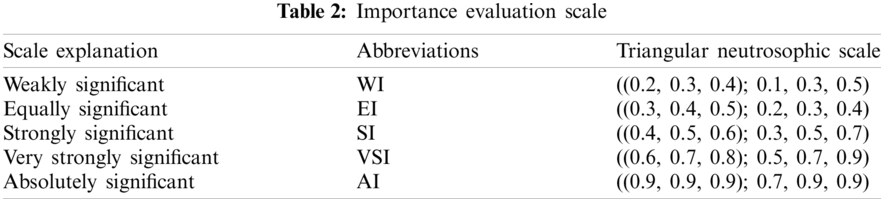
Step 3. According to the decision maker's preferences as in Tab. 2, construct the pairwise comparison matrix based on the neutrosophic evaluation scale to find the weights of inputs and outputs by the AHP method. In this step, the consideration of uncertainty and inconsistency of the decision maker's evaluation will improve the accuracy of evaluation results.
Step 4. In order to improve the decision matrix, check the decision matrix consistency by calculating the consistency index (CI) and consistency ratio (CR) using Eq. (11).
where,

Figure 1: The executive framework of the proposed study

Step 5. Calculate the mean of each row and use the de-neutrosophication function as in Eq. (12) to determine the importance weight of each input and output.
Step 6. Obtain the final weight of inputs and outputs.
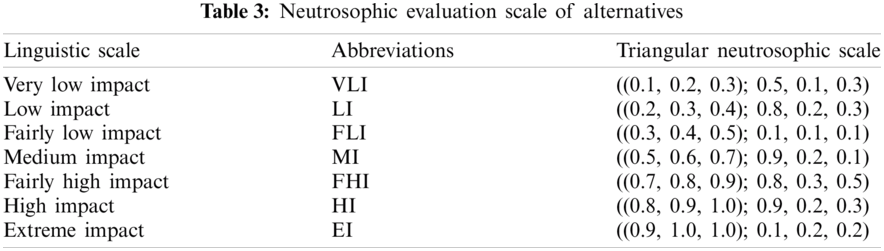
Step 7. Obtain evaluation information by integrating a committee of decision-makers who have experience in healthcare institution management. Using the neutrosophic evaluation scale in Tab. 3, K decision-makers evaluate the DMUs (EDs) according to the inputs and outputs.
Step 8. Construct the evaluation inputs and outputs matrices based on plithogenic set in order to consider uncertainty information.
Step 9. Aggregate the K evaluation matrix based on plithogenic aggregation operation according to defined contradiction degree, as mentioned in Eqs. (7)–(9). In this step, the aggregation matrix will be more accurate because of the contradiction degree provided by plithogenic set.
Step 10. Normalize the aggregated evaluation inputs and outputs using Eq. (13) for both input and output matrix.
where
Step 11. Obtain the weighted aggregated input and output matrix by multiplying the normalized aggregated by the weights calculated using the AHP method.
Step 12. Apply the input-oriented CRS model for comparison of the DMUs. CRS model is given in the following:
where
Step 13. Finally, according to
5 Application of the Proposed Approach
5.1 Evaluation of 20 Private and General Hospital in Egypt
Healthcare institutions is a critical organization in any country that cares about the human quality of life. Therefore, evaluating these institutions based on criteria, including ensuring an acceptable and satisfying level of life for humans, is one of the most significant topics to be studied from different aspects. Thus, in this study, we proposed an integrated framework to evaluate the emergency department in 20 private (P) and general (G) hospitals in Egypt. As we mentioned before, ED is one of the most crowded places in healthcare centres, if it's not the most overcrowded at all. As a result, there are several issues that the hospital may face. In this research, the efficiency of ED in 12 private hospitals and eight general hospitals in Egypt will be determined using the proposed framework. The names of hospitals are not shared according to their privacy guidelines. Three experts in healthcare institution management are participating in this evaluation.
In this study, we consider 11 inputs that affect the operations of ED directly and indirectly manner. These inputs have been verified by experts and some previous studies as in [39]. The inputs as the criticality of the department, number of vacant bed, number of a competent nurse, assignment preference related to the patient's pathology, the average time in the system (length of stay LOS), number of exiting ambulance, hospitalization, admission transfer rate, ambulance off-loading time, medical equipment, and number of efficient doctors. On the other hand, the two selected outputs are the effect on patient's life quality and the number of treated patients.
5.2 Weighting Inputs and Outputs Using AHP
According to decision-makers preferences, the importance of inputs and outputs are determined based on the neutrosophic importance scale in Tab. 2. The pairwise comparison matrix is shown in Tab. 4. After checking the consistency ratio using Eq. (11), Tab. 5 and Fig. 2 shows the weights of inputs and outputs obtained from applying the AHP method by decision makers.
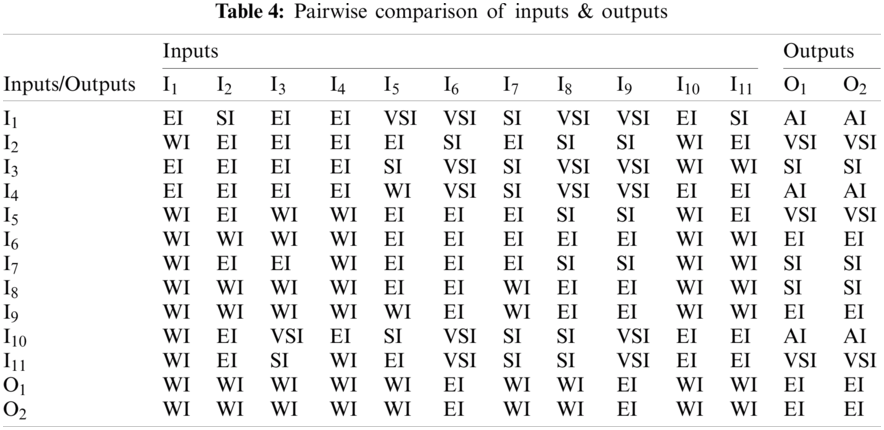

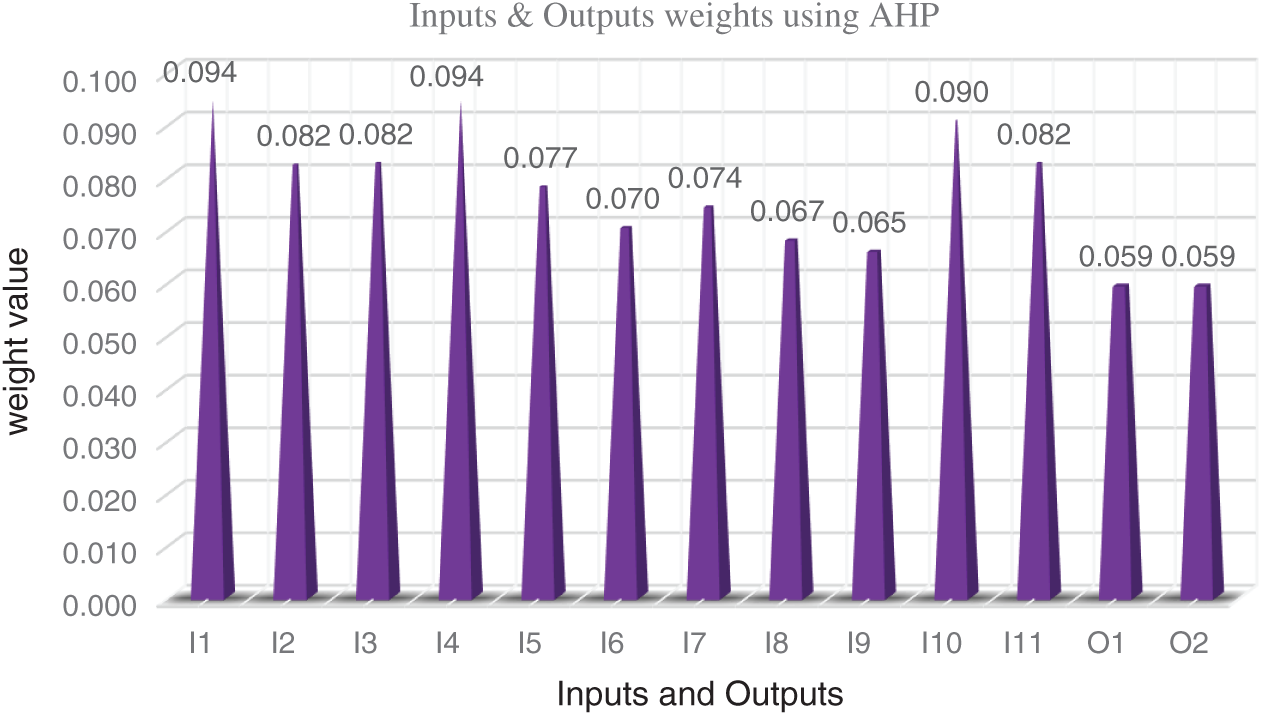
Figure 2: Weights of inputs and outputs
5.3 Aggregation of Evaluation Matrices Based on Plithogenic Set
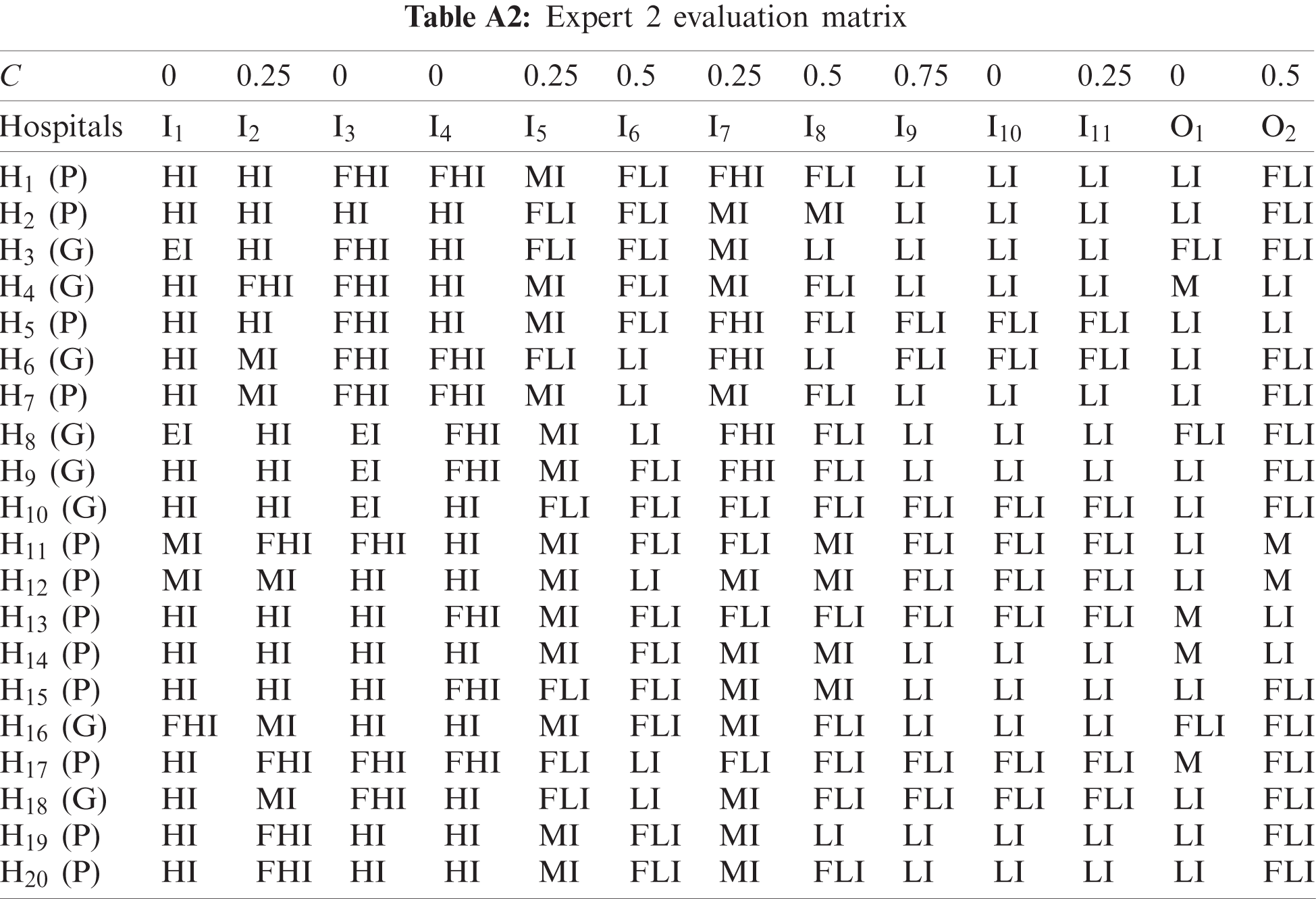
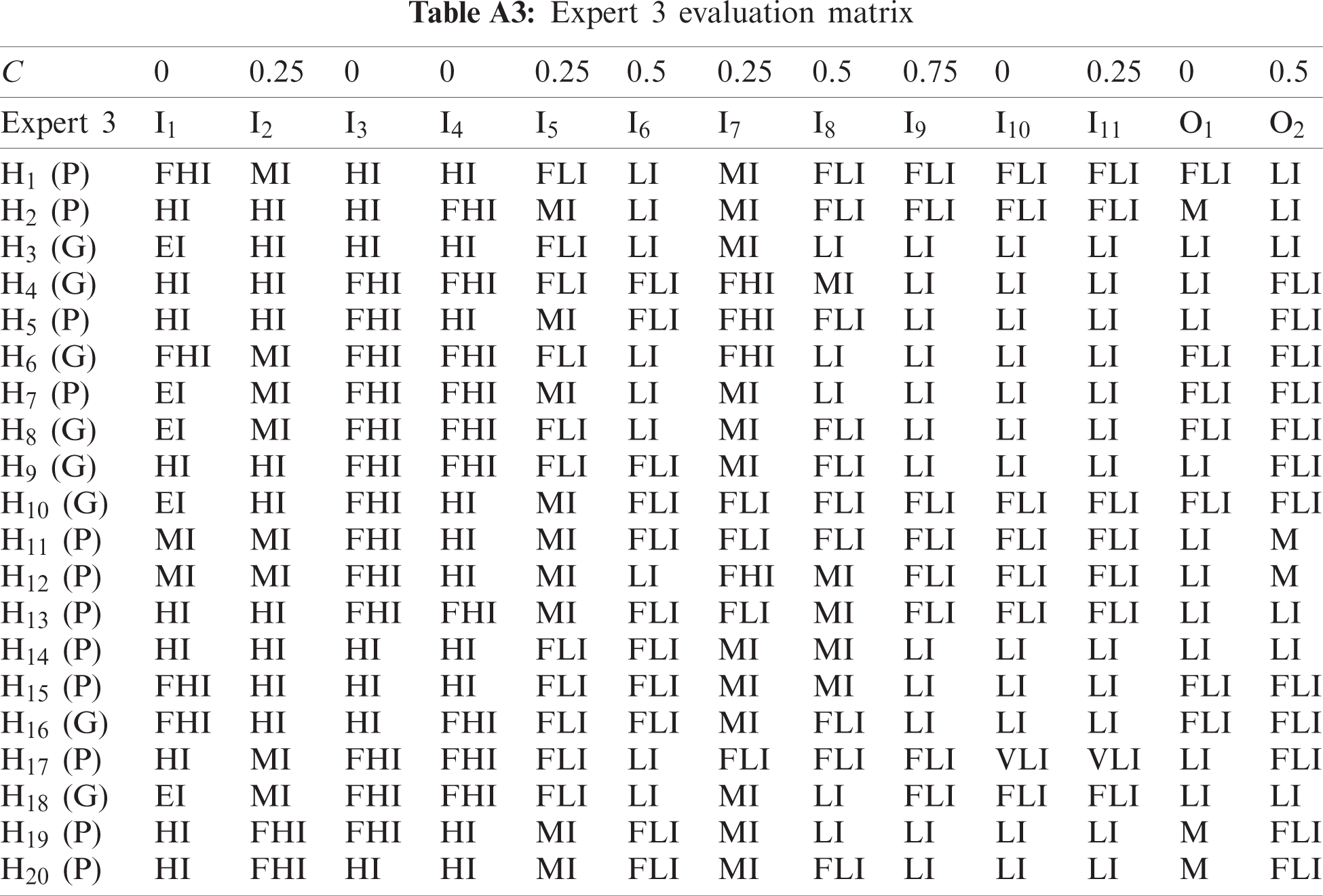
One of the main contributions of this study is improving the consideration of uncertainty in the evaluation process. So, the aggregation of evaluation matrices is based on contradiction degree that improves the accuracy of aggregation operation. The three experts evaluate the 20 EDs according to the inputs and outputs based on Tab. 3 neutrosophic scale as shown in Tabs. A1–A3.
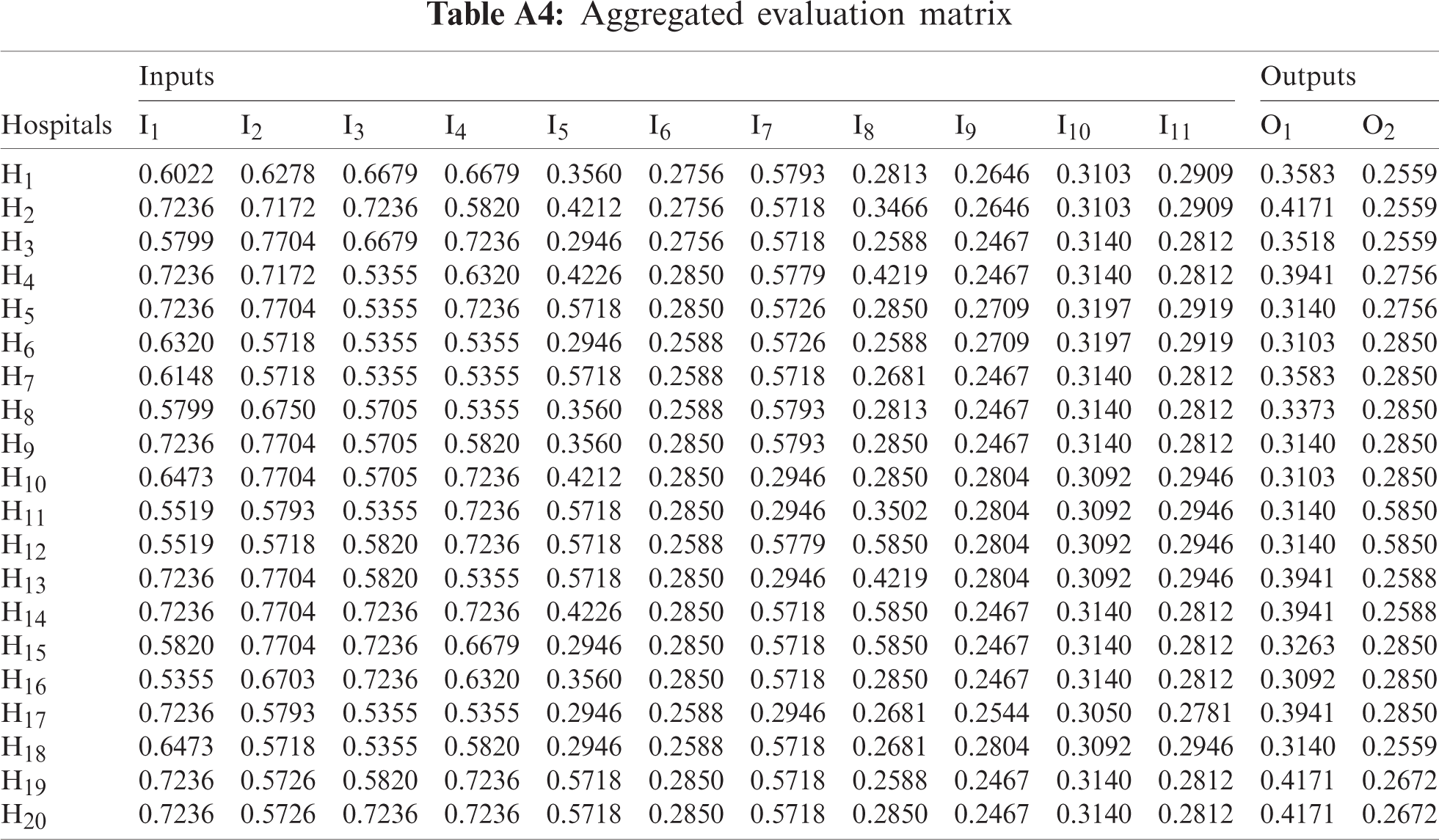
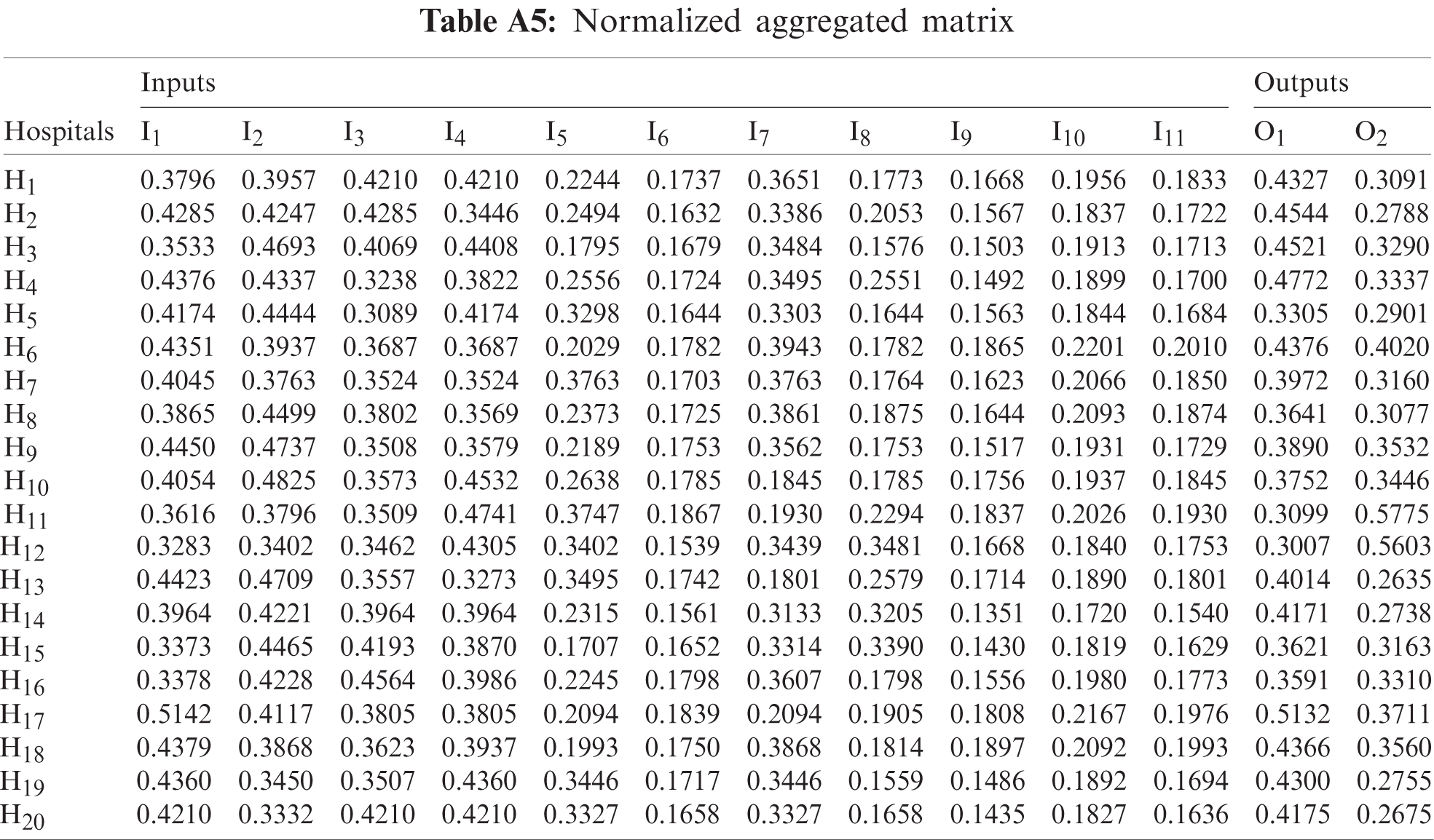
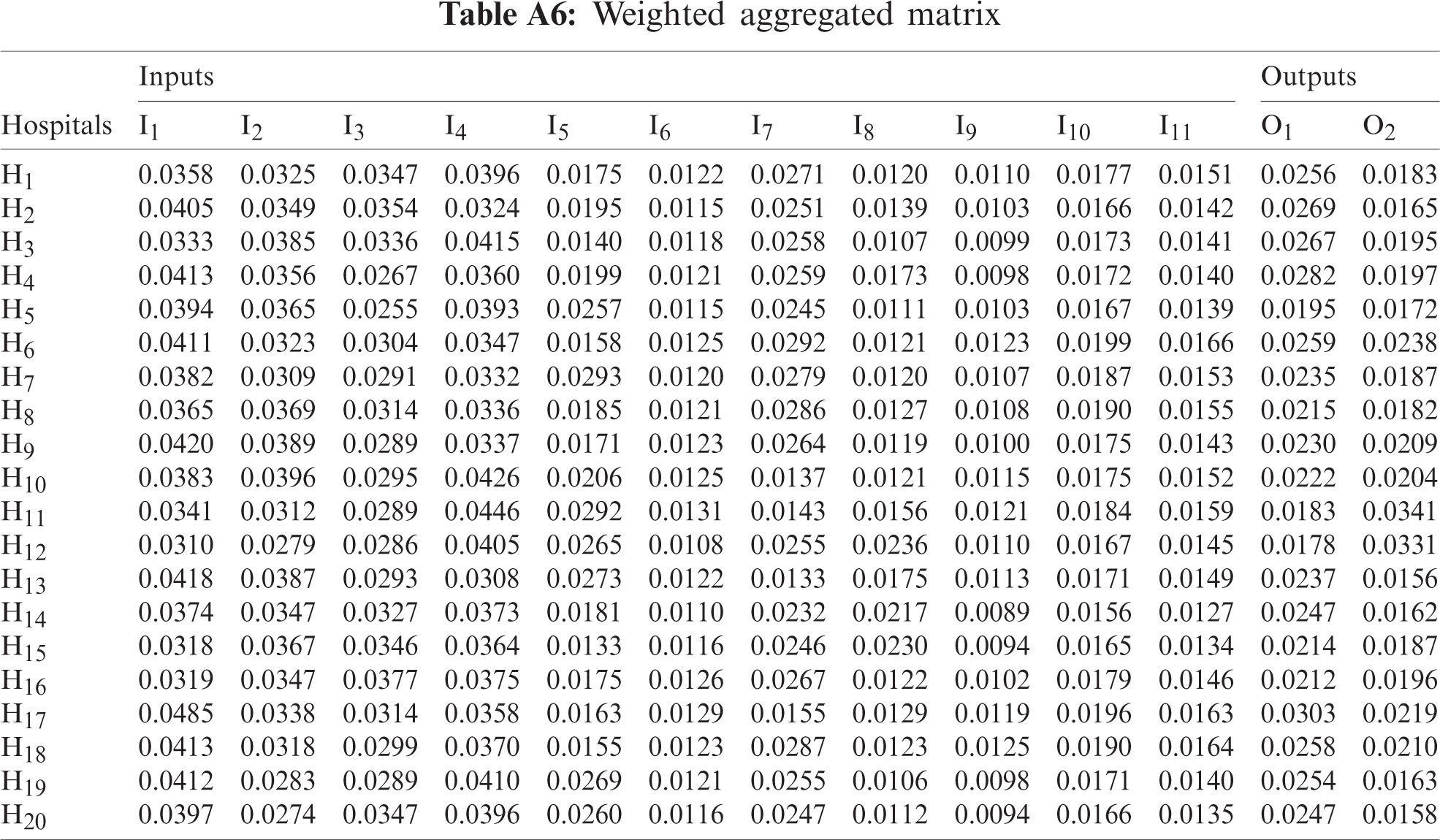
Contradiction degree C is determined between each attribute value with respect to the most preferred (dominant) attribute value. Then, aggregate the three evaluation matrices based on defined contradiction degree by decision-maker using Eqs. (7)–(9). Convert the aggregated neutrosophic evaluation into crisp values using Eq. (12). The final aggregated evaluation matrix as shown in Tab. A.4. Using Eq. (13), normalize the aggregated evaluation matrix as shown in Tab. A5. Tab. A6 shows the weighted aggregated evaluation matrix by multiplying the normalized aggregated matrix by the weight of inputs and outputs that calculated using the AHP method in Tab. 5.
Using weighted aggregated matrix (Tab. A6), the CRS-DEA model has been applied. Tab. A7 shows the result of the proposed approach. The results show that H1, H2, H3, H4, H6, H11, H12, H17, H19, H20 has efficient emergency departments. The rest of hospitals emergency department are ranked as H9 > H15 > H18 > H14 > H10 > H7 > H16 > H13 > H8 > H5 as shows in Fig. 3. The analysis of results defines that 58% of private hospitals ED are efficient and 38% of general hospitals ED are efficient. Fig. 3 shows the relationship between 20 emergency departments (alternatives) on the horizontal axis and weight value on the vertical axis.

Figure 3: The result of the proposed framework
It is worth to mention the result of weighting the inputs and outputs of emergency departments based on the AHP method shown in Fig. 2. As shown in Tab. 5 and Fig. 2, the criticality of the department (I1) and assignment preference related to the patient's pathology (I4) are the two most important inputs with weight 0.094 that may affect the operations of ED. While, admission transfer rate (I8) and ambulance off-loading time (I9) are the least effective inputs with weight 0.067 and 0.065 respectively, but that doesn't mean that they are not effective for ED operations. On the side of outputs, the effect on patient's life quality and the number of treated patients have the same important level to evaluate the emergency department efficiency with weight 0.059.
To explain the importance of input slacks and output slacks on inefficient EDs, let's look to H5. We can find that criticality of the department (I1), number of vacant bed (I2), assignment preference related to the patient's pathology (I4), number of exiting ambulance (I6), hospitalization (I7), and number of efficient doctors (I11) must be reduced by 0.002, 0.008, 0.007, 0.001, 0.010, and 0.001, respectively.
If H5 may achieve that, its emergency department will be efficient. However, suppose H5 may reduce the number of vacant beds (I2), the number of competent nurses (I3), assignment preference related to the patient's pathology (I4), and admission transfer rate (I8) by 0.002, 0.008, 0.005, and 0.006, respectively. In that case, its ED will not be efficient until it increases the number of treated patients (O2) by 0.001. That is why decision-makers should seriously consider the values of inputs slacks and outputs slacks.
Healthcare institutions’ evaluation is a high-priority research field on account of the importance of improving the human quality of life. Especially, evaluation of the emergency department in any healthcare institution became a critical field of study regarding many issues that may happen because of the overcrowding of this department. This research proposed an integrated framework that assists the healthcare institution managers to evaluate the overall efficiency of ED. Due to the uncertainty in many healthcare evaluation problems, this framework is based on a plithogenic set that improves the accuracy of the evaluation process by considering the contradiction degree between attribute values. In this study, the proposed framework integrates the AHP and DEA method to evaluate ED in 20 hospitals in Egypt. The evaluation was made based on 11 input measures and two main output measures. AHP method was applied to assess the weight of inputs and output. In contrast, the DEA method was applied to measure the efficiency of EDs. The evaluation results show that 50% of these EDs are operating efficiently, while the other 50% are inefficient with uneven ratios. The traditional DEA method was applied in various evaluations related to the healthcare industry. Thus, it has some limitations in handling the uncertain environment. That's why one of the main contributions of this research is to improve the accuracy of decision-making under uncertainty. Moreover, applying the DEA method based on AHP evaluation of inputs and outputs improved decision-making accuracy.
In future works, evaluation of inputs and outputs may be applied using any other MCDM methods such as Best-Worst Method (BWM). Additionally, many other departments in healthcare institutions have many problems that need more consideration from decision-making researchers. For instance, the allocation of ambulance centres based on different standards is a significant problem.
Funding Statement: The authors received no specific funding for this study.
Ethical Approval: This article does not contain any studies with human participants or animals performed by any of the authors.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. H. Omrani, K. Shafaat and A. Emrouznejad, “An integrated fuzzy clustering cooperative game data envelopment analysis model with application in hospital efficiency,” Expert Systems with Applications, vol. 114, no. 3, pp. 615–628, 2018. [Google Scholar]
2. C. Hsu, L. Liang, Y. Chang and W. Juang, “Emergency department overcrowding: Quality improvement in a Taiwan medical center,” Journal of the Formosan Medical Association, vol. 118, no. 1, pp. 186–193, 2019. [Google Scholar]
3. I. Otay, B. Oztaysi, S. Onar and C. Kahraman, “Multi-expert performance evaluation of healthcare institutions using an integrated intuitionistic fuzzy AHP&DEA methodology,” Knowledge-Based Systems, vol. 133, no. 2, pp. 90–106, 2017. [Google Scholar]
4. M. Cavalieri, C. Guccio and I. Rizzo, “On the role of environmental corruption in healthcare infrastructures: An empirical assessment for Italy using DEA with truncated regression approach,” Health Policy, vol. 121, no. 5, pp. 515–524, 2017. [Google Scholar]
5. S. Kohl, J. Schoenfelder, A. Fügener and J. O. Brunner, “The use of data envelopment analysis (DEA) in healthcare with a focus on hospitals,” Health Care Management Science, vol. 22, no. 2, pp. 245–286, 2019. [Google Scholar]
6. A. Ji, Y. Qiao and C. Liu, “Fuzzy DEA-based classifier and its applications in healthcare management,” Health Care Management Science, vol. 220, no. 3, pp. 1–9, 2019. [Google Scholar]
7. A. Singh and A. Prasher, “Measuring healthcare service quality from patients’ perspective: Using fuzzy AHP application,” Total Quality Management & Business Excellence, vol. 30, no. 3, pp. 284–300, 2019. [Google Scholar]
8. M. Hsieh, E. Wang, W. Lee, L. Li, C. Hsieh et al., “Application of HFACS, fuzzy TOPSIS, and AHP for identifying important human error factors in emergency departments in Taiwan,” International Journal of Industrial Ergonomics, vol. 67, no. 4, pp. 171–179, 2018. [Google Scholar]
9. F. Smarandache, “Plithogenic set, an extension of crisp, fuzzy, intuitionistic fuzzy, and neutrosophic sets-revisited,” Infinite Study, vol. 13, no. 2, pp. 1–13, 2018. [Google Scholar]
10. E. Glonek, K. Załuska, M. Oberc, E. Lewicka, K. Torres et al., “Evaluation of patients’ satisfaction and quality of life in selected healthcare institutions in southern-eastern Poland,” Polish Journal of Public Health, vol. 124, no. 4, pp. 183–186, 2015. [Google Scholar]
11. T. Lupo, “A fuzzy framework to evaluate service quality in the healthcare industry: An empirical case of public hospital service evaluation in sicily,” Applied Soft Computing, vol. 40, no. 3, pp. 468–478, 2016. [Google Scholar]
12. G. Narayanamurthy and A. Gurumurthy, “Is the hospital lean? A mathematical model for assessing the implementation of lean thinking in healthcare institutions,” Operations Research for Health Care, vol. 18, no. 2, pp. 84–98, 2018. [Google Scholar]
13. I. Chiu, Y. Lin, Y. Syue, C. Kung, K. Wu et al., “The influence of crowding on clinical practice in the emergency department,” The American Journal of Emergency Medicine, vol. 36, no. 1, pp. 56–60, 2018. [Google Scholar]
14. L. Laker, C. Froehle, J. Windeler and C. Lindsell, “Quality and efficiency of the clinical decision-making process: Information overload and emphasis framing,” Production and Operations Management, vol. 27, no. 12, pp. 2213–2225, 2018. [Google Scholar]
15. R. Yazdanparast, M. Hamid, M. Azadeh and A. Keramati, “An intelligent algorithm for optimization of resource allocation problem by considering human error in an emergency department,” Journal of Industrial and Systems Engineering, vol. 11, no. 1, pp. 287–309, 2018. [Google Scholar]
16. M. Yousefi, M. Yousefi, R. Ferreira, J. Kim and F. Fogliatto, “Chaotic genetic algorithm and adaboost ensemble metamodeling approach for optimum resource planning in emergency departments,” Artificial Intelligence in Medicine, vol. 84, no. 3, pp. 23–33, 2018. [Google Scholar]
17. D. Daldoul, I. Nouaouri, H. Bouchriha and H. Allaoui, “A stochastic model to minimize patient waiting time in an emergency department,” Operations Research for Health Care, vol. 18, no. 4, pp. 16–25, 2018. [Google Scholar]
18. J. Crilly, J. Boyle, M. Jessup, M. Wallis, J. Lind et al., “The implementation and evaluation of the patient admission prediction tool: Assessing its impact on decision-making strategies and patient flow outcomes in 2 Australian hospitals,” Quality Management in Health Care, vol. 24, no. 4, pp. 169–176, 2015. [Google Scholar]
19. J. Helm and M. Oyen, “Design and optimization methods for elective hospital admissions,” Operations Research, vol. 62, no. 6, pp. 1265–1282, 2014. [Google Scholar]
20. A. Gharahi, A. Kheirkhah, A. Bagheri and M. Ahmadi, “Improving patient flow management process in emergency department using simulation and PROMETHEE method,” Journal of Health Administration, vol. 17, no. 57, pp. 20–32, 2014. [Google Scholar]
21. F. Smarandache, Neutrosophy: Neutrosophic probability, set, and logic: Analytic synthesis & synthetic snalysis. Rehoboth, NM: American Research Press, 1998. [Google Scholar]
22. M. Abdel-Basset and M. Mohamed, “A novel and powerful framework based on neutrosophic sets to aid patients with cancer,” Future Generation Computer Systems, vol. 98, no. 3, pp. 144–153, 2019. [Google Scholar]
23. F. Smarandache, “Plithogeny, plithogenic set, logic, probability, and statistics,” Infinite Study, Publ. Hse., GoogleLLC, Mountain View, California, USA, vol. 141, no. 2, pp. 12–25, 2017. [Google Scholar]
24. M. Abdel-Basset, M. El-hoseny, A. Gamal and F. Smarandache, “A novel model for evaluation hospital medical care systems based on plithogenic sets,” Artificial Intelligence in Medicine, vol. 121, no. 2, pp. 101710, 2019. [Google Scholar]
25. M. Abdel-Basset, R. Mohamed, A. Zaied and F. Smarandache, “A hybrid plithogenic decision-making approach with quality function deployment for selecting supply chain sustainability metrics,” Symmetry, vol. 11, no. 7, pp. 903–923, 2019. [Google Scholar]
26. D. Chang, W. Wang and R. Wang, “Identifying critical factors of sustainable healthcare institutions’ indicators under Taiwan's national health insurance system,” Social Indicators Research, vol. 140, no. 1, pp. 287–307, 2018. [Google Scholar]
27. Z. Anas, N. Sefiani, K. Reklaoui and H. Azzouzi, “A SCOR based performance evaluation system of the hospital supply chain,” in 2018 Int. Colloquium on Logistics and Supply Chain Management (LOGISTIQUATangier, Morocco, IEEE, pp. 182–187, 2018. [Google Scholar]
28. V. Oliveira, J. Sobral and M. Ribeiro, “Development of a tool for selection and acquisition of medical devices based on the analytic hierarchy process,” in 2019 IEEE 6th Portuguese Meeting on Bioengineering (ENBENGLisbon, Portugal, IEEE, pp. 1–4, 2019. [Google Scholar]
29. A. Esfahani, H. Ahmadi, M. Nilashi, M. Alizadeh, A. Bashiri et al., “An evaluation model for the implementation of hospital information system in public hospitals using multi-criteria-decision-making (MCDM) approaches,” International Journal of Engineering and Technology (UAE), vol. 7, no. 1, pp. 1–18, 2018. [Google Scholar]
30. X. Zuo, B. Li, X. Huang, M. Zhou, C. Cheng et al., “Optimizing hospital emergency department layout via multiobjective tabu search,” IEEE Transactions on Automation Science and Engineering, vol. 16, no. 3, pp. 1137–1147, 2019. [Google Scholar]
31. M. Yousefi and M. Yousefi, “Human resource allocation in an emergency department: A metamodel-based simulation optimization,” Kybernetes, vol. 13, no. 2, pp. 12–25, 2019. [Google Scholar]
32. K. Qi, Q. Wang, Q. Duan, L. Gong, J. Sun et al., “A multi criteria comprehensive evaluation approach for emergency response capacity with interval 2-tuple linguistic information,” Applied Soft Computing, vol. 72, no. 2, pp. 419–441, 2018. [Google Scholar]
33. T. L. Saaty, “A scaling method for priorities in hierarchical structures,” Journal of Mathematical Psychology, vol. 15, no. 3, pp. 234–281, 1977. [Google Scholar]
34. F. Abastante, S. Corrente, S. Greco, A. Ishizaka and I. Lami, “A new parsimonious AHP methodology: Assigning priorities to many objects by comparing pairwise few reference objects,” Expert Systems with Applications, vol. 127, no. 3, pp. 109–120, 2019. [Google Scholar]
35. M. Moallem, C. Derbel, M. Ammar, N. Béji and D. Dhouib, “Risk prioritization using the analytic hierarchy process (AHP) in a Tunisian healthcare department: A real-world case study,” Multiple Criteria Decision Making, vol. 13, no. 1, pp. 9–28, 2018. [Google Scholar]
36. A. Mardani, R. Hooker, S. Ozkul, S. Yifan, M. Nilashi et al., “Application of decision making and fuzzy sets theory to evaluate the healthcare and medical problems: A review of three decades of research with recent developments,” Expert Systems with Applications, vol. 137, no. 3, pp. 202–231, 2019. [Google Scholar]
37. S. Barak and J. Dahooei, “A novel hybrid fuzzy DEA-fuzzy MADM method for airlines safety evaluation,” Journal of Air Transport Management, vol. 73, no. 2, pp. 134–149, 2018. [Google Scholar]
38. A. Emrouznejad and G. Yang, “A survey and analysis of the first 40 years of scholarly literature in DEA: 1978–2016,” Socio-Economic Planning Sciences, vol. 61, no. 1, pp. 4–8, 2018. [Google Scholar]
39. C. Akkan, M. Karadayi, Y. Ekinci, F. Ülengin, N. Uray et al., “Efficiency analysis of emergency departments in metropolitan areas,” Socio-Economic Planning Sciences, vol. 69, no. 2, pp. 100679, 2020. [Google Scholar]
40. A. Kazley and Y. Ozcan, “Electronic medical record use and efficiency: A DEA and windows analysis of hospitals,” Socio-Economic Planning Sciences, vol. 43, no. 3, pp. 209–216, 2009. [Google Scholar]
41. P. Mitropoulos, M. Talias and I. Mitropoulos, “Combining stochastic DEA with Bayesian analysis to obtain statistical properties of the efficiency scores: An application to Greek public hospitals,” European Journal of Operational Research, vol. 243, no. 1, pp. 302–311, 2015. [Google Scholar]
42. H. Chowdhury and V. Zelenyuk, “Performance of hospital services in ontario: DEA with truncated regression approach,” Omega, vol. 63, no. 3, pp. 111–122, 2016. [Google Scholar]
43. J. Khushalani and Y. Ozcan, “Are hospitals producing quality care efficiently? an analysis using dynamic network data envelopment analysis (DEA),” Socio-Economic Planning Sciences, vol. 60, no. 2, pp. 15–23, 2017. [Google Scholar]
44. M. Abdel-Basset, A. Atef and F. Smarandache, “A hybrid neutrosophic multiple criteria group decision making approach for project selection,” Cognitive Systems Research, vol. 57, no. 2, pp. 216–227, 2019. [Google Scholar]
45. M. Abdel-Baset, I. Hezam and F. Smarandache, “Neutrosophic goal programming,” Neutrosophic Sets & Systems, vol. 11, no. 1, pp. 12–37, 2016. [Google Scholar]


 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |