Computers, Materials & Continua DOI:10.32604/cmc.2022.019579
Article

Torsional Wave in a Dissipative Cylindrical Shell Under Initial Stresses

Mahmoud M. Selim1,2,* and Khaled A. Gepreel3

1Department of Mathematics-College of Sciences & Humanities in Al Aflaj, Prince Sattam bin Abdulaziz University, Al-Aflaj, 11912, KSA
2Department of Mathematics, Suez Faculty of Science, Suez University, Egypt
3Department of Mathematics, Faculty of Science, Taif University, Taif, 21944, Saudi Arabia
*Corresponding Author: Mahmoud M. Selim. Email: m.selim@psau.edu.sa
Received: 18 April 2021; Accepted: 01 June 2021

Abstract: The dispersion relation of torsional wave in a dissipative, incompressible cylindrical shell of infinite length incorporating initial stresses effects is investigated. The governing equation and closed form solutions are derived with the aid of Biot's principle. Phase velocity and damping of torsional wave are obtained analytically and the influences of dissipation and initial stresses are studied in details. We proposed a new method for obtaining the phase and damping velocities of torsional wave in a complex form. Numerical results analyzing the torsional wave propagation incorporating initial stress effects are analyzed and presented in graphs. The analytical and numerical solutions reveal that, the dissipation as well as the initial stresses have notable impacts on the phase velocity of torsional wave in a pre-stressed dissipative cylindrical shell. The numerical results reveal that, the initial stresses and dissipation, considerably, effect the phase velocity of the torsional wave. It has been observed that, any change in dissipation parameter (δ) produces a substantial change in damping velocity of torsional wave. In addition, it can be seen that, the phase velocity increases as the initial stress parameter increases. Finally, the result of numerical simulation illustrated the influence of dissipation and initial stresses on damping and phase velocities of torsional wave propagation. The conclusion made shown the consistency with the Biot's incremental deformation theory, and the effective on model such as engineering mechanics and displacement of particles.

Keywords: Propagation; torsional wave; dissipation; cylindrical shell; initial stress

1  Introduction

Waves propagation in the elastic media is an interesting topic for numerus scientists due to the needs of the complete understanding of different medium characteristics. The early literature studied the waves propagation in the elastic media, is the book of Ewing et al. [1]. After Ewing`s published his book, many research papers have been published. More attention are paid to study the torsional waves propagation in elastic media, and less attention is paid on the dissipative media based on the torsional wave how to model and get the solutions to the governing equations. Xie et al. [2] studied the propagation of transient torsional wave in a transversely isotropic medium. Kudlicka [3–4] studied the dispersion of torsional wave in transversely isotropic thick-walled cylinder of infinite length. In addition, Yokoyama et al. [5] studied the distribution of shear stress of torsional wave propagation in a strengthening rod. Wang [6] analyzed the propagation of wave in a coated cylinder with piezoelectric layer. Xi et al. [7] proposed a layered element method to analysis dispersive behaviors of torsional waves in a laminated composite cylinder surrounded by a fluid. It is well known that the actual Earth crust is an initially stressed medium due to various reasons, such as change of temperatures and gravity variation, etc. Gupta et al. [8] reported a new result about the torsional surface wave propagation in a heterogeneous layer over pre-stressed heterogeneous half-space. Kepceler [9] analyzed the dispersion relation of torsional wave in an initially stressed bi-material compounded cylinder. In recent years, the phenomena of initial stresses impacts have been a subject of continued researcher's interest due to its importance in seismology and earthquake engineering fields. The main important information about the physical effects of initial stresses on the waves propagation in the elastic media are contained in the famous book with the title “Mechanics Incremental Deformations” by Biot [10]. References can be made to Dey et al. [11–13], Selim [14–18] for their contributions in studying the torsional wave propagation in the elastic media under various conditions. Nowadays, torsional wave propagation in the nanostructures has received more attention in nanotechnology fields. Adeli et al. [19] employed the strain gradient theory to achieve the free torsional vibration of nonlinear homogenous and isotropic nano-cone. Asad Ullah et al. [20,21] studied the thermal behavior of nanofluids on an inclined rotating surface.

Based on Kelvin-Voigt model, El-Borgi et al. [22] have reported a novel model to investigate the vibrational behavior of the viscoelastic nanorods. Zhu et al. [23] have used the nonlocal integral elasticity to study Longitudinal and torsional vibrations of nanorods. Nazemnezhad and Fahimi [24] have discussed the effects of surface energy on the free torsional vibration of cracked nanobeams at different boundary conditions based on the surface elasticity theory. Yayli [25] and Huang [26] investigated the torsional vibrations of restrained nanotubes subjected to constraint of surface elasticity. Taking the effect of nonlocal strain, Yayli et al. [27] investigated the effects of torsional restraints on the vibration of cracked carbon nanotubes. Khosravi et al. [28] analyzed the torsional vibrations of nanowire. The existence of dissipation and initial stresses are common occurred in Earth crust. Such existence play an important role on the vibrational analysis of torsional wave propagation [29–32].

It is obvious that the dissipation and the initial stress parameter influences the behavior of the torsional wave propagation in a cylindrical shell. Hence, it is of great importance to study propagation of torsional wave in a dissipative cylindrical shell incorporating initial stress effects. Thus, the present work proposed a new method to analysis the impacts of initial stress and medium`s dissipation on the phase velocities of torsional wave propagation in a pre-stressed, dissipative, incompressible cylindrical shell. The analysis are carried based on Biot's incremental deformation theory.

2  Formulation of the Problem and Its Solution

Let us consider a dissipative incompressible elastic cylindrical shell with radius a under compressional initial stress P. The cylindrical coordinates (r,θ,z) are shown in Fig. 1. The equations of motion with the initial stress (SZZ=−P) and dissipation (γ) effects are [10]:

∂srr∂r+1r∂srθ∂θ+∂srz∂z+srr−sθθr−P∂ωθ∂z=ρ∂2u∂t2+γ∂u∂t,(1)

∂srθ∂r+1r∂sθθ∂θ+∂sθz∂z+2srθr+P∂ωr∂z=ρ∂2v∂t2+γ∂v∂t,(2)

∂srz∂r+1r∂sθz∂θ+∂szz∂z+srzr−P[∂ωθ∂r−∂ωr∂θ]=ρ∂2w∂t2+γ∂w∂t,(3)

where ρ is the density, Srr,Sθθ,Szz,Srz,Srθ and Sθz are the stress components, u,v,w are the displacement components and ωr,ωθ are the rotational components which are given by [10]:

ωr=12(∂w∂θ−∂v∂z),ωθ=12(∂u∂z−∂w∂r).(4)

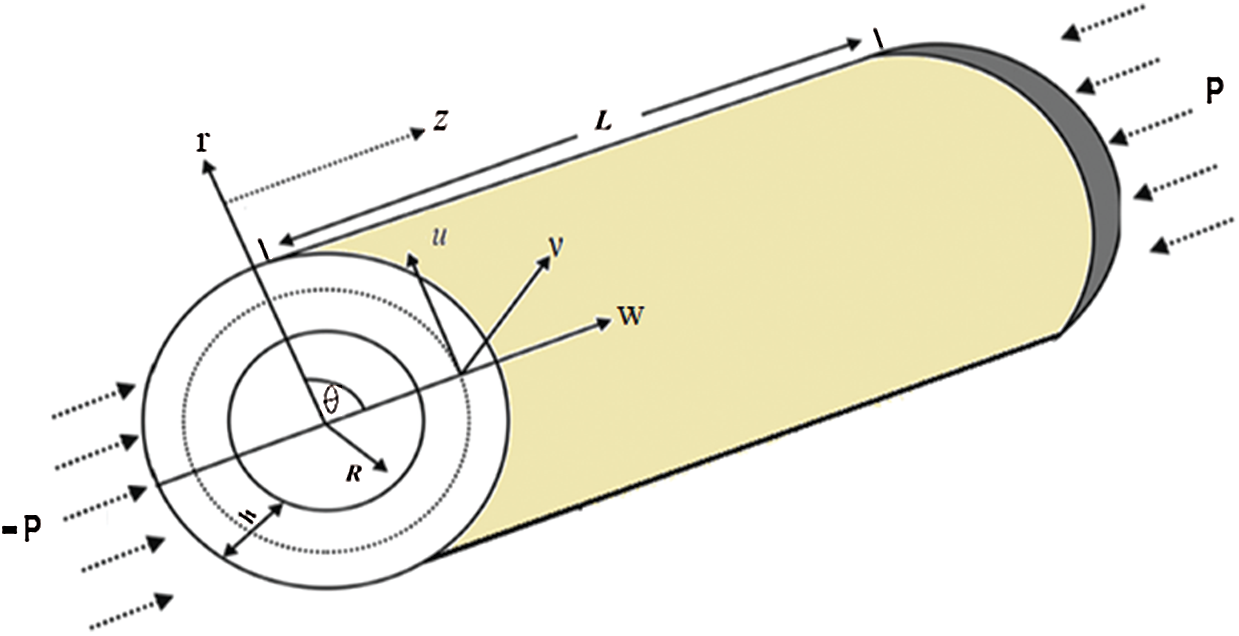
Figure 1: Geometry of initially stressed cylindrical shell

Eqs. (1)–(3) contains the dissipation (damping) term (γ), which is proportional to the velocity.

The tress-strain relations in our case, can be written in the following form [10]:

Srr=B11err+B12eθθ+B13ezz,Sθθ=B21err+B22eθθ+B23ezz,Szz=B13err+B23eθθ+B33ezz,SθZ=2Q1eθZ,SrZ=2Q2erZ,Srθ=2Q3erθ,(5)

where Bmn(m,n=1,2,3) and Qm are the incremental constants and shear coefficients, respectively.

The incremental strain components can be written as a function of the displacements u,v and w as follows:

err=∂u∂r,eθθ=1r(∂v∂θ+u),ezz=∂w∂z,erz=ezr=12(∂u∂z+∂w∂r),eθz=ezθ=12(∂v∂z+1r∂w∂θ),erθ=eθr=12(1r∂u∂θ−vr+∂v∂r).(6)

The present study investigates the torsional wave propagation in a dissipative cylindrical shell. Then, the propagation having θ symmetry, then it can be easily observed that Eqs. (1) and (3) are automatically satisfied as u=w=0. Using relation (4), the Eq. (2) takes the form:

∂srθ∂r+∂sθz∂z+2srθr−P2∂2v∂z2=ρ∂2v∂t2+γ∂v∂t.(7)

The relations (5) in this case may be written as:

sθz=2Q2eθz,srθ=2Q1erθ,(8)

where Q1 and Q2 are the incremental elastic coefficients and can be written by Biot [10] as follows:

Q1=μ2(λr2+λθ2),Q2=μ2(λθ2+λz2)(9)

Where μ is the elastic modulus of unstressed cylindrical shell and λr,λθ,λz are the extension ratios.

The incompressibility condition can be written as:

λrλθλz=1.(10)

From the relation obtained by Biot [10], between the initial stresses and extension ratios we can get:

λr2=λθ2=1λz=1λ(say),(11)

P=μλ(1−λ3)(12)

Inserting relations (4)–(6), (8)–(12) in (7) one gets:

∂2v∂r2+λ3∂2v∂z2+1r∂v∂r−vr2=ρλμ∂2v∂t2+γλμ∂v∂t.(13)

Assuming harmonic wave solution eik(z−ct) and the general solution for torsional displacement components in the cylindrical shell becomes:

v(r,z,t)=V(r)eik(z−ct)(14)

From Eq. (14) into Eq. (13) one gets:

r2d2Vdr2+rdVdr+[η2r2−1]V=0,(15)

where

η2=k2(c2λβ2−λ3)+ikcλγμ,(16)

and β=(μρ)12 is the phase velocity of torsional wave propagating in unstressed cylindrical shell; c is the phase velocity in an initially stressed cylindrical shell. Eq. (15) is so-called parametric Bessel equation, which its general solution can be defined as follows:

V(r)=AJ1(ηr)+BY1(ηr),(17)

where J1(ηr) and Y1(ηr) are Bessel's functions.

3  Boundary Conditions

Let us consider no external forces, then the surface of cylindrical shell will be free from initial stresses and the displacement component at the free surface r=0 will be remained finite.

The boundary conditions in the case of torsional wave may be written as follows:

srθ=μ(dVdr−Vr)at the surface r=a.(18)

The second part of Bessel function (17) will be removed from the solution [28]. Then, substitute solution (14) in the boundary condition (18), one gets:

ξJ1′(ξ)−J1(ξ)=0,(19)

where ξ=ηa and the prime denotes that, the derivatives with respect to the radius r.

The solution of Eq. (19) gives a multiple roots of ξ. In our problem we will use the first three roots which are 0, 5.136 and 8.418 [11]. From Eq. (16), we can get:

c2β2−cβI−R=0,(20)

wherec is the phase velocity of torsional wave in the pre-stressed cylindrical shell, and

I=−iδρk,R=[(ξka)2∙1λ+λ2],(21)

where δ=γa, is the damping (dissipation) parameter.

Solving Eq. (20), we can get the phase velocity of torsional wave (c) as follows:

cβ=12(I+Ω),(22)

where

Ω=I2+4R,(23)

Eq. (22) gives the phase and damping velocities of torsional wave. The real part represents the phase velocity and the imaginary part represents the damping velocity. Appearing of the parameters δ and λ in Eq. (22) told us that, the phase and damping velocities of torsional wave influences by the dissipation as well as initial stresses present in the medium.

4  Particular Cases

4.1 Particular Case 1

If the cylindrical shell is non-dissipative medium (i.e.,δ=0), the phase velocity can be defined from the following relation:

cβ=[(ξka)2∙1λ+λ2]12,(24)

Which agree with the result obtained by Dey and Dutta [11].

4.2 Particular Case 2

The existence of the parameter λ in Eq. (21) told us that, the phase velocity of torsional wave is effected by the initial stress parameter present in the medium. Thus, if the cylindrical shell is unstressed medium, (i.e.,λ=1), then the phase velocity can be defined from the following relation:

cβ=[(ξka)2+1]12(25)

Which coincide with the result of Kolsky [33].

5  Numerical Results and Discussion

To examine the influences of various parameters on dispersion relation of torsional wave propagation in a dissipative, incompressible initially stressed cylindrical shell of infinite length, we have taken ρ=2.15g/cm3 to calculate the phase velocity from Eq. (22) for different values of initial stress and dissipation parameters. The Effects of initial stress and dissipation parameters are discussed and presented graphically in Figs. 2–4.

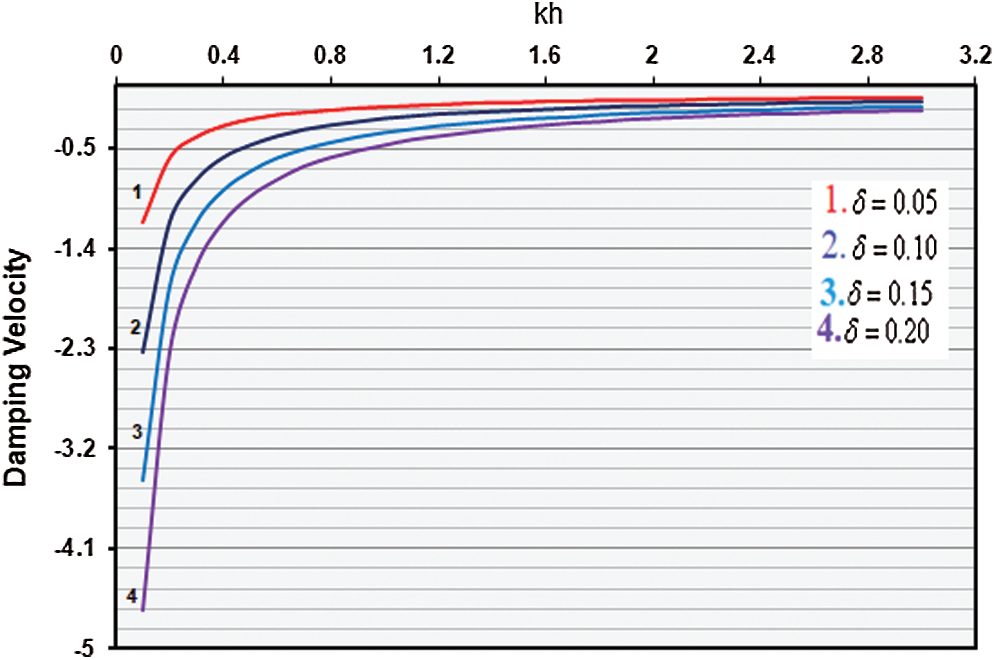
Figure 2: Variation of damping velocity vs. wave number (ka) at different values of dissipation parameter δ

The phase velocity c/β are computed numerically at different values of dissipation parameter (δ=0.05, 0.1 0.15, 0.2). In addition, the phase velocity c/β are computed numerically with two different values ξ=ηa=5.136 and 8.418 in two cases: a) λ < 1 (existence of initial stress parameter), b) λ=1(absent of the initial stresses parameter). The dispersion curves have been calculated with different wave number (ka) and the results are presented graphically in Figs. 2–4.

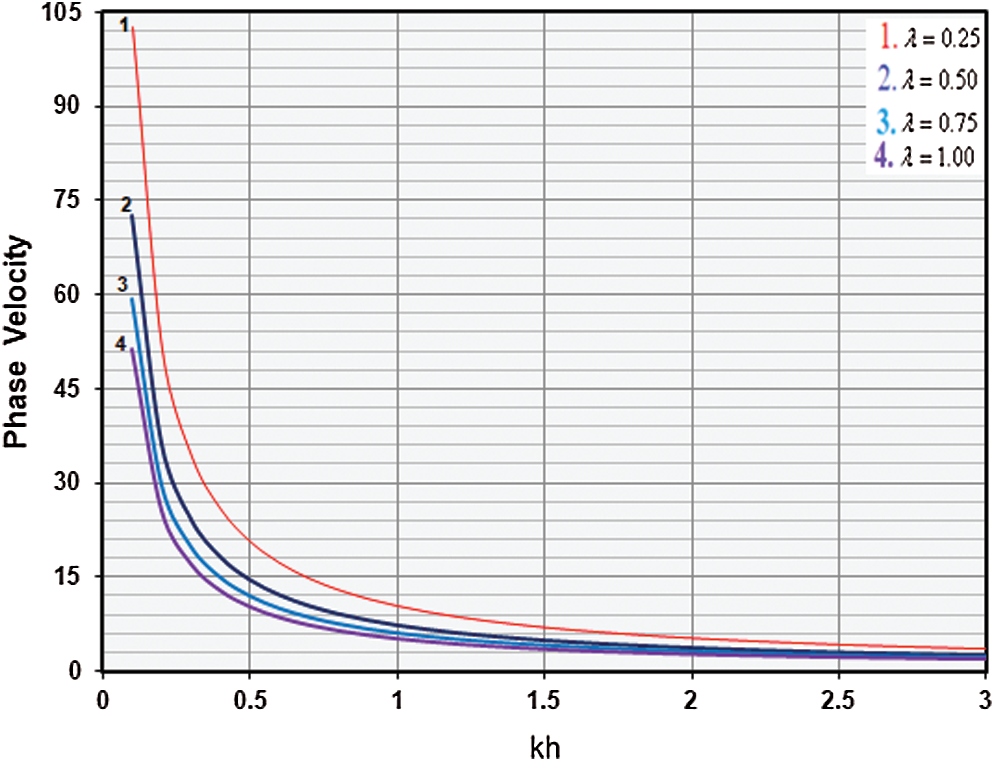
Figure 3: Variation of phase velocity (c/β) vs. wave number (ka)atξ=5.136

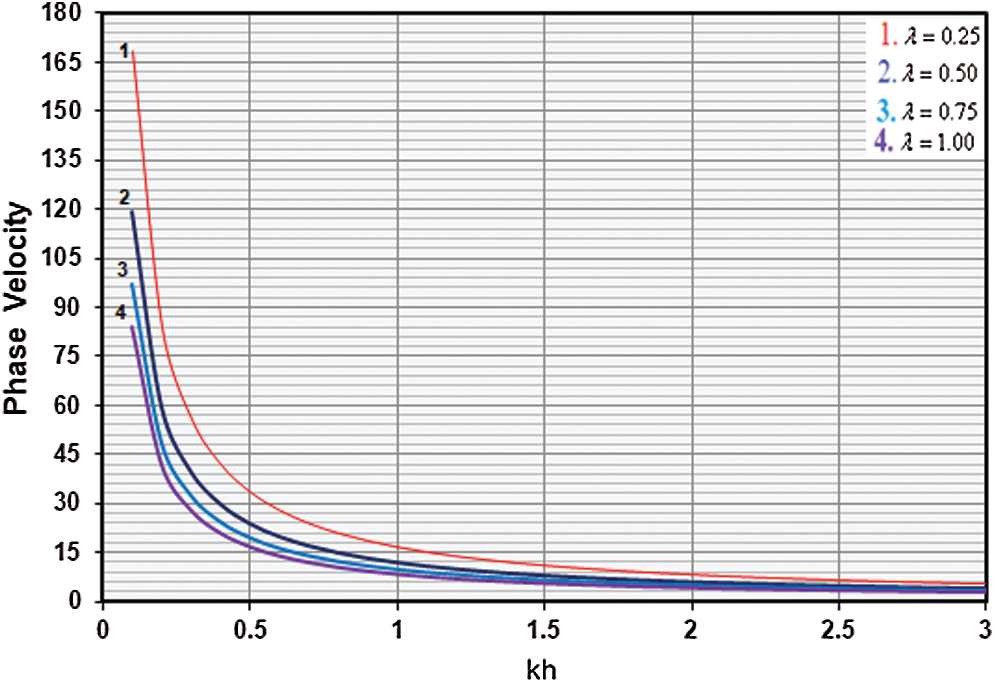
Figure 4: Variation of phase velocity (c/β) vs. wave number (ka)atξ=8.418

Fig. 2 shows the variation of damping vs. wave number (ka) at different dissipation parameter (δ=0.05, 0.10, 0.15, 0.20). The dispersion curves reveal clearly that, the change of dissipation parameter (δ) produces a substantial change in damping velocity of torsional wave.

Fig. 3 shows variation of phase velocity (c/β) vs. wave number (ka) for different values of the initial stress parameter λ at (ξ=5.136). The dispersion curves obtained in Fig. 3 show that, the phase velocity of torsional wave increases as the initial stress parameter increases. This means that, the presence of initial compressional stresses, considerably, effects the phase velocity of torsional wave in a dissipative cylindrical shell.

Fig. 4 gives the variation of phase velocity (c/β) vs. wave number (ka) for the different values of initial stress parameter λ at (ξ=8.418). The obtained dispersion curves of in Fig. 4 support the results obtained and shown in the dispersion curves of Fig. 3.

6  Conclusions

In the present work, the dispersion of torsional wave in a dissipative, incompressible cylindrical shell of infinite length incorporating initial stresses effects is investigated. The analysis of this study reported a novel governing equation of torsional wave propagation in a pre-stressed dissipative cylindrical shell based on Biot`s incremental deformation theory. We proposed a new method for obtaining the phase and damping velocities of torsional wave in a complex form. Numerical results analyzing the torsional wave propagation incorporating initial stress effects are discussed and presented in graphs. The dimensionless phase velocity c/β are computed numerically at different values of dissipation parameter (δ=0.05, 0.1 0.15, 0.2). In addition, the values of c/β are computed numerically for two different values of the parameter ξ=ηa=5.136 and 8.418 in two cases: a) λ<1 (existence of initial stress parameter), b) λ=1(absent of the initial stresses parameter). The dispersion curves have been plotted for different value of wave number (ka) and the results presented graphically. The analytical and numerical solutions reveal that, the dissipation as well as the initial stress parameter have notable effects on the phase velocities of torsional wave in a pre-stressed dissipative cylindrical shell.

The numerical results also, reveal clearly that, every little change in the dissipation parameter (δ) produces a substantial change in the damping velocity of torsional wave. In addition, it can observed that, the phase velocity of torsional wave increases as the initial stress parameter increases. Finally, numerical results and simulation gave the figures with the change of parameters initial stress and dissipation module of the component, so the present research on the dispersion of torsional wave propagation in the dissipative, incompressible cylindrical shell of infinite length can be useful in modelling and analyzing the particle displacement, engineering mechanics and many engineering applications.

Acknowledgement: The authors thank Taif university researchers for supporting project number (TURSP-2020/16), Taif University, Taif, Saudi Arabia. The first author would like to acknowledge the supports provided by the Deanship of Scientific Research of Prince Sattam bin Abdulaziz University during this research work.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  W. M. Ewing, W. S. Jardetzky and F. Press, “Elastic waves in layered media,” Mcgraw-hill, New York, 1957. [Google Scholar]

 2.  S. Xie, K. Liu, “Transient torsional wave propagation in a transversely isotropic tube,” Archive of Applied Mechanics, vol. 68, pp. 589–596, 2021. [Google Scholar]

 3.  J. K. Wka, “Energy flow of axisymmetric elastic waves in a three-layered, transtropic–isotropic–transtropic, composite cylinder,” Journal of Sound and Vibration, vol. 277, pp. 1093–1100, 2004. [Google Scholar]

 4.  J. K. Wka, “Dispersion of torsional waves in a thick-walled transversely isotropic circular cylinder of infinite length,” Journal of Sound and Vibration, vol. 294, pp. 368–373, 2006. [Google Scholar]

 5.  T. Yokoyama and K. Liu, “A numerical and experimental study of transient torsional waves in stepped circular bars,” International Journal of Engineering Science, vol. 38, pp. 287–307, 2000. [Google Scholar]

 6.  Q. Wang, “Axi-symmetric wave propagation in a cylinder coated with a piezoelectric layer,” International Journal of Solids and Structures, vol. 39, pp. 3023–3037, 2002. [Google Scholar]

 7.  Z. C. Xi, G. R. Liu, K. Y. Lam and H. M. Shang, “Dispersion of waves in immersed laminated composite hollow cylinders,” Journal of Sound and Vibration, vol. 250, no. 2, pp. 215–227, 2002. [Google Scholar]

 8.  S. Gupta, S. Kundu and S. K. Vishwakarma, “Propagation of torsional surface waves in an inhomogeneous layer over an initially stressed inhomogeneous half-space,” Journal of Vibration and Control, vol. 21, no. 7, pp. 1286–1298, 2015. [Google Scholar]

 9.  T. Kepceler, “Torsional wave dispersion relations in a pre-stressed bi-material compounded cylinder with an imperfect interface,” Applied Mathematical Model, vol. 34, no. 12, pp. 4058–4073, 2010. [Google Scholar]

10. M. A. Biot, “Mechanics of incremental deformation,” John wiley & sons, New York, 1965. [Google Scholar]

11. S. Dey and A. Dutta, “Torsional wave propagation in an initially stressed cylinder,” Proc. of the Indian National Science Academy, vol. 58, no. 5, pp. 425–429, 1992. [Google Scholar]

12. S. Dey, A. K. Gupta, and S. Gupta,“ Torsional surface waves in nonhomogeneous and anisotropic medium,” The Journal of the Acoustical Society of America, vol. 99, no. 5, pp. 2737–2741, 1996. [Google Scholar]

13. S. Dey, S. Gupta, A. K. Gupta, and A. M. Prasad,“ propagation of torsional surface waves in a heterogeneous half-space under a rigid layer,” Acta Gephysica Polonica, vol. 49, no. 1, pp. 113–118, 2001. [Google Scholar]

14. M. M. Selim, “Static deformation of an irregular initially stressed medium,” Applied Mathematics and Computation, vol. 188, pp. 1274–1284, 2007. [Google Scholar]

15. M. M. Selim, “Propagation of torsional surface waves in heterogeneous half-space with irregular free surface,” Journal of Nanofluids, vol. 9, no.2, pp. 128–131, 2020. [Google Scholar]

16. M. M. Selim, “Torsional vibration of carbon nanotubes under initial compression stress,” Brazilian Journal of Physics, vol. 40, no. 3, pp. 283–287, 2010. [Google Scholar]

17. M. M. Selim, S. Abe and K. Harigaya, “Effects of initial compression stress on wave propagation in carbon nanotubes,” European Physical Journal B, vol. 69, no.4, pp. 523–528, 2009. [Google Scholar]

18. H. Khalifa, S. A. El-Safty, A. Reda, M. A. Shenashen, M. M. Selim et al., “Experimental sets of choice anode/Cathode architectonics for high-performance full-scale LIB built-up models,” Nano-Micro Letters, vol. 11, pp. 84, 2019. [Google Scholar]

19. M. M. Adeli1, A. Hadi, M. Hosseini, and H. H. Gorgani, “Torsional vibration of nano-cone based on nonlocal strain gradient elasticity theory,” The European Physical Journal Plus, vol. 132, pp. 393, 2017. [Google Scholar]

20. A. Ullah, Z. Shah, P. Kumam, M. Ayaz, S. Islam et al., “Viscoelastic MHD nanofluid thin film flow over an unsteady vertical stretching sheet with entropy generation,” Processes, vol. 7, pp. 262, 2019. [Google Scholar]

21. Z. Shah, A. Ullah, E. Bonyah, M. Ayaz, S. Islam et al., “Hall effect on titania nanofluids thin film flow and radiative thermal behavior with different base fluids on an inclined rotating surface,” AIP Advances, vol. 9, pp. 55113, 2019. [Google Scholar]

22. S. El-Borgl, P. Rajendran, M. I. Friswell, M. Trabelss and J. N. Reddy, “Torsional vibration of size-dependent viscoelastic rods using nonlocal strain and velocity gradient theory,” Composite Structures, vol. 186, pp. 274–292, 2018. [Google Scholar]

23. X. Zhu and L. Li, “Longitudinal and torsional vibrations of size-dependent rods via nonlocal integral elasticity,” International Journal of Mechanical Sciences, vol. 133, pp. 639–650, 2017. [Google Scholar]

24. R. Nazemnezhad, P. Fahimi, “Free torsional vibration of cracked nanobeams incorporating surface energy effects,” Applied Mathematics and Mechanics English Edition, vol. 38, no. 2, pp. 217–230, 2017. [Google Scholar]

25. M. O. Yayli, “Torsional vibrations of restrained nanotubes using modified couple stress theory,” Microsystem Technologies, vol. 24, pp. 3425–3435, 2018. [Google Scholar]

26. Z. Huang, “Torsional wave and vibration subjected to constraint of surface elasticity,” Acta Mechanica, vol. 229, pp. 1171–1182, 2018. [Google Scholar]

27. M. O. Yayli, S. Y. Kandemir and A. E. Cercevik, “Torsional vibration of cracked carbon nanotubes with torsional restraints using eringen's nonlocal differential model,” Journal of Low Frequency Noise, Vibration and Active Control, vol. 38, no. 1, pp. 70–87, 2019. [Google Scholar]

28. F. Khosravi, S. A. Hosseini and B. A. Hamidi, “On torsional vibrations of triangular nanowire,” Journal of Thin–Walled Structures, vol. 148, pp. 106591, 2020. [Google Scholar]

29. W. H. Su, D. Baleanu, X. J. Yang and H. Jafari, “Damped wave equation and dissipative wave equation in fractal strings within the local fractional variational iteration method,” Fixed Point Theory and Applications, vol. 89, pp. 1–11, 2013. [Google Scholar]

30. D. Baleanu and H. K. Jassim, “Approximate solutions of the damped wave equation and dissipative wave equation in fractal strings,” Fractal and Fractional, vol. 3, no. 26, pp. 1–12, 2019. [Google Scholar]

31. N. A. Adnan, U. Khan, N. Ahmed, S. T. Mohyud-Din, D. Baleanu et al., “Second Law analysis of magneto radiative GO-moS2/H2O–(CH2OH)2 hybrid nanofluid,” Computers, Materials & Continua, vol. 68, no. 1, pp. 213–228, 2021. [Google Scholar]

32. M. M. Selim and M. K. Ahmed, “Propagation and attenuation of seismic body waves in dissipative medium under initial and couple stresses,” Applied Mathematics and Computation, vol. 182, no. 2, pp. 1064–1074, 2006. [Google Scholar]

33. H. Kolsky, “Stress Wave in Solids”, Oxford University Press, London, 1953. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.