Computers, Materials & Continua DOI:10.32604/cmc.2022.019562
Article

Blockchain-Based SQKD and IDS in Edge Enabled Smart Grid Network

Abdullah Musaed Alkhiari1, Shailendra Mishra2,* and Mohammed AlShehri1

1Department of Information Technology, College of Computer and Information Sciences, Majmaah University, Majmaah, 11952, Saudi Arabia
2Department of Computer Engineering, College of Computer and Information Sciences, Majmaah University, Majmaah, 11952, Saudi Arabia
*Corresponding Author: Shailendra Mishra. Email: s.mishra@mu.edu.sa
Received: 17 April 2021; Accepted: 20 May 2021

Abstract: Smart Grid is a power grid that improves flexibility, reliability, and efficiency through smart meters. Due to extensive data exchange over the Internet, the smart grid faces many security challenges that have led to data loss, data compromise, and high power consumption. Moreover, the lack of hardware protection and physical attacks reduce the overall performance of the smart grid network. We proposed the BLIDSE model (Blockchain-based secure quantum key distribution and Intrusion Detection System in Edge Enables Smart Grid Network) to address these issues. The proposed model includes five phases: The first phase is blockchain-based secure user authentication, where all smart meters are first registered in the blockchain, and then the blockchain generates a secret key. The blockchain verifies the user ID and the secret key during authentication matches the one authorized to access the network. The secret key is shared during transmission through secure quantum key distribution (SQKD). The second phase is the lightweight data encryption, for which we use a lightweight symmetric encryption algorithm, named Camellia. The third phase is the multi-constraint-based edge selection; the data are transmitted to the control center through the edge server, which is also authenticated by blockchain to enhance the security during the data transmission. We proposed a perfect matching algorithm for selecting the optimal edge. The fourth phase is a dual intrusion detection system which acts as a firewall used to drop irrelevant packets, and data packets are classified into normal, physical errors and attacks, which is done by Double Deep Q Network (DDQN). The last phase is optimal user privacy management. In this phase, smart meter updates and revocations are done, for which we proposed Forensic based Investigation Optimization (FBI), which improves the security of the smart grid network. The simulation is performed using network simulator NS3.26, which evaluates the performance in terms of computational complexity, accuracy, false detection, and false alarm rate. The proposed BLIDSE model effectively mitigates cyber-attacks, thereby contributing to improved security in the network.

Keywords: Smart grid; edge computing; intrusion detection system; blockchain; quantum key distribution; deep reinforcement learning

1  Introduction

In recent years, there is an increasing requirement of properly managing renewable resources and distribution of power based on the requirement. The smart grid has been evolved as a promising technology for proper management of the power resources by providing a decentralized supply of power from all sources. The smart grid network’s clean distribution and operational efficiency has been achieved by integrating the electric flow and communication network [1]. This integration results in an increased number of security threats to the smart grid network. The security requirement for the smart grid network has been stated as confidential, full of integrity and availability (CIA). Several existing works implemented authentication of smart meters to provide anonymity to the users, but most of the users end in improper key distribution, ultimately affecting the performance of the network [2,3].

Few random tree methods were incorporated for attack detection. However, only known attacks were detected which will not be sufficient for the overall security of the smart grid network [4]. Few asymmetric encryption functions were deployed to ensure authentication of users, but these functions had higher complexity, which increased the latency of the smart grid network [5]. Various methods deployed multi agents and Q learning approaches in edge server and in the neighbor gateway in order to take precise decision in attack circumstances [6]. Several works implemented homomorphic encryption of data, to provide data integrity, but it degraded the performance as it had high overhead. Various monitoring techniques have emerged to improve the security on the server-side by deploying significant techniques, including blockchain however, these methods had their own limitations and were not suited for smart grid networks [7,8].

The prekeying technique emerged as an alternative keying method in which the key for the upcoming data was generated priory to reduce the latency involved in it; nevertheless, this method also had a key distribution problem [9]. Some methods implemented dynamic detection of attacks in the smart grid network, but they had less efficiency in learning which affected the network’s performance [10]. Few unique methods constructed graphs for better visualization of attacks, but they also addressed only prevailing attacks [11]. The network similarity was observed, and the odd one out method was practiced to detect the attack, which was considered simple and significant in detecting them.

Few existing works were used for the correction of parameters for the detection of most prevailing false data injection attacks. The integrity of the data was improved by executing the digital signature of packets for anomaly device detection in the smart grid-based edge network [12]. Smart grid network has been emerged as an on-demand technology to satisfy the increasing requirements of energy resources. Several existing works addressed the cyber security of the smart grid network but the overall solution for the security problems is not provided till now. Additionally, the following research problems are encountered, Lack of user anonymity, Poor key distribution and improper user privacy management. Motivated by these problems, the objectives of this research work address the cybersecurity threats in the smart grid network and to provide the solutions to ensure unconditional security in the power network.

The goal of the research are;

•   To maximize the anonymity of the users by authenticating only the legitimate users in the smart grid network and to improve the security using blockchain technology,

•   To maximize the integrity of the data by performing lightweight encryption of data without increasing the latency of the network, to overcome the key distribution problem, and to provide a secure transmission channel for transmission of data packets,

•   To maximize the scalability in the smart grid network by optimal selection of the edge node (gateway) based on significant parameters,

•   To maximize the security of the smart grid network in the control center side by implementing intrusion detection,

•   To maximize the availability of the smart grid network in real-time by properly managing the users and providing updated and revocation phases.

To meet the abovementioned research objectives, in this paper, we proposed a Blockchain-based secure quantum key distribution and Intrusion Detection System in Edge Enabled Smart Grid Network (BLIDSE) model; we summarize our research contributions as;

•   Firstly, we proposed a lightweight block cipher algorithm for smart meters’ authentication, namely, Camellia cipher, which is in comparison with the Advanced Encryption Standard (AES) quite easier to use. It is a symmetric block cipher that provides better security compared to AES with an ultralow latency.

•   Secondly, we particularly forwarded the data from the smart meters using an encrypted format and for particularly that, the procedure of Camellia is put to use. Confidentiality of the data is being secured and protected against transmission is ensured by implementation of lightweight Camellia encryption as well as the key distribution problem is overcome by performing quantum key distribution in which the key is transmitted in the form of photon, thereby providing unconditional security.

•   Thirdly, we proposed a multi-constraints-based edge selection model which was presented for optimum selection to avoid any packet loss. The proper selection of edge nodes is carried out by performing a perfect matching algorithm that considers distance, load, makespan time, connectivity, delay and congestion, thereby facilitating reliable transmission of data. Here edge nodes are constructed into a hypergraph, and a perfect edge node is selected based on multiple constraints.

•   Fourthly, we proposed Bi-Fold IDS in which the D-DQN is used in sync with historical data and the classification of data is done based on the dynamic threshold is performed, which will detect the new attacks as it computes the threshold for normal data. The D-DQN is trained with historical data from which the received data will be checked and the classification of data based on the dynamic threshold is performed, thereby the false alarm rate associated with the physical failure of devices will be reduced resulting in precise ID’s. The training of the proposed D-DQN is carried out with comparatively low time consumption, thereby improving the proposed work’s performance. The proposed work provides security to the users through blockchain-based secure authentication and provides security as well as the integrity of the data by executing Bi-Fold IDS which is performed to mitigate the physical attacks.

Finally, the optimal user privacy management ID’s carried out by FBI optimizer solves the optimization problem involved in updation and revocation to improve the security and scalability of the smart grid network. In the final analysis, the performance of the BLIDSE model is analyzed and evaluated during experiments, and we proved that as an outcome, it is more significant than the earlier models.

This paper is organized as follows; Section 1: Literature of intrusion detection in smart grid network, and edge assisted energy management is discussed, while in Section 2: A background of research problems is summarized and discussed in related work section. In Section 3: A detailed discussion of the proposed BLIDSE model is discussed, while, in Section 4: An experimental analysis of the proposed model and the previous works are compared. Further, this particular section covers the performance evaluation and security analysis of the proposed model. Finally, in the Section 5: there is a conclusion of the paper by stating the future directions and aspects of the same.

2  Related Work

A multi-agent-based attack resilient system is presented for [13] protecting the integrity of a smart grid. The Multi-Agent System (MAS) was deployed in the substations to protect the system’s integrity. The data sources available for the MAS are physical measurements such as voltage magnitude, power injection, relative phase angle, power flow, brake status, and frequency of the system. This multi-agent system integrity protection method is suitable for accountability and confidentiality attacks where user authentication and data encryption is necessary. All the users in the network were first registered to the smart grid network, then the private key and public key for the user is generated and only the public key of the user is revealed during the transaction. The load balancing between two users was performed using blockchain and was found obtaining efficient load balancing with less energy consumption, but when the number of nodes increased, the efficiency degraded [14]. A multi-step attack detection model is presented [15] based on alerts of smart grid monitoring systems. The multi-step attack detection model based on alerts is not suitable for real-world scenarios in which there are many node failure reasons to raise an alert and it should not be considered as an attack.

In [16], the authors proposed detecting dynamic attacks in smart grids using a spiking delay feedback reservoir-based computing. The proposed attack detection approach implemented a spike in neural network for dynamic detection of attacks but it has major limitation of learning the data, which affects the accuracy of the approach. Authors in [17] proposed an approach to detect hidden electricity theft by exploiting multiple pricing schemes in smart grids. The purpose and possibilities of hidden electricity theft were addressed, and an optimization problem was proposed to increase the detection of these types of attacks, and two algorithms were designed to overcome these attacks. The vulnerabilities of the smart meters were demonstrated, and the detection of these intrusions was addressed [18]. The intrusion detection process involved two phases in which initially the abnormal behavior of the smart meters was observed by implementing the support vector machine, while the attack events were identified by generating the attack routes by temporal failure propagation graph (TFPG) technique.

A cyber-physical security model is presented in [19] for smart grids based on parameter correction against unbalanced false data injection attacks. Authors in [20] proposed a lightweight privacy-preserving Q learning-based energy management for the internet of things enabled smart grid. However, the Q learning model deployed for the lightweight privacy management is a reinforcement learning model which is efficient, but the optimal result will be made through the trial, and error method which will affect the performance of the smart grid network. In [21], the authors proposed, permissioned blockchain model for enhancing privacy in the smart grid network. The proposed model consists of three layers: super nodes, edge nodes, and intelligent contact layer.

Two authorization methods are involved in validating the edge nodes in the proposed system, such as identity authorization and convert channel authorization. To manage security, and privacy, a blockchain-based anonymous authentication. With key management is presented for smart grid edge computing infrastructure. Mostly, attackers use hardware for capturing-sensitive energy-related information. A lightweight mutual authentication-based PUF scheme is presented for addressing the insider attacks. The unique properties of PUF are considered for authentication.

Machine learning (ML) approaches are used for intrusion detection and mitigation to protect cloud-based enterprise solutions [22]. Using machine learning algorithms to predict, and distinguish the DDoS attack from normal traffic prediction, detection, and mitigation are fast and effective. In [23], a highly randomized tree-based scheme is presented for stealthy cyber-attack detection in the smart grid network. A secure load frequency control of smart grid using AES is presented in [24]. This method is based on comparing the obtained statistics of the state with that of the predicted future statistics. The statistical features selected for the comparison were mean, and standard deviation. Then, [25] Elliptical Curve Cryptography was implemented to ensure secure authentication of Home Area Network Gateway (HAN-GW) into the smart grid network. Particularly, these aspects have several drawbacks as follows: In [24], the model based data integrity method implemented AES encryption, a symmetric cryptography function that has a major issue of key distribution and management in large scale smart grid system.

The model-based data integrity method used public key encryption for the purpose of digital signature, but these methods are vulnerable to man-in-the-middle attacks, affecting the data integrity of the method. Also, it detects the attack by comparing the variation of statistics from the predicted statistics of the state; this causes unnecessary false alarms as the obtained values may vary due to other reasons. The lightweight authentication scheme as stated in [25], used elliptical curve cryptography which is an asymmetric key cryptography, and it posed as a limitation of increased computational complexity for resource smart meters. The parameters considered for the purpose of registration of the HAN-GW was not mentioned in the lightweight authentication scheme; this affects the integrity of the scheme. The updation and revocation of the same were not addressed by the lightweight authentication scheme which limited the use of this scheme in a real-time smart grid network.

3  BLIDSE Model

3.1 System Model

Fig. 1 represents the overall architecture model in edge enabled smart grid network. Firstly, a HAN model is discussed, consisting of several smart meters and other IoT-based devices, sensors, and actuators. Every smart meter is connected with the Internet, and protects its communication with each other. Further, smart meters’ authenticity, confidentiality, and integrity requirements are analyzed for improving their security strength. It is achieved by integrating blockchain technology with a lightweight block cipher algorithm without increasing the energy consumption of smart meters, and latency of the smart grid network. However, smart meters in the smart grid network is used to measure the energy consumption, and demand of the HAN in which all smart devices in the home is connected to the smart meter.

It demands the need for user authentication in which only authorized users can access the smart grid network and provide anonymity for legitimate users, and thus the privacy of smart meters is protected. Secondly, the measurements of energy consumption and demand of every HAN are collected by the control center to generate and distribute the power from various sources. The data gathered from the HANs are encrypted before being transmitted in order to improve the confidentiality of the data.

Thirdly, edge servers ES(i) are also authenticated to the blockchain to ensure data security in transmission. Therefore, an optimum ES(i) is selected by multi-criteria. Then, the control center receives data monitored in the HAN area and further precedes billing and power generation processes. Therefore, the received data must be a credible one without any suspicious code in it. The availability is one of the important factors in the smart grid network. The scalability and availability of the smart grid network are increased through the optimal management of user privacy. This is carried out by performing update and revocation of smart meters.

Figure 1: Proposed BLIDSE model architecture

3.2 Threat Model

Through the BLIDSE model, three kinds of attacks are considered for detection and mitigation in this research i.e., Man-in-the-Middle (MITM) attacks, Physical attacks, Insider attacks. The proposed BLIDSE model consists of five phases as blockchain-based secure user authentication via Quantum Key Distribution, Lightweight Data Encryption, Multi-constraint based Edge Selection, Bi-Fold Intrusion Detection System and Optimal User Privacy Management. Blockchain technology records all the network transactions, and the smart grid users check the validity of data.

All the transactions are stored in the blocks with the format of hashing which is not tampered by any attackers. The hash code is generated and received by Double SHA-256 hash function. Each block is connected with existing blocks. Smart grid network faces many security challenges for that we introduced blockchain in smart grid network which improves security. Blockchain has many benefits described as follows; Blockchain is a distributed ledger that supports multifactor verification that improves security. It avoids deploying the third party into the verification process network, thus reducing energy and cost.

Blockchain has four metrics such as block validation processing time, storage cost, transaction processing time and rate of hash.

(a) Block validation processing time: This metric is used to compute the block validation time which computes the difference between block validation beginning time and block validation ending time.

(b) Cost of Storage: This metric calculates the storage cost of the blockchain-based on data storage size. Storage cost for each block cycle is calculated as follows,

SC=CB×TB (1)

where, SC represents storage cost, and CB is a cycles of block, and TB represent time taken to create a new block.

(c) Processing time of Transaction: This metric evaluates the processing time of transactions, for that it calculates the time difference between the transaction starting time, and ending time which is defined as follows,

PT=2−CMC19562−inline−1 (2)

where, PT represent the processing time of transaction, and 2 represent transaction ending time, and CMC19562−inline−1 is a transaction starting time.

(d) Rate of hash: Hashrate is calculated based on the count of block cycles which is defined as follows,

RH=SBBT×NH (3)

where, RH represent the rate of hash, and SB represented the size of block, and BT represent processing time of block, and NH is a number of hash. Based on the procedure of blockchain, the complete smart grid based edge environment is working.

3.3 Blockchain-Based Secure User Authentication

Initially, the smart meter users (Ui)={U1,…,Un} are registered to the blockchain by using the parameters such as physically unclonable function (PUF), local time, and geographical location. Then the key for the meter is generated by the proposed Camellia encryption mechanism and is registered in the blockchain. After that the blockchain ID for the meter is provided. All the users (Ui) in the network are registered to the blockchain in which the details, and transactions of each node are stored in blocks. Once the user (Ui) is registered in the blockchain it will communicate by using its ID and its key is erased from its memory, by doing so, even when the node is compromised physically, the attacker cannot retrieve its key. This way, the register users (Ui) are capable to access the data. The registered users (Ui) are authenticated to enter, and access the data in the smart grid network. The secret key (SKi) is verified, and permits to access the smart grid. In case the verification is failed then the user does not allow to access the smart grid network. This provides the improved confidentiality and anonymous nature of the users in the smart grid network.

Fig. 2 represents the process of user authentication. Initially, the user registers their device PUF, location time, and geographical location to the blockchain. After completed registration, the blockchain generates secret key with the help of this formula, (SKi). This SKi={SKi,…,SKi} for providing security. SKi is shared via a quantum channel to enhance security, which can detect the presence of an attack or any third party try to gain the information of the key or data. The key distribution drawback of symmetric encryption is overcome by implementing QKD in which the key is distributed in terms of photon, and it is proved to provide unconditional security during the transmission of data. During authentication, the user validates the key and device ID; if it is verified then the user allows to access the smart grid network otherwise, the user will be avoided. The process of QKD is shown in Fig. 3

Figure 2: Blockchain-based user authentication

Figure 3: Process of QKD

3.4 Lightweight Data Encryption

The control center collects the energy consumption and demand of every home area network (HAN) to generate and distribute the power from various sources. The data generated from the HAN are encrypted before being transmitted to improve the integrity of the data. For this purpose, a lightweight symmetric encryption cipher named Camellia is used, which is as secure as the standard AES, and computes with ultralow latency. The encryption is done by using the (SKi), which is shared through the sequence of photons. Then the sender compares the emitters which have sent every photon. The photons collected from the wrong beam collector are discarded and collect only a specific sequence of bits.

This sequence of bits is used as key for encrypting the data. In this work, we consider the block length is 128 bits, and the key length is 128 bits. The encryption and decryption are done based on the secret key. The key is divided into two sub keys; each one has a 64-bit length. We consider two variables with the size of 128 bits, and four variables with the size of 64 bits, which is defined as follows,

kll=left bit of kl(64) (4)

klr=right bit of kl(64) (5)

krl=left bit of kr(64) (6)

krr=right bit of kr(64) (7)

This connection is determined for the length of the secret key k. For 128-bit length key consist

where, the four 128 bit length created the variables kl,kr,ka and kb that calculates all the sub keys which has 64 bit length kn, kwn, and kln. Sub keys are used for encryption, and decryption. In our work we generate the key with the length of 128 bits. Camellia algorithm includes five functions: S function, P function, F function, FL function, and FL−1 function. S function is placed inside the F function. The input key (64 bits) is replaced by other 8 bytes that return for further processing. The input is split into eight bytes I1,…,I8. I1 has 8 leftmost bits, and I8 have final rightmost bits. S blocks change the received bits into other bits. S function of the camellia is defined as follows,

J1=S1(I1),J2=S2(I2),J3=S3(I3),J4=S4(I4),J5=S5(I5),J6=S6(I6),J7=S7(I7),J8=S8 (8)

where J represents the output bits, and I represent the input bits. The next function is the P function which is also run inside the F function which also takes the input (8 bit), and modifies the input as like the S function. In p function performs the XOR function, which is defined as follows, J1=I1XORI3XORI4XORI6XORI7XORI8,...,J8=I1XORI4XORI5XORI6XORI7. The next function is the F function, one of the main functions in camellia used in encryption, and decryption during generating sub keys. The F function result is modified by the two functions S and P, which is defined as follows,

(I,kl)→(Il‖Ir,Ill‖Ilr)→Jl∣∣Jr (9)

Next function is the FL function which is performed during encryption and decryption, which is defined as follows,

(J,kl)→I→(Jl‖Jr,Jll‖Jlr)→Jl∣∣Jr (10)

Finally, the data is encrypted by using the camellia algorithm. The process of encryption and decryption of camellia is shown in Fig. 4. With the use of lightweight cipher, the energy consumption of smart meters is reduced. And also, it is a strong security algorithm.

Figure 4: Encryption and decryption block diagram of camellia

In the following, data encryption and decryption is discussed. After completing authentication, the user (Ui) data are encrypted by using SKi.

•   Step 1: Initially, Ui sends a request blockchain server for getting SKi.

•   Step 2: Blockchain server send a response to the user Ui to send their UserID that is encrypted by the proposed encryption method for verification.

•   Step 3: Ui sends the encrypted UserID using quantum method.

•   Step 4: Server decrypts the UserID using key which is obtained by quantum key distribution.

•   Step 5: If is it matched then the blockchain server ready to share SKi, using quantum method.

•   Step 6: During this process session key is generated by server that is used to encrypt the overall communication to provide confidentially of the data.

By doing so, the most prevailing attacks such as MITM, physical attacks, insider attacks, and eavesdropping are mitigated, hence the confidentiality of the data is ensured.

3.5 Multi-Constraint Based Edge Selection

When multiple edge nodes are presented in the smart grid network, there is a huge likelihood for smart meters that may reside in the coverage area of multiple edge nodes. Some characteristics inherit from the proposed architecture as follows.

•   Smart meters transmit measurements from HAN to the nearby ES(i), and it receives real-time data from the smart meters for processing, and storing of records.

•   Measure data from sensors, actuators and other devices collects information by ES(i) that stores and processes the collected data for further processing.

The HAN network transmits the data to the perfect edge server from the available number of server based on the parameters such as distance  d, makespan  m\raisebox{-2pt}{j}, load  CMC19562−inline−1, connectivity  C, congestion rate −1ptCMC19562−inline−2, delay  −3ptCMC19562−inline−3 in order to facilitate the proper transmission of data. A problem here is to search for optimum edge servers to the arrived data i.e., perfect matching over the HyperGraph. Furthermore, an optimum edge selection is considered the bipartite matching problem in which agents compute edges for data in bipartite matching theory for different parameters. This selection of optimal edge server is carried out by perfectly matching 2 algorithm in which the edge nodes are constructed as a hypergraph, and an optimal edge node is selected based on the condition. A hypergraph with perfect matching for edge selection is illustrated in Fig. 5.

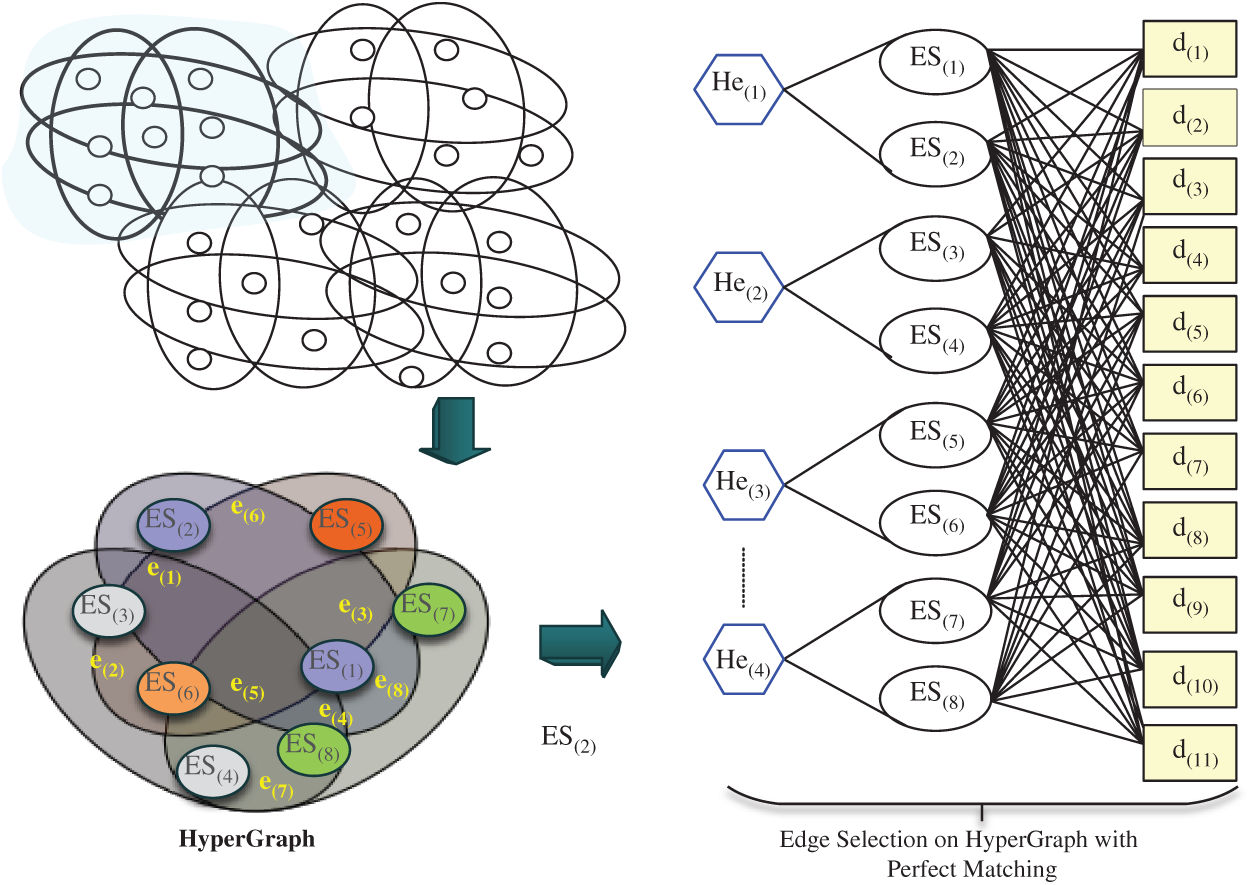
Figure 5: Hypergraph for edge node selection

HyperGraph Construction: In this study, we use a HyperGraph which is asymmetric to represents the relationship between data, and edge servers.

HG={v1,…,n,e1,…,e} (11)

where v1,…,n, and e1,…,e represent the vertices (edge servers), and weight values of edge servers, respectively. In this paper, a hypergraph is constructed by similarity among ES(i). Edges in the graph are connected from one node in the category to the other node in the same category. For that similarity, Si is computed between two edge servers.

A mathematical formulation of the above bipartite matching problem is represented by follows. X={x1,x2,…,xm} is the set of agents (edge servers) on one side, and Xi is the ith server i.e., i∈I={1,2,…,m}. Similarly, Y={y1,y2,…,ym} is the set of agents (data) on the other side where n≥m, and Yi is the ith data i.e., j∈J={1,2,…,n}. Here, ai is computed between Xi, and Yi, which is the matching aspiration that is determined by the multiple constraints of XiYi. Therefore, it is given by,

ai(Xi,Yi)=∑(i,j)∈Mw(i,j) (12)

where w(i,j) is the weighted score between edge servers and data. M represents the matching allocation for node pairs Xi and Yi. The maximum weight of edge servers are selected as the final solutions. Hence, the above equation is redefined by follows,

ai(Xi,Yi)=MAX∑(i,j)∈Mw(i,j) (13)

3.6 Bi-Fold IDS

In the control center, the received data are monitored to obtain each HAN’s energy consumption and further precede with billing and power generation processes. Therefore, the received data must be a credible one without any suspicious code in it. The false data injection attack is most commonly occurring in the smart grid network in which the smart meters are either compromised logically or physically, and the false data are manipulated with the original data before being transmitted to the control center. These types of attacks affect the performance of the power grid. To ensure that the received data is legitimate and doesn’t contains any false data. The Bi-Fold IDS is performed in which the packet flow based firewall is deployed which will drop all the irrelevant packets and this is performed based on the parameters such as source IP, destination IP, IP protocol, source port number, destination port number, APDU type, ASDU type, cause of transmission.

To ensure that the received data is legitimate and doesn’t contain any false data. The Bi-Fold IDS is performed in which the packet flow based firewall is deployed, which will drop all the irrelevant packets, and this is performed based on the parameters such as source IP, destination IP, IP protocol, source port number, destination port number, APDU type, ASDU type.

The next layer of IDS checks the integrity of the relevant message packets and classifies the data into three classes: normal, physical failure and attack. On both firewall features and packets are considered as F. The proposed Bi-Fold IDS as shown in Fig. 6 is executed by D-DQN in which the output of the first DQN is led into the processing of the second one, which is trained by the historical data, and a dynamic threshold value is generated form the trained data, which is used for the purpose of classification.

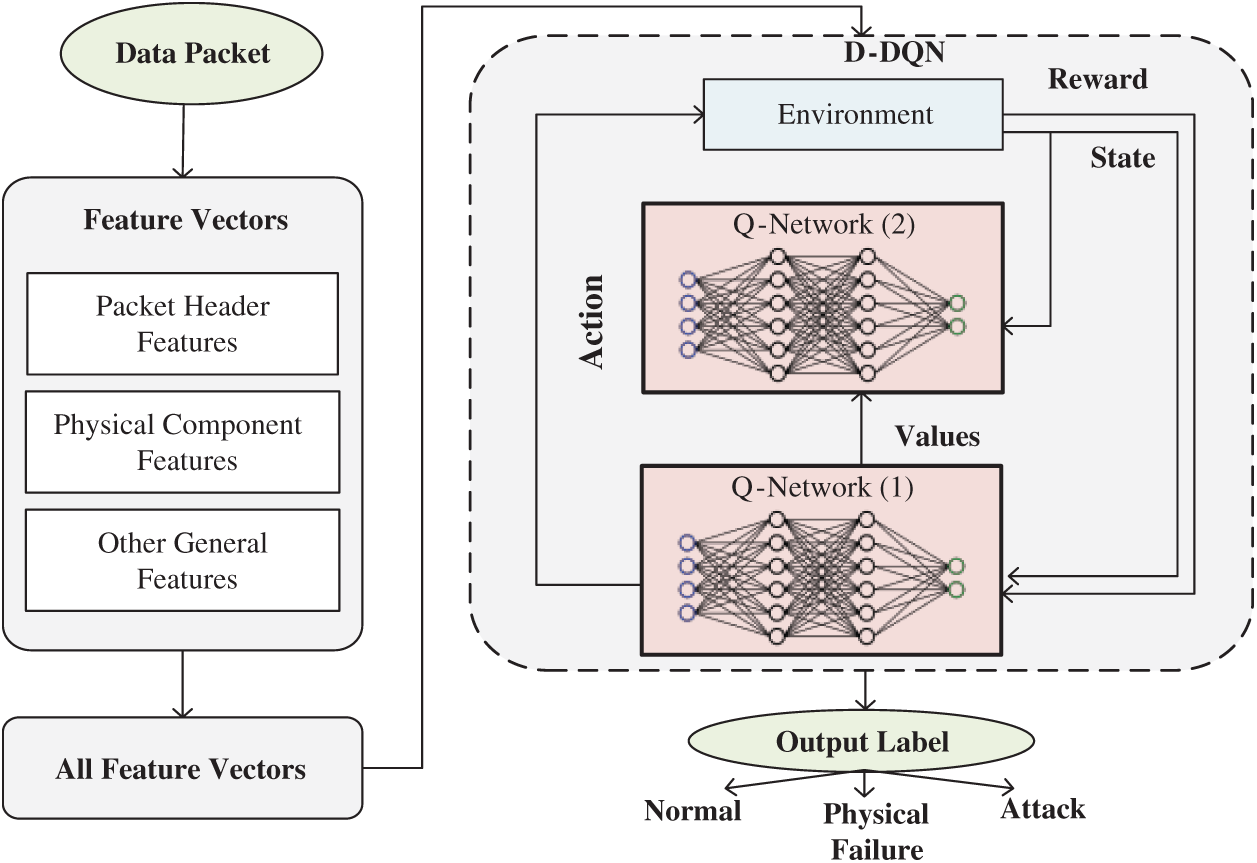
Figure 6: Double DQN for bi-fold IDS

D-DQN belongs to the Q-learning family, and it is the updated method that works similar to the Q-target of DQN as follows,

YtDQN=Nt+1+rmaxaQ(St+1,a,θt−) (14)

where θt− represents the integral Q-parameters and in single DQN accumulated i.e., optimized reward is not possible, larger than the actual value. To address this issue, double DQN is presented which selects the best action than DQN and the value of Q-target is computed as follows,

YtDQN=Nt+1+rQ(St+1argmaxaQ(St+1,a,θt)θt− (15)

For two different DQNs, θt and θt− are used. In D-DQN, mean μi and standard deviation σi of data packets are computed as follows,

μi=∑di=1nw(i)tjN (16)

σi=∑di=1n(witj−μ1(i))2N (17)

where w(i) is the weight value computed for all data packets for time interval tj. Based on the threshold values computation for the number of packets in D-DQN, the classification of abnormal behaviors are executed. It is defined by follows,

Bi−IDSC={1if D(i)=Class1(Attack)0if D(i)=Class2(Normal)−1if D(i)=Class3(Physical Failure) (18)

The algorithm for Bi-Fold IDS using Double DQN is given above. This algorithm is used to detect the abnormal packets transmitted from the smart meter is predicted. For temporal and spatial constraints between the packet, D-DQN learns the inputs and predicts the corresponding result. Through this process, the security of the smart grid network is ensured.

3.7 Optimal User Privacy Management

The availability is one of the important factors in the security; the scalability and availability of the smart grid network are increased by means through the optimal management of user privacy. This is carried out by performing updation and revocation of smart meters. The optimal updation and revocation is performed by implementing the Forensic Based Investigation optimization (FBI), which has improved convergence speed and convergence time than many other optimization algorithms. This algorithm has two phases such as investigation phase and the pursuit phase. The investigation phase investigates the suspected location. The investigation is executed if the user’s timeout for the key is attained or when the meter is suspicious.

In (L1), the new suspected location (SL1i) from SLi is assumed based on SLi and data that is related to the suspected locations. Every move is under the effect of other individuals. That is defined as follows,

where j = 1:d and d represent the dimension number, R and x represents the random integer in the range [−1, 1] and [0, 1], respectively. x1 represent the individual number that is affecting the movement of SLij.

{m,n,i}∈{1,2,…,NP} (19)

Eq. (19) represents the updated suspected location of SL1i. Where, m and n represent the randomly selected location, and i represent the current location, d and NP are the numbers of dimensions and number of locations for the suspect, respectively. In (L2), represent direct inquiry section. Pmin represent the minimum probability that is the minimum objective value, where, Pmax and SLmax are the maximum possibility and the optimal location, respectively.

Pb(SLi)=(Pmin−PSLi)/(Pmin−Pmax) (20)

Based on L1 and L2, the movement is defined as follows,

SL2i=SLmax+∑y=1x2xy×SLyix2∈{1,2,…,n−1} (21)

where, SLmax represent the optimal location and x2 represent individual number that affect the move of SL2i, y=1,2,…,x2,xb represent the effective coefficient of other individual to move with the range of [−1, 1]. The suspected location is updated by follows,

SL2ij=SLmax+SLdj+R5×(SLfj−SLej){d,e,f,i}∈{1,2,…,NP} (22)

where, SLmax represents the optimal location and R5 denotes the random value between zero and one, and d,e,f,i represent the four suspected locations.

In (M1) every Mi agent updates the position, which has the maximum value of the objectives. The new position is changed when it finds an optimal fitness compared to the previous one.

SM1ij=R6×SMij+R7×(SMmax−SMij)j=1,2,…,d (23)

where Smax represent the optimal location which is provided by the investigators, R7 and R8 represent the integer within the range [0, 1].

In (M2), every agent Mi coordinates with the other and Mi shift in the position of direction of the optimal location, The updated location of the agent is defined as follows,

SM2ij=SMrj+R8×(SMrj−SMij)+R9×(Smax−SMrj) (24)

SM2ij=SMij+R10×(SMij−SMrj)+R11×(Smax−SMij) (25)

where, Smax represent the optimal location. The revocation of the user is executed when the meter is found to be compromised or when a user wants to leave the network. All the updation and revocation are stored in the blockchain in the form of hashed values for further retrieval. The optimal management of users is necessary to improve the security in smart grid network.

The accuracy is an important factor in determining the intrusions of the smart grid system. The accuracy can be formulated as,

Accuracy=TrP+TrNTrP+TrN+FlP+FlN (26)

4  Experimental Result and Analysis

The experimentation of the proposed BLIDSE model is performed with extensive simulations. The simulation of the proposed BLIDSE model is carried out using NS 3.26. The validation of BLIDSE model is performed by creating a smart grid network of 1000 m×800 m consisting of number of smart meters, gateways and a control center. Initially, the smart meters are authenticated to improve the anonymity of the users. Then the data from smart meter are encrypted and then sent to the controller. In the controller side, the validation of packets is executed to ensure the security of the smart grid network. Fig. 7 illustrates the accuracy of the proposed BLIDSE models with other existing model like Blockchain-Based Anonymous Authentication with Key Management for Smart Grid Edge Computing Infrastructure (BAKM) [23] for the number of compromised meters. The accuracy in detecting the intrusions decreases gradually with an increase in the number of compromised meters.

The proposed BLIDSE model is found to have higher accuracy particularly; even when the number of compromised meters increases above 21 the accuracy is maintained with negligible reduction. This is due to the implementation of Bi-Fold IDS in which initially the firewall is deployed to filter the packets based on flow parameters, and further, the detection of intrusions is carried out by D-DQN packets are classified into three classes based on the dynamic threshold. This facilitates the accurate detection of both already occurred and new intrusions in the network. Once the meter is compromised, the FBI-based update and revocation are carried out to preserve the privacy of other users.

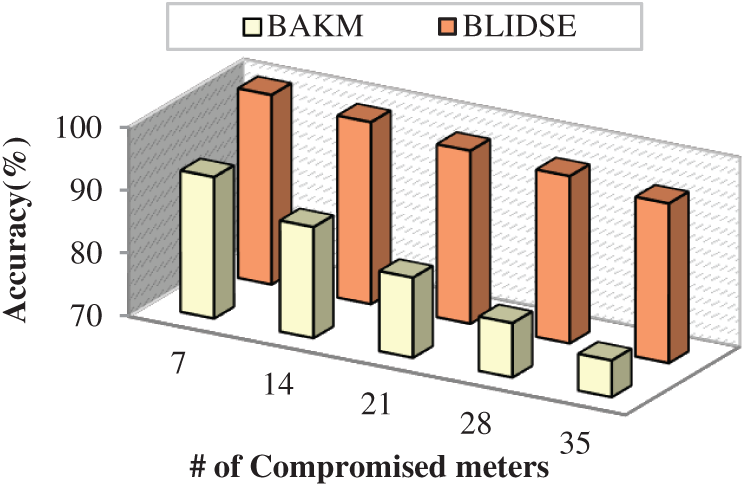
Figure 7: Number of compromised meters vs. accuracy

The accuracy of the proposed BLIDSE model is also compared with existing models for number of training samples, as shown in Fig. 8. The accuracy of intrusion detection increases with an increase in the number of training samples.

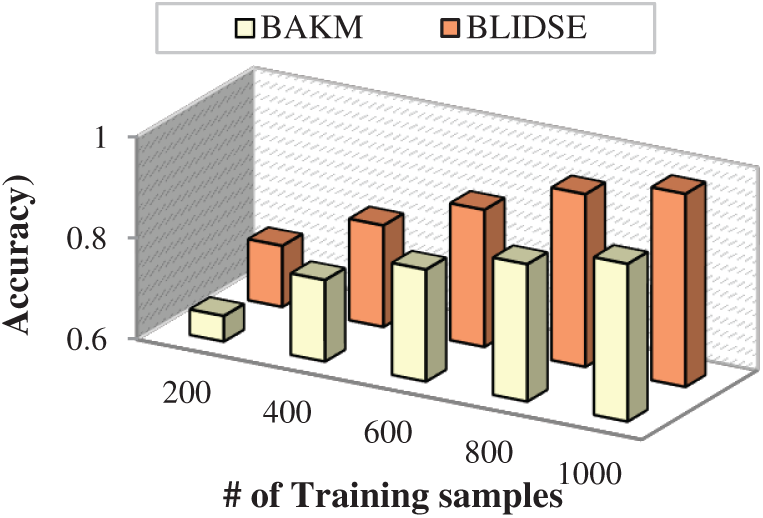
Figure 8: Number of training samples vs. accuracy

The proposed BLIDSE model is found to have high accuracy mainly. When the number of training samples is 1000, the accuracy in detection of intrusion reaches to about 100%, whereas the existing models have accuracy lesser than the proposed model. This is due to the variation of threshold in detecting normal, physical failure and attack packets based on the training samples. Through this, the accuracy of identifying the attack packets is achieved, thereby improving the integrity of the user data.

4.1 Impact of Computational Overhead

The computational overhead is referred to as the additional load that restricts the reliability of the smart grid network. The overhead in the network is due to the increased number of requests from the meters in a particular time. This is caused mainly due to inappropriate selection of edge nodes, which causes interference resulting in increased latency in the transmission of data. Fig. 9 depicts the computational overhead of the proposed BLIDSE model and other existing models for the number of smart meters in the network. The computational overhead increases with increase in the number of smart meters. The proposed BLIDSE model has less computational overhead compared to other model due to the execution of multi-constraint based edge selection. The optimal edge server is selected by constructing a hyper graph and implementing perfectly matching algorithm. The results in a reduced overhead of about 12 KB, whereas the existing approaches acquire overhead up to 20 KB when the number of meters is 100 leading to increased latency. Hence, the existing approaches possess less reliability in data transmission, which will not be suitable for smart grid networks.

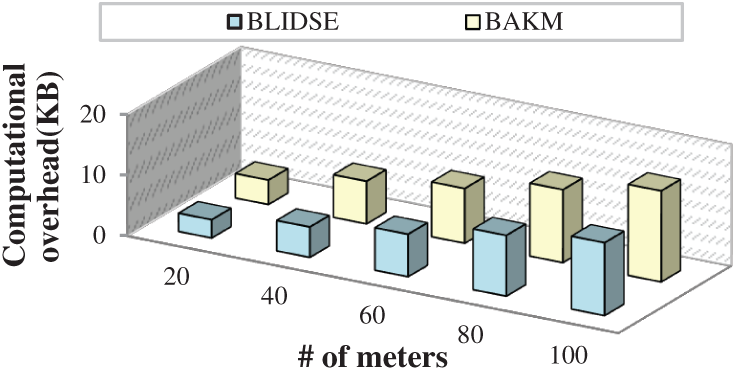
Figure 9: Number of meters vs. computational overhead

4.2 Impact of Attack Packets

The attack packets in the smart grid network are detected in order to achieve confidentiality, integrity and availability. The number of detected attack packets is a measure of accurate detection of intrusions in the network. The number of detected attack packets increases with increase in the time taken for detection. Fig. 10 presents the comparison of detected attack packets of BLIDSE model and other existing for detection time. When the detection time is 200 s, the BLIDSE, and BAKM [23] model detected 10 attack packets; similarly, when the detection time is 300 s, the BAKM detects only 12 packets, but the proposed BLIDSE model detected 15 attack packets. This proves the efficiency of the proposed BLIDSE model in identifying and detecting the attack packets. This characteristic of the BLIDSE model is due to the implementation of Bi-Fold IDS in which initially the firewall is used to filter the packets based on flow parameters; then the IDS is performed by D-DQN, which precisely classifies the attack packets based on a dynamic threshold.

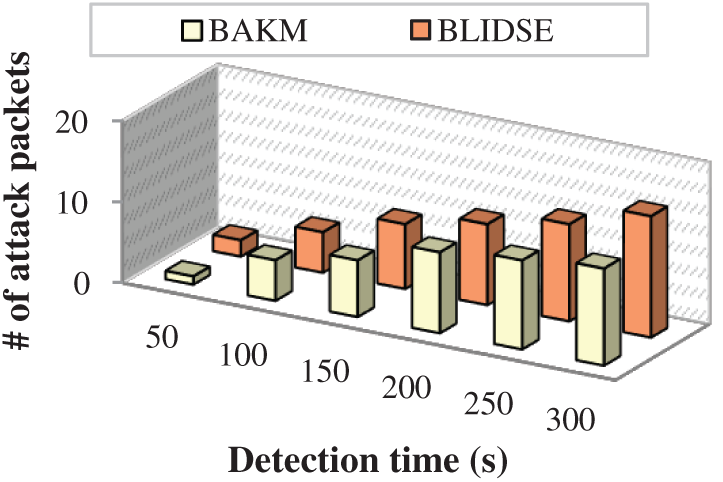
Figure 10: Detection time vs. number of attack packets

4.3 Impact of False Alarm Rate

The false alarm rate is a significant metric in assessing the efficiency of a model. The false alarm rate in the smart grid network is caused due to the inaccurate classification of packets into attack packets which causes unwanted revocation of smart meters from the network. Fig. 11 depicts the comparison of the proposed BLIDSE model’s false alarm rate with other existing model for number of packets. The false alarm rate gradually increases with an in the number of packets. The BLIDSE model is found to have a reduced false alarm rate than other existing models. From Fig. 11, when 800 packets are analyzed, the BLIDSE model produces a false alarm rate of 8, which is negligible, whereas the BAKM model produces a false alarm rate of 17, which affects the efficiency of those models. The BLIDSE model classifies the packets based on the dynamic threshold by considering the physical failures such as CPU overloading and RAM exhaustion which affects the normal pattern of the packets. The lack of consideration of these deviations results increased false alarm in the existing approaches.

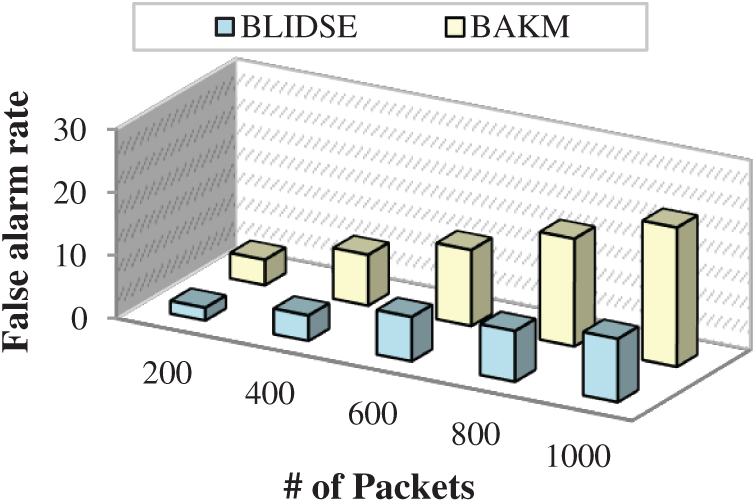
Figure 11: Number of packets vs. false alarm rate

4.4 Impact of False Detection

The false detection of intrusions is affected by the threshold by which it is determined. The purpose of the threshold is to act as a boundary above which the packets are termed as attack packets. The threshold must be set accordingly to detect the attack packets accurately. Fig. 12 presents the comparison of false detection of the proposed model and other existing models to a threshold value. The variation in the threshold to the optimal value reduces the false detection in the network. For instance, when the threshold value is 60, the false detection of the BLIDSE model is 14% but when the threshold value varies to 80, the false detection is also reduced to 10%. The existing models detected intrusions based on distance and other metrics which is inefficient as it doesn’t consider the spatial and temporal features.

Figure 12: Threshold vs. false detection

The comparison results of the proposed BLIDSE model in ensuring the security of the smart grid network is presented as a numerical representation in Tab. 1.

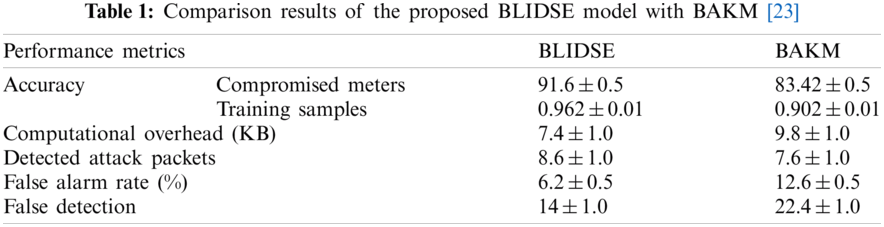
Due to the following reasons, the proposed BLIDSE model has obtained the better performance, and they are listed as follows,

•   The PUF based authentication of smart meters is carried out in which each node is authenticated in the blockchain, which mitigates insider attacks and physical attacks, thereby ensuring the anonymity of users. Previous works have presented centralized security mechanisms that do not resist security attackers.

•   The key generation is carried out by implementing camellia cryptography in order to improve the confidentiality of the data, and the limitation of symmetric key distribution is overcome by implementing QKD, thereby mitigating MITM attacks. The user’s anonymity is improved by performing blockchain-based secure user authentication by considering the factors such as PUF, geographical location, and local time.

•   The computational overhead of the smart grid network is reduced by optimally selecting the edge server, which is performed by using a perfectly matching theorem.

•   The intrusion detection is executed by using Bi-Fold IDS in which the firewall is implemented to filter the packets based on flow parameters and the D-DQN is used to classify the packets into three classes namely normal, physical failure and attack based on the dynamic threshold thereby increasing the accuracy and F1 score.

•   The updation and revocation of smart meters is executed by using FBI optimizer which ensures the data integrity and reduces false alarm rate in the smart grid network.

5  Conclusion

In this paper, the BLIDSE model is proposed for intrusion detection in edge enabled smart grid network. Our work solves the problems discussed in the above studies related to intrusion detection in smart grid networks. The proposed BLIDSE model mitigates MITM, physical, insider, and DDoS attacks in an effective manner, thereby contributing to improved security in the network. The main objective of this research is to provide security for smart grid networks. Blockchain-based secure user authentication is proposed to improve the network’s security. For this, we shared the secret key through the quantum channel during transmission. By using camellia, the user data is encrypted with the secret key, which improves the security and mitigates various attacks in the network such as MITM, insider attacks, and eavesdropping attacks. To achieve efficient transmission of data, we select the optimal edge server using a perfect matching algorithm. In this research, we perform two layers through Bi-Fold IDS, to improve the accuracy of the network. In the first level, the firewall is used to drop the irrelevant packets; in the second level of IDS, the integrity of the relevant message packets is checked, and the data is classified into three classes such as normal, physical error, and attack. For this we propose the DDQN algorithm, the D-DQN is used to classify the packets into three classes namely normal, physical failure and attack based on the dynamic threshold thereby increasing the accuracy and F1 score. Finally, user privacy is managed to improve security. The comparison results of the proposed BLIDSE model in ensuring the security of the smart grid network is presented as a numerical representation in Tab. 1. The performance of the proposed BLIDSE model is compared with the existing work BAKM [23] for validation purpose. The computational overhead of the smart grid network is reduced by optimally selecting the edge server, which is performed by using a perfectly matching theorem. This is done by updating and revoking the smart counters, which is done by the optimization algorithm of forensic investigation (FBI). The proposed model has been tested in NS 3.26 network simulator, and our work provides high security and detects intrusion in smart grid networks accurately. In the future, trust management in smart grid network will be further focused improving energy management's security and privacy. In addition, blockchain technology will be modified to reduce the energy consumption of smart meters.

Acknowledgement: The authors sincerely acknowledge the support from Majmaah University, Saudi Arabia for this research.

Funding Statement: The authors would like to thank the Deanship of Scientific Research at Majmaah University for supporting this work under Project Number No-R-2021-137.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  C. Peng, H. Sun, M. Yang and Y. Wang, “A survey on security communication and control for smart grids under malicious cyber-attacks,” IEEE Transactions on Systems, Man, and Cybernetics: Systems, vol. 49, no. 8, pp. 1554–1569, 2019. [Google Scholar]

 2.  X. Jiang, M. Liu, C. Yang, Y. Liu and R. Wang, “A blockchain-based authentication protocol for wlan mesh security access,” Computers, Materials & Continua, vol. 58, no. 1, pp. 45–59, 2019. [Google Scholar]

 3.  P. Kumar, Y. Lin, G. Bai, A. Paverd, J. Dong et al., “Smart grid metering networks: A survey on security, privacy and open research issues,” IEEE Communications Surveys & Tutorials, vol. 21, no. 3, pp. 2886–2927, 2019. [Google Scholar]

 4.  M. Z. Gunduz and R. Das, “Cyber-security on smart grid: Threats and potential solutions,” Computer Networks, vol. 169, pp. 107094, 2020. [Google Scholar]

 5.  F. Wei, Z. Wan and H. He, “Cyber-attack recovery strategy for smart grid based on deep reinforcement learning,” IEEE Transactions on Smart Grid, vol. 11, no. 3, pp. 2476–2486,2020, 2020. [Google Scholar]

 6.  W. Han and Y. Xiao, “Edge computing enabled non-technical loss fraud detection for big data security analytic in smart grid,” Journal of Ambient Intelligence and Humanized Computing, vol. 11, no. 4, pp. 1697–1708, 2020. [Google Scholar]

 7.  M. Ferrag and L. Maglaras, “DeepCoin: A novel deep learning and blockchain-based energy exchange framework for smart grids,” IEEE Transactions on Engineering Management, vol. 67, no. 4, pp. 1285–1297, 2020. [Google Scholar]

 8.  A. Jindal, G. Aujla, N. Kuma and M. Villari, “Guardian: Blockchain-based secure demand response management in smart grid system,” IEEE Transactions on Services Computing, vol. 13, no. 4, pp. 613–624, 2020. [Google Scholar]

 9.  Z. Ni and S. Paul, “A multistage game in smart grid security: A reinforcement learning solution,” IEEE Transactions on Neural Networks and Learning Systems, vol. 30, no. 9, pp. 2684–2695, 2019. [Google Scholar]

10. S. M. Taghavinejad, M. Taghavinejad, L. Shahmiri and M. Zavvar, “Intrusion detection in IoT-based smart grid using hybrid decision tree,” in 2020 6th Int. Conf. on Web Research, Tehran, Iran, University of Science and Culture, pp. 152–156, 2020. [Google Scholar]

11. P. I. Grammatikis, P. G. Sarigiannidis, G. Efstathopoulos and E. Panaousis, “ARIES: A novel multivariate intrusion detection system for smart grid,” Sensors, vol. 20, no. 18, pp. 5305, 2020. [Google Scholar]

12. E. Hossain, I. Khan, F. U. Noor, S. S. Sikander and M. S. Sunny, “Application of big data and machine learning in smart grid, and associated security concerns: A review,” IEEE Access, vol. 7, pp. 13960–13988, 2019. [Google Scholar]

13. P. Wang and M. Govindarasu, “Multi-agent based attack-resilient system integrity protection for smart grid,” IEEE Transactions on Smart Grid, vol. 11, no. 4, pp. 3447–3456, 2020. [Google Scholar]

14. R. Khalid, N. Javaid, A. S. Almogren, M. U. Javed, S. Javaid et al., “A blockchain-based load balancing in decentralized hybrid P2P energy trading market in smart grid,” IEEE Access, vol. 8, pp. 47047–47062, 2020. [Google Scholar]

15. H. Zhang, X. Jin, Y. Li, Z. Jiang, Y. Liang et al., “A multi-step attack detection model based on alerts of smart grid monitoring system,” IEEE Access, vol. 8, pp. 1031–1047, 2020. [Google Scholar]

16. K. Hamedani, L. Liu, S. Hu, J. Ashdown, JWu Wu et al., “Detecting dynamic attacks in smart grids using reservoir computing: A spiking delayed feedback reservoir based approach,” IEEE Transactions on Emerging Topics in Computational Intelligence, vol. 4, no. 3, pp. 253–264, 2020. [Google Scholar]

17. Y. Liu, T. Liu, H. Sun, K. Zhang and P. Liu, “Hidden electricity theft by exploiting multiple-pricing scheme in smart grids,” IEEE Transactions on Information Forensics and Security, vol. 15, pp. 2453–2468, 2020. [Google Scholar]

18. C. Sun, D. J. Cardenas, A. Hahn and C. Liu, “Intrusion detection for cybersecurity of smart meters,” IEEE Transactions on Smart Grid, vol. 12, no. 1, pp. 612–622, 2021. [Google Scholar]

19. T. Zou, A. Bretas, C. Ruben, S. Dhulipala and N. Bretas, “Smart grids cyber-physical security: Parameter correction model against unbalanced false data injection attacks,” Electric Power Systems Research, vol. 187, pp. 106490, 2020. [Google Scholar]

20. Z. Wang, Y. Liu, Z. Ma, X. Liu and J. Ma, “LiPSG: Lightweight privacy-preserving q-learning-based energy management for the IoT-enabled smart grid,” IEEE Internet of Things Journal, vol. 7, no. 5, pp. 3935–3947, 2020. [Google Scholar]

21. J. Wang, L. Wu, K. R. Choo and D. He, “Blockchain-based anonymous authentication with key management for smart grid edge computing infrastructure,” IEEE Transactions on Industrial Informatics, vol. 16, no. 3, pp. 1984–1992, 2020. [Google Scholar]

22. S. Mishra, S. K. Sharma and M. A. Alowaidi, “Multilayer self-defense system to protect enterprise cloud,” Computers, Materials & Continua, vol. 66, no. 1, pp. 71–85, 2021. [Google Scholar]

23. M. R. Acosta, S. Ahmed, C. E. Garcia and I. Koo, “Extremely randomized trees-based scheme for stealthy cyber-attack detection in smart grid networks,” IEEE Access, vol. 8, pp. 19921–19933, 2020. [Google Scholar]

24. H. Yang, S. Liu and C. Fang, “Model-based secure load frequency control of smart grids against data integrity attack,” IEEE Access, vol. 8, pp. 159672–159682, 2020. [Google Scholar]

25. D. Sadhukhan, S. Ray, M. S. Obaidat and M. Dasgupta, “A secure and privacy preserving lightweight authentication scheme for smart-grid communication using elliptic curve cryptography,” Journal of Systems Architecture, vol. 114, no. 11, pp. 101938, 2021. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.