DOI:10.32604/cmc.2022.019541

| Computers, Materials & Continua DOI:10.32604/cmc.2022.019541 |  |
| Article |
Fast Intra Mode Selection in HEVC Using Statistical Model
1Department of Computer Science & Engineering, HITEC University, Taxila, Pakistan
2L@BISEN, Equipe LSL, Yncrea Oust, 20 rue Cuirasse Bretagne, Brest, 29200, France
3Department of IT and CS, Pak-Austria Fachhochschule, Haripur, Pakistan
4Department of Electrical Engineering, Jouf University, Sakaka, KSA
*Corresponding Author: Junaid Tariq. Email: junaid.tariq@hitecuni.edu.pk
Received: 16 April 2021; Accepted: 31 May 2021
Abstract: Comprehension algorithms like High Efficiency Video Coding (HEVC) facilitates fast and efficient handling of multimedia contents. Such algorithms involve various computation modules that help to reduce the size of content but preserve the same subjective viewing quality. However, the brute-force behavior of HEVC is the biggest hurdle in the communication of multimedia content. Therefore, a novel method will be presented here to accelerate the encoding process of HEVC by making early intra mode decisions for the block. Normally, the HEVC applies 35 intra modes to every block of the frame and selects the best among them based on the RD-cost (rate-distortion). Firstly, the proposed work utilizes neighboring blocks to extract available information for the current block. Then this information is converted to the probability that tells which intra mode might be best in the current situation. The proposed model has a strong foundation as it is based on the probability rule-2 which says that the sum of probabilities of all outcomes should be 1. Moreover, it is also based on optimal stopping theory (OST). Therefore, the proposed model performs better than many existing OST and classical secretary-based models. The proposed algorithms expedited the encoding process by 30.22% of the HEVC with 1.35% Bjontegaard Delta Bit Rate (BD-BR).
Keywords: Statistical; HEVC; angular mode; reduce time
The founder of Facebook, Mark Zuckerberg, said that videos will play an important role in the future. According to online statistics, 100% of TV advertisements consist of video, around 80% of the businesses do marketing using video and 59% of the executives prefer learning from video than reading text. One more interesting fact is that around 1 billion hours of content are watched on YouTube and out of which 75% of the content is watched on mobile. This content is usually HD (High Definition) at 15–30 fps (Frames per Second) as it gives a realistic experience to the viewer. In order to support the availability of this content, the size of the video is reduced by applying compression algorithms. These compression algorithms reduce the size of the video with no loss in the subjective quality of the video.
A large number of compression standards exist and HEVC [1] is the latest among them. It is also known as H.265 and it uses 50% [2] less bits than the previous standard i.e., H.264. HEVC achieves this bit reduction by using big block sizes for smooth regions and small block sizes for the textured area of the frame. Then each of these blocks is either intra predicted (within a frame) or inter predicted (between frames) to achieve compression. In order to achieve the best possible compression, HEVC tries all the block sizes and predictions. This increased the complexity of HEVC and made it unfit of real-time situations. In order to handle this issue, fast algorithms are proposed for HEVC which reduces the computation time of encoding with negligible bit-rate overhead.
Before discussing the fast algorithm, let's understand the working of the HEVC to have some idea about various elements involved in the compression. For this purpose, we will use the HEVC test model (HM) software [3]. In order to compress the video, HM receives video frame by frame, and then it makes square blocks for each frame known as coding-tree-unit (CTU) or coding-unit (CU) of size 64 × 64 pixels. Then this CTU (biggest block in the frame) is predicted using intra technique, in which data from the current frame is used. The CTU can be predicted using inter technique, in which data from the previous frame is used. However, this paper will focus only on intra prediction. The Prediction Unit (PU) concept handles the prediction related data achieved for this CTU. This prediction for 64 × 64 pixels CTU has some RD (rate-distortion) cost associated with it. To see if a better RD cost is possible, the CTU is divided into 4 square blocks of equal sizes i.e., 32 × 32 pixels and the same prediction concept is applied on each 32 × 32 block. The sum of 4 RD costs will be compared with the RD cost of 64 × 64 block. The block size that gives the least RD cost is selected as the best. In HEVC, the block division does not stop at 32 × 32, and each of these 32 × 32 CU will be further divided into 4 blocks. This process will continue until the CU size becomes 8 × 8. Dividing the frames in recursive block structure and predicting the content for each block size makes HEVC very computationally extensive.
HEVC has many features [4], but this article will focus on intra technique [5] of HEVC. So far we have known the block structure of HEVC, and now we focus on intra prediction technique. The intra prediction uses the pixels of the above and left CU. These pixels are then copied on the area of the current block in order to predict it. This copying of pixels is carried out in 33 different ways that are called intra modes in HEVC. These intra modes are graphically shown in Fig. 1 [6]. Such a large number of intra modes tend to handle different type of textures present in the frame. In order to predict the smooth region, Planar and DC modes are proposed by HEVC. For example, in DC mode, the average of neighboring pixels is copied on the area of the current block. HEVC applies these modes on each block size and selects the mode that gives the least RD cost. No doubt this process will give us the least RD cost, but it will also result in huge complexity. Another shortcoming is found by the author is that due to small angle deviation among the modes; some modes give the same RD cost for the current block. This shows that applying all the intra modes will just result in complexity explosion and nothing else. To show the width of this problem, we have encoded the first 20 frames of two videos, Johnny_1280 × 720 and BasketballDrill_832 × 480. During this encoding experiment, we noted those blocks that have the same RD cost among their intra modes. The output of this experiment is graphically presented in Fig. 2. It can be observed that this problem is very common among all types of block sizes. Furthermore, it becomes worse in the case of 8 × 8 and 4 × 4 block sizes in which 30% and 50%, respectively, of the blocks, have the same RD cost among their intra modes.

Figure 1: Graphical representation of angular modes in HEVC

Figure 2: Blocks having the similar RD cost
The proposed work got motivated by the current trend and advancement in the field of computer vision. The statistical models proposed for computer vision improved the performance of many applications. The proposed work further explores the statistical foundation of optimal stopping theory and applies it in HEVC. In the proposed work, in order to utilize the available information in the prediction, the probability is incorporated based on the guidance-filter [7] concept. Such guidance not only efficiently alters the working of the algorithm but dynamically adjusts itself to the contents of the video. Some of the contributions of this article include:
I. A statistical model is proposed that is based on statistic's basic principle.
II. The model is simple and as a result, it requires less computation.
III. The performance of the proposed model is better than many existing classical secretary-based models.
This article is structured as related-works, motivation, proposed-model, and results are presented in Sections 2–5, respectively. In the end, the article is concluded in Section 6.
Literature is full of fast algorithms, and one reason behind the popularity of intra mode is that it is a very challenging area. Because one mode has to be selected from 35 modes. Hence, the probability of selecting the correct option is only 0.02%.
In [8], 30% of the encoding time is saved by the classical secretary problem-based algorithm. This work evaluates a minimum of two modes to compute the stopping point. In [9], the pixel values of the left and above block are used to decide the planar mode. This results in a 14% time reduction in the encoding process. Zhu et al. in [10] saved 16.1% of the encoding time. In this work, Hadamard transform is used instead of DCT. The author of [11] saved 28% of the time by proposing a model that performs intra modes selection in an iterative process. In each iteration, few intra modes are selected from the available pool (i.e., 35 modes). In [12], 60% time-saving is achieved. This work tries a sub-set of modes. Ying in [13] saved 38% of the time by proposing a model that utilizes RD as a stopping point. Zhang in [14] saved 38% of the time by proposing a model that consists of three phases. In [15], a model is proposed that utilizes the complexity of the block to form three groups. Yeh in [16] computes the RD cost using the co-located information. Then this RD cost is used to compute the stopping point.
In [17], the RDOQ module is customized. This work utilizes the coefficients of the transform to predict the RD cost. Around 63% of the time is saved by this work. Zhang in [18] perform intra prediction using the gradient of the block. In [19], Hu saved 55% of the time by proposing a regression-based algorithm. Tariq in [20] saved 35% of the time by proposing a stopping-theory based algorithm. In [21], Kuanar saved 45% of the time by using CNN to perform fast encoding of the multimedia content. Huang in [22] performed optimization of intra modes. According to Huang, this model can be utilized for an early decision of CU and PU. The time saving is around 66% on average. The author of [23] saved 58% of the time by using random-forest-based algorithm to perform fast encoding of the multimedia content. In [24], 52% time is saved. This work first applies the planar mode on the current block and then uses its result to perform the fast angular mode decision on the same block. Tian in [25] saved 20.45% of the time. This work utilizes the deviation among the pixels values of the current CU and selects the intra mode for the current CU. In [26], Gwon saved 31.54% of the time by proposing a model that uses a Hadamard-cost-based classifier. In [27], an uncertainty-based model is presented to achieve fast intra mode decisions. Therefore, it dynamically adjusts itself to various situations. In [28], Munagala enhanced the holoentropy of HEVC. As a result, the PSNR is approved compared to the original HEVC. Improvement in PSNR is directly related to the improvement in the subjective quality of the content. Therefore, this algorithm gives a realistic experience to the user. Liu in [29], proposed a method that accurately predicts the features from video sequences. This method helped in overcoming stability and quantity issues of feature matching techniques. More features mean more information and hence, such an algorithm gives a more accurate prediction. However, more features mean more computation. Therefore, only those features should be used that efficiently represent the original data. Bahce in [30], proposed a 3D-SPECK method for the encoding of geometry videos.
The proposed work, in comparison to the state-of-the-art works presented above, tries to extract information for the current CU. In the proposed work, the probability of each intra mode is found out using the modes of the neighboring CUs because neighboring CUs and current CU has a strong correlation. This correlation is due to the existence of symmetry in natural images. The proposed work uses these probabilities of the intra modes to find out the stopping point. This early stopping will help in reducing the complexity of HEVC. The probabilities of intra modes not only act as a guide, but also help in making efficient early decisions about the intra mode. No doubt, the probability is just simple information, but it is the most relevant information too.
This section will present the motivation of doing this research. Also, we will explain how our research got inspired by the ‘guided filter’ [7]. The most important concept of this filter is that it not only takes an input image, but also accepts a guidance image. This guidance image can be any natural image that will tell the filter to preserve the important information present in the input image. For example, the output image of the guided filter will contain an edge, if there is really an edge because it is guided by the guidance image. This means that if guidance is provided, we can efficiently early terminate the intra mode decision process.
The probability of any intra mode i ∈ 1, 2, …, 35 can be obtained by consulting the intra mode s of the neighboring CUs. If m1, m2, …, mN are the modes shortlisted for the current CU, then the probabilities of these modes can be obtained from the pre-computed matrix. Let pi denotes the probabilities of these shortlisted intra modes that are arranged in a list, and we have evaluated (seen) up to k elements of this list. Then by using the sum of probability rule, we get:
where N is the total number of intra modes for the current CU, p is the probability of a specific intra mode i, and k is the current intra mode that is evaluated for the current CU such that the value of k is [1, N).
The left side of (1) can be treated as a success while the other side as a failure. The simplest and efficient stopping point can be found when success becomes greater than failure. Consider the Tab. 1 data that contains 5 elements. To make an optimal decision, one has to evaluate/see all the 5 options. Another way is to consider any additional information that can guide us to the optimal decision in less time. Therefore, the probabilities (p) of each of these options are used that are also provided in Tab. 1. These probabilities guide us like what is the chance of selecting any particular mode. Moreover, if we know that the first option is selected 60% of the time, then these probabilities do make sense.

For example, consider Tab. 1 that has 5 elements and each of them has a probability of 0.2. Suppose we evaluated the first element (k = 1) but the question is that can we stop here? Even we know that the first option is best in 60% of the cases but we can't stop because it's a very risky decision. Look at it from another angle, the success of making the right decision is only 0.2 and the probability of making a wrong decision is 0.8, which is too high. Suppose we evaluated another option (k = 2), and this means that we have seen two elements so far and now we have some more idea about the situation. The probability of making the right decision now is increased to 0.4 and the probability of making a wrong decision has decreased to 0.6. Similarly, one can say that we should evaluate another option so that we can increase the chance of making the right decision. Therefore, for k = 3, the probability of making the right decision is 0.6 and the probability of making a wrong decision is 0.4.
Kindly note that different modes are selected for the CU in HEVC and therefore, their related probabilities will be different too. Hence, sometimes this 50% success or 0.5 probability can be achieved early and sometimes it can be delayed. This process is presented in Fig. 3 which shows that both the probabilities intersect at point 0.5. This is the neutral point that indicates a satisfactory level of success i.e., 50%. Moreover, this intersection point will change depending upon the values of the elements. For example, if the probability is large for early elements present in the list, then the intersection will occur early. However, if the probability is small for the early elements present in the list, then the intersection will occur late. Therefore, the authors argue that whenever an intersection is found, the intra mode decision process should be terminated. In the next section, three different examples will be used to present this intersection concept graphically. This will help in understanding the early and late occurrence of the intersection.

Figure 3: Success and failure concept
An algorithm will be presented in this section that will achieve fast intra mode decisions. As mentioned in the motivation section that the probabilities of intra mode can be used as guidance. This guidance (probability) will only give limited information like what is the likelihood of any particular mode to be selected. The probability of any intra mode S can be obtained if M is the mode of neighboring CU. This simply means that to save the count of M when modes were S. A 2D matrix can easily hold this information. This 2D matrix is shown in Fig. 4 for easy understanding. Fig. 4 shows that some modes have a high probability (big peaks in the figure) and some have less probability (small peaks in the figure). The issue is that less probability doesn't mean they are not selected and high probability doesn't mean they are always selected. That's why we have to evaluate elements until we reach a point the tells us a satisfactory number of elements have been seen.
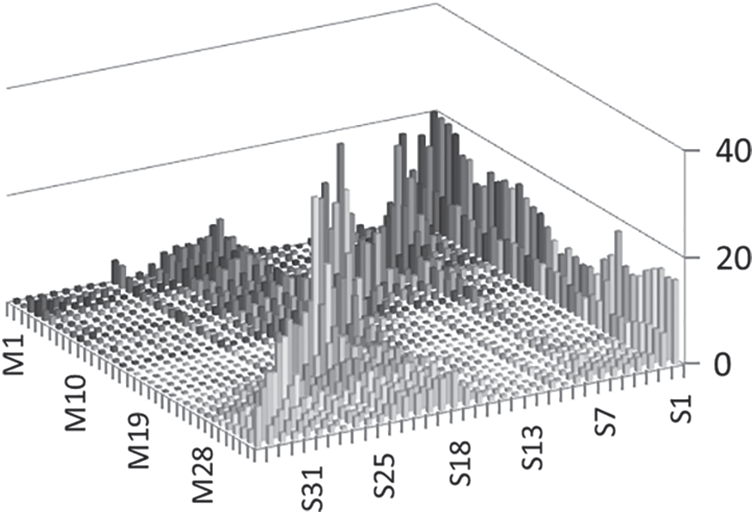
Figure 4: Probabilities of intra mode based on its neighboring blocks
In this section, the work mentioned in (1) and Fig. 3 will be extended. By extension, we mean that if the probability is high, then the intersection should take place early and if the probability is low, then the intersection should be delayed. A model with such a characteristic will be considered as a satisfactory contribution to the area of classical-secretary-problem and optimal-stopping-theory. In order to construct such a model, we take the help of the basic statistical formulation:
From (2), we can also get:
Using (4) in (3), we get:
Eq. (5) can be simplified to:
The simplification of (5) into (6) holds because the R.H.S of (5) is added by a big value i.e.,
Now this concept will be further explained with the help of examples and visual evidences. Denote the left side of (7) as L.H.S and the right side of (7) as R.H.S. Three examples are constructed that are shown in Tabs. 2–4. In these tables, p is the probability, L.H.S is the L.H.S of (7) and R.H.S is R.H.S of (7). The output of (7) for these examples, give in Tabs. 2–4, are graphically presented in Fig. 5. The first example given in Tab. 2 contains small values which indicate the probability is less or we are uncertain in this situation. The second example, given in Tab. 3, represents an intermediate situation in which probability is increased. In example 3, given in Tab. 4, the probabilities of early elements are set high to indicate that they have a high chance to be selected.




Figure 5: Three examples for concept clarification
The output of (7) is very interesting for these three aforementioned examples. Let's discuss the first example. The R.H.S of (7) is obtained by dividing the sum of probabilities i.e., 0.5 by the sum of probabilities up to the first element that is 0.1 in this case, and the answer is 5. The L.H.S is simply the addition of the sum of probabilities up to the first element plus 1.0, and we get 1.1. Similarly, the second value for Tab. 2 is obtained by dividing the sum of probabilities (0.5) by the sum of probabilities up to the second element i.e., 0.2 and the answer is 2.5 in this case. The L.H.S is simply the addition of 1 plus 0.2 and the answer is 1.2. The same process is repeated to obtain the remaining values. The visual result of this example is shown in Fig. 5a. Fig. 5a shows that the termination point, in this case, will be found at element 4. This delay in termination is due to the small probabilities of the elements.
Now we discuss the third example that is given in Tab. 4. The sum of probabilities, in this case, is 0.77 and when it is divided by the probability of the first element i.e., 0.4, the answer is 1.92. The L.H.S is simply the addition of 1 and 0.4, and the answer is 1.4 in this case. Similarly, the second value in Tab. 4 is obtained by dividing 0.77 by 0.6, and the answer is 1.28, and so on. Fig. 5c shows the visual output of this example. Fig. 5c shows that the termination is performed at element 2. This early termination is due to the high probabilities of the early elements in the list. Example-2 represents the intermediate case and the same procedure is applied to it. The output of example-2 is presented in Fig. 5b which shows that the termination is performed at element 3, because (7) has ≥ sign in it. These examples show that the proposed algorithm handles various situations efficiently and dynamically adjust itself according to the elements. Moreover, the formulation of this early termination model is very simple and as a result, it requires less computation. The flowchart of the proposed algorithm is shown in Fig. 6. The changes made to the RDO module are shown in the RDO box. For each CU, the RMD module calculates 35 intra modes and chooses N modes. Then the proposed algorithm evaluates the intra modes given by the RMD module one by one until it finds the termination point, i.e., the point found using (7).

Figure 6: Flowchart of the proposed algorithm
This section will present and discuss the encoding results of the proposed algorithm for HEVC. The limitation of this algorithm will also be presented with facts and figures. In the end, the comparison will be conducted with the existing algorithms. HM software, 16.0 version is downloaded from [3] and the proposed algorithm is implemented in it to obtain the encoding results. Following settings are used during the encoding process to make a fair comparison with existing algorithms: 4 QPs i.e., {22, 27, 32, and 37}, videos from A-F classes and All-Intra-Main configuration are selected as directed in [31]. Three performance matrices i.e., Time-saving (ΔT), BD-BR and BD-PSNR are used as directed in [32]. The ΔT is measured using:
5.1 Encoding Results of Probability Based Early Termination in HEVC
The results of the probability-based intra mode decision algorithm for the HEVC data set are presented in Tab. 5. Tab. 5 shows that the probability-based model saved 30% of the total encoding time and bit rate increment is only 1.35% on average. The probability model's time saving is due to its simplicity and guidance information. It is already discussed in the previous section that if a model does not provide real-time response then it is useless. This fast intra mode decision is a very good practical example of this situation. Secondly, the guidance has to be as useful as possible. The probability of intra mode is obtained in this work by using the neighboring intra mode's information. This allows the model to dynamically adjust itself based on the guidance. This adjustment means the movement of the intersection point presented in Fig. 5.

The two most important, relevant and recent intra mode decision algorithms [20,33] are implemented and test on the same platform. The output of these algorithms is also summarized in Tab. 6. The result of the proposed algorithm is also placed in Tab. 6 for easy comparison. Tab. 6 shows that [20] saves 29% of the encoding time, while [33] saves 20% of the total encoding time. Tab. 6 also shows that the proposed probability-based algorithm saves more time than the two aforementioned algorithms. Moreover, Tab. 6 shows that the proposed probability algorithm gives a satisfactory proportion between ΔT and ΔR.

Fig. 7 analyzes the proposed algorithm from another perspective. Fig. 7 presents the information that which intra modes are usually selected by proposed models, as it will give a unique working signature/behavior of the proposed algorithms. To make things interesting and comparative, Fig. 7 contains the results for the proposed algorithm, [20] (Tariq), [33] (Zhao) and [34] (FFA) algorithms. From Fig. 7, one can easily decide how and where an algorithm is saving time. Because if an algorithm picks early intra modes for the blocks as we see in the case of Tariq ([20]); then time-saving will be huge as its not evaluating lots of modes for the blocks and hence, bit-rate will be high. In contrast, if an algorithm tries many options (intra modes) for the blocks as we see in the case of Zhao ([33]); then time-saving will be marginal but the bit-rate increase will be minimal. Fig. 8 shows that the proposed probability algorithm saves time but selects the first option only 60% of the time, which is 10% less compared to FFA. But, the good thing about the probability model is that it evaluates less number of options than FFA to draw the stopping decision.
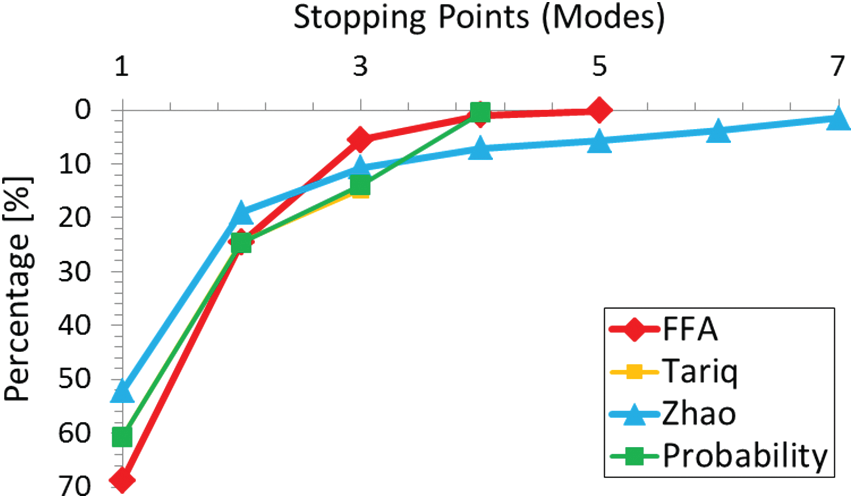
Figure 7: Histogram of stopping-points selected by various algorithms

Figure 8: Visual comparison between HEVC and the proposed algorithm. (a) HEVC output (b) Proposed output
Literature is full of fast intra algorithms. Out of which, some of the novel algorithms are presented in Tab. 7. Algorithms that were applied on both H.264 and HEVC (e.g., gradient algorithm) are presented only once. Also, algorithms that were combining CU/TU/PU/intra-mode are dropped and only intra mode focused algorithms are presented. As this will be unfair to compare intra mode time saving with the CU algorithm proposed for intra frame. Some articles claim huge time saving, that's why we conducted an experiment in which 1 intra mode per block (CU) is evaluated. The results of this experiment show that the total overall time saving of HEVC is 43.65%. Moreover, this experiment is conducted on the HM 16.9 version which is the latest version. Lastly, the bit-rate in such a case is too high to be acceptable for any publication. Therefore, the time saving reported by any article over 43% is a question mark.

Secondly, some articles are combining early CU, early PU, early TU, and early intra-mode algorithms. Such algorithms neither fall in the fast CU category, nor fall in fast intra mode decision. Therefore, we have proposed a fast intra mode decision algorithm and compared it with only fast intra mode decision algorithms. The term Prob in Tab. 7 represents the proposed algorithm. Tab. 7 shows that Prob gives a satisfactory proportion between the increase in ΔR and ΔT.
Finally, the reconstruction quality of the proposed algorithm is shown in Fig. 8. Fig. 8a shows the reconstruction quality of HEVC and Fig. 8b shows the reconstruction quality of the proposed algorithm. It can be seen in Fig. 8 that the picture obtained using HEVC is very smooth. Whereas the picture obtained using the proposed algorithm contains some rough/sharp edges at some places, but altogether, there is not much difference.
The intra mode computation procedure of HEVC is expedited by employing the guidance idea. The proposed algorithm proved that the algorithm that is light weight such as probability improves the performance of the fast algorithm and supports real-time applications. The proposed algorithm is applied to various statistics and HEVC examples, and its performance was satisfactory. The proposed algorithm solves the same problem as the existing works in the literature, but its methodology is very unique. Moreover, the proposed probability-based algorithm outperforms [34,38] that are the latest fast intra algorithms proposed to reduce the complexity of HEVC. In order to improve the time-saving of the proposed model, a threshold can be introduced in (7). This threshold will assign weight and as a result, it will accelerate the early termination process. Hence, will result in more time-saving
Acknowledgement: The authors acknowledge Dr. Junaid Ali Khan who did the proofreading of this paper.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. U. Kemal, K. Andersson, A. Fuldseth, G. Bjontegaard, L. P. Endresen et al., “High performance, low complexity video coding and the emerging HEVC standard,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 20, no. 12, pp. 1688–1697, 2010. [Google Scholar]
2. J. R. Ohm, G. J. Sullivan, H. Schwarz, T. K. Tan and T. Wiegand, “Comparison of the coding efficiency of video coding standards including high efficiency video coding (HEVC),” IEEE Transactions on Circuits and Systems for Video Technology, vol. 22, no. 12, pp. 1669–1684, 2012. [Google Scholar]
3. G. R. Ohm and G. J. Sullivan, HEVC Test Model, Heinrich Hertz Institute, Berlin, Germany. [Online]. Available: https://hevc.hhi.fraunhofer.de/svn/svn_HEVCSoftware. 2020. [Google Scholar]
4. J. Tariq, S. Kwong and H. Yuan, “Spatial/temporal motion consistency based MERGE mode early decision for HEVC,” Journal of Visual Communication and Image Representation, vol. 44, pp. 198–213, 2017. [Google Scholar]
5. J. Tariq, S. Kwong and H. Yuan, “HEVC intra mode selection based on rate distortion (RD) cost and sum of absolute difference (SAD),” Journal of Visual Communication and Image Representation, vol. 35, pp. 112–119, 2016. [Google Scholar]
6. M. Zhan, X. Zhai and Z. Liu, “Fast and adaptive mode decision and CU partition early termination algorithm for intra-prediction in HEVC,” EURASIP Journal on Image and Video Processing, vol. 1, pp. 1–11, 2017. [Google Scholar]
7. K. He, J. Sun and X. Tang, “Guided image filtering,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 35, no. 6, pp. 1397–1409, 2012. [Google Scholar]
8. J. Tariq, “Intra mode selection using classical secretary problem (CSP) in high efficiency video coding (HEVC),” Multimedia Tools and Applications, vol. 78, no. 22, pp. 31533–31555, 2019. [Google Scholar]
9. L. L. Wang and W. C. Siu, “Novel adaptive algorithm for intra prediction with compromised modes skipping and signaling processes in HEVC,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 23, no. 10, pp. 1686–1694, 2013. [Google Scholar]
10. J. Zhu, Z. Liu, D. Wang, Q. Han and Y. Song, “Fast prediction mode decision with hadamard transform based rate-distortion cost estimation for HEVC intra coding,” in 20th IEEE Int. Conf. on Image Processing, Melbourne, Australia, pp. 1977–1981, 2013. [Google Scholar]
11. L. Zhao, L. Zhang, S. Ma and D. Zhao, “Fast mode decision algorithm for intra prediction in HEVC,” in Visual Communications and Image Processing, vol. 1, pp. 1–4, 2011. [Google Scholar]
12. H. Zhang and Z. Ma, “Fast intra mode decision for high efficiency video coding (HEVC),” IEEE Transactions on Circuits and Systems for Video Technology, vol. 24, no. 4, pp. 660–668, 2014. [Google Scholar]
13. K. Y. Liao, J. F. Yang and M. T. Sun, “Rate-distortion cost estimation for H. 264/AVC,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 20, no. 1, pp. 38–49, 2010. [Google Scholar]
14. H. Zhang and Z. Ma, “Fast intra prediction for high efficiency video coding,” in Pacific-Rim Conf. on Multimedia, Berlin, Heidelberg, pp. 568–577, 2012. [Google Scholar]
15. P. Wang, C. Ni, G. Zhang and K. Li, “R-Lambda model based CTU-level rate control for intra frames in HEVC,” Multimedia Tools and Applications, vol. 78, no. 1, pp. 125–139, 2019. [Google Scholar]
16. C. H. Yeh, M. F. Li, M. J. Chen, M. C. Chi, X. X. Huang et al., “Fast mode decision algorithm through inter-view rate-distortion prediction for multiview video coding system,” IEEE Transactions on Industrial Informatics, vol. 10, no. 1, pp. 594–603, 2014. [Google Scholar]
17. Z. Sheng, D. Zhou, H. Sun and S. Goto, “Low-complexity rate-distortion optimization algorithms for HEVC intra prediction,” in Int. Conf. on Multimedia Modeling, Cham, pp. 541–552, 2014. [Google Scholar]
18. T. Zhang, M. T. Sun, D. Zhao and W. Gao, “Fast intra-mode and CU size decision for HEVC,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 27, no. 8, pp. 1714–1726, 2017. [Google Scholar]
19. Q. Hu, Z. Shi, X. Zhang and Z. Gao, “Fast HEVC intra mode decision based on logistic regression classification,” in IEEE Int. Symposium on Broadband Multimedia Systems and Broadcasting (BMSBNara, Japan, pp. 1–4, 2016. [Google Scholar]
20. J. Tariq and S. Kwong, “Adaptive stopping strategies for fast intra mode decision in HEVC,” Journal of Visual Communication and Image Representation, vol. 51, pp. 1–13, 2018. [Google Scholar]
21. S. Kuanar, K. R. Rao, M. Bilas and J. Bredow, “Adaptive CU mode selection in HEVC intra prediction: A deep learning approach,” Circuits, Systems, and Signal Processing, vol. 38, no. 11, pp. 5081–5102, 2019. [Google Scholar]
22. B. Huang, Z. Chen, Q. Cai, M. Zheng and D. Wu, “Rate-distortion-complexity optimized coding mode decision for HEVC,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 30, no. 3, pp. 795–809, 2019. [Google Scholar]
23. Z. Yan, S. Y. Cho and S. Welsen, “Fast intra prediction mode decision for HEVC using random forest,” in 2019 Int. Conf. on Image, Video and Signal Processing, Shanghai, China, pp. 45–49, 2019. [Google Scholar]
24. E. Hosseini, F. Pakdaman, M. R. Hashemi and M. Ghanbari, “A computationally scalable fast intra coding scheme for HEVC video encoder,” Multimedia Tools and Applications, vol. 78, no. 9, pp. 11607–11630, 2019. [Google Scholar]
25. R. Tian, Y. Zhang, M. Duan and X. Li, “Adaptive intra mode decision for HEVC based on texture characteristics and multiple reference lines,” Multimedia Tools and Applications, vol. 78, no. 1, pp. 289–310, 2019. [Google Scholar]
26. D. Gwon and H. Choi, “Relative SATD-based minimum risk Bayesian framework for fast intra decision of HEVC,” KSII Transactions on Internet and Information Systems (TIIS), vol. 13, no. 1, pp. 385–405, 2019. [Google Scholar]
27. J. Tariq, “High-performance intra-mode accelerator for HEVC,” The Visual Computer, vol. 35, no. 10, pp. 1–15, 2019. [Google Scholar]
28. V. Munagala and S. Kodati, “Enhanced holoentropy-based encoding via whale optimization for highly efficient video coding,” Visual Computer, vol. 36, no.10, pp. 1–22, 2020. [Google Scholar]
29. H. Liu, S. Tang and D. Lei, “Accurate estimation of feature points based on individual projective plane in video sequence,” Visual Computer, vol. 36, no. 10, pp. 2091–2103, 2020. [Google Scholar]
30. C. G. Bahce and U. Bayazit, “Compression of geometry videos by 3D-sPECK wavelet coder,” Visual Computer, vol. 36, no. 5, pp. 1–19, 2020. [Google Scholar]
31. F. Bossen, “Common test conditions and software reference configurations,” in Joint Collaborative Team on Video Coding (JCT-VCJCTVC-F900, Redmond, WA 98052 USA, vol. 1, 2011. [Google Scholar]
32. G. Bjontegaard, “Calculation of average PSNR differences between RD-curves,” in Video Coding Experts Group (VCEGThirteenth Meeting, Austin, Texas, USA, vol. 1, 2001. [Google Scholar]
33. T. Zhao, S. Kwong, H. Wang and C. C. J. Kuo, “H. 264/SVC mode decision based on optimal stopping theory,” IEEE Transactions on Image Processing, vol. 21, no. 5, pp. 2607–2618, 2012. [Google Scholar]
34. J. Tariq, A. Armghan, A. Ijaz and I. Ashraf, “Pure intra mode decision in HEVC using optimized firefly algorithm,” Journal of Visual Communication and Image Representation, vol. 68, no. 1, pp. 102766, 2020. [Google Scholar]
35. J. Tariq, “RD-Cost as statistical inference for early intra mode decision in HEVC,” Multimedia Tools and Applications, vol. 78, no. 12, pp. 16783–16801, 2019. [Google Scholar]
36. J. Tariq and S. Kwong, “Efficient intra and most probable mode (MPM) selection based on statistical texture features,” in 2015 IEEE Int. Conf. on Systems, Man, and Cybernetics (SMCKowloon, Hong Kong, pp. 1776–1781, 2015. [Google Scholar]
37. J. Tariq and S. Kwong, “Hybrid fast intra mode decision and early termination of prediction unit (PU) splitting for HEVC,” in 2015 IEEE Int. Conf. on Systems, Man, and Cybernetics (SMCKowloon Tong, Hong Kong, pp. 1782–1786, 2015. [Google Scholar]
38. W. Si, Q. Zhang, Z. Shi, B. Wang, T. Yan et al., “A fast mode decision algorithm for intra prediction in high efficiency video coding,” Journal of Medical Imaging and Health Informatics, vol. 10, no. 2, pp. 496–501, 2020. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |