DOI:10.32604/cmc.2022.019448

| Computers, Materials & Continua DOI:10.32604/cmc.2022.019448 |  |
| Article |
Deep Reinforcement Learning Model for Blood Bank Vehicle Routing Multi-Objective Optimization
1Director of Advanced Manufacturing and Industry 4.0 Center, King Abdul-Aziz City for Science and Technology Riyadh, Saudi Arabia
2Data Science and AI Senior Manager Vodafone, Cairo, Egypt
3Information System Department, Al Imam Mohammad Ibn Saud Islamic University, Riyadh, Saudi Arabia
*Corresponding Author: Meteb M. Altaf. Email: maltaf@kacst.edu.sa
Received: 14 April 2021; Accepted: 25 June 2021
Abstract: The overall healthcare system has been prioritized within development top lists worldwide. Since many national populations are aging, combined with the availability of sophisticated medical treatments, healthcare expenditures are rapidly growing. Blood banks are a major component of any healthcare system, which store and provide the blood products needed for organ transplants, emergency medical treatments, and routine surgeries. Timely delivery of blood products is vital, especially in emergency settings. Hence, blood delivery process parameters such as safety and speed have received attention in the literature, as well as other parameters such as delivery cost. In this paper, delivery time and cost are modeled mathematically and marked as objective functions requiring simultaneous optimization. A solution is proposed based on Deep Reinforcement Learning (DRL) to address the formulated delivery functions as Multi-objective Optimization Problems (MOPs). The basic concept of the solution is to decompose the MOP into a scalar optimization sub-problems set, where each one of these sub-problems is modeled as a separate Neural Network (NN). The overall model parameters for each sub-problem are optimized based on a neighborhood parameter transfer and DRL training algorithm. The optimization step for the sub-problems is undertaken collaboratively to optimize the overall model. Pareto-optimal solutions can be directly obtained using the trained NN. Specifically, the multi-objective blood bank delivery problem is addressed in this research. One major technical advantage of this approach is that once the trained model is available, it can be scaled without the need for model retraining. The scoring can be obtained directly using a straightforward computation of the NN layers in a limited time. The proposed technique provides a set of technical strength points such as the ability to generalize and solve rapidly compared to other multi-objective optimization methods. The model was trained and tested on 5 major hospitals in Saudi Arabia’s Riyadh region, and the simulation results indicated that time and cost decreased by 35% and 30%, respectively. In particular, the proposed model outperformed other state-of-the-art MOP solutions such as Genetic Algorithms and Simulated Annealing.
Keywords: Optimization; blood bank; deep neural network; reinforcement learning; blood centers; multi-objective optimization
Logistics costs and consumed time are major challenges in both the private and public sectors. Therefore, lowering the cost of logistics and operations, as well as maximizing time efficiency, is a priority. The key performance indicators of blood banks are the location besides distribution decisions based on their logistic network [1]. For decades, logistics specialists have examined location-routing problems that embrace location and routing decisions [2]. Delays in the delivery of blood products can directly influence population health and even lead to deaths [2].
There are several terminologies relating to blood transfer. A “Blood Establishment” is defined as an organization that leads or engages in actions such as the collection, testing, processing, storage, and distribution of human blood or blood components (excluding hospitals) when it is intended for transfusion [3]. Meanwhile, a “Hospital Blood Bank” is defined as an entity that stores, executes compatibility testing, and issues human blood or its components for exclusive internal usage [4]. There are different models for blood bank organization [4]. One common model of development is a centralized national blood supplier, in which all steps toward blood supply provision are performed by one central organization. Examples of this model include Canadian Blood Services (CBS) and Hema Quebec (HC), for which all blood products in Canada are collected by CBS-HC. An alternative model is “hospital-based”, which exists commonly in many countries and allows for the collection process to occur within hospitals. Also, it permits the entire vein-to-vein transfusion chain to be completed on hospital premises.
In the Kingdom of Saudi Arabia (KSA), a large proportion of the country’s blood collection and manufacturing activities occur under the hospital-based model. At the same time, the country has a limited number of regional blood banks that are managed and operated by the Ministry of Health (MOH), which are not attached to specific hospitals. In the KSA, the blood bank logistics system consists of hospital centers and regional blood centers. All centers are responsible for blood testing, blood donation processes, and 1-to-1 transfusion. The whole blood is separated into three blood products: erythrocytes, platelets, and plasma. The requested products are saved or transported to hospitals using vehicles [4,5]. In previous research works, location and routing problems are typically solved together, but some researchers divide the problem into two sub-problems. Although total delivery cost is a major concern, it is also true that in some cases, especially in the health sector, cost optimization is not the priority.
In this work, routing time and cost are minimized simultaneously using a mathematical programming model, which is applied for both regional and hospital blood banks using Deep Reinforcement Learning (DRL). Multi-objective Optimization Problems (MOPs) appear frequently in the real world when the aim is to optimize two or more objective functions simultaneously. An MOP can be formulated as follows:
where F(x) consists of (n) different objective functions and (X) is a d-dimensional vector of decision variables. Since the (n) objective functions are not guaranteed to be free from conflict, a set of trade-off solutions known as Pareto-optimal (PO) solutions is defined as a compromising solution.
In recent decades, Multi-objective Evolutionary Algorithms (MOEAs) have shown superiority in solving MOPs. This superiority derives from their ability to obtain a set of solutions in a single run. The two most common MOEAs are NSGA-II and MOEA/D [6–8], both of which have been implemented and applied in many practical problems. Moreover, multiple handcrafted heuristics have been addressed, including the Lin–Kernighan heuristic and the 2-opt local search [9]. Other methods have been implemented to solve MOTSP such as Pareto local search, multi-objective genetic local search, and other close variations [10]. In the previous decade, Deep Neural Networks (DNNs) emerged as one of the leading machine learning methods, especially in computer vision. DNNs generally concentrate on making predictions, whereas DRL is typically exploited to learn decision-making. Consequently, DRL is a potential methodology for learning how to solve different optimization problems without human intervention or pre-determined input heuristics or strategies.
In this research, the possibility of exploiting DRL to solve MOPs for the blood bank vehicle routing problem is addressed. The optimal set of solutions can be obtained directly using a forward calculation pass through a trained Neural Network (NN). The NN model is trained using DRL error and can be perceived as a heuristic approach.
The main contributions of this research can be summarized as follows:
— The research proposes a mathematical model that expresses the blood transfer process in the KSA. The problem can be modeled as an MOP with two objective functions to minimize: namely, time and cost.
— The research devises a DRL-based solution with superior characteristics in terms of efficiency, generalization ability, and the lack of a need for retraining.
The rest of this paper is organized as follows: Section 2 introduces related work; Section 3 offers the problem statement; Section 4 shows the mathematical model formulation; Section 5 describes the proposed solution; and Section 6 presents the discussion, study summary, and considers future work.
Researchers have addressed location-routing problems using both exact and heuristic approaches. One study examined problems involving capacity constraints and proposed a branch and price method as a solution [11]. Alumur et al. [12] proposed a solution for the problem of locating and routing waste, where the model defined two objective functions. The solution relied on a mixed-integer approach and was applied for 92 nodes. Boyer et al. [13] introduced a model with two objectives: total cost minimization and transportation risk. Both objective functions were supposed to be minimized. The model was tested in Markazi province in Iran. Ceselli et al. [14] proposed a “branch and price and cut” solution that considered prices, strengthening cuts, distribution, and generalized location heuristics. Practically, exact deterministic solutions are most likely intended to address problems of medium-scale instances due to the intensive requirements in terms of computation resources. Consequently, a set of studies have adopted heuristic methods [15–17]. Duhamel et al. [18] proposed a platform for fleet assignment and routing based on greedy randomized adaptive search approach hybridized with evolutionary local search. Doulabi et al. [19] introduced a mixed-integer programming model for a location problem and also proposed an algorithm based on a heuristic approach within simulated annealing.
Some researchers have addressed the location and routing problem for blood centers specifically, proposing recommendations for the optimal locations and counts of blood centers. Jafarkhan et al. [20] conducted a study in Chicago to ensure hospital demand was satisfied. The problem was divided into two sub-problems due to its complexity. Price et al. [21] proposed a model for blood donation location; the researchers considered Virginia blood products for all phases such as collection process, blood testing, and distribution. The distribution model was studied and they proposed two models to improve the results. The first model targeted the minimization of the distance between blood collecting positions and the blood bank itself. Meanwhile, the second model addressed the minimization of the distance between the blood bank and the demanding hospital minimize. Recently, Wang et al. [22] proposed a heuristic algorithm to solve a fresh food location-routing problem, where carbon emissions were considered in the model as an objective to be minimized. Also, Eskandari-Khanghahia et al. [2] focused their study on the blood supply chain, in which they examined inventory, routing, and location problems. The authors developed simulated annealing and harmony as an algorithm to resolve the larger instances. Obviously, the use of heuristics and handcrafted rules can improve performance and results. Meanwhile, progressive advances in machine learning have demonstrated their ability to replace handcrafted subjective features in solving diverse problems. For example, Convolution Neural Networks (CNNs) have shown superiority compared to engineered features in computer vision research and practice. While deep learning techniques concentrate on prediction making, Deep Reinforcement Learning (DRL) is basically exploited to capture and learn how to engage in decision-making. Consequently, in this work, we are confident that DRL is a potential candidate that will be effective in solving different optimization problems without any intervention.
This paper examines the potential of DRL to solve Multi-objective Optimization Problems (MOPs) in general and, more specifically, in blood location and routing problems. The optimal settings can be obtained explicitly using a forward propagation for the pre-trained network. Training the network model is performed using a trial and error process of DRL and can be regarded as a black-box heuristic and a meta-rule-based system associated with credible heuristics. Due to the exploratory properties of the DRL training process, the output model should have proven generalization capabilities. In particular, it should have the ability to resolve instances of the problem that have not been seen before. This work is fundamentally inspired by recent solutions based on the neural network single-objective Traveling Salesman Problem (TSP), which begins by proposing a pointer network that uses an attention mechanism to forecast permutations of the cities. Accordingly, the model is trained in a supervised way that demands large TSP instances and the corresponding optimal solutions. These instances and the corresponding optimal solution represent the training dataset. Unfortunately, the supervised training procedure exhibits the model from achieving better solutions than the exposed in the training set. To avoid this problem, Bello et al. [23] proposed and developed an actor-critic DRL training algorithm to train the pointer network while eliminating the need to provide optimal solutions. Nazari et al. [24] proposed a simplified model and considered dynamic elements input to expand the model to propose solutions for the vehicle-routing problem.
In this study, a new system is proposed to address the issues that are associated with the centralized structure. Normally, a subset of hospitals in a specific district or region are labeled as a “Distribution Center”. These represent the additional layer between “Regional Blood Center” and the hospitals that distribute blood products. The model finds a solution for the optimal number and location of distribution centers (see Fig. 1 below) and it optimizes the routes (RBC to DC and DC to hospitals).
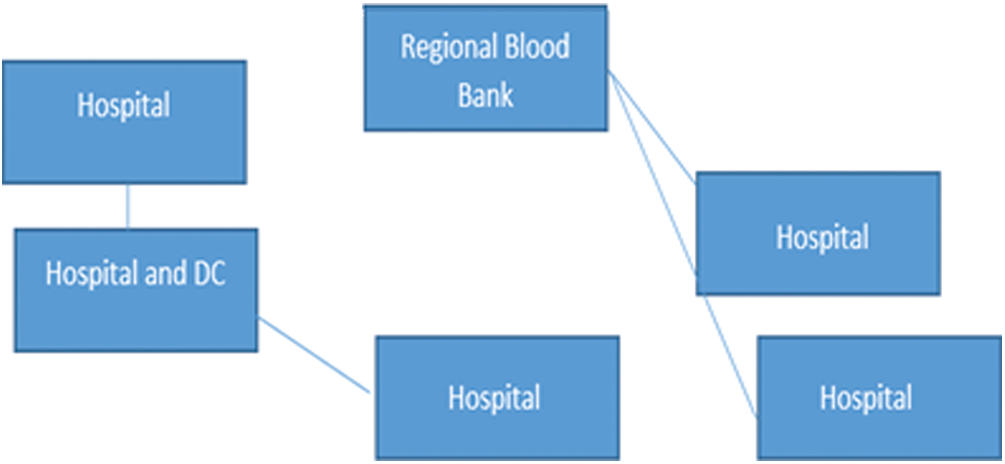
Figure 1: DC location assigning
In this research, the following assumptions are considered:
• One RCB is considered and has zero opening cost
• No existing constraints inhibit any hospital or RBC from being authorized as DC
• Expenses are well-known and defined for 10 years
• The launch date is at the year head
• In the first model, the problem is regarded as a multi-level one: (RBC to DC) and (DC to hospitals)
• The second model is regarded as a single-level one: (DC to the hospitals)
• The deterministic nature of hospitals’ blood needs is well-established
• Free restriction number of DCs
• The distribution vehicles have upper-limit capacities for each blood product type
• Every DC has a transfer once per week from RBC, while every hospital receives three deliveries per week from DC.
As mentioned earlier, the problem is reformulated into two problems due to its complexity. The first one involves optimizing the average distances between (RBC and DC) and (DC and hospitals). Meanwhile, the second problem addresses the minimization of the transportation costs between (DC and hospitals). For convenience, the notations used in the problem modeling are shown in Tab. 1.
Also, a decision variable (Y_j) takes a value of 1 if DC is at point (j), whereas a decision variable (X_ij) equals 1 if hospital (i) is assigned to DC (j). A decision variable (Zijk) will be 1 if vehicle (k) travels from (i) to (j) and 0 otherwise. Vk is a decision variable that is set to 1 when vehicle (k) is used, and Tipk is set to 1 when blood product (p) is distributed by hospital (i) using vehicle (k). The complete model for the cost minimization problem can be formulated as follows:
Minimize:
Subject to:
Constraint (3) ensures that each hospital is mapped to a single DC no more, and constraint (4) delimits the budget for a new DC. Constraint (5) ensures that the distance between DC and the hospitals is delimited by the maximum distance parameter. The last constraint (6) states that every hospital must be assigned to itself in case a DC opens in that hospital. On the other hand, the model for the routing problem can be formulated as follows:
Minimize:
Subject to:
The second objective function (8) aims to minimize both the annual operating expenses of the vehicles and the cost of the demand-weighted distances between DC and the hospitals. Constraint (9) emphasizes the total product need in the vehicle, which is bounded by the vehicle capacity parameter. Constraint (10) ensures that the vehicle’s start and end points are the same. The final constraint illustrates that product (p) is delivered to the hospital by the vehicle only if the hospital is on the route from DC to the hospital.
In this work, a Deep Reinforcement Learning (DRL)-based model is proposed to solve Multi-objective Optimization Problems (MOPs). The research methodology defines the solution in two stages:
1. Introduce a “decomposition strategy” to split the MOP into a set of sub-problems, each of which is modeled as a DNN.
2. Optimize and tune the set of these sub-problems’ model parameters in a collaborative way based on the neighborhood parameter transfer strategy.
In the decomposition phase, the idea of decomposing a problem is a reliable method to analyze and solve an MOP. Specifically, the overall blood donation routing problem is explicitly decomposed into a group of scalar sub-problems and solved using a collaborative methodology. Finding the optimization sub-problems tends to guide toward a Pareto-optimal (PO) solution. Many approaches can be used for the decomposition phase, including Weighted Sum, Chebyshev, and the penalty-based boundary intersection [25–28]. A group of uniformly spread weight vectors (V1,V2, Vn) is given for a two-objective function problem (see Fig. 2) [29,30].
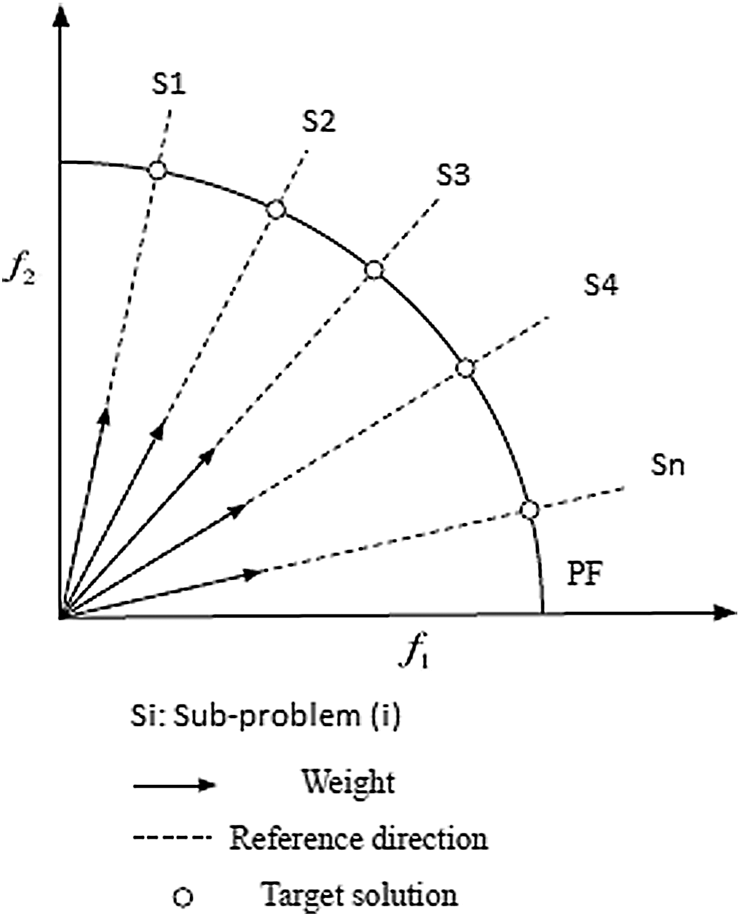
Figure 2: Decomposition phase
Each weight vector Vj, can be formulated as (Vj1,Vj2,…,Vjm) where (m) corresponds to the number of objective functions to optimize. The main MOP problem is mapped into (N) sub-problems using a “weighted-sum” method [31]. The formulation of the jth objective function can be stated as following:
Minimize
To solve each sub-problem using DRL, they are modeled as Neural Networks (NNs). Afterward, the optimization is solved in a collaborative manner among the sub-problems using the neighborhood-based parameter transfer strategy, which can be summarized as follows [32,33]:
Based on Eq. (14), it is noticed that two neighboring sub-problems could have very close minimal solutions since the weight vectors are close. Therefore, a solution for a sub-problem can be found by the surrounding sub-problems’ knowledge.
For more details, sub-problems in this research are modeled as NNs, where the network’s (i − 1) sub-problem parameters can be stated as (W(i − 1), b(i − 1)) weights and biases. The network parameters are propagated from the preceding sub-problem to the next one in the order (see Fig. 3).
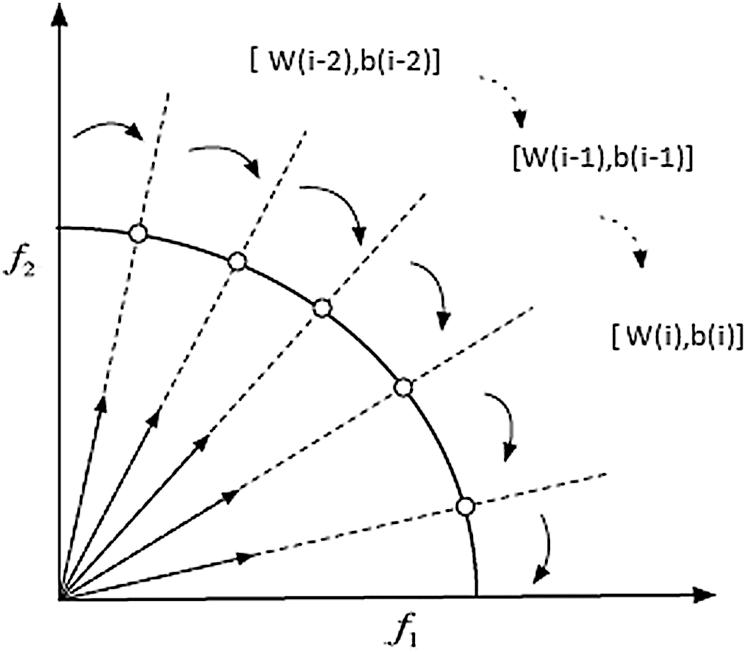
Figure 3: Parameter transfer strategy
The idea of parameter transfer saves the time amount needed for training the sub-problems set. The detailed steps are shown in the flowchart in Fig. 4.
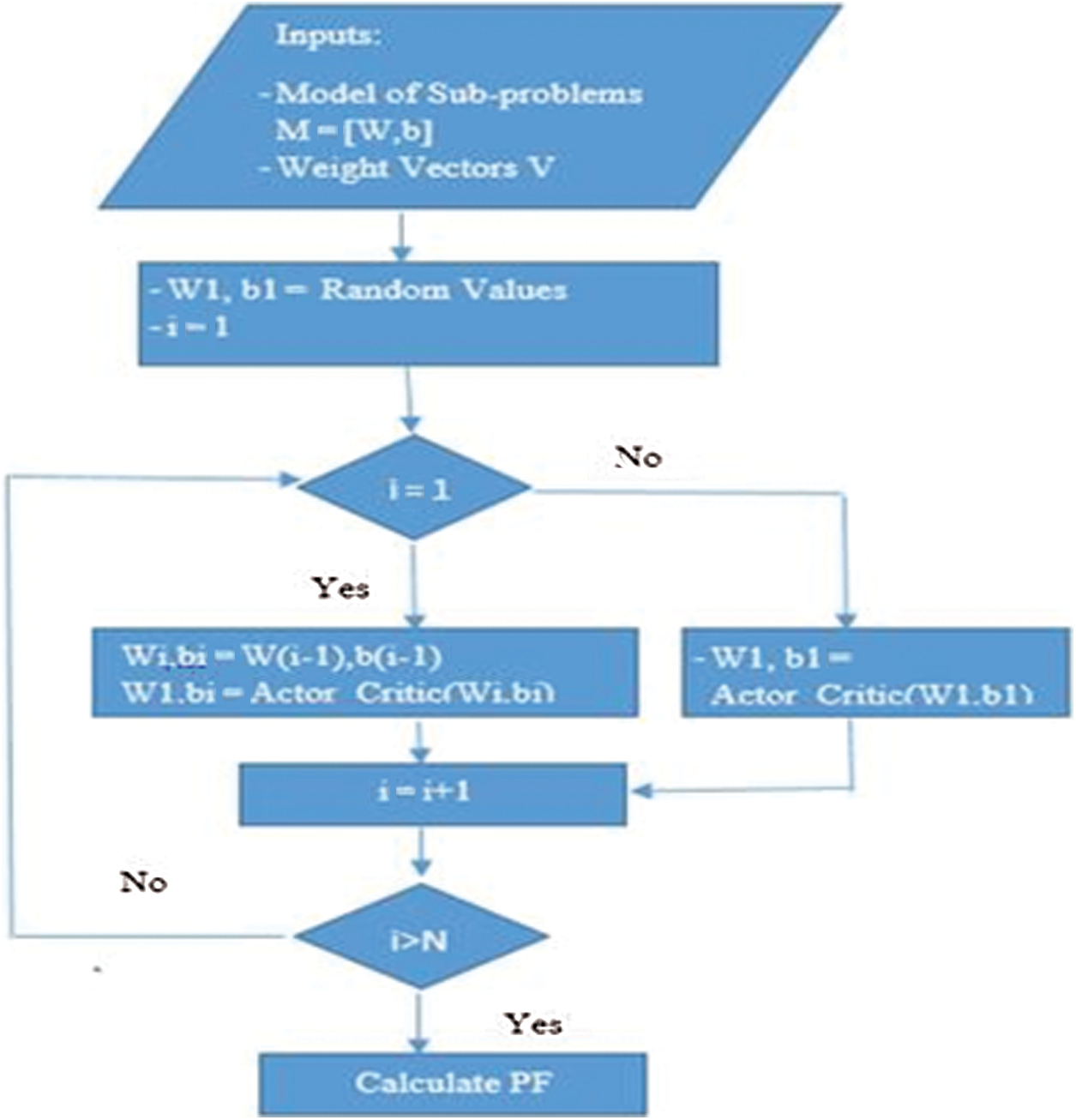
Figure 4: Detailed steps involved in parameter transfer strategy
5 Detailed Implementation and Discussion
The main MOP is formalized using the system of equations from (2) to (13), and the input/output network structure model can be illustrated as:
Let the given set of inputs be X = {Si: i from 1 to n}, where (n) is the number of blood banks. Each blood bank is represented by (x_i; y_i), the x and y coordinates of the blood bank (i), and is called for to calculate the distance between two blood banks. To obtain the desired output (Y) from the input (X), we follow the probability chain rule:
Afterward, a modified pointer network is exploited to model (14). It has the “Sequence to Sequence” structure architecture, which is a novel and successful model in the field of machine learning that creates a mapping from one sequence to another. Fundamentally, the generic “Sequence to Sequence” model is composed of Recurrent Neural Networks (RNNs): encoder and decoder. The first component, the encoder, performs input sequence encoding into a code vector that maintains the input extracted knowledge. The second RNN does the reverse operation; it is used for vector knowledge decoding to a target sequence. Accordingly, the methodology that underpins the “Sequence to Sequence” model, which converts one input sequence into an output sequence, is convenient.
To solve the routing sequence optimization problem …
After training every sub-problem model, Pareto solutions were directly calculated using a straightforward propagation of the models.
In this paper, the proposed model and implementation are exploited on two objective functions relating to the field of blood banks. All trials and results were conducted using a single GeForce GTX 1650 super GPU, and Python 3.6 was used as the development language.
The hyperparameter values of the network model are listed in Tab. 2, where Di represents the input dimension. A 1-layer GRU RNN with a hidden size of 256 was used for the decoder. Regarding the Critic network, the hidden size was also set to 256. Training for both the actor network and critic network was completed using the Adam optimizer with a learning rate of 0.0005 and a batching size of 150. The weights for the post sub-problems were set using the proposed neighborhood-based parameter transfer methodology.

The implementation was applied and tested for a test sample consisting of 5 major hospitals in Saudi Arabia’s Riyadh region. Other hyperparameters were input from the user GUI, including location, different types of costs, routing costs, and the number of vehicles. Experiments were simulated 100 times and the performance was compared to existing state-of-the-art systems. The proposed system reduced the time by between 35% and 38% and cost by 30%. In the future, the proposed system can be used as a benchmark for further studies to build on.
Since the dataset is not a benchmark dataset, it was necessary to implement other meta-heuristics such as Genetic Algorithms (GA) and Evolution Strategies (ES), which exploit natural (problem-dependent) representations, fundamentally selection beside mutation represent search operators. Usually, with evolutionary techniques, these operators run within a loop, where each loop iteration is referred to as a “generation”. In the case of simulated annealing, this is usually applied when the search space is defined as discrete. It depends on the idea that finding an approximate global optimum is more important than finding an accurate local solution in a fixed time.
In this experiment, the selected parameter values for GA were as follows: crossover probability and the mutation probability (PC, PM) = (0.5, 0.2) (0.5, 0.3) (0.5, 0.5) (0.6, 0.4) (0.7, 0.5) (0.7, 0.6) (0.8, 0.3) (0.8, 0.5), and the best pair was PM = 0.6 and PM = 0.4. The implementations of GA and SA yielded a time reduction of 23% and 21%, respectively, and cost reductions of 18% and 17.5%.
This work presents a solution for optimizing the routing process between blood banks by decomposing the MOP into a scalar optimization sub-problems set, where each one of these sub-problems is modeled as a separate Neural Network. The optimization for the overall model parameters is being done by optimizing the sub-problems neighborhood parameter and DRL training algorithm. The major technical contribution of this approach is that once the trained model is trained it becomes available without any scalability concerns. The proposed technique provides a set of technical strength points such as the ability to generalize and solve rapidly compared to other multi-objective optimization methods. The model was trained and tested on 5 major hospitals in Saudi Arabia’s Riyadh region, and the simulation results indicated that time and cost decreased by 35% and 30%, respectively. In particular, the proposed model outperformed other state-of-the-art MOP solutions such as Genetic Algorithms and Simulated Annealing. This work can be extended by enriching the model with more data points and working toward building a benchmark dataset for KSA blood banks.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. S. Keitel, Guide to the Preparation, Use and Quality Assurance of Blood Components. France: European Directorate for the Quality of Medicines & HealthCare (EDQM) Council of Europe, 2011. [Google Scholar]
2. M. Eskandari-Khanghahia, R. Tavakkoli-Moghaddam, A. A. Taleizadeh and S. H. Amin, “Designing and optimizing a sustainable supply chain network for a blood platelet bank under uncertainty,” Engineering Applications of Artificial Intelligence, vol. 71, no. 2, pp. 236–250, 2018. [Google Scholar]
3. J. Koistinen, “Building sustainable blood services in developing countries,” Transfusion Alternatives in Transfusion Medicine, vol. 10, no. 2, pp. 53–60, 2008. [Google Scholar]
4. L. Ifland, “Promoting national blood systems in developing countries,” Current Opinion in Hematology, vol. 21, no. 6, pp. 497–502, 2014. [Google Scholar]
5. S. Cheraghi and S. M. Hosseini-Motlagh, “Optimal blood transportation in disaster relief considering facility disruption and route reliability under uncertainty,” International Journal of Transportation Engineering, vol. 4, no. 3, pp. 225–254, 2017. [Google Scholar]
6. L. Ke, Q. Zhang and R. Battiti, “MOEA/D-ACO: A multiobjective evolutionary algorithm using decomposition and antcolony,” IEEE Transactions on Cybernetics, vol. 43, no. 6, pp. 1845–1859, 2013. [Google Scholar]
7. B. A. Beirigo and A. G. dos Santos, “Application of NSGA-II framework to the travel planning problem using real-world travel data,” in 2016 IEEE Congress on Evolutionary Computation, Canada, pp. 746–753, 2016. [Google Scholar]
8. W. Peng, Q. Zhang and H. Li, “Comparison between MOEA/D and NSGA-II on the multi-objective travelling salesman problem,” in Multi-Objective Memetic Algorithms. Berlin, Heidelberg: Springer, pp. 309–324, 2009. [Google Scholar]
9. E. Angel, E. Bampis and L. Gourvès, “A dynasearch neighborhood for the bicriteria traveling salesman problem,” in Metaheuristics for Multiobjective Optimisation. Berlin, Heidelberg: Springer, pp. 153–176, 2004. [Google Scholar]
10. T. Lust and J. Teghem, “The multiobjective traveling salesman problem: A survey and a new approach,” in Advances in Multi-Objective Nature Inspired Computing. Berlin, Heidelberg: Springer, pp. 119–141, 2010. [Google Scholar]
11. Z. Akca, R. T. Berger and T. K. Ralphs, “Modeling and solving location routing and scheduling problems,” in Proc. of the Eleventh INFORMS Computing Society Meeting, USA, pp. 309–330, 2008. [Google Scholar]
12. S. Alumur and B. Y. Kara, “A new model for the hazardous waste location-routing problem,” Computer and Operations Research, vol. 34, no. 5, pp. 1406–1423, 2007. [Google Scholar]
13. O. Boyer, T. Sai Hong, A. Pedram, R. B. Mohd Yusuff and N. Zulkifli, “A mathematical model for the industrial hazardous waste location-routing problem,” Journal of Applied Mathematics, vol. 2013, no. 7, pp. 1–10, 2013. [Google Scholar]
14. A. Ceselli, G. Righini and E. Tresoldi, “Combined location and routing problems for drug distribution,” Discrete Applied Mathematics, vol. 165, no. 1, pp. 130–145, 2014. [Google Scholar]
15. İ. Muter, Ş. İ. Birbil and G. Şahin, “Combination of metaheuristic and exact algorithms for solving set covering-type optimization problems,” INFORMS Journal on Computing, vol. 22, no. 4, pp. 603–619, 2010. [Google Scholar]
16. T. Vidal, T. G. Crainic, M. Gendreau and C. Prins, “Heuristics for multi-attribute vehicle routing problems: A survey and synthesis,” European Journal Operational Research, vol. 231, no. 1, pp. 1–21, 2013. [Google Scholar]
17. D. Tuzun and L. I. Burke, “A two-phase tabu search approach to the location routing problem,” European Journal Operational Research, vol. 116, no. 1, pp. 87–99, 1999. [Google Scholar]
18. C. Duhamel, P. Lacomme, C. Prins and C. Prodhon, “A memetic approach for the capacitated location routing problem,” in Proc. of the 9th EU/Meeting on Metaheuristics for Logistics and Vehicle Routing, Troyes, France, vol. 38, pp. 39, 2008. [Google Scholar]
19. S. H. H. Doulabi and A. Seifi, “Lower and upper bounds for location-arc routing problems with vehicle capacity constraints,” European Journal Operational Research, vol. 224, no. 1, pp. 189–208, 2013. [Google Scholar]
20. F. Jafarkhan and S. Yaghoubi, “An efficient solution method for the flexible and robust inventory-routing of red blood cells,” Computer& Industrial Engineering, vol. 117, no. 2, pp. 191–206, 2018. [Google Scholar]
21. W. L. Price and M. Turcotte, “Locating a blood bank,” Interfaces (Providence), vol. 16, no. 5, pp. 17–26, 1986. [Google Scholar]
22. S. Wang, F. Tao and Y. Shi, “Optimization of location-routing problem for cold chain logistics considering carbon footprint,” International Journal of Environmental Research and Public Health, vol. 15, no. 1, pp. 86, 2018. [Google Scholar]
23. I. Bello, H. Pham, Q. V. Le, M. Norouzi and S. Bengio, “Neural combinatorial optimization with reinforcement learning,” arXiv preprint arXiv: 1611.09940, 2016. [Google Scholar]
24. M. Nazari, A. Oroojlooy, L. V. Snyder and M. Takáč, “Reinforcement learning for solving the vehicle routing problem,” arXiv preprint arXiv: 1802.04240, 2018. [Google Scholar]
25. R. Wang, Z. Zhou, H. Ishibuchi, T. Liao and T. Zhang, “Localized weighted sum method for many-objective optimization,” IEEE Transactions on Evolutionary Computation, vol. 22, no. 1, pp. 3–18, 2016. [Google Scholar]
26. S. Gronauer and K. Diepold, “Multi-agent deep reinforcement learning: A survey,” Artificial Intelligence Review, vol. 34, no. 6, pp. 26, 2021. [Google Scholar]
27. A. M. A. Zador, “A critique of pure learning and what artificial neural networks can learn from animal brains,” Nature Communications, vol. 10, pp. 1–7, 2019. [Google Scholar]
28. C. Zhang, O. Vinyals, R. Munos and S. Bengio, “A study on overfitting in deep reinforcement learning,” arXiv preprint arXiv: 1804.06893, 2018. [Google Scholar]
29. Z. Zheng, J. Oh and S. Singh, “On learning intrinsic rewards for policy gradient methods,” in Advances in Neural Information Processing Systems, Montreal, pp. 4644–4654, 2018. [Google Scholar]
30. O. Vinyals, I. Babuschkin, W. M. Czarnecki, M. Mathieu, A. Dudzik et al., “Grandmaster level in starcraft II using multi-agent reinforcement learning,” Nature, vol. 575, no. 7782, pp. 350–354, 2019. [Google Scholar]
31. G. Wayne, C.-C. Hung, D. Amos, M. Mirza, A. Ahuja et al., “Unsupervised predictive memory in a goal-directed agent,” arXiv preprint arXiv: 1803.10760, 2018. [Google Scholar]
32. M. Fellows, A. Mahajan, T. G. J. Rudner and S. Whiteson, “Virel: A variational inference framework for reinforcement learning,” in Advances in Neural Information Processing Systems, Canada, pp. 7120–7134, 2019. [Google Scholar]
33. T. Haarnoja, A. Zhou, P. Abbeel and S. Levine, “Soft actor-critic: Offpolicy maximum entropy deep reinforcement learning with a stochastic actor,” arXiv preprint arXiv: 1801.01290, 2018. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |