DOI:10.32604/cmc.2022.019440

| Computers, Materials & Continua DOI:10.32604/cmc.2022.019440 |  |
| Article |
Database Recovery Technique for Mobile Computing: A Game Theory Approach
1Institute of Graduate Studies and Research, Alexandria University, Alexandria, Egypt
2Assistant General Manager, IT Department, Egyptian Petrochemicals Co., Alexandria, Egypt
*Corresponding Author: Saad Darwish. Email: saad.darwish@alexu.edu.eg
Received: 13 April 2021; Accepted: 27 June 2021
Abstract: Contact between mobile hosts and database servers presents many problems in the Mobile Database System (MDS). It is harmed by a variety of causes, including handoff, inadequate capacity, frequent transaction updates, and repeated failures, both of which contribute to serious issues with the information system’s consistency. However, error tolerance technicality allows devices to continue performing their functions in the event of a failure. The aim of this paper is to identify the optimal recovery approach from among the available state-of-the-art techniques in MDS by employing game theory. Several of the presented recovery protocols are chosen and evaluated in order to determine the most critical factors affecting the recovery mechanism, such as the number of processes, the time required to deliver messages, and the number of messages logged-in time. Then, using the suggested payout matrix, the game theory strategy is adapted to choose the optimum recovery technique for the specified environmental variables. The NS2 simulator was used to carry out the tests and apply the chosen recovery protocols. The experiments validate the proposed model’s usefulness in comparison to other methods.
Keywords: Mobile computing; game theory; decision making; mobile database recovery
Through the advancement in networking capabilities, mobile communication has been one of the most vital aspects of our lives. Mobile Computing (MC) refers to a variety of nodes or devices that allow citizens to access information or data regardless of their location [1]. However, the mobile environment has a number of shortcomings that make managing mobile data transfers difficult, such as periodic disconnections [2–5]. The primary transaction management issues stem from the versatility of the Mobile Host (MH) and the limited wireless bandwidth [6–9]. Numerous recovery modules have been created by researchers to ensure that sensitive information can be retrieved after a malfunction. They take into account the difficulties associated with wireless networking when working with the mobile database, such as electricity shortages, frequent server disconnections, and handoff issues. There are two styles of recovery approaches described in the literature in this regard: forward recovery and backward recovery; for more details, see [9,10]. Recovery is a time-consuming and resource-intensive method, and these protocols necessitate an abundance of both. Since managing the log is considered the most costly operation in recovery protocols, an economical and effective log management scheme is needed for the MDS [11–13].
Due to the fact that the majority of nodes are mobile, the MD recovery mechanism becomes extremely difficult. Despite this, numerous parameter requirements are required for the recovery module in order to achieve a dynamic recovery protocol that adapts to changing environmental conditions [7–10]. The challenge here is determining the most appropriate recovery approach for the environmental circumstances. Thus, the optimal approach must find an acceptable balance between the used recovery algorithm and efficiency at all operational stages. Thus, this proposal seeks to implement a selective approach (decision making) that utilizes the game theory to pick the best recovery algorithm from a pool of usable algorithms taking into account the circumstances surrounding the disruption. This will significantly increase device stability and include high availability data storage for handoff and disconnected operations. The fundamental distinction between existing recovery methods in the literature and the suggested game theory-based approach is that the former seeks a suitable recovery solution based on specific parameters, while the latter is used to render a judgment based on the utility function with a large number of conflicting parameters.
The majority of current database recovery procedures make a little exception for the conditions surrounding the disconnection in a mobile world. Thus, the objective is to create a novel intelligent strategy for mobile database recovery that takes into account a variety of environmental variables through the use of game theory. Game theory is used here since no one optimum approach exists for all recovery scenarios using available recovery protocols. Game theory is an appropriate method for determining the optimal strategy (best solution) for each player based on their utility function (alternative recovery approaches are represented as players) [12–16].
Mobile systems are often exposed to a variety of external conditions, which can result in data loss or contact failure. As a result, traditional recovery methods cannot be strictly applied to these systems. The following are the primary problems confronting conventional mechanisms: (1) Some recovery protocols rely on unstable and limited MH storage; (2) certain protocols affect the logging scheme, which can result in machine load overhead; (3) certain schemes necessitate a large amount of data transfer; (4) certain protocols may be slow during the recovery process, depending on the distance between the MH and the Base Station (BS); and (5) some of the algorithms failure in terms of the number of repeated processes and exchanged messages. In general, considering the attempts made to resolve mobile database recovery, there is still room for substantial improvement.
The novelty of the proposed model is that it enables efficient recovery treatment in MDS by using a novel smart strategy focused on players (different recovery protocols) within the game theory paradigm as a decision-maker for selecting the most efficient recovery procedure. Since the main issue is not selecting one of the well-known recovery methods, but rather selecting the most suitable approach in light of the adjustments introduced by the operational environment, which is often ambiguous and unpredictable? In this regard, the current work would ensure that the best possible recovery approach through game theory model is chosen based on its critical parameters. The proposed study compares a variety of various recovery strategies. These techniques demonstrate the impact of various parameters on the complex efficiency of the protocol under consideration. The work shows that using ideal parameters greatly enhanced efficiency, demonstrating the proposed method’s enormous potential. Additionally, the proposed model exhibits a strong degree of versatility by incorporating cutting-edge regeneration techniques that can significantly increase the performance.
This paper is a substantial extension of our conference paper [17]. Compared with this small version, further details of the suggested method are presented, and a more extensive performance evaluation is conducted. We also give a more comprehensive literature review to introduce the background of the offered method and make the paper more self-contained. Therefore, this version of the paper provides a more comprehensive and systematic report of the previous work. In this version, three algorithms were used as players within the game theory for giving the opportunity to a larger number of algorithms to enter the competition, which improves the effectiveness of decision-making according to different environmental conditions.
Apart from this introduction, the following sections are planned: Section 2 discusses current state-of-the-art MD recovery strategies, Section 3 outlines the proposed mobile database recovery model, Section 4 describes the standards for evaluating the proposed game theory strategy of MD recovery and presents the results, and Section 5 concludes and suggests potential work directions.
While recovery in the MDS field of research is not recent, there are still numerous opportunities for improving established protocols and developing new ones [18,19]. In general, there exist three types of checkpointing; coordinated checkpointing, uncoordinated checkpointing, and communication induced checkpointing. In the coordinated checkpointing, there must be coordination in the participating processes to form a globally consistent state and it gives a good performance for rollback recovery. In the uncoordinated checkpointing, no need for processes to coordinate their checkpoints. The disadvantage of uncoordinated checkpointing is the susceptibility of the Domino effect and also recovery process is complicated as compared to coordinated checkpointing. In communication-induced checkpointing, communication patterns of the application are used to do the checkpointing. The advantage of communication-induced checkpointing is the absence of a domino effect and coordination is not required in it.
Authors in [20] discussed an effective failure recovery scheme for mobile database applications that relies on movement-based checkpointing and logging. Current methods employ periodic checkpoints regardless of the mobility activity of mobile users. Their movement-based checkpointing scheme only performs a checkpoint when a predefined number of mobility handoffs is met. The optimum threshold is determined by the mobile host’s failure rate, log arrival rate, and mobility rate. This enables per-user tuning of the checkpointing rate. They determined the optimum travel threshold that minimizes the cost of recovery per failure as a function of the mobility rate, failure rate, and log arrival rate of the mobile node. On the other side, selecting the versatility hand-off threshold incorrectly may have a negative effect on results. Additionally, if the checkpoint rate is very low, the last checkpoint may be existing very far from the mobile support station. Additionally, a significant number of logs through several mobile support station can be scattered, resulting in a lengthy recovery period.
In [21], the authors defined a mechanism for recovering applications in a mobile computing setting by integrating movement-based checkpointing and message logging. The system’s objective is to impose minimal overhead on standard application execution as a result of the recovery scheme. Costs associated with locating the mobile host, the number of messages sent over wireless media, and the scale of recovery-related data collected on a mobile host have also been limited. The adaptability of a node is used to determine whether a checkpoint must be taken. They used the storage at a Base Transceiver Station (BTS) to store the MH’s checkpoints and message logs. Additionally, the sender-based logging system avoids the packet from being copied to the BTS. When message logging is integrated with the underlying contact protocol, no additional overhead is incurred for message logging at the sender BTS. Numerous criteria have been used in this system, including the number of MH registrations in the region, the number of regions, and the number of handoffs. This work can be particularly useful in vast networks with multiple regions. In comparison, it can cause additional costs while operating in confined spaces.
In [22], the authors defined a rollback recovery algorithm focused on independent checkpoints and message logging. The algorithm is novel in that it makes use of mobile agents to manage message logs and checkpoints. Additionally, if a mobile node travels a long distance from its most recent checkpoint, the agents manage to relocate the checkpoint and message logs that are located in remote Mobile Service Stations. Thus, the period required for a mobile node to recover would never reach a predefined threshold. By logging messages, it is possible to store just one checkpoint in permanent storage. The primary benefit of this work is the small size of the message log, which cannot be massive due to the network’s minimal message substitution. Additionally, if a process communicates on a regular basis, it can reduce its interval checkpointing. Nonetheless, this approach happens in a limited number of circumstances which can result in increased network activity during recovery. In particular, if the duration of the mobility profile exceeds the number of distinct mobile service stations at some stage, it is necessary to consolidate the logs into a single location. The contribution of [23] is a suggestion for a modern checkpointing algorithm that is appropriate for mobile computing systems. This algorithm is distinguished by its reliability and optimization in terms of time-space overhead experienced during checkpointing and regular application operation.
Checkpointing is a time-consuming mechanism since it requires all systems to take a checkpoint in order to maintain global continuity. This will sometimes result in needless checkpointing and the exchanging of several messages. A decrease in the period required for log unification or checkpointing results in a decrease in recovery time. It is possible to create a list of dependent processes that need checkpointing and insert it in a mobile agent that travels with the mobile host. The wok resented in [24] defined a log management and low-latency no-blocking checkpointing scheme that minimizes recovery time by using a mobile-agent-based architecture. Due to their exclusive properties, mobile agents are ideal for this scheme. In this system, the checkpoint algorithm compels a small number of processes to take checkpoints, each of which is based on the previous operation. This protocol improved recovery time by reducing the number of messages exchanged. On the contrary, especially where multiple agents are required, it may increase complexity, which can absorb some additional execution costs.
The authors of [25] introduced a log management scheme for a mobile computing system that significantly reduces the overall cost of failure recovery as compared to current lazy and pessimistic schemes. Additionally, their strategy allows recovery from a base station other than the one where it crashed and minimizes handoff costs, log replication costs, and failure recovery period. The primary advantage of the suggested log management approach is its simplicity of implementation, while the primary disadvantage is probably the recovery time if the home agent has located a long distance from the mobile unit [26,27].
The authors in [28] presented a recovery method that is dependent on database and mobile device synchronization. A synchronization algorithm is a technique or process used to allow the sharing of data between two or more entities. As a result, the replication mechanism ensures the data is consistent for all organizations. In the opposite, existing data in the mobile database’s synchronization algorithm between a server-side database and a mobile database reveals existing holes in the mobile database’s data synchronization. The authors concluded this study by suggesting a Synchronization Algorithm focused on the Message Digest (SAMD). Two message digest tables are built based on data tables, one on the server and one on the mobile device/client. The data tables are where the real company data is stored.
In their work, the message digest is a hash function that is used to compare hash values in order to identify rows that need synchronization. If the values are identical, no synchronization (recovery) is required; if they are not identical, an error occurs, and synchronization is required and proceeds according to the algorithm’s rules. The drawback of this algorithm is that it does not make use of database objects such as triggers, recorded procedures, or timestamps, which means that there is no additional expense associated with the retrieval mechanism on the database side. Additionally, the SAMD algorithm is very stable due to its use of a message digest and is simple to enforce on both the server-side and mobile database. One disadvantage of this algorithm is that, although it makes use of hash functions, it does not ensure data integrity during transmission to the server, since the hash values are stored in a database table on both ends.
According to the review given, the majority of the works presented were classified as follows: (1) The majority of recovery studies used a variety of techniques in the recovery process, including log management, checkpointing, movement-based checkpointing, and an agent-based logging scheme; (2) Since these methods are so dissimilar, one of them does not work as a substitute for another; this means that each algorithm has a unique parameter set and different assumptions. (3) Although certain plans attempted to combine several techniques into a single contribution (hybrid method), they were still harmed by the difficulty of choosing the right fusion from this pool of approaches. As a result, recovery costs may be large, and the recovery mechanism may be overly complex; (4) Finally, most schemes did not regard environmental variables as influencing factors in the recovery process. As a result of the above, the realistic application of recovery algorithms is constrained. It is necessary to create a scheme that optimizes success by selecting the most appropriate recovery strategies for the current scenario. Thus, game theory was used due to its importance for decision making, as it utilizes conflict analysis or interactive decision theory to choose the optimal solution through competition between the strategies presented for each recovery protocol.
A traditional MDS architecture contains a tiny database fragment originating from the main database that resides on the MH. This architecture is intended to manage the accessibility constraints that MHs and Mobile Satellite Services (MSS) can alleviate. If the MH is present in the cell served by the MSS, a nearby MH may interact directly with it. The MH will freely switch between cells, and each cell contains a BS and many MHs. The BSs also configured stations to provide a wireless gateway that allows them to connect with the MHs and transmit data through the wireless network. Each MH can communicate with the BS via a wireless channel; the BS communicates with the database server via wired links, and the MH cannot communicate directly with the database server without the BS [11,29]. The concentration of this research is on how to employ GT to find the optimal recovery protocol from alternative recovery algorithms in the MC. Herein, three important selected recovery algorithms, according to their algorithmic architecture, are implemented. The proposed model has been prototyped using a three-player game theory. The proposed work differs from other recovery systems as it takes into account some important variables in the mobile environment during handoffs or service outages, which are different in situations. While conventional recovery algorithms depend on some assumptions in the environment and built their works on these assumptions. Fig. 1 depicts the suggested model’s architecture.
To illustrate the technical significance of the system recovery model in the MDS, we analyzed the most important developed algorithms for MD recovery in order to determine which of these algorithms should be investigated. In this scenario, we grouped the usable recovery algorithms according to their operation or characteristics. As mentioned in [9–13], these groups vary in terms of how the recovery technique is implemented. We chose three recovery protocols for our proposal: log monitoring (act as player 1) [25], mobile agent (act as player 2) [22], and a hybrid approach that merged movement-based checkpointing and message logging as a (act as player 3) [20].
Each player must develop a set of strategies in order to compete against other players. To obtain these strategies, feature analysis and extraction are performed on each selected recovery protocol to ascertain the most powerful features of each protocol. Thus, in the game theory, each chosen protocol is described by a player, and each player’s strategies are determined by the way each protocol’s variable is used. For example, the first protocol (player 1) took into account many variables, including log arrival rate, handoff rate, average log size, and mobility rate. Similarly, the second protocol (player 2) made use of many variables, including the number of processes in the checkpoint, a handoff threshold, and the log duration. The third procedure makes use of many parameters, including the total number of registrations in the region, the total number of regions, and the total number of hand-offs. For further detail about how these protocols operate, see [13–25].
To prepare the parameters for the requisite recovery algorithms using game theory as a decision-making strategy, we first apply the selected protocols using the selected critical factors on which each protocol is dependent. Each algorithm is applied using actual database transactions to evaluate the strategies of each player. A package with an objective function for overall recovery cost is measured, which is calculated differently for each algorithm. Based on the preceding steps, we construct the payoff matrix for each protocol output value in game theory. These outcomes are referred to as each player’s utility or payoff. These payoffs or benefits estimate the satisfaction degree of a player extracted from the conflicting situation. Generally, the game theory could be described as follows: (1) a set of players (the selected algorithms for negotiation); (2) a pool of strategies for each player (the strategies reflect the assumed values of significant coefficients in each protocol that also reflect the possible environmental changes); (3) the benefits or payoffs (utility) to any player for every possible list of the strategy chosen by the players. Tab. 1 lists the set of symbols used to describe the game for the proposed model.
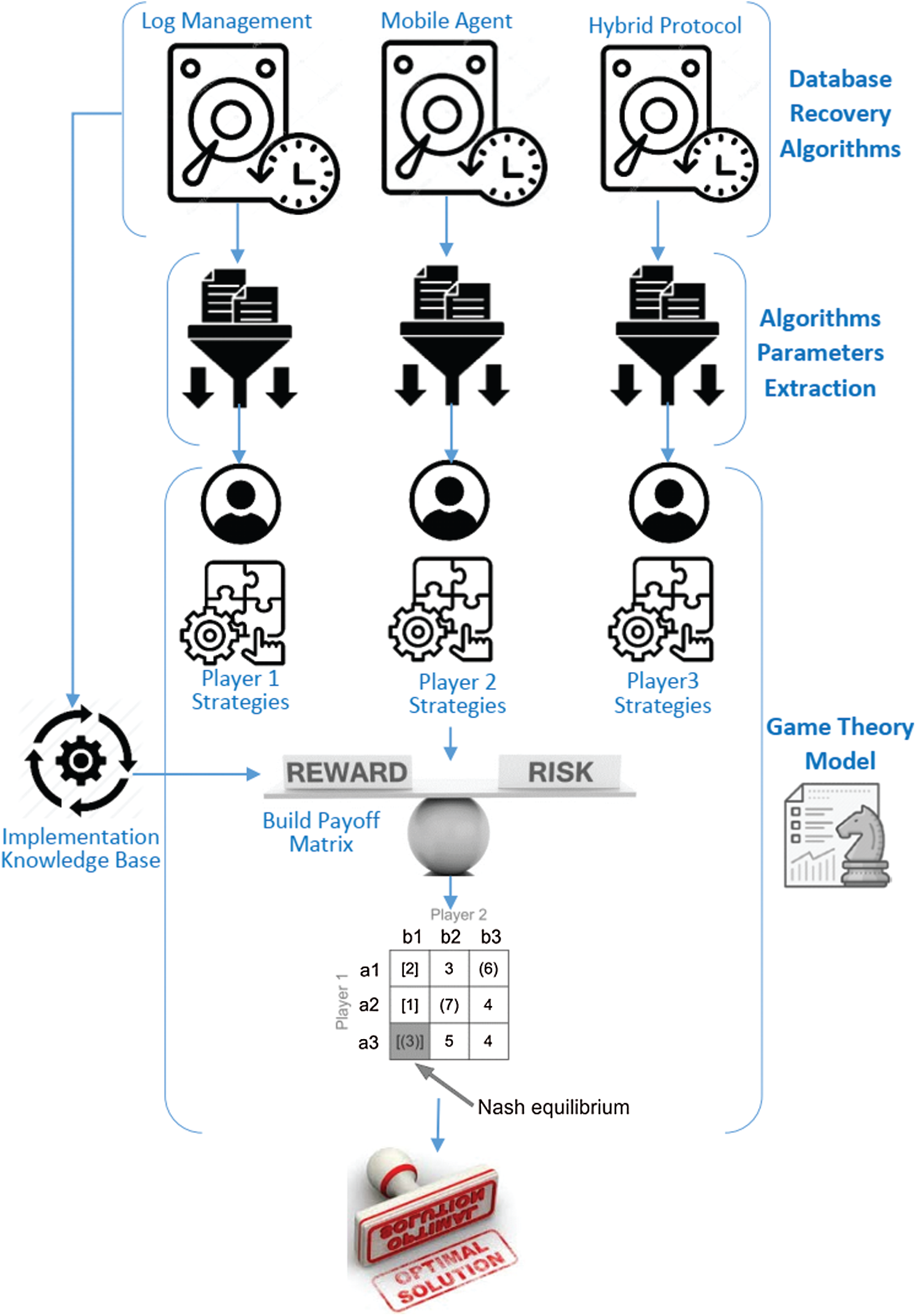
Figure 1: The proposed MDS recovery model
Within the game of the suggested model, a finite set of players

We construct one matrix for each of player 3’s actions (strategies); thus player 1 chooses a row, player 2 chooses a column, and player 3 chooses a table. The bi-matrix for three players’ game with its payoff is illustrated in Tab. 2. Accordingly, each third player strategy
for every list of

Estimating the amount of payoff in the game depends on other players’ decisions by their choices. Therefore, choosing a strategy for a player impacts the gain value of the other player. In this proposal, there are three utility functions that are used as benchmarks for performance and evaluation of the candidate protocols. The functions are; the amount of time used during the operation of the protocol (TIMEi) for each strategy, the amount of memory used during the operation (MEMOi) for each strategy, and the rate that expresses the percentage of completion of the recovery work “recovery completion” (DONE_PROBi) for each strategy. After studying and implementing the protocols, it was found that the operation of each algorithm falls between 0 and 5 s, so the value of the return function from the time measurement will be distributed as follows:
where
Finally, with regard to estimating the recovery process’s completion level
Thus, the player’s total gain in this game is the sum of the reward values of the variables (
The simulation is used to evaluate the proposed game theory-based recovery model in MD. In this regard, we used two software to implement the prototype NS2 software and Matlab. The NS2 simulation software is a simulator for a discrete event intent at networking research that helps developers to improve their business in real-time. It also supports many protocols like TCP, routing, and multicast protocols over wired and wireless networks, and works on several platforms such as Linux, and Windows [34,35]. So, we exploit this program to implement the stage of collecting work environment data at different levels to simulate the change in the work environment. Then, Matlab software is running for game theory building to evaluate the alternative recovery protocols by entering the output values of the simulation stage in it to search for the best decision. For our implementation, we used some mobile log files of a different size that contains several process data items to be recovered according to each algorithm’s mechanism.
Tab. 3 summarizes the NS2 simulation parameters. Herein, the distributed coordination function of IEEE 802.11 for wireless large area networks as the Medium Access Control (MAC) layer protocol is used. The movements of the mobile client node are gained from a movement file. The node has the transmission range of the mobile client node that is 250 m. The system uses two cells every cell has one base station. The initial location and movements of the nodes are obtained via a Random Waypoint (RWP) model. The RWP model is a simple random mobility model based on random destinations, speeds, and pause times. The prototype was developed in a modular manner and implemented and evaluated on a DellTM InspironTM N5110 Laptop device, manufactured by Dell Computer Corporation in Texas. Intel (R) Core (TM) i5–2410M processor running at 2.30 GHz, 4.00 GB of RAM, Windows 7 64–bit. Herein, the execution time and recovery probability are used to evaluate the efficiency of the suggested model. See [22,25] for more details.
From the literature, based on the evaluation of selected recovery protocols, the most appropriate values for the set of protocol’ factors (strategies) were chosen to reflect the performance of the protocol in different environments. The first set of experiments was conducted to assess the proposed recovery model performance in terms of real execution time as a function of log file size. In general, the recovery cost for any scheme is very low as the entire log information is present at the current base station. When the MH travels far away from the first BS the degree of recovery algorithm’s complexity increases to find and transfer the log file. Increasing the file size leads to an increase in the cost of the transfer. As revealed in Fig. 2, the proposed game theory-based recovery model achieves less execution time with an increase in file size in different mobile environments according to the changing nature of the simulation. One possible explanation of these results is that as the suggested model relies on a knowledge base that was built after the pre-implementation of each selected recovery protocol in different simulation environments, it selects the most appropriate recovery protocol suitable with the current situation (variation of log file size). As a consequence, for many runs of the simulation, the suggested model takes less time for execution.

The proposed recovery model depends in its work on building a knowledge base, which is only built once and through which the most appropriate protocol is chosen based on the payoff matrix and the dominant equilibrium technique. Herein, the selection is made based on the integration of the three utility functions that are used as benchmarks for performance and evaluation of the candidate protocols. Fig. 3 reveals that the increase in recovery cost will be more if the mobility rate increases. As mentioned above, the recovery cost will be low as the entire log information is present at the current base station. But the recovery cost will be higher when recovery is in the same base station where the mobile node got failed. The results in Fig. 3 indicate that the log management and agent-based algorithms generally suffer from increasing implementation time in the long run despite achieving good competition in the small areas. On the contrary, the hybrid method may be effective in a large environment rather than a small region because it takes the checkpoint once before MH transfers from region to region which leads to saving some time.
For a recovery process’s completion, there is a positive relationship between the increase in the handoff rate and the possibility to complete the recovery. Handoff is the process of transferring a mobile station (MS) from one base station (BS) or channel to another. A handoff algorithm with fixed parameters cannot perform well in different system environments. Specific characteristics of the communication systems should be taken into account while designing handoff algorithms. When a mobile node moves from one network to another, if the preparation time of fast handoff is larger than WLAN sojourn time related to mobile node speed, the handoff failed and occurred the packet loss. If the mobile node speed is too slow in the case of the fixed threshold value, instead, handoffs are triggered too late and thus WLAN service time is reduced. The handoff cost includes the cost of transferring the checkpoint state, message log, and an acknowledgement. Fig. 4 displays the recovery process’s completion vs. increases in the hand-off threshold rates. The recovery probability with the log management method is dramatically decreased while the hand-off threshold rate increased. Whereas, other methods got down slowly with increasing the threshold value. This proves that the log method is only valid in small work environments. Whereas the hybrid method and the agent-based equally achieved good performance for multi regions or the region farther from the point of retrieval. As expected, the recovery probability is better for the proposed model when compared with the other schemes in the long run in the different simulation environments.
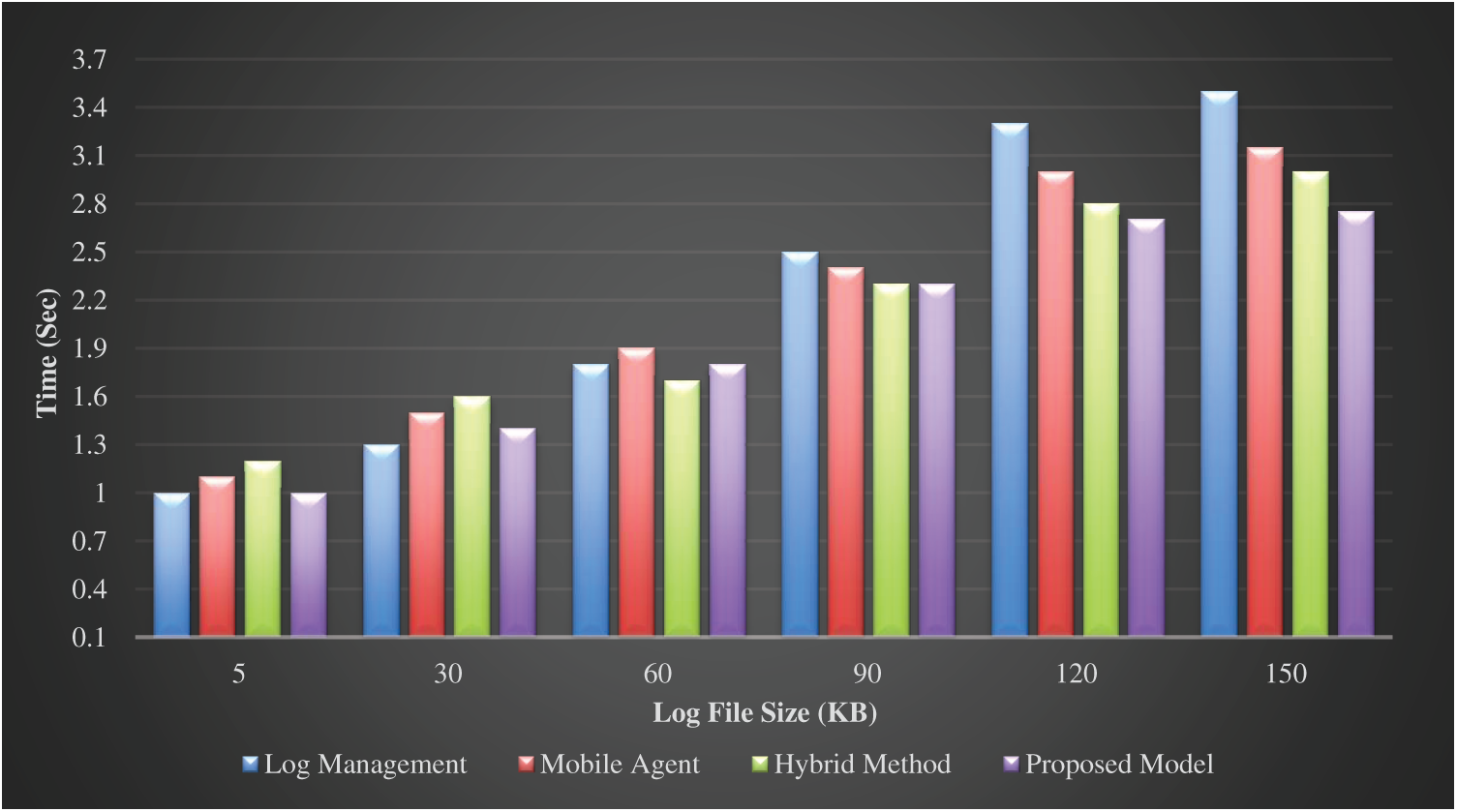
Figure 2: Execution time as a function of log file size
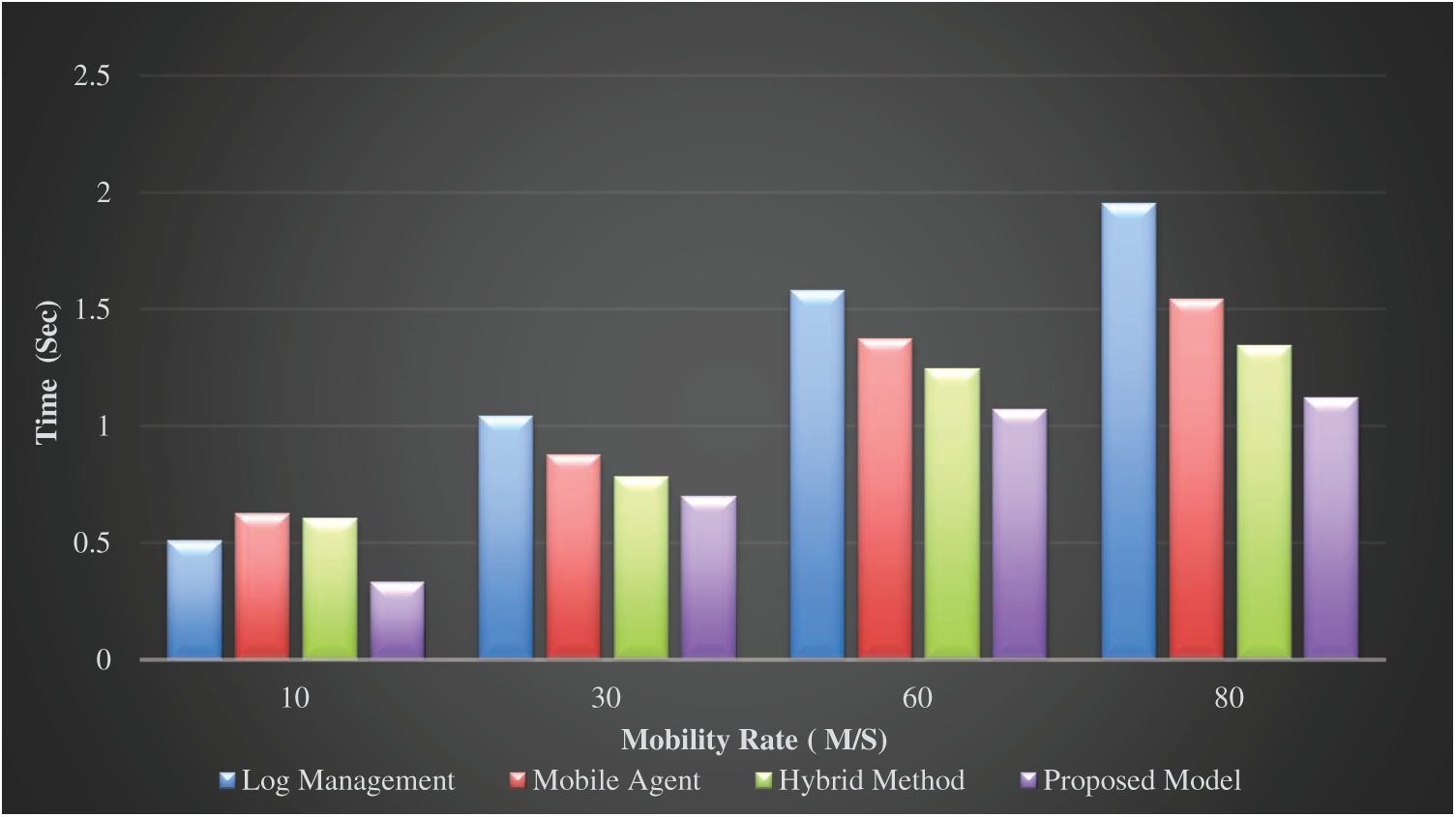
Figure 3: Execution time as a function of mobility rate
In the same context, Fig. 5 presents the recovery process’s completion vs. log arrival rates. The graph clarifies that the recovery probability reduced as the log arrival rate raised. Herein, the mobile agent appeared a good result comparing to other methods. That’s because the checkpoint takes once in this method and if a process frequently communicates, then its interval checkpointing can be reduced whenever the MH proceeds far away from the last registered checkpoint the agents manage to move the checkpoint and message logs with it.
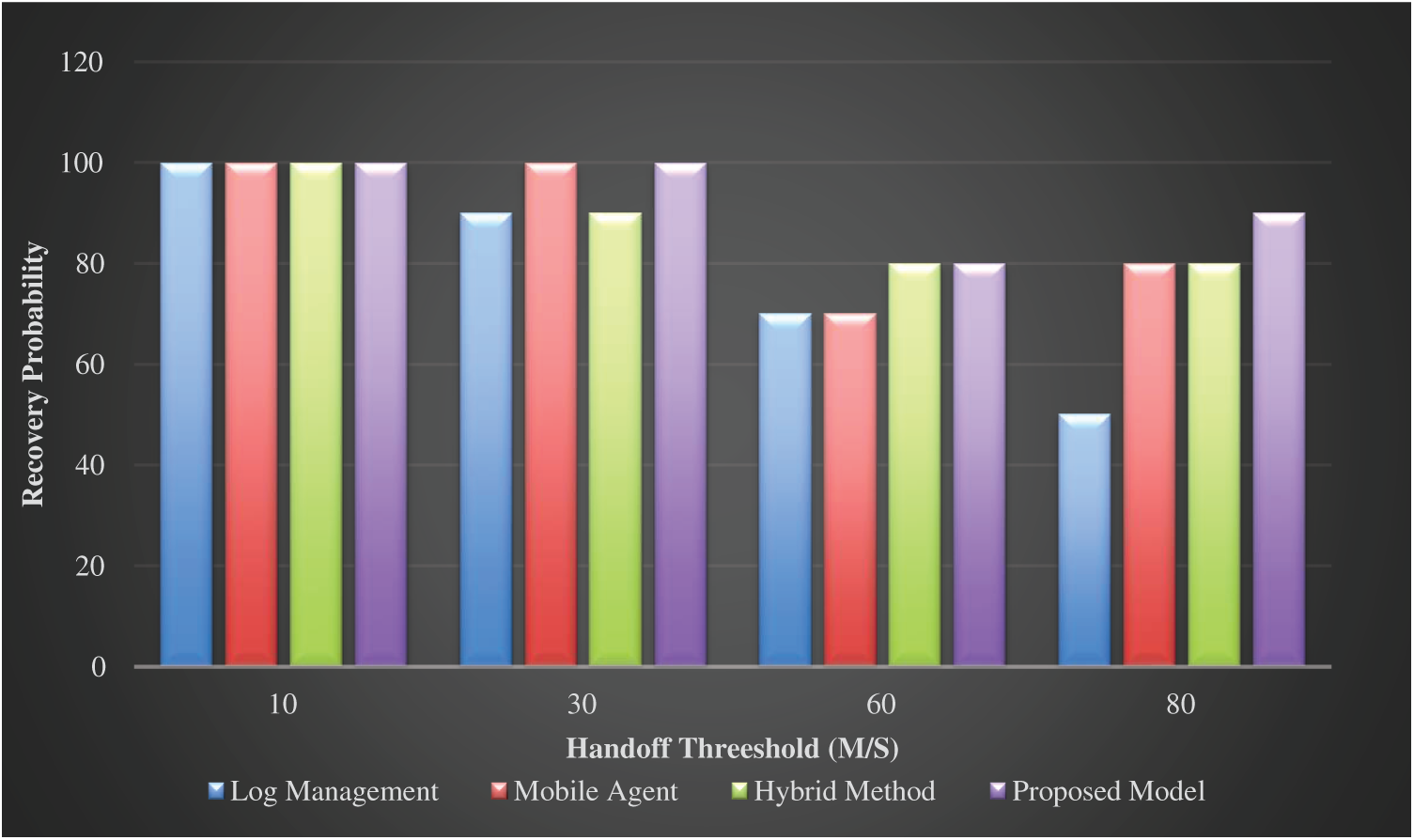
Figure 4: Recovery probability vs. handoff threshold
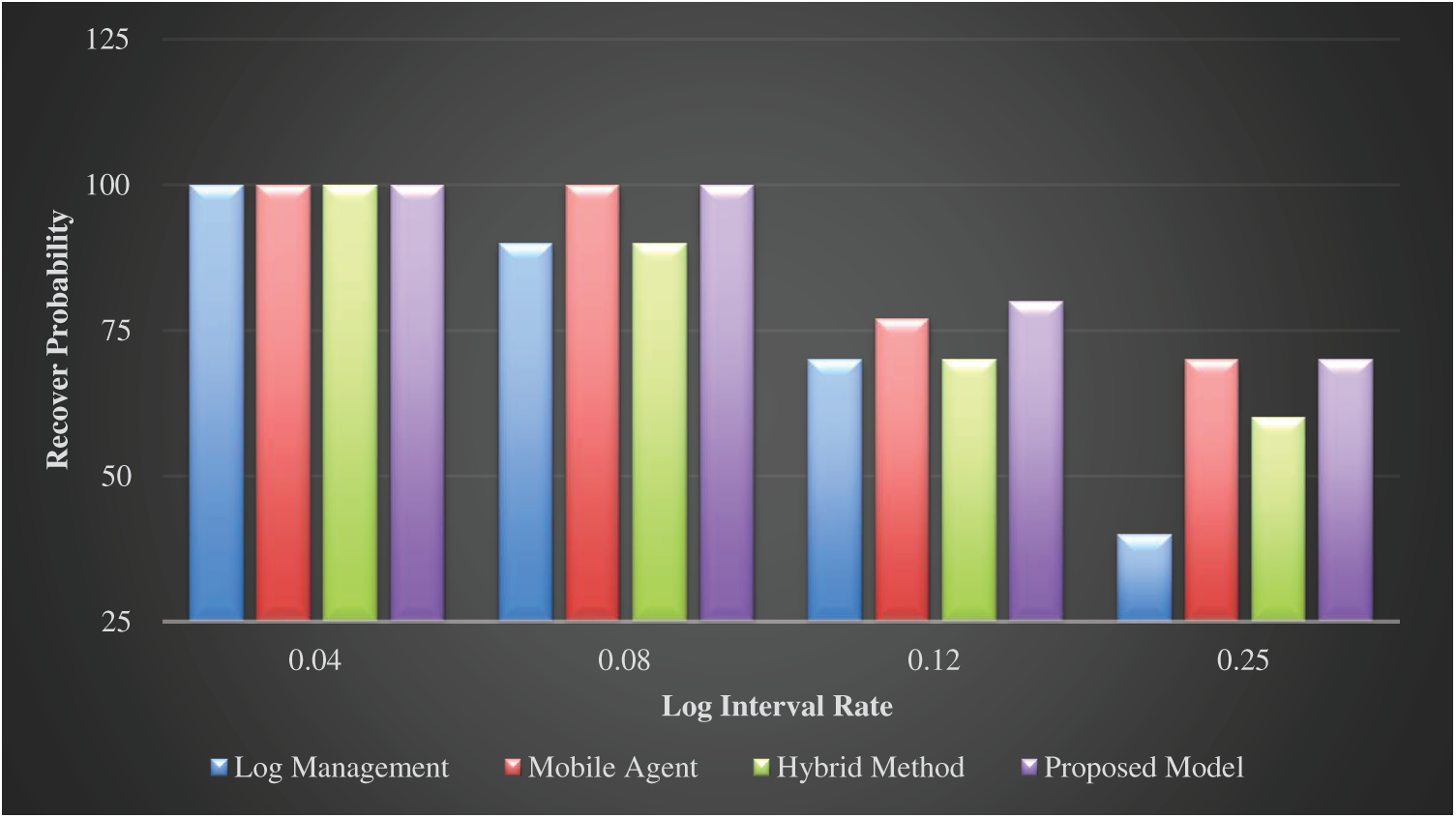
Figure 5: Recovery probability vs. log arrival rate
This article aims to suggest a novel game theory model for determining the optimal recovery solution in MDS. The new algorithm was demonstrated in a competitive setting against two of the most widely used MDS recovery protocols. The concept behind game theory is that each algorithm selects the most suitable approach in terms of message delivery time and message count to detect the correct recovery solution based on environmental variables. A critical phase in a game-theoretic study is determining which approach is the better solution of a recovery procedure to the strategies selected by others. The suggested recovery model is focused on the creation of a knowledge base that is created once and used to choose the most suitable procedure based on the payoff matrix and dominant equilibrium technique. The experimental results support the proposed recovery model’s superiority. In the future, it could be necessary to allow for additional recovery protocols to maximize the performance of the proposed model. Additionally, a hybrid approach focused on game theory and the proposed paradigm of cloud algorithms was used to achieve a better outcome.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. R. Rathika, T. Prakash and A. Aloysius, “A survey on mobile computing security,” International Journal of Research and Analytical Reviews, vol. 6, no. 2, pp. 645–649, 2019. [Google Scholar]
2. M. Anandhakumar, E. Ramaraj and N. Venkatesan, “Query issues in mobile database systems,” Asia Pacific Journal of Research, vol. I, no. XX, pp. 24–36, 2014. [Google Scholar]
3. F. Ibikunle and A. Adegbenjo, “Management issues and challenges in mobile database system,” International Journal of Engineering Sciences & Emerging Technologies, vol. 5, no. 1, pp. 1–6, 2013. [Google Scholar]
4. H. Su, “The processing technology in mobile database transaction system,” International Journal of Database Theory and Application, vol. 8, no. 2, pp. 51–60, 2015. [Google Scholar]
5. P. Patil, “Mobile computing: Issues and limitations,” International Journal of Computer Science and Mobile Applications, vol. 4, no. 8, pp. 1–6, 2016. [Google Scholar]
6. J. Nisar and O. N. Trumboo, “Database for mobile application,” International Journal of Trend in Scientific Research and Development, vol. 2, no. 3, pp. 853–854, 2018. [Google Scholar]
7. A. Mobarek, S. Abdel-Rhman, A. Abdel-Mutal, S. Adam, N. Elbadri et al., “Transaction processing, techniques in mobile database: An overview,” International Journal on Computational Sciences and Applications, vol. 5, no. 1, pp. 1–10, 2015. [Google Scholar]
8. D. Selvarani and T. Ravi, “A survey on data and transaction management in mobile databases,” International Journal of Database Management Systems, vol. 4, no. 5, pp. 1–20, 2012. [Google Scholar]
9. V. Ramaj, Y. Januzaj and Y. Januzaj, “Transactions management in mobile database,” International Journal of Computer Science Issues, vol. 13, no. 3, pp. 39–44, 2016. [Google Scholar]
10. I. Ahmed, H. Karvonen, T. Kumpuniemi and M. Katz, “Wireless communications for the hospital of the future: Requirements challenges and solutions,” International Journal of Wireless Information Networks, vol. 27, no. 1, pp. 4–17, 2020. [Google Scholar]
11. P. Kumar, “Fault tolerance approach in mobile distributed systems,” International Journal of Computer Applications, vol. 2015, no. 2, pp. 15–19, 2015. [Google Scholar]
12. A. Chandna, “Mobile database design: A key factor in mobile computing,” in Proc. of the 5th National Conf. on Computing for Nation Development, New Delhi, India, pp. 1–4, 2011. [Google Scholar]
13. V. Kumar, Mobile database recovery. In: Fundamentals of Pervasive Information Management Systems, 2nd ed., Hoboken, New Jersey, USA: John Wiley & Sons, pp. 219–238, 2013. [Google Scholar]
14. D. Murthy and N. Jack, “Game theoretic modelling of service agent warranty fraud,” Journal of the Operational Research Society, vol. 68, no. 11, pp. 1399–1408, 2017. [Google Scholar]
15. S. Bonau, “A case for behavioral game theory,” Journal of Game Theory, vol. 6, no. 1, pp. 7–14, 2017. [Google Scholar]
16. D. Satria, D. Park and M. Jo, “Recovery for overloaded mobile edge computing,” Future Generation Computer Systems, vol. 70, pp. 138–147, 2017. [Google Scholar]
17. Y. F. Mokhtar, Saad, M. Darwish and M. M. Madbouly, “An enhanced database recovery model based on game theory for mobile applications,” Advances in Intelligent Systems and Computing, vol. 1261, pp. 16–25, 2021. [Google Scholar]
18. B. K. Saraswat, R. Suryavanshi and D. S. Yadav, “A comparative study of checkpointing algorithms for distributed systems,” International Journal of Pure and Applied Mathematics, vol. 118, no. 20, pp. 1595–1603, 2018. [Google Scholar]
19. A. Silberschatz, H. F. Korth and S. Sudarshan, “Recovery system,” in Database System Concepts, 7th edition, New York, USA: McGraw-Hill Education, pp. 907–957, 2020. [Google Scholar]
20. S. E. George and I. R. Chen, “Movement-based checkpointing and logging for failure recovery of database applications in mobile environments,” Distributed and Parallel Databases, vol. 23, no. 3, pp. 189–205, 2008. [Google Scholar]
21. P. Jaggi and A. Singh, “Log based recovery with low overhead for large mobile computing systems,” Journal of Information Science and Engineering, vol. 29, no. 5, pp. 969–984, 2013. [Google Scholar]
22. C. Chowdhury and S. Neogy, “Checkpointing using mobile agents for mobile computing system,” International Journal of Recent Trends in Engineering, vol. 1, no. 2, pp. 26–29, 2009. [Google Scholar]
23. H. Mansouri, N. Badache, M. Aliouat and A. Pathan, “A new efficient checkpointing algorithm for distributed mobile computing,” Control Engineering and Applied Informatics, vol. 17, no. 2, pp. 43–54, 2015. [Google Scholar]
24. M. Mahmoodi, A. Baraani and M. Khayyambashi, “Recovery time improvement in the mobile database systems,” in Proc. of the Int. Conf. on Signal Processing Systems, Singapore, Singapore, pp. 688–692, 2009. [Google Scholar]
25. M. J. Pamila and K. Thanushkodi, “Log management support for recovery in mobile computing environment,” International Journal of Computer Science and Information Security, vol. 3, no. 1, pp. 1–6, 2009. [Google Scholar]
26. R. S. Chowhan, “Mobile agent programming paradigm and its application scenarios,” International Journal of Current Microbiology and Applied Sciences, vol. 7, no. 5, pp. 3269–3273, 2018. [Google Scholar]
27. A. Belghiat, E. Kerkouche, A. Chaoui and M. Beldjehem, “Mobile agent-based software systems modeling approaches: A comparative study,” Journal of Computing and Information Technology, vol. 24, no. 2, pp. 149–163, 2016. [Google Scholar]
28. M. Kekgathetse and K. Letsholo, “A survey on database synchronization algorithms for mobile device,” Journal of Theoretical and Applied Information Technology, vol. 86, pp. 1–9, 2016. [Google Scholar]
29. A. R. Bhagat and V. B. Bhagat, “Mobile database review and security aspects,” International Journal of Computer Science and Mobile Computing, vol. 3, no. 3, pp. 1174–1182, 2014. [Google Scholar]
30. X. Liang and Z. Yan, “A survey on game theoretical methods in human-machine networks,” Future Generation Computer Systems, vol. 92, no. 1, pp. 674–693, 2019. [Google Scholar]
31. H. Shaha, V. Kakkada, R. Patela and N. Doshi, “A survey on game theoretic approaches for privacy preservation in data mining and network security,” Procedia Computer Science, vol. 155, no. 2, pp. 686–691, 2019. [Google Scholar]
32. B. Z. Orbay and L. Sevgi, “Game theory and engineering applications,” IEEE Antennas and Propagation Magazine, vol. 56, no. 3, pp. 256–267, 2014. [Google Scholar]
33. G. Gerasimou, “Dominance-solvable multi-criteria games with incomplete preferences,” Economic Theory Bulletin, vol. 7, no. 2, pp. 165–171, 2019. [Google Scholar]
34. H. Trivedi and M. Mali, “A review on network simulator and its installation,” International Journal of Research and Scientific Innovation, vol. I, no. IX, pp. 115–116, 2014. [Google Scholar]
35. C. Gayathri and R. Vadivel, “An overview: Basic concept of network simulation tools,” International Journal of Advanced Research in Computer and Communication Engineering, vol. 6, no. 1, pp. 19–22, 2017. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |