Computers, Materials & Continua DOI:10.32604/cmc.2022.019120
Article

Diffusion Based Channel Gains Estimation in WSN Using Fractional Order Strategies

Nasir Mahmud Khokhar1, Muhammad Nadeem Majeed2 and Syed Muslim Shah3,*

1Department of Computer Engineering, University of Engineering and Technology, Taxila, 47050, Pakistan
2Punjab University College of Information Technology, University of Punjab, Lahore, 54000, Pakistan
3Department of Electrical Engineering, Capital University of Science and Technology, Islamabad, 44000, Pakistan
*Corresponding Author: Syed Muslim Shah. Email: s.m.shah@ieee.org
Received: 02 April 2021; Accepted: 17 May 2021

Abstract: In this study, it is proposed that the diffusion least mean square (LMS) algorithm can be improved by applying the fractional order signal processing methodologies. Application of Caputo’s fractional derivatives are considered in the optimization of cost function. It is suggested to derive a fractional order variant of the diffusion LMS algorithm. The applicability is tested for the estimation of channel parameters in a distributed environment consisting of randomly distributed sensors communicating through wireless medium. The topology of the network is selected such that a smaller number of nodes are informed. In the network, a random sleep strategy is followed to conserve the transmission power at the nodes. The proposed fractional order modified diffusion LMS algorithms are applied in the two configurations of combine-then-adapt and adapt-then-combine. The average squared error performance of the proposed algorithms along with its traditional counterparts are evaluated for the estimation of the Rayleigh channel parameters. A mathematical proof of convergence is provided showing that the addition of the nonlinear term resulting from fractional derivatives helps adjusts the autocorrelation matrix in such a way that the spread of its eigenvalues decreases. This increases the convergence as well as the steady state response even for the larger step sizes. Experimental results are shown for different number of nodes and fractional orders. The simulation results establish that the accuracy of the proposed scheme is far better than its classical counterparts, therefore, helps better solves the channel gains estimation problem in a distributed wireless environment. The algorithm has the potential to be applied in other applications related to learning and adaptation.

Keywords: Diffusion strategies; distributed channel gains; fractional derivatives; mean squared error

1  Introduction

Adaptive algorithms provide solutions including learning and inference to a class of problems arising in signal processing, instrumentations, control systems, machine learning and evolutionary computations which are all related to applied sciences and engineering [1,2,3]. The workhorse or the performance metric in these algorithms is the minimization of Mean Squared Error (MSE) in one way or the other. The MSE is the expected value of the squared error which is difference between the desired output and the model or the estimated output. In the recent past, fractional calculus (FC) theory has been applied in the optimization process for algorithms based on the MSE to develop Fractional-Order (FO) adaptive frameworks. Their applications include solution of quadratic Riccati equation [4], electromagnetic field theory [5], railway track model [6], continues and discrete time fractional linear systems [7,8], active noise control systems [9], and tracking of time varying fading channels characterized by high Doppler shifts in a vehicular communication system [10]. In comparison to the standard integer order calculus where the orders of the differentiation operation are classified in a commensurate manner of 1st, 2nd, 3rd and so on, the fractional order calculus generates the same results not only for these integer orders but are also applicable with different fractional orders. Least Mean Square (LMS) based diffusion strategies have recently been applied to model adaptive networks. These especially useful when there are limited number of informed agents involved to achieve an objective in a collaborative manner [11]. The applications include distributed sensing and estimation, online machine learning, intrusion detection, and target localization. One of the important problems is the channel gains estimation in a distributed wireless sensor network (WSN) [12]. In WSN, mostly a random sleep strategy is applied to conserve transmission energy. In the case of randomly positioned sensors, estimation of the initial channel gains become very important for adjusting the transmission power which helps prolong the operation time. The duty cycling scheme is mostly used [13–16] where a small number of nodes are in awakening mode. In the recent past, one of the most suitable and applied technique is the Diffusion Least Mean Square (DLMS) algorithm [11,13] in distributed applications since it does not require any prior information about the distribution. The DLMS algorithm, however, has the disadvantage of slow convergence even for the maximum step size of unity as compared to algorithms requiring prior information such expectation propagation approach [12], although the latter is as computationally expensive. Recently, FO Signal Processing (FOSP) techniques [17,18] have been found useful in applications such as the development of FO variant of filtered error LMS for active noise control systems [9] and the FO constant modulus algorithm [8] for blind equalization, and [10] tracking of multipath channels. FC relies on new feature space in comparison with the traditional integer order derivatives such as treatment of FO chaotic systems [19,20] and exploited for the solution of different problems arising in applied physics and engineering such as modified least mean square [21], complex domain LMS and NLMS algorithms for channel equalization [22], active noise control systems [23], Improved design of digital fractional-order differentiator [24], and chemotaxis model involving fractional operators [25]. The FC adaptive strategies have seen its importance in system identification of Hammerstein type and outperform the standard counterparts such as vibration control [26], uncertain chaotic systems [27], FO constant modulus blind algorithms [8], tracking of Rayleigh fading sequences [10], momentum LMS for parameter estimation of Hammerstein systems [28]. We have observed that different variants of the diffusion LMS have been proposed [12,13,29] and applied to the problems of distributed sensing and estimation [30–33], machine learning [34–37], intrusion detection [38–40] and target localization [41], and channel gains estimation [8,42–44]. In this study, we propose a fractional variant of the Diffusion LMS and apply in its two configurations. This paper contributes by proposing FO DLMS and its formulation for the estimation of channel gains in distributed WSN. We consider modelling of the channel gains [8,19], which are generated using the path loss and log-normal effects [38–46]; and then the estimation of these gains through the FO DLMS. Recently, similar techniques for non-distributed environments published in reputed databases includes RC circuit modelled with nonlinear differential order system [47], design of multi-innovation fractional LMS algorithm [48], fractional evolutionary processing [49], power signal parameter estimation [50], and design of momentum fractional LMS for Hammerstein nonlinear system identification [51]. Evaluation through numerical experimentation is performed for different number of sleep cycles, compare the results with conventional DLMS and for different fractional orders. The performance metric of average squared error is used for the assessment. The contributions of the study are:

•   Development of FO Diffusion Least Mean Square (FO DLMS) for application of channel estimation in distributed wireless sensor networks.

•   Development of FO variant of the LMS algorithm to have fast convergence with stable MSE performance for larger step size.

•   There will be few nodes alive/informed to conserve energy by reducing communication overhead. The random sleep strategy will be used for this purpose.

•   Modification for both combine-then-adapt (CTA) and adapt then-combine (ATC) configurations suggested and experimentations.

•   Mathematical convergence analysis for performance for the proof of concept and simulation comparison of proposed strategies will be compared with existing techniques.

•   Conclusion and future enhancement applications will be stated.

The paper is organized as follows. Sections 2 and 3 describe the channel estimation problem in a two nodes communications perspective. Section 4 presents introduction to fractional derivatives especially for polynomial functions. Section 5 presents a distributed wireless channel gains estimation using the DLMS algorithm and Section 6 discuss the channel gains estimation for the CTA and ATC mechanisms using fractional derivative based DLMS. In Section 7, Simulation results and computational performance is presented and finally the main concluding remarks and future work is proposed.

2  System Model and MSE Based Adaptive Algorithms

Designing adaptive algorithms requires that the filter weights are progressively adjusted according to an optimization criterion. This criterion is mostly based on the input environment and the resulting error. To make a reliable communication between nodes, it is necessary that channel gains be estimated properly. In a distributed environment with limited power at the nodes, early channel parameters estimation helps improve frame efficiency through small number of training or pilot symbols possible and the conservation of power through the avoidance of re-transmissions. This section is divided in two subsections including (a) two nodes channel estimation as shown in Fig. 1, and (b) channel gains estimation in a distributed wireless sensor network in which the nodes are positioned randomly. The basic principle is to send training or pilot symbols to estimate the channel, then send a block of useful data and using the already obtained channel estimates for compensation of the channel effects. We consider the transmission of Binary Phase Shift Keying (BPSK) symbols drawn from a finite alphabet set x through a channel with memory, modelled as an Mth order Finite Impulse Response (FIR) filter. This is represented by the vector hlk(n)=[hlk(n),hlk(n−1),…,hlk(n−M+1)]T; where (.)T represents the vector transpose and the subscript lk represents link between nodes l and k. The received signal is formed from the channel output, that is, ∑i=0M−1hlk(i)x(k−i) and is corrupted by the additive noise. The corresponding input regression vector is represented by xlk(n)=[xlk(n),xlk(n−1),…,xlk(n−N+1)]T. In the training phase, the transmitted signal sequence x(n) is known to the receiver and is convolved with the estimated channel response of the adaptive filter to produce an output denoted by ylk(n)=∑i=0M−1h^lk(t)x(n−i). The estimator relies on an FIR filter for the estimation of the channel gains at a particular node and an adaptation and step size adjustment for progressively adjusting the FIR filter weights to ensure stability and convergence. Ideally, h^lk(n)=dlk(n). The estimation error is the difference between the channel and the filter outputs, that is, e(n)=d(n)−d^(n), and the optimization objective is to keep the error e(n) as small as possible.

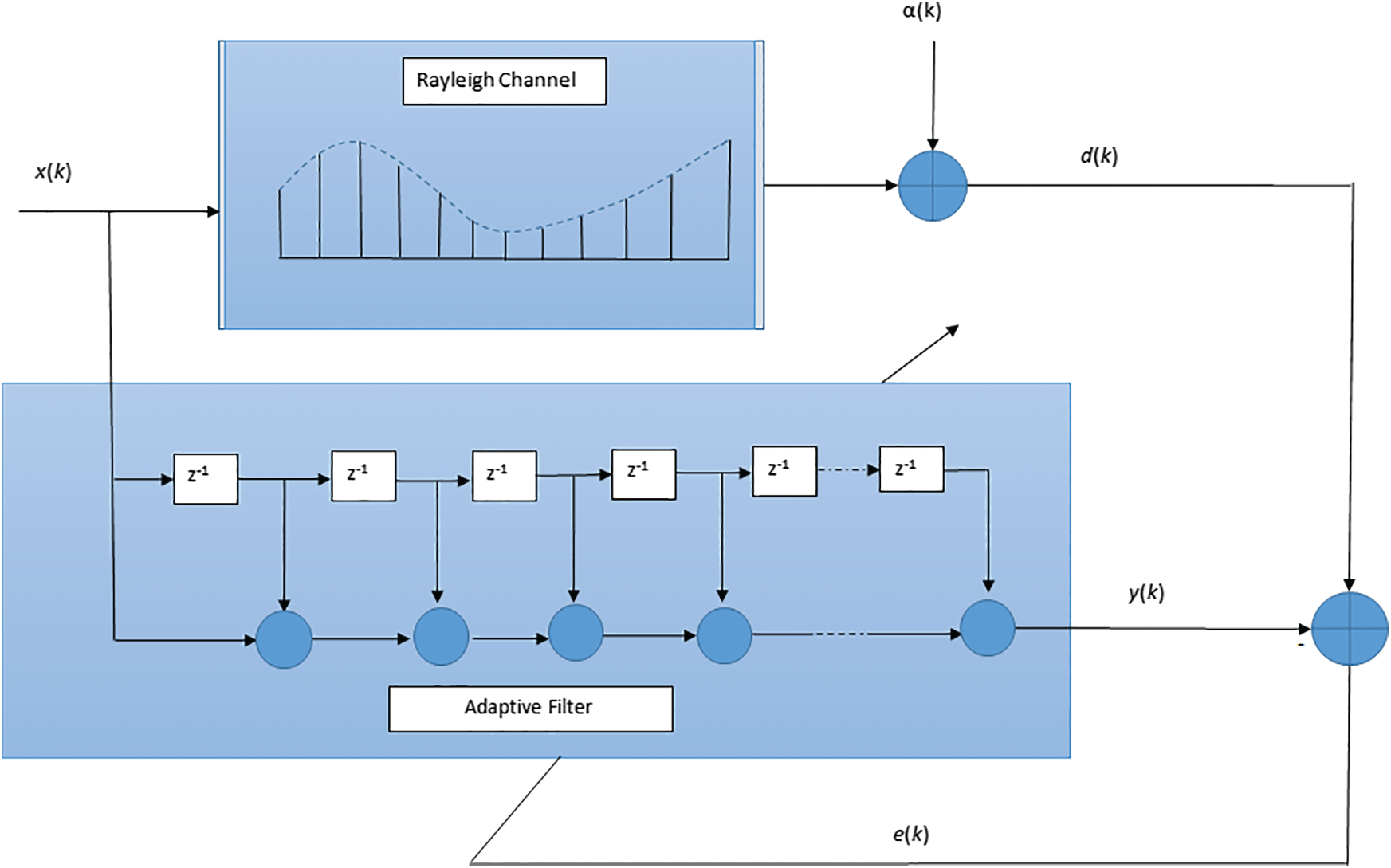
Figure 1: Block diagram for channel estimation on a single node

Fig. 2 shows a block diagram of the system with discrete-time Mth order FIR filter representing the channel h(n)=[h0,h1,h2,…,hM−1]T at time instant n, the channel output samples d(n) are acquired in the presence of noise which is modelled as additive Gaussian random variable with zero mean and unit variance, that is, d(n)=∑i=0M−1hlk(i)x(n−i)+δ(n). An FIR filter is used to estimate a desired signal d(n), with u(n)=[u0,u1,u2,…,uM−1]T as the input vector, where n is the index or sample number. It is assumed that u(n) and d(n) are obtained from infinite length random processes. The symbol y(n)=uT(n)h(n)=hT(n)u(n) represents the output of the FIR filter and e(n) is the estimation error given by the difference e(n)=d(n)−uT(n)h(n). The output of the filter is adjusted iteratively so that it matches the desired signal d(n) and the error between the desired response and output of the filter is progressively minimized. The Mean Square Error (MSE) is one of the criterions used for the design of adaptive filters and is expressed as follows:

ξ(n)=E[|e2(n)|] (1)

where the operator E[.] represents the statistical expected value. The MSE criterion is best suited for the performance comparison because it is mathematically tractable, physically relevant to energy and has a single global minimum (or maximum) point resulting in optimal values of the filter coefficients [46]. Particularly, in the case of absence of noise, it produces an unbiased estimation. This is characteristic of non-recursive FIR filters that have a smooth performance surface with continuous derivatives. The performance function ξ(n) is, therefore, a bowl-shaped hyper paraboloid with one minimum point. This point represents the optimal filter coefficients that are the true or desired weights for an adaptive filter to achieve optimal performance in the given application. In (1), the expectation operation applied to the squared error results in the generation of auto-correlation matrix and cross correlation vector. However, the auto and cross correlation coefficients need to be known beforehand and the method is not practically applicable. Moreover, for the Wiener Filter case, the calculation of optimal weights requires computationally complex matrix operations of multiplication and inverse. An iterative algorithm, on the other hand is more appropriate for practical use and suits the framework of an adaptive system with changing environment [46]. The basic philosophy in such cases is to minimize the MSE at each time instant n, by applying a correction term Δh(n) to the filter weights h(n) to form a new set of coefficients at time n + 1, that is:

h(n+1)=h(n)+Δh(n) (2)

The design objective of the adaptive filters is determining the correction term such that the filter weights converge to the desired response as early as possible and adjust the weights when in the steady state of operation. The most commonly techniques using first order derivative based gradient search method include the Least Mean Squares (LMS) and the Recursive Least Squares (RLS) algorithms. The first is based on the instantaneous error which makes it attractive for real time applications but has relatively slow convergence. The second recursively approximates the autocorrelation matrix leading to a faster convergent algorithm [34,40], but it is computationally expensive.

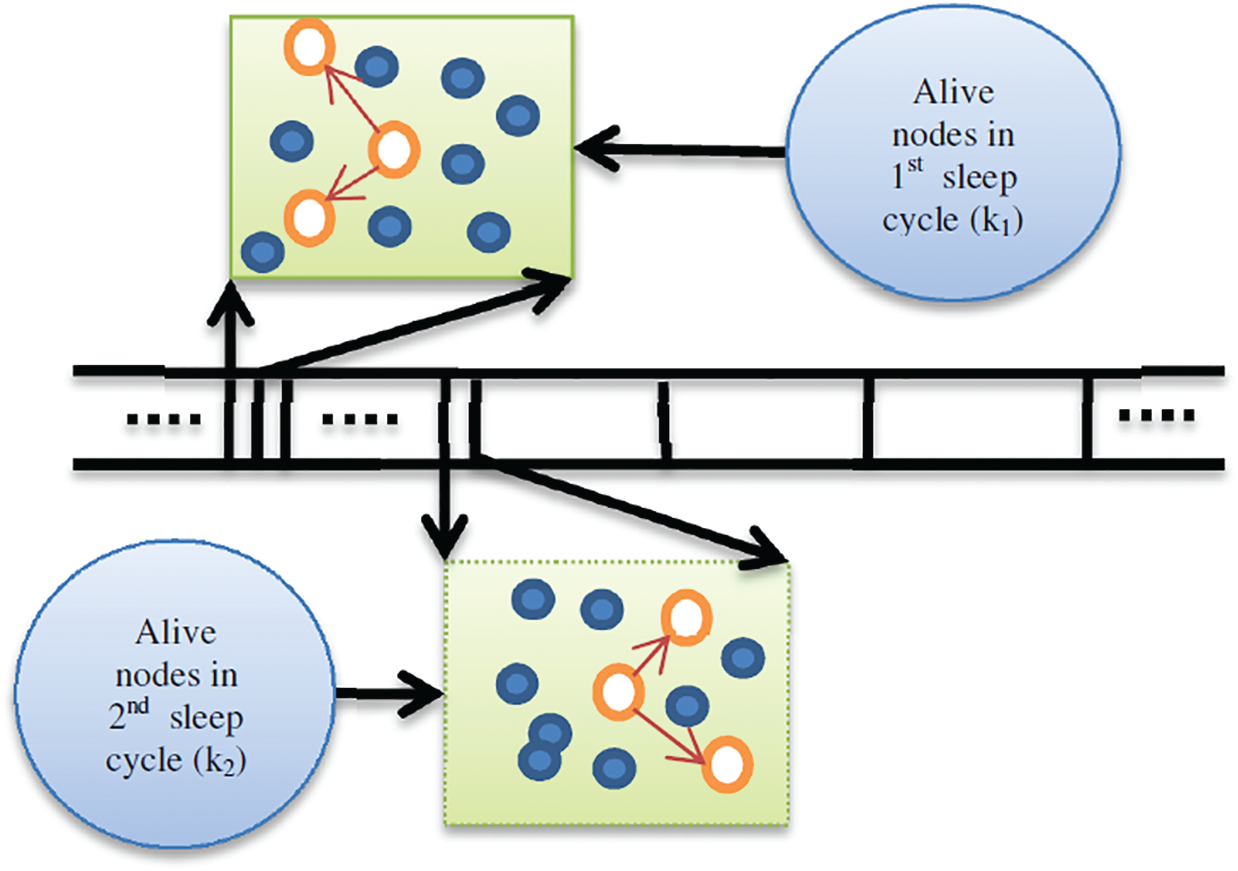
Figure 2: Random set of awaken sensor nodes during two different sleep cycles

The LMS algorithm approximates the stochastic gradient steepest descent technique. The LMS updates the tap weights iteratively in the direction of the negative gradient of the squared amplitude of instantaneous error signal [41] converging to the Wiener or optimal solution. The convergence is controlled by a step size parameter μ≤1 that for large values results in faster convergence but degrading performance in the steady-state behavior. The smaller values of step size results in slower convergence but better steady-state behavior performance. The suitability of the LMS algorithm for real world applications is owed to their low computational cost that do not require complex operations (e.g., squaring, averaging, differentials, matrix inversion or measurement of the correlation functions [42,46]) such as mean or correlation coefficients. For an N-tap adaptive FIR filter system, the correction term for the LMS algorithm can be expressed as:

−∇Jh(n)=e(n)u(n) (3)

Incorporating (3) in (2), for the correction term Δh(n)=−∇Jh(n), we obtain a generalized update equation for the channel estimates at each iteration for the LMS algorithm given by:

h^(n+1)=h^(n)+μe(n)u(n) (4)

As already stated, if μ is too small, the filter takes too long to converge, and if μ is too big, the filter may diverge in the steady state. The complexity of the LMS algorithm is O(N) [46] and constitutes a good choice for online computations in adaptive filtering.

3  Fractional Diffusion LMS Algorithm for Distributed Channel Gains Estimation

Consider the scenario of N active sensors with each one interested in estimating the unknown channel response with M-taps, that is, h^k(n)=[h^k,0,h^k,1,h^k,2,…,h^k,M−1]T. At sample index n, each sensor k independently probes h and observe its response rk(n) to the input uk(n)=[uk,0,uk,1,uk,2,…,uk,M]T in the presence of additive noise δk(n) modelled as zero mean Gaussian noise with variance σk,N2(n)=E[δk(n)δk(n)]. The desired response for each sensor k is written as [11,12]:

dk(n)=∑i=0M−1hk,iuk,i(n−i)+δk(n)=hkT(n)uk(n)+δk(n) (5)

where hk(n) represents the exact or optimal weights vector of the channel. The network objective is to choose the estimated channel vector h^k(n) such that to minimize the cost function:

minh^∑m=1NJk(n) (6)

where Jk(n)=dk(n)−h^kT(n)uk,j(n). Using random sleep strategy [12,23] for the channel estimation, now consider the first sleep cycle. Suppose that the node i is awake at sleep cycle instant k and it transmits its training sequence of length M which is denoted by uk,j(n). Each node j receives the output rk,j,i,m from the channel having gain hi,j where m∈{1,2,…,M}. The received signal at a given node will be:

rk,j,i,m=hi,jui,m+δk,j,i,m (7)

The network nodes i′∈S(k)∖{i} can use the diffusion LMS algorithm [7] to estimate hi,i′. Denote the estimate of hi,i′ at time instant m of sleep cycle instant k by h^i,i′k,m. Then, the diffusion update becomes:

h^i,i′k,m=h^i,i′k,m−1+μui,mek,i′,i,m (8)

where μ is the step size and ek,i′,i,m is the error and is equal to the difference of rk,i′,i,m and the estimator outpout h^i,i′k,m−1ui,m. At the end of each sleep cycle instant k, the nodes that are awake diffuse their estimates to get the combined estimate h~k as:

h~k=∑i∈S(k)α(k,i)h~ik (9)

where h~ik is the estimate of h at node i at the end of the sleep cycle instant k and α(k,i) satisfy ∑i∈S(k)α(k,i)=1. The nodes i∈S(k) use the combined estimate h~k for estimation during the later sleep cycle instants. The coefficients α(k,i) are free parameters that are chosen by the designer and their careful selection influences the performance of the algorithm. To further refine the estimation of channel gains, a fractional order modified diffusion LMS algorithm is proposed. The FrDLMS relies on fractional derivative based term in the standard LMS. Having the estimated channel gain h^k and the error ek,i′,i,m, the cost function that a given node has to minimize is the mean square error defined as:

J(n)=E[(rk,i′,i,m−h^i,i′k,m−1ui,m)2] (10)

The network objective is to minimize the cost function, that is, each node chooses the channel estimates h^ such that, minh^∑i=1NJi(n)=E[ei2(n)]. For minimizing, taking the partial derivative of the squared error in (10) with respect to h^ such that at a given cycle h^=h^i,i′k,m−1, we have,

∂J(n)∂h^=2e(n)∂∂h^i,i′k,m−1(rk,i′,i,m−h^i,i′k,m−1ui,m) (11)

which results in the second part of Eq. (3). To introduce fractional part [47–51], we introduce the Caputo fractional derivative of order ν such that n−1<ν<n of a function g(t)=tp, for p≥0 as given in [14,46–51] as:

Dνg(t)={Γ(p+1)Γ(p−ν+1)tp−νp>n−1 (12)

For p≤n−1, the fractional derivatives of the polynomial function g(t)=tp is zero. In (12), the operator Dν corresponds to the fractional derivative and Γ denotes the gamma function and is calculated with integral function Γ(t)=∫0∞xt−1e−xdx. Applying the Caputo derivative of Eq. (12) in (11) we have the partial derivatives as:

∂νJ(n)∂h^ν≅−2e(n)ui,m∂∂(h^i,i′k,m−1)ν(rk,i′,i,m−h^i,i′k,m−1ui,m) (13)

and on further simplifying, we have,

∂νJ(n)∂h^ν≅−2[e(n)ui,m⊙h^1−ν(n−1)Γ(2−ν)] (14)

The symbol ⊙ represents element-wise multiplication between two vectors ui,m and h^. The update expression utilizes both integer and fractional-order derivatives together; the algorithm rely on two step-sizes for learning rate control, that is, μ1 and μf and the fractional order ν which is between 0 and 1. For 0 < ν < 1 and p = 1, the Γ function always operate on R+. It is worth mentioning to note that the fractional or real power of a negative number results in a complex number. To have all the real weights, we use the following identical equation h1−ν(n)=|h|1−ν(n)sgn(h(n)) to avoid the generation of complex numbers [18]. Here, sgn is the sign function. We modify the update Eq. (4) with the correction term Δh(n) as the sum of integer order derivative as in (11) and the fractional part as in (14), and is given as:

h^i,i′k,m=h^i,i′k,m−1+μ1ui,mek,i′,i,m+μfui,mek,i′,i,m⊙h^1−ν(n−1)Γ(2−ν) (15)

where μf is step size for the fractional part in the adaptation Eq. (15). This is the final equation used to estimate the channel gains in the distributed environments and the weights so obtained would be used in the fusion Eq. (9).

Fig. 3 shows the effects of varying a weight w with different fractional powers while changing the weight from 0 to 1. The nonlinear behavior can be seen where the left side curves show the effects of different fractional orders when one considers the combined factor of F1=w2−ν/Γ(3−ν) considering both integer and fractional derivatives for the optimization while the right side shows the effects of fractional order of only the fractional part, that is, F2=w1−ν/Γ(2−ν). As opposed to the standard linear techniques, this approach helps adjust the weights according to its importance as required by partial update functions [46].

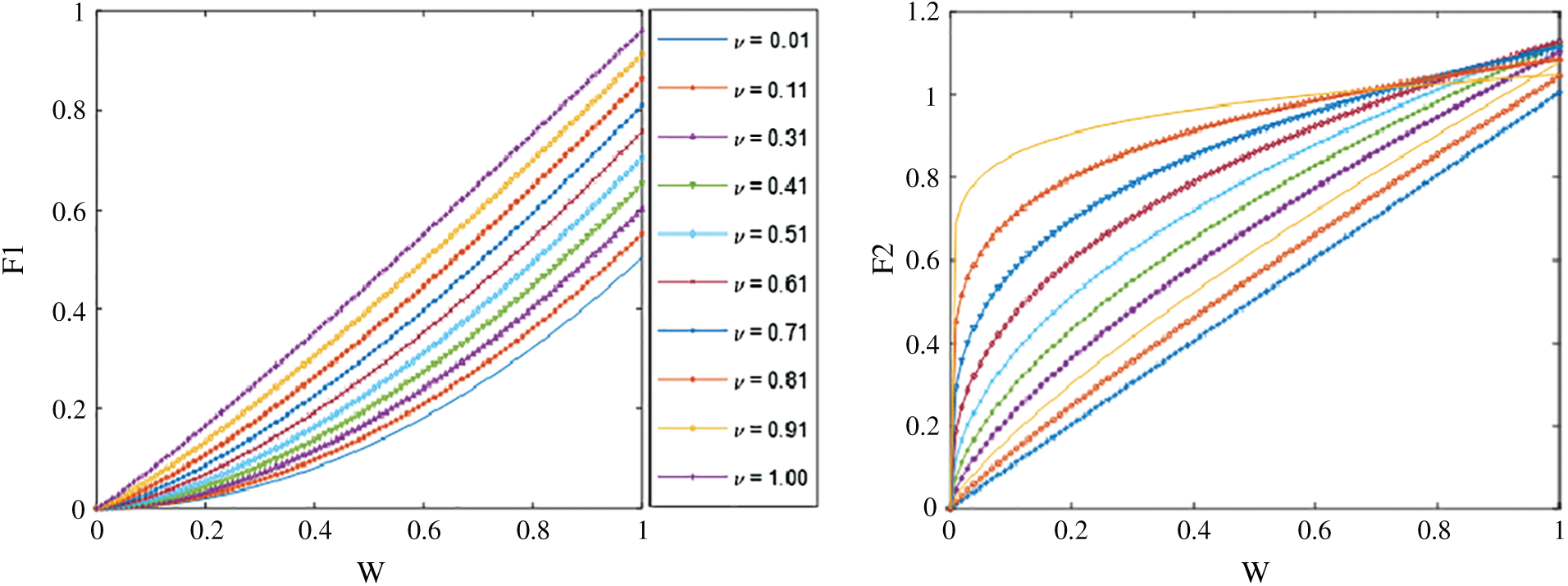
Figure 3: Weight behavior for different fractional orders

We would be considering this implementation for the two configurations of the diffusion strategies, that is, combine-then-adapt (CTA) and Adapt-then-Combine (ATC). These algorithms utilize an accumulation step [12,23] in the adaptation mechanism to fuse information obtained from the local neighborhoods. At every instant i, all the agents in the CTA strategy performs the two steps, that is, a combination step where the agent j aggregates the channel gains estimations from its neighbors to obtain the intermediate estimations of previous step i−1 and the adaptation step where agent k uses its data to update its intermediate estimations of the channel gains. The intermediate state allows information to diffuse through the network. ATC is an alternative form of the CTA diffusion strategy and is obtained by swapping the order of the combination and adaptation steps. Tab. 1 shows a summary of the fractional order diffusion algorithm implementing the ATC strategy and Tab. 2 shows the implementation of fractional order for CTA based approach. Both algorithms rely on same input and controlling parameters or data, only the adaptation parts of the algorithms are modified.

The computational complexity of the FrDLMS is a-bit higher than the DLMS, the former requires PKd(2(d−1)M+dN(N−12) additions [12] while the later require PKd(2(d−1)M+dN(N−12)+3M additions. Similarly, the number of multiplications required for the DLMS are PKd((d−1)(2M+N(N−12) while for FrDLMS are PKd((d−1)(2M+N(N−12)+MX where X is the number of fractional powers. The FrDLMS also require the calculation of fractional power of the weight vector. The memory requirements for the FrDLMS and DLMS is same, that is, (MN+N(N−12), however, the FrDLMS require two other adaptation parameters, namely, a step size and fractional order.

4  Convergence Analysis

To get the convergence properties of the fractional LMS algorithm in (15), we convert to a different frame of reference. We define an error vector v(n) at instant n as:

v(n)=h^(n)−h^o (16)

where, ho represents the optimum channel gains vector. The error due to these gains is given by:

eo(n)=r(n)−uT(n)h^o (17)

In terms of v(n), the relationship in Eq. (15) can further be written for a future gain at index n+1 as:

v(n+1)=v(n)+μ1e(n)u(n)+μfe(n)u(n)⊙v1−ν(n)Γ(2−ν) (18)

For simplicity, we put μf=Γ(2−ν)μ1 and using the value of eo(n) and taking the expectation on both sides to apply the principle of orthogonality, one would arrive at the following relation:

E[v(n+1)]=[I−μR+μR⊙E[|v(n)|1−ν]]E[v(n)] (19)

which, in simplified form can be written as:

E[v(n+1)]=[I−μR(I−I⊙E[|v(n)|1−ν])]E[v(n)] (20)

Representing the product I⊙E[|v(n)|1−ν] by F(h^(n),ν), the relation can be written as:

E[v(n+1)]=[I−μR(I−F(h^(n),ν))]E[v(n)] (21)

The mean power of the weight difference should be a decreasing function of the number of iterations and at steady state, we have,

limn→∞‖E[v(n)‖2=0 (22)

which is only possible for −1−μ(R−F(h^(n),ν))<1. This results in a simplified form:

0<μ<2R−F(h^(n),ν) (23)

In terms of maximum eigenvalue λmax, it can be written as:

0<μ<2λmax−F(h^(n),ν) (24)

This equation provides the selection of step size parameter to ensure convergence of the FLMS algorithm. It can be seen in (23), (24) that the addition of nonlinear term resulting from fractional derivatives helps adjusts the autocorrelation matrix in such a way that the spread of its eigenvalues decreases and hence, the convergence improves as well as the steady state response even for the larger step sizes.

5  Simulation Results

A logical diagram of the proposed algorithm and its application to the estimation of channel gains in a distributed environment is depicted in Fig. 4. The simulation procedure includes the initialization of parameters related to the wireless sensor network such as the number of sensor nodes N, the length of the training sequence M, the number of time instants k in the sleep cycle and the number of nodes d awake at a time. Other controlling parameters include the step sizes μ;1 and μ;f, fractional order v, and calculating a value of gamma function based on the given fractional order. The number of times a node is awake is kd/N, while the number of edges is kd.

First of all, the prior statistics of mean and covariance based on 20 thousand experiments is generated for the channel gains using only the path loss effect with path loss exponent of 4 [12]. This is followed by Monte Carlo loop. In the start, the shadowing effect based on normal distribution is added. After this, a random sleep strategy (RSS) is applied. The nearest neighbors (first and second) are found, and links are established after first, second and third sleep cycles. For each time event, a random sequence u drawn from independent and identically distributed gaussian process and modulated as binary phase shift keying symbols. The symbols are input to the channel. The output of the channel at a node is the desired reference for the error of the diffusion algorithm. The adaption algorithm based on the proposed methodology is applied for the estimates of the channel and is followed by the diffusion process. The estimates are obtained after the diffusion, the process repeats, and the average error is calculated.

We would be considering this implementation for the CTA in the given two configurations of the diffusion strategies as this is the most widely used one. Simulations results are presented for both the standard DLMS [12] and FrDLMS algorithms, plots are shown for the estimation errors. The performance metric for comparison is the average squared error. We estimate the channel gains vector h while considering a WSN having 20 nodes, it employs random sleep strategy with K=10 and d=4. The sensor positions are generated as i.i.d. with Gaussian distribution having zero mean and unit variance. The true channel gains which need to be estimated are generated with path loss and log-normal shadowing effects [33–36]. Five hundred binary phase shift keying symbols have been used for training purpose, unit variance of noise is considered for the experiments and the averaged mean squared error is obtained using 50 independent Monte Carlo runs. The performance metric of average MSE against the number sleep cycles is used for comparison purpose; three different cases with l=1,2,3 are considered. In the simulations, the step size parameter is kept at 1.0 for the fastest convergence possible for the DLMS algorithm.

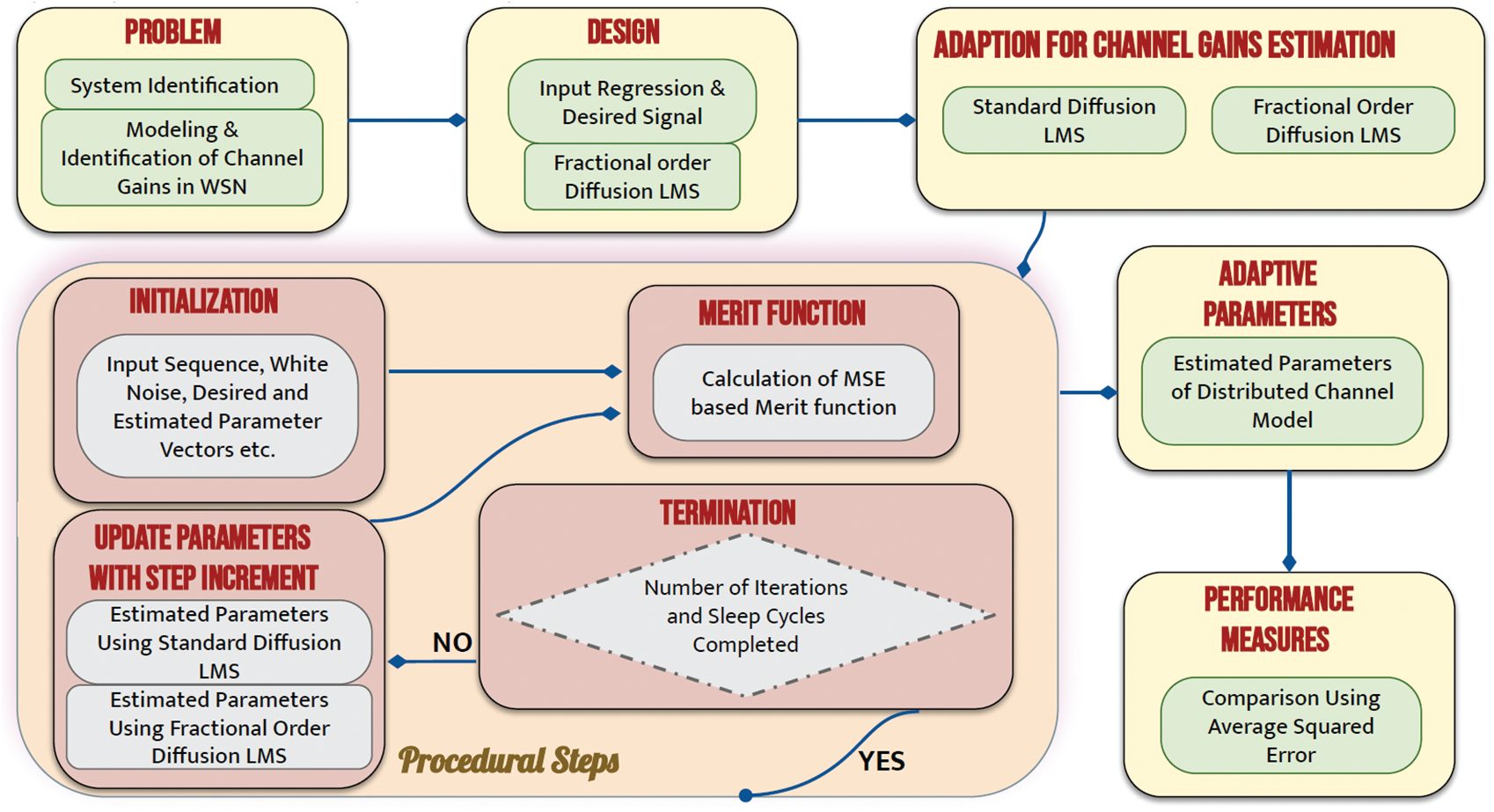
Figure 4: Logical diagram of simulation results generation

Fig. 5 shows the average squared error performance vs. the number of sleep cycles for the DLMS algorithm [12]. In the simulation, the fractional order is fixed at 0.9. It can be seen that FrDLMS performs well than DLMS, helping the WSN nodes to estimate the channel gains in small number of sleep cycles. The proposed FrDLMS algorithm has much superior performance than the DLMS algorithm. It is with almost an 8-dB gain over the DLMS algorithm.

Fig. 6 shows the average squared error performance vs. the number of sleep cycles (20) for the DLMS and FrDLMS algorithms for all the three cases, that is, ‘Case 1,’ ‘Case 2’ and ‘Case 3’ with the step size kept at 1.0 and the fractional order is set to 0.3 to see the effects of fractional order on the convergence. Again, it can be seen clearly that the FrDLMS algorithm offer better performance than the standard DLMS algorithm for this is the network conditions in which small numbers of sleep cycles are used for the estimation of channel gains. The proposed FrDLMS has much superior performance than DLMS with almost a 6-dB gain over the DLMS algorithm for all the cases. One can observe that the convergence improves with increasing the fractional order.

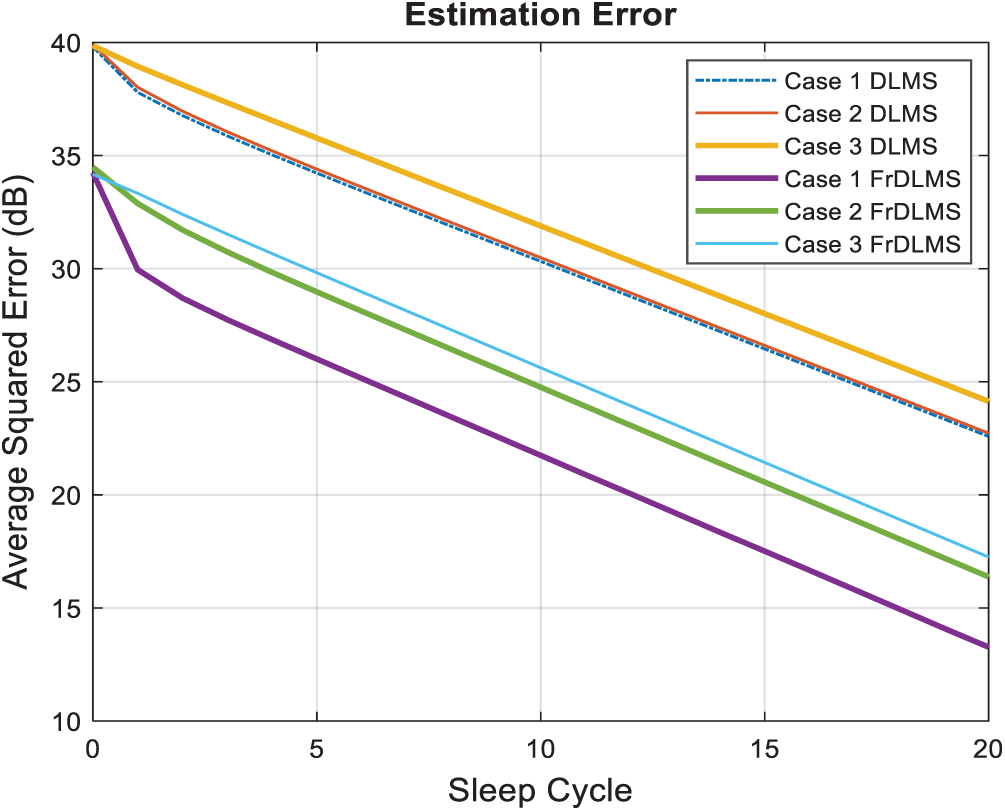
Figure 5: DLMS vs. FrDLMS for three Cases with v = 0.9

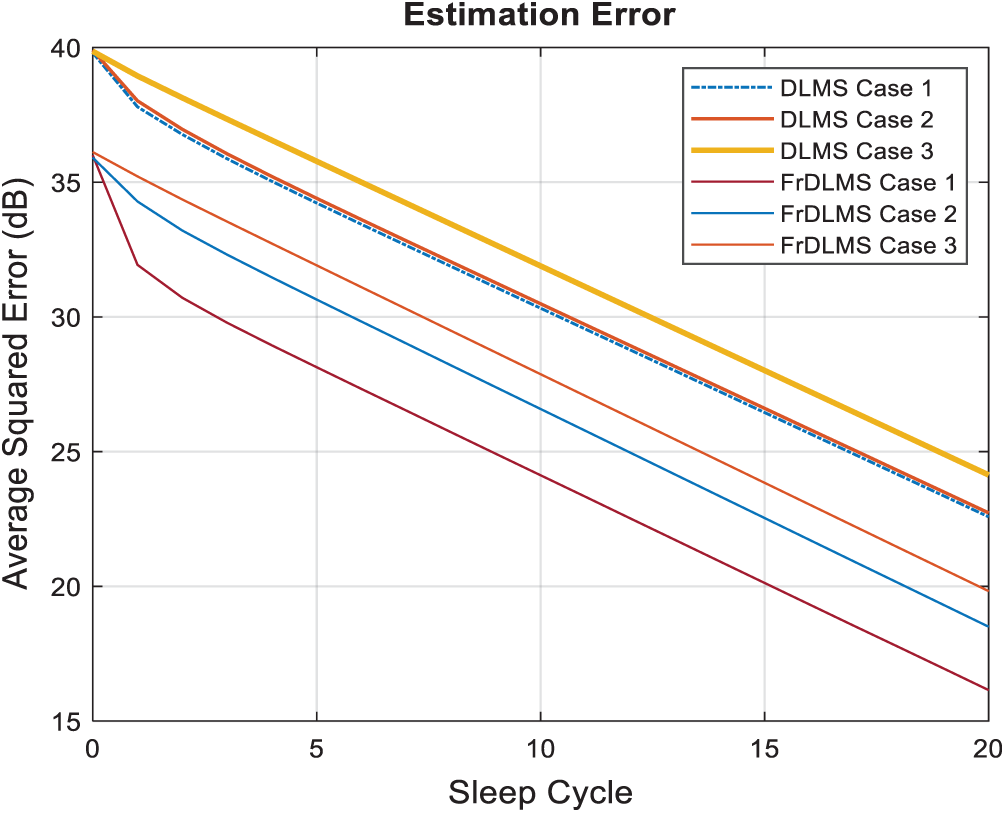
Figure 6: DLMS vs. FrDLMS for three Cases with v = 0.3

6  Conclusions

We proposed a novel fractional order modified diffusion least mean square algorithm and applied for the estimation of channel gains in a wireless sensor network. We considered different cases of the random sleep strategy; using the average squared error as the performance metric, we found that the proposed algorithm has much superior performance than its conventional counterpart. The results were generated for different fractional orders, and it was found that that the gain is of the order of 6-8-dB when 0-dB additive noise is considered at each node. The performance in terms of convergence speed increases when we increase the fractional order. We believe that the fractional order DLMS is a useful addition in fractional order signal processing; it is open to further research and can be applied in a other applications such as distributed sensing and estimation, online machine learning, intrusion detection and target localization.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  K. B. Oldham and J. Spanier, The Fractional Calculus. New York: Academic Press, 1974. [Google Scholar]

 2.  W. Shaowei and X. Mingyu, “Exact solution on unsteady Couette flow of generalized Maxwell fluid with fractional derivative,” Journal of ActaMechanica, vol. 187, no. 1, pp. 103–112, 2006. [Google Scholar]

 3.  B. Mbodje and G. Montseny, “Boundary fractional derivative control of the wave equation,” IEEE Transactions on Automatic Control, vol. 40, pp. 378–382, 1995. [Google Scholar]

 4.  Z. Odibat and S. Momani, “Modified homotropy perturbation method: Application to quadratic Riccati differential equation of fractional order,” Chaos Solitons & Fractals, vol. 36, no. 1, pp. 167–174, 2008. [Google Scholar]

 5.  N. Engheta, “On the role of fractional calculus in electromagnetic theory,” IEEE Antennas and Propagation Magazine, vol. 39, pp. 35–46, 1997. [Google Scholar]

 6.  A. Fenander, “A fractional derivative rail-pad model included in a railway track model,” Journal of Sound and Vibration, vol. 212, no. 5, pp. 889–903, 2000. [Google Scholar]

 7.  M. D. Ortiguerira, “Introduction to fractional linear systems—Part 2: Discrete-time case,” IEE Proceedings- Vision, Image and Signal Processing, vol. 147, pp. 71–78, 2000. [Google Scholar]

 8.  S. M. Shah, R. Samar, S. M. Naqvi and J. A. Chambers, “Fractional order constant modulus blind algorithms with application to channel equalization,” Electronics Letters, vol. 50, no. 23, pp. 1702–1704, 2014. [Google Scholar]

 9.  S. M. Shah, R. Samar, M. A. Z. Raja and J. A. Chambers, “Fractional normalized filtered-error least mean squares algorithm for applications in active noise control systems,” Electronics Letters, vol. 50, no. 14, pp. 973–975, 2014. [Google Scholar]

10. S. M. Shah, R. Samar and M. A. Z. Raja, “Fractional-order algorithms for tracking Rayleigh fading channels,” Nonlinear Dynamics, vol. 92, pp. 1243–1259, 2018. [Google Scholar]

11. A. H. Sayed, S. Y. Tu, J. Chen, X. Zhao and J. Z. Towfic, “Diffusion strategies for adaptation and learning over networks: An examination of distributed strategies and network behavior,” IEEE Signal Processing Magazine, vol. 30, no. 3, pp. 155–171, 2013. [Google Scholar]

12. S. Ramanan and J. M. Walsh, “Distributed estimation of channel gains in wireless sensor networks,” IEEE Transactions on Signal Processing, vol. 58, no. 6, pp. 3097–3107, 2010. [Google Scholar]

13. S. Y. Tu and A. H. Sayed, “On the influence of informed agents on learning and adaptation over networks,” IEEE Transactions on Signal Processing, vol. 61, no. 6, pp. 1339–1356, 2013. [Google Scholar]

14. J. M. Walsh, S. Ramanan and P. A. Regalia, “Optimality of expectation propagation based distributed estimation for wireless sensor network initialization,” in IEEE 9th Int. Workshop on Signal Processing Advances for Wireless Communications, Recife, Brazil, pp. 620–624, 2008. [Google Scholar]

15. K. Kredo II and P. Mohapatra, “Medium access control in wireless sensor networks,” Computer Networks, vol. 51, no. 4, pp. 961–994, 2007. [Google Scholar]

16. G. Scutari, S. Barbarossa and L. Pescosolido, “Distributed decision through self-synchronizing sensor networks in the presence of propagation delays and asymmetric channels,” IEEE Transactions on Signal Processing, vol. 56, no. 4, pp. 1667–1684, 2008. [Google Scholar]

17. A. A. Khan, S. M. Shah, M. A. Z. Raja, N. I. Chaudhary, Y. He et al., “Fractional LMS and NLMS algorithms for line echo cancellation,” Arabian Journal of Science and Engineering, pp. 1–14, 2021. https://doi.org/10.1007/s13369-020-05264-1. [Google Scholar]

18. H. Sheng, Y. Chen and T. Qiu, Fractional Processes and Fractional—Order Signal Processing: Techniques and Applications. Springer-Verlag London Limited, 2012. [Google Scholar]

19. J. B. Andersen, T. S. Rappaport and S. Yoshida, “Propagation measurements and models for wireless communications channels,” IEEE Communications Magazine, vol. 33, no. 1, pp. 42–49, 1995. [Google Scholar]

20. S. M. Shah, “Riemann–Liouville operator‐based fractional normalised least mean square algorithm with application to decision feedback equalisation of multipath channels,” IET Signal Processing, vol. 10, no. 6, pp. 575–582, 2016. [Google Scholar]

21. R. M. A. Zahoor and I. M. Qureshi, “A modified least mean square algorithm using fractional derivative and its application to system identification,” European Journal of Scientific Research, vol. 35, no. 1, pp. 14–21, 2009. [Google Scholar]

22. S. M. Shah, R. Samar, N. M. Khan and M. A. Z. Raja, “Design of fractional order variants of complex LMS and NLMS algorithms for adaptive channel equalization,” Nonlinear Dynamics, vol. 88, pp. 839–858, 2017. [Google Scholar]

23. S. M. Shah, R. Samar, N. M. Khan and M. A. Z. Raja, “Fractional-order adaptive signal processing strategies for active noise control systems,” Nonlinear Dynamics, vol. 85, no. 3, pp. 1363–1376, 2016. [Google Scholar]

24. C. C. Tseng, “Improved design of digital fractional-order differentiator using fractional sample delay,” IEEE Circuits and System Transactions, vol. 53, pp. 193–203, 2006. [Google Scholar]

25. V. F. Morales-Delgado, J. F. Gmez-Aguilar, S. Kumar and M. A. Taneco-Hernndez, “Analytical solutions of the Keller-Segel chemotaxis model involving fractional operators without singular kernel,” European Physical Journal Plus, vol. 133, no. 200, 2018. [Google Scholar]

26. M. Zilletti, S. J. Elliott and M. G. Tehrani, “Adaptive vibration control of a mechanical system with nonlinear damping excited by a tonal disturbance,” Journal of the Acoustical Society of America, vol. 137, pp. 2258, 2015. [Google Scholar]

27. M. Afshari, “Global sliding mode control via linear matrix inequality approach for uncertain chaotic systems with input nonlinearities and multiple delays,” Journal of Computational and Nonlinear Dynamics, vol. 13, no. 3, pp. 31008, 2018. [Google Scholar]

28. N. I. Chaudhary, S. Zubair and M. A. Z. Raja, “Design of momentum LMS adaptive strategy for parameter estimation of Hammerstein controlled autoregressive systems,” Neural Computing and Applications, vol. 30, pp. 1133–1143, 2018. [Google Scholar]

29. C. G. Lopes and A. H. Sayed, “Diffusion least-mean squares over adaptive networks: Formulation and performance analysis,” IEEE Transactions on Signal Processing, vol. 56, no. 7, pp. 3122–3136, 2008. [Google Scholar]

30. A. H. Sayed, S. Y. Tu, J. Chen, X. Zhao and Z. J. Towfic, “Diffusion strategies for adaptation and learning over networks,” IEEE Signal Processing Magazine, vol. 30, no. 3, pp. 155–171, 2013. [Google Scholar]

31. X. Zhao and A. H. Sayed, “Clustering via diffusion adaptation over networks,” in Proc. of Int. Workshop Cognitive Information Proc., Parador de Baiona, Spain, pp. 1–6, 2012. [Google Scholar]

32. A. H. Sayed, “Diffusion adaptation over networks,” in E-Reference Signal Processing, R. Chellapa, S. Theodoridis, (Eds.Amsterdam, The Netherlands: Elsevier, 2012, see also arXiv: 1205.4220v1 [cs.MA]. [Google Scholar]

33. A. Goldsmith, Wireless Communications. New York, USA: Cambridge University Press, 2005. [Google Scholar]

34. L. Gordon and G. L. Stuber, Principles of Mobile Communication, 2nd ed., Norwell, Mass, USA: Kluwer Academic Publishers, 2001. [Google Scholar]

35. A. Ribeiro and G. B. Giannakis, “Bandwidth-constrained distributed estimation for wireless sensor networks—Part i: Gaussian case,” IEEE Transactions on Signal Processing, vol. 54, no. 3, pp. 1131–1143, 2006. [Google Scholar]

36. I. F. Akyildiz, W. Su, Y. Sankarasubramaniam and E. Cayirci, “Wireless sensor networks: A survey,” in Computer Networks, vol. 38, no. 4, pp. 393–422, 2002. [Google Scholar]

37. D. Cassioli, M. Z. Win and A. F. Molisch, “The ultra-wide bandwidth indoor channel: From statistical model to simulations,” IEEE Journal on Selected Areas in Communications, vol. 20, no. 6, pp. 1247–1257, 2002. [Google Scholar]

38. E. Green and M. Hata, “Microcellular propagation measurements in an urban environment,” in IEEE Int. Sym. on Personal, Indoor and Mobile Radio Communications, UK, pp. 324–328, 1991. [Google Scholar]

39. C. F. Hsin and M. Liu, “Randomly duty-cycled wireless sensor networks: Dynamics of coverage,” IEEE Transactions on Wireless Communications, vol. 5, no. 11, pp. 3182–3192, 2006. [Google Scholar]

40. A. Saleh and R. Valenzuela, “Statistical model for indoor multipath propagation,” IEEE Journal on Selected Areas in Communications, vol. 5, no. 2, pp. 128–137, 1987. [Google Scholar]

41. A. Ephremides, “Energy concerns in wireless networks,” IEEE Wireless Communications, vol. 9, no. 4, pp. 48–59, 2002. [Google Scholar]

42. V. Kawadia and P. R. Kumar, “Principles and protocols for power control in wireless ad hoc networks,” IEEE Journal on Selected Areas in Communications, vol. 23, no. 1, pp. 76–88, 2005. [Google Scholar]

43. O. Dousse, P. Mannersalo and P. Thiran, “Latency of wireless sensor networks with uncoordinated power saving mechanisms,” in Proc. of the 5th ACM Mobihoc, Tokyo, Japan, pp. 109–120, 2004. [Google Scholar]

44. K. S. Miller and B. Ross, An Introduction to the Fractional Calculus and Fractional Differential Equations. New York: Wiley, 1993. [Google Scholar]

45. Y. Wang, “Dynamic analysis and synchronization of conformable fractional-order chaotic systems,” European Physical Journal Plus, vol. 133, pp. 481, 2018. [Google Scholar]

46. S. M. Shah, “Applications of fractional derivatives in adaptive signal processing systems,” Ph.D Thesis, Capital University of Science and Technology, Islamabad, Pakistan, 2019. [Google Scholar]

47. M. A. Z. Raja, A. Mehmood, S. A. Niazi and S. M. Shah, “Computational intelligence methodology for the analysis of RC circuit modelled with nonlinear differential order system,” Neural Computing and Applications, vol. 30, no. 6, pp. 1905–1924, 2018. [Google Scholar]

48. N. I. Chaudhary, M. A. Z. Raja, Y. He, Z. A. Khan and J. A. T. Machado, “Design of multi-innovation fractional LMS algorithm for parameter estimation of input nonlinear control autoregressive systems,” Applied Mathematical Modelling, vol. 93, pp. 412–425, 2021. [Google Scholar]

49. Y. Muhammad, R. Akhtar, R. Khan, F. Ullah, M. A. Z. Raja et al., “Design of fractional evolutionary processing for reactive power planning with FACTS devices,” Scientific Reports, vol. 11, no. 1, pp. 1–29, 2021. [Google Scholar]

50. N. I. Chaudhary, R. Latif, M. A. Z. Raja and J. A. T. Machado, “An innovative fractional order LMS algorithm for power signal parameter estimation,” Applied Mathematical Modelling, vol. 83, pp. 703–718, 2020. [Google Scholar]

51. N. I. Chaudhary, S. Zubair, M. S. Aslam, M. A. Z. Raja and J. A. T. Machado, “Design of momentum fractional LMS for Hammerstein nonlinear system identification with application to electrically stimulated muscle model,” European Physical Journal Plus, vol. 134, no. 407, pp. 1–15, 2019. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.