Computers, Materials & Continua DOI:10.32604/cmc.2022.019833
Article

Improving Supply Chain Performance Through Supplier Selection and Order Allocation Problem

Chia-Nan Wang1, Ming-Cheng Tsou2,*, Chih-Hung Wang3, Viet Tinh Nguyen4 and Pham Ngo Thi Phuong5

1Department of Industrial Engineering and Management, National Kaohsiung University of Science and Technology, Kaohsiung, 80778, Taiwan
2Department of Shipping Technology, National Kaohsiung University of Science and Technology, Kaohsiung, 80778, Taiwan
3Department of International Business, Shih Chien University, Taipei, 80778, Taiwan
4Faculty of Commerce, Van Lang University, Ho Chi Minh City, 70000, Vietnam
5Faculty of Industrial Engineering and Management, International University, Ho Chi Minh City, 70000, Vietnam
*Corresponding Author: Ming-Cheng Tsou. Email: mingchengtsou891@gmail.com
Received: 26 April 2021; Accepted: 27 May 2021

Abstract: Suppliers play the vital role of ensuring the continuous supply of goods to the market for businesses. If businesses do not maintain a strong bond with their suppliers, they may not be able to secure a steady supply of goods and products for their customers. As a result of failure to deliver products, the production and business activities of the business can be delayed which leads to the loss of customers. Normally, each trading enterprise will have a variety of commodity supply chains with multiple suppliers. Suppliers play an important role and contribute to the value of the entire supply chain. Should any supplier encounters a problem, the whole supply chain of businesses will be affected and could lead to not guaranteeing the stable supply to the market. Thus, suppliers can be seen as a threat to businesses where they have the ability to increase input prices or decrease the quality of the required products and services they provide. The quantity of the business, and the supply lead time directly affect the operations and reduce the profitability of the business. The paper mainly focuses on the supplier selection problem under a variety of price level and product families when using a two-phase fuzzy multi-objective linear programming. The objectives of the proposed model are to minimize the total purchasing and ordering cost in order to reduce the quantity of defective materials and the late-delivery components from suppliers. Moreover, the piecewise linear membership function is applied in the model to determine an optimal solution which is based on the requirement of decision makers under their fuzzy environment. The results of this study can be applied in various business environment and provide a reliable decision tool for choosing potential suppliers relating to these objectives. Based on the results, the company can make a good decision on supplier selection; therefore, the company can improve the quality and quantity of their final product. This is because, the best supplier can supply raw material using just-in-time application and reduce production risk on the manufacturing process.

Keywords: Supplier selection; multi-objective; linear programming; multi-price level; multi-product; fuzzy sets

1  Introduction

In the current international competitive environment, most companies attempt to meet the customers’ demand, improve quality, and reduce manufacturing cost. As a result, they focus heavily on production cost and supplier selection. When the raw materials cost increase, the final price of the product will also increase. Choosing an appropriate supplier who have significant influence on manufacturers’ performance can potentially reduce the purchasing cost, decrease production lead time and increase customer satisfaction.

Order allocation is one of a strategic purchasing decision, which directly affects the relationship between a company and suppliers. Buyers usually order from many suppliers since this will reduce the strengthen of suppliers’ power [1].

Multiple Criteria Decision Making (MCDM) is a process that people apply in order to determine decisions under two or more conflicting criteria. The reason for the conflict between objectives is that the improvement in an objective can only be made if there are sacrifices from other objectives. There is no optimal solution for this selection problem because all the decisions are selected based on the decision makers’ preferences.

According to the raw material requirements, the supplier selection problem, which involves several conflicting factors such as price, quality, and delivery [1], can be categorized into two types [2]:

—The best supplier selected from a pool of available suppliers who can satisfy all customers’ requirement.

—The selection of potential suppliers from multi sourcing can meet demand which none of individual supplier can meet.

There is a discrepant method of MCDM [3] which are categorized in terms of articulation for preferences in solving engineering problems. Firstly, priority articulation of preferences method allows the users or designers to specify preferences, which is clustered in terms of relative importance of different objectives using methods such as Linear Aggregation, Weighted Sum Method, Compromise Programming Method, Weighted Min-Max Method, Goal Programming, Exponential Weighted Method, and many more. Second, a posteriori articulation of preference method such as Genetic Algorithm, Normal boundary intersection method, and normal constraint method. The decision makers have difficulty in expressing an explicit approximate of the preference function. As a result, this method can assist decision makers, setting their preferences into the parameter set that can be used to choose from a range of solutions. Last, methods with no articulation of preferences: decision makers cannot identify what they prefer. Additionally, this method does not require any articulation of preferences and significantly ease without weight. This method includes compromise function, objective sum, and objective product and so on.

The variety range of the uncertainty factor will affect the optimal solution in reality; therefore, fuzzy method applied in linear programming is used to improve flexibility and robustness [4]. This fuzzy linear programming system considers all the possible of a specific domain of linear programming problems, hence it provides integration-oriented, adaptation and learning feature (as Fig. 1) [5].

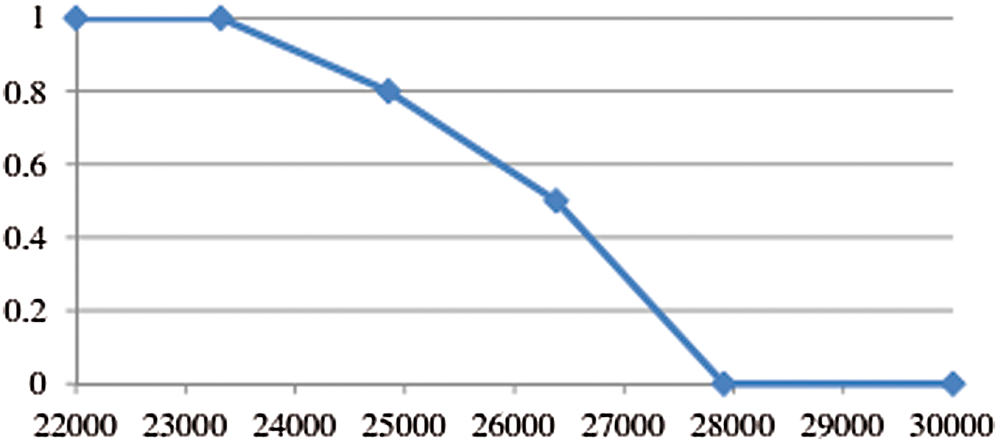
Figure 1: The membership function using fuzzy linear programming [5]

The decision-making process consists of the high discrepancy level of fuzziness. Moreover, the input information and the objective function are often uncertain and unclear. As a result, the best tool to handle uncertainty and vagueness is the fuzzy set theory which was initial introduced by Zadeh [6].

Due to the conflict among the three objective functions: minimize the total purchasing and ordering cost, minimize the net number of late delivered goods ordered from suppliers, and minimize the net number of rejected items form the suppliers, a fuzzy goal approach is proposed in this research to solve the model under multi-price level and product families. In a price discount environment and product families, Tsai and Wang [1] stated that the price per unit will decrease while the number of units purchased increase but may increase inventory risk.

The aim of the research is to develop a two-phase fuzzy multi-objective linear programming model to support the supplier selection and order allocation process under vary price level and multi-product condition. The objective of the proposed model is to minimize the total purchasing and ordering cost, reduce the quantity of defective materials and late delivered components from suppliers. The remaining sections of this paper are organized as follow: Section 2 includes a literature review while Section 3 explains the model of supplier selection and allocation problem. The numerical example is illustrated in Section 4. Lastly, Section 5 presents conclusion to this research.

2  Literature Review

As the competitiveness among companies increases over time, many people attempt to meet the demand of suppliers, reduce existing cost, and increase quality. In most industries, the most considered method is to minimize the cost of raw materials and components since they can affect the final pricing of a product. Weber et al. [7] claims that the raw materials cost may increase to 80% of total cost in hi-tech production environment. Moreover, the late delivered goods and the high rate of rejected items are also considered as future risks of the company. Therefore, selecting a potential and proper supplier can significantly improve purchasing order cost, reduce production lead time which will raise the satisfaction of customers and strengthen corporate competitiveness.

Researchers have determined and define various criteria for supplier selection problem [8–12]. Pan [13] showed that choosing the best vendor could reduce the total cost by twenty percentage when using an adaptive-fuzzy genetic algorithm. When suppliers have more power of negotiation, the profit of organizations can be put at risk due to the increase of material cost from suppliers. As a result, the suppliers can put pressure such as component cost, payment methods, or quality on the organizations that are purchasing their products. Nazari-Shirkouhi et al. [5] used an extended mixed-integer linear programming to apply in an uncertain environment and to provide a tool for logistics managers and practitioners to adopt strategies and policies in purchasing activities when choosing potential vendors. The authors state that the solution of the single-objective models is quite different from multi-objective models. Moreover, in fact, the decision makers require to minimize the total purchasing and ordering cost, the net number of rejected items ordered from suppliers and the net number of late delivered components from suppliers although these requirements are conflicting with one another. Therefore, the solution may perform well for one objective but will trade-off the remaining objectives. Narasimhan et al. [14] proposed a fuzzy multi-objective linear programming model for supplier selection problem for solving the problem in multi-product and discount environment while considering the competitive bidding mechanism for supplier selection.

There have been multiple optimization models developed to solve the supplier selection and order allocation problems [15–19]. Most of the proposed approach is a combination of MADM methods with MODM models. Hamdan and Cheaitou [20] developed a dynamic decision support system for a green supplier selection problem with quantity discounts and changing availability. The proposed model was built upon the combination of Analytical Hierarchy Process (AHP), fuzzy Technique for Order of Preference by Similarity to Ideal Solution (fuzzy TOPSIS), and integer linear programming methods. Vahidi et al. [21] approached the sustainable supplier selection and order allocation problem under operational and disruption risks with a hybrid MCDM model. The proposed model is based on Strengths, Weaknesses, Opportunities, and Threats (SWOT) analysis, Quality Function Deployment (QFD) method, and a novel mixed possibilistic-stochastic model. Lo et al. [22] introduced an integrated model that solved a green supplier selection and order allocation problem. The introduced model utilized the Best–Worst method (BWM), TOPSIS model, and fuzzy multi-objective linear programming (FMOLP) technique to evaluate the performance of potential suppliers and optimize order allocation among qualified suppliers. Gören [23] developed a decision support system for the supplier selection and order allocation problem. The model considered sustainability performance of the supply chain and the ability to satisfy customer demands. Fuzzy Decision-making Trial and Evaluation Laboratory (DEMATEL) is applied in combination with Taguchi Loss Functions to calculate the performance of the potential suppliers. Then, a novel bi-objective mathematical model is developed to determine the optimal order allocation among qualified suppliers with the objective of minimizing lost sales. Demirtas et al. [24] approached the problem with an Analytic Network Process (ANP) and Multi-objective Mixed Integer Linear Programming (MOMILP) based model. The ANP method is applied to calculate the ranking of potential suppliers based on relevant criteria and the MOMILP model is used to determine the order allocation among these suppliers, with the objectives of minimizing budget and defect rate.

In this study, the supplier selection and order allocation problem under changing price level for multi products is approached with a two-phase fuzzy multi-objective linear programming model with the objective of minimize the total purchasing and ordering cost, reduce the quantity of defective materials and late delivered components from suppliers.

3  Methodology

The supplier selection problem in the current paper has three objectives solved by apply multi-objective function (as Fig. 2):

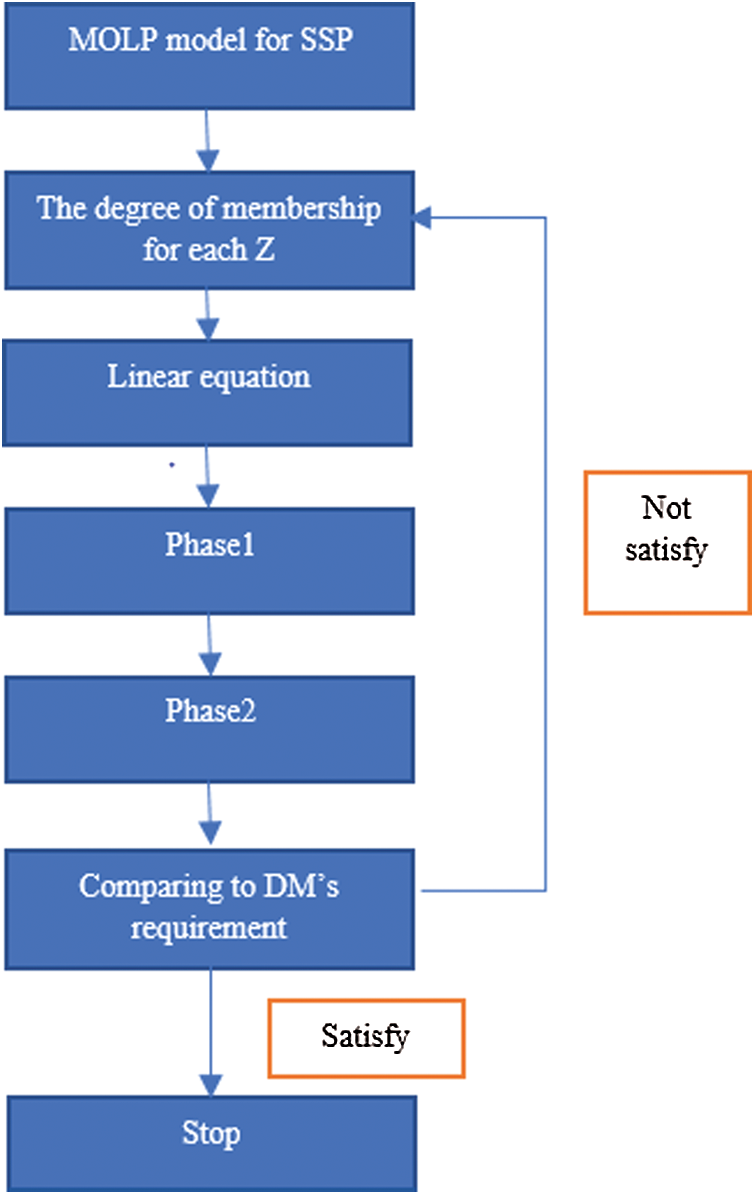
Figure 2: The block diagram of the interactive two-phase FMOLP model development

Minimize: the total purchasing and ordering cost.

Minimize: the net number of rejected items order from suppliers.

Minimize: the net number of late delivered items.

Considered parameters:

—Shortage of each item is not allowed from each supplier.

—One or more items can be supplied from each supplier.

—Quantity discount is offered by each supplier.

—Constant and known parameters: demand of the items, unit cost, price and so on.

—Capacity of each supplier is finite.

4  Notation

4.1 Index Set

i: Index of item, i∈I;

s: Index of supplier, s∈S;

p: Index of price levels offered by supplier, p∈P;

m: Index of points on the membership function, m∈M;

h: Index of objective function, h∈H.

4.2 Parameters

Di: Total demand of the ith item;

bisp: Upper limit purchased volume for the item i of the supplier s at the price level p;

pisp: Unite price for the item i of the supplier s at the price level p;

ois: Ordering cost for the item i of the supplier s;

qisp: Percentage of rejected units in the item i of the supplier s at the price level p;

disp: Percentage of late delivered units in the item i of the supplier s at the price level p;

cis: Capacity of supplier s for the item i;

fis: Flexibility of supplier quota allocation of supplier s for the item i;

Fis: Lower bound of quota flexibility of supplier s required by item i;

sis: Service level of supplier s for item i;

Si: Lower bound of service level required for item i;

ris: Rating value of supplier s for item i;

Ri: Lower bound of rating value on item i;

Amh: The value of objective function h at point m belonging to membership function h;

Bmh: The value of membership function h at point m;

μh: The membership function of objective function h;

φmh: Be the value of membership function h if the solution creating the poi;

BigM: A very large number.

4.3 Decision Variable

Xisp: Number of item i ordered from supplier s at level price p;

Yis = 1: If item i provided by supplier s otherwise = 0;

Ui = 1: If at least 1 item is provided by supplier s otherwise = 0.

4.4 Mathematical Model

Model constrains:

MinZ1=∑i∈I∑s∈S∑p∈PpispXisp+∑i∈I∑s∈SoisUs (1)

MinZ2=∑i∈I∑s∈S∑p∈PqispXisp (2)

MinZ3=∑i∈I∑s∈S∑p∈PdispXisp (3)

Subject to:

∑s∈S∑p∈PXisp=Di,∀i; (4)

Yisp≤Xisp≤cisYisp,∀i,s,p; (5)

∑p∈PYisp≤1,∀i,s; (6)

∑s∈Sfis∑p∈Pxisp≥FiDi,∀i; (7)

∑j=1numSsij∑k=1numPxijk≥SiDi,∀i; (8)

∑s∈Sris∑p∈PXisp≥RiDi,∀i; (9)

bis,p−1Yisp≤Xijp≤bispYisp,∀i,s,p; (10)

Us≤∑i∈I∑p∈PYisp≤BigM×Us,∀s; (11)

Xisp≥0,∀i,s,p; (12)

Yisp,Zs∈{0,1}∀i,j,k (13)

Constraint (4) implies that the total of item i provided by supplier s at price range p should be met the overall demand. Constraint (5) shows the limitation of supplier capacity. Constraint (6) defines that if item i is supplied by supplier j, there is one or non-price level which will be applied for ordering cost. Constraint (7)–(9) implies that the quota flexibility, service level and rating values must be greater than or equal a given bound. Constraint (10) represent that at each level of price requires a quantity of item ordered from supplier. Constraint (11) guarantee that all the product purchased from the same supplier will be placed in one order. Constraint (12) and (13) requires all the ordered item should be integer and greater or equal 0 as well as must be binary.

4.5 Interactive Two-Phase Fuzzy Multi-Objective Linear Programming Model

The above problem is solved separately for each objective function regarding to Eqs. (1)–(3). These results are recorded for later usage and for helping us to construct the membership function for each objective. Tab. 1 shows illustration data for constructing a membership function μh.

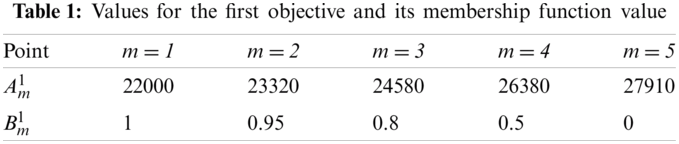
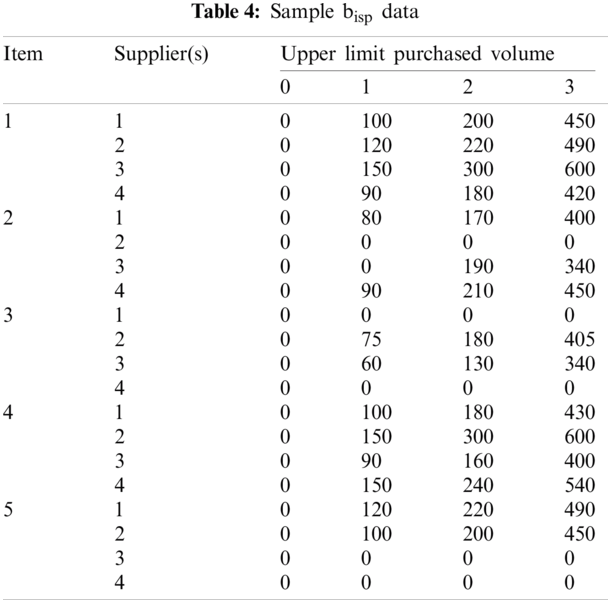
Using these values, the membership function μ1 can be identified as Fig. 3.

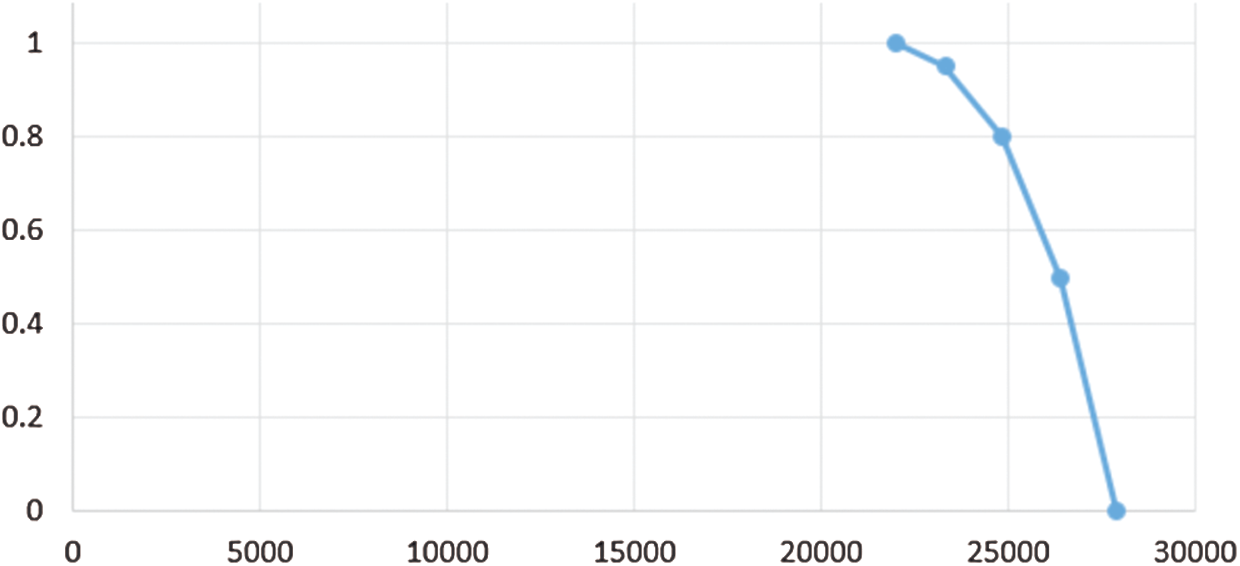
Figure 3: The membership function for the first objective

Using the piecewise linear membership function, the original multi-objective linear programming can be converted to an interactive two-phase fuzzy multi-objective linear programming. The algorithm consists of the following step:

Step 1: Specify a degree of a membership function for several values of each objective function.

Step 2: Draw the piecewise linear membership function.

Step 3: Formulate the linear equations.

Step 4: Apply the two-phase approach to introduce the auxiliary variable so that the problem can be transformed into the equivalent ordinary linear programming problem.

Step 5: Execute and modify the interactive decision process comparing with the requirement of decision makers.

Phase 1:

Phase 1 is accounted for finding a lower bound, i.e., α, for decision maker’s satisfaction regarding to all objectives. The constraints (15)–(17) linearize the membership function μh for each interval between points m and point m + 1. Constraints (18)–(20) force α must be belonged to only one interval between points m and point m + 1. If the lower bound is not between points m and point m + 1 then value of φmh=0. Constraint (21) set the upper bound for α. Constraints (4)–(13) are considered in phase 1 to ensure the feasibility of the solution. In phase 2, the solution is improved by finding a new solution whose all membership function values are always greater than α finding in phase 1.

maximize α (14)

Subject to:

∑i∈I∑s∈S∑p∈PPispXisp+∑i∈I∑s∈SoisZs=∑m∈M(Am1−Am+11Bm1−Bm+11φm1+Am+11Vm1) (15)

∑i∈I∑s∈S∑p∈PqispXisp=∑m∈M(Am2−Am+12Bm2−Bm+12φm2+Am+12Vm2) (16)

∑i∈I∑s∈S∑p∈PdispXisp=∑m=1(Am3−Am+13Bm3−Bm+13φm3+Am+13Vm3) (17)

Bm+1h+BigM(Vmh−1)≤φmh≤Bmh+BigM(1−Vmh);∀m∈M,h∈H (18)

Bm+1hVmh≤φmh≤BmhVmh,∀m∈M,h∈H; (19)

∑m∈MVmh=1;h=1,..,3; (20)

α≤∑m∈Mφmh;∀h∈H; (21)

And constraints: (4)–(13)

Phase 2:

Phase 2 will maximize the total membership function values of all objectives.

Maximize β=∑m∈Mφmh (22)

Subject to:

α≤∑m∈Mφmh,∀h∈H (23)

And constraint: (4)–(13); (15)–(20);

5  Numerical Example

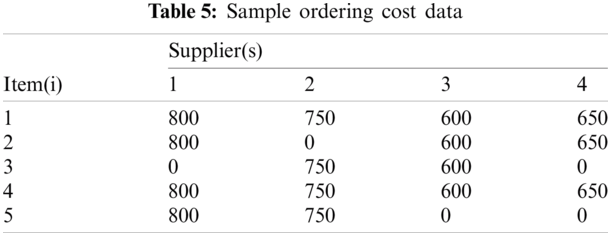
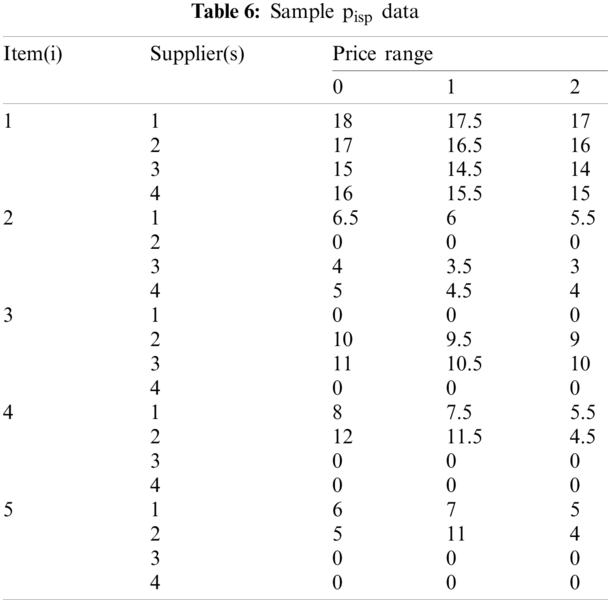
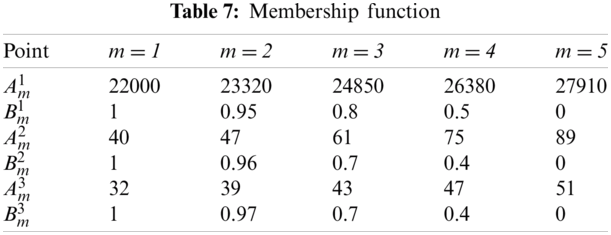
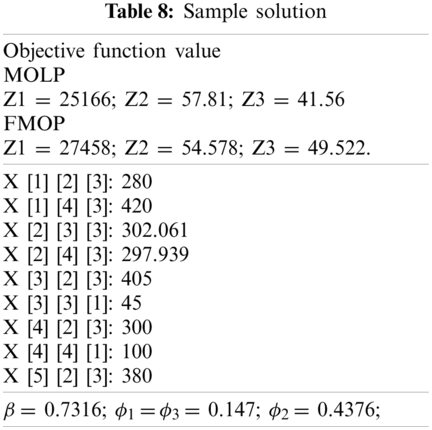
This section provides a numerical example for illustration. In this example, buyer plans to purchase five items (raw materials) from four suppliers. Each supplier proposes three levels of price and quantity of product. The parameters for the example are shown in Tabs. 2–6. Each objective function is solved separately then the optimal results are recorded. These results have the membership function values are equal to one. Based on these results the decision makers are interviewed to identify his membership function for the objective set. Tab. 7 represents the interview results for constructing each membership function. The shapes of these functions are displayed in the Figs. 3–6. When all the membership functions are available phase 1 is conducted. With α=0.147 obtained in phase 1, then phase 2 is computed. The solution details are given in Tab. 8. Since decision maker can adjust the membership function depending on his favor, it gives considerable flexibilities to solve the real problem.

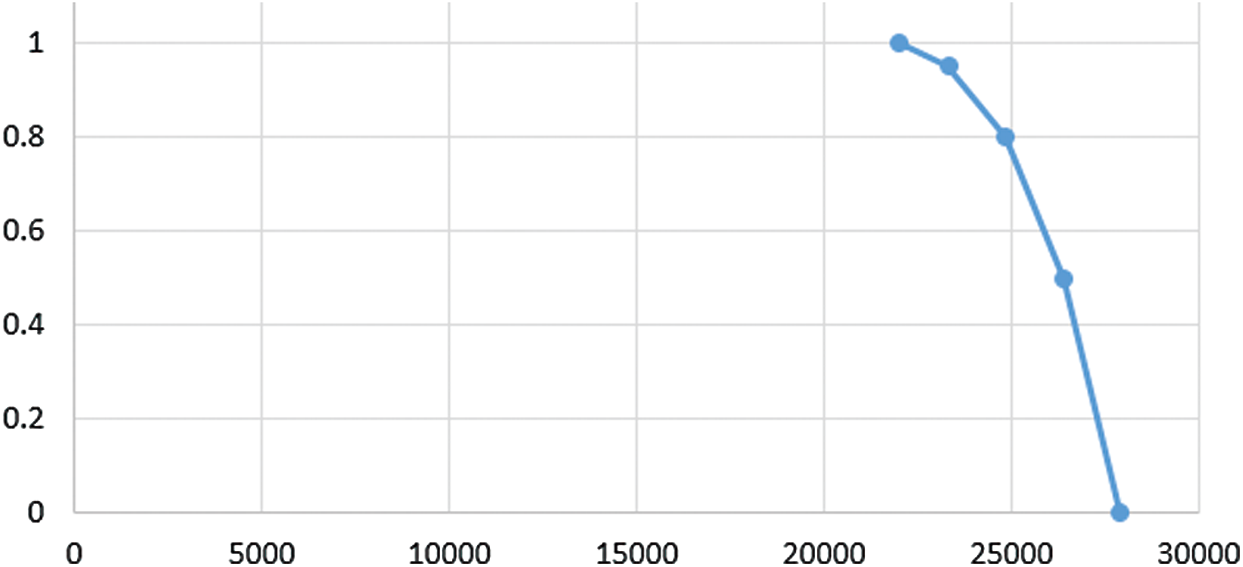
Figure 4: Shape of membership function μ1

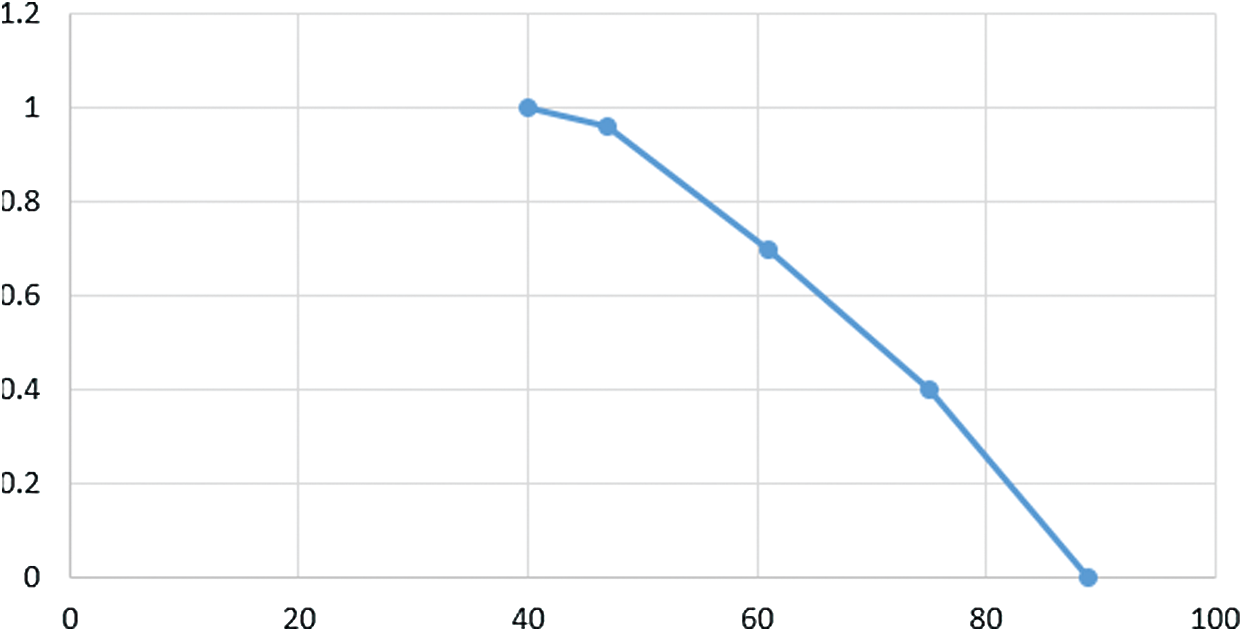
Figure 5: Shape of membership function μ2

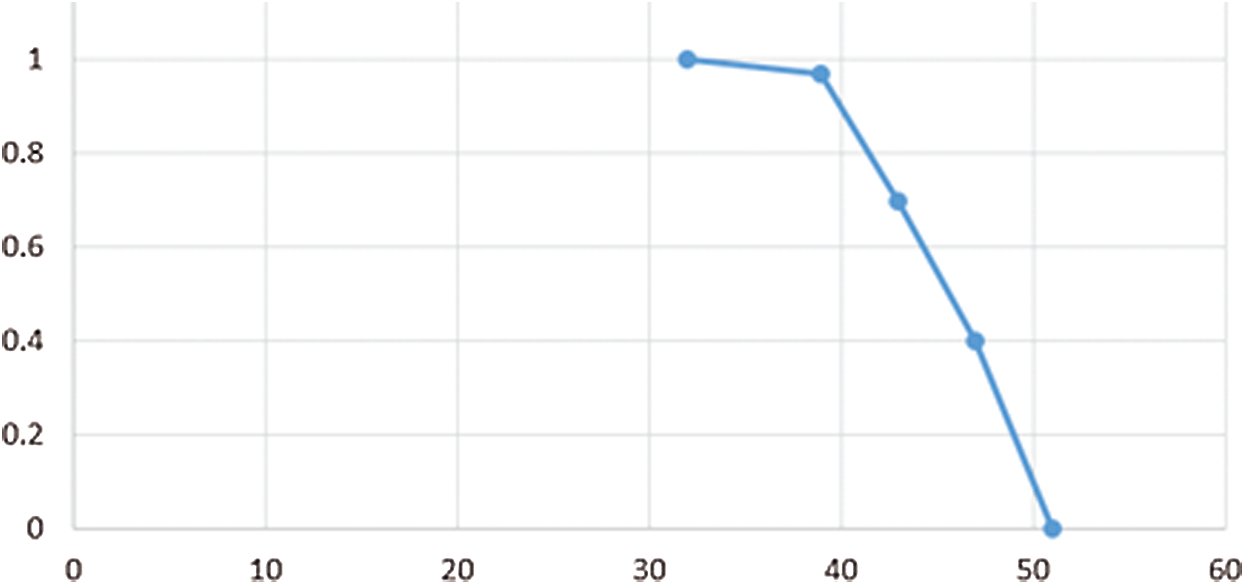
Figure 6: Shape of membership function μ3

6  Conclusions

Supplier selection and order allocation problem is one of the most important decision-making problems for supply chains. In order to ensure the effectiveness of the decision-making process, multicriteria decision-making models are frequently employed to support the decision-makers. In this research, the supplier selection and order allocation problem under multi-price and multi-product condition is approached by developing a two-phase FMOLP model. The objective of the model is to minimize the total purchasing and ordering cost, reduce the quantity of defective materials and late delivered components from suppliers. The proposed model is then tested using a numerical example using the CPLEX software. The results show that there is no conflict between constraints and the model is feasible providing feasible solutions.

The proposed mathematical model can handle uncertain environments and provide a decision-making supporting tool for managers and decision maker in solving supplier selection and order allocation problems under multi-price and multi-product conditions in different industry. Future research can look into the problem and expand the model to work under more complicate environments such as stochastic demand or allowing shortages.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  W. Tsai and C. Wang, “Decision making of sourcing and order allocation with price discounts,” Journal of Manufacturing Systems, vol. 29, no. 1, pp. 47–54, 2010. [Google Scholar]

 2.  S. Ghodsypour and C. O’Brien, “A decision support system for supplier selection using an integrated analytic hierarchy process and linear programming,” International Journal of Production Economics, vol. 56–57, pp. 199–212, 1998. [Google Scholar]

 3.  G. Odu and O. E. Charles-Owaba, “Review of multi-criteria optimization methods—Theory and applications,” IOSR Journal of Engineering, vol. 3, no. 10, pp. 1–14, 2013. [Google Scholar]

 4.  Y. Lai and C. Hwang, “Interactive fuzzy linear programming,” Fuzzy Sets and Systems, vol. 45, no. 2, pp. 169–183, 1992. [Google Scholar]

 5.  S. Nazari-Shirkouhi, H. Shakouri, B. Javadi and A. Keramati, “Supplier selection and order allocation problem using a two-phase fuzzy multi-objective linear programming,” Applied Mathematical Modelling, vol. 37, no. 22, pp. 9308–9323, 2013. [Google Scholar]

 6.  L. Zadeh, “Fuzzy sets,” Information and Control, vol. 8, no. 3, pp. 338–353, 1965. [Google Scholar]

 7.  C. Weber, J. Current and W. Benton, “Vendor selection criteria and methods,” European Journal of Operational Research, vol. 50, no. 1, pp. 2–18, 1991. [Google Scholar]

 8.  M. Yazdani, P. Chatterjee and E. K. Zavadskas, “Integrated QFD-MCDM framework for green supplier selection,” Journal of Cleaner Production, vol. 142, pp. 3728–3740, 2017. [Google Scholar]

 9.  C. N. Wang, V. T. H. Viet, T. P. Ho, V. T. Nguyen and V. T. Nguyen, “Multi-criteria decision model for the selection of suppliers in the textile industry,” Symmetry (Basel), vol. 12, no. 6, p. 979, 2020. [Google Scholar]

10. S. Hamdan and A. Cheaitou, “Supplier selection and order allocation with green criteria: An MCDM and multi-objective optimization approach,” Computers & Operations Research, vol. 81, pp. 282–304, 2017. [Google Scholar]

11. H. C. Liu, M. Y. Quan, Z. W. Li and Z. L. Wang, “A new integrated MCDM model for sustainable supplier selection under interval-valued intuitionistic uncertain linguistic environment,” Information Sciences, vol. 486, pp. 254–270, 2019. [Google Scholar]

12. M. Yazdani, Z. Wen, H. Liao, A. Banaitis and Z. Turskis, “A grey combined compromise solution (CoCoSo-G) method for supplier selection in construction management,” Journal of Civil Engineering and Management, vol. 25, no. 8, pp. 858–874, 2019. [Google Scholar]

13. F. Pan, “The optimization model of the vendor selection for the joint procurement from a total cost of ownership perspective,” Journal of Industrial Engineering and Management, vol. 8, no. 4, pp. 1251–1269, 2015. [Google Scholar]

14. R. Narasimhan, S. Talluri and S. Mahapatra, “Multiproduct, multicriteria model for supplier selection with product life-cycle considerations,” Decision Sciences, vol. 37, no. 4, pp. 577–603, 2006. [Google Scholar]

15. S. Prasanna Venkatesan and M. Goh, “Multi-objective supplier selection and order allocation under disruption risk,” Transportation Research Part E: Logistics and Transportation Review, vol. 95, pp. 124–142, 2016. [Google Scholar]

16. P. Ghadimi, F. Ghassemi Toosi and C. Heavey, “A multi-agent systems approach for sustainable supplier selection and order allocation in a partnership supply chain,” European Journal of Operational Research, vol. 269, no. 1, pp. 286–301, 2018. [Google Scholar]

17. D. Kannan, R. Khodaverdi, L. Olfat, A. Jafarian and A. Diabat, “Integrated fuzzy multi criteria decision making method and multi-objective programming approach for supplier selection and order allocation in a green supply chain,” Journal of Cleaner Production, vol. 47, pp. 355–367, 2013. [Google Scholar]

18. J. Scott, W. Ho, P. Dey and S. Talluri, “A decision support system for supplier selection and order allocation in stochastic, multi-stakeholder and multi-criteria environments,” International Journal of Production Economics, vol. 166, pp. 226–237, 2015. [Google Scholar]

19. A. Mohammed, R. Setchi, M. Filip, I. Harris and X. Li, “An integrated methodology for a sustainable two-stage supplier selection and order allocation problem,” Journal of Cleaner Production, vol. 192, pp. 99–114, 2018. [Google Scholar]

20. S. Hamdan and A. Cheaitou, “Dynamic green supplier selection and order allocation with quantity discounts and varying supplier availability,” Computers & Industrial Engineering, vol. 110, pp. 573–589, 2017. [Google Scholar]

21. F. Vahidi, S. Torabi and M. Ramezankhani, “Sustainable supplier selection and order allocation under operational and disruption risks,” Journal of Cleaner Production, vol. 174, pp. 1351–1365, 2018. [Google Scholar]

22. H. Lo, J. Liou, H. Wang and Y. Tsai, “An integrated model for solving problems in green supplier selection and order allocation,” Journal of Cleaner Production, vol. 190, pp. 339–352, 2018. [Google Scholar]

23. H. Gören, “A decision framework for sustainable supplier selection and order allocation with lost sales,” Journal of Cleaner Production, vol. 183, pp. 1156–1169, 2018. [Google Scholar]

24. E. Demirtas and Ö. Üstün, “An integrated multiobjective decision making process for supplier selection and order allocation,” Omega, vol. 36, no. 1, pp. 76–90, 2008. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.