DOI:10.32604/cmc.2022.019798

| Computers, Materials & Continua DOI:10.32604/cmc.2022.019798 |  |
| Article |
Improved RC6 Block Cipher Based on Data Dependent Rotations
1Department of Information Technology, College of Computers and Information Technology, Taif University, P.O. Box 11099, Taif, 21944, Saudi Arabia
2Department of Electrical Communications, Faculty of Engineering, Kafrelsheikh University, Kafrelsheikh, Egypt
3Department of Computer Engineering, College of Computers and Information Technology, Taif University, P.O. Box 11099, Taif, 21944, Saudi Arabia
4Department of Electronics and Electrical Communications, Faculty of Electronic Engineering, Menoufia University, Menouf, 32952, Egypt
5Department of Electrical Engineering, Faculty of Engineering, Menoufia University, Shebin El-Kom, 32511, Egypt
6Department of Informatics, Electronic Research Institute (ERI), Cairo, Egypt
*Corresponding Author: Osama S. Faragallah. Email: o.salah@tu.edu.sa
Received: 26 April 2021; Accepted: 08 June 2021
Abstract: This paper introduces an Improved RC6 (IRC6) cipher for data encryption based on data-dependent rotations. The proposed scheme is designed with the potential of meeting the needs of the Advanced Encryption Standard (AES). Four parameters are used to characterize the proposed scheme. These parameters are the size of the word (w) in bits, the number of rounds (r), the length of the secret key (b) in bytes, and the size of the block (L) in bits. The main feature of IRC6 is the variable number of working registers instead of just four registers as in RC6, resulting in a variable block size for plaintext and ciphertext. The IRC6 cipher is designed to improve the robustness against attacks by increasing the diffusion for each round and providing greater security with fewer rounds. The effectiveness of the proposed IRC6 scheme is verified against theoretical attacks. The proposed IRC6 scheme depends on full diffusion and confusion mechanisms regardless of the utilized block size. The proposed IRC6 scheme saves 70% of the encryption time and 64% of the decryption time of RC6. The simulation results prove that the IRC6 achieves a better encryption/decryption time compared to the traditional RC6. Therefore, the proposed IRC6 is anticipated to fulfill the market needs and system security requirements.
Keywords: Cryptography; block cipher; RC6, IRC6, AES
Security is the process of protecting data from unwanted behavior. Security can be achieved through security services that satisfy integrity, availability, and confidentiality. Encrypting of data is the operation of substitution or scrambling of the data through a computer system or any communication system. Later, authorized parties may reverse the process to reconstruct and reveal the original data [1]. Fig. 1 depicts a data security model [2]. The source message is described as a plaintext (X) and transformed into a ciphertext (Y) through the encryption process [3]. This encryption process is applied by performing an algorithm with a secret key K. The encryption produces different outputs based on the secret key. For decryption, the ciphertext can be converted to the plaintext again via performing the decryption algorithm using the same key employed for encryption. The cryptanalysis process tries to discover the plaintext or/and key by creating a plaintext value (Xe) or/and the secret key value (Ke) [1–3].
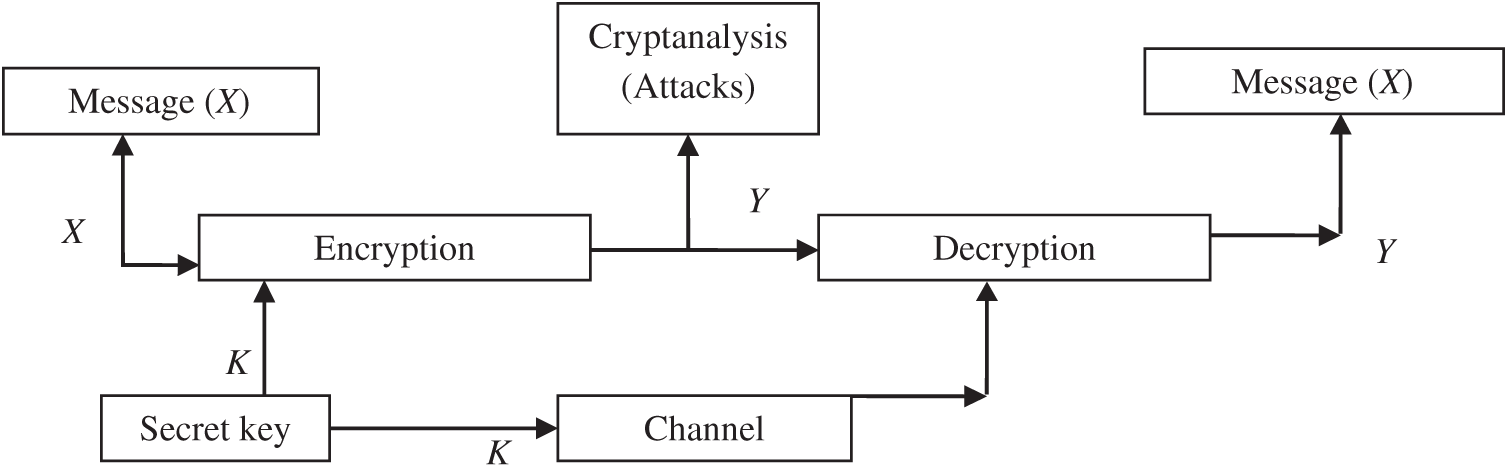
Figure 1: Symmetric system model for data security
Some of the almost widely used traditional ciphers involve RC5 [4–7] and RC6 [8–12]. The RC5 employs the ideas of data-dependent rotation, word size variation, variation of the number of rounds, and secret key length variation. RC6 may be considered as an extension of RC5, where it uses four running registers instead of two running registers, in addition to integer multiplication [9–12]. With multiplication, the diffusion spread per round can be significantly increased, increasing security, reducing rounds, and increasing throughput. Since declaration of the proposals of RC5 and RC6, many studies have improved the understanding of how structures and operations contribute to security [4–19]. Such investigations offered a theoretical attack depending on the fact that RC5 rotations do not rely on each bit in the register.
The proposal introduces a data encryption algorithm based on data-dependent rotations (IRC6). Unlike RC6, the proposed IRC6 relies on four variables. w denotes the word size in bits, r is the number of non-negative rounds, b is the length of the secret key in bytes, and L is the block size. The number of working registers m can be found by dividing L by w. The employment of integer multiplication extremely enhances the diffusion spread accomplished per round and can provide enhanced security. The IRC6 consists of two major components, the cipher algorithm and the confusion/diffusion network, which depends on the XOR operation between permuted bytes, called ‘’Permuted XORed Bytes’’ (PXB). Fig. 2 shows the general description of the proposed encryption/decryption process of IRC6.
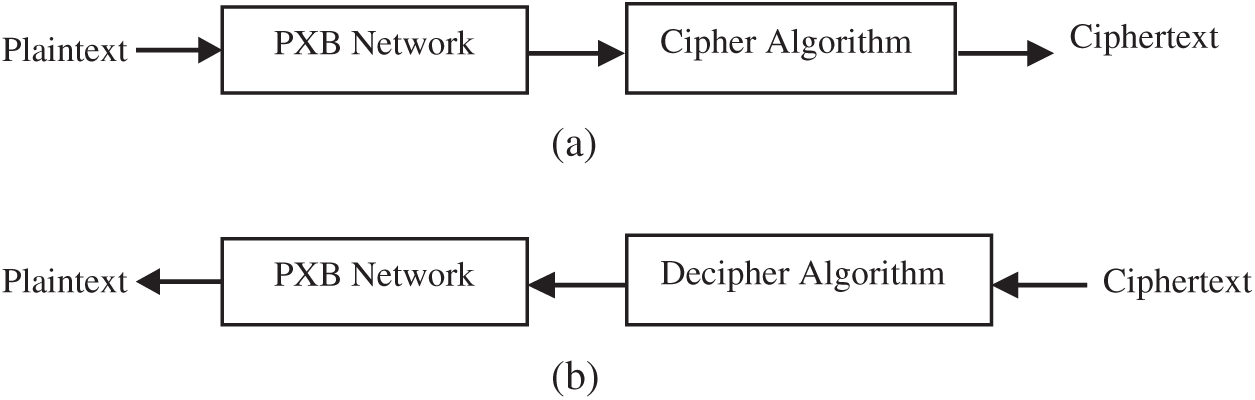
Figure 2: Description of the proposed encryption/decryption processes of IRC6 (a) The encryption process (b) The decryption process
These proposed modifications offer the advantages of enhancing the number of rotations for each round and utilizing further data bits to evaluate the number of rotations for each round. Therefore, integer multiplication can be considered as an effective diffusion primitive and can be utilized to calculate the number of rotations in the proposed IRC6. Consequently, the proposed IRC6 shows an increase in the diffusion spread compared with all other block ciphers. In addition, the IRC6 can run with less rounds with an efficient increase in security and throughput.
The work presented in this paper offers several significant contributions to the security field as follows:
a) A detailed survey of the RC6 encryption algorithm is presented. It is noticed that RC6 cannot provide full confusion and diffusion properties to the encrypted data.
b) A proposed cipher (IRC6), which is an advanced version of RC6, is introduced. This cipher has a variable block length, which makes it more flexible.
c) The proposed algorithm achieves full diffusion and confusion, and it is divided into two parts. The first one is the PXB network, which mixes the bytes of the data. If there are any small changes in the plaintext, they result in changes in all bytes of the ciphertext, and these changes are magnified in the cipher, resulting in full diffusion and confusion properties regardless of the block size.
d) The proposed cipher has good flexibility and effectiveness. This appears in the variable block size and the high throughput.
e) A good comparative analysis is introduced. This is achieved by performing a comparison of the proposed algorithm with RC6 for theoretical attacks.
The rest of the paper is organized as follows. Section 2 provides the RC6 literature overview. Section 3 presents the functional and design parameters of the proposed IRC6. Section 4 explores the architecture of the proposed IRC6. The implementation issues are given in Section 5. Section 6 introduces theoretical attacks on the proposed IRC6 cipher. A comparative analysis of the proposed IRC6 and the state-of-the-art RC6 is introduced in Section 7. The conclusion is given in Section 8.
The RC6 is characterized as an encryption algorithm that belongs to the fully-parameterized family [4–7,9–12]. RC6 is a version of block ciphers specified as RC6-ww/rr/bb, where ww denotes the word size in bits, rr denotes the number of rounds, and bb denotes the length in bytes of the key. These parameters are shown in Tab. 1. In all variants, RC6-ww/rr/bb works in units of four w-bit words input/output (plaintext/ciphertext), It may be considered as a word-oriented algorithm. The RC6 has three processes: the key schedule algorithm, encryption, and decryption algorithms.

The key schedule routine extends the secret key K to fill the extended key array SS. So, SS is similar to a random binary array of words tt = 2rr + 4 specified by KK. The key schedule routine utilizes two magic constants [4–7] and has three algorithmic parts: converting, initializing, and mixing, respectively.
• Converting: The user secret key KK[0…bb−1] is copied into the L[0…cc−1] array of words cc = [bb/uu], where the number of bytes/word is denoted as uu = ww/8. Fill each consecutive word from LL, low byte to high byte, using consecutive key bytes of KK. The unfilled byte positions in LL are padded with zeros as follows: Fill each consecutive word from LL, low byte to high byte, using consecutive key bytes of KK. The unfilled byte positions in LL are padded with zeros, as given below.
cc = max (b, ll)/uu;
for ii = bb − 1 down to 0 do
LL[ii/u] = (LL[ii/uu] <<< 8) + KK[ii];
• Initializing: The array SS is initialized with a specific fixed pseudo-random bit pattern based on modulo 2w using the two magic constants Pw and Qw.
SS [0] := Pw;
for ii := 1 to tt − 1 do
SS[ii] := SS[ii − 1] + Qw;
• Mixing: This stage starts by mixing the user’s secret key into SS and LL arrays. More accurately, because SS and LL can have unequal sizes, the larger array is processed for one time, and the other is processed three times.
begin
AA := BB := ii := jj := 0;
vv := 3* max{c, 2rr + 4}
for ss := 1 to vv do
begin
AA = SS[ii] = (SS[ii] + AA + BB) <<< log2(ww);
AA = LL[jj] = (LL[jj] + AA + BB) <<< (AA + BB);
ii = (ii + 1) mod (2rr + 4);
jj = (jj + 1) mod cc;
end;
end.
2.2 RC6 Encryption/Decryption Processes
The RC6 encryption is explored and detailed as follows. It is assumed that the input block is provided to the four ww-bit registers AA, BB, CC and DD, and the output is stored in AA, BB, CC, and DD registers.
begin
BB = BB + SS[0];
DD = DD + SS[1]
for ii := 1 to rr do
begin
kk = (BB*(2BB + 1) <<< log2(ww),
ll = (DD*(2DD + 1) <<< log2(ww),
AA = ((AA ⊕ kk) <<< l) + SS[2ii],
CC = ((CC ⊕ ll) <<< kk) + SS[2ii + 1]
end;
AA = AA + SS[2rr + 2];
CC = CC + SS[2rr + 3],
end.
The RC6 decryption process can be easily derived from the RC6 encryption process [9–12].
3 Features and Design Parameters of IRC6
The IRC6 consists of two parts, the cipher algorithm and the Permuted-XORed Bytes Network (PXB).
Similar to RC5 and RC6 ciphers, the IRC6 is a family of fully-parameterized cryptographic algorithms. The proposed IRC6 is more precisely designated as IRC6-w/r/b/L; in which w denotes the word size in bits, r denotes the number of rounds, L denotes the encryption key length in bytes and b is the block size. IRC6-w/r/b/L works in m units of w-bit words, where m is the number of working registers. The IRC6 works with m-word input/output (plaintext/ciphertext). So it may be considered as a word-oriented algorithm. As seen, we have input with w-bit words and output with all computational operations. So, the IRC6 first design parameter is w. The normal selection for w is 32 bits, and IRC6 operates on 32 ∗ m bits of plaintext and ciphertext block size (L). For simplicity, only values of 16, 32 and 64 are suggested [9–12].
The second IRC6 design parameter is the number of rounds r. An extended key table S is derived from the secret key provided by the user. Table S with size t depends on the number of rounds r with t =
The IRC6 third design parameter is the secret key length determined by b and K parameters. The parameter b denotes the secret key number of bytes for K [0], K [1], K [2],…, K [b−1]. The permissible values of b are 0, 1, 2, 3,…, 255.
Block size is the fourth design parameter of IRC6. The variable block size comes from using a variable number of registers in the encryption/decryption process, unlike RC6, resulting in more flexibility. The test results show that with the increase in the number of working registers, the security and throughput are improved, and the dependency between the data increases.
3.2 Primitive Operations of IRC6-w/r/b/L
The proposed IRC6-w/r/b/L block cipher uses the following primitive operations as shown in Tab. 2. log2(x) represents the x base-two logarithm.

3.3 The Permuted-XORed Bytes Network
The Permuted–XORed Bytes (PXB) is the network of substitution-transposition that is responsible for providing the confusion/diffusion mechanism of the IRC6. The proposed PXB is utilized to increase the confusion/diffusion characteristics of IRC6 by mixing bytes of data. First, the XOR chain operations are performed between the plaintext bytes. K1 is the sub-key that acts as the first XORing initial key and results in a XORing with the next block until reaching the end of the plaintext. Then, all blocks resulting from this XOR series are transposed bit by bit, as illustrated in Fig. 1. After that, a block-based transposition is employed. Finally, another XOR chain is employed starting from the sub-key K2. The advantage of the PXB is that one round is fair enough to make a complete confusion/diffusion of the plaintext and it does not consume too much time.
4 Architecture and Implementation of IRC6
The IRC6 algorithm, likes RC6, has three processes: the key expansion process, the encryption processes, and the decryption processes. These processes are shown in the following subsections.
4.1 IRC6 Encryption/Decryption
In the encryption process, the plaintext is firstly processed by PXB, and then it is delivered to the IRC6 cipher. The IRC6 has m w-bit registers Wi with i = 1, 2, 3,…, m. The registers include the initial input of the plaintext and output ciphertext of the encryption. The initial byte of either plaintext or ciphertext is put in W1, and the final byte is put in Wm. A parallel assignment is performed and this can be expressed as (Wl, W2, W3,…, Wm−1, Wm) = (W2, W3, W4, Wm−1, Wm, W1).
The pseudo-code of the encryption with IRC6-w/r/b/L is as follows:
Begin // PXB
P1(1) = P(1) ⊕ subkey1
for i = 1 to L − 1 do
begin
P1(i + 1) = P(i + 1) ⊕ P1(i)
end
P2 = BitPermutation(P1)
P3(1) = P2(L) ⊕ subkey2
for i = 1 to L − 1 do
begin
P3(i + 1) = P3(i) ⊕ P2(L − i)
end
for j := 2 step 2 to m do //The cipher
begin
W(j) = W(j) + S[((j/2) − 1) mod 352];
end;
for i := 1 to r do
begin
for j := 1 to m/2 do
begin
k(j) = (W(2 ∗ j) ∗ (2 W(2 ∗ j) ∗ 1) <<< lg w
end;
for j := 1 step 2 to m − 3 do
begin
W(j) = ((W(j) ⊕ k((j + 1)/2) <<< k((j + 1)/2 + 1)) ∗ S [i ∗ (m/2) + (j−1)/2 mod 352]
W(j + 2) = ((W(j + 2) ⊕ k((j + 1)/2 + 1) <<< k((j + 1)/2)) + S[i ∗ (m/2) + (j − 1)/2 + 1 mod 352]
end;
end.
for j := 1 step 2 to m − 1 do
begin
W(j) = W(j) + S [(m/2) ∗ (r + 1) + (j − 1)/2 mod 352]
end;
end;
The pseudo-code of the decryption of IRC6-w/r/b/L is as follows:
Begin // IRC6 decipher
for i := j step 2 to m − 1 do
begin
W(j) = W(j) − S [(m/2) ∗ (r + 1) + (j − 1)/2 mod 352]
end;
for i = r down to 1 do
begin
for j := 1 to m/2 do
begin
k(j) = (W(2 ∗ j) ∗ (2 W(2 ∗ j) + 1) <<< lg w
end;
for j := m − 3 stepdown 2 to 1 do
begin
W(j) = ((W(j) -+ S [i ∗ (m/2) + (j − 1)/2 mod 352]) >>> k((j + 1)/2 + 1))) ⊕ k((j + 1)/2)
W(j + 2) = ((W(j) -+ S [i ∗ (m/2) + (j − 1)/2 + 1 mod 352]) >>> k((j + 1)/2))) ⊕ k((j + 1)/2 + 1)
end;
end;
for j := m stepdown 2 to 2 do
begin
W(j) = W(j) − S[((j/2) − 1) mod 352];
end;
Begin // PXB
for i = L − 1 down to 1 do
begin
P2(L − i) = P3(i) ⊕ P3(i + 1)
end
P2(L) = P3(1) ⊕ subkey2
P1 = BitPermutation(P2)
for i = L − 1 down to 1 do
begin
P(i + 1) = P1(i + 1) ⊕ P1(i)
end
P1(1) = P(1) ⊕ subkey1
4.2 Key Expansion Algorithm for IRC6
The main schedule of IRC6 is substantially the same as the main key schedule of RC5 and RC6, using the magic constants Pw, Qw. The difference in IRC6 is the number of w-bit words generated for the addition round key t =
If the block size is large, i.e., (
The key re-usage function is used to update table S with new values in the encryption/decryption processes resulting in more security. The equation of the update is
for v = 0 to 351 do
Begin
S[v] = S[v] <<< (v mod 13)
end;
And in the decryption process:
for v = 0 to 351 do
Begin
S[v] = S[v] > > > (v mod 13)
end;
The IRC6-w/r/b/L uses
For the previous block cipher and the modified cipher, the selected transform is the left rotation by the function f(x) followed by the log2(w) bit position (log2 (w) = 5 for w = 32). The f(x) function is a one-to-one modulo 2w, and f(x) bits with a higher-order estimate of the rotation amount are highly dependent on every bit of x [9–12]. The rotation is performed by the log2(w) bits, but taking into account the hardening differential and linear cryptographic analysis.
Another issue is that in the decryption process, the key must be prepared first before beginning the decryption process by applying the key re-usage function of the encryption process along the length of the ciphertext to get the value of S[t − 1]. This disadvantage results in a slight increase in the decryption time compared to the encryption one.
6.1 Basic Cryptanalytic Attack
The brute-force attack is the most commonly employed for IRC6 cryptographic analysis via searching the encryption key space for the b-bytes encryption key. Hence, if the key provided by the user is long, the search focuses on the extending round key array [20]. A meet-in-the-middle attack, which is resource-intensive, can decrease the number of operations to min {28b, min {
6.2 Confusion/Diffusion Mechanism
A desirable property of the proposed encryption system is that it is susceptible to small changes in plaintext (just one plaintext bit changes). Usually, the other party can make minor changes, like changing just only 1 byte of the source plaintext and notifying the result modification. Through this technique, one can figure out a meaningful relationship between plaintext and ciphertext. However, this attack would be practically useless and inefficient if the ciphertext could be changed drastically due to minor changes in the plaintext [22].
In Shannon’s original definitions, confusion means complicating the relationship between the key and the ciphertext. The main purpose of the confusion is to make the key hard to be determined, even when there are many plaintext-ciphertext pairs generated with the same key. So, each ciphertext bit has to depend differently on the whole key and the other bits in the key. Specifically, if we change just one key bit, the ciphertext must be changed completely [22].
In the IRC6 cryptosystem, due to PXB and the variable working registers (m), one can encrypt a huge amount of data (ex: 1GB) by processing the data with the PXB network, and then dividing it into m working registers. These registers are all encrypted with each other in each round, giving a complete self-diffusion mechanism. Furthermore, the key re-usage function can generate new values of keys in the encryption/decryption processes, resulting in full dependence of the data on the key.
A comparative analysis is held between IRC6 and RC6 to assess the encryption/decryption procedures. The effect of the number of rounds on the encryption quality is investigated for IRC6 and compared with that on RC6 in different modes of operation at r = 20, which gives the best encryption quality in RC6 [20–22]. The measurement for normalized throughput of encryption/decryption is also considered. The analysis of confusion/diffusion properties is presented. The results are explained in sections 7.1 to 7.4.
7.1 The Effect of Number of Rounds on Encryption Quality
Let F and F′ denote the plaintext and ciphertext, respectively, each of size L bytes, and denote H(F) as the occurrence number of each byte value from 0 to 255 in the plaintext and H(F′) as the number of occurrences of each byte value from 0 to 255 in the ciphertext. So, the encryption quality can be expressed as:
The test was made on data with a size of 256 KB using IRC6−32/r/16/256 K, i.e., the data was treated as one block. The encryption quality of RC6 in ECB, CBC, and OFB modes at r = 20 is shown in Tab. 3. From Tab. 3 and Fig. 3, we can see that:
1. The best result of IRC6 is at r = 2 with a value of 737.1875.
2. Comparing these results with those of RC6, one can see that with only two rounds of IRC6, the encryption quality is better than that of RC6.
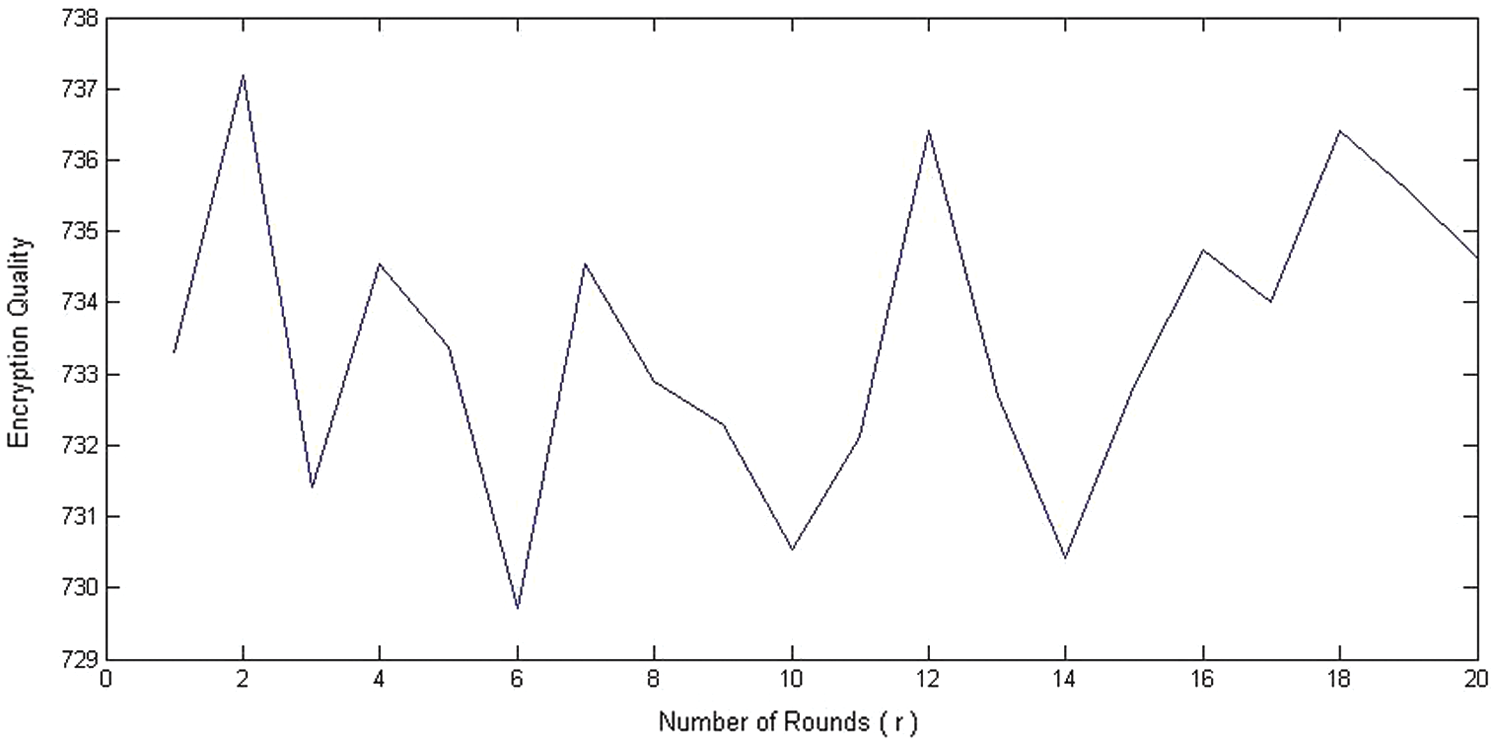
Figure 3: The effect of the number of rounds on IRC6 encryption quality

7.2 Encryption/Decryption Throughput
The encryption/decryption throughput (Th) can be estimated as the encryption or decryption amount of data per time unit (MB/Sec). In addition, the throughput normalization is tested on data with a size of 64 KB and computed for RC6-32/20/16 and IRC6-32/2/16/64 K. The results show that IRC6 takes only 30% of the encryption time of RC6, but in decryption, the percentage is increased to 36% of the decryption time of RC6. This is attributed to the key preparation process before decryption.
The diffusion of an algorithm can be tested by two factors: the Number of Pixels Changing Rate (NPCR) and the Unified Average Change Intensity (UACI) [23–25]. Considering the two ciphers, C1 and C2, whose plaintexts have only one-bit difference. Also, let C1(i) and C2(i) represent C1 and C2 at ith byte. Assume a bipolar array, D of equivalent size as C1 and C2. Hence, the values of C1(i) and C2(i) give D(i). If C1(i) = C2(i), then D(i) = 0; otherwise, D(i) = 1. The NPCR can be computed as:
where L is C1 or C2 length. The NPCR detects the percentage of different bytes between the two ciphers.
The UACI can be computed as:
which estimates the difference in average intensity between the two ciphers. The test was made on data of 64 KB. The results are shown in Tab. 4. From these results, one can see that:
1. The best mode that makes the most significant diffusion in RC6 is the CBC mode.
2. The IRC6 has the best results compared to all other RC6 modes.

We have tested the confusion by ciphering a 64 KB plaintext with two different keys. The first is key1 = ‘0000000000000000’16 and the second is key2 = ‘0000000000000001’16. The correlation between these two ciphers is calculated. For IRC6-32/2/16/64 K, the correlation is −0.0013 indicating a high deviation between these two ciphers due to a one-bit change in the key.
This paper introduced an IRC6, which is considered as an improved extension of RC5 and RC6 ciphers. Its salient feature is the utilization of a variable number of working registers instead of constant four registers in the RC6 round resulting in varying plaintext/ciphertext block size resulting and more flexibility. The processes of IRC6 include encryption, decryption and key expansion. Experiments have been conducted to demonstrate that the proposed encryption algorithm is robust against theoretical attacks. Furthermore, the IRC6 is verified as a full diffusion/confusion mechanism regardless of the block size. Finally, the comparative analysis for the IRC6 was considered, and its results were compared to those of RC6. The obtained results demonstrate that IRC6 has less encryption/decryption times and higher throughput compared to RC6 in other modes of operation. Using this architecture, the IRC6 w/r/b/L provides a compact, simple, and dynamic block cipher that satisfies the Advanced Encryption Standard and the computer security developers’ goals.
Acknowledgement: The authors would like to thank the Deanship of Scientific Research, Taif University Researchers Supporting Project number (TURSP-2020/08), Taif University, Taif, Saudi Arabia for supporting this research work.
Funding Statement: This study was funded by the Deanship of Scientific Research, Taif University Researchers Supporting Project number (TURSP-2020/08), Taif University, Taif, Saudi Arabia.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. A. Kuznetsov, V. Frolenko, E. Eremin and O. Zavgorodnia, “Research of cross-platform stream symmetric ciphers implementation,” in IEEE 9th Int. Conf. on Dependable Systems, Services and Technologies (DESSERTKyiv, UKraine, pp. 300–305, 2018. [Google Scholar]
2. R. Roman, J. Lopez and M. Mambo, “Mobile edge computing, Fog et al.: A survey and analysis of security threats and challenges,” Future Generation Computer Systems, vol. 78, pp. 680–698, 2018. [Google Scholar]
3. K. Bhushan and B. B. Gupta, “Security challenges in cloud computing: State-of-art,” International Journal of Big Data Intelligence, vol. 4, no. 2, pp. 81–107, 2017. [Google Scholar]
4. I. S. Farahat, A. S. Tolba, M. Elhoseny and W. Eladrosy, “Data security and challenges in smart cities,” Security in Smart Cities: Models Applications, and Challenges, vol. 2, pp. 117–142, 2019. [Google Scholar]
5. O. S. Faragallah, “Digital image encryption based on the RC5 block cipher algorithm,” Sensing and Imaging: An International Journal, vol. 12, no. 3, pp. 73–94, 2011. [Google Scholar]
6. O. S. Faragallah, “An enhanced chaotic key-based RC5 block cipher adapted to image encryption,” International Journal of Electronics, vol. 99, no. 7, pp. 925–943, 2012. [Google Scholar]
7. O. S. Faragallah, A. I. Sallam and H. S. El-Sayed, “Visual protection using RC5 selective encryption in telemedicine,” Intelligent Automation & Soft Computing, 2021. https://doi.org/10.32604/iasc.2021.019348. [Google Scholar]
8. M. Büscher, S. Perng and M. Liegl, “Privacy, security, and liberty: ICT in crises, cyber law, privacy, and security: Concepts, methodologies, tools, and applications,” Information Resources Management Association, IGI, vol. 13, pp. 248–266, 2019. [Google Scholar]
9. A. Sallam, E. EL-Rabaie and O. S. Faragallah, “HEVC selective encryption using RC6 block cipher technique,” IEEE Transactions on Multimedia, vol. 20, no. 7, pp. 1636–1644, 2018. [Google Scholar]
10. O. S. Faragallah, H. S. El-sayed, A. Afifi and S. F. El-Zoghdy, “Small details gray scale image encryption using RC6 block cipher,” Wireless Personal Communications, vol. 118, no. 2, pp. 1559–1589, 2021. [Google Scholar]
11. A. Sallam, E. EL-Rabaie and O. S. Faragallah, “CABAC-Based selective encryption for HEVC using RC6 in different operation modes,” Journal of Multimedia Tools and Applications, vol. 77, no. 21, pp. 28395–28416, 2018. [Google Scholar]
12. O. S. Faragallah, A. Afifi, W. El-Shafai, H. S. El-sayed, M. A. AlZain et al., “Efficiently encrypting color images with few details based on RC6 and different operation modes for cybersecurity applications,” IEEE Access, vol. 8, pp. 103200–103218, 2020. [Google Scholar]
13. P. J. Alvarez, C. K. Chan, M. Elimelech, N. J. Halas and D. Villagrán, “Emerging opportunities for nanotechnology to enhance water security,” Nature Nanotechnology, vol. 13, no. 8, pp. 634–641, 2018. [Google Scholar]
14. O. S. Faragallah, H. S. El-sayed, A. Afifi and W. El-Shafai, “Efficient and secure opto-cryptosystem for color images using 2D logistic-based fractional Fourier transform,” Optics and Lasers in Engineering, vol. 137, no. 106333, pp. 1–15, 2021. [Google Scholar]
15. S. Rajesh, V. Paul, V. G. Menon and M. R. Khosravi, “A secure and efficient lightweight symmetric encryption scheme for transfer of text files between embedded IoT devices,” Symmetry, vol. 11, no. 2, pp. 393, 2019. [Google Scholar]
16. O. S. Faragallah, W. El-Shafai, A. Afifi, I. Elashry, M. A. AlZain et al., “Efficient three-dimensional video cybersecurity framework based on double random phase encoding,” Intelligent Automation & Soft Computing, vol. 28, no. 2, pp. 253–367, 2021. [Google Scholar]
17. A. Priya, K. Sinha, M. P. Darshani and S. K. Sahana, “A novel multimedia encryption and decryption technique using binary tree traversal,” Proc. of the second Int. Conf. on Microelectronics, Computing & Communication Systems (MCCS 2017pp. 163–178, 2019. [Google Scholar]
18. R. Siregar, “Performance analysis of AES-blowfish hybrid algorithm for security of patient medical record data,” Journal of Physics: Conf. Series, vol. 1007, no. 1, pp. 1–10, 2018. [Google Scholar]
19. M. Büscher, S. Y. Perng and M. Liegl, “Privacy, security, and liberty: ICT in crises,” International Journal of Information Systems for Crisis Response and Management, vol. 6, no. 4, pp. 76–92, 2014. [Google Scholar]
20. M. Rashid, M. Imran, A. R. Jafri and T. F. Al-Somani, “Flexible architectures for cryptographic algorithms—A systematic literature review,” Journal of Circuits, Systems and Computers, vol. 28, no. 3, 1930003, pp. 1–35, 2019. [Google Scholar]
21. A. H. Zahid, M. J. Arshad and M. Ahmad, “A novel construction of efficient substitution-boxes using cubic fractional transformation,” Entropy, vol. 21, no. 3, pp. 245, 2019. [Google Scholar]
22. D. S. Wong and X. Tian, “E–mail protocols with perfect forward secrecy,” International Journal of Security and Networks, vol. 7, no. 1, pp. 1–5, 2012. [Google Scholar]
23. O. S. Faragallah, A. Afifi, W. El-Shafai, H. S. El-sayed, E. A. Naeem et al., “Investigation of chaotic image encryption in spatial and FrFT domains for cybersecurity applications,” IEEE Access, vol. 8, pp. 42491–42503, 2020. [Google Scholar]
24. S. Thakur, A. K. Singh, S. P. Ghrera and M. Elhoseny, “Multi-layer security of medical data through watermarking and chaotic encryption for telehealth applications,” Multimedia Tools and Applications, vol. 78, no. 3, pp. 3457–3470, 2019. [Google Scholar]
25. O. S. Faragallah and H. S. El-Sayed, “Secure opto-audio cryptosystem using XORing mask and hartley transform,” IEEE Access, vol. 9, pp. 25437–25449, 2021. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |