DOI:10.32604/cmc.2022.019611

| Computers, Materials & Continua DOI:10.32604/cmc.2022.019611 |  |
| Article |
BHGSO: Binary Hunger Games Search Optimization Algorithm for Feature Selection Problem
1Department of Computer Science and Engineering, Kongu Engineering College, Perundurai, 638060, Tamil Nadu, India
2Department of Electrical and Electronics Engineering, Dayananda Sagar College of Engineering, Bengaluru, 560078, Karnataka, India
3Rajasthan Rajya Vidyut Prasaran Nigam, Sikar, 332025, Rajasthan, India
4Department of Computer Science and Engineering, Guru Nanak Institute of Technology, Hyderabad, 501506, Telangana, India
5Mathematics Department, College of Science, Jouf University, Sakaka, P.O. Box: 2014, Saudi Arabia
6Department of Mathematics, College of Arts and Sciences, Prince Sattam bin Abdulaziz University, Wadi Aldawaser, 11991, Saudi Arabia
*Corresponding Author: Kottakkaran Sooppy Nisar. Email: n.sooppy@psau.edu.sa
Received: 18 April 2021; Accepted: 19 May 2021
Abstract: In machine learning and data mining, feature selection (FS) is a traditional and complicated optimization problem. Since the run time increases exponentially, FS is treated as an NP-hard problem. The researcher’s effort to build a new FS solution was inspired by the ongoing need for an efficient FS framework and the success rates of swarming outcomes in different optimization scenarios. This paper presents two binary variants of a Hunger Games Search Optimization (HGSO) algorithm based on V- and S-shaped transfer functions within a wrapper FS model for choosing the best features from a large dataset. The proposed technique transforms the continuous HGSO into a binary variant using V- and S-shaped transfer functions (BHGSO-V and BHGSO-S). To validate the accuracy, 16 famous UCI datasets are considered and compared with different state-of-the-art metaheuristic binary algorithms. The findings demonstrate that BHGSO-V achieves better performance in terms of the selected number of features, classification accuracy, run time, and fitness values than other state-of-the-art algorithms. The results demonstrate that the BHGSO-V algorithm can reduce dimensionality and choose the most helpful features for classification problems. The proposed BHGSO-V achieves 95% average classification accuracy for most of the datasets, and run time is less than 5 sec. for low and medium dimensional datasets and less than 10 sec for high dimensional datasets.
Keywords: Binary optimization; feature selection; machine learning; hunger games search optimization
Due to the significant advancement of technology, including the Internet in various areas, many databases were recently developed, and the complexity and diversity have also grown. Nevertheless, high-dimensional databases have some drawbacks, including lengthy model building periods, incomplete features, and deteriorated efficiency, making data analysis challenging [1,2]. Feature selection (FS) is a robust data pre-processing phase that can limit the features count and dataset dimensions, improve model generalization, and reduce overfitting. The process of deciding the attributes to be used in a classification problem is known as FS [3]. FS aims to select a set of attributes to improve accuracy rate or reduce the size of the framework while substantially reducing the classifier’s accuracy rate using only the FS process. For machine learning experts who must handle complicated data, FS is essential. It is frequently used in machine learning, data mining, and pattern recognition [3–5]. FS methods have previously been seen in video classification, image retrieval, gender classification, vehicle identification, and other applications [6,7]. By removing unwanted or noisy features, FS may reduce the dimensions of the given dataset. This decreases the complexity and data processing burden and lowers the computation complexity of the classification model, and saves resources while improving the algorithm’s efficiency. The FS approach helps to reduce the dimensionality of real-world problems. Investigators have produced a series of FS methods up to date. FS approaches may be classified as filter or wrapper approaches depending on whether an assessment tool is accessible [8,9]. Filter-based approaches pick the dataset’s attributes first, then train the learner. The fundamental premise is to assign a weight to each element, with the weight representing the dimension feature’s value, and then ranking the attributes based on the weight. Wrapper-based approaches use the classification model (for example, classification) as the function subset’s performance measure explicitly. The key concept is to approach subset choice as a search optimization problem, generating multiple types, evaluating them, and comparing them to other configurations. The wrapper outperforms the filter in terms of learning classification accuracy but at a high computational complexity.
Conventional optimization approaches are incapable of solving complex optimization tasks, and obtaining acceptable results is challenging. As a result, a more efficient approach, known as the metaheuristic algorithm, was already suggested and used by many researchers. Optimization algorithms have several benefits, including their ease of use, independence from the problem, versatility, and gradient-free design [10]. Evolutionary algorithms, human-based and physics-based, and swarm intelligence (SI) approaches are the four types of metaheuristic algorithms. A genetic algorithm (GA) is an example of an evolutionary algorithm, in which three steps, such as crossover, selection, and mutation, are utilized to update an individual and attain a global solution. Differential evolution (DE) algorithm is also included in this category. The social behavior of animals influenced swarm intelligence, which shares all personal knowledge during the optimization procedure. Ant colony optimization, Dragonfly Algorithm, Grey wolf optimizer (GWO), Salp Swarm Algorithm (SSA), particle swarm optimization, artificial bee colony, flower pollination algorithm, Marine Predator Algorithm (MPA), and satin bowerbird optimizer are few examples of SI algorithms. The sailfish optimizer, emperor penguin optimizer, whale optimization algorithm (WOA), harris hawk’s optimization (HHO), and Artificial Butterfly Optimization Algorithm [ABOA] are few recent algorithms in the SI category. Various researchers have utilized the SI algorithms due to their versatility and simplicity. Laws of physics inspire physics-based algorithms. For instance, gravitational search algorithm, simulated annealing, Sine-Cosine Algorithm (SCA), Atom Search Optimization (ASO) algorithm, Equilibrium Optimizer (EO), multi-verse optimizer, and Henry gas solubility algorithm (HGSA) belongs to this category. Human behavior and interaction in society inspire Human-based techniques. For instance, teaching-learning-based optimization, cultural evolution algorithm, and the volleyball premier league [11–16]. The advantage of using such techniques to solve real-world problems is that they deliver the best outcomes in a short period, even for huge problem sets [17–19]. To address the FS problem, all the above-said algorithms and their binary variants have been used.
The authors of [19] suggested a binary GWO (BGWO) algorithm hybridized with a two-stage mutation scheme for the FS problem by utilizing the sigmoid function to map the basic version to the binary version. The authors of [20] presented a binary SSA accompanied by crossover for the feature selection problem using various transfer functions to alter the SSA into its binary version. To overcome the FS challenge, the authors of [21] proposed a binary variant of ABOA by using two transfer functions: V-shaped and S-shaped. The authors of [22] presented binary DA (BDA) for FS based on eight transfer functions. The benefit is that the likelihood of changing the location of an individual during the initial stages is strong, making it easier to discover different solutions from the initial population. The authors of [23] presented an improved BDA version by combining a hyper learning scheme called HLBDA. The sigmoid function is utilized to convert the algorithm into binary search space. The authors of [24] proposed a binary symbiotic organism search algorithm based on the wrapper technique that uses a time-varying mechanism as the FS process. To address the FS problem, the authors of [25] utilized HGSA, in which k-nearest neighbor (kNN) and Support Vector Machine (SVM) were used to validate the selected features. The authors of [26] presented a binary SCA (BSCA) for the FS problem using eight transfer functions to alter into its binary version. The authors of [27] presented a binary ASO (BASO) for the wrapper FS problem using eight transfer functions to alter into its binary version. The authors of [21] suggested binary EO (BEO) and its improved versions for the wrapper-based FS problems using the Sigmoid function. The authors of [28] suggested binary MPA (BMPA) and its improved versions for wrapper-based FS problems. The continuous version of MPA is converted into binary variants using Sigmoid and eight transfer functions. Often seen as research approaches for wrappers-FS problems are metaheuristic techniques such as the simulated annealing, GA, DE, ant lion optimization algorithm, harmony search algorithm, and particle swarm optimization algorithm. Please see the literature [29] for more information on metaheuristics for the FS problem. The authors of [30,31] introduced quadratic HHO and enhanced WOA for high dimensional feature election problems. Can conventional systems be helpful to address the FS problem? As discussed earlier, metaheuristics have many advantages. The free lunch theorem (NFL) is the solution to this situation, stating that no algorithm can address all classification problems [32]. For FS problems, one algorithm’s final output for a database would be excellent, while another algorithm’s success may be impaired.
Therefore, in this paper, a binary variant of a recently proposed Hunger Games Search Optimization (HGSO) algorithm [33] is proposed to handle the feature selection problem. The suggested HGSO is based on animals’ hunger-driven and social behaviors. This dynamic, strength and conditioning search approach uses the basic principle of “Hunger” as one of the essential homeostatic incentives and explanations for behavior, actions, and decisions to allow the optimization technique to be more intuitive and straightforward for the researcher’s existence of all species. The following are the reasons for using the HGSO techniques to optimize the FS problem in this study. Initially, the two segments demonstrate that the metaheuristic procedure outperforms other state-of-the-art techniques in solving these problems. As a result, we’d like to put the latest HGSO algorithm on the examination. Second, the HGSO method is a brand-new metaheuristic algorithm that has yet to be implemented to FS problems effectively. Finally, an evaluation of the proposed algorithm with sophisticated, recent, and high-efficient algorithms indicates that the proposed HGSO algorithm possesses the optimal or suboptimal solution with typically higher classification efficiency for problems studied (i.e., fewer iterations or less runtime). This paper suggests two new discrete HGSO versions, called BHGSO-V and BHGSO-S, to make the FS problem easier to handle. The HGSO algorithm uses V- and S-shaped transfer functions to convert a continuous HGSO algorithm to a binary form. To validate the number of selected features, the kNN algorithm is used in this paper. The following are the highlights of the paper.
• A new binary variant of the HGSO algorithm is formulated using different transfer functions.
• BHGSO-V and BHGSO-S algorithms are applied to low, medium, and high dimensional FS problems.
• The performance of the BHGSO algorithm is compared with other state-of-the-art algorithms.
• Statistical tests, such as Friedman’s test and Wilcoxon Signed Rank test, have been conducted.
The structure of the paper is organized as follows. Section 2 explains the basic concepts of the HGSO algorithm. Section 3 explains how the continuous HGSO algorithm is altered to a binary version using V- and S-shaped transfer functions. Section 4 discusses the results and further discussion while validating the performance of the proposed algorithm using 16 UCI datasets. Section 5 concluded the paper.
2 Hunger Games Search Optimization (HGSO) Algorithm
The Hunger Games Search Optimization (HGSO) algorithm was introduced by Yang et al. [33] in 2021 for continuous optimization problems. The HGSO algorithm is inspired by the everyday actions of animals, such as nervousness of being slain by predators and hunger. This section of the paper explains the mathematical modeling of the HGSO algorithm. The modeling is based on social choice and hunger-driven actions.
The approaching behavior of hunger is mathematically modeled in this subsection. The game instructions are presented in Eq. (1), which describes the foraging hunger and individual supportive communication actions. The mathematical expression given in Eq. (1) imitates the contraction mode.
where
where
where
The hunger behavior of all individuals during the search is mathematically modeled in this subsection. The expression for
The expression for
where N denotes the population size,
where AllFitness(i) denotes the cost function value of each population in the current iteration. A new starvation H is supplementary based on the actual starvation. The expression for H is denoted in Eq. (8).
where H is restricted to a lower bound,

Figure 1: Flowchart of the HGSO algorithm

3 Proposed Binary Hunger Games Search Optimization (BHGSO) Algorithm
The HGSO algorithm is a recently developed population-based algorithm that imitates hunger hunting behavior for food. In terms of avoidance of local optima, exploitation, exploration, and convergence, the HGSO algorithm outperforms the other population-based algorithms. It is proved by the inventors of the HGSO algorithm that the HGSO performs better on benchmark functions. Due to a better balance between the exploration and exploitation phases of the HGSO algorithm, the convergence and solution diversity is better in the HGSO algorithm. Therefore, the benefits mentioned above motivated the researchers to use the HGSO algorithm in real-world applications, including wrapper-based FS problems, due to its appealing properties.
In the wrapper-based FS process, the classification model is used for training and validation at each phase, and then a sophisticated optimization technique is used to reduce the number of iterations. Besides, the search space is likely to be highly nonlinear, with numerous local optima. Generally, continuous optimization techniques predict feature combinations that optimize classification efficiency, and populations are used in the search space with d-dimension at positions [0, 1]. In contrast, binary versions are supposed to perform well if used similarly since the search space is restricted to two values for every dimension (0, 1). Furthermore, binary operators are easier to understand than continuous operators [34]. The primary reason for creating a binary representation of the HGSO algorithm is that the solutions to FS problems are restricted to binary values of 1 and 0. For the FS problem, a new binary HGSO (BHGSO) algorithm is suggested in this study. It can be shown that each individual can change its location using either the local or global search stages. To do so, a transfer function (TF) must be used to assign the hungry values to the probabilities of starvations so that the position can be updated. In other terms, a TF describes the likelihood of changing the hunger location vector between 0 to 1 or 1 to 0. Essentially, the binary search space is a hypercube, with the populations of the HGSO algorithm only being able to shift to the hypercube’s far edges by swapping different bit numbers. The proposed binary versions of the HGSO algorithm work based on updating the hunger location with the likelihood of its food. To accomplish this, a TF must be used to map the values to probability to update the hunger positions. To put it another way, a TF determines the probability of changing the vector position from 0 to 1 and 1 to 0. Two TFs, S- and V-shaped TFs, are used to create two binary variants, BHGSO-S and BHGSO-V, respectively.
3.1 S-Shaped Binary Hunger Games Search Optimization (BHGSO-S) Algorithm
As discussed, the new positions of the hunger found through local or global search can have continuous output, but these continuous positions should be converted into binary. This transformation is accomplished by changing continuous positions of each dimension utilizing a Sigmoidal (S-shaped) TF, which directs the hunger to travel in a binary location [35]. As shown in Eq. (10) and Fig. 2a, the S-shaped is a typical TF.
where
where

Figure 2: Characteristic curves; (a) S-shaped TF, (b) V-shaped TF
3.2 V-Shaped Binary Hunger Games Search Optimization (BHGSO-V) Algorithm
Rather than an S-shaped TF, a V-shaped TF approach is defined in this paper, and Eqs. (12) and (13) are used to accomplish this process [36,37]. Fig. 2b shows the steps involved in using the proposed TF to force hunger to direct in a binary position.
Eq. (12) can be rewritten as follows.
The threshold directions can be mathematically denoted in Eq. (14).
Eq. (12) is used as the TF in this binary method to convert the position of hunger to the probabilities of adjusting the components of the location vectors. As a result, the location vectors of hunger are modified using the rules of Eq. (14). The V-Shaped TF has the advantage of not forcing hunger to take a value of 0 or 1. To put it another way, it allows hunger to turn to the compliments only after the fitness values are high; then, the hunger would remain in the current location due to their low fitness value.
3.3 Binary Hunger Games Search Optimization Algorithm for FS Problem
FS is a binary optimization process in which the populations can only choose between [1 or 0]. A one-dimensional vector represents any solution; the length is determined by the number of attributes (nf) in the database. Any cell may have one of two values, either 0 or 1, in which 1 specifies that the respective feature is chosen and 0 specifies that the feature is not chosen.
In general, the FS problem is a multi-objective optimization problem in which two conflicting objectives, such as choosing the smallest nf while maintaining the highest classification accuracy. The proposed binary optimization approaches are used to solve this multi-objective FS problem. In an FS problem, the less nf and the highest classification accuracy are considered the best. The fitness function evaluates each solution using the KNN classifier to measure the accuracy rate and the nf chosen. The fitness function in Eq. (15) is used to test the strategies, the foreordained goal of finding a balance between the nf and classification accuracy.
where

Figure 3: Overall flowchart of BHGSO algorithm for the FS problems
Sixteen benchmark datasets from the UCI data source were selected for experimentation to verify the output of the proposed binary approaches. Tab. 1 shows the identified datasets, including the number of instances and features in each dataset. The motive behind choosing such datasets is that they include a range of instances and features that reflect various issues that the proposed binary strategies would be evaluated on. A collection of high-dimensional datasets is also chosen to evaluate the efficiency of the suggested technique in high search spaces. Each dataset is split into cross-validation groups for assessment purposes. In K-fold cross-validation, the dataset is split into several folds, with K − 1 folds used for training and the remaining set used for testing. This operation is repeated for M times. As a result, for each dataset, each algorithm is evaluated K × M times. The training portion is used to train the classifier during the optimization, while the testing portion is used to test the classifier’s output while it is being optimized. The validation portion is used to evaluate the attribute set chosen by the trained classifier.

Based on the KNN classifier, a wrapper-based method for FS has been used in this paper, with the best option (k = 5) being used on all datasets. Each population represents a single set of features during the training phase. The training fold is used to measure the efficiency of the KNN classifier on the validation fold during the optimization phase to direct the optimal feature subclass selection criteria. In contrast, the test fold is kept private from the process and is only used for ending assessment purposes. The suggested FS approaches are compared to some state-of-the-art approaches, including BEO, BMPA, BASO, BGWO, HLBDA, and BSCA. Tab. 2 details the parameter settings of all algorithms. The proposed and other selected algorithms are implemented in MATLAB, which runs on Intel Core™ i5-4210U CPU @2.40 GHz with Windows 8 operating system. All algorithms run 30 times for fair comparison on each dataset.

In each run of all algorithms, the following procedures are applied to the datasets.
Classification Accuracy: It is a metric that defines how accurate a classification model is for a given set of features, i.e., the number of features accurately categorized, and it is measured as follows:
where N signifies the number of test setpoints, M signifies the number of runs, Ci denotes the output label for datapoint i, match denotes the comparator that returns 0 when two labels are not identical, and 1 when they are same, and Li denotes the reference label for i.
Average Selected Features: It represents the average of the nf over M times and is defined as follows.
where
Statistical Mean: It shows the average solutions obtained by running each method M times and can be expressed as a collection of follows.
where
Statistical Standard Deviation (STD): It describes the variety of the optimal fitness produced by running algorithm M times and can be expressed in the following way.
Statistical Best: It describes the best fitness attained by running an algorithm over M times.
Statistical Worst: It describes the worst fitness attained by running an algorithm over M times.
Average Run Time (RT): It describes each algorithm’s real RT in seconds over diverse runs, and it is expressed as follows.
Wilcoxon Rank-Sum Test (WSRT) and Friedman’s Rank Test (FRT): WSRT and FRT statistical tests are utilized to see whether the solutions of the suggested algorithm were statistically dissimilar from other techniques. In WSRT, all of the values are assumed to rank as a single group, and then the ranks of each group are introduced. The null premise states that the two data points come from a similar individual and that any variances in the rank sums are due to sampling error. This statistical test generates a p-value parameter used to compare the implication stages of two techniques. Similarly, FRT also helps in assigning the rank based on the best solutions obtained over the M runs of all algorithms.
The convergence curves of proposed BHGSO-V and BHGSO-S algorithms and other selected algorithms on sixteen datasets are shown in Fig. 4. It is discovered that the proposed BHGSO-V and BHGSO-S algorithms can typically deliver excellent convergence behavior, outperforming other approaches in the analysis of optimal feature subsets. Out of two proposed algorithms, the BHGSO-V algorithm can converge faster to discover the best optimum in all high-dimensional datasets (Colon, Leukemia, TOX_171, COIL20, Lung, and ORL). The outcome strongly suggests the proposed BHGSO-V’s dominance in high-dimensional FS problems. The characteristic that the hunger maintains strengthened and finds the best solutions is one reason why BHGSO shows high convergence speed.
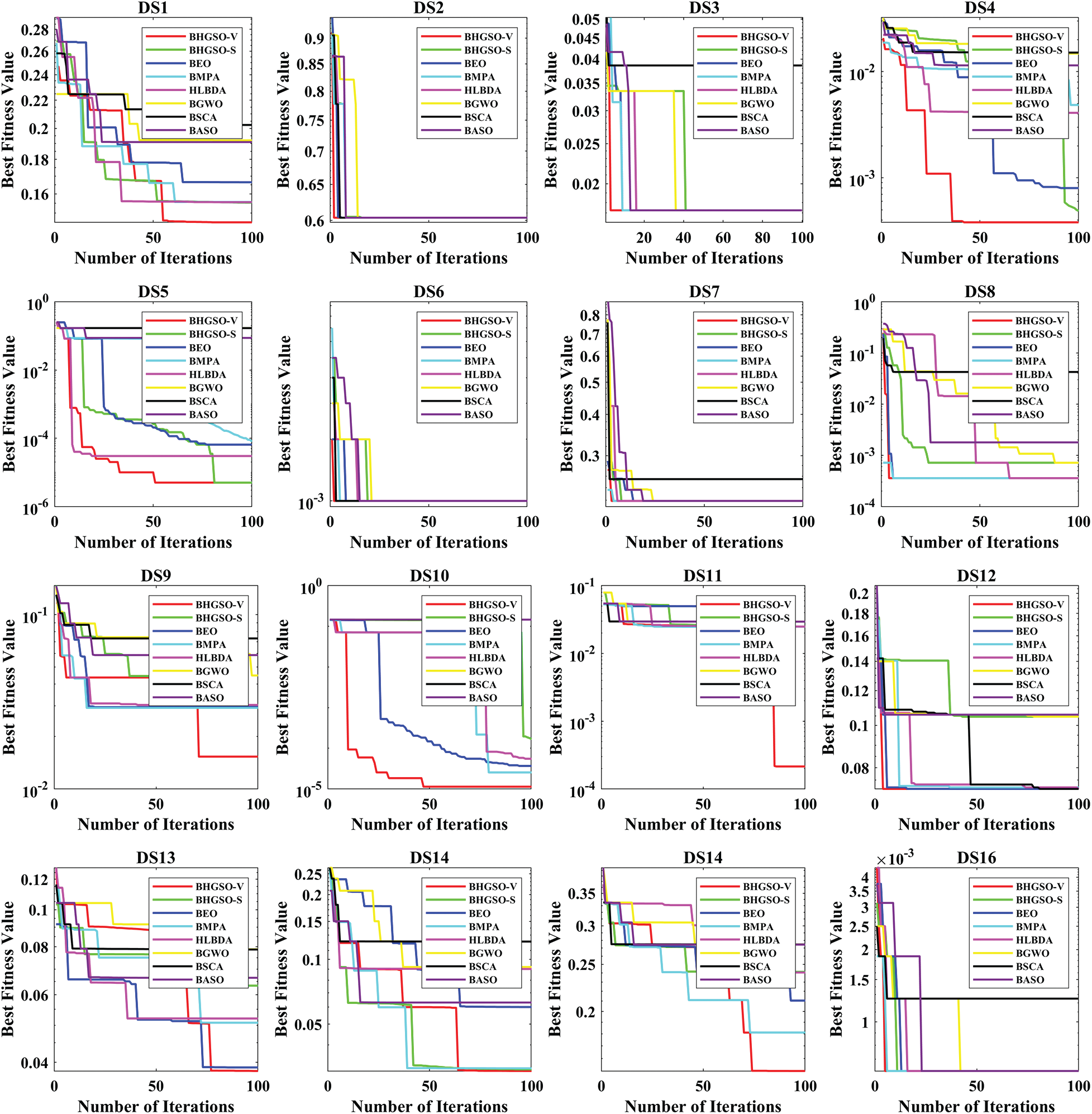
Figure 4: Convergence curves of all algorithms on all selected datasets
The best fitness, mean fitness, worst fitness, and standard deviation (STD) of fitness obtained by all algorithms are presented in Tabs. 3–6, respectively. On all 16 datasets, BHGSO-V perceived the optimum best fitness values, as shown in Tab. 3. However, BHGSO-S obtained the best fitness only for five datasets out of 16 datasets. Next to BHGSO-V, BMPA, BEO, HLBDA, BGWO, BHGSO-S, BASO, and BSCA gives the best fitness values. Out of all algorithms, the proposed BHGSO-V has consistently shown a high level of commitment when dealing with FS tasks. According to Tab. 4, in most cases (11 datasets), the proposed BHGSO-V algorithm responded to the optimum mean fitness value, followed by BEO (nine datasets), BMPA (six datasets), BHGSO-S (five datasets), BGWO (five datasets). As a result, the BHGSO-V algorithm can frequently find the optimal solution feature subset, resulting in acceptable outcomes. The V-shaped transfer function is mainly responsible for BHGSO-V’s excellent search capability in addressing the FS problem. The STD of the objective function value obtained by the BHGSO-V algorithm is less compared to all selected algorithms, followed by BMPA, BGWO, BEO, BHGSO-S, BASO, and BSCA, as shown in Tab. 5. In comparison to all, the proposed BHGSO-V algorithms can provide highly reliable performance. Boldface in all tables indicates the best result among all algorithms.




The average accuracy and STD of the classification accuracy values obtained by all algorithms are listed in Tabs. 6 and 7, respectively. As seen in Tab. 6, the average accuracy obtained by BHGSO-V is better (i.e., 15 datasets), followed by BMPA, BEO, BHGSO-S, BGWO, HLBDA, BASO, and BSCA. As seen in Tab. 7, the STD of the classification accuracy obtained by the proposed BHGSO-V algorithm is better (i.e., 12 datasets), which means the reliability of the algorithm is better related to other techniques. As shown, the BHGSO-V algorithm outperformed other approaches in obtaining the best feature subset in most datasets. The boxplot analysis of eight algorithms, on the other hand, is shown in Fig. 5. In the present research, the proposed BHGSO algorithm gave the best median and mean values, as shown in Fig. 5. The outcomes show that the BHGSO algorithm is effective in maintaining better classification accuracy.
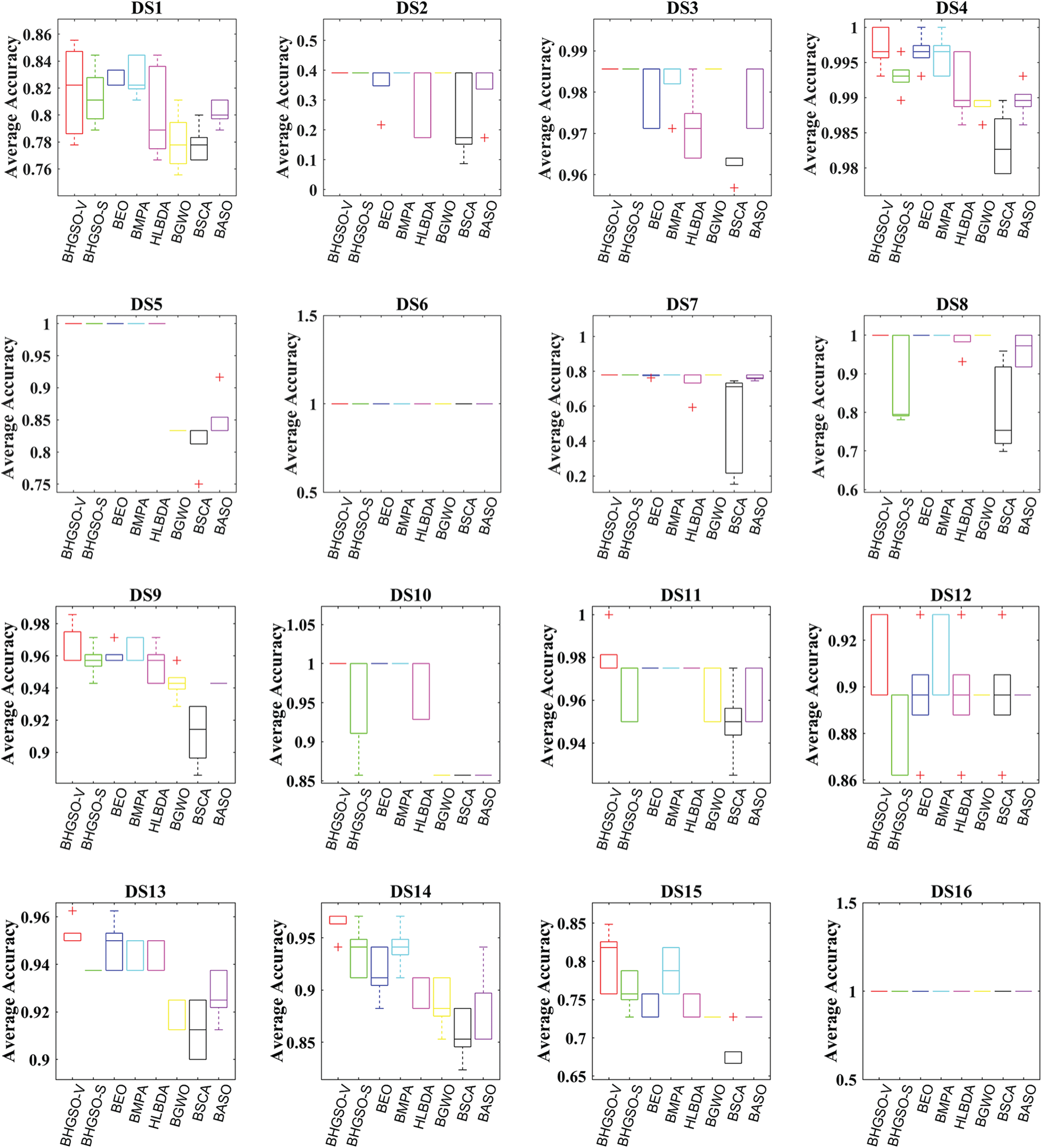
Figure 5: Boxplot analysis of all algorithms on all selected datasets

The mean and STD of the selection of the features from the large datasets are shown in Tabs. 8 and 9, respectively. In sixteen datasets, the proposed BHGSO-V had the smallest feature size (12 datasets), followed by BMPA, according to the findings (nine datasets). Unlike BSCA, BASO, BGWO, HLDBA, BEO, and BMPA, the BHGSO algorithm can typically find a small subset of best features that better represent the target definition. The BHGSO algorithm can avoid local optima and efficiently interpret the best FS solution. The lowest values of STD obtained by BHGSO prove the reliability of the algorithm.


A few statistical techniques are used to assess the proposed BHGSO algorithm’s efficacy. Several statistical non-parametric tests are discussed in the literature. The statistical analysis in this study is separated into two parts. First, the Friedman rank test (FRT) is utilized to assess all algorithms’ accuracy. The authors discovered that there is a substantial difference among all algorithms in this paper. The FRT of all algorithms is shown in Tab. 10. Based on the score obtained by all algorithms, the ranking is provided to all algorithms. The proposed BHGSO algorithm stands first among all selected algorithms for all datasets. For pairwise comparisons, the Wilcoxon signed-rank test (WSRT) is used in this paper. If the p-value is larger than 0.05, the results of the two techniques are considered to be identical; otherwise, the two methods are significantly different. The WSRT of the BHGSO algorithm against all other methods is shown in Tab. 11. According to the findings, the suggested BHGSO’s classification results were significantly higher than those of other competitors. Overall, the proposed HGSO algorithm provides the highest classification accuracy while also reducing dimensionality. Another performance metric called RT is illustrated in Fig. 6. From Fig. 6, it is observed that the RT of both versions of the BHGSO algorithm is significantly less for more than 10 datasets.

Figure 6: RT of all algorithms on all selected datasets


The proposed BHGSO algorithm was determined to be the best FS method based on the findings. The BHGSO-V algorithm enhanced the global optimum detection over the complex databases in terms of convergence and a minimum feature selection. The proposed BHGSO algorithms can able to sustain a decent acceleration during the iterations. The results in Tabs. 3–5 demonstrated the superiority of the BHGSO algorithms in terms of best, mean, and STD of the fitness values. The average accuracy and STD of the classification accuracy shown in Tabs. 6 and 7 prove the performance of the algorithm in classifying the datasets. The selected features shown in Tabs. 8 and 9 show the superiority of the BHGSO algorithms in selecting the optimal features. Furthermore, the BHGSO performed more consistently than the traditional binary algorithms, as evidenced by lower STD values. According to the experimental analysis results, the suggested BHGSO algorithm can often outperform the BEO, BMPA, BGWO, HLBDA, BASO, and BSCA classification. Clearly, the BHGSO features selected can typically provide high-quality data, which helped to improve prediction ability. The BHGSO effectively selected appropriate attributes and omitted most of the obsolete ones in a high-dimensional dataset like Colon, Leukemia, TOX_171, COIL20, Lung, and ORL. Compared to all selected algorithms, the suggested BHGSO is more capable of choosing significant features.
Binary versions of the HGSO algorithm are introduced and used to address the FS problems in wrapper form in this study. Either using S-shaped or V-shaped TFs, the continuous variant of the HGSO is converted to a binary variant. The proposed techniques can be used for FS in machine learning to evaluate various algorithms’ searching abilities. The FS problem is expressed as a multiobjective problem with an objective function reflecting dimensionality reduction and classification accuracy. To evaluate the output, 16 datasets from the UCI repository were selected. For evaluation, the suggested BHGSO are used in the FS problems, and the experimental outcomes have been compared to advanced FS methods such as BEO, BMPA, HLBDA, BGWO, BSCA, and BASO. To evaluate various aspects of results, the assessment uses a collection of evaluation criteria. On most datasets, experimental findings showed that the proposed BHGSO lead to better outcomes than other strategies. Furthermore, the findings, such as classification accuracy (>95%) and run time (<5 s for low and medium dimensional problems and <10 s for high dimensional problem), demonstrate that using a BHGSO with a V-shaped TF can expressively boost the performance of HGSO in terms of the number of features selected and classification accuracy. The experimental results reveal that the BHGSO-V searches the feature set more efficiently and converges to the best solution faster than other optimizations. The continuous HGSO was also successfully transformed into binary variants that can address several discrete problems, including the task scheduling, traveling salesman, and knapsack problems.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. H. H. Albaity and N. Almutlaq, “A new optimized wrapper gene selection method for breast cancer prediction,” Computers, Materials & Continua, vol. 67, no. 3, pp. 3089–3106, 2021. [Google Scholar]
2. Y. Xue, N. Wang, Y. Niu, P. Zhong, S. Niu et al., “Robust re-weighted multi-view feature selection,” Computers, Materials & Continua, vol. 60, no. 2, pp. 741–756, 2019. [Google Scholar]
3. Y. Gültepe, “Performance of lung cancer prediction methods using different classification algorithms,” Computers, Materials & Continua, vol. 67, no. 2, pp. 2015–2028, 2021. [Google Scholar]
4. W. Guo, T. Liu, F. Dai and P. Xu, “An improved whale optimization algorithm for feature selection,” Computers, Materials & Continua, vol. 62, no. 1, pp. 337–354, 2020. [Google Scholar]
5. T. Ma, H. Zhou, D. Jia, A. Aldhelaan, M. Aldhelaan et al., “Feature selection with a local search strategy based on the forest optimization algorithm,” Computer Modeling in Engineering & Sciences, vol. 121, no. 2, pp. 569–592, 2019. [Google Scholar]
6. S. Sayed, M. Nassef, A. Badr and I. Farag, “A nested genetic algorithm for feature selection in high-dimensional cancer microarray datasets,” Expert Systems with Applications, vol. 121, pp. 233–243, 2019. [Google Scholar]
7. L. Brezočnik, I. Fister and V. Podgorelec, “Swarm intelligence algorithms for feature selection: A review,” Applied Science, vol. 8, no. 9, pp. 1521, 2018. [Google Scholar]
8. S. Yu and J. C. Príncipe, “Simple stopping criteria for information theoretic feature selection,” Entropy, vol. 21, no. 1, pp. 99, 2019. [Google Scholar]
9. N. El Aboudi and L. Benhlima, “Review on wrapper feature selection approaches,” in Proc. of Int. Conf. on Engineering & MIS, Agadir, Morocco, pp. 1–5, 2016. [Google Scholar]
10. S. Mirjalili, “Dragonfly algorithm: A new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems,” Neural Computing and Applications, vol. 27, pp. 1053–1073, 2016. [Google Scholar]
11. A. Darwish, “Bio-inspired computing: Algorithms review, deep analysis, and the scope of applications,” Future Computing and Informatics Journal, vol. 3, no. 2, pp. 231–246, 2018. [Google Scholar]
12. T. Dokeroglu, E. Sevinc, T. Kucukyilmaz and A. Cosar, “A survey on new generation metaheuristic algorithms,” Computer and Industrial Engineering, vol. 137, pp. 106040, 2019. [Google Scholar]
13. M. Premkumar, T. Sudhakar Babu, S. Umashankar and R. Sowmya, “A new metaphor-less algorithms for the photovoltaic cell parameter estimation,” Optik, vol. 208, pp. 164559, 2020. [Google Scholar]
14. M. Premkumar, P. Jangir, R. Sowmya, H. H. Alhelou, A. A. Heidari et al., “MOSMA: Multi-objective slime mould algorithm based on elitist non-dominated sorting,” IEEE Access, vol. 9, pp. 3229–3248, 2021. [Google Scholar]
15. M. Premkumar, P. Jangir and R. Sowmya, “MOGBO: A new multiobjective gradient-based optimizer for real-world structural optimization problems,” Knowledge-Based Systems, vol. 218, pp. 106856, 2021. [Google Scholar]
16. M. Premkumar, R. Sowmya, P. Jangir, K. S. Nisar and M. Aldhaifallah, “A new metaheuristic optimization algorithms for brushless direct current wheel motor design problem,” Computers, Materials & Continua, vol. 67, no. 2, pp. 2227–2242, 2021. [Google Scholar]
17. M. Premkumar, P. Jangir, R. Sowmya, R. Madurai Elavarasan and B. Santhosh Kumar, “Enhanced chaotic JAYA algorithm for parameter estimation of photovoltaic cell/modules,” ISA Transactions, Article in Press, pp. 1–22, 2021. [Google Scholar]
18. X. Fan, W. Sayers, S. Zhang, Z. Han, L. Ren et al., “Review and classification of bio-inspired algorithms and their applications,” Journal of Bionic Engineering, vol. 17, pp. 611–631, 2020. [Google Scholar]
19. R. Alwajih, S. J. Abdulkadir, N. Aziz, Q. Altashi and N. Talpur, “Hybrid binary grey wolf with harris hawks optimizer for feature selection,” IEEE Access, vol. 9, pp. 31662–31677, 2021. [Google Scholar]
20. Y. Yin, Q. Tu and X. Chen, “Enhanced salp swarm algorithm based on random walk and its application to training feedforward neural networks,” Soft Computing, vol. 24, pp. 14791–14807, 2020. [Google Scholar]
21. Y. Gao, Y. Zhou and Q. Luo, “An efficient binary equilibrium optimizer algorithm for feature selection,” IEEE Access, vol. 8, pp. 140936–140963, 2020. [Google Scholar]
22. M. Mafarja, I. Aljarah, A. A. Heidari, H. Faris, P. Fournier-Viger et al., “Binary dragon fly optimization for feature selection using time-varying transfer functions,” Knowledge-Based Systems, vol. 161, pp. 185–204, 2018. [Google Scholar]
23. J. Too and S. Mirjalili, “A hyper learning binary dragonfly algorithm for feature selection: A COVID-19 case study,” Knowledge-Based Systems, vol. 212, pp. 106553, 2021. [Google Scholar]
24. C. Han, G. Zhou and Y. Zhou, “Binary symbiotic organism search algorithm for feature selection and analysis,” IEEE Access, vol. 7, pp. 166833–166859, 2019. [Google Scholar]
25. N. Neggaz, E. H. Houssein and K. Hussain, “An efficient henry gas solubility optimization for feature selection,” Expert Systems and Applications, vol. 152, pp. 113364, 2020. [Google Scholar]
26. L. Kumar and K. K. Bharti, “A novel hybrid BPSO-sCA approach for feature selection,” Natural Computing, vol. 20, pp. 39–61, 2021. [Google Scholar]
27. J. Too and A. R. Abdullah, “Binary atom search optimization approaches for feature selection,” Connection Science, vol. 32, no. 4, pp. 406–430, 2020. [Google Scholar]
28. M. A. Elaziz, A. A. Ewees, D. Yousri, H. S. N. Alwerfali, Q. A. Awad et al., “An improved marine predators algorithm with fuzzy entropy for multi-level thresholding: Real-world example of COVID-19 CT image segmentation,” IEEE Access, vol. 8, pp. 125306–125330, 2020. [Google Scholar]
29. M. Sharma and P. Kaur, “A comprehensive analysis of nature-inspired meta-heuristic techniques for feature selection problem,” Archives of Computational Methods in Engineering, vol. 28, pp. 1103–1127, 2021. [Google Scholar]
30. J. Too, A. R. Abdullah and N. Mohd Saad, “A new quadratic binary harris hawk optimization for feature selection,” Electronics, vol. 8, no. 10, pp. 1130, 2019. [Google Scholar]
31. W. Sheng-Wu and C. Hong-Mei, “Feature selection method based on rough sets and improved whale optimization algorithm,” Journal of Computer Science, vol. 47, no. 2, pp. 44–50, 2020. [Google Scholar]
32. D. H. Wolpert and W. G. Macready, “No free lunch theorems for optimization,” IEEE Transactions on Evolutionary Computation, vol. 1, no. 1, pp. 67–82, 1997. [Google Scholar]
33. Y. Yang, H. Chen, A. A. Heidari and A. H. Gandomi, “Hunger games search: Visions, conception, implementation, deep analysis, perspectives, and towards performance shifts,” Expert Systems and Applications, vol. 177, pp. 114864, 2021. [Google Scholar]
34. S. Arora and P. Anand, “Binary butterfly optimization approaches for feature selection,” Expert Systems and Applications, vol. 116, pp. 147–160, 2019. [Google Scholar]
35. S. Mirjalili and S. Z. M. Hashim, “BMOA: Binary magnetic optimization algorithm,” International Journal of Machine Learning and Computing, vol. 2, no. 3, pp. 204, 2012. [Google Scholar]
36. S. Mirjalili and A. Lewis, “S-shaped versus v-shaped transfer functions for binary particle swarm optimization,” Swarm and Evolutionary Computation, vol. 9, pp. 1–14, 2013. [Google Scholar]
37. A. G. Hussien, D. Oliva, E. H. Houssein, A. A. Juan and X. Yu, “Binary whale optimization algorithm for dimensionality reduction,” Mathematics, vol. 8, no. 10, pp. 1821, 2020. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |