Computers, Materials & Continua DOI:10.32604/cmc.2022.019604
Article

Medical Image Compression Method Using Lightweight Multi-Layer Perceptron for Mobile Healthcare Applications

Taesik Lee1, Dongsan Jun1,*, Sang-hyo Park2, Byung-Gyu Kim3, Jungil Yun4, Kugjin Yun4 and Won-Sik Cheong4

1Kyungnam University, Changwon, 51767, Korea
2Kyungpook National University, Daegu, 41566, Korea
3Sookmyung Women’s University, Seoul, 04310, Korea
4Electronics and Telecommunications Research Institute, Daejeon, 34129, Korea
*Corresponding Author: Dongsan Jun. Email: dsjun9643@kyungnam.ac.kr
Received: 19 April 2021; Accepted: 14 June 2021

Abstract: As video compression is one of the core technologies required to enable seamless medical data streaming in mobile healthcare applications, there is a need to develop powerful media codecs that can achieve minimum bitrates while maintaining high perceptual quality. Versatile Video Coding (VVC) is the latest video coding standard that can provide powerful coding performance with a similar visual quality compared to the previously developed method that is High Efficiency Video Coding (HEVC). In order to achieve this improved coding performance, VVC adopted various advanced coding tools, such as flexible Multi-type Tree (MTT) block structure which uses Binary Tree (BT) split and Ternary Tree (TT) split. However, VVC encoder requires heavy computational complexity due to the excessive Rate-distortion Optimization (RDO) processes used to determine the optimal MTT block mode. In this paper, we propose a fast MTT decision method with two Lightweight Neural Networks (LNNs) using Multi-layer Perceptron (MLP), which are applied to determine the early termination of the TT split within the encoding process. Experimental results show that the proposed method significantly reduced the encoding complexity up to 26% with unnoticeable coding loss compared to the VVC Test Model (VTM).

Keywords: Mobile healthcare; video coding; complexity reduction; multi-layer perceptron; VVC; intra prediction; multi-type tree; ternary tree; neural network

1  Introduction

Image or video compression is widely used to facilitate real-time medical data communication in mobile healthcare applications. This technology has several applications, including remote diagnostics and emergency incidence responses, as shown in Fig. 1 [1]. Mobile healthcare is one of the key aspects of telemedicine in which clinicians perform a broad range of clinical tasks remotely. At the same time, patients communicate with clinicians on hand-held devices with a limited hardware platform. Therefore, there is a need to develop a low-complexity video codec that achieves minimum bitrates with better coding performance while still maintaining high perceptual quality for seamless delivery of medical data within a constrained network bandwidth.

Figure 1: Visual representation of remote healthcare applications [1]

The state of the art video coding standard, Versatile Video Coding (VVC) [2] has been developed by the Joint Video Experts Team (JVET) of ITU-T Video Coding Experts Group (VCEG) and ISO/IEC Moving Picture Experts Group (MPEG) in 2020. It can significantly improve the coding performance compared with High-Efficiency Video Coding (HEVC) [3]. According to [4], VVC test model (VTM) has higher compression performance by 25% when compared with HEVC test model (HM) under the All Intra (AI) configuration recommended by JVET Common Test Conditions (CTC) [5]. This improvement was achieved as a result of newly adopted coding tools, such as flexible block structure, Position Dependent intra Prediction Combination (PDPC) [6], Cross Component Linear Model intra prediction (CCLM) [7], Wide Angular Prediction (WAP) [8], and Matrix weighted Intra Prediction (MIP) [9]. Although VVC can significantly improve the coding performance, the encoder’s computational complexity also substantially increased by approximately 26 times [10] compared to HEVC. Therefore, it is essential to reduce the encoding complexity of VVC to facilitate its real-time implementation in low-end mobile devices.

One of the main differences between HEVC and VVC is the block structure scheme. Both HEVC and VVC commonly specify Coding Tree Unit (CTU) as a basic coding unit with an interchangeable size based on the encoder configuration. In addition, to adapt to the various block properties, CTU could be split into four Coding Units (CUs) using a Quad-Tree (QT) structure. In HEVC, a leaf CU could be further partitioned into one, two, or seven Prediction Units (PUs) according to the PU partitioning types. After obtaining the residual block derived from the PU level using either intra or inter prediction, a leaf CU can be further partitioned into multiple Transform Units (TUs) according to a Residual Quad-Tree (RQT) that is structurally similar to that of the CU split. Therefore, the block structure of HEVC has multiple partition concepts, including CU, PU, and TU, as shown in Fig. 2 [11].

Figure 2: Multiple partition concepts for the coding unit (CU), prediction unit (PU), and transform unit (TU) in HEVC [11]

On the other hand, VVC replaces the concepts of multiple partition unit types (CU, PU, and TU) of HEVC with another block structure, named QT-based Multi-type Tree (QTMTT). In VVC, a MTT can be partitioned into either Binary Tree (BT) or Ternary Tree (TT) to support more flexible CU shapes. As shown in Fig. 3, VVC specifies a single QT split type and four MTT split types. These include quad-tree split (SPLIT_QT), vertical binary split (SPLIT_BT_VER), horizontal binary split (SPLIT_BT_HOR), vertical ternary split (SPLIT_TT_VER), and horizontal ternary split (SPLIT_TT_HOR), respectively. While the minimum BT and TT sizes are both 4 × 4, the maximum BT and TT sizes are 128 × 128 and 64 × 64, respectively. Note that a QT node with a square shape can be further partitioned into either sub QT or MTT node, while a MTT node can be only partitioned into MTT node, as shown in Fig. 4 [11]. Here, a QT or a MTT leaf node is considered as a CU, and it is used in the unit of the prediction and transform processes without any further partitioning schemes. It means that a CU in VVC can have either a square or a rectangular shape, while a CU in HEVC always has a square shape.

Figure 3: VVC block structure consisting of a quad-tree (QT) and a multi-type tree (MTT) where MTT is classified into binary tree (BT) and ternary tree (TT) splits in the horizontal and vertical direction. (a) QT split (b) BT split (c) TT split

Figure 4: CU partitions corresponding to the QT or MTT node in VVC [11]

Although the block structure of VVC is superior to that of HEVC in terms of the flexibility of CU shapes, it causes heavy computational complexity on VVC encoder due to the excessive Rate-distortion Optimization (RDO) calculations required to search for the optimal QT, BT, and TT block mode decision. Furthermore, VVC adopted a dual-tree structure in the intra-frame so that a CTU can have different block structures according to the color of each component. It means that a luma CTU and a chroma CTU can have their own QTMTT structures. This dual-tree concept significantly improves the coding performance in the chroma components but comes at the cost of increasing the computational complexity [12]. Therefore, we propose a fast MTT decision method with two Lightweight Neural Networks (LNNs) using Multi-layer Perceptron (MLP), which are applied to determine the Early Termination (ET) of the TT split within the encoding process. In this paper, we implemented two LNNs before the RDO process of the TT split. These are denoted as HTS-LNN and VTS-LNN for the ET of the horizontal and the vertical TT split, respectively.

In this study, we investigated four input features to use as an input vector on the proposed two LNNs with MLP structure. With the proposed four input features, two LNNs were designed to provide high accuracy with the lowest complexity. In addition, various ablation works were performed to evaluate their effectiveness how these features would affect the accuracy of the proposed LNNs. We then proposed a fast MTT decision method using the two LNNs to determine the early termination of the horizontal and the vertical TT splits required in the CU encoding process. Finally, we implemented the proposed method on top of the VTM and evaluated the trade-off between the complexity reduction and the coding loss on medical sequences as well as JVET test sequences.

The remainder of this paper is organized as follows. In Section 2, we review the related fast encoding schemes used to reduce the complexity of the video encoder. Then, the proposed method is described in Section 3. Finally, experimental results and conclusions are given in Sections 4 and Section 5, respectively.

2  Related Works

Several methods have been proposed to reduce the computational complexity of HEVC and VVC encoders. Shen et al. proposed a fast CU size decision algorithm for HEVC intra prediction, which exploited RD costs and intra mode correlations among previously encoded CUs [13]. Goswami et al. [14] designed a fast block mode decision method using the Markov-Chain-Monte-Carlo model and the Bayesian classifier to determine the optimal CU partitioning shapes. Min et al. [15] proposed a fast CU partition algorithm based on the analysis of edge complexity. As described in [16], Min et al. addressed a fast QTBT decision method based on the RD costs of the previously encoded CUs in VVC. Yang et al. [17] also proposed a fast QTBT decision method using the properties of intra prediction mode. Cho et al. proposed a fast CU splitting and pruning method for sub-optimal CU partitioning with Bayes decision rules in the intra prediction of HEVC [18]. In [19,20], the proposed schemes exploited both texture properties and spatial correlations derived from neighboring CUs. In [21], a fast CU mode decision method was proposed to estimate the optimal prediction mode in HEVC. Recently, Park et al. [22] proposed a context-based fast TT decision (named C-TTD) method using the correlation according to the directional information between BTs and TTs. Saldanha et al. [23] proposed a novel fast partitioning decision scheme for VVC intra coding to reduce the complexity of the QTMT structure. This scheme is composed of two strategies that explore the correlation of the intra prediction modes and samples of the current CU for deciding the split direction of binary and ternary partitions. Fu et al. designed two fast encoding schemes to speed up the CU splitting procedure for VVC intra-frame coding [24]. Lei et al. [25] proposed a look-ahead prediction based on a CU size pruning algorithm to cut down redundant MTT partitions. Wu et al. [26] investigated a support vector machine (SVM) based fast CU partitioning algorithm for VVC intra coding designed to terminate redundant partitions by using CU texture information. Fan et al. [27] proposed a fast QTMT partition algorithm using the texture properties such as variance and gradient to reduce the computational complexity of VVC CU partitions. This method exploited RD costs obtained from the previously encoded CU data based by using a probabilistic approach.

While the aforementioned methods evaluated statistical coding correlations between a current CU and neighboring CUs, recent researches have studied new fast decision schemes using Convolutional Neural Network (CNN) or Multi-layer Perceptron (MLP) to avoid the redundant block partitioning within video encoding processes. Xu et al. [28] defined a Hierarchical CU Partition Map (HCPM) with nine convolutional layers in order to determine the optimal CU partition structure in HEVC. Kim et al. [29] designed simple neural networks using MLP to estimate the optimal CU depth in HEVC. Galpin et al. [30] proposed a CNN-based block partitioning method for fast intra prediction in HEVC by exploiting texture analysis of CTU blocks to predict the most probable splits inside each potential sub-block. Wang et al. [31] proposed a QTBT partitioning decision in order to determine the optimal CU depth as a multi-classification problem in the inter prediction. Jin et al. [32] proposed a fast QTBT partition method with a CNN model to predict the depth range of QTBT according to the inherent texture richness of the image. Li et al. [33] addressed a deep learning approach to predict QTMT-based CU partition to accelerate the encoding process in the intra prediction of VVC. Lin et al. [34] proposed a CNN-based intra mode decision method with two convolutional layers and a fully connected layer. Zhao et al. [35] developed an adaptive CU split decision method with the deep learning and multi-featured fusion. Zaki et al. [36] also proposed a CtuNet framework to support CTU partitioning using deep learning techniques. As the aforementioned methods are mainly focused on speeding up QT or BT, fast encoding schemes for the TT split are still needed in VVC.

3  Proposed Method

The RD-based encoding procedures for the current CU are illustrated in Fig. 5, whereby the gray rectangles represent the newly adopted MTT (BT and TT) block structures in VVC. In order to find the optimal block structure, the encoder conducts the RD competitions for all MTT split types, including QT split according to the order illustrated in Fig. 5. In this paper, we propose a fast MTT decision method to determine the early termination of the TT split in the CU encoding process. Note that the proposed method can only be applied for cases wherein a further MTT split is allowed. For the implementation of the proposed method, we deployed two early termination networks for the horizontal and vertical TT splits, which are denoted as HTS-LNN and VTS-LNN, respectively.

Figure 5: CU encoding procedures of VVC

As shown in Fig. 6, the proposed method has two modules which are feature aggregation and early TT decision consisting of HTS-LNN and VTS-LNN. In the feature aggregation module, the Network Input Features (NIF) of the two LNNs are extracted halfway through encoding processes according to the TT direction. These are then fed into the two LNNs in order to be used as the input vectors, which are denoted as x¯h, NIF and x¯v, NIF, respectively. Finally, the horizontal and vertical TT splits are determined by the neurons (yh and yv) output values of LNNs.

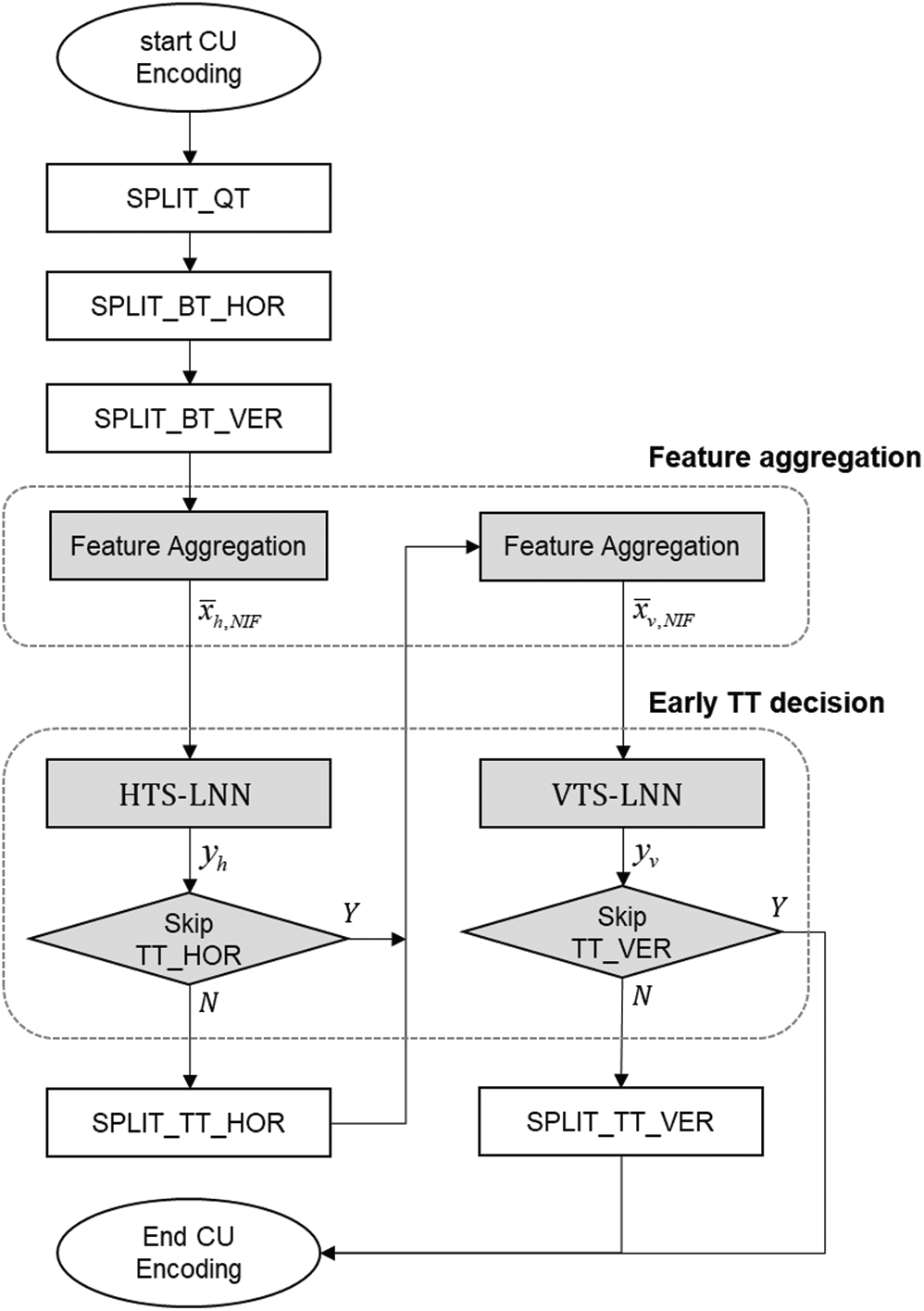
Figure 6: Proposed CU encoding procedures. The gray rectangles represent the proposed feature aggregation and early TT decision

3.1 Feature Aggregation

In this paper, we defined the relationship between the parent CU and current CUs used to extract the network input features. The parent CU can be either a QT node with a square shape or a MTT node with either a square or a rectangular shape covering the area of the current CU. For example, the divided QT, BT, and TT CUs can have the same parent CU, which is the QT node with 2 N × 2 N, as illustrated in Fig. 7a. Similarly, a MTT node is also regarded as a parent CU for further partitioned sub-MTT nodes, as depicted in Fig. 7b.

Figure 7: Graphical representation of the parent and current CUs. (a) An example of regarding QT as a parent CU (b) An example of regarding MTT as a parent CU

Because CNN generally requires heavy convolution operations between input features and filter weights, the proposed LNNs were designed to use fewer input features that can be easily extracted during the current CU encoding process. In this paper, we proposed four input features which are named as Ratio of Block Size (RBS), Optimal BT Direction (OBD), Ratio of the Number of Direction (RND), and TT Indication (TTI), respectively, as described in Tab. 1.

3.2 Early TT Decision with LNNs

We implemented two LNNs with MLP architectures before the TT split, defined as HTS-LNN and VTS-LNN, according to the early termination of the horizontal and vertical TT splits, respectively. Through feature aggregation, a 1-dimensional (1D) column vector with four features as an input vector was identified for both HTS-LNN and VTS-LNN. As shown in Fig. 8, HTS-LNN consisted of four input nodes, one hidden layer with 15 hidden nodes, and one output node. Conversely, VTS-LNN consisted of four input nodes, two hidden layers with 30 and 15 hidden nodes, and one output node. The value of the output node finally determined the horizontal or vertical TT splits.

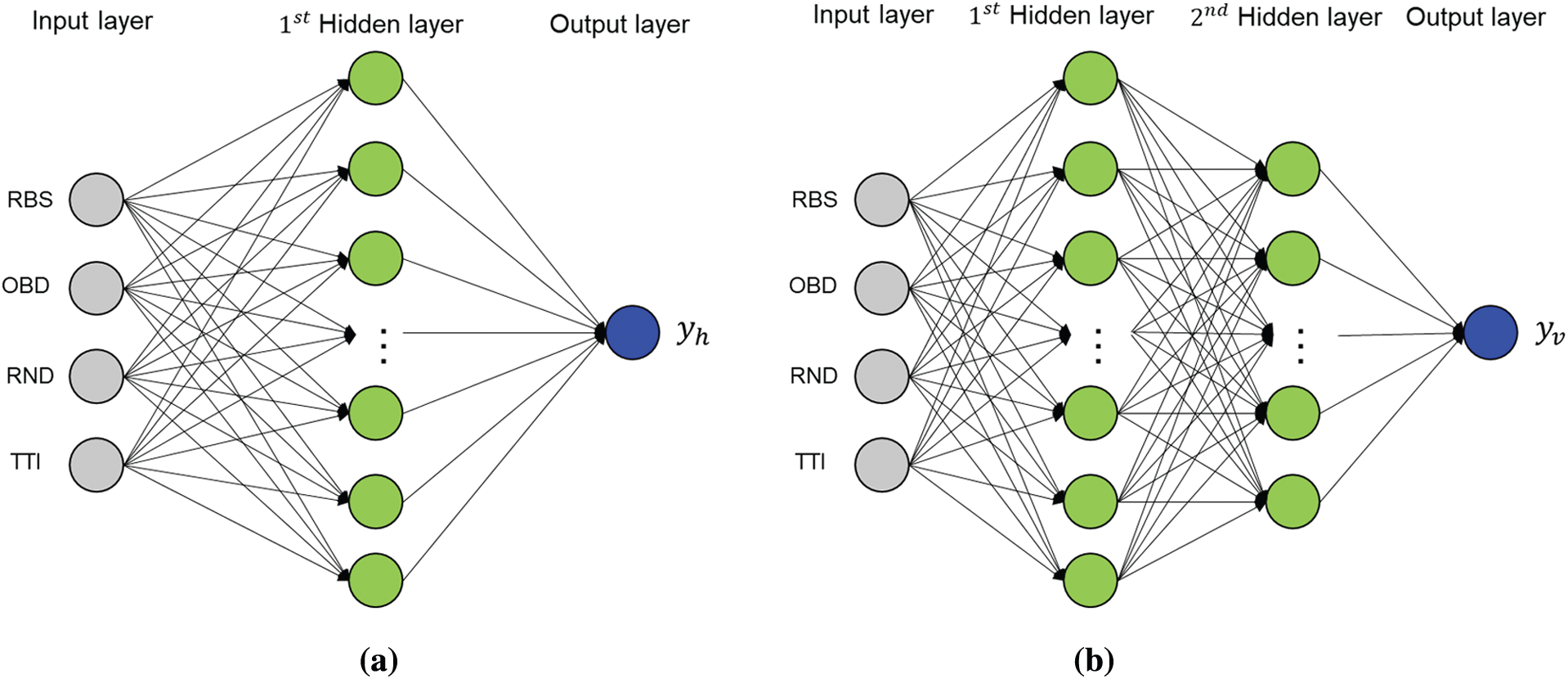
Figure 8: Proposed LNN architectures. (a) HTS-LNN with one hidden layer having 15 nodes (b) VTS-LNN with two hidden layers having 30 and 15 nodes

We implemented both HTS-LNN and VTS-LNN on PyCharm 2020.3.2 using the Keras library. In the process of network training, the output of the jth neuron were computed by Eq. (1):

hj=f(∑iw¯jix¯i+bj),wherej=1,…,φ(1)

where x¯i, w¯j,i, bj, φ and f(⋅) denote the ith input feature, the filter weight corresponding to the jth neuron of the ith input feature, the bias value of the jth neuron, the number of neurons within each layer, and the logistic sigmoid function as an activation function, respectively. The output of each network (yh or yv) had a value between 0 and 1, and it determined whether the TT split of the current CU could be skipped or not with a predefined threshold value. Note that when the output values of the models are close to 1, then the TT should be split and vice versa. Since the threshold value was set to 0.5 in this paper, the encoder performed the TT split when the value of the output neuron was larger than the threshold value.

Tab. 2 shows the measured weight and bias parameters as well as the total memory size. Since the parameters were stored as a 4-byte floating number, the total memory of the proposed networks was less than 3 KB.

Under the AI configuration of JVET CTC [5], we collected training datasets halfway through the encoding by VTM 10.0 [4] to train the proposed networks. A Quantization Parameter (QP) of 30 was selected to separate the training conditions from the testing conditions. The input features were then extracted with the type of floating number, which ranged from 0 to 1. The total numbers of input vectors for the training HTS-LNN and VTS-LNN were 185,988 and 209,337, respectively. In addition, 20% of them were used as the validation set. Note that the training datasets had to be extracted evenly for both the TT non-split and the TT split because the TT split was rarely encoded as the best block.

The selected hyperparameters are presented in Tab. 3. The weight values of the proposed networks were optimized using a Stochastic Gradient Descent (SGD) with a momentum value of 0.9 and a weight decay of 1e-6 [37]. The batch size and learning rate were set at 128 and 0.01, respectively. The initialization of all MLP weights was performed according to Xavier’s normalized initialization procedure [38], whereby the optimized model parameters were updated iteratively within the predefined epoch number, and the Mean Squared Error (MSE) was used as a loss function. Finally, we implemented the trained models on top of VTM 10.0.

4  Experimental Results

All experiments were run on an Intel Xeon Gold 6138 40-cores 2.00 GHz processors having 256GB RAM operated by the 64-bit Windows server 2016. In the class A (3,840 × 2,160) and B (1,920 × 1,080) sequences of JVET CTC, the proposed method was evaluated under AI configuration and we compared our method with the previous method [22], where VTM 10.0 was used as an anchor.

4.1 Performance Measurements

In order to evaluate the coding loss, we measured the Bjontegaard Delta Bit Rate (BDBR) [39]. In general, a BDBR increase of 1% corresponds to a BD-PSNR decrease of 0.05 dB where the positive increment of BDBR indicates the coding loss. Eq. (2) represents the weighted average BDBR of Y, U, and V color components in the test sequences recommended by JVET CTC. For comparison of the computational complexity, we measured time-saving (ΔT) as expressed by Eq. (3):

BDBRYUV=6×BDBRY+BDBRU+BDBRV8(2)

ΔT=14∑QPi∈{22,27,32,37}Torg(QPi)−Tfast(QPi)Torg(QPi)(3)

where Torg and Tfast denote the total encoding time of the anchor and the fast encoding methods, respectively. In terms of BDBRYUV and ΔT, performance comparisons between the proposed method and the compared method [22] are measured in Tab. 4. Compared to the anchor, the proposed method achieved an average time saving of 26%. In particular, the maximal time saving of 30% was obtained in the Tango2 sequence. Furthermore, the proposed method enhances the time saving up to 10% on average compared to the previous method [22]. The effectiveness of this technique was further verified on 29 colonoscopy medical sequences obtained from the Computer Vision Center-Clinic Database (CVC-ClinicDB) [40]. As shown in Tab. 5, the results had similar trends to those obtained from the JVET test sequences, whereby an average time saving of up to 35% was noted with almost the same visual quality as the anchor, as shown in Fig. 9.

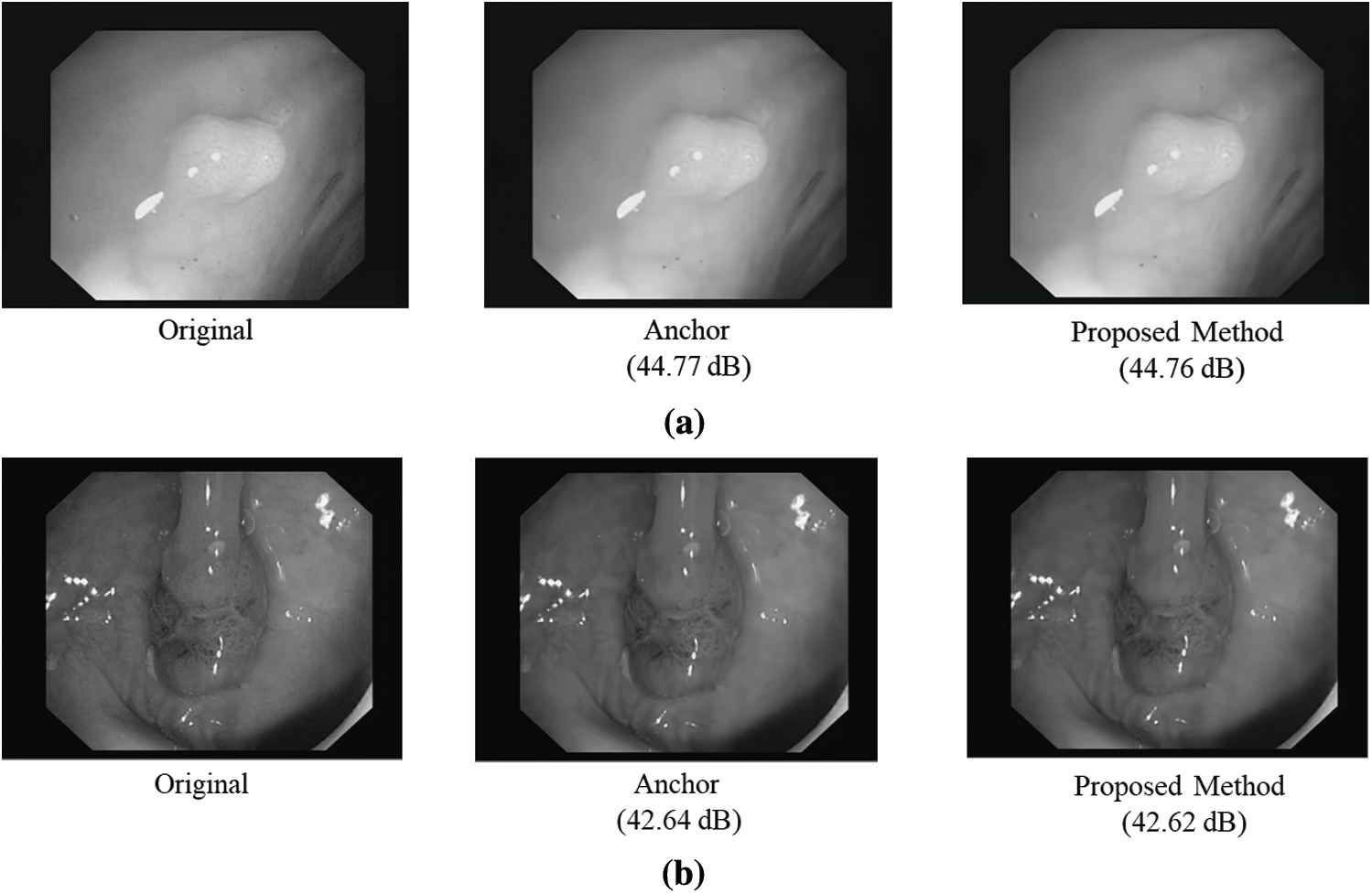
Figure 9: Visual comparison on CVC-ClinicDB [40]. (a) 2nd sequence (b) 6th sequence

4.2 Ablation Works

In order to optimize the proposed network architecture, it is essential to determine the valid input features, the number of hidden layers, and the number of nodes per hidden layer. Tool-off tests on both validation and training datasets were performed to measure the effectiveness of the four input features. This test involved measuring the efficacy of all input features combined (“all features”) and then by subsequently omitting one of the four input features. The results of the tool-off tests are illustrated in Tabs. 6 and 7. Since the “all features” input exhibited the best accuracy and the lowest coding loss, the effectiveness of each of the tool-off tests was determined as a proportion of the “all feature” category. Based on these findings, we confirmed that the proposed four input features affected the performance of our networks in different ways. In particular, the TTI and RND were identified as the most effective input features in the HTS-LNN and VTS-LNN, respectively.

In terms of the number of hidden layers and the number of nodes per hidden layer, we investigated a few neural network models using different numbers of nodes and hidden layers, as shown in Tabs. 8 and 9. Note that the maximum number of hidden layers was set to two for all the lightweight network designs. After considering both the accuracy and the loss of networks, HTS-LNN was optimized under one hidden layer with 15 nodes. On the other hand, VTS-LNN was optimized under two hidden layers with 30 nodes in one of the layers and 15 nodes in the second layer.

5  Conclusions

In this paper, we proposed two LNNs with MLP architectures to determine the early termination of the TT split in the encoding process, namely HTS-LNN and VTS-LNN for the early termination of the horizontal and vertical TT splits, respectively. HTS-LNN consisted of four input nodes, one hidden layer with 15 hidden nodes, and one output node. On the other hand, VTS-LNN consisted of four input nodes, two hidden layers with 30 and 15 hidden nodes, and one output node. The various verification tests of those networks were conducted to determine the optimal network structure. In order to identify the effectiveness of this method for the transfer of medical images, we evaluated the performance of our approach using colonoscopy medical sequences obtained from the CVC-ClinicDB and JVET CTC sequences. Our experimental results indicate that the proposed method can significantly reduce the average encoding complexity by 26% and 10% with unnoticeable coding loss compared to the anchor and the previous method, respectively. Through visual comparison, we demonstrated that the proposed method could provide almost the same visual quality compared to the anchor.

Acknowledgement: This work was supported by Institute for Information & communications Technology Planning & Evaluation (IITP) grant funded by the Korea government (MSIT) (No. 2017-0-00072, Development of Audio/Video Coding and Light Field Media Fundamental Technologies for Ultra Realistic Tera-media)

Funding Statement: The author received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  B. Atty, A. M. Iliyasu, H. Alaskar and A. Latif, “A robust quasi-quantum walks-based steganography protocol for secure transmission of images on cloud-based E-healthcare platforms,” Sensors, vol. 20, no. 11, pp. 1–19, 2020. [Google Scholar]

 2.  B. Bross, J. Chen, S. Liu and Y. K. Wang, “Versatile video coding (Draft 10),” in Joint Video Experts Team of ITU-T SG 16 WP 3 and ISO/IEC JTC 1/SC 29/WG 11 Document JVET-S2001, Teleconference (Online2020. [Google Scholar]

 3.  G. J. Sullivan, J. R. Ohm, W. J. Han and T. Wiegand, “Overview of high efficiency video coding standard,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 22, no. 12, pp. 1649–1668, 2012. [Google Scholar]

 4.  Fraunhofer Heinrich Hertz Institute, Joint Video Experts Team (JVET“JVET, test model 10 of versatile video coding (VTM 10),” 2020. [Online]. Available: https://vcgit.hhi.fraunhofer.de/jvet/VVCSoftware_VTM. [Google Scholar]

 5.  F. Bossen, J. Boyce, K. Sühring, X. Li and V. Seregin, “VTM common test conditions and software reference configurations for SDR video,” in Joint Video Experts Team of ITU-T SG 16 WP 3 and ISO/IEC JTC 1/SC 29/WG 11 Document JVET-T2010, Teleconference (Online2020. [Google Scholar]

 6.  G. Auwera, V. Seregin, A. Said, A. Ramasubramonian and M. Karczewicz, “CE3: Simplified PDPC (Test 2.4.1),” in Joint Video Experts Team of ITU-T SG 16 WP 3 and ISO/IEC JTC 1/SC 29/WG 11 Document JVET-K0063, Ljubljana, SI, 2018. [Google Scholar]

 7.  X. Ma, H. Yang and J. Chen, “CE3: Tests of cross-component linear model in BMS1.0 (Test 4.1.8, 4.1.9, 4.1.10, 4.1.11),” in Joint Video Experts Team of ITU-T SG 16 WP 3 and ISO/IEC JTC 1/SC 29/WG 11 Document JVET-K0190, Ljubljana, SI, 2018. [Google Scholar]

 8.  F. Racapé, G. Rath, F. Urban, L. Zhao, S. Liu et al., “CE3-related: Wide-angle intra prediction for non-square blocks,” in  Joint Video Experts Team of ITU-T SG 16 WP 3 and ISO/IEC JTC 1/SC 29/WG 11 Document JVET-K0500, Ljubljana, SI, 2018. [Google Scholar]

 9.  J. Pfaff, B. Stallenberger, M. Schäfer, P. Merkle, P. Helle et al., “CE3: Affine linear weighted intra prediction,” in Joint Video Experts Team of ITU-T SG 16 WP 3 and ISO/IEC JTC 1/SC 29/WG 11 Document JVET-N0217, Geneva, CH, 2019. [Google Scholar]

10. F. Bossen, X. Li, A. Norkin and K. Suhring, “JVET AHG report: Test model software development (AHG3),” in Joint Video Experts Team of ITU-T SG 16 WP 3 and ISO/IEC JTC 1/SC 29/WG 11 Document JVET-T0003, Teleconference (Online2020. [Google Scholar]

11. Y. Ahn, T. Hwang, D. Sim and W. Han, “Implementation of fast HEVC encoder based on SIMD and data-level parallelism,” EURASIP Journal on Image and Video Processing, vol. 16, pp. 1–19, 2014. [Google Scholar]

12. W. J. Chien, J. Boyce, Y. W. Chen, R. Chernyak, K. Choi et al., “JVET AHG report: Tool reporting procedure (AHG13),” in Joint Video Experts Team of ITU-T SG 16 WP 3 and ISO/IEC JTC 1/SC 29/WG 11 Document JVET-T0013, Teleconference (Online2020. [Google Scholar]

13. L. Shen, Z. Zhang and P. An, “Fast CU size decision and mode decision algorithm for HEVC intra coding,” IEEE Transactions on Consumer Electronics, vol. 59, no. 1, pp. 207–213, 2013. [Google Scholar]

14. K. Goswami and B. Kim, “A design of fast high efficiency video coding scheme based on markov chain monte carlo model and Bayesian classifier,” IEEE Transactions Industrial Electronics, vol. 65, no. 11, pp. 8861–8871, 2018. [Google Scholar]

15. B. Min and R. C. C. Cheung, “A fast CU size decision algorithm for the HEVC intra encoder,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 25, no. 5, pp. 892–896, 2015. [Google Scholar]

16. P. H. Lin, C. L. Lin, Y. J. Chang, C. C. Lin and Y. H. Ju, “AHG5: Enhanced fast algorithm of JVET-e0078,” in Joint Video Experts Team of ITU-T SG 16 WP 3 and ISO/IEC JTC 1/SC 29/WG 11 Document JVET-F0063, Hobart, AU, 2017. [Google Scholar]

17. H. Yang, L. Shen, X. Dong, Q. Ding, P. An et al., “Low complexity CTU partition structure decision and fast intra mode decision for versatile video coding,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 30, no. 6, pp. 1668–1682, 2020. [Google Scholar]

18. S. Cho and M. Kim, “Fast CU splitting and pruning for suboptimal CU partitioning in HEVC intra coding,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 23, no. 9, pp. 1555–1564, 2013. [Google Scholar]

19. L. Shen, Z. Zhang and Z. Liu, “Effective CU size decision for HEVC intra-coding,” IEEE Transactions on Image Processing, vol. 23, no. 10, pp. 4232–4241, 2014. [Google Scholar]

20. L. Shen, Z. Liu, X. Zhang, W. Zhao and Z. Zhang, “An effective CU size decision method for HEVC encoders,” IEEE Transactions on Multimedia, vol. 15, no. 2, pp. 465–470, 2013. [Google Scholar]

21. D. Jun, “A fast coding unit mode decision method based on mode inheritance of upper coding unit for low-complexity compression of smart contents,” Displays, vol. 55, pp. 3–9, 2018. [Google Scholar]

22. S. Park and J. Kang, “Context-based ternary tree decision method in versatile video coding for fast intra coding,” IEEE Access, vol. 7, pp. 172597–172605, 2019. [Google Scholar]

23. M. Saldanha, G. Sanchez, C. Marcon and L. Agostini, “Fast partitioning decision scheme for versatile video coding intra-frame prediction,” in Proc. ISCAS, Seville, Spain, pp. 1–5, 2020. [Google Scholar]

24. T. Fu, H. Zhang, F. Mu and H. Chen, “Fast CU partitioning algorithm for H.266/VVC intra-frame coding,” in Proc. ICME, Shanghai, China, pp. 55–60, 2019. [Google Scholar]

25. M. Lei, F. Luo, X. Zhang, S. Wang and S. Ma, “Look-ahead prediction based coding unit size pruning for VVC intra coding,” in Proc. ICIP, Taipei, Taiwan, pp. 4120–4124, 2019. [Google Scholar]

26. G. Wu, Y. Huang, C. Zhu, L. Song and W. Zhang, “SVM based fast CU partitioning algorithm for VVC intra coding,” in Proc. ISCAS, Daegu, Korea, pp. 1–5, 2021. [Google Scholar]

27. Y. Fan, J. Chen, H. Sun, J. Katto and M. Jing, “A fast QTMT partition decision strategy for VVC intra prediction,” IEEE Access, vol. 8, pp. 107900–107911, 2020. [Google Scholar]

28. M. Xu, T. Li, Z. Wang, X. Deng, R. Yang et al., “Reducing complexity of HEVC: A deep learning approach,” IEEE Transactions on Image Processing, vol. 27, no. 10, pp. 5044–5059, 2018. [Google Scholar]

29. K. Kim and W. Ro, “Fast CU depth decision for HEVC using neural networks,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 29, no. 5, pp. 1462–1473, 2019. [Google Scholar]

30. F. Galpin, F. Racap, S. Jaiswal, P. Bordes, F. Le Lannec et al., “CNN-Based driving of block partitioning for intra slices encoding,” in Proc. DCC, Snowbird, UT, USA, pp. 162–171, 2019. [Google Scholar]

31. Z. Wang, S. Wang, X. Zhang, S. Wang and S. Ma, “Fast QTBT partitioning decision for interframe coding with convolution neural network,” in Proc. ICIP, Athens, Greece, pp. 2550–2554, 2018. [Google Scholar]

32. Z. Jin, P. An, C. Yang and L. Shen, “Fast QTBT partition algorithm for intra frame coding through convolutional neural network,” IEEE Access, vol. 6, pp. 54660–54673, 2018. [Google Scholar]

33. T. Li, M. Xu, R. Tang, Y. Chen and Q. Xing, “DeepQTMT: A deep learning approach for fast QTMT-based CU partition of intra-mode VVC,” ArXiv Preprint ArXiv, vol. 2006, pp. 1–14, 2021. [Google Scholar]

34. T. Lin, K. Liang, J. Huang, Y. Tu and P. Chang, “Convolutional neural network based fast intra mode prediction for H.266/FVC video coding,” in Proc. DCC, Snowbird, UT, USA, pp. 380, 2020. [Google Scholar]

35. J. Zhao, Y. Wang and Q. Zhang, “Adaptive CU split decision based on deep learning and multifeatured fusion for H.266/VVC,” Hindawi, vol. 2020, pp. 1–11, 2020. [Google Scholar]

36. F. Zaki, A. Mohamed and S. Sayed, “Ctunet: A deep learning-based framework for fast CTU partitioning of H265/HEVC intra-coding,” Ain Shams Engineering Journal, vol. 12, pp. 1859–1866, 2021. [Google Scholar]

37. S. Ruder, “An overview of gradient descent optimization algorithms,” ArXiv Preprint ArXiv, vol. 1609, pp. 1–14, 2017. [Google Scholar]

38. X. Glorot and Y. Bengio, “Understanding the difficulty of training deep feedforward neural networks,” Journal of Machine Learning Research, vol. 9, pp. 249–256, 2010. [Google Scholar]

39. G. Bjontegaard, “Calculation of average PSNR differences between RD curves,” in ITU-T SG 16 Q6 Document VCEG-M33, Austin, TX, USA, 2001. [Google Scholar]

40. J. Bernal, J. F. Sánchez, G. Fernández-Esparrach, D. Gil, C. Rodríguez et al., “WM-Dova maps for accurate polyp highlighting in colonoscopy: Validation vs. saliency maps from physicians,” Computerized Medical Imaging and Graphics, vol. 43, pp. 99–111, 2015. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.