DOI:10.32604/cmc.2022.019342

| Computers, Materials & Continua DOI:10.32604/cmc.2022.019342 |  |
| Article |
Hybrid Teaching Learning Approach for Improving Network Lifetime in Wireless Sensor Networks
1Easwari Engineering College, Chennai, 600089, India
2Computer Science and Engineering, RVS College of Engineering & Technology, Coimbatore, 641402, India
*Corresponding Author: P. Baskaran. Email: baskarcse06@gmail.com
Received: 10 April 2021; Accepted: 12 June 2021
Abstract: In a wireless sensor network (WSN), data gathering is more effectually done with the clustering process. Clustering is a critical strategy for improving energy efficiency and extending the longevity of a network. Hierarchical modeling-based clustering is proposed to enhance energy efficiency where nodes that hold higher residual energy may be clustered to collect data and broadcast it to the base station. Moreover, existing approaches may not consider data redundancy while collecting data from adjacent nodes or overlapping nodes. Here, an improved clustering approach is anticipated to attain energy efficiency by implementing MapReduction for regulating mapping and reducing complexity in routing mechanisms for eliminating redundancy and overlapping. In order to optimize the network performance, this work considers intelligent behaviors’ to adapt with network changes and to introduce computational intelligence ability. In the proposed research, improved teaching learning based optimization is used to evaluate the coordinates of target nodes and nodes upgradation for determining energy consumption. Node upgradation is performed by integrating Map reduction to attain modification in Hop size of nodes. This variation reduces communication complexities. Therefore, network lifetime is increased, and redundancy is reduced. While comparing with existing approaches here, sleep and wake-up nodes are considered for data transmission. The proposed algorithm clearly demonstrates 50%, 16% & 12% improvement in nodes lifetime, residual energy and throughput respectively compared to other models. Also it shows progressive improvement in reducing average waiting time, average queuing time and average energy utilization as 30%, 20% and 46% respectively. Simulation has been done in NS-2 environment for distributed heterogeneous networks.
Keywords: Map reduction; optimization; Teaching-learning; energy efficiency; network lifetime; heterogeneous network
Wireless Sensor Networks (WSN) gathers information of data locality among nodes via constant monitoring and prominently used in wide area network (WAN) as it is extremely cheaper and route establishment procedure is also considered to be simpler. WSN is used for monitoring military tracking, fire, temperature and so on [1]. WSN is used for the short range that helps in monitoring environmental factors [2]. Sensor node [SN] design is based on parameters like energy constraints, restricted computation and storage capacities like collaborating sensors in performing measures [3]. The sensor controls over harsh environment leads to control over placed sensors with hectic confronts (Fig. 1). In every routing protocols of WSN, application functionality may change with variations in goal [4]. The functionality of WSN is based on the battery functionality of SNs as battery-based sensors that are accountable for network lifetime [5]. Similarly, clustering is a technique that deals with SNs energy consumption for forming groups termed as clusters, with individual Cluster Head’s (CH) [6]. SNs comes under a single cluster and they involve themselves in broadcasting the data collected to CHs which is communicated to sink nodes either by single or multi-hop communication [7].
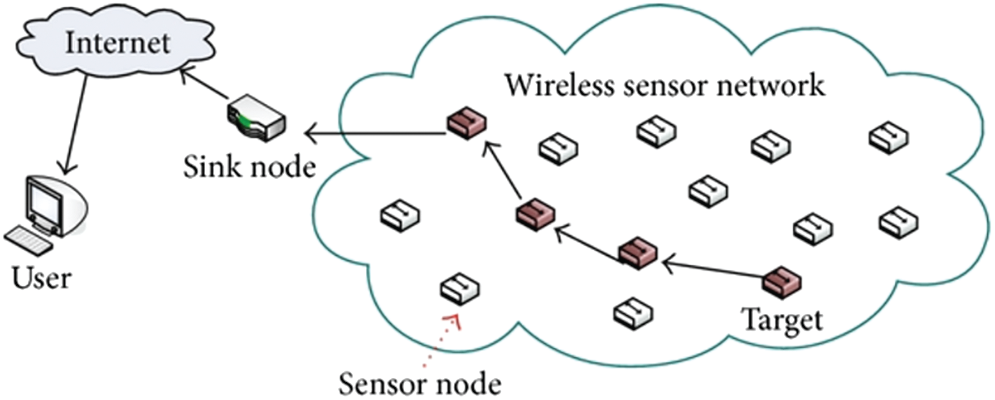
Figure 1: WSN architecture
WSN possesses huge amount of limitations like topology, energy and SNs’ bandwidth to model a transmission protocol [8]. With the idea for handling constraints, there are clusters based on a multi-hop algorithm. Some cluster based protocols includes low energy adaptive clustering hierarchy and Fuzzy C-means may fulfill superior network lifetime [9]. The effectual solution for WSN energy efficiency lies over the network layer, routing protocol and path where lifetime and energy of network will be optimized. Energy optimization is one amongst the prime cause related to network lifetime, which is handled by various algorithms. Some investigators provide simpler assumptions towards sensors of homogeneous environment comprises node with the same energy with the ability for processing and sensing [10]. In practical cases, various networks comprise heterogeneous sensors that have diverse features with changing modalities. Diversity in SN can improve network performance such as network lifetime [11].
The routing protocol selection is based on network resources and application requirements. Henceforth, modeling of routing protocol is based on improving network lifetime for higher time period with resource utilization available over the network more economically [12]. Moreover, routing leads to huge challenges owing to restricted resource availability, limited energy and limited communication in SNs [13]. Thus, routing is carried out with complexity related to communication overhead and routing which is relieved. WSN carries out two communication mode known as query-driven and event-driven routing protocols [14]. The former model facilitates the node to request Base Station (BS) for collecting information regarding the present scenario. Similarly, the latter model is used for data transmission from SN to BS. Huge broadcast and multi-cast protocols are used in WSN routing.
This investigation aims to handle the crucial problems related to routing with optimization algorithm [15]. With a multi-objective optimization algorithm, the anticipated model is designed to map the routing spectrum and reduce the complexity associated with routing. It works on various objectives like distance, energy, mobility, and delay and nodes lifetime [16]. The anticipated hybrid optimization technique uses various constraints and performs certain functionality to the given optimal solution in cluster head formation. The hybridized model is mapping the route with Teaching task and reducing the complexity by learning the difficulties in route establishment. This is termed as MapReduction based Teaching Learning Optimization (MR-TLO). The main objective is to proved optimal solution for improving network lifetime. Data transmission will be initiated over network where transmission is followed for energy constraints during communication process based on CH mapping. The essential contribution of the anticipated model is:
• Initially, the complexities over route established by mapping and teaching process. Then, the constraints are reduced by reduction task and by learning task for further route optimization. This helps in scheduling the task properly for transmission and shows certain merits in determining effectual trade-off among them. Therefore, effectual communication is established.
• This work considers intelligent behaviors’ to adopt with network changes and to introduce computational intelligence ability. Here, improved teaching learning based optimization is used to evaluate the target nodes coordinates and nodes upgradation for determining energy consumption. Node upgradation is performed by integrating Map reduction to attain modification in Hop size of nodes.
The remainder of this investigation is organized as: Section 2 with background knowledge over recent multi-objective functions and the factors related to it. Sections 3 & 4 discusses in detail about mapping and reduction task by integrating Teaching-Learning Optimization. Section 5 depicts numerical values and analysis related to it. Section 6 shows the conclusion of the anticipated model and directions for further research.
Cao et al. in [17], described a multi-objective fuzzy-based clustering for enhancing network lifetime and fulfilling the inadequacy encountered due to energy hole issues and hotspots in developing and stationary networks. Energy based constraints are handled among them with tentative CN for selecting optimal CH and it is provided with a certain probabilistic model. The anticipated model selects the distributed competitive algorithm using probabilistic approach. This model is measured as a distributed competitive algorithm targeting appropriate ranges of uncertainty CH. Evaluation and performance analysis are performed with clustering procedures which is most popular.
Sitanavah et al. in [18], discusses about routing constraints in Multi-media WSNs for offering multi-objective approaches. It deals with Quality of Service[QoS] by handling delay and expected transmission count. QoS factors and single objective systems are optimized with traditional approximation and it will not determine the parametric nature that provides sub-optimal solutions. Some case studies determine appropriate improvements over QoS routing solutions. For instance, delay, approximated mean enhancement ratio for scenarios and time. Imran et al. in [19], depicted alliance functionality via multi-objective optimization for sensing coverage for enhances nodal coverage efficiency. This work offers a proportionate relationship for renovating energy functionality between the neighborhood and active nodes. This relationship is utilized for determining mobile nodes with lesser energy. Thus, energy stability with complete network and resources has to be maintained. The simulation outcomes validate that this model enhances network coverage quality, reduces node energy depletion more effectually. Therefore, it enhances network life cycle.
Hwang et al. in [20], utilized Multi-objective particle swarm optimization to anticipate a Multi-objective load balancing approach. Reliability and energy efficiency is measured as an objective function. With the appropriate residual energy of CH, energy efficiency is determined. Here, reliability is generated on inter-cluster routing based communication cost. Load balancing is performed with mixing up functionalities of next hop and CH in all iteration. Fuzzy based decision making is determined with a compromise solution for selecting nodes. The performance of anticipated and prevailing approaches has been analyzed based on energy efficiency, Packer Drop Ration (PDR), network lifetime, accuracy and number of active nodes. With all these parameters, coverage and scalability are chosen for quality evaluation provided with multi-objective optimization model.
Kimence et al. in [21] depicts multi-objective function with Particle Swarm Optimization (PSO) algorithm to model energy efficiency for various mobile sinks. With well-determined particle based encoding patterns and derivation with multi-objective fitness function certain algorithms are given. To determine both global and local solutions for all particles with Parento analysis is utilized. With this model, various simulation experiments are done and results are computed with prevailing approaches like energy aware sink re-location and tree cluster based data gathering. The outcomes determine that anticipated achieves superior functionality with the evaluated metrics. Also, statistical analysis is performed with authenticated Analysis of Variance (ANOVA) and least significant differences for post ad-hoc analysis.
The total amount of added relays are deployed for fulfilling every SN in the initial design model with k-length bounded vertex disjoint shortest paths to sink and paths to reduce the total amount of deployed relays. Fatih et al. in [22], attempted to analyze overlap encountered among communication ranges to reduce the minimal amount of added nodes required for k-connectivity repair.
In distributed actor based recovery model, the neighborhood node failure has to be replaced. The finest candidate selection is based on physical proximity and lowest node degree towards failure. Similarly, Senel et al. in [23], anticipated the least distance based movement recovery process where the direct neighborhood set of failed node moves from failed node position while original position is substituted with the nearest vertex actor. Borkar et al. in [24], anticipates an algorithm for constructing a complete graphic terminal and for evaluating minimal spanning tree utilizing the kruskal algorithm. This is constructed with tree edges. Some three step procedure for network segmentation through steiner tree approximation. Shah et al. [25] designed grid based area deployment for equal sized cells anticipating relay node placement algorithm. Here, bio-inspired relay node placement is anticipated.
Khabiri et al. in [26] utilized multi-objective connectivity factor for restoring network connectivity; however, it works back-ward with diverse partitioning to determine the bi-directional connection and to provide data to sink node. Here, segments are considered as SN collection and set apart from prevailing models. Thus, the modeling of WSN is considered to be more complicated with substantial aspects over various parameters like energy, delay, PDR, routing, cost and efficiency over real time application. Therefore, to enhance network lifetime this investigation uses a Multi-objective function integrated with MapReduction concept to identify the central information processing over WSN.
Data is handled by each node in distributed creation strategies, and decisions are made locally and are restricted to the node’s immediate vicinity (single-hop neighbors). The below are the key features of distributed networks:
• Self-contained devices are available.
• Each node communicates with its immediate vicinity. It is appropriate for distributed applications (multi-agent systems, self-organized systems, etc.)
• Much of the data is routed into a single node.
• Interconnection equipment (routers, bridges, and so on) are optional.
• Because of their adaptability, they can be used to target harsh conditions.
The complexity of the information forwarding mechanism necessitates the use of robust algorithms. The proposed work must ensure that complex activities are completed with equivalent results to centralized solutions.
In the anticipated model, clustering and routing are considered as a major factor for analysis. Therefore, the hybridization approach known as MapReduction based Teaching-Learning optimization approach. This is designed by Rao, which is inspired based on Teacher’s influence and learner’s interaction. This model outperforms various Meta-heuristic approaches and compared with benchmark standards. This approach is hybridized into two phases. They are: Mapping based on Teacher’s influence and reduction with learner’s activeness. The flow diagram of proposed model is given in Fig. 2.

Figure 2: Flow diagram of a proposed model
Based on various nature-inspired algorithms, Teaching-Learning Optimization (TLO) utilizes population solutions to the give global solution. Here, the initial population is set of learners and study materials are considered as design variables. Compute the entire population with ‘fitness function’ best solution is considered as a teacher. Here, the teacher holds an influence towards shifting learners (mean) to knowledge level. Then, the set of new learners is evaluated with Eq. (1):
The difference among teacher and mean learners is provided as in Eq. (2):
where
Here, students attempt to enhance knowledge via interaction with one another. By forming a group of students, the level will be increased. Here,
To attain the beneficial factors form TLO, this work hybridizes the MapReduction for routing and scheduling data transmission.
MapReduction is performed in computing clusters in various nodes. This cluster uses multi-level hierarchical network architecture. When a job enters into the network, it brings various random amounts of map tasks that have to be performed by machines. The incoming data will be of data chunks with fixed size and every chunk is replicated and placed in various locations. Here, tasks are allocated with clustered nodes. When the processing is launched, machine will not initiate till all the available chunk arrives. Here, this model is used for task scheduling and routing. This is termed as a co-operative scheduler. This is partitioned into two phases: allocate incoming tasks to network nodes or initiate network communication when tasks reach the cluster and route the task arrived for network communication. Initially, queuing architecture of the network model has to be determined. Every cluster node has to process the queue. The scheduler must keep track of the loading queue to buffer tasks for system allocation and assign data to machines for remote processing. Thus, tasks are ready for processing.
It is generally known that WSN are strict towards energy constraints and possess limited energy replacement abilities. Therefore, it is essential to optimize energy consumption during routing; thus, it may prolong the network lifetime. Here, MR-TLO is not a centralized network model where the algorithm is subjected to work in every node. Here, the process is initiated with the population path and determines the optimum path for further transmission. The anticipated method uses TLBO for routing purpose.
Source node has to transmit a message to neighbors where request raised has to ask for an available route to final destination. It has to choose the data chunks from various clustered nodes which may be lead to sink node. When the request is received and data are accumulated from various clustered nodes, it has to maintain routing table. When a route prevails, source node has to receive data directly. Else, the receiver has to request neighbors. This SN has to initiate population based on total paths to sink. Population path is specified as
Population initialization is measured as a task carried out by set of nodes. For instance, the source has to identify events from request to neighbors. The neighbor has to validate the routing table, where the route towards sink was stored and informs the source. Else, it has to check the corresponding routing table when sink was stored and informs the source node. After a certain waiting time, all data chucks from various nodes are received by the source node; this may collects data and generates population by random number of paths. The waiting time during data chunk collection is deployed over the simulation environment.
When population is initiated, source node has to partition the raw data into pieces to handle bandwidth. This comprises of time and data, event identification regarding event detection (mapping events). Before establishing communication, every data is related to parameters. It has to identify the possible nodes based on the path towards sink and sequence number. When queuing time or waiting time considered for prolonged time, data chunk will be reduced, known as reducing task.
Here, routing problem is considered with various steps. Optimization parameter based initialization is used to resolve a Multi-objective function. The first process is population size which is based on the number of nodes over network queuing time. Nodes will wait initially for receiving any request from neighbors to paths from source to sink. This number is determined as population size. Next is termination criteria, when a path is revisited huge amount of time during various iterations, this is determined as solution. Accordingly, for evaluating objective function, solution may produce finest outcomes based on lifetime and energy consumption. Here, variables are considered to be in discrete form, i.e., data chunks are determined to be discrete with the number of nodes over given path. Here, the energy function of WSN is determined with an approximate energy model. Energy is consumed during power transmission and reception. For transmitting certain bit to a remote location with distance ‘d’, transmitter consumes some energy as in Eq. (5):
Similarly, for receiving data the energy consumed is given below in Eq. (6):
When the transmission path is longer, energy consumed during transmission for
When
where
Here, the path size is not essential, where
4.2.1 Teaching Based Node Mapping
Here, compute the mean of actively available nodes over the cluster where it cannot be provided analytically (number of paths). Hence, some mathematical operations have to be redefined using the mapping process. The node connectivity is mapped using an edge re-combination operator to model inherits of offspring with essential information from parental structures. Consider that the simulation setup for node connectivity is determined by 50 nodes, where the source has to identify the events. The node population is determined by mapping nodes connectivity from source to sink.
The population mean is
With the difference, the new solution will be determined as
Here, choose random
For every time slot, chunk that arrives to the system are allocated to a queue where total chunk arrival is specified as
The transmission also considers bandwidth constraints, service process of queues in network is determined as follows:
The service process initiated with queuing process is specified as
The queue length is determined as vector as in Eq. (18):
This statistical assumption is performed during learning process with co-operative scheduler with queuing process
Node identifies a co-operative scheduling process for data transmission to sink with a solution attained from the learning process. When the node fails, the node which holds information constructs a new path using the teaching-learning process. When the task is completed, BS holds the received paths and generates raw data. When the packet is missed, the source receives warning message from the sink over the same path. Thereby, it will re-broadcast the missing packets and follows this procedure till the end. Data transmission from source to destination is attained and network capacities are optimized. To validate this, the routing protocol is performed. By computing the overall functionality, the algorithm model is designed as below.

The above mentioned process is carried out for routing in WSN with MR-TLO. Here, the population is initialized and the path has to be identified based on time to live process of nodes. The mean vector is determined with edge re-combination operator. The best solution has to be determined and the solution has to be validated with the maximal objective function. The node which is no longer alive will be terminated and also node that holds prolonged waiting time will also be terminated.
The proposed routing model is implemented over NS-2 simulator with 64 bits OS. This experimentation is performed in a PC with Intel(R) i5 3.20 GHz and 4 GB RAM. The parameter settings are provided as in Tab. 1.

To validate the performance of the proposed model in terms of efficiency, there are a number of metrics that is utilized for comparing the variations in the number of nodes, coverage and total packets. The energy consumption model encounters certain limitations such as energy level is set as 10 J for all nodes, network topology holds till 200 nodes with uniform distribution. To compute the efficiency of the anticipated routing protocol, consider certain conditions utilized for experimental and events occur in the same place and all packets are sent from source node. For generating a routing protocol, there are roughly about 1000 packets used for transmission. Average CPU time is given and it is measured based on number of nodes, random deployment and simulation region against sink. Nodes lifetime is determined based on initial battery energy and power with Eq. (19):
Based on packets received at sink, the anticipated model gives superior outcomes in various scenarios. Huge residual energy gives lesser cost (Tab. 2). It specifies more energy compared to other models for transmitting packet size to sink node. The residual energy influences a longer network lifetime with maximal residual energy. It is proven that MR-TLO works superiorly while prolonging network lifetime than other routing model. While conducting certain experimentation, huge amount of packets are transferred from source to sink nodes. This model shows superior outcomes by extending network lifetime.

This work considers five different parameters like throughput, an average waiting time of data packets in the queue, average queuing time, average energy utilization and residual energy. This helps in determining the efficiency of routing model to improve network lifetime. Here, packets travel from source to sink, where packet consideration average varies from 50, 100, 150, 200, 300, 400, 500 and 600 respectively. The anticipated MR-TLO is compared with standard algorithms like Artificial Bee Colony Optimization (ABC), Particle Swarm Optimization (PSO) and Ant Colony Optimization (ACO) respectively. The throughput attained by MR-TLO is 89, 90, 94, 110, 115, 130, 145 and 150 respectively when packet size changes. MR-TLO shows an average waiting time of 1.80, 3.00, 3.15, 3.80, 4.25, 4.50, 5.5 and 6.5 ms for collecting data chunks from the nodes of a cluster (Tab. 3).

Similarly, average queuing time is determined as 0.126, 0.186, 0.190, 0.225, 0.295, 0.352, 0.400 and 0.410 ms respectively (Tab. 4). The energy utilization of nodes during data transmission is determined in Joules. During packet transmission the average energy consumed is 2.653, 3.578, 4.254, 5.152, 6.157, 7.154, 8.147 and 9.152 J respectively (Tab. 5). Similarly the average residual energy after the completion of task is 75, 85, 98, 112, 126, 132, 142, 154, 160 and 165 J respectively (Tab. 6). When the residual energy is higher it is directly proportional to the nodes lifetime. Nodes lifetime is increased when residual energy is higher. It is measured in seconds.

From nodes 10–100, nodes lifetime is determined as 20, 26, 35, 46, 50, 64, 72, 89, 98 and 110 s respectively (Tab. 7). Fig. 3 depicts the throughput of MR-TLO and other approaches like ABC, ACO and PSO. The throughput of MR-TLO is higher than other models. Fig. 4 depicts the average waiting time (AWT) of MR-TLO and other approaches like ABC, ACO and PSO. The AWT of MR-TLO is lesser than other models. Fig. 5 depicts the Average Queuing time (AQT) of MR-TLO and other approaches like ABC, ACO and PSO. The AQT of MR-TLO is lesser than other models. Fig. 6 depicts the Average Energy utilization (AEU) of MR-TLO and other approaches like ABC, ACO and PSO. The AEU of MR-TLO is lesser than other models. Fig. 7 depicts the residual energy of MR-TLO, ABC, ACO and PSO. Due to the structural framework of proposed model, the residual energy remains higher than other models. Fig. 8 depicts the nodes lifetime. When residual energy is higher, nodes lifetime is also higher.




Figure 3: Throughput

Figure 4: Average waiting time

Figure 5: Average queuing time

Figure 6: Average energy utilization

Figure 7: Residual energy

Figure 8: Nodes lifetime
Network lifetime can be achieved with effectually node clustering, residual energy, throughput attained during routing in WSN. Various challenges are associated with routing and clustering. This work offers an effective routing strategy using the Map-Reduction based Teaching-Learning optimization. This model is considered more robust in energy consumption, network lifetime, throughput, average waiting time and queuing time. The experimentation is carried out in various scenarios with 100–200 nodes and with 600 packet transmission. The outcomes are compared with conventional approaches like ABC, ACO and PSO. The anticipated MR-TLO shows better trade-off in contrary to prevailing approaches. The research direction in the future will be moved in enhancing the QoS of network system and performing real time implementation of this model. Hybridized optimization approach will be attempted to validate the network lifetime.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. V. Potdar, A. Sharif and E. Chang, “Wireless sensor networks: A survey,” in Int. Conf. on Advanced Information Networking and Applications Workshops, Bradford, UK, pp. 636–641, 2009. [Google Scholar]
2. A. Gogu, D. Nace, A. Dilo and N. Mertnia, “Optimization problems in wireless sensor networks,” in Int. Conf. on Complex, Intelligent and Software Intensive Systems, Seoul, Korea, IEEE, pp. 302–309, 2011. [Google Scholar]
3. R. V. Kulkarni and G. K. Venayagamoorthy, “Particle swarm optimization in wireless-sensor networks: A brief survey,” IEEE Transactions on Systems, Man, and Cybernetics, Part C (Applications and Reviews), vol. 41, no. 2, pp. 262–267, 2011. [Google Scholar]
4. A. El. Ghazi and B. Ahiod, “Particle swarm optimization compared to ant colony optimization for routing in wireless sensor networks,” in Proc. of the Mediterranean Conf. on Information & Communication Technologies, Saïdia, Morocco, Springer, pp. 221–227, 2015. [Google Scholar]
5. A. M. S. Saleh, B. M. Ali, M. F. A. Rasid and A. Ismail, “A survey on energy awareness mechanisms in routing protocols for wireless sensor networks using optimization methods,” Transactions on Emerging Telecommunications Technologies, vol. 25, no. 12, pp. 1184–1207, 2014. [Google Scholar]
6. P. S. Mann and S. Singh, “Artificial bee colony metaheuristic for energy-efficient clustering and routing in wireless sensor networks,” Soft Computing, vol. 21, no. 22, pp. 6699–6712, 2017. [Google Scholar]
7. B. Zeng and Y. Dong, “An improved harmony search based energy-efficient routing algorithm for wireless sensor networks,” Applied Soft Computing, vol. 41, no. 4, pp. 135–147, 2016. [Google Scholar]
8. A. El Ghazi, B. Ahiod and A. Ouaarab, “Improved ant colony optimization routing protocol for wireless sensor networks,” in Networked Systems. NETYS 2014. Lecture Notes in Computer Science, G. Noubir, M. Raynal, (Eds.vol. 8593. London, UK: Hindawi, 2014. [Google Scholar]
9. B. Jan, H. Farman, H. Javed, B. Montrucchio, M. Khan et al., “Energy efficient hierarchical clustering approaches in wireless sensor networks: A survey,” Wireless Communications and Mobile Computing, vol. 2017, pp. 6457942, 2017. [Google Scholar]
10. B. K. Sahu, S. Pati, P. K. Mohanty and S. Panda, “Teaching-learning based optimization algorithm based fuzzy-pid controller for automatic generation control of multi-area power system,” Applied Soft Computing, vol. 27, pp. 240–249, 2015. [Google Scholar]
11. A. Nayya and R. Singh, “A comprehensive review of simulation tools for wireless sensor networks (WSNs),” Journal of Wireless Networking and Communications, vol. 5, no. 1, pp. 19–47, 2015. [Google Scholar]
12. A. Naik, K. Parvathi, S. C. Satapathy, R. Nayak and B. Panda, “QoS multicast routing using teaching learning based optimization,” in Proceedings of International Conference on Advances in Computing. Advances in Intelligent Systems and Computing, M. A. Kumar, S. R., T. Kumar, (Eds.vol. 174. Berlin, Germany: Springer, 2013. [Google Scholar]
13. R. Negra, I. Jemili and A. Belghith, “Wireless body area networks: Applications and technologies,” Procedia Computer Science, vol. 83, no. 3, pp. 1274–1281, 2016. [Google Scholar]
14. R. Kumar and D. Kumar, “Multi-objective fractional artificial bee colony algorithm to energy aware routing protocol in wireless sensor network,” Wireless Network, vol. 22, pp. 1461–1474, 2016. [Google Scholar]
15. B. Moradi, “The new optimization algorithm for the vehicle routing problem with time windows using multi-objective discrete learnable evolution model,” Soft Computing, vol. 24, no. 9, pp. 6741–6769, 2020. [Google Scholar]
16. X. M. Zhang, Y. Zhang, F. Yan and A. V. Vasilakos, “Interference based topology control algorithm for delay-constrained mobile Ad hoc networks,” IEEE Transactions on Mobile Computing, vol. 14, no. 4, pp. 742–754, 2015. [Google Scholar]
17. X. Han, X. Cao, E. L. Lloyd and C. Shen, “Fault-tolerant relay node placement in heterogeneous wireless sensor networks,” IEEE Transactions on Mobile Computing, vol. 9, no. 5, pp. 643–656, 2010. [Google Scholar]
18. L. Sitanayah, K. N. Brown and C. J. Sreenan, “A fault-tolerant relay placement algorithm for ensuring k vertex-disjoint shortest paths in wireless sensor networks,” Ad Hoc Networks, vol. 23, no. 4, pp. 145–162, 2014. [Google Scholar]
19. M. Imran, M. Younis, N. Haider and M. A. Alnuem, “Resource efficient connectivity restoration algorithm for mobile sensor/actor networks,” EURASIP Journal on Wireless Communications and Networking, vol. 347, no. 1, pp. 393, 2012. [Google Scholar]
20. S. Hwang, W. Chao, C. Wu and C. Dow, “2-Connected relay node placement scheme in disjoint wireless sensor networks,” in IEEE 5th Int. Conf. on Software Engineering and Service Science, Beijing, China, pp. 1039–1043, 2014. [Google Scholar]
21. S. Kimence and I. Bekmezci, “Weighted relay node placement for wireless sensor network connectivity,” Wireless Networks, vol. 20, no. 4, pp. 553–562, 2014. [Google Scholar]
22. F. Senel and M. Younis, “Relay node placement in structurally damaged wireless sensor networks via triangular steiner tree approximation,” Computer Communications, vol. 34, no. 16, pp. 1932–1941, 2011. [Google Scholar]
23. F. Senel and M. Younis, “Optimized interconnection of disjoint wireless sensor network segments using k mobile data collectors,” in IEEE Int. Conf. on Communications, Ottawa, Ontario, Canada, pp. 492–496, 2012. [Google Scholar]
24. G. M. Borkar and A. R. Mahajan, “‘A secure and trust based on demand multipath routing scheme for self-organized mobile adhoc networks,” Wireless Networks, vol. 23, no. 8, pp. 2455–2472, 2016. [Google Scholar]
25. M. A. Shah, G. Abbas, A. B. Dogar and Z. Halim, “Scaling hierarchical clustering and energy aware routing for sensor networks,” Complex Adaptive Systems Modeling, vol. 3, no. 5, pp. 1–23, 2015. [Google Scholar]
26. M. Khabiri and A. Ghaffari, “‘Energy-aware clustering-based routing in wireless sensor networks using cuckoo optimization algorithm,” Wireless Personal Communication, vol. 98, no. 3, pp. 2473–2495, 2018. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |