Computers, Materials & Continua DOI:10.32604/cmc.2022.019295
Article

Joint Channel and Multi-User Detection Empowered with Machine Learning

Mohammad Sh. Daoud1, Areej Fatima2, Waseem Ahmad Khan3, Muhammad Adnan Khan4,5,*, Sagheer Abbas3, Baha Ihnaini6, Munir Ahmad3, Muhammad Sheraz Javeid7 and Shabib Aftab3

1College of Engineering, Al Ain University, Abu Dhabi, 112612, UAE
2Department of Computer Science, Lahore Garrison University, Lahore, 54792, Pakistan
3School of Computer Science, National College of Business Administration and Economics, Lahore, 54000, Pakistan
4Riphah School of Computing and Innovation, Faculty of Computing, Riphah International University, Lahore, 54000, Pakistan
5Pattern Recognition and Machine Learning Lab, Department of Software Engineering, Gachon University, Seongnam, 13557, South Korea
6Department of Computer Science, College of Science and Technology, Wenzhou Kean University, 325060, USA
7Department of Computer Science, Hameeda Rasheed Institute of Science and Technology, Multan, 66000, Pakistan
*Corresponding Author: Muhammad Adnan Khan. Email: adnan.khan@riphah.edu.pk
Received: 09 April 2021; Accepted: 10 May 2021

Abstract: The numbers of multimedia applications and their users increase with each passing day. Different multi-carrier systems have been developed along with varying techniques of space-time coding to address the demand of the future generation of network systems. In this article, a fuzzy logic empowered adaptive backpropagation neural network (FLeABPNN) algorithm is proposed for joint channel and multi-user detection (CMD). FLeABPNN has two stages. The first stage estimates the channel parameters, and the second performs multi-user detection. The proposed approach capitalizes on a neuro-fuzzy hybrid system that combines the competencies of both fuzzy logic and neural networks. This study analyzes the results of using FLeABPNN based on a multiple-input and multiple-output (MIMO) receiver with conventional partial opposite mutant particle swarm optimization (POMPSO), total-OMPSO (TOMPSO), fuzzy logic empowered POMPSO (FL-POMPSO), and FL-TOMPSO-based MIMO receivers. The FLeABPNN-based receiver renders better results than other techniques in terms of minimum mean square error, minimum mean channel error, and bit error rate.

Keywords: Channel and multi-user detection; minimum mean square error; multiple-input and multiple-output; minimum mean channel error; bit error rate

1  Introduction

Communication systems are ubiquitous and are plagued with the perennial problem of limited channel capacity. We strive to enhance the channel capacity without compromising system performance for optimal utilization of bandwidth. The multiple-input and multiple-output (MIMO) method has been used to improve the data rates of communication systems and resolve channel capacity issues [1–4]. Raut et al. [5] estimated the signals at both the sender and receiver antennas using different algorithms. The data rates increase due to the bandwidth of the channel capacity [6–9]. In [10], the authors used multiple transmitter and receiver antennas to improve the system’s communication technique. The transmitted information is calculated on different transmission paths that depend on the data conveyed by the MIMO framework increments [10].

Some antennas collect received information on the receiver end, perform calculations to gather the information, then reestablish the data on the receiver end. The MIMO technique is the midpoint for unconnected communication because the amount of information increases without any extra transmitting power or capacity in the data transfer [11,12].

Fuzzy systems have fuzzy logic and fuzzy sets through which modeling, in the ordinary sense, is carried out. These systems have non-stationary uncertainty, an inherent property that cannot be uncertain. Fuzzy logic control (FLC) is a primitive application of fuzzy sets, and a part of many successful applications. In these applications, efficient control approaches are used for nonlinear, complex, and non-analytic systems [13]. In 1975, Mamdani and Asselin developed the first FLC, which was applied to a small steam engine. Earlier researchers contributed considerably to both the theoretical and applied aspects of FLC [14].

The widespread usage of modern multimedia services and wireless internet underlies the increased demand for high data rates, presenting problems such as inter-symbol interference (ISI) and scattered fading channels (SFC) to address this demand [15]. The specific processing is required on the receiver end to resolve these issues when data arrives. Evolutionary techniques like the genetic algorithm (GA) are used to improve the multi-user detection (MUD) of multi-carrier systems. Cultural evolutionary and cooperative coevolutionary algorithms are applied to find new dimensions of MUD for fast convergence and an attractive bit error rate [16].

An early system is known as a single input and single output used a single antenna for both the transmitter and receiver, which did not use the maximum bandwidth, which is one of the most important factors in communication systems. To overcome this issue, MIMO systems provide a solution through multiple antennas used at both ends [15].

The proposed method can also be used with multi-carrier code division multiple accesses (MC-CDMA) and orthogonal frequency division multiplexing (OFDM) to enhance the capacity of a communication channel [16–19].

Other techniques include total opposite mutant particle swarm optimization (TOMPSO), partial opposite mutant particle swarm optimization (POMPSO), and particle swarm optimization (PSO) [16,17,19,20]. Differential equations (DE), GA, island DE, and island GA can also be used to enhance the performance of a digital communication system [21–23]. The proposed method performs channel estimation (CE) for effective data rates at both ends.

Some distortion accumulates in the signal during communication [24,25]. The antenna at the receiver end cannot determine the correct information due to the weak signal strength. We use fuzzy logic [26] to resolve this issue and improve the data and channel estimation process. The proposed method introduces a new variant for the communication system: fuzzy logic-powered opposite particle swarm optimization that uses PSO on the applied side.

The remainder of this paper is organized as follows. Section 2 discusses essential concepts such as the MIMO model system and fuzzy logic empowered adaptive backpropagation neural network (FLeABPNN)-based optimization. The problem is formulated in Section 3. Section 4 describes the simulation of the proposed framework. Section 5 provides concluding remarks.

2  System Model

The MIMO system uses a transmitting antenna A and receiving antenna B, with a flat fading stationary channel during the communication process of the Q (transmitted) symbols. The received signal at B is

rb(i)=∑a=1Ahb.ada(i)+vb(i),(1)

where vb(i) is additive white Gaussian noise (AWGN). E[|vb(i)|2]=2σV2, da(i) is the ith transmitted symbol form with antenna A, taking the value from the symbol set { −1, +1} of the binary phase shift key (BPSK); hb.a is the flat fading channel coefficient that links transfer antenna A to receiving antenna B; and i is the index of the symbol.

Eq. (1) can also be written as

r(i)=Hd(i)+v(i),(2)

where v(i) represents AWGN, and

v(i)=[v1(i)v2(i)…vB(i)]T.(3)

The transmitted symbol vector is

and the received signal vector is

The channel gain at the receiving antenna can always be normalized to unity:

We define a B×V-dimensional received data matrix and A×V-dimensional transmitted data matrix as

R=[r(1)r(2)…r(Q)] (4)

D=[d(1)d(2)…d(Q)] (5)

Eqs. (4) and (5) represent the received vector at the receiver end and the transmitted symbols/vector at the transmitter end, respectively.

Prob(RH,D)=12πσv2BQe-12σv2∑i=1Q∥r(n)-Hd(i)∥2(6)

Eq. (6) represents the probability function from which we find the probability of R given the channel matrix (H) and transmitted symbol matrix(D) from all users.

JML(D̃,H̃)=1B×Q∑i=Q∥r(i)-H̃d̃(i)∥2(7)

Eq. (7) represents the cost function, which we want to minimize such that the optimum value of the estimated transmitted symbols (D̃) and estimated channel matrix coefficients (H̃) are used.

Eq. (7) can be written as

JML(D̃,H̃)=arg{minS̃,H̃JML(D̃,H̃)}.(8)

The enhanced cost function can be written as:

JML(D̃,H̃)=1B*Q[∑i=1Qr2(i)-2∑i=1Qr(i)H̃d̃(i)+∑i=1Q∥H̃d̃(i)∥2]JML(D̃,H̃)=1B*Q[∑i=1Qr2(i)-{2∑i=1Qr(i)H̃d̃(i)-∑i=1Q∥H̃d̃(i)∥2}](9)

Let

CML(D̃,H̃)=2∑i=1Qr(i)H̃d̃(n)-∑i=1Q∥H̃d^(i)∥2.(10)

After substituting the values from Eq. (10) in Eq. (9), we have

JML(D̃,H̃)=1B×Q[∑i=1Qr2(i)-CML(D̃,H̃)].(11)

As we know that we want to minimize the cost function, Eq. (9) can also be written as

JML(D̃,H̃)=[minD̃,Ȟ[∑i=1Qr2(i)-CML(D̃,H̃)]].(12)

Therefore, the following applies:

JML(D̃,H̃)= maxD̃̃,H̃^CML(D̃,H̃).(13)

The proposed method is fuzzy logic empowered adaptive backpropagation neural network (FLeAPBNN) for the joint estimation of the channel and MUD. FLeAPBNN is a hybrid fuzzy logic and adaptive backpropagation neural network. Eq. (12) is considered a fitness function and is used to evaluate the performance of the proposed algorithm.

3  Proposed FLeABPNN-Based MIMO Receiver Model

Fig. 1 shows the proposed FLeABPNN-based MIMO receiver model in which the received signal is down-converted for the uth user. The cyclic prefixes are removed in the first step after the signal is transferred from the serial to the parallel mode. FLeABPNN is used to optimize the weights of the receiver after the fast Fourier transform (FFT).

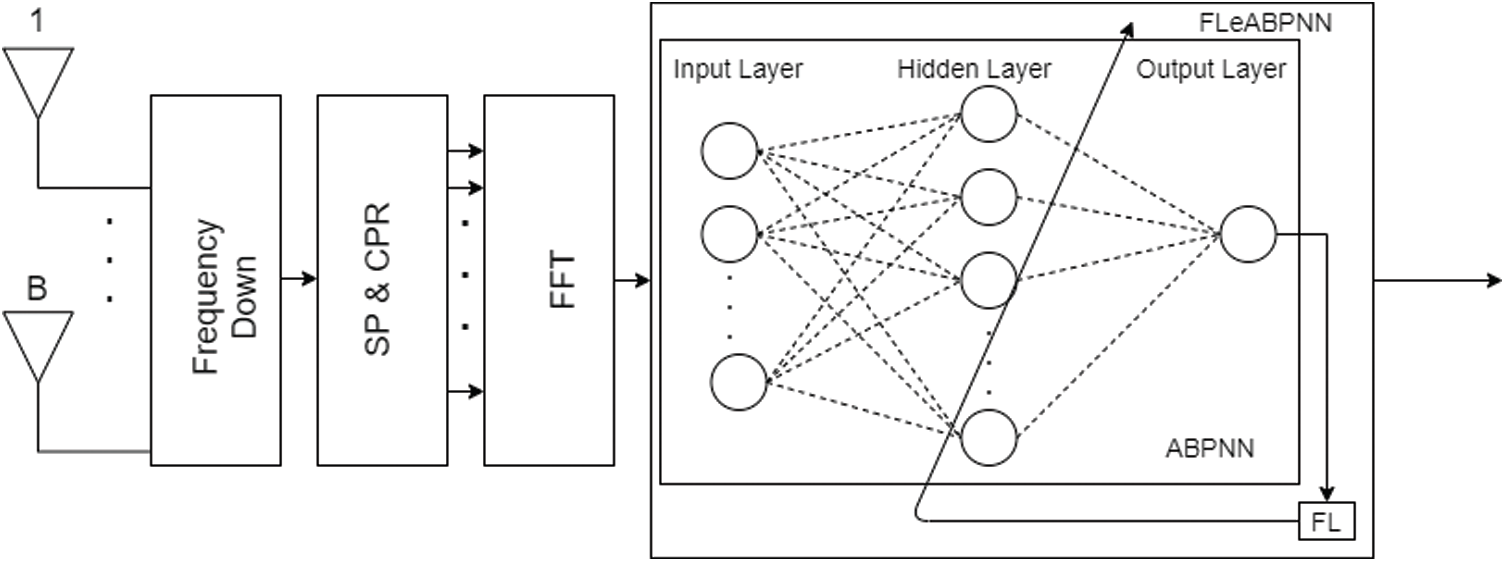
Figure 1: FLeABPNN-based receiver system

The proposed methodology (FLeABPNN), the input layer, a hidden layer, and an output layer are used. The proposed algorithm has steps including weight initialization, feedforward, backpropagation of error, and updating of weight and bias, as shown in Tab. 1. A hidden layer has many neurons, each with an activation function in form f(x) = sigmoid(x). The sigmoid function for the input and hidden layer of FLeABPNN can be written as:

ώd=i1+∑c=1o(ϖcd*ϒc) (14)

𝓑d=11+e-ώdwhered=1,2,3,…,z. (15)

The input taken from the output layer is

ώq=i2+∑d=1z(ύdq*𝓑d).(16)

The output layer activation is

𝓑q=11+e-ώqwhereq=1,2,3,…,ϒ.(17)

In the case of channel estimation, Eq. (18) is used to calculate the minimum mean squared channel error.

È=12∑q(ⵍ⌣q-𝓑q)2.(18)

In the case of MUD estimation, Eq. (19) is used to calculate the minimum mean squared bit error.

Ès=12∑Jb(ᘤJb-𝓑q)2.(19)

Eq. (19) represents the backpropagation error, where ⵍq and outq are the desired and estimated output, respectively.

The rate of change in weight for the output layer is:

ΔЖ∝-∂È∂ЖΔύd,q=-Ξ∂È∂ύd,q,(20)

where Ξ is constant. After applying the chain rule, Eq. (20) can be written as

Δύd,q=-Ξ∂È∂𝓑q×∂𝓑q∂ώq×∂ώq∂ύd,q.(21)

After substituting the values of partial derivates of ∂È∂𝓑q, ∂𝓑q∂ώq, and ∂ώq∂ύd,q in Eq. (21), the value of the change in weights between the dth hidden layer neuron and the qth output layer neuron can be obtained as:

Δύd,q=Ξ(ⵍ⌣q-𝓑q)×𝓑q(1-𝓑q)×(𝓑d)Δύd,q=Ξζq𝓑d,(22)

where

Updating the weights between the input and hidden layers, we apply the chain rule:

where Ξ is a constant. After substituting the above partial derivatives, the change in weights between the cth input layer neuron and dth hidden layer neuron can be written as

After simplification, the above equation for the change in weights between the cth input layer neuron and dth hidden layer neuron can be written as

where

ζd=[∑qζq(ύd,q)]×𝓑d(1-𝓑d)ζd=[∑qζq(ύd,q)]×𝓑d(1-𝓑d)(23)

Updating the weights between the output and hidden layers for the channel and MUD estimation, we use:

ύd,q+=ύd,q+λϜΔύd,q(24)

Updating the weights between the hidden and input layers, we use

ϖc,d+=ϖc,d+λϜΔϖc,d(25)

where λϜ is the learning rate of FLeABPNN. The convergence of FLeABPNN depends upon the careful selection of λϜ. In this article, λϜ is updated using fuzzy logic, as follows:

λϜ=FLC(эჷ,Δэჷ).(26)

where es and Δes are the mean square error and normalized mean square error, respectively, of FLeABPNN, and

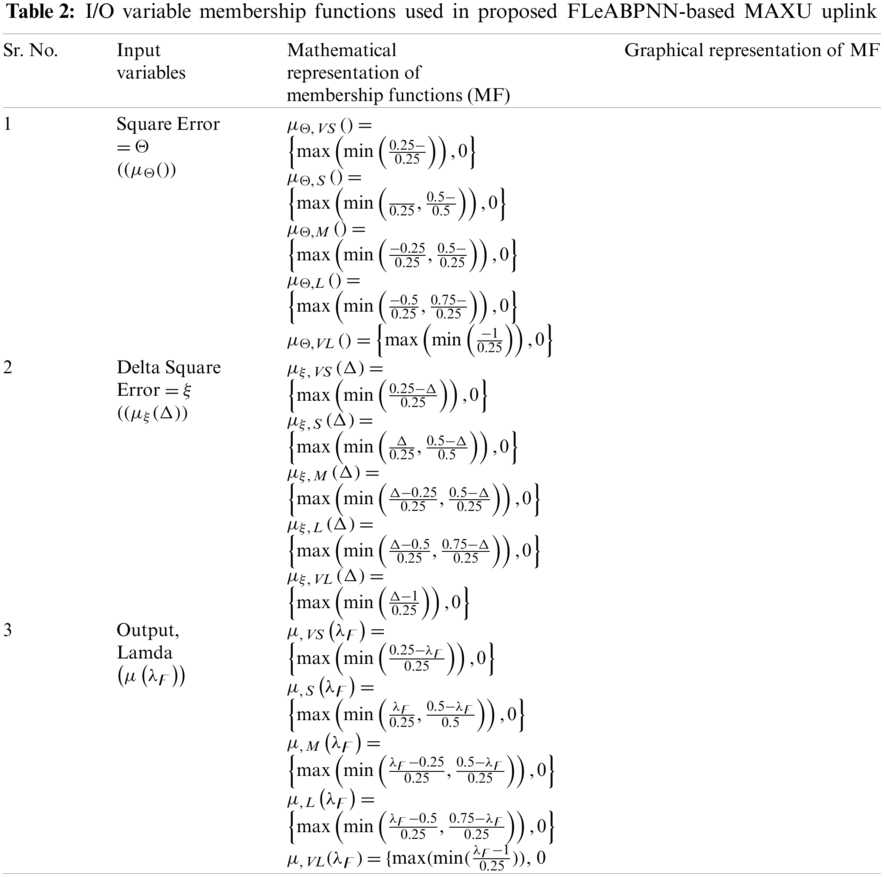
Tab. 2 shows the input/output variable membership functions used in the FLeABPNN-based system, both mathematically and graphically.

The fuzzy system has four main parts: fuzzy propositions, lookup table, inference engine, and de-fuzzifier.

The fuzzy preposition t-norm function is written as

t:эჷ,Δэჷ→λϜ.(27)

Eq. (27) can also be written in terms of fuzzy sets as

t:[0,1]×[0,1]→[0,1] (28)

[(μΘ(эჷ),(μξ(Δэჷ)]=μΘ,ξ(эჷ,Δэჷ)= min[(μΘ(эჷ),(μξ(Δэჷ)]. (29)

We estimate channels using Eq. (18). We apply MUD to the result of Eq. (18), using Eq. (19).

4  Results and Discussion

The MIMO system was implemented using BPSK signaling, and the data sequence length of Q was 50. The transmitters were equipped with A = 3 transmit antennas, while the base station had B = 3 antennas. The Rayleigh selective fading channel was implemented in four parts. The Doppler frequency was set to 25 Hz, which corresponded to a transmitter using a 900 MHz carrier frequency and moving at a speed of 30 km/h. The channel taken for simulation was 3k MIMO, with k = 10 users, the data population was 100, and the number of cycles for both algorithms was five. We chose a population size of 5Ph, where Ph is the channel matrix size. However, the performance in the simulation can also be measured by minimum mean channel error (MMCE), defined as

MMCE=1A*B∑a=1A∑B=1B|ha,b-H̃*(a,b)|(30)

The performance of FLeAPBNN for channel and data estimation of the MIMO system is expressed in terms of minimum mean square error (MMSE) and bit error rate (BER), respectively, in Figs. 2 and 3. The performance of FLeABPNN in terms of MMCE is shown in Fig. 4.

The number of cycles (NoC) vs. MMSE of the FLeAPBNN-based MIMO system with SNR set at 25 dB and 15 users is shown in Fig. 2. Conventional POMPSO and conventional TOMPSO [24,25] gave MMSE values of 10−3 and 10−5.4 at the 160th and 180th NoCs, respectively. FL-POLMPSO and FL-TOLMPSO [25] converged with MMSE values of 10−3.5 and 10−5.5 at the 150th & 160th NoCs, respectively. FLeABPNN gave an MMSE of 7.327 * 10−5.9 at the 170th NoC. FLeABPNN gave better MMSE results than previous approaches [24,25] at the cost of NoC, and FLeABPNN converged faster than TOMPSO [24,25].

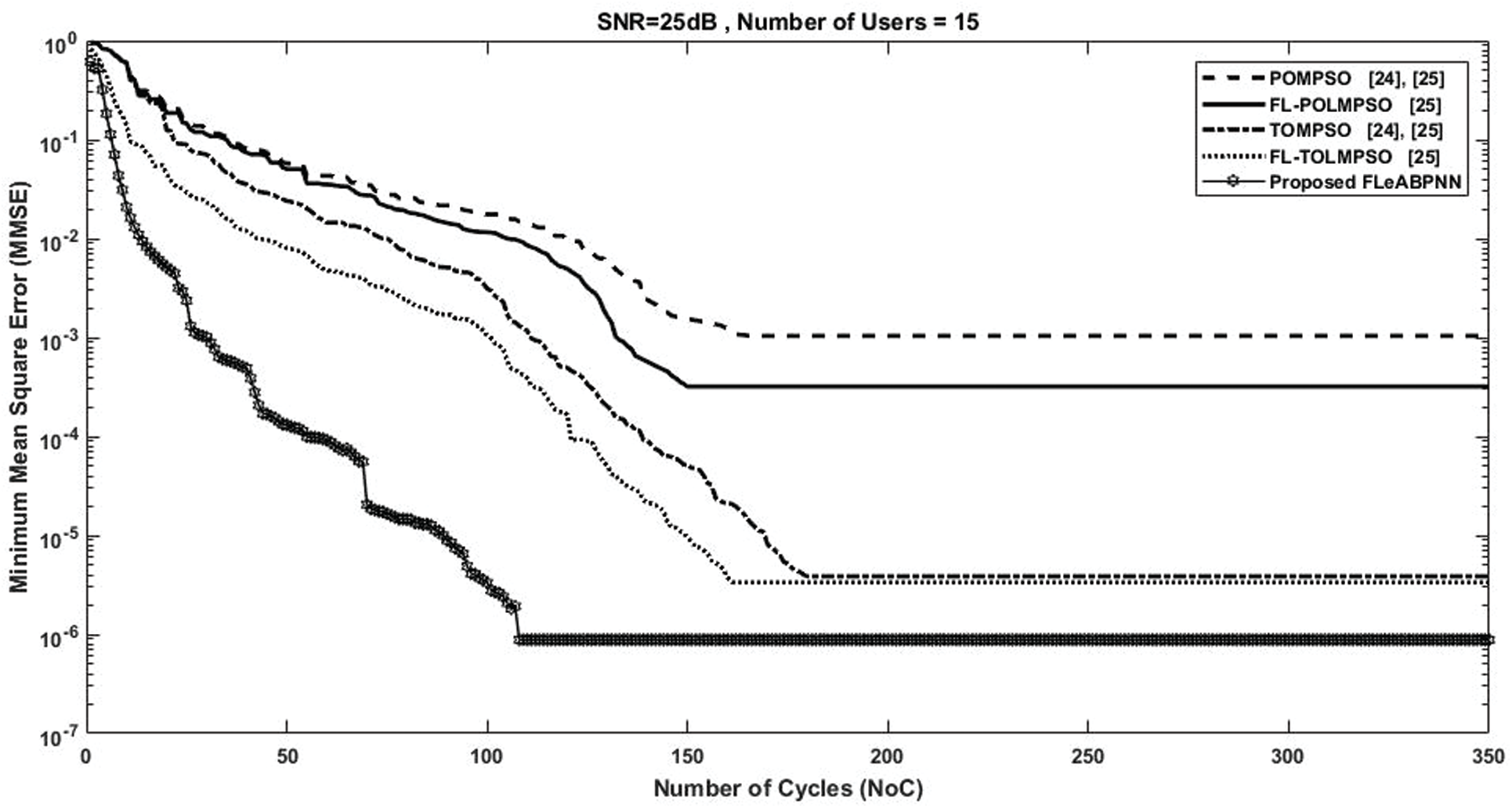
Figure 2: NoC vs. MMSE of proposed FLeAPBNN

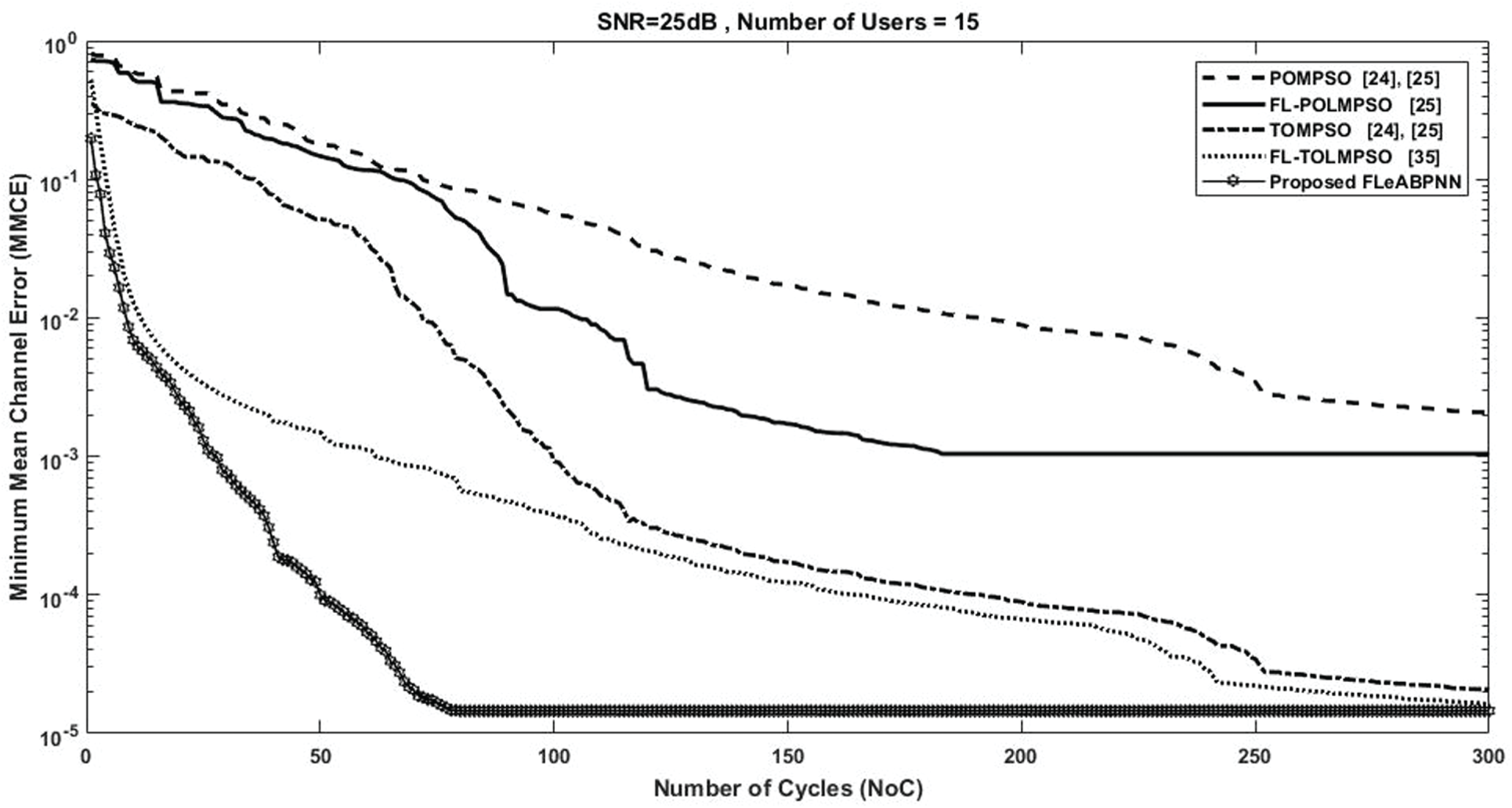
Figure 3: NoC vs. MMCE of proposed FLeAPBNN

The performance of the FLeABPNN-based solution in terms of NoCs vs. MMCE is shown in Fig. 3. The SNR was fixed at 25, and the number of users was 15. Conventional POMPSO and conventional TOMPSO [24,25] had MMCE values of 10−2 and 10−4, respectively. FL-POLMPSO and FL-TOLMPSO [25] converged at MMCE values of 10−3 and 10−4.2, respectively. FLeABPNN had an MMCE value of 8.9002 * 10−5.3. These statistics confirm that the proposed FLeABPNN algorithm gives better results than previous approaches [24,25] in terms of MMCE.

The performance of the proposed FLeABPNN-based solution in terms of signal-to-noise ratio (SNR) vs. bit error rate (BER) is shown in Fig. 4. The NoCs were fixed to 180, and the number of users was 15. Conventional POMPSO and conventional TOMPSO [24,25] had BER values of 10−3 and 3.205 * 10−4, respectively. FL-POLMPSO and FL-TOLMPSO [25] converged at BER values of 10−3 and 10−4.2, respectively. The proposed FLeABPNN had a BER of 10−6. The proposed FLeABPNN algorithm,, therefore, gives better results than previous approaches [24,25] in terms of BER.

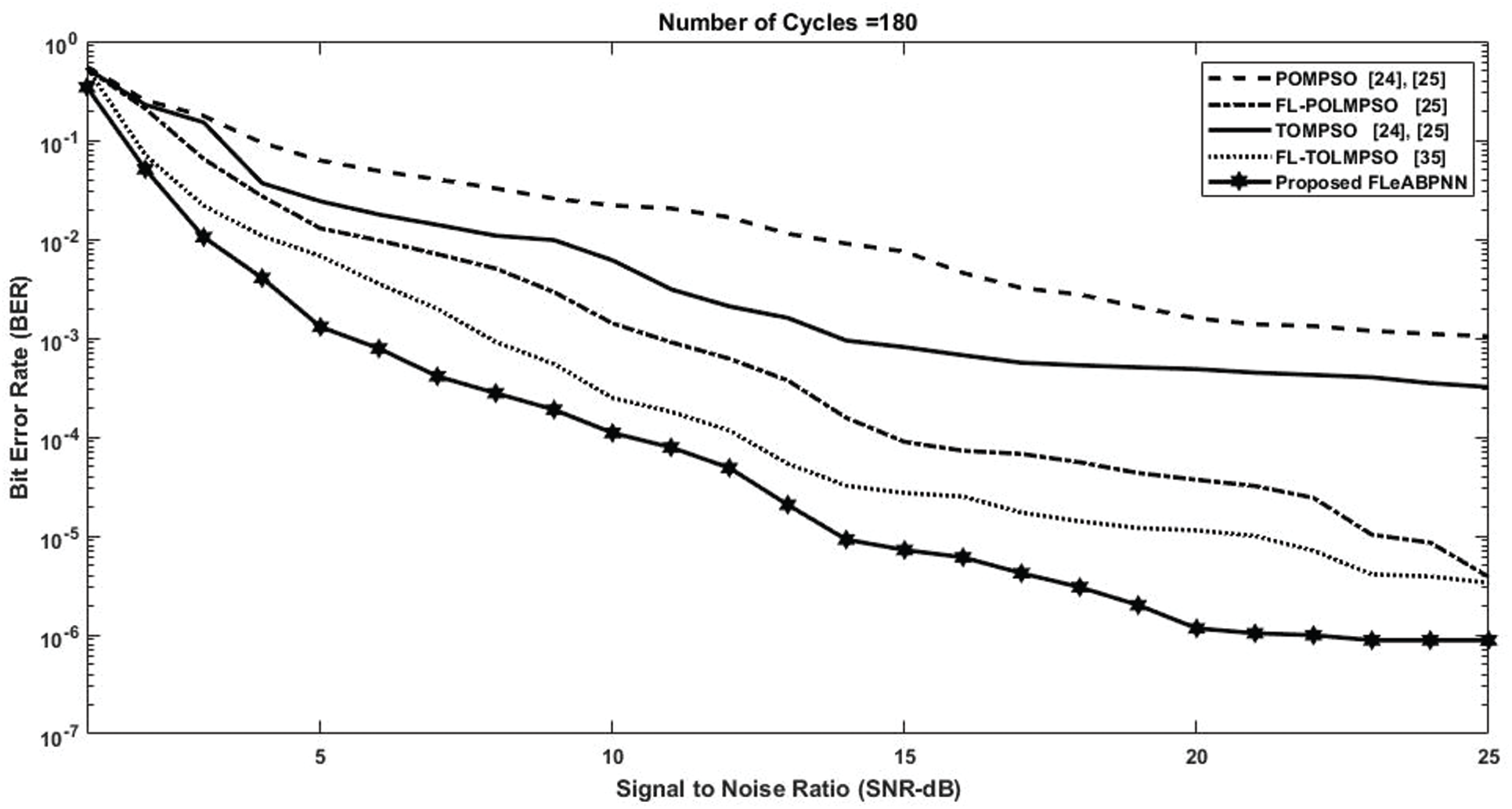
Figure 4: SNR vs. BER of proposed FLeAPBNN

5  Conclusion

Joint channel and multi-user detection were performed using a fuzzy logic empowered adaptive backpropagation neural network algorithm. The proposed approach exploits a neuro-fuzzy hybrid system combining the competencies of fuzzy logic and neural networks. The simulation showed that the proposed FLeABPNN-based MIMO receiver gives better results than approaches such as POMPSO, TOMPSO, FL-POMPSO, and FL-TOMPSO in terms of MMCE, MMSE, and BER.

6  Future Work

In the future, the efficiency of the proposed system can be tested for massive MIMO systems, and the current study can be extended to such systems. Computational complexity analysis in multiplication, addition, division and flops will also be carried out.

Acknowledgement: Thanks to our families and colleagues, who supported us morally.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  T. Abdelkader, K. Mokhtar and O. Abdelaziz, “New space time coding for joint blind channel estimation and data detection through time varying mimo channels,” International Journal of Computer Science Issues, vol. 11, no. 5, pp. 33–38, 2014. [Google Scholar]

 2.  M. A. Khan, M. Umair and M. A. S. Choudry, “Island differential evolution based adaptive receiver for mc-cdma system,” in Int. Conf. on Information and Communication Technologies, Karachi, Pakistan, pp. 1–6, 2015. [Google Scholar]

 3.  A. Mezghani and A. L. Swindlehurst, “Blind estimation of sparse multi-user massive mimo channels,” in 21th Int. Itg Workshop on Smart Antennas, Berlin, Germany, pp. 2–6, 2017. [Google Scholar]

 4.  M. N. Seyman and N. Taspinar, “Symbol detection using the differential evolution algorithm in mimo-ofdm systems,” Turkish Journal of Electrical Engineering and Computer Sciences, vol. 21, no. 2, pp. 373–380, 2013. [Google Scholar]

 5.  P. W. Raut and S. L. Badjate, “Mimo-future wireless communication,” International Journal of Innovative Technology and Exploring Engineering, vol. 2, no. 5, pp. 102–106, 2013. [Google Scholar]

 6.  M. Zubair, M. A. S. Choudhry and I. M. Qureshi, “Multi-user detection using soft particle swarm optimization along with radial basis function,” Turkish Journal of Electrical Engineering and Computer Sciences, vol. 22, no. 6, pp. 1476–1483, 2014. [Google Scholar]

 7.  M. Zubair, M. A. Saleem and I. M. Qureshi, “Multi-user detection using soft particle swarm optimization for asynchronous mc-cdma,” Information, vol. 16, no. 3, pp. 2093–2099, 2013. [Google Scholar]

 8.  M. Asif, M. A. Khan, S. Abbas and M. Saleem, “Analysis of space & time complexity with pso based synchronous mc-cdma system,” in 2nd Int. Conf. on Computing, Mathematics and Engineering Technologies, Karachi, Pakistan, pp. 1–5, 2019. [Google Scholar]

 9.  M. Saleem, M. A. Khan, S. Abbas, M. Asif, M. Hassan et al., “Intelligent fso link for communication in natural disasters empowered with fuzzy inference system,” in Int. Conf. on Electrical, Communication, and Computer Engineering, Karachi, Pakistan, pp. 1–6, 2019. [Google Scholar]

10. M. A. Khan, Multi user detection using computational intelligence in multi-carrier communication systems. Pakistan: Islamabad Campus, ISRA University, 2016. [Google Scholar]

11. M. Umair, M. A. Khan and M. A. S. Choudhry, “Island genetic algorithm-based mud for mc-cdma system,” in Int. Conf. on Information and Communication Technologies, Karachi, Pakistan, pp. 1–6, 2015. [Google Scholar]

12. N. Ali, M. A. Khan and M. Adeel, “Genetic algorithm based adaptive receiver for mc-cdma system with variation in mutation operator,” International Journal of Computer Science and Information Security, vol. 14, no. 9, pp. 215–222, 2016. [Google Scholar]

13. M. Umair, M. A. Khan and M. A. S. Choudhry, “Piranha fish optimization for multi user detection in ofdma system,” International Journal of Advanced and Applied Sciences, vol. 3, no. 6, pp. 35–40, 2016. [Google Scholar]

14. R. Prasad and S. Hara, “An overview of multi-carrier cdma,” in Int. Symp. of Spread Spectrum Techniques and Applications, Prague, Czech, pp. 107–114, 1996. [Google Scholar]

15. M. Zubair, M. A. Choudhry, A. Naveed and I. M. Qureshi, “Particle swarm with soft decision for multi-user detection of synchronous multi-carrier cdma,” IEICE Transactions on Communications, vol. 91, no. 5, pp. 1–12, 2008. [Google Scholar]

16. S. Y. Siddiqui, A. Athar, M. A. Khan, S. Abbas, Y. Saeed et al., “Modelling, simulation and optimization of diagnosis cardiovascular disease using computational intelligence approaches,” Journal of Medical Imaging and Health Informatics, vol. 10, no. 5, pp. 1005–1022, 2020. [Google Scholar]

17. S. Y. Siddiqui, M. A. Khan, S. Abbas and F. Khan, “Smart occupancy detection for road traffic parking using deep extreme learning machine,” Journal of King Saud University-Computer and Information Sciences, pp. 1–7, 2020. In press, https://doi.org/10.1016/j.jksuci.2020.01.016. [Google Scholar]

18. M. W. Nadeem, M. A. A. Ghamdi, M. Hussain, M. A. Khan, K. M. Khan et al., “Brain tumor analysis empowered with deep learning: A review, taxonomy, and future challenges,” Brain Sciences, vol. 10, no. 2, pp. 118–139, 2020. [Google Scholar]

19. R. Lammare and R. Sampaio, “Blind adaptive mimo receivers for space-time block-coded ds-cdma systems in multipath channels using the constant modulus criterion,” IEEE Transactions on Communications, vol. 58, no. 1, pp. 21–27, 2010. [Google Scholar]

20. M. A. Khan, M. Umair and M. A. S. Choudry, “Accelerated assistant to sub optimum receiver for multi carrier code division multiple access system,” in Int. Conf. on Future Trends in Computing and Communication Technologies, Malaysia, pp. 26–29, 2012. [Google Scholar]

21. M. Umair, M. A. Khan and M. A. S. Choudry, “Ga backing to stbc based mc-cdma systems,” in Int. Conf. on Intelligent Systems, Modelling and Simulation, Bankok, Thailand, pp. 503–506, 2013. [Google Scholar]

22. M. A. Khan, M. Umair and M. A. S. Choudhry, “Ga based adaptive receiver for mc-cdma system,” Turkish Journal of Electrical Engineering & Computer Sciences, vol. 15, no. e-1, pp. 2267–2277, 2015. [Google Scholar]

23. M. A. Khan, M. Umair and M. A. S. Choudhry, “Island differential evolution based adaptive receiver for mc-cdma system,” in Int. Conf. on Information and Communication Technologies, Karachi, Pakistan, pp. 1–6, 2015. [Google Scholar]

24. M. A. Khan, A. Nasir and M. Umair, “Time complexity of tompso algorithm,” in Int. Conf. on Statistical Sciences: Advances in Statistics and Data Management: Its Role in National Growth and Socio-Economic Developments, Pakistan, pp. 89–100, 2018. [Google Scholar]

25. M. Asadullah, M. A. Khan and S. Abbas, “Blind channel and data estimation using fuzzy logic-empowered opposite learning-based mutant particle swarm optimization,” Computational Intelligence and Neuroscience, vol. 2018, no. 5, pp. 1–17, 2018. [Google Scholar]

26. N. S. Naz, M. A. Khan, S. Abbas, A. Ather and S. Saqib, “Intelligent routing between capsules empowered with deep extreme machine learning technique,” SN Applied Sciences, vol. 2, no. 1, pp. 108–116, 2020. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.