DOI:10.32604/cmc.2022.019148

| Computers, Materials & Continua DOI:10.32604/cmc.2022.019148 |  |
| Article |
Design of Computer Methods for the Solution of Cervical Cancer Epidemic Model
1Department of Mathematics, National College of Business Administration and Economics Lahore, Pakistan
2Department of Mathematics, Faculty of Sciences, University of Central Punjab, Lahore, 54500, Pakistan
3Mathematics Department, College of Science, Jouf University, P. O. Box: 2014, Sakaka, Saudi Arabia
4Department of Mathematics and Statistics, The University of Lahore, Lahore, Pakistan
5Department of Mathematics, College of Science Al-Zulfi, Majmaah University, Al-Majmaah, 11952, Saudi Arabia
6Department of Mathematics, College of Arts and Science at Wadi Aldawaser, Prince Sattam bin Abdulaziz University, Alkharj, 11991, Kingdom of Saudi Arabia
7Department of Mathematics, Technische Universitat Chemnitz, Germany
*Corresponding Author: Ilyas Khan. Email: i.said@mu.edu.sa
Received: 04 April 2021; Accepted: 15 May 2021
Abstract: Nonlinear modelling has a significant role in different disciplines of sciences such as behavioral, social, physical and biological sciences. The structural properties are also needed for such types of disciplines, as dynamical consistency, positivity and boundedness are the major requirements of the models in these fields. One more thing, this type of nonlinear model has no explicit solutions. For the sake of comparison its computation will be done by using different computational techniques. Regrettably, the aforementioned structural properties have not been restored in the existing computational techniques in literature. Therefore, the construction of structural preserving computational techniques are needed. The nonlinear model for cervical cancer is constructed by parametric perturbation technique. Well-known computer methods are considered for the computation of cervical cancer dynamics. The well-known existing methods in literature are Euler Maruyama, Euler and Runge Kutta. Nonstandard finite difference method or Implicitly driven explicit method is first time considered for aforesaid model under the assumptions given by Mickens in a stochastic way. Unfortunately, the aforementioned existing methods did not reinstate structural properties of cervical cancer dynamics in the human population. Our planned method is structural preserving and a powerful tool for all nonlinear models of biomedical engineering problems. We have verified that existing computational methods do not preserve dynamical properties. But, the implicitly driven explicit method is a good device for dynamical properties. In the support of assertions, convergence analysis of implicitly driven explicit method is presented.
Keywords: Cervical cancer model; differential equations; computer methods; convergence analysis
Irregular development of cells into the cervix is the basic cause of cervical cancer which may grow to the nearby parts of the body. At early stages, cervical cancer has no specific sign. After some time, when the disease grows up violently, irregular vaginal bleeding, pelvic pain and having discomfort sex activity are realized as symptoms of the disease. Teenaged women may also suffer from cervical cancer. Commonly, 80% cases of this disease are found in developing states. Because of the disease, almost 200,000 deaths befell out of 500,000 in a year throughout the world. This slow-growing disease may have chances of prevention and treatment, if it is detected at early stages. Many women in the age of 20 s and 30 s are identified with precancerous variations, but mostly women in the age of mid-50 s are identified that they have cervical cancer [1,2]. This is the age difference in which precancerous changes are measured and detected. In this age, when cancer is explored, it can be prevented by specific diets. Body of every one is constructed by a number of various living cells. Ordinary body cells are produced and split into new cells in the early years of life. Cells split faster in the children than that of adults, as they require faster growth. Gradually, when any one gets adult; the cell division substitutes the dead cells and repairs the worn-out cells. When cells of any part of the body get out of appropriate development control, cancer occurs. There are numerous types of cancers. But every type of cancer twitches only due to irregular development of cells. Generally, the cancer is named by the part where it grooms initially, later on it may spread to other parts of the body. Cervical cancer is an anomalous type of cancer which initiates in the uterine, the finishing lower side of the uterus that is linked with the upper vagina. Cervical cancer cases are occurred throughout the world, particularly, it is considered the second largest cancer world-widely in women. About 530,000 fresh belongings to cervical cancer are noticed and analyzed every year. According to modern global study, almost 275,000 women expire due to this cancer. Only in the U.K. almost 2,800 examples of the disease are reported per annum out of which about 1,000 are women expired. In 2004, the ratio was 282 cases and in 2005 due to this cancer 127 women expired. The existence rate in during five years in Scotland from 1997 to 2001 was 70.6%. It was reported from Canada in 2008 that almost 1,300 women were noticed and diagnosed from which 380 women were expired. The ratio of expiry in women is 80%, which regularly ensue in developed countries. The fourth utmost cancer in women in Pakistan is cervical carcinoma. In Pakistan, the cervical cancer is low as associated with the several western states, but the amount of mortality is higher. Nearly, all types of cervical cancer are because of long standing, associated with Human Papillomavirus Infection (HPV). There are over 100 types of HPVs and only certain types are caused by cancer [3–6]. Other HPV types develop warts on the skin or genital parts called “high risk.” HPV types cause cancer of cervix as well as cancer of the penis in men. HPVs may also cause the cancer of the mouth, throat and anus in people of both sexes. HPV is a very common sexually transmitted infection (STI) and epidemiology of this infection and the molecular studies show its etiologic management for cervical cancer. There are more than 40 kinds of HPV affecting the puberty parts of males and females, the outer skin of the penis, vulva (range external from vagina), anus, inside layer of vagina, rectum and cervix. Mostly people remain totally unaware that HPV has infected them. HPV-16 is one of the highly risky types of HPV (more than 56%) of all cervical cancers. Around 70% of all cancers are because of HPV-16 and HPV-18. Nearby, 500,000 precancerous cells change of the vulva, vagina and cervix are identified. Even though all types of cervical cancers are associated with HPV, mostly genital infections may not be the source of cervical cancer in the United States. Almost twenty million American people are presently affected from HPV. At any time, at least half of sexually active (50%) males and females may attain genital HPV infection in their lives. Among the age of 15 to 25 years, nearly half of the infection is found. It was found that most of the genital HPV spreads through genital meeting during vaginal, oral and anal sex. It also turns over from the body fluid and mother-child transformation through birth. Having several sexual spouses or having intercourses by such males who have several sexual spouses, may increase the risk of the disease in women. In June 2006 a vaccine was introduced by the food and drugs administration (FDA) for the anticipation of protection from HPV-16 and HPV-18 (that causes 70% of all cervical cancers). These types of HPV infection after being detected at its initial stage having a pap smear or Papanicolaou test may be treated [7–12].
A qualitative study was conducted by Wal boomers et al. in 1999, with eight focus groups (having 102 number of samples) with eleven questions drawn from “the health belief model.” The findings from the focus groups were that here was a deficiency of factual information around cervical cancer. So, the womenfolk stood unaware of the causal features and protective approaches concerning cervical cancer. The results exposed that main structural fences were lack of information as well as time and financial aspects. Denied misunderstandings and anxiety are the main psychological barriers to undertaking Pap tests and medical education advice impacts on contributors. To increase inspiration and knowledge, and to lessen certain barriers, recommendations are made [13,14]. In 2004, Raley et al. [15] suggested that HPV infection is the contributing agent of genital warts and cervical neoplasia. To prevent infection with HPV, a vaccine has been developed recently that may become a part of gynaecology. A survey was conducted by the researcher of American college of obstetricians and Gynaecologists (ACOG) to explore approaches towards vaccination of HPV. In 2004, Allison Friedman recommended that human papillomavirus (HPV) infection is the utmost mutual sexually transmitted and causing cervical cell irregularities, genital warts and cervical cancer in females in U.S.A. to prevail information about this virus in the individuals of general public, 35 groups were made stratified by, gender, race and location. The groups enhanced their information, thoughts and ideas about hypothetical HPV and HPV vaccines. In 2005 Sheila and Twin took a model of 467 Chinese women respectively to determine information about cervical cancer. The results revealed that female’s information around cervical cancer and precautionary or protective approaches play an important role in their screening practices. In 2006, the infectious disease obstetric Gynaecology journal recommended that in the near future, vaccines for cervical cancer (HPV 16 and HPV 18 types) will be available in the market. HPV vaccines being prophylactic, would be directed earlier to the detection of the virus at the age of adolescence or before or preadolescence. In 2007, Kwan et al. supervised a study to seek Chinese women's vision about the HPV vaccine and their will to be vaccinated. The results showed that only 38% of the members had ever heard of HPV cancer while 50% had some knowledge of its vaccination and only 88% of them showed their concern about the cancer and wanted to be vaccinated. In 2007, Nubia Munoz et al. took an experimental group of 17,622 women of 15 to 26 years of age. These all were registered in one of the two placebo-controlled efficiency tribunals used for HPV (6, 11, 16 and 18) vaccine (first patient on 28 December 2001 and studies accomplished on 31 July 2007). The vaccine was dosed on day 1st, 2nd month and 6th month. Cervical vaginal sampling from the women was collected for pap testing at day one of every month up to 12 months regularly. The result showed 100% effectiveness of the vaccine to lessen the dangers of HPV (16 and 18) as well as HPV-11 and genital warts [16–18]. Chao et al. presented in 2007, the learning amongst 34,193 women who were using HPV vaccination. The results showed that the completion rate was 47.1% amongst the patients of age 18 to 26 years and 41.9% amongst the patients of age from 9 to 17 years. In 2008, Caron et al, took college women to conduct a cross-sectional study. The results showed HPV as the main cause of cervical cancer and second ordinary source of cancer related mortality among the women. Foremost objective behind this analysis is to find out the alertness of HPV and its vaccine named Gardasil, along with reorganization accessed by the college women. The results showed that 14% of them identified as precancerous and got necessary treatment. 24% of them did not pay heed during primarily three months after receiving the results. To localize the cancer about 96% of the women were not aware. For the females, by helpful pap test, these results may be useful to select treatment modalities or fitness activities in developing intervention strategies to assist them. A study on HPV vaccination was supervised by Licht et al. in 2009. Main purpose of the analysis was to observe hazards and perceptions, linked in the direction of HPV which concerned the use of HPV vaccine amongst girls who studied in colleges. A concluded self-administered review was made amongst 406 enrolled women from the age of 18 to 26 years in two public universities by cross-sectional design [19–24]. Mathematical modelling is a comprehensive way to study the dynamics of diseases in the human population. That is the reason, we have done stochastic modelling with structure preserving analysis of cervical cancer due Papillomavirus infection in humans. After this analysis, we will be capable of predicting its extinction and persistence scenarios. There are different mathematical models of cervical cancer disease that have been considered in [25]. The all-explicit schemes for ODE’s and SDE’s have produced non-physical oscillation for certain parameters So, these schemes are less reliable and unstable. It is notable that stochastic schemes do not protect the dynamical properties in stochastic context. Here a question arises: Can we get protection of dynamical properties for stochastic dynamical systems?
This is our real idea to construct the implicitly driven explicit scheme namely as S-NSFD for stochastic cervical cancer model. The strategy of our paper is as follows: In Section 3, we shall call deterministic and stochastic cervical cancer models and their equilibria. In Section 4, we shall describe the numerical methods for stochastic models and results are related with deterministic solutions. In Section 5, we shall discuss the covariance among the sub populaces. Finally, we shall discuss the future framework of our research.
3 Deterministic Cervical Cancer Model
In this part, we consider the cervical cancer model due to human papillomavirus infection. Let at any time
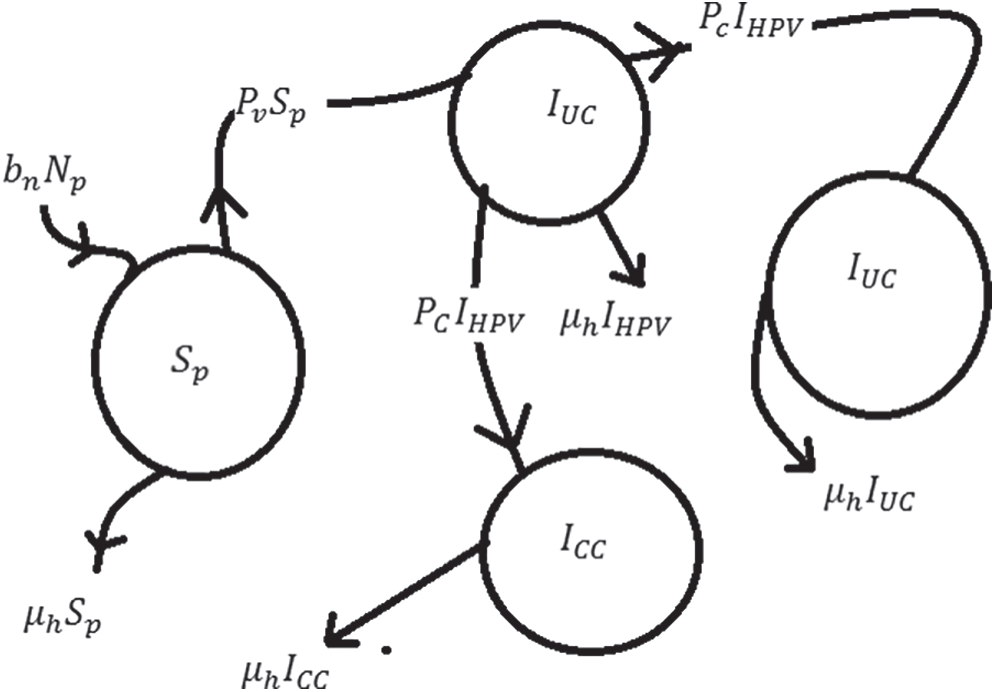
Figure 1: Flow map of cervical cancer model
The model parameters are labelled as:
The reduced form of system (1)–(4) is as follows:
where,
3.1 Equilibria of Cervical Cancer Model
Two types of equilibria of the model (3.5–3.7) as: Cervical-free equilibrium = CFE is
Note that
3.2 Stochastic Cervical Cancer Model
Now, we study the vector

The expectancy of the model (5)–(7) is given as:
The drift and diffusion of model is as follows:
So, we can easily write the SDE as:
with terms
For the solution of SDE (8), we shall use the fundamental technique, Euler Maruyama and selected values of parameters are presented in Tab. 2.
where the step size is represented ‘

4 Parametric Perturbation Model
We shall introduce the stochastic environmental factors
where,
The system (10)–(12) can be written as follows:
where “h” is called the time step size and
4.2 Stochastic Runge-Kutta Method
The system (10)–(12) can be written as follows.
First Stage
Second Stage
Third Stage
Fourth Stage
Final Stage
where “h” is called the time step size and
The system (10)–(12) can be written by using this method and presented in [27]:
where “h” is called the time step size and
Theorem 1: Let for (
Theorem 2: The set
Proof: The system (17)–(19) may be written as:
By adding all the equations, we have
nearly sure.
Theorem 3: The system (17)–(19) will be stable, if all eigen values of given system should lie in a unit circle.
For this we consider F, G and H as follows:
The Jacobian matrix
where,
Put,
The eigen values are
Thus, all eigen values of discrete dynamical system for cancer free equilibria (CFE) lies in unit circle. So, the system (17)–(19) is stable.
In this unit, we shall discourse the simulations of above methods and the values of constants are presented in [26].
The simulations of system (9) are presented as follows:
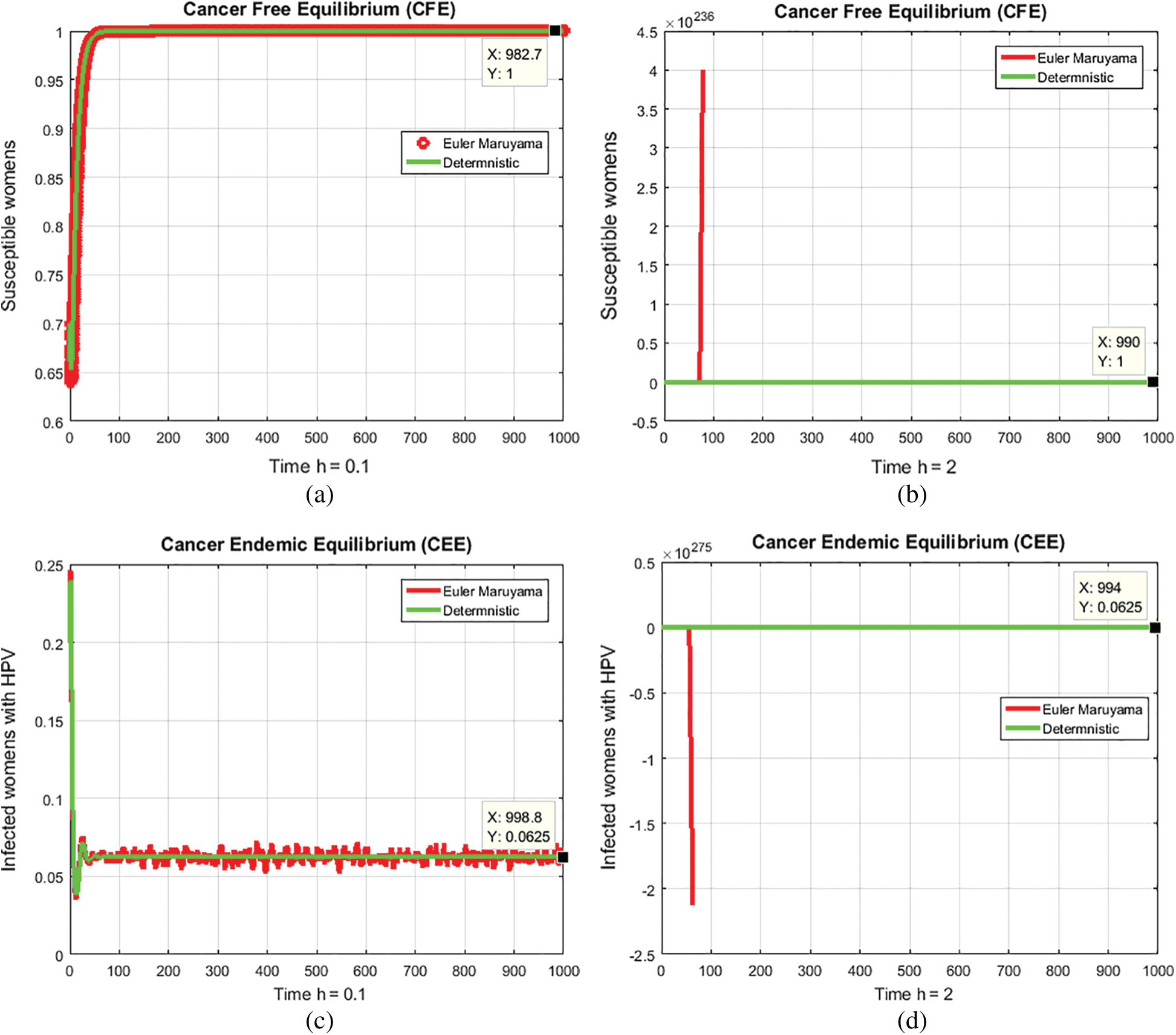
Figure 2: (a) Susceptible women’s at CFE for h = 0.1 (b) Susceptible women’s at CFE for h = 2 (c) Infected women at CEE for h = 0.1 (d) Infected women at CEE for h = 2
Remarks: The aforesaid method converges for parameter h = 0.1 in Figs. 2a and 2c But diverges in Figs. 2b and 2d.
The simulations of system (13)–(15) are as follows:
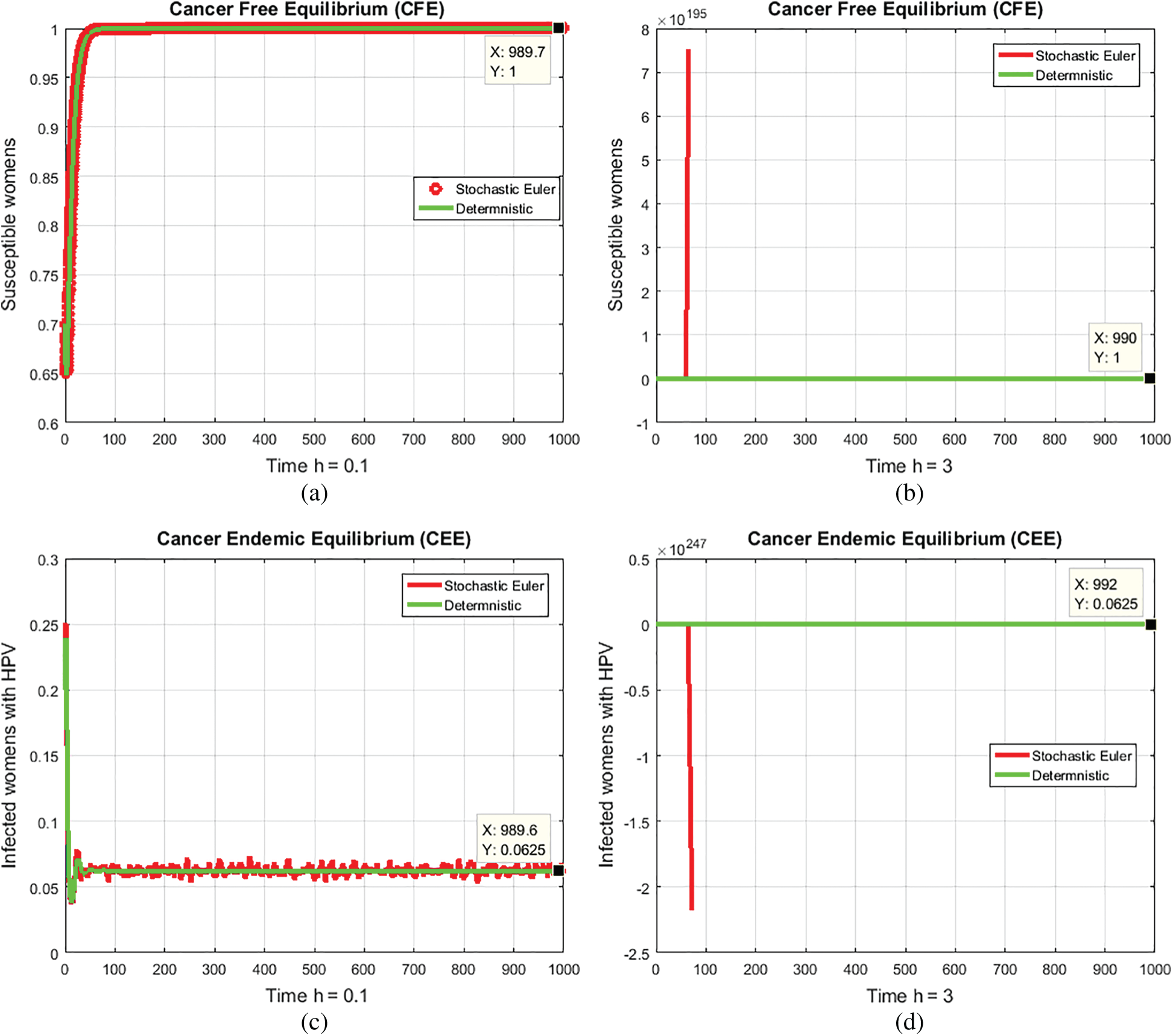
Figure 3: (a) Susceptible women’s’ at CFE for h = 0.1 (b) Susceptible women’s at CFE for h = 3 (c) Infected women at CEE for h = 0.1 (d) Infected women at CEE for h = 3
Remarks: The aforesaid method converges for parameter h = 0.1 in Figs. 3a and 3c But diverges and shows negativity in Figs. 3b and 3d.
5.3 Stochastic Runge Kutta Method
The simulations of system (16) are described as follows:
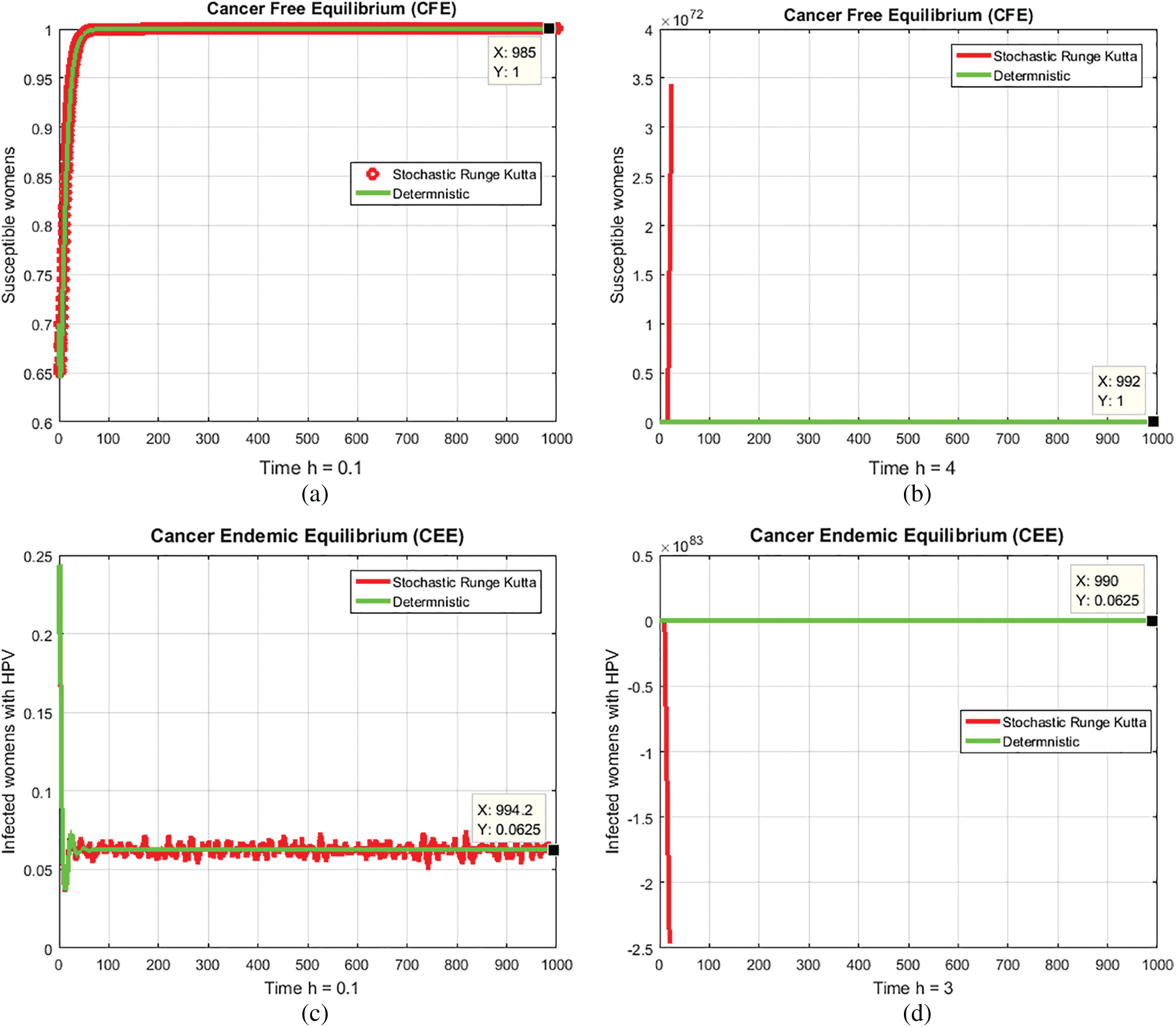
Figure 4: (a) Susceptible women’s at CFE for h = 0.1 (b) Susceptible women’s at CFE for h = 4 (c) Infected women at CEE for h = 0.1 (d) Infected women at CEE for h = 3
Notes: The aforesaid method converges for parameter h = 0.1 in Figs. 4a and 4c But diverges and shows negativity in Figs. 4b and 4d Its means the sbove stochastic explicit methods are time dependent. We can not observe long term qualtative behavior of system.
The simulations of system (17)–(19) are as follows:
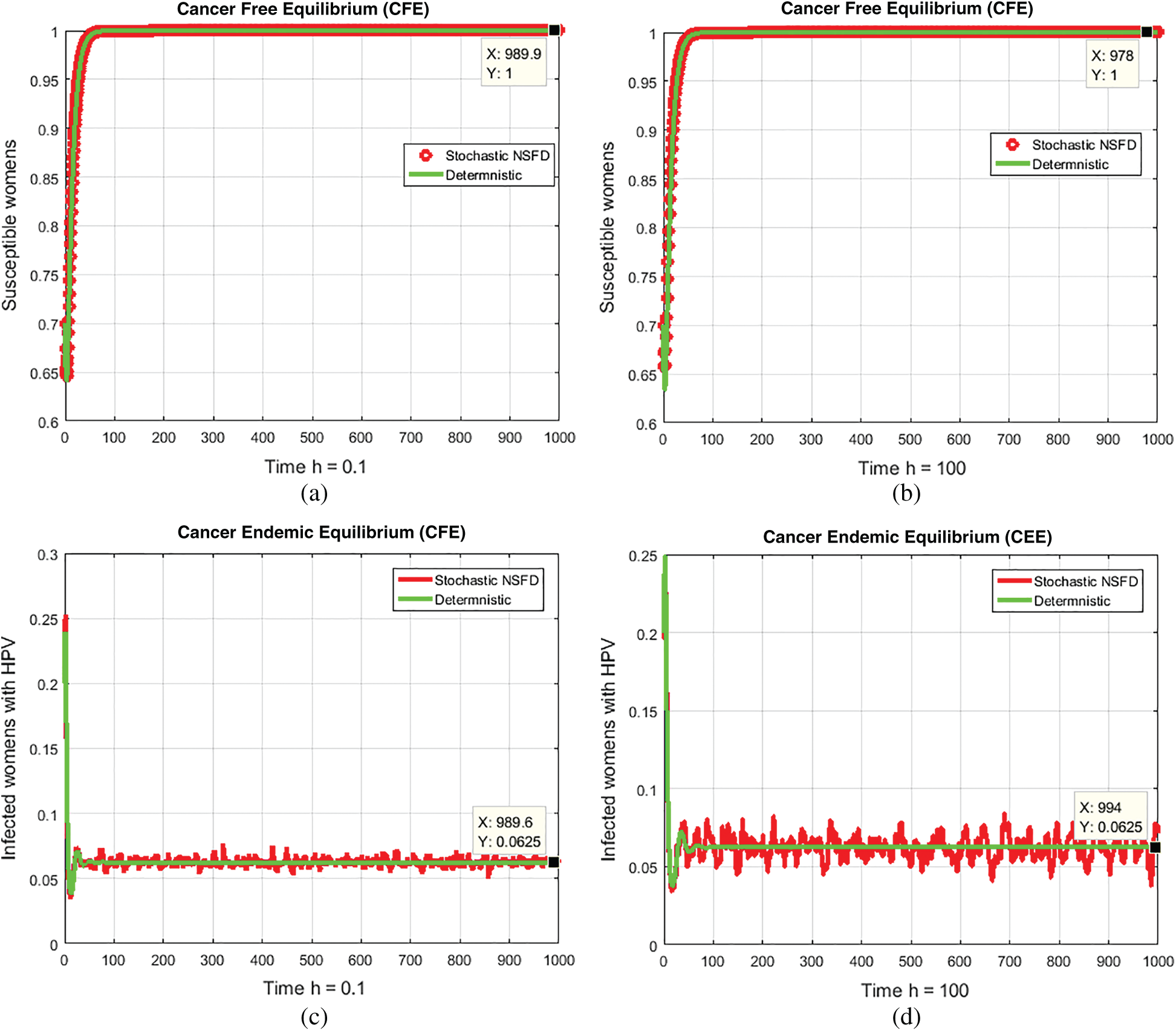
Figure 5: (a) Susceptible women’s at CFE for h = 0.1 (b) Susceptible women’s at CFE for h = 100 (c) Infected women at CEE for h = 0.1 (d) Infected women at CEE for h = 100
Notes: The aforesaid method converges at any step sizre of time in as shown Figs. 5a and 5d.
We shall draw a comparison of aforesaid techniques as presented in Fig. 6 as follows:
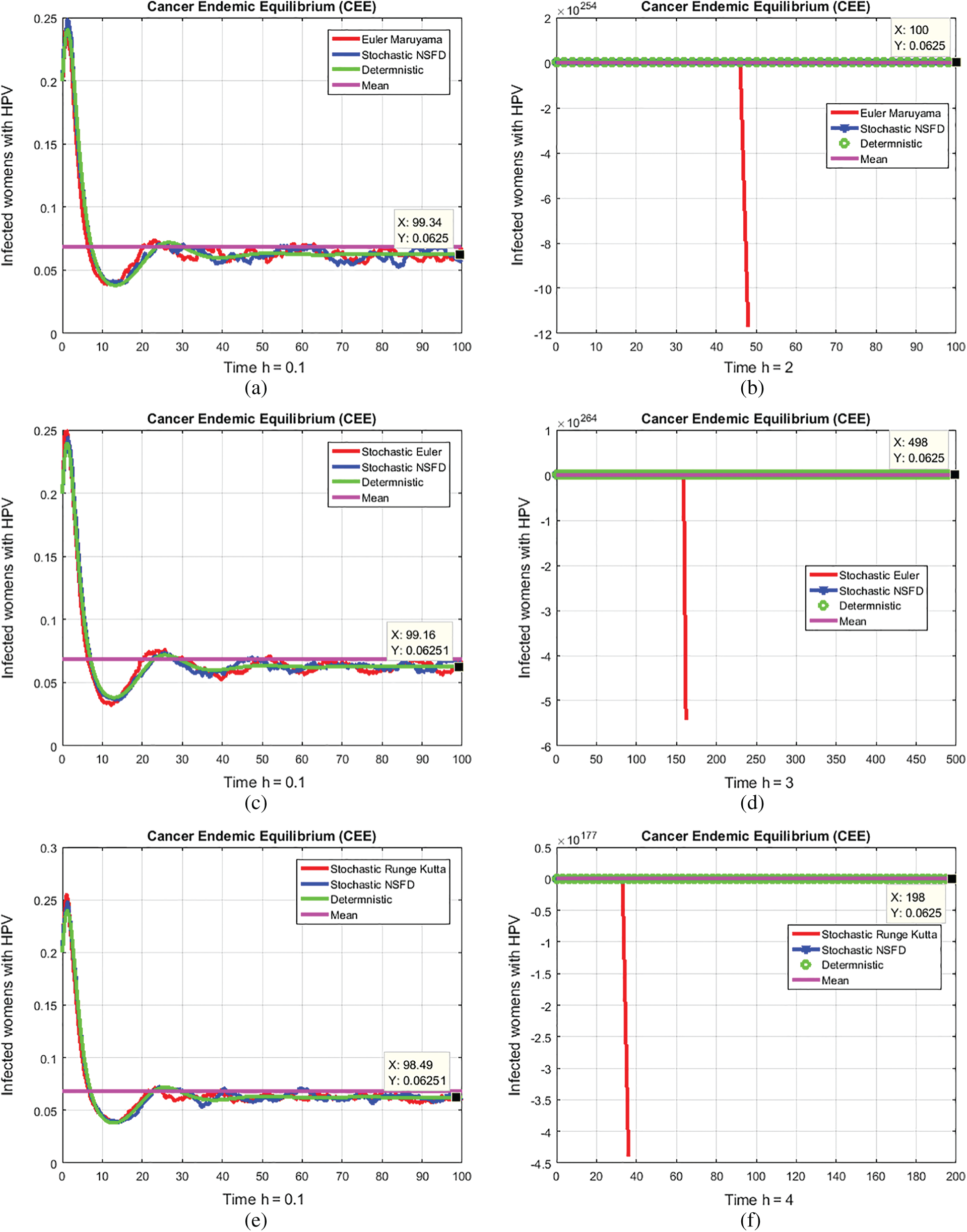
Figure 6: (a) Comparison of infected women with HPV compartment at h = 0.1 (b) Comparison of infected women with HPV compartment at h = 2. Euler Maruyama produce negativity. (c) Comparison of infected women with HPV compartment at h = 0.1 (d) Comparison of infected women with HPV compartment at h = 3 and stochastic Euler produce negativity. (e) Comparison of infected women with HPV compartment at h = 0.1 (f) Comparison of infected women with HPV compartment at h = 4 and stochastic Runge Kutta produce negativity
The covariance of population for nonlinear cervical cancer model due to human papillomavirus infection is studied here. Now, we shall calculate the correlation coefficients for checking the covariance of the model and results are described below.

In Tab. 3, we can observe the terms among the compartmental population. The inverse relation holds in susceptible women and the other two populations. The population will be cancer free if there is an increase in susceptible women and decrease in remaining compartments.
6 Conclusion and Future Frame Work
We have claimed that SDEs analysis of models is most effective and real as compared to ODE’s analysis of models. No doubt they are connected to each other. The stochastic explicit methods are conditionally convergent and depend on time step size. But, the NSFD method is independent of time step size. This scheme is an unconditionally convergent technique as compared to other explicit stochastic methods. This scheme preserves all dynamical properties of stochastic models such as consistency, stability, positivity and boundedness in the stochastic framework. In future, we shall extend our work in all disciplines of stochastic calculus. Moreover, we shall extend this idea in stochastic fractional models and stochastic fuzzy models as presented in [28–30].
Acknowledgement: We always warmly, thanks to anonymous referees.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. N. Wentzensen, M. Arbyn, J. Berkhof, M. Bower, K. Canfell et al., “How HPV knowledge is changing screening practice,” International Journal of Cancer, vol. 140, no. 1, pp. 2192–2200, 2017. [Google Scholar]
2. A. Hammer, A. Rositch, F. Qeadan, P. E. Gravitt, J. Blaakaer et al., “Age-specific prevalence of HPV genotypes in cervical cancer: A systematic review and meta-analysis,” International Journal of Cancer, vol. 138, no. 2, pp. 2795–2803, 2016. [Google Scholar]
3. A. R. Giuliano, A. G. Nyitray, A. R. Kreimer, C. M. Campbell, M. T. Goodman et al., “Differences in human papillomavirus infection natural history transmission and human papillomavirus-related cancer incidence by gender and anatomic site of infection,” International Journal of Cancer, vol. 136, no. 2, pp. 2752–2760, 2015. [Google Scholar]
4. D. Mesher, K. Cuschieri, S. Hibbitts, J. Jamison, A. Sargent et al., “Type-specific HPV prevalence in invasive cervical cancer in the UK prior to national HPV immunization programme baseline for monitoring the effects of immunisation,” Journal of Clinical Pathology, vol. 68, no. 2, pp. 135–140, 2015. [Google Scholar]
5. D. Saslow, D. Solomon, H. W. Lawson, M. D. M. Killackey, S. L. Kulasingam et al. “American Society for colposcopy and cervical pathology, and American society for clinical pathology screening guidelines for the prevention and early detection of cervical cancer,” American Journal of Clinical Pathology, vol. 137, no. 2, pp. 516–542, 2012. [Google Scholar]
6. K. Abodayeh, A. Raza, M. S. Arif, M. Rafiq, M. Bibi et al., “Stochastic numerical analysis for impact of heavy alcohol consumption on transmission dynamics of gonorrhoea epidemic,” Computers, Materials & Continua, vol. 62, no. 3, pp. 1125–1142, 2020. [Google Scholar]
7. A. K. Chaturvedi, E. A. Engels, R. M. Pfeiffer, B. Y. Hernandez, W. Xiao et al., “Human papillomavirus and rising or pharyngeal cancer incidence in the United States,” Journal of Clinical Oncology, vol. 29, no. 32, pp. 4294–4301, 2011. [Google Scholar]
8. H. Muller and C. Bauch, “When do sexual partnerships need to be accounted for in transmission models of human papillomavirus,” International Journal of Environmental Research and Public Health, vol. 1, no. 2, pp. 635– 650, 2010. [Google Scholar]
9. J. Herbert and C. Janis, “Reducing patient risk for human papillomavirus infection and cervical cancer,” Journal of the American Osteopathic Association, vol. 108, no. 10, pp. 65–70, 2008. [Google Scholar]
10. M. L. Gillison, A. K. Chaturvedi and D. R. Lowy, “HPV prophylactic vaccines and the potential prevention of noncervical cancers in both men and women,” European Journal of Cancer Supplements, vol. 13, no. 10, pp. 3036–3046, 2008. [Google Scholar]
11. P. W. Lee, T. T. Kwan, K. F. Tam, K. K. Chan, M. P. Young et al., “Beliefs about cervical cancer and human papillomavirus and acceptability of HPV vaccination among Chinese women in Hong Kong,” Preventive Medicine Journal, vol. 45, no. 1, pp. 130–134, 2007. [Google Scholar]
12. J. Godfrey and M. D. Harper, “Discusses the HPV vaccine and prevention of cervical cancer,” Journal of Women’s Health, vol. 16, no. 10, pp. 139–1401, 2007. [Google Scholar]
13. R. Winer, J. Hughes and Q. Feng, “Condom use and the risk of genital human papillomavirus infection in young women,” New England Journal of Medicine, vol. 354, no. 26, pp. 45–54, 2006. [Google Scholar]
14. C. Radecki, H. C. Pearson and M. D. Breltkopf, “Poor knowledge regarding the pap test among low-income women undergoing routine screening,” Perspectives on Sexual and Reproductive Health, vol. 35, no. 22, pp. 78–84, 2005. [Google Scholar]
15. J. C. Raley, K. A. Followwill, G. D. Zimet and K. A. Ault, “Gynecologists attitudes regarding human papilloma virus vaccination: A survey of fellows of the American college of obstetricians and gynecologists,” Infectious Diseases in Obstetrics and Gynecology, vol. 1, no. 12, pp. 127–133, 2004. [Google Scholar]
16. T. H. Pham, T. H. Nguyen and R. Herrero, “Human papillomavirus infection among women in south and north Vietnam,” International Journal of Cancer, vol. 104, no. 2, pp. 213–220, 2003. [Google Scholar]
17. G. M. Clifford, J. S. Smith, M. Plummer, N. Munoz, S. Franceschi et al., “Human papillomavirus types in invasive cervical cancer worldwide: A meta-analysis,” British Journal of Cancer, vol. 88, no. 2, pp. 63–73, 2003. [Google Scholar]
18. K. McCaffrey, S. Forrest, J. Waller, M. Desai, A. Szarwski et al., “Attitudes towards HPV testing: A qualitative study of beliefs among Indian, Pakistani, African, Caribean and white British women in the UK,” British Journal of Cancer, vol. 88, no. 1, pp. 42–46, 2003. [Google Scholar]
19. J. S. Mandelblatt, W. F. Lawrence, S. M. Womack, D. J. Jacobson, T. Y. Hwang et al., “Benefits and costs of using HPV testing to screen for cervical cancer,” Journal of American Medical Association, vol. 287, no. 23, pp. 72–81, 2002. [Google Scholar]
20. S. Collins, S. Mazloomzadeh and H. Winter, “High incidence of cervical human papillomavirus infection in women during their first sexual relationship,” British Journal of Obstetrics and Gynaecology, vol. 109, no. 1, pp. 96–98, 2002. [Google Scholar]
21. H. Z. Hausen, “Papillomaviruses causing cancer evasion from host-cell control in early events in carcinogenesis,” Journal of National Cancer Institute, vol. 96, no. 1, pp. 690–698, 2000. [Google Scholar]
22. J. M. Walboomers, M. V. Jacobs, M. M. Manos, F. X. Bosch, J. A. Kummer et al., “Human papillomavirus is a necessary cause of invasive cervical cancer worldwide,” The Journal of Pathology, vol. 189, no. 1, pp. 12–19, 1999. [Google Scholar]
23. G. Y. H. Bierman, L. Beardsley, C. J. Chang and R. D. Burk, “Natural history of cervical-vaginal papillomavirus infection in young women,” The New England Journal of Medicine, vol. 338, no. 1, pp. 423–428, 1998. [Google Scholar]
24. A. Akgul, N. Ahmed, A. Raza, Z. Iqbal, M. Rafiq et al., “A fractal fractional model for cervical cancer due to human papillomavirus infection,” Fractals: An Interdisciplinary Journal on The Complex Geometry of Nature, vol. 1, no. 2, pp. 1–18, 2021. [Google Scholar]
25. A. Raza, M. S. Arif and M. Rafiq, “A reliable numerical analysis for stochastic gonorrhea epidemic model with treatment effect,” International Journal of Biomathematics, vol. 12, no. 5, pp. 445–465, 2019. [Google Scholar]
26. P. Pongsumpun, “Mathematical model of cervical cancer due to human papillomavirus infection,” Mathematical Methods in Science and Engineering, vol. 1, no. 1, pp. 157–161, 2020. [Google Scholar]
27. A. Raza, D. Baleanu, M. Rafiq, M. S. Arif, M. Naveed et al., “Competitive numerical analysis for stochastic HIV/AIDS epidemic model in a two-sex population,” IET Systems Biology, vol. 13, no. 6, pp. 305–315, 2019. [Google Scholar]
28. A. Ahmadian, S. Salahshour, C. S. Chan and D. Baleanu, “Numerical solutions of fuzzy differential equations by an efficient Runge–Kutta method with generalized differentiability,” Fuzzy Sets and Systems, vol. 331, no. 1, pp. 47–67, 2018. [Google Scholar]
29. A. Ahmadian, M. Suleiman and S. Salahshour, “An operational matrix based on Legendre polynomials for solving fuzzy fractional-order differential equations,” Abstract and Applied Analysis, vol. 13, no. 1, pp. 1–18, 2013. [Google Scholar]
30. M. Rafiq, A. Ahmadian, A. Raza, D. Baleanu, M. S. Ahsan et al., “Numerical control measures of stochastic malaria epidemic model,” Computers, Materials & Continua, vol. 65, no. 1, pp. 33–51, 2020. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |