Computers, Materials & Continua DOI:10.32604/cmc.2022.019048
Article

Utilization of Machine Learning Methods in Modeling Specific Heat Capacity of Nanofluids

Mamdouh El Haj Assad1, Ibrahim Mahariq2, Raymond Ghandour2, Mohammad Alhuyi Nazari3 and Thabet Abdeljawad4,5,6,*

1Sustainable and Renewable Energy Engineering Department, University of Sharjah, P. O. Box 27272, Sharjah, UAE
2College of Engineering and Technology, American University of the Middle East, Kuwait
3Faculty of New Sciences and Technologies, University of Tehran, Tehran, Iran
4Department of Mathematics and General Sciences, Prince Sultan University, Riyadh, 11586, Saudi Arabia
5Department of Medical Research, China Medical University, Taichung, 40402, Taiwan
6Department of Computer Science and Information Engineering, Asia University, Taichung, Taiwan
*Corresponding Author: Thabet Abdeljawad. Email: tabdeljawad@psu.edu.sa
Received: 31 March 2021; Accepted: 01 May 2021

Abstract: Nanofluids are extensively applied in various heat transfer mediums for improving their heat transfer characteristics and hence their performance. Specific heat capacity of nanofluids, as one of the thermophysical properties, performs principal role in heat transfer of thermal mediums utilizing nanofluids. In this regard, different studies have been carried out to investigate the influential factors on nanofluids specific heat. Moreover, several regression models based on correlations or artificial intelligence have been developed for forecasting this property of nanofluids. In the current review paper, influential parameters on the specific heat capacity of nanofluids are introduced. Afterwards, the proposed models for their forecasting and modeling are proposed. According to the reviewed works, concentration and properties of solid structures in addition to temperature affect specific heat capacity to large extent and must be considered as inputs for the models. Moreover, by using other effective factors, the accuracy and comprehensive of the models can be modified. Finally, some suggestions are offered for the upcoming works in the relevant topics.

Keywords: Specific heat capacity; nanofluid; artificial neural network; concentration

1  Introduction

Literature demonstrates that by suspending solids with nanodimension in traditional operating fluids, heat transfer rate can be improved, mainly due to increment in the effective thermal conductivity [1–3]. Addition of solid phase in the base fluid results in changes in different thermophysical properties such as density, thermal conductivity and specific heat capacity [4–6]. Variations in these properties are contingent on different items including concentration of solids, temperature and properties of the base fluid [7,8]. In general, increase in volume fraction of nanostructures causes increase in both viscosity and thermal conductivity [9,10]. Despite the advantages of high thermal conductivity for heat transfer purposes, the increase in dynamic viscosity is unfavorable; consequently, there is an optimum concentration in the majority of the cases [11,12]. In comparison with specific heat capacity of nanofluids, more attentions have been attracted by dynamic viscosity and thermal conductivity; however, several studies have focused on this property of the nanofluids due to its substantial role in heat transfer of operating fluids.

Nanofluids are employable in different energy-related mediums and technologies for performance enhancement including renewable energy systems, air conditioners and heat pipes, as shown in Fig. 1 [13–17]. For instance, Hosseinzadeh et al. [18] applied three different nanofluids in an indirect solar cooker and compared the performance with a case of using thermal oil without any nanoparticle. They observed that with the thermal oil, utilizing SiO2/oil, TiO2/oil, and SiC/oil led to around 1.17%, 3.54% and 4.27% enhancement in the efficiency, respectively. In another work [19], performance of spirally-coiled twisted-tube was compared using water and Cu/water nanofluid. They found that the maximum performance index of the device was 1.39 and 1.88 for cases of using water and the nanofluid, respectively. Ahmed et al. [20] investigated the effect of using TiO2/water nanofluid as coolant in a car radiator and observed that using the nanofluid resulted in up to 47% enhancement in the performance compared with pure water. Ahmed et al. [21] used nanofluid as external cooling jacket in vicinity of air conditioner condenser. It was observed that using nanolfuids, Cu/water and Al2O3/water in 5% concentration resulted in 29.4% and 22.1% improvement in coefficient of performance, respectively. Another energy-related device with high potential for performance improvement by employing nanofluid is heat pipe. As an example, Zhou et al. [22] applied graphene oxide/water in a pulsating heat pipe and observed that by using this nanofluid, thermal performance could be enhanced up to 54.34% in optimal operating condition in comparison with pure water.

Figure 1: Some of the main energy-related applications of nanofluids

Different approaches have been applied for modeling the properties of nanofluids including regressive correlations, artificial neural networks (ANNs) and support vector machines (SVMs). Studies have demonstrated that employing artificial intelligence for modeling results in higher accuracy compared with the correlations. For instance, Komeilibirjandi et al. [23] applied both GMDH NN and correlation for predicting thermal conductivity of nanofluids with CuO particles. The determined values for R-squared of the models based on ANN and correlation were 0.9996 and 0.9862, respectively. Higher accuracy of the models based on ANNs in comparison with correlations has been observed for the predictive models used for dynamic viscosity of nanofluids [24].

There are some review papers on the models proposed for predicting thermal conductivity and dynamic viscosity of nanofluids [25,26]; however, there is not any up to date review article on the specific heat capacity. In this work, studies carried out on specific heat of nanofluids are reviewed; afterwards, the proposed models with focus on artificial intelligence are reviewed and represented. Finally, some suggestions are recommended for upcoming works in the relevant topics.

2  Specific Heat Capacity of Nanofluids

Specific heat capacity of nanofluids is one of the properties that play substantial role in heat transfer ability of nanofluids. Mainly, suspension of solid materials with nanodimensions in the base fluid changes the overall specific heat. Depending on the intended application, decreased or increased specific heat would be desirable. Variation in specific heat depends on several elements that are discussed and reviewed in this section. For instance, concentration of the particles notably influences the variation in the specific heat [27–29]. Tiwari et al. [30] measured the specific heat of graphene nanoplatelet/water-EG for various concentrations of solid phase. As shown in Fig. 2, they noticed that the increase in the volume fraction resulted in a reduction in the specific heat of the nanofluid. In addition to the volume fraction, other factors including base fluid and temperature influence specific heat capacity of nanofluids. In a study done by Akilu et al. [31], the effect of dispersion of SiO2 particles in different base fluids, including glycerol (GC), ethylene glycol (EG) and their mixture (GC/EG) and concentrations were discussed. As shown in Fig. 3 they observed that by increasing the fraction of particles in fluid, reduction in the specific heat became more noticeable. Furthermore, they found that a decrease in the specific heat of nanofluid with GC/EG base fluid was higher than the others. In addition, by comparing the specific heat of the nanofluids at two temperatures, 25 and 50∘C, it was concluded that temperature influenced the variations in specific heat to a small extent. Particle size is another element that affects the specific heat capacity of nanofluids. In a study, the effect of particle size on the specific heat capacity of Fe3O4/kerosene was investigated [32]. It was observed that the increase in the size of particles resulted in more reduction in specific heat capacity; however, some studies have reported different findings about the effect of particle size on this property of nanofluids.

Figure 2: Specific heat capacity of GN/water-EG nanofluid vs. concentration [30]

Contrary to the nanofluids with conventional base fluids, specific heat capacity of the ones with molten salt base fluids can be increased by adding solid particles with nanometer dimensions [33]. Qiao et al. [34] measured the specific heat capacity of molten nitrate salt-based nanofluids with SiO2particles for different concentrations. According to their measurement for potassium nitrate based nanofluid, there was an optimum value at which the maximum value of the specific heat capacity was obtained, by more increase in concentration, the specific heat capacity of the nanofluid was reduced. Among the considered concentrations of the nanoparticles, 0%, 0.5%, 1%, 2% and 4% wt, the highest specific heat capacity of the nanofluid was observed for 1% wt. In addition to the concentration, the size of particles is an influential factor in variation of specific heat. According to findings of a study done by Lu et al. [35] on the molten salt-based nanofluid containing alumina particles, the decrease in the particle size caused reduction in the specific heat capacity, attributed to the nanolayer effect, since contribution of nanolayer increased by reducing the size of particles. In addition to size, temperature and volume fraction, type of particles and base fluid specification influence the variations in specific heat capacity [36].

Figure 3: Variations in specific heat capacity of nanofluids with different base fluids [31]

In another work [37], the effect of dispersing SiO2 particles on the specific heat capacity of a molten salt, mixture of lithium carbonate and potassium carbonate (62:38 ratio), was investigated. It was observed that the nanoparticle dispersion in the molten salt, with 1% wt concentration, led to 19−24% improvement in the specific heat capacity. In another study [38], specific heat capacity of a molten salt, with 60% NaNO3 and 40% KNO3 with SiO2 nanoparticles in different concentrations were measured. As shown in Fig. 4, there was an optimum concentration at which it reached a maximum value. In addition to binary base fluids, the specific heat capacity of a molten salt nanofluid with ternary base fluid was investigated by Sang et al. [39]. The ternary base fluid was composed of K2CO3,\; Li2CO3\;  and Na2CO3 with various composition ratios. It was observed that the specific heat capacity of the nanofluid could increase up to 113.7%. Moreover, they noticed that the composition of the base fluid affects enhancement value of specific heat capacity. In another work [40], the effect of particle material on the specific heat capacity of a nanofluid with ternary molten salt composed of K2CO3,\; Li2CO3\;  and Na2CO3 was investigated. In their study, four nanoparticles including Al2O3,\; CuO,\; SiO2 and TiO2were considered. They found that for the same condition, adding SiO2 caused the maximum improvement in the specific heat capacity in the range of 78% to 116.8%, which was followed by CuO in the range of 50.67% to 73.9%.

Hybrid nanofluids, that are composed of nanostructures with two dissimilar materials, have gained attentions in recent years for various purposes [41,42]. In this regard, the specific heat of these nanofluids, similar to their other properties, has been investigated by some researchers. Wole-Osho et al. [41] carried out a work on specific heat capacity of Al2O3−ZnO/water nanofluid. In their work, three mixture ratios including 1:1, 1:2, and 2:1 were examined to investigate its effect on the variations of specific heat. They observed that the maximum reduction in specific heat capacity of nanofluid in comparison with the pure base fluid was around 30.12% in mixture ratio of 2:1. In another research, Gao et al. [43] measured the specific heat capacity of a hybrid nanofluid, GO-Al2O3/water nanofluid for different concentrations and temperatures. They found that by increasing the concentration, the specific heat capacity of the nanofluid was decreased and this reduction was more noticeable at lower temperatures. Reduction in the specific heat capacity of hybrid nanofluids by increasing the volume fraction hybrid nanostructures has been observed in other studies; however, the effect of the temperature was not the same [44].

Figure 4: Specific heat capacity of 60% NaNO3 and 40% KNO3 with SiO2 nanoparticles different concentrations

3  Proposed Models for Specific Heat Capacity

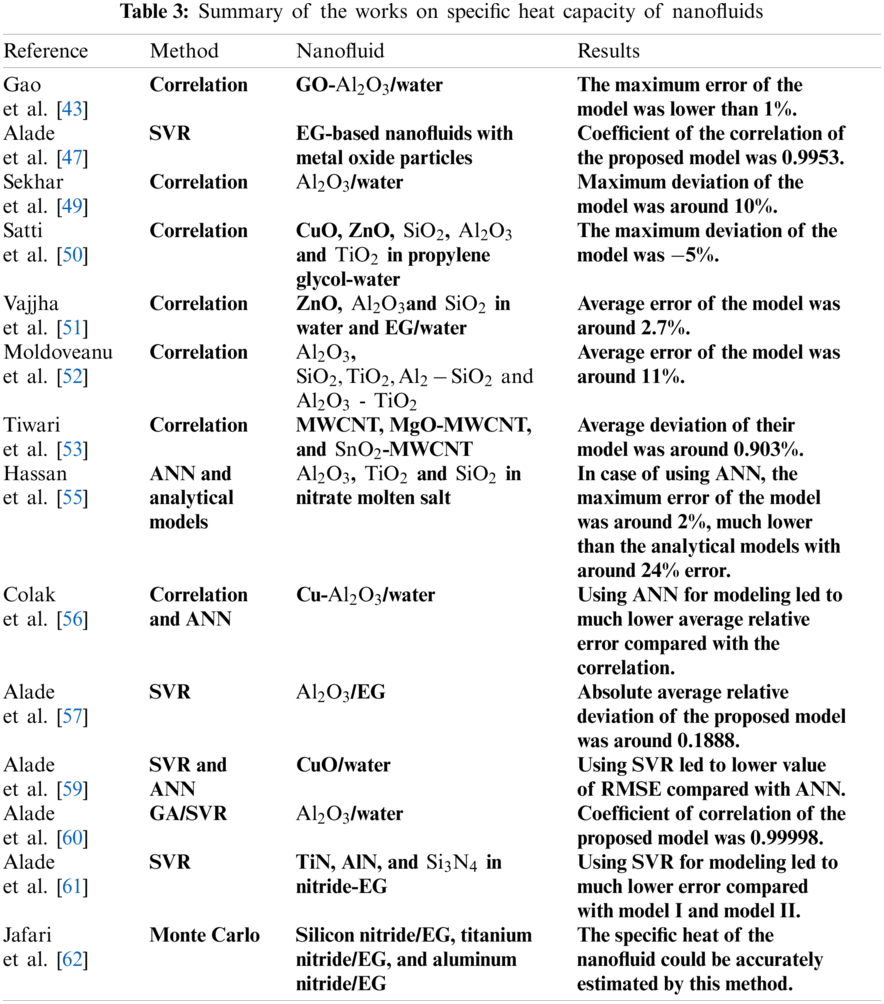
Similar to dynamic viscosity and thermal conductivity [45], variety of methods have been applied for modeling specific heat of nanofluids. There are two general methods that are applicable for rough estimation of specific heat capacity [46]. The first one is based on the idea of mixing theory for ideal gases (model I) which is defined as follows [47]:

CP,nf=φCP,n+(1−φ)CP,bf(1)

where subscripts nf, n and bf refer to nanofluid, nanoparticle, and base fluid, respectively. Another correlation is proposed based on the thermal equilibrium of nanoparticles and base fluid, which is defined as follows (model II) [47]:

CP,nf=φρnCP,n+(1−φ)ρbfCP,bfφρn+(1−φ)ρbf(2)

where ρ refers to the density. In comparison with the previous model, it has higher precision in predicting specific heat capacity in majority of cases [48]. Besides the above mentioned models, applicable for all of the nanofluids, there are some correlations that can be used for specific types of nanofluids with higher accuracy [49]. Satti et al. [50] proposed a correlation for specific heat capacity of nanofluids with various particles including CuO, ZnO, SiO2, Al2O3 and TiO2 with propylene glycol-water as base fluid. The proposed correlation is as follows:

ρnfCP,nfρbf0CP,bf0=0.371641+1.00713φ+0.345370(TT0)+0.039107(ρnpCP,npρbfCP,bf)(3)

where T0=273K. It should be noted that this correlation is valid for 243K \lt T \lt 363\; K and 0<φ<0.06. The maxium deviation of this correlation in determination of specific heat capacity of the nanofluids is −5%. Similar correlations have been proposed for hybrid nanofluids. For instance, Gao et al. [43] proposed a correlation for specific heat capacity of GO-Al2O3/water by considering concentration and temperature as the inputs, which is:

CP,nf=a+bφ+cT+dφ2+eφT+fT2(4)

The determined values of the coefficients are mentioned in Tab. 1. The maximum error of this correlation in determining the specific heat capacity of the nanofluid is 0.86%.

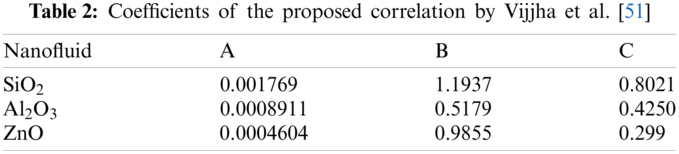
There are some correlations with higher degree of comprehensiveness by including more inputs. For instance, Vajjha et al. [51] proposed a correlation for specific heat capacity of nanofluids with different particles including ZnO, Al2O3 and SiO2. The first two were dispersed in EG-water while the third was dispersed in water. In their model, the specific heat capacities of the base fluids, particles, volume concentration and temperatures were included in the correlation as follows:

CP,nfCP,bf=(AT)+B(CP,npCP,bf)(C+φ)(5)

The coefficients of the above mentioned correlation are presented in Tab. 2. Average error of their model is around 2.7%.

In addition to the conventional nanofluids, the specific heat capacity of hybrid nanofluids could be modeled by using correlations [52]. Tiwari et al. [53] compared the specific heat capacity of three hybrid nanofluids with CuO-MWCNT, MgO-MWCNT, and SnO2-MWCNT nanostructure. The base fluid of the nanofluids was water and CTAB was utilized as surfactant. In their study, the effects of temperature, specific heat and size of nanostructures in addition to concentration were considered for modeling. The proposed correlation in their work was as follows:

CP,nf=CP,bf(1−10.6364×(TT0)−0.771×φ0.448×(dnpd0)−0.474×(CP,npCP,bf)1.027×(ρnfρbf)−2.742)(6)

where dP refers to the size of metal oxide nanoparticles and d0 is equal to 20 nm. The average deviation of the proposed model was 0.903%, revealing acceptable accuracy of the model. Despite these correlations are simple to use and able to estimate the specific heat capacity of various nanofluids, their accuracy may not be as high as desirable [54]. In this regard, other models have been proposed by focusing on special types of nanofluids and/or employing powerful approaches such as ANNs. For instance, Hassan et al. [55] compared prediction accuracy of the models based on ANN with analytical models for nanofluids with various particles including silica, titania and alumina dispersed in molten nitrate salt. They found that ANN-based model, at optimal condition, had much higher accuracy compared with the analytical models. The maximum error of ANN-based model was around 2% while the corresponding value of the analytical models was about 24%. ANNs are also usable for modeling specific heat capacity of hybrid nanofluids. For instance, Colak et al. [56] applied ANN to propose a model for the specific heat capacity of Cu−Al2O3/water by considering temperature and volume fraction. Average relative error of the model, based on ANN was around 5.84×10−9, while the corresponding value for the proposed correlation was about 0.005%, indicating higher precision of the model based on ANN.

In addition to correlations and ANNs, other intelligent methods are applicable for specific heat capacity modeling of nanofluids [57,58]. Alade et al. [59] compared performance of support vector regression and ANN with the classical models for modeling specific heat capacity of CuO/water nanofluid. As shown in Fig. 5, based on the values of root mean squared error (RMSE), using support vector regression led to the highest accuracy which was followed by ANN. In another work, Alade et al. [47] applied support vector regression (SVR) for modeling the specific heat capacity of EG-based nanofluids with different metal oxide particles including CuO and Al2O3 particles. Inputs of their model were the specific heat capacity values of the base fluid and nanoparticles in addition to temperature and volume fraction of solid phase. In their model, Bayesian algorithm was employed for obtaining the optimum hyperparameters to reach the highest possible accuracy. Coefficient of correlation of their model was 0.9953 and the root mean square error was 0.0127, revealing the precision of the proposed model. They compared the accuracy of the proposed regression with two conventional models based on mixing theory of ideal gas (model I) and thermal equilibrium (model II) and observed much higher accuracy as shown in Fig. 6. Different optimization techniques can be applied in SVR-based models proposed for specific heat capacity prediction. In a study [60], genetic algorithm (GA) was coupled with SVR to model specific heat of Al2O3/water nanofluid. It was noticed that the proposed model was very accurate, and its correlation coefficient was 0.99998. Comprehensiveness of the models can be further improved by considering more inputs. For instance, Alade et al. [61] applied SVR for modeling specific heat of nanofluids with various particles including TiN, AlN, and Si3N4, which were dispersed in nitride/EG. In their model, the effect of particle material and size was considered by adding the particle size and molar mass. Moreover, temperature and volume fraction were used as other inputs. Mean percentage absolute error of their model was 0.123, much lower than model I and models II with 3.997 and 1.339, respectively. In addition to SVR, other novel methods are applicable for modeling specific heat capacity of nanofluids. As an example, Monte Carlo approach has been applied for modeling isobaric heat capacity of nanofluids with EG base fluid [62]. The model considered nanofluids with various particles including silicon nitride, titanium nitride, and aluminum nitride. It was found that by using this approach it would be possible to model the output with great reliability. The summary of the researches on the modeling of specific heat capacity is given in Tab. 3.

Figure 5: Root mean squared error of the models for specific heat capacity of CuO/water nanofluid

Figure 6: RMSE of the models applied for modeling specific heat capacity of nanofluids with EG base fluid and metal oxide particles

4  Suggestions for Upcoming Studies

Based on the performed literature review, several models have been introduced for determination of the specific heat capacity of nanofluids; however, the provided models have some defects or restrictions which necessitate some modification and further attempt. First of all, the majority of the models are limited to special type of nanofluids with certain number of particles. In this regard, the applicability of the models can be broadened by using more variables such as properties of the base fluids and nanostructures. By including these parameters as the inputs, specific heat capacity of more nanofluids could be modeled and predicted. Moreover, there are few studies that applied ANN despite their desirable performance in modeling complex system. It is suggested to develop various types of ANNs, such as GMDH, for proposing models which are simple to use [63]. Furthermore, due to the dependency of ANN performance on the architecture of network, it is crucial to examine different structures to obtain more precise and reliable models [64]. In addition, utilizing various functions in the architecture of the ANNs would be useful for upcoming research.

Besides ANNs, other intelligent methods with different structures and algorithms can be used for specific heat capacity modeling. Adaptive neuro-fuzzy inference system (ANFIS) [65] and least square SVM (LSSVM) [66] would be appropriate and attractive options for modeling this property with remarkably high accuracy. Coupling novel and powerful optimization algorithms with the currently used intelligent methods for minimizing error is another idea for proposing better predictive models. Finally, performing sensitivity analysis would be very useful since detailed and brilliant insight into the effect of each factor can be provided. Summary of the suggestions for upcoming research are shown in Fig. 7.

Figure 7: Suggestions for upcoming research

5  Conclusion

In this article, parameters influencing the specific heat capacity of different nanofluids in addition to the proposed models are reviewed. The main findings of the study are as follows:

•   For the nanofluids with conventional base fluids, in contrary to molten salts, increase in the volume fraction of nanostructure leads to reduction in the specific heat capacity.

•   Temperature of nanofluids influences the specific heat capacity and its increasing or decreasing trend with temperature is dependent on the base fluid.

•   Analytical models, based on thermal equilibrium or ideal gas idea, could be applicable for rough estimation of nanofluids specific heat capacity.

•   Several correlations have been proposed for modeling specific heat capacity of nanofluids with higher accuracy compared with analytical models.

•   Different intelligent models have been proposed for modeling the specific heat of nanofluids with higher precision compared with correlations.

•   Including more parameters in the models improve comprehensiveness of the models.

•   Different optimization algorithms can be coupled with models for minimizing the errors.

•   It is suggested to consider other intelligent methods such as ANFIS and LSSVM for upcoming studies with similar topics.

Funding Statement: This work was supported by College of Engineering and Technology, the American University of the Middle East, Kuwait. Homepage: https://www.aum.edu.kw.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  M. Mohammadi, M. Mohammadi, A. R. Ghahremani, M. B. Shafii and N. Mohammadi, “Experimental investigation of thermal resistance of a ferrofluidic closed-loop pulsating heat pipe,” Heat Transfer Engineering, vol. 35, no. 1, pp. 25–33, 2014. [Google Scholar]

 2.  A. Gandomkar, M. H. Saidi, M. B. Shafii, M. Vandadi and K. Kalan, “Visualization and comparative investigations of pulsating ferro-fluid heat pipe,” Applied Thermal Engineering, vol. 116, no. 3, pp. 56–65, 2017. [Google Scholar]

 3.  M. El Haj Assad and M. Alhuyi Nazari, “Heat exchangers and nanofluids,” in Design and Performance Optimization of Renewable Energy Systems, Cambridge, MA, USA: Academic Press, pp. 33–42, 2021. [Google Scholar]

 4.  M. H. Ahmadi, F. Hajizadeh, M. Rahimzadeh, M. B. Shafii and A. J. Chamkha, “Application GMDH artificial neural network for modeling of Al2O3/water and Al2O3/ethylene glycol thermal conductivity,” International Journal of Heat and Technology, vol. 36, no. 3, pp. 773–782, 2018. [Google Scholar]

 5.  A. H. Saeedi, M. Akbari and D. Toghraie, “An experimental study on rheological behavior of a nanofluid containing oxide nanoparticle and proposing a new correlation,” Physica E: Low-Dimensional Systems and Nanostructures, vol. 99, no. 10, pp. 285–293, 2018. [Google Scholar]

 6.  D. Dey, P. Kumar and S. Samantaray, “A review of nanofluid preparation, stability, and thermo-physical properties,” Heat Transfer-Asian Research, vol. 46, no. 8, pp. 1413–1442, 2017. [Google Scholar]

 7.  M. H. Hamzah, N. A. C. Sidik, T. L. Ken, R. Mamat and G. Najafi, “Factors affecting the performance of hybrid nanofluids: A comprehensive review,” International Journal of Heat and Mass Transfer, vol. 115, no. 7, pp. 630–646, 2017. [Google Scholar]

 8.  A. Maleki, A. Haghighi and I. Mahariq, “Machine learning-based approaches for modeling thermophysical properties of hybrid nanofluids: A comprehensive review,” Journal of Molecular Liquids, vol. 322, no. 18, pp. 114843–114853, 2021. [Google Scholar]

 9.  M. H. Esfe, H. Rostamian, S. Esfandeh and M. Afrand, “Modeling and prediction of rheological behavior of Al2O3-mWCNT/5w50 hybrid nano-lubricant by artificial neural network using experimental data,” Physica A: Statistical Mechanics and its Applications, vol. 510, no. 2, pp. 625–634, 2018. [Google Scholar]

10. M. H. Esfe, S. Esfandeh, M. Afrand, M. Rejvani and S. H. Rostamian, “Experimental evaluation, new correlation proposing and ANN modeling of thermal properties of EG based hybrid nanofluid containing ZnO-dWCNT nanoparticles for internal combustion engines applications,” Applied Thermal Engineering, vol. 133, no. 4, pp. 452–463, 2018. [Google Scholar]

11. M. A. Nazari, R. Ghasempour, M. H. Ahmadi, G. Heydarian and M. B. Shafii, “Experimental investigation of graphene oxide nanofluid on heat transfer enhancement of pulsating heat pipe,” International Communications in Heat and Mass Transfer, vol. 91, no. 10, pp. 90–94, 2018. [Google Scholar]

12. B. Bakthavatchalam, K. Habib, R. Saidur, N. Aslfattahi, M. Yahya et al., “Optimization of thermophysical and rheological properties of mxene ionanofluids for hybrid solar photovoltaic/Thermal systems,” Nanomaterials, vol. 11, no. 2, pp. 320–335, 2021. [Google Scholar]

13. M. Alhuyi Nazari, M. H. Ahmadi, R. Ghasempour and M. B. Shafii, “How to improve the thermal performance of pulsating heat pipes: A review on working fluid,” Renewable and Sustainable Energy Reviews, vol. 91, no. 11, pp. 630–638, 2018. [Google Scholar]

14. M. Ramezanizadeh, M. Alhuyi Nazari, M. H. Ahmadi and E. Açıkkalp, “Application of nanofluids in thermosyphons: A review,” Journal of Molecular Liquids, vol. 272, no. 11, pp. 395–402, 2018. [Google Scholar]

15. E. Bellos and C. Tzivanidis, “Thermal analysis of parabolic trough collector operating with mono and hybrid nanofluids,” Sustainable Energy Technologies and Assessments, vol. 26, no. 17, pp. 105–115, 2018. [Google Scholar]

16. A. Kumar, M. A. Hassan and P. Chand, “Heat transport in nanofluid coolant carradiator with louvered fins,” Powder Technology, vol. 376, no. 20, pp. 631–642, 2020. [Google Scholar]

17. M. Izadi and M. E. Assad, “Use of nanofluids in solar energy systems,” Design and Performance Optimization of Renewable Energy Systems, vol. 12, no.3, pp. 221–250, 2021. [Google Scholar]

18. M. Hosseinzadeh, R. Sadeghirad, H. Zamani, A. Kianifar, S. M. Mirzababaee et al., “Experimental study of a nanofluid-based indirect solar cooker: Energy and exergy analyses,” Solar Energy Materials and Solar Cells, vol. 221, no. 20, pp. 110879–110893, 2021. [Google Scholar]

19. M. K. Aliabadi, S. F. Khaligh and Z. Tavassoli, “An investigation of heat transfer in heat exchange devices with spirally-coiled twisted-ducts using nanofluid,” Applied Thermal Engineering, vol. 143, no. 9, pp. 358–375, 2018. [Google Scholar]

20. S. A. Ahmed, M. Ozkaymak, A. Sözen, T. Menlik and A. Fahed, “Improving car radiator performance by using TiO2-water nanofluid,” Engineering Science and Technology, an International Journal, vol. 21, no. 5, pp. 996–1005, 2018. [Google Scholar]

21. F. Ahmed and W. A. Khan, “Efficiency enhancement of an air-conditioner utilizing nanofluids: An experimental study,” Energy Reports, vol. 7, no. 3, pp. 575–583, 2021. [Google Scholar]

22. Y. Zhou, H. Yang, L. Liu, M. Zhang, Y. Wang et al., “Enhancement of start-up and thermal performance in pulsating heat pipe with GO/water nanofluid,” Powder Technology, vol. 384, no. 4, pp. 414–422, 2021. [Google Scholar]

23. A. Komeilibirjandi, A. H. Raffiee, A. Maleki, M. A. Nazari and M. Safdari Shadloo, “Thermal conductivity prediction of nanofluids containing CuO nanoparticles by using correlation and artificial neural network,” Journal of Thermal Analysis and Calorimetry, vol. 139, no. 4, pp. 2679–2689, 2020. [Google Scholar]

24. M. Afrand, A. Nadooshan, M. Hassani, H. Yarmand and M. Dahari, “Predicting the viscosity of multi-walled carbon nanotubes/water nanofluid by developing an optimal artificial neural network based on experimental data,” International Communications in Heat and Mass Transfer, vol. 77, no. 20, pp. 49–53, 2016. [Google Scholar]

25. M. Ramezanizadeh, M. A. Nazari, M. H. Ahmadi, G. Lorenzini and I. Pop, “A review on the applications of intelligence methods in predicting thermal conductivity of nanofluids,” Journal of Thermal Analysis and Calorimetry, vol. 138, no. 1, pp. 115–127, 2019. [Google Scholar]

26. M. Ramezanizadeh, M. H. Ahmadi, M. A. Nazari, M. Sadeghzadeh and L. Chen, “A review on the utilized machine learning approaches for modeling the dynamic viscosity of nanofluids,” Renewable and Sustainable Energy Reviews, vol. 114, no. 4, pp. 109345–109355, 2019. [Google Scholar]

27. B. X. Wang, L. P. Zhou, X. F. Peng, X. Z. Du and Y. P. Yang, “On the specific heat capacity of CuO nanofluid,” Advances in Mechanical Engineering, vol. 20, no. 3, pp. 1–10, 2010. [Google Scholar]

28. B. Barbés, “Thermal conductivity and specific heat capacity measurements of Al2O3 nanofluids,” Journal of Thermal Analysis and Calorimetry, vol. 111, no. 2, pp. 1615–1625, 2013. [Google Scholar]

29. Y. Ueki, T. Aoki, K. Ueda and M. Shibahara, “Thermophysical properties of carbon-based material nanofluid,” International Journal of Heat and Mass Transfer, vol. 113, no. 1, pp. 1130–1134, 2017. [Google Scholar]

30. C. Selvam, D. Mohan Lal and S. Harish, “Thermal conductivity and specific heat capacity of water–ethylene glycol mixture-based nanofluids with graphene nanoplatelets,” Journal of Thermal Analysis and Calorimetry, vol. 129, no. 2, pp. 947–955, 2017. [Google Scholar]

31. S. Akilu, A. T. Baheta, K. V. Sharma and M. A. Said, “Experimental determination of nanofluid specific heat with SiO2 nanoparticles in different base fluids,” in AIP Conf. Proc, AIP Publishing LLC, vol. 1877, pp. 090001, 2017. [Google Scholar]

32. S. A. Angayarkanni, V. Sunny and J. Philip, “Effect of nanoparticle size, morphology and concentration on specific heat capacity and thermal conductivity of nanofluids,” Journal of Nanofluids, vol. 4, no. 3, pp. 302–309, 2015. [Google Scholar]

33. B. Jo and D. Banerjee, “Enhanced specific heat capacity of molten salt-based carbon nanotubes nanomaterials,” Journal of Heat Transfer, vol. 137, no. 9, pp. 1–12, 2015. [Google Scholar]

34. G. Qiao, M. Lasfargues, A. Alexiadis and Y. Ding, “Simulation and experimental study of the specific heat capacity of molten salt based nanofluids,” Applied Thermal Engineering, vol. 111, no. 2, pp. 1517–1522, 2017. [Google Scholar]

35. M. C. Lu and C. H. Huang, “Specific heat capacity of molten salt-based alumina nanofluid,” Nanoscale Research Letters, vol. 8, no. 1, pp. 1–7, 2013. [Google Scholar]

36. S. M. S. Murshed, “Determination of effective specific heat of nanofluids,” Journal of Experimental Nanoscience, vol. 6, no. 5, pp. 539–546, 2011. [Google Scholar]

37. D. Shin and D. Banerjee, “Enhanced specific heat of silica nanofluid,” Journal of Heat Transfer, vol. 133, no. 2, pp. 1–9, 2011. [Google Scholar]

38. P. A. Cabedo, R. Mondragon, L. Hernandez, R. M. Cuenca, L. Cabedo et al., “Increment of specific heat capacity of solar salt with SiO2 nanoparticles,” Nanoscale Research Letters, vol. 9, no. 1, pp. 582–593, 2014. [Google Scholar]

39. L. Sang, W. Ai, T. Liu, Y. Wu and C. Ma, “Insights into the specific heat capacity enhancement of ternary carbonate nanofluids with SiO2 nanoparticles: The effect of change in the composition ratio,” RSC Advances, vol. 9, no. 10, pp. 5288–5294, 2019. [Google Scholar]

40. L. Sang and T. Liu, “The enhanced specific heat capacity of ternary carbonates nanofluids with different nanoparticles,” Solar Energy Materials and Solar Cells, vol. 169, no. 3, pp. 297–303, 2017. [Google Scholar]

41. I. Wole-Osho, E. C. Okonkwo, D. Kavaz and S. Abbasoglu, “An experimental investigation into the effect of particle mixture ratio on specific heat capacity and dynamic viscosity of Al2O3-znO hybrid nanofluids,” Powder Technology, vol. 363, no. 9, pp. 699–716, 2020. [Google Scholar]

42. J. Qu, R. Zhang, Z. Wang and Q. Wang, “Photo-thermal conversion properties of hybrid CuO-mWCNT/H2O nanofluids for direct solar thermal energy harvest,” Applied Thermal Engineering, vol. 147, no. 5, pp. 390–398, 2019. [Google Scholar]

43. Y. Gao, Y. Xi, Y. Zhenzhong, A. Sasmito, A. Mujumdar et al., “Experimental investigation of specific heat of aqueous graphene oxide Al2O3 hybrid nanofluid,” Thermal Science, vol. 1, no. 4, pp. 381–381, 2019. [Google Scholar]

44. H. Yarmand, S. Gharehkhani, S. F. Shirazi, M. Goodarzi, A. Amiri et al., “Study of synthesis, stability and thermo-physical properties of graphene nanoplatelet/platinum hybrid nanofluid,” International Communications in Heat and Mass Transfer, vol. 77, no. 8, pp. 15–21, 2016. [Google Scholar]

45. P. C. Kumar and R. Kavitha, “Regression analysis for thermal properties of Al2O3/H2O nanofluid using machine learning techniques,” Heliyon, vol. 6, no. 6, pp. 3966–3972, 2020. [Google Scholar]

46. T. P. Teng and Y. Hung, “Estimation and experimental study of the density and specific heat for alumina nanofluid,” Journal of Experimental Nanoscience, vol. 9, no. 7, pp. 707–718, 2014. [Google Scholar]

47. I. O. Alade, M. A. Rahman, A. Bagudu, Z. Abbas, Y. Yaakob et al., “Development of a predictive model for estimating the specific heat capacity of metallic oxides/ethylene glycol-based nanofluids using support vector regression,” Heliyon, vol. 5, no. 6, pp. 1882–1891, 2019. [Google Scholar]

48. S. Q. Zhou and R. Ni, “Measurement of the specific heat capacity of water-based Al2O3 nanofluid,” Applied Physics Letters, vol. 92, no. 9, pp. 93123–93130, 2008. [Google Scholar]

49. Y. R. Sekhar and K. V. Sharma, “Study of viscosity and specific heat capacity characteristics of water-based Al2O3 nanofluids at low particle concentrations,” Journal of Experimental Nanoscience, vol. 10, no. 2, pp. 86–102, 2015. [Google Scholar]

50. J. R. Satti, D. K. Das and D. Ray, “Specific heat measurements of five different propylene glycol based nanofluids and development of a new correlation,” International Journal of Heat and Mass Transfer, vol. 94, no. 1, pp. 343–353, 2016. [Google Scholar]

51. R. S. Vajjha and D. K. Das, “Specific heat measurement of three nanofluids and development of new correlations,” Journal of Heat Transfer, vol. 131, no. 7, pp. 1–7, 2009. [Google Scholar]

52. G. M. Moldoveanu and A. A. Minea, “Specific heat experimental tests of simple and hybrid oxide-water nanofluids: Proposing new correlation,” Journal of Molecular Liquids, vol. 279, no. 20, pp. 299–305, 2019. [Google Scholar]

53. A. K. Tiwari, N. S. Pandya, H. Shah and Z. Said, “Experimental comparison of specific heat capacity of three different metal oxides with MWCNT/water-based hybrid nanofluids: Proposing a new correlation,” Applied Nanoscience, vol. 7, no. 20, pp. 1–11, 2020. [Google Scholar]

54. H. Hanley, J. Buongiorno, T. McKrell and L. W. Hu, “Measurement and model correlation of specific heat capacity of water-based nanofluids with silica, alumina and copper oxide nanoparticles,” in ASME International Mechanical Engineering Congress and Exposition, vol. 54, no. 1, pp. 1209–1214, 2011. [Google Scholar]

55. M. A. Hassan and D. Banerjee, “A soft computing approach for estimating the specific heat capacity of molten salt-based nanofluids,” Journal of Molecular Liquids, vol. 281, no. 18, pp. 365–375, 2019. [Google Scholar]

56. A. B. Çolak, O. Yıldız, M. Bayrak and B. S. Tezekici, “Experimental study for predicting the specific heat of water based Cu-Al2 O3 hybrid nanofluid using artificial neural network and proposing new correlation,” International Journal of Energy Research, vol. 44, no. 9, pp. 7198–7215, 2020. [Google Scholar]

57. I. O. Alade, M. A. Rahman and T. A. Saleh, “Predicting the specific heat capacity of alumina/ethylene glycol nanofluids using support vector regression model optimized with Bayesian algorithm,” Solar Energy, vol. 183, no. 11, pp. 74–82, 2019. [Google Scholar]

58. B. Bakthavatchalam, N. B. Shaik and P. B. Hussain, “An artificial intelligence approach to predict the thermophysical properties of MWCNT nanofluids,” Processes, vol. 8, no. 6, pp. 693–699, 2020. [Google Scholar]

59. I. O. Alade, M. A. Rahman, Z. Abbas, Y. Yaakob and T. A. Saleh, “Application of support vector regression and artificial neural network for prediction of specific heat capacity of aqueous nanofluids of copper oxide,” Solar Energy, vol. 197, no. 21, pp. 485–490, 2020. [Google Scholar]

60. I. O. Alade, M. A. Rahman and T. A. Saleh, “Modeling and prediction of the specific heat capacity of Al2O3/water nanofluids using hybrid genetic algorithm/support vector regression model,” Nano-Structures and Nano-Objects, vol. 17, no. 1, pp. 103–111, 2019. [Google Scholar]

61. I. O. Alade, M. A. A. Rahman and T. A. Saleh, “An approach to predict the isobaric specific heat capacity of nitrides/ethylene glycol-based nanofluids using support vector regression,” Journal of Energy Storage, vol. 29, no. 3, pp. 101313–101321, 2020. [Google Scholar]

62. K. Jafari and M. H. Fatemi, “A new approach to model isobaric heat capacity and density of some nitride-based nanofluids using monte carlo method,” Advanced Powder Technology, vol. 31, no. 7, pp. 3018–3027, 2020. [Google Scholar]

63. M. Moghadam and S. Asgharzadeh, “On the application of artificial neural network for modeling liquid-liquid equilibrium,” Journal of Molecular Liquids, vol. 220, no. 7, pp. 339–345, 2016. [Google Scholar]

64. M. Ghalandari, H. Fard, A. K. Birjandi and I. Mahariq, “Energy-related carbon dioxide emission forecasting of four european countries by employing data-driven methods,” Journal of Thermal Analysis and Calorimetry, vol. 7, no. 20, pp. 1–10, 2020. [Google Scholar]

65. I. M. Alarifi, H. M. Nguyen, A. N. Bakhtiyari and A. Asadi, “Feasibility of ANFIS-pSO and ANFIS-gA models in predicting thermophysical properties of Al2O3-mWCNT/Oil hybrid nanofluid,” Materials, vol. 12, no. 21, pp. 1–8, 2019. [Google Scholar]

66. M. Esfe, A. Tatar, M. R. H. Ahangar and H. Rostamian, “A comparison of performance of several artificial intelligence methods for predicting the dynamic viscosity of TiO2/SAE 50 nano-lubricant,” Physica E: Low-Dimensional Systems and Nanostructures, vol. 96, no. 2, pp. 85–93, 2018. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.