Computers, Materials & Continua DOI:10.32604/cmc.2022.018947
Article

Network Analysis for Projects with High Risk Levels in Uncertain Environments

Mohamed Abdel-Basset1, Asmaa Atef1, Mohamed Abouhawwash2,3, Yunyoung Nam4,* and Nabil M. AbdelAziz1

1Faculty of Computers and Informatics, Zagazig University, Zagazig, 44519, Egypt
2Department of Mathematics, Faculty of Science, Mansoura University, Mansoura, 35516, Egypt
3Department of Computational Mathematics, Science, and Engineering (CMSE), Michigan State University, East Lansing, 48824, MI, USA
4Department of Computer Science and Engineering, Soonchunhyang University, Asan, 31538, Korea
*Corresponding Author: Yunyoung Nam. Email: ynam@sch.ac.kr
Received: 26 March 2021; Accepted: 27 April 2021

Abstract: The critical path method is one of the oldest and most important techniques used for planning and scheduling projects. The main objective of project management science is to determine the critical path through a network representation of projects. The critical path through a network can be determined by many algorithms and is useful for managing, monitoring, and controlling the time and cost of an entire project. The essential problem in this case is that activity durations are uncertain; time presents considerable uncertainty because the time of an activity is not always easily or accurately estimated. This issue increases the need to use neutrosophic theory to solve the critical path problem. Real-world problems are characterized by a lack of precision, consistency, and completeness. The concept of neutrosophic sets has been introduced as a generalization of fuzzy, intuitionistic fuzzy, and crisp sets to overcome the ambiguity surrounding real-world problems. Truth-, falsity-, and indeterminacy-membership functions are used to express neutrosophic elements. This study was performed to examine a neutrosophic event-oriented algorithm for determining the critical path in activity-on-arc networks. The activity time estimates are presented as trapezoidal neutrosophic numbers, and score and accuracy functions are used to obtain a crisp model of the problem. An appropriate numerical example is then used to explain the proposed method.

Keywords: Project management; project life cycle; project planning; project scheduling; CPM; neutrosophic set theory; trapezoidal neutrosophic number

1  Introduction

A project is a venture to accomplish a set of interrelated jobs; when these jobs are accomplished, the project is considered completed. Each job requires specific amounts of time and resources, which are governed by specific relations. A project is a unique set of activities meant to produce a defined outcome within an established time frame using specific allocations of resources. Three fundamental components are related to the project definition: (1) the goal that answers the question, “What do we want?;” (2) the objectives that answer the question, “How do we want it?”; (3) and the scope that answers the question, “How much of it do we want?” Whether the project is any good is also a consideration. Project management is the application of knowledge, skills, methods, experience, tools, and techniques to project activities to meet the project objectives. The study and understanding of projects involve three axes, namely, the project objectives, the project constituents, and the basic composition of the related jobs or activities, which are important because they consume time and resources and are responsible for project completion. Fig. 1 shows the different types of projects, including personal, local-neighborhood, organizational, national, and global projects.

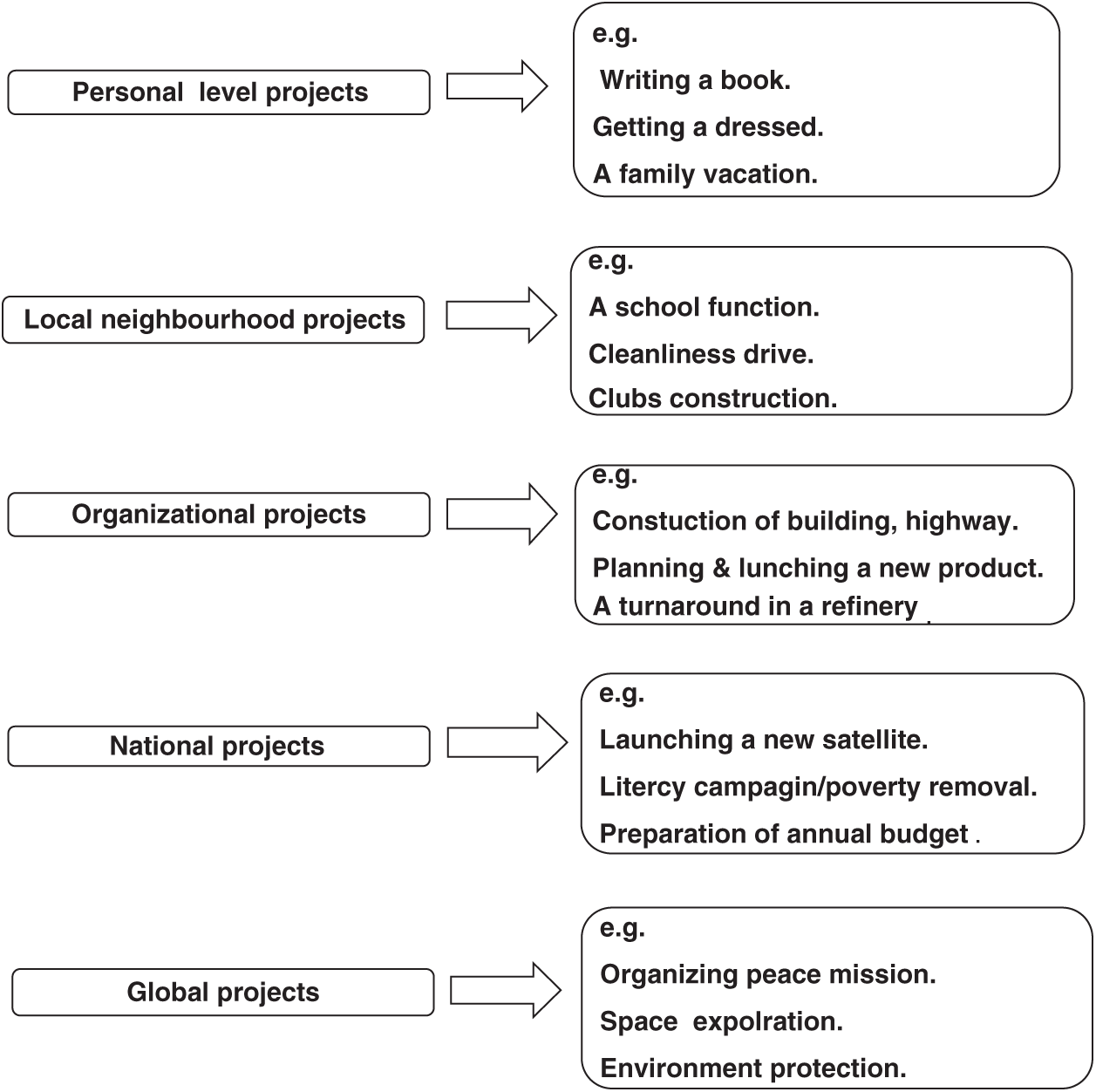
Figure 1: Different types of projects

Despite the tremendous variety of the nature and size of different projects, all projects feature a number of common characteristics or features. Regardless of whether the project is personal or organizational, finding and defining the features of the project is necessary. The common features of projects are used to plan, lead, and control various types of projects, which is the goal of project management science. These features are summarized in Fig. 2. Each project has a life cycle that begins with selecting the appropriate project from among several alternatives to achieve definite goals. A number of studies have discussed project scheduling, project life cycles, project planning, the critical path method (CPM), and advanced project management science [1–5]. The project life cycle begins with the client choosing the best project alternative from the available project set. In terms of life cycles, when a project is undertaken to accomplish a goal, a path that leads to a specific desired state, one that is distinct from the current state, is constructed. Several different projects could lead to the same desired state from the same current state, as shown in Fig. 3.

Figure 2: Common features of different projects

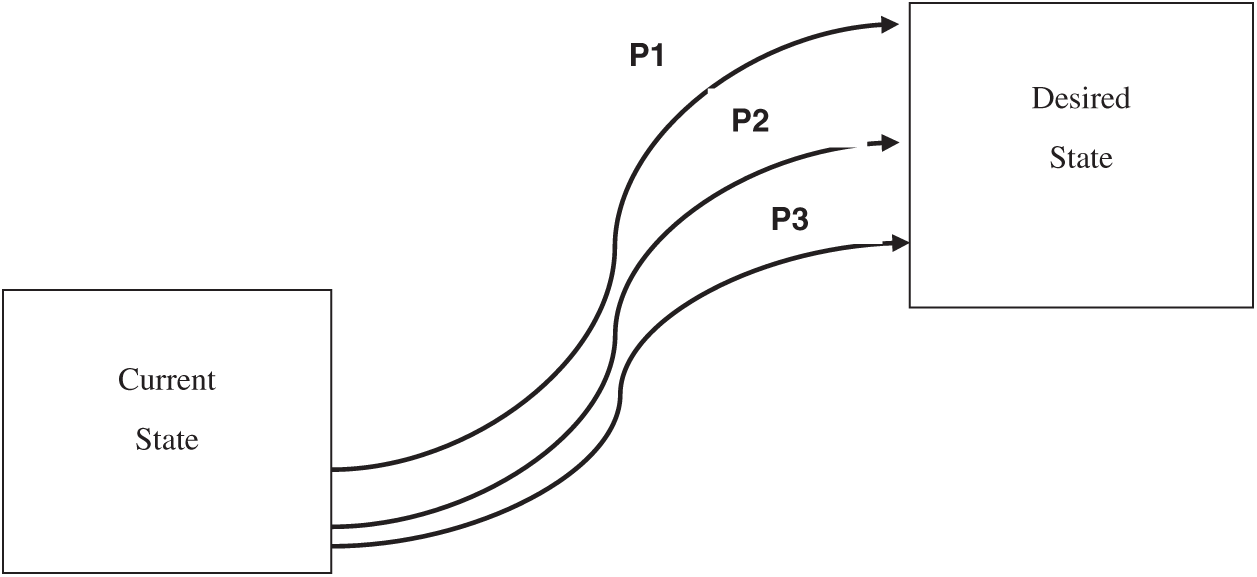
Figure 3: Alternatives pathways as projects

Once the appropriate project has been selected, the project must be planned and then implemented. Finally, upon project completion, an audit is performed. The project life cycle is summarized in Fig. 4. This paper addresses the scheduling sub-phase of the planning stage in detail.

The second stage of the project life cycle is planning, as described below:

•   Determine the project team and its leader.

•   Define the scope and terms of reference.

•   Create a work breakdown structure.

•   Determine the basic process of scheduling.

•   Evaluate time/expenditure tradeoffs.

•   Consider resources.

The basic scheduling sub-phase in the planning stage involves:

•   Project representation as a network.

•   Estimates of activity durations.

•   Calculation of forward and backward passes.

•   Determination of activity floats.

•   Determination of the critical path.

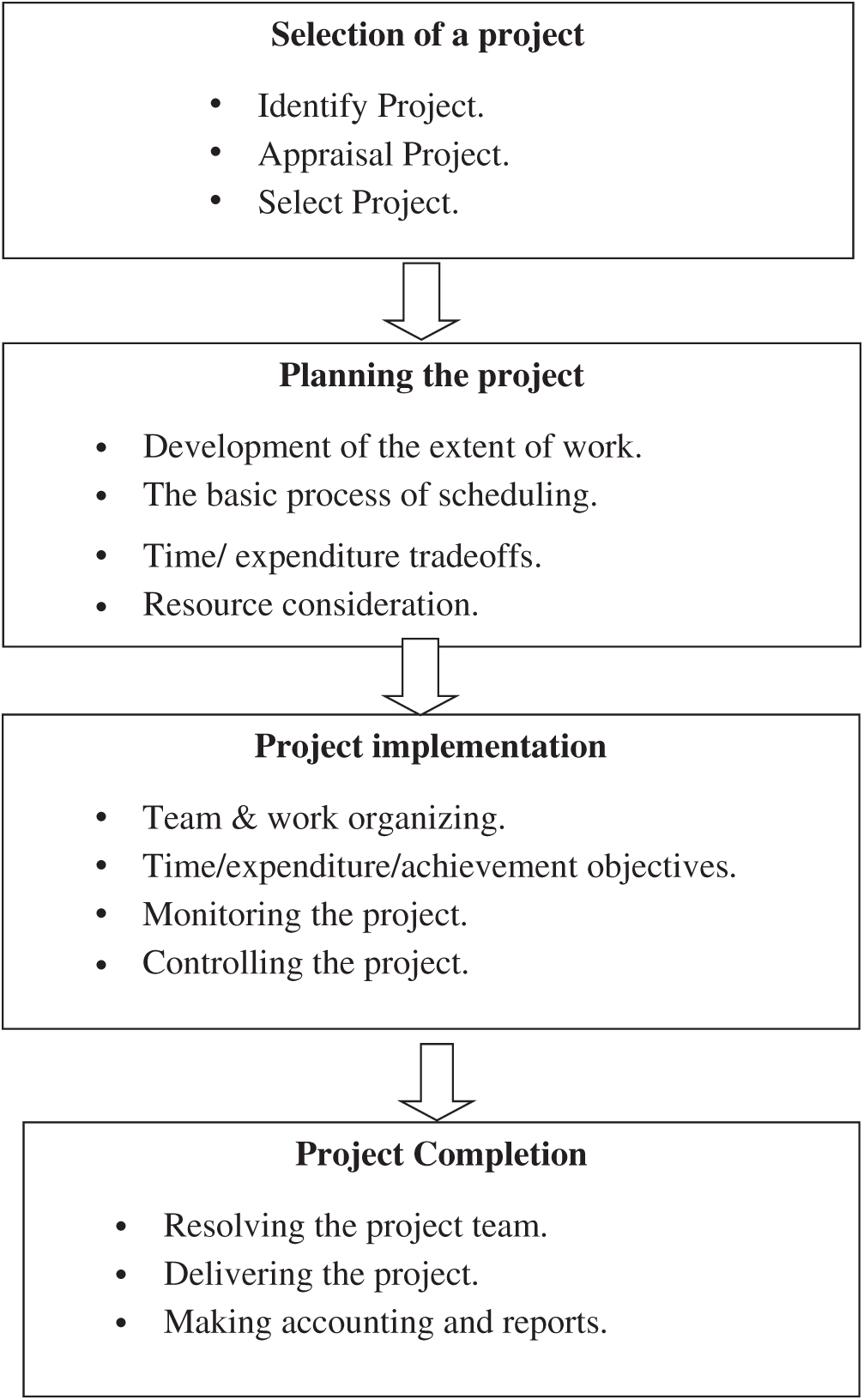
Figure 4: Project life cycle

2  Preliminaries

Neutrosophic theory was developed by the authors in [6]. Some concepts regarding neutrosophic sets are presented below.

Definition 1: Let X be a space of points and x ∈ X. A neutrosophic set A in X is defined by a truth-membership function TA(x), an indeterminacy-membership function IA(x), and a falsity-membership function FA(x), and TA(x), IA(x), and FA(x) are real standard or real nonstandard subsets of [−0, +1].

Definition 2: Let αa~, θa~, and βa~ ϵ [0, 1] and a1, a2, a3, and a4∈ R, where a1 ≤ a2≤ a3 ≤ a4. Then, a single-value trapezoidal neutrosophic number ã = 〈(a1, a2, a3, a4); αa~, θa~, βa~〉 is a special neutrosophic set on the real line set R, with truth-, indeterminacy-, and falsity-membership functions defined as:

Ta~(x)={αa~(x−a1a2−a1)(a1≤x≤a2)αa~(a2≤x≤a3)αa~(a4−xa4−a3)(a3≤x≤a4)0otherwise, (1)

Ia~(x)={(a2−x+θa~(x−a1))(a2−a1)(a1≤x≤a2)αa~(a2≤x≤a3)(x−a3+θa~(a4−x))(a4−a3)(a3≤x≤a4)1otherwise, (2)

Fa~(x)={(a2−x+βa~(x−a1))(a2−a1)(a1≤x≤a2)αa~(a2≤x≤a3)(x−a3+βa~(a4−x))(a4−a3)(a3≤x≤a4)1otherwise, (3)

where αa~, θa~, and βa~ depict the maximum truth-membership degree, the minimum indeterminacy-membership degree, and the minimum falsity-membership degree, respectively.

3  Methodology

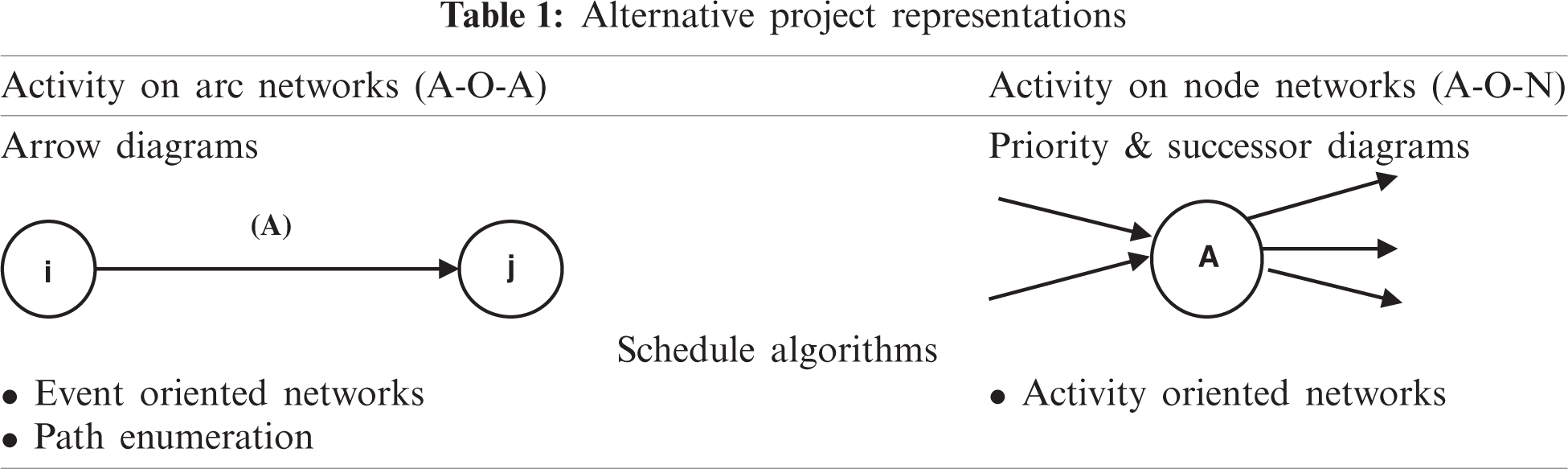
In this section, we discuss the basic neutrosophic scheduling of an activity-on-arc (AOA) network. The primary contribution of the program evaluation and review technique (PERT) and CPM is the development of project schedules, which is one of the core topics in PERT and CPM use. Projects can be broadly represented in two modes, i.e., the AOA mode and the activity-on-node mode. A number of common terms are used in network (arrow) diagrams, such as “activity,” which is a task that requires time and resources. An activity is represented by an arrow; the tail represents the start, and the head represents the completion of the activity. The length, shape, and direction of the arrows are not related to the size of the activity. The events or nodes are the beginning and endpoints of an activity and represent specific points in time. Each activity has start and finish events. It does not consume any resources and is represented by a cycle. The tail event is the (ith) event, and the head event is the (jth) event where (j > i). The path is an unbroken chain of activity arrows connecting the initial event to some other event. Arrow (network) diagrams are graphical depictions of sequentially connected arrows and nodes representing the activities and events of a project. Tab. 1 summarizes the differences between the two modes of project representation. Care is required when deciding the type of representation to use for various activities in the project network and activity durations, as we shall see how uncertain activity times or random activity durations can be accommodated in the project scheduling framework using the neutrosophic CPM methodology. The essential problem in this case is that activity durations are uncertain; time presents considerable uncertainty because the time required to complete an activity is not always easily or accurately estimated. Therefore, neutrosophic theory is used to estimate the times of activities in a project assuming various estimates based on expert opinion; these times are expressed as trapezoidal neutrosophic numbers.

Our objective is to determine the critical path, which is the longest path in the network. The critical path places a lower boundary on the project completion time so that the project cannot be accomplished at a time shorter than the length of the critical path. A project may take a longer time to accomplish, but the critical path is the minimum possible completion time of the project. The critical path also presents a means of providing control for project management. Because it determines the project duration, the critical path identifies a subset of (critical) activities that will allow the comprehensive monitoring and control of the entire project. This approach allows control of the project duration and, to a large extent, the project cost. The critical path can be determined in several ways. One of the simplest methods for determining the critical path is by listing and enumerating all network paths yielding not only the longest path but also the next longest path and all other paths in the project network. This method is useful in many other areas, such as project crashing, which simply means a project is failing because more resources than initially estimated are spent being on activities. When activity times are reduced, the critical path must be made shorter. Then, other paths become critical, and keeping track of these various other paths is important. Event-based computations on AOA networks is another method of determining the critical path. Many studies have applied fuzzy set theory to determine and calculate the critical path in AOA networks, but these works focus only on membership values [7–17]. Intuitionistic fuzzy set theory deals with both membership and non-membership values. Neutrosophic set theory developed by Smarandache treats uncertainty and ambiguity by adding indeterminacy-membership functions, in addition to truth-membership and falsity-membership functions [18–22].

The framework of the proposed model is shown in Fig. 5. Here, we present a neutrosophic event-oriented algorithm to define the critical path in an AOA network as follows:

Neutrosophic event-oriented algorithm in AOA networks

Step 1: Represent the project as an AOA network.

Step 2: Assess the activity durations as a trapezoidal neutrosophic number.

Step 3: Obtain a crisp model of the neutrosophic duration times of the activities.

The means by which any two single-value trapezoidal neutrosophic numbers are compared depends on the score and accuracy functions. Let a~ (a single-value trapezoidal neutrosophic number)=⟨(a1,b1,c1),αa~,θa~,βa~⟩, then

Score function, S(a~)=116[a1+b1+c1+d1]×(2+αa~−θa~−βa~) (4)

and

Accuracy function, A(a~)=116[a1+b1+c1+d1]×(2+αa~−θa~+βa~). (5)

The crisp model applies the score and accuracy functions of a~, in addition to the truth-membership, indeterminacy-membership, and falsity-membership functions, to represent a neutrosophic CPM model using Eqs. (1)–(5), respectively.

Step 4: Calculate the forward pass.

In any network, the forward pass calculations are performed as follows (Fig. 5):

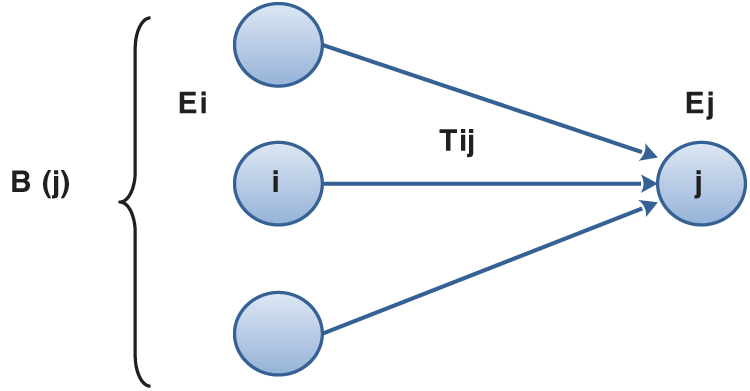
Figure 5: Forward pass calculations

● Initialization step:

E1 (or the earliest occurrence time of the first node, project start time, S) = 0

(E1=0, for all source or starting nodes) (6)

● Ej (or the earliest occurrence time of node j) = Max (Ei + Tij) for all i before node j.

(set B(j) (set of all immediately predecessor nodes of node j)). (7)

Step 5: Calculate the backward pass.

In any network, the backward pass calculations are performed as follows (Fig. 6):

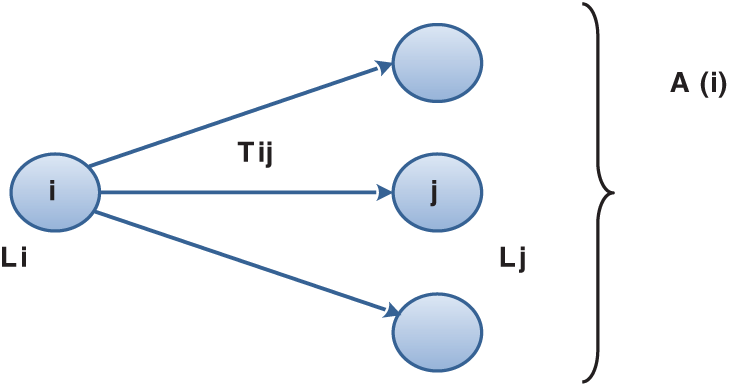
Figure 6: Backward pass calculations in AOA networks

● Initialization step:

Ln (latest occurrence of all finishing nodes)=project duration, T as determined in the forward pass. (8)

● Li (or the latest occurrence time of node i) = Min (Lj − Tij) overall successor nodes j of the node II being investigated.

(set A[i] [the set of all immediate successor nodes of node i]). (9)

Step 6: Calculate the activity schedule from event times.

Determination of an activity schedule from the event times, the forward pass, and the backward pass gives us information on the Early Start (ES), Early Finish (EF), Late Start (LS), and Late Finish (LF) for all activities in the network (Fig. 7).

Figure 7: Event time calculations

FORWARD PASS:

ES of activity ij=ES(ij)=Ei (10)

EF of activity ij=EF(ij)=ES(ij)+Tij (11)

BACKWARD PASS:

LF of activity ij=LF(ij)=Lj (12)

LS of activity ij=LF(ij)−Tij (13)

Step 7: Calculate the event slack and float.

•   Event slack (Fig. 8)

Figure 8: Event slack calculations

Slack on node i=Li−Ei. (14)

Slack on node j=Lj−Ej. (15)

● Activity float

In general, all activities have both predecessors and successors. Activity floats depend on how these elements accommodate the activity. Four types of float are possible. If the successors are performed as late as possible and predecessors are performed as early as possible, giving the maximum, a total float is obtained. If the successors and predecessors are performed as early as possible, a free float is obtained. If the predecessors are performed as late as possible and successors are performed as early as possible, leaving very little time left for other activities, an independent float is obtained. Finally, when the successors and predecessors are performed as late as possible, a safety float is obtained. These four types of floats are shown in Fig. 9.

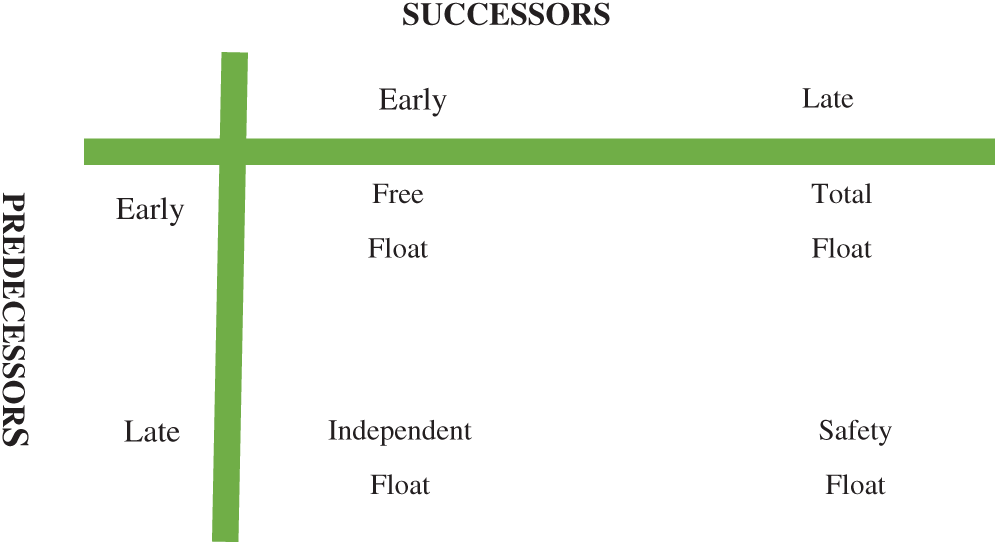
Figure 9: Interpretation of four types of floats

Total Float=TF(ij)=Lj−Ei−Tij=LS−ES=LF−EF. (16)

Safety Float=SF(ij)=Lj−Li−Tij=TF−Slack on preceding node. (17)

Free Float=FF(ij)=Ej−Ei−Tij=TF−Slack on succeeding node. (18)

Independent Float=IF(ij)=Max(0,Ej−Li−Tij)=Max(0,Total float−Slack on succeeding and preceding nodes). (19)

Step 8: Determine the critical path, which consists of activities in which the four types of floats are equal to zero, in the AOA network representation of the project. The framework of the proposed algorithm is summarized in Fig. 10.

Figure 10: Framework of the proposed model

4  Illustrative Example

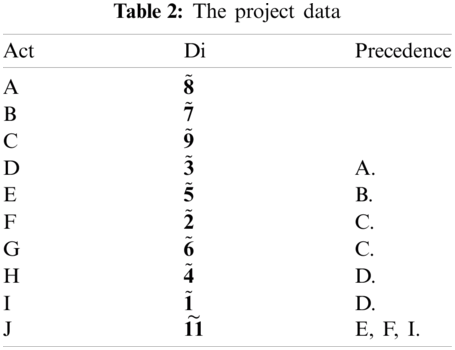
Consider a project of publishing a new children’s book that has 10 activities: (A) assigning lunch group members, (B) completing a questionnaire, (C) scheduling interviews, (D) designing and ordering marketing materials, (E) setting a kick-off book launch meeting, (F) preparing book profit and loss statements, (G) planning the author’s travel itinerary, (H) completing the book launch form, (I) preparing book sales, and (J) distributing the internal marketing materials. The project data are summarized in Tab. 2. Here, the task is to determine the critical path and compute the completion time of the project.

Solution:

a. Apply the proposed neutrosophic event-oriented algorithm as discussed above.

•   The network representation is shown in Fig. 11.

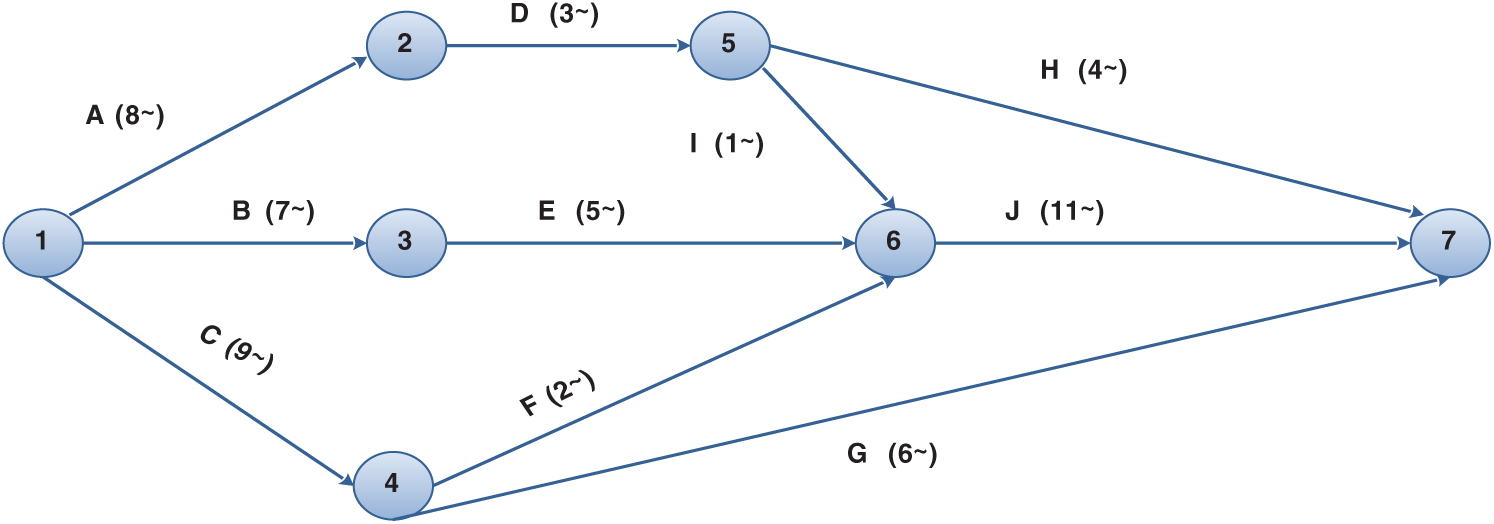
Figure 11: AOA network representation

b. Estimate the duration of activities as trapezoidal neutrosophic numbers. Let

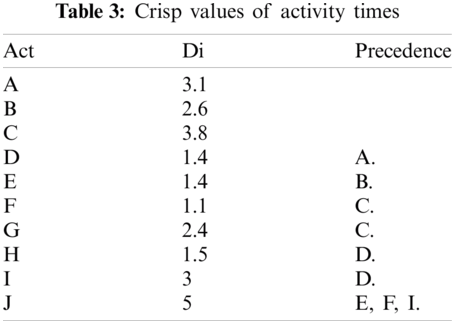
c. Compute the crisp values and score functions of each trapezoidal neutrosophic number by using Eq. (4). The results of these calculations are presented in Tab. 3.

d. Calculate the forward pass using Eqs. (6) and (7) and place the results in a rectangle above each node, as shown in Fig. 12.

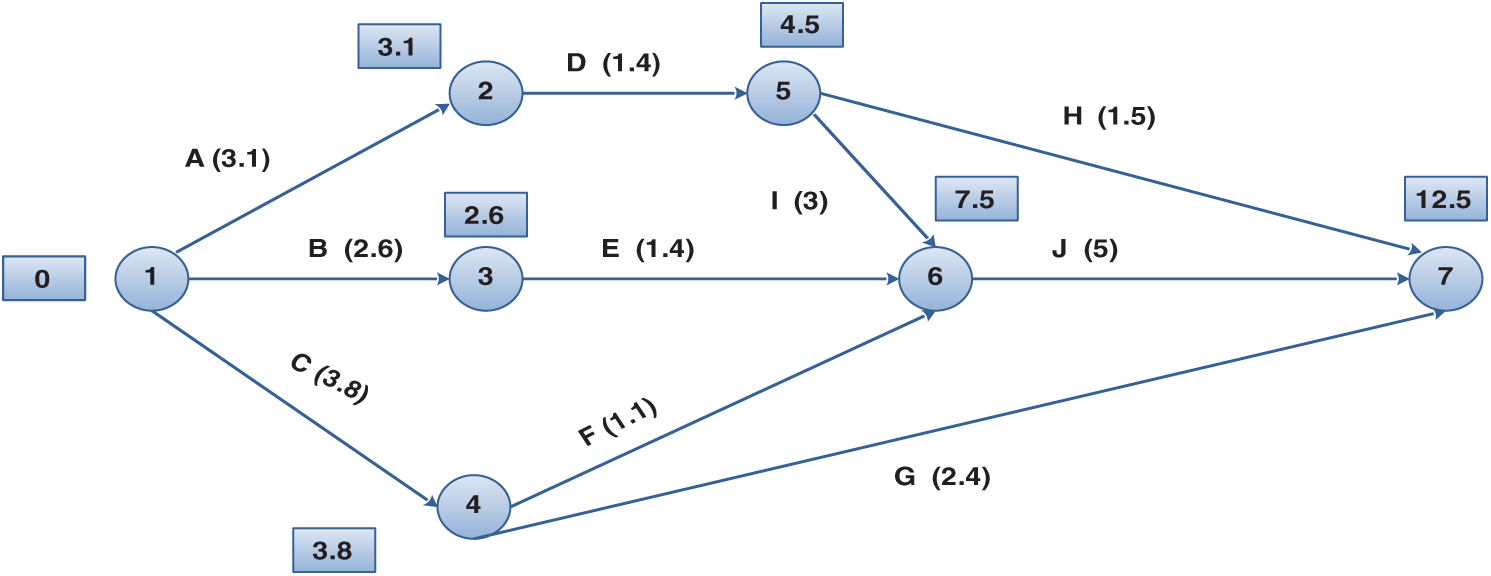
Figure 12: Forward pass calculations

e. Calculate the backward pass using Eqs. (8) and (9) and place the results above each node, as shown in Fig. 13.

Figure 13: Backward pass calculations

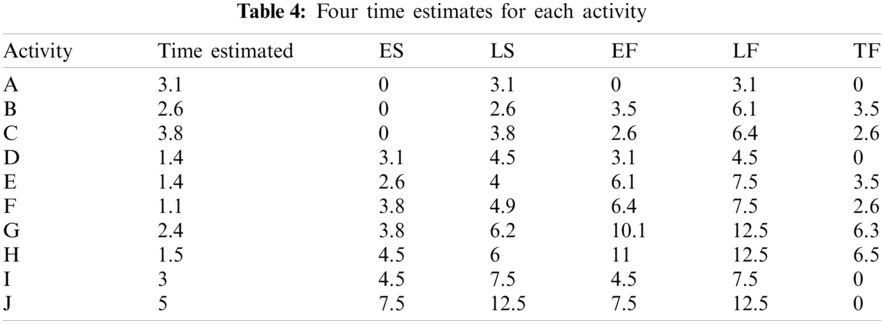
f. Calculate four times (ES, EF, LS, and LF) for each activity in our illustrative example by using Eqs. (10)–(13). The results of these calculations are presented in Tab. 4.

g. Calculate four types of floats for each activity using Eqs. (14)–(19). The results of the float calculations are shown in Tab. 5.

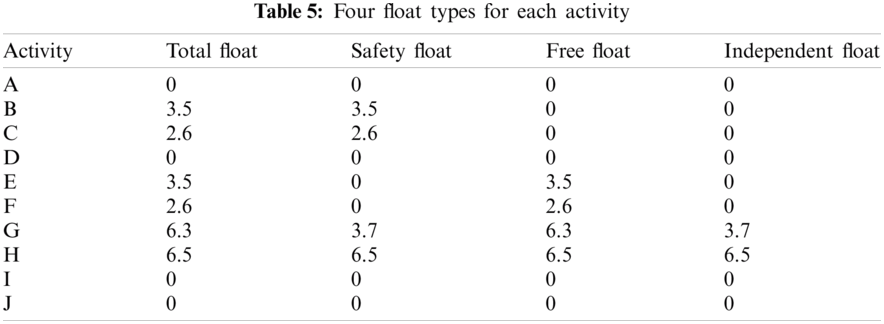
h. Determine the critical path after completing the computations of all types of floats; here, the critical path consists of activities in which the four types of floats equal to zero.

From Tab. 4, we know that the critical activities are A, D, I, and J and that the four types of floats for these activities are equal to zero. The critical path is A–D–I–J, as shown in Fig. 14. The expected project completion time is TA + TD + TI + TJ = 12.5

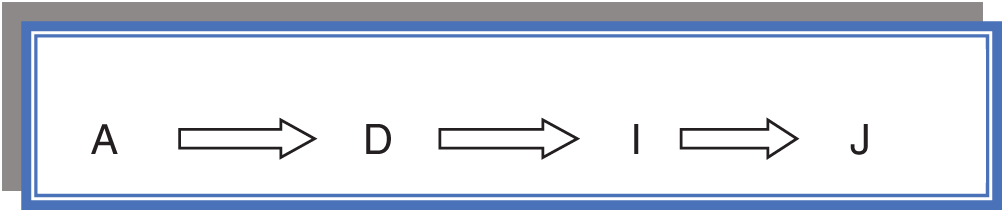
Figure 14: The critical path

We can also track and obtain the critical path using a Gantt chart, a method to represent the activity scheduling of a project. In the present example, activities A, D, I, and J are critical activities because they have no floats. These critical activities have a fixed duration and must occupy time slots as shown in Fig. 15. In addition, we find that the duration times of these activities are equal to the completion time of the project. However, the remaining activities, e.g., activity H, can be performed early or late, as shown in the Gantt chart. If activity H is performed early, it starts at 4.5 and finishes at 6 units of time; if H is performed late, it starts at 11 with a flexibility equal to 5 units of time. This situation is also true for all other non-critical activities (i.e., B, C, E, F, G, and H), which similarly have a great deal of flexibility, as shown in the Gantt chart. The critical path in our example Gantt chart is indicated by red lines.

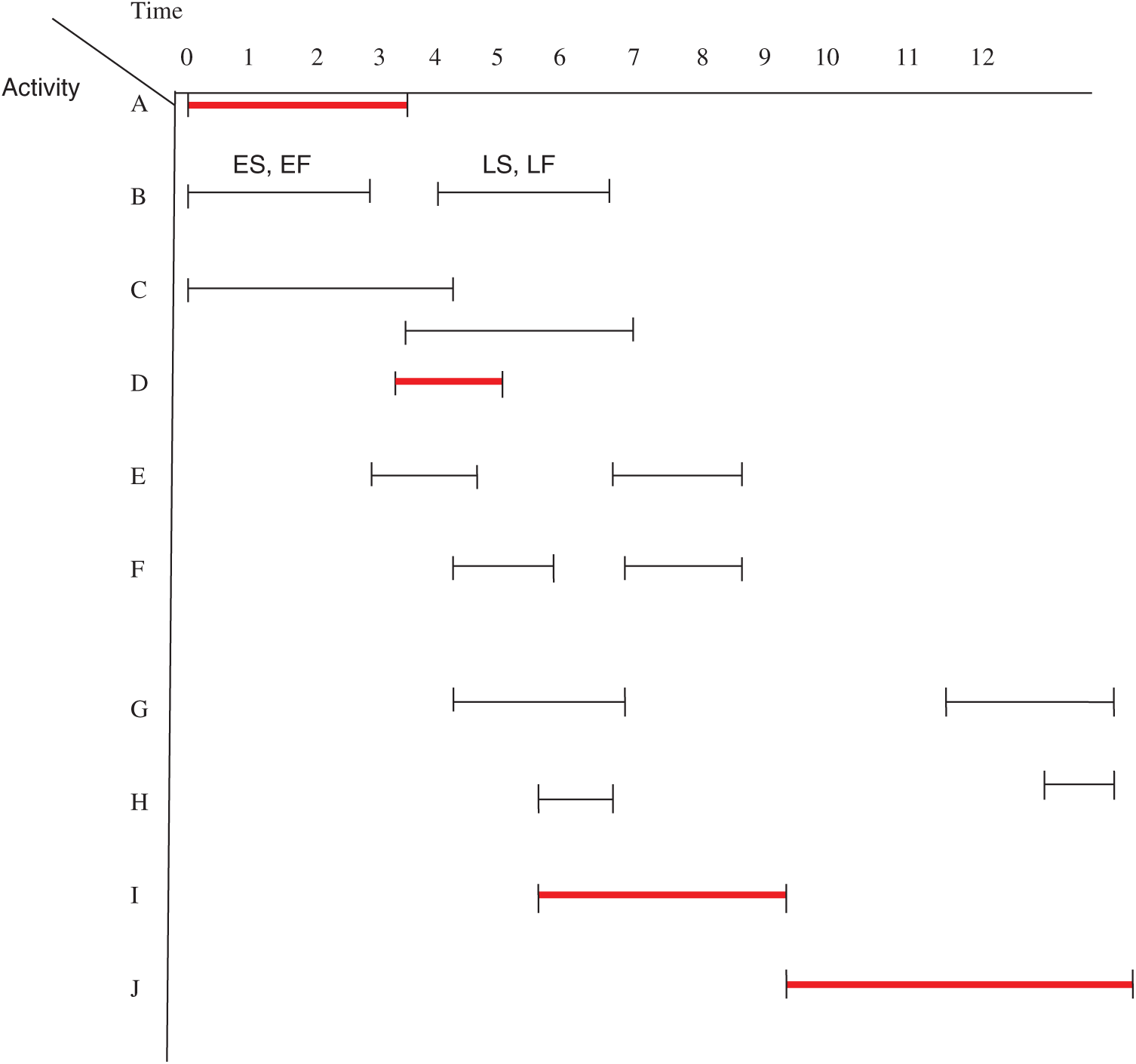
Figure 15: Tracking of the critical path through the Gantt chart of a project

5  Conclusion

Little emphasis on the clarity of decision-making processes in daily life real-world problems has been made, and the resulting decisions are always ambiguous and uncertain. Neutrosophic sets have been introduced as a generalization of fuzzy, intuitionistic fuzzy, and crisp sets to overcome the ambiguity surrounding real-world problems. Neutrosophic elements are expressed using not only truth- and falsity-membership functions but also indeterminacy-membership functions. In this paper, we solved the problem of finding the critical path in AOA networks by using a neutrosophic event-oriented algorithm. The activity time estimates are presented as trapezoidal neutrosophic numbers, and a crisp model of the problem was obtained by applying score and accuracy functions.

Funding Statement: This work was supported by the Soonchunhyang University Research Fund.

Ethical Approval: This article does not contain any studies with human participants or animals performed by any of the authors.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  J. P. Lewis, Project Planning, Scheduling, and Control: The Ultimate Hands-on Guide to Bringing Projects in on Time and on Budget: The Ultimate Hands-on Guide to Bringing Projects in on Time and on Budget. New York, New York, United States: McGraw Hill Professional, 2010. [Google Scholar]

 2.  F. Harrison and D. Lock, Advanced Project Management: A Structured Approach. London: Routledge, 2017. [Online]. Available: https://doi.org/10.4324/9781315263328. [Google Scholar]

 3.  J. W. Hinze, Construction Planning and Scheduling. vol. 228. Upper Saddle River, NJ: Pearson/Prentice Hall, pp. 229, 2004. [Google Scholar]

 4.  R. Burke, Project Management: Planning and Control Techniques. New Jersey, USA: Wiley, 2013. [Google Scholar]

 5.  H. Kerzner and H. R. Kerzner, Project Management: A Systems Approach to Planning, Scheduling, and Controlling. New Jersey, United States: John Wiley & Sons, 2017. [Google Scholar]

 6.  M. Abdel-Basset, M. Mohamed, F. Smarandache and V. Chang, “Neutrosophic association rule mining algorithm for big data analysis,” Symmetry, vol. 10, no. 4, pp. 106, 2019. [Google Scholar]

 7.  M. Masmoudi and A. Hait, “Project scheduling under uncertainty using fuzzy modeling and solving techniques,” Engineering Applications of Artificial Intelligence, vol. 26, no. 1, pp. 135–149, 2013. [Google Scholar]

 8.  M. Hapke, A. Jaszkiewicz and R. Slowinski, “Fuzzy project scheduling system for software development,” Fuzzy Sets and Systems, vol. 67, no. 1, pp. 101–117, 1994. [Google Scholar]

 9.  S. P. Chen and Y. J. Hsueh, “A simple approach to fuzzy critical path analysis in project networks,” Applied Mathematical Modeling, vol. 32, no. 7, pp. 1289–1297, 2008. [Google Scholar]

10. S. P. Chen, “Analysis of critical paths in a project network with fuzzy activity times,” European Journal of Operational Research, vol. 183, no. 1, pp. 442–459, 2007. [Google Scholar]

11. N. R. Shankar, V. Sireesha and P. P. B. Rao, “An analytical method for finding critical path in a fuzzy project network,” International Journal of Contemporary Mathematical Sciences, vol. 5, no. 20, pp. 953–962, 2010. [Google Scholar]

12. G. S. Liang and T. C. Han, “Fuzzy critical path for project network,” Information and Management Sciences, vol. 15, no. 4, pp. 29–40, 2004. [Google Scholar]

13. N. R. Shankar, V. Sireesha and P. P. B. Rao, “An analytical method for finding critical path in a fuzzy project network,” International Journal of Contemporary Mathematical Sciences, vol. 5, no. 20, pp. 953–962, 2010. [Google Scholar]

14. S. Chanas and P. Zieliński, “Critical path analysis in the network with fuzzy activity times,” Fuzzy Sets and Systems, vol. 122, no. 2, pp. 195–204, 2001. [Google Scholar]

15. C. T. Chen and S. F. Huang, “Applying fuzzy method for measuring criticality in project network,” Information Sciences, vol. 177, no. 12, pp. 2448–2458, 2007. [Google Scholar]

16. S. Elizabeth and L. Sujatha, “Fuzzy critical path problem for project network,” International Journal of Pure and Applied Mathematics, vol. 85, no. 2, pp. 223–240, 2013. [Google Scholar]

17. F. A. Zammori, M. Braglia and M. Frosolini, “A fuzzy multi-criteria approach for critical path definition,” International Journal of Project Management, vol. 27, no. 3, pp. 278–291, 2009. [Google Scholar]

18. M. Abdel-Basset, A. Gamal, R. K. Chakrabortty and M. Ryan, “A new hybrid multi-criteria decision-making approach for location selection of sustainable offshore wind energy stations: A case study,” Journal of Cleaner Production, vol. 280, no. 9, pp. 124462, 2021. [Google Scholar]

19. M. Abdel-Basset, G. Manogaran and M. Mohamed, “A neutrosophictheory based security approach for fog and mobile-edge computing,” Computer Networks, vol. 157, no. 2, pp. 122–132, 2019. [Google Scholar]

20. M. Abdel-Basset, A. Gamal, R. K. Chakrabortty and M. J. Ryan, “Evaluation of sustainable hydrogen production options using an advanced hybrid MCDM approach: A case study,” International Journal of Hydrogen Energy, vol. 46, no. 5, pp. 4567–4591, 2021. [Google Scholar]

21. N. A. Nabeeh, M. Abdel-Basset, H. A. El-Ghareeb and A. Aboelfetouh, “Neutrosophic multi-criteria decision making approach for iot-based enterprises,” IEEE Access, vol. 7, pp. 59559–59574, 2019. [Google Scholar]

22. A. Kumar, K. Rajalakshmi, S. Jain, A. Nayyar and M. Abouhawwash, “A novel heuristic simulation-optimization method for critical infrastructure in smart transportation systems,” International Journal of Communication Systems, vol. 33, no. 11, pp. e4397, 2020. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.