Computers, Materials & Continua DOI:10.32604/cmc.2022.017971
Article

A Cost-Effective Approach for NDN-Based Internet of Medical Things Deployment

Syed Sajid Ullah1, Saddam Hussain1, Abdu Gumaei2,3,*, Mohsin S. Alhilal4, Bader Fahad Alkhamees4, Mueen Uddin5 and Mabrook Al-Rakhami2

1Department of Information Technology, Hazara University Mansehra, KPK, 21120, Pakistan
2Research Chair of Pervasive and Mobile Computing, Department of Information Systems, King Saud University, Riyadh, 11543, Saudi Arabia
3Department of Computer Science, Faculty of Applied Sciences, Taiz University, Taiz, 6803, Yemen
4Department of Information Systems, College of Computer and Information Sciences, King Saud University, Riyadh, 11543, Saudi Arabia
5Digital Science, Faculty of Science, Universiti Brunei Darussalam, Jln Tungku link, Gadong, Brunei, BE1410, Darussalam
*Corresponding Author: Abdu Gumaei. Email: agumaei.c@ksu.edu.sa
Received: 19 February 2021; Accepted: 30 April 2021

Abstract: Nowadays, healthcare has become an important area for the Internet of Things (IoT) to automate healthcare facilities to share and use patient data anytime and anywhere with Internet services. At present, the host-based Internet paradigm is used for sharing and accessing healthcare-related data. However, due to the location-dependent nature, it suffers from latency, mobility, and security. For this purpose, Named Data Networking (NDN) has been recommended as the future Internet paradigm to cover the shortcomings of the traditional host-based Internet paradigm. Unfortunately, the novel breed lacks a secure framework for healthcare. This article constructs an NDN-Based Internet of Medical Things (NDN-IoMT) framework using a lightweight certificateless (CLC) signature. We adopt the Hyperelliptic Curve Cryptosystem (HCC) to reduce cost, which provides strong security using a smaller key size compared to Elliptic Curve Cryptosystem (ECC). Furthermore, we validate the safety of the proposed scheme through AVISPA. For cost-efficiency, we compare the designed scheme with relevant certificateless signature schemes. The final result shows that our proposed scheme uses minimal network resources. Lastly, we deploy the given framework on NDN-IoMT.

Keywords: Internet of Medical Things; healthcare; Named Data Networking

1  Introduction

The Internet of Medical Things (IoMT) is an IoT subsidiary capable of compiling all medical things for collecting, analyzing, and exchanging patient-related data over the traditional IP-based Internet paradigm [1]. The data such as respiration rate, blood pressure, electrocardiogram (ECG), and body temperature, etc., can be sensed by biomedical sensors and managed via edge devices (i.e., smartwatches, computers, smartphones, or a specific embedded device) [2,3]. Additionally, IoMT can also monitor ecological conditions such as room conditions, laboratory transition time, treatment time, and patient rates from staff.

The edge devices are connected to gateways via short-distance wireless technologies such as WiFi, ZigBee, and Bluetooth Low Energy (BLE). BLE has robust features like low power consumption, unlicensed band, and moderate data rate, making it a highly desirable option for attaching wearable sensor nodes [4]. In a healthcare automation system, patient details are maintained in an electronic health table, accessible to medical experts when the patients visit a hospital. Yet, IoMT exchanges data using conventional models and protocols with the risks allied with mobility, privacy, and security.

To tackle this, a new Internet model known as Named Data Networking (NDN) has been proposed [5]. NDN paradigm is specially designed to add some interesting features such as in-network caching, named based routing, and mobility support, that provides efficient information access to end-users [6,7]. Considering the positives of NDN, some frameworks for NDN-based healthcare have been introduced [8–10]. However, there is no concrete cryptographic scheme that can secure NDN-IoMT communications, but the authentication information that NDN-IoMT needs can be achieved through a digital signature.

The digital signature has been widely adopted for plenty of schemes. Conversely, the traditional Public Key Cryptography needs additional support from the Public Key Infrastructure (PKI) [11]. In PKI, a third party, called Certificate Authority (CA), allocates and distributes customer authentication. Unfortunately, PKI has certificate management issues like distribution, revocation, and verification.

In 1984, Shamir [12] presented Identity Based Cryptography (IBC) to solve the PKI's problems. IBC selects each party's IP address, email address, etc., as his/her public key without CA verification. A third party called the private Key Generation Center (KGC) calculates and sends participants' secret keys via a private channel. However, this makes KGC a target for rivals, commonly referred to as the Key Escrow Problem (KEP).

To solve this problem, Al-Riyami and Paterson [13] construct novel cryptography known as Certificateless Cryptography (CLC). The new cryptosystem is born from the achievements of IBC and PKC. CLC has introduced a unique concept for calculating private and public keys using KGC's partial private key (PPK). CLC allows each user to have a set of keys, such as a secret key and a PPK. The secret value of each participant is randomly selected, but KGC calculates the PPK using its master secret key [14].

Since most IoT devices have limited system power and communication bandwidth, we aim to decrease the complexity of resource-limited devices of NDN-IoMT. Currently, bilinear pairing, ECC, and HCC are providing services for effective communication. However, both bilinear pairing and ECC are not effective for resource-limited devices [15].

Due to the aforementioned discussion, we are motivated to use HCC which uses a smaller key compared to bilinear pairing, and ECC which fits NDN-IoMT environments with limited computing power, storage space, and bandwidth [16]. In this work, the communication efficiency and computational cost of the CLC signature scheme are improved by proposing a more efficient CLC signature scheme for NDN-IoMT using HCC.

We summarize the main contributions of our proposed work as follows:

•   We present the basic syntax of our scheme (NDN-IoMT).

•   We provide a concrete construction for the proposed NDN-IoMT scheme.

•   We provide detailed security proof under the ROM, which shows that the given scheme can resist both Type−I(TI) and Type−II (TII) adversaries.

•   We compare the designed scheme with previously recommended solutions based on computational time and communicational overhead, and the results show that the proposed scheme is efficient.

•   We present a detail deployment of our proposed scheme on NDN-IoMT.

•   Finally, we simulate our proposed scheme with help of AVISPA.

The paper is organized as follows. Section 2 provides the related work. Section 3 provides preliminaries. Section 4 presents the construction of our scheme. Section 5 comprises of security analysis while Section 6 is dedicated to comparative analysis. Section 7 shows the robust deployment of our scheme. Finally, in Section 8 we conclude our research.

2  Related Work

The work related to our scheme divided into two parts i.e., NDN-based healthcare schemes and CLC schemes.

2.1 Healthcare Schemes for NDN Network

Saxena et al. [8] provided an NDN-based health setup. The given solution can find network-based healthcare. Later, Saxena and Raychoudhury [9] provided an alternative NDN-based scheme for emergency messages in healthcare. The recommended scheme aims to authenticate the source of emergency messages. Unfortunately, in both solutions, the authors do not provide a definitive security plan for healthcare in NDN settings.

Recently, Wang and Kai [10] designed a monitoring model for protecting NDN-enabled healthcare using Edge and cloud services. The authors took the advantage of NDN to improve the effectiveness of clinical data. However, due to heavy map-to-map functions of bilinear pairing, the scheme was inefficient for healthcare systems.

2.2 Certificateless Signature Solutions

He et al. [17] constructed a pairing-free CLC signature scheme based on ECC, hence affected by high computation and communication costs [14]. Moreover, Tsai et al. [18] and Huang [19] claim that the scheme was not secure and improved. Gong and Li [20] found that the designed approach of Tsai et al. [18] was not secure, and construct a whole CLC signature scheme built on ECC.

After two years, Yeh et al. [21] prove that the designed approach of Gong and Li [20] was insecure. Moreover, the authors presented an efficient CLC signature scheme constructed on ECC. Wang et al. [22] present a new and improve version of Yeh et al. [21]. Later, Wang et al. [23] launch a CLC signature approach for limited-resource devices.

Yeh et al. [24] constructed a lightweight CLC signature approach for IoT-based smart objects. However, the security complexity of the given approach was constructed on ECC, which is not an ideal choice for devices with limited resources.

One year later, Karati et al. [25] launched a lightweight CLC signing approach for the Industrial Internet of Things (IIoT). Zhang et al. [26] found that this scheme was insecure against internal and external adversaries. Additionally, its security is constructed on bilinear pairing, which makes it costly for the IIoT infrastructure.

In this context, Pakiniat and Vanda [27], claim that the scheme of [25], is not secure, so they constructed a modified version. Unfortunately, the improved scheme was built on ECC. Zhang et al. [26] present a modified version of [25], by tossing a concrete CLC signing approach for IIoT via ECC. Later, Rezaeibagha et al. [28] introduce an improved version of [25], by throwing out an efficient approach using the bilinear pairing for IIoT. After that, Thumbur et al. [29] developed a CLC signing scheme using ECC. Although the given scheme reduces the cost complexities to some extent, it still needs some improvement as it is constructed on ECC [14].

3  Preliminaries

3.1 Hyperelliptic Curve Discrete Logarithm Problem (HDLP)

Suppose β∈{1,2,….(n−1)} and W= β.D, finding β and W is called HDLP.

3.2 Generic Syntax

The given scheme includes seven algorithms, as mentioned below.

•   Setup: The Network Manager (NM) runs this algorithm. It takes the security parameter (l), generates the master secret key (K) and the master public key (S), and sets the system public parameter (Q).

•   Extraction of PPK: This step is executed by the NM. It takes the identities (IDP),K, S, and system public parameter (Q) as in input and generates the users PPK (O).

•   Set Secret Values: In this step, both entities set their secret values.

•   Key Generations: This algorithm runs on the user's side and produces a private key (Ptp) and a public key (Pkp).

•   Sign: This algorithm is executed by the provider. It takes the content c, IDp, Pkp, and υ as in input and generates a signed tuple (Ω).

•   Verification: This algorithm is performed by the consumer. It takes content (c), Pkp,IDp, and Ω as input to verify the signed content (Ω).

3.3 Threat Model

For our security explanation, we consider two types of adversaries: Type−I (TI) and Type−II (TII).

•   Type−I (TI) Adversary: The TI adversary is generally known as outsider adversary which can request for the participants public key for the replacement of its own.

•   Type−II (TII) Adversary: The TI adversary is generally known as insider adversary or malicious KGC which can make a participants PPK with help of a master secret key. However, it is unable to replace users’ public keys.

4  Proposed Scheme for NDN-IoMT

4.1 Design Network Model

For NDN-IoMT environments, the intended data must not be changed, and the source of data is reliable and authentic during the entire transmission. Hence, our aim is concentrated on the authenticity and integrity of NDN-IoMT data while concurrently aiming to minimize the bandwidth and computational cost of NDN-IoMT devices. Fig. 1 shows our network model, containing four elements: a Network Manager (NM), consumers, producers, and NDN routers.

•   Network Manager (NM): This NM is primarily responsible for establishing a secure connection between consumers and producers. Moreover, the NM produces system parameters and PPKs.

•   Consumer: Here in the given network model, a consumer can be an IoMT device such as a smartphone, hospital, ambulance, patient, etc., or can be a user that can request some content related to Medical.

•   Provider: Here in the given network model, a provider can be an IoMT device such as a smartphone, hospital, ambulance, patient, etc., or can be a user that can provide content related to Medical.

•   NDN Routers: NDN routers are in-between nodes that carry interest with caching capability.

For successful registration, both participants send their respective identities to the NM as illustrated in Fig. 3. Next, NM produces a PPK for participants and delivers it using a secure channel. Upon receipt, both participating parties take the PPK with their chosen secret value to create their keys (private and public).

Now, whenever the consumer requests some content, the intermediate routers forward the request to a potential content provider. The content provider signs the requested content and forwards it to the intended receiver. The intermediate router R1 caches the forwarded content utilizing its CS. After getting the requested content, the consumer can verify the validity of the content.

4.2 Construction of the Designed IoMT-NDN Scheme

The designed algorithm is a generalized version of G. Thumbur et al. [29], as it is based on HCC. The notations used in our proposed scheme are given in Tab. 1.

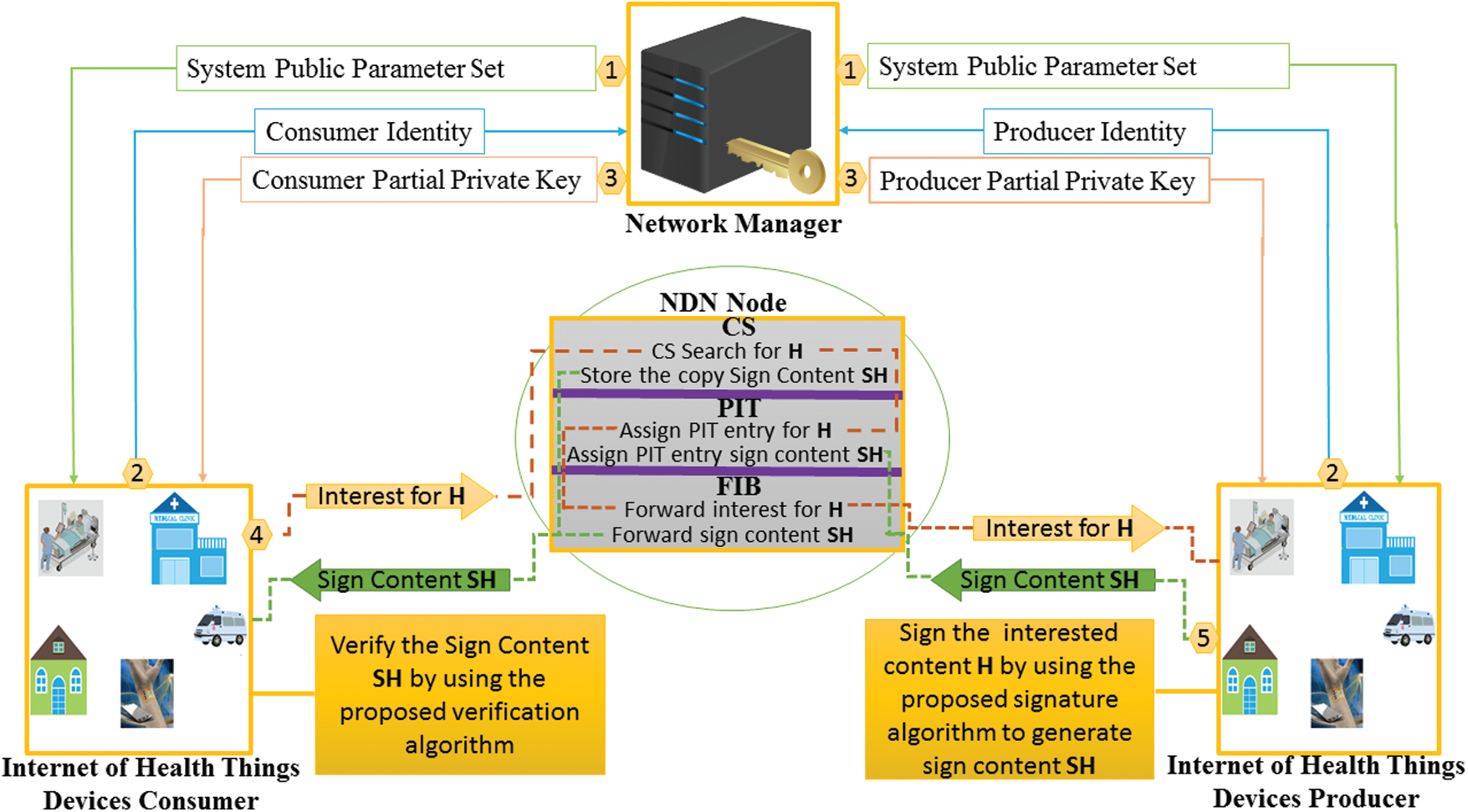
Figure 1: Proposed network model for NDN-IoMT

Setup

The Network Manager (NM) initializes the system to generate K, S and Q using a security parameter (l) to complete the subsequent steps.

•   Select (D) as a devisor of HCC of order n

•   Select K∈{1,2,…,(n−1)}and calculate S=K.D

•   Choose three secure hash functions (SHA−512) = H1, H2, H3

•   Initialize public parameter set Q = {n,H0,H1,H2,S,D}

The NM then publishes Q and keeps K secret.

Partial Private Key Setting

After receiving the identities IDP, both participants complete the subsequent computations to generate PPK keys for both participating entities.

•   The KGC randomly picks Rn ∈{1,2,…,(n−1)}

•   Compute private number Pn = Rn. D

•   Compute h0= H0 (IDp ,S,Pn, Ꞃ)

•   Compute λ= (Rn + Kh0) mod n

•   Produce a PPK O = (λ,Pn) for both participants.

Later the participants can check the validity of O from λ.D = Rn+h0S.

Key Settings

The participants obtain the computed PPKs from the NM and set their secret values. They then compute their private and public keys, respectively.

The participants pick a number at random υ∈{1,2…,(n−1)}, and set it as their secret values. Further, the user’s computers calculate V=υ.D.

Then the users set the private key (Ptp) and public keys (Pkp) by performing the following computations.

h1= H1(IDp,V)

Υ=Pn+h1V

Finally, the users set Ptp= (λ,υ) and Pkp= (Υ,Pn)

Sign

Here, the content provider produces signed content, by doing the following computations.

•   Pick a number at random ϑ∈{1,2,…(n−1)}

•   Compute private number δ=ϑ.D.

•   Compute h1= H1(IDp,V)

•   Compute h2= H2 (c, IDp, Pkp, δ, Ꞃ)

•   Compute ω = ϑ + h2(λ+h1.υ) mod n

Finally, the provider generates signed content Ω = (δ,ω) and delivers it to the requested consumer.

Verify

Here, the consumer takes Q, Pkp, IDp, Ω = (δ, ω), and c to verify the signature (Ω) on the received tuple by doing the following steps.

•   Compute h0 = H0 (IDp, S,Pn, Ꞃ)

•   Compute h2 = H2 (c, IDp, Pkp, δ, Ꞃ)

•   Finally, verify the equation ω.D = δ + h2(Υ+h0.S). If it holds, accept the content. Otherwise reject the content.

Correctness

ω.D = ϑ + h2(λ+h1.υ)

= (ϑ + h2(λ+h1.υ)). D

= (ϑ + h2((Rn + h0K )+h1.υ)). D

= (ϑ.D + h2((Rn.D + h0K.D )+h1.υ.D))

= δ+ h2Pn + h0S+h1.V

= δ+ h2(Υ +h0S)

5  Threat Model and Security Analysis

Here, we performed the security analysis of the given scheme against TI and TII adversaries by supposing the hardness of HDLP. For the security model, we follow the model presented by Thumber et al. [29].

Theorem I:

Under HDLP, the given scheme is existentially unforgeable against TI.

Proof:

Suppose TI can forge a valid signature with the help of a polynomial algorithm (ψ). Now we construct ψ that can solve the HDLP using TI. For (D, Υ =KD) of HDLP, the aim of ψ is to find K. Let ψ take IDp∗ as a target identity of TI on content c∗.

Setup Phase:

ψ sets S =Υ= KD and executes the setup algorithm.

Query Phase:

In this phase, TI requests with multiple queries which should be responded to by ψ. Initially, ψ maintains empty lists such as l0, l1, l2, lCU, and lpsk.

Queries on H0

When TI requests a query on H0 (IDp, S, Pn), if the tuple already exists in l0, ψ delivers h0. If not, ψ selects h0∈ {1,2,…,(n−1)}, sets H0 (IDp, S, Pn, Ꞃ)= h0, delivers it to TI, and adds the given (IDp, S, Pn, h0) into l0.

Queries on H1

When TI requests a query on H1 (IDp, V), if the tuple already exists in l1, ψ delivers h1. If not, ψ selects h1∈ {1,2,…,(n−1)}, sets H1 (IDp,V)=h1 , delivers it to TI, and adds the given (IDp,V,h1) into l1.

Queries on H2

When TI requests a query on H2 (c, IDp, Pkp, δ), if the tuple already exists in l2, ψ delivers h2. If not, ψ selects h2∈ {1,2,…,(n−1)}, sets H2 (c, IDp, Pkp, δ)= h2, delivers it to TI, and adds the given H2 (c, IDp, Pkp, δ,η,h2) into l2.

Reveal Partial Secret Key Oracle

When TI requests a query on PSK (O), if the tuple already exists in lpsk, ψ delivers O = (λ,Pn). If O=O∗, ψ aborts. Otherwise, ψ selects α,β∈ {1,2,…,(n−1)} and sets λ = α, H0 (IDp, S, Pn) = β, and Pn = αD−βS. ψ , then adds (IDp, S,Pn, β) to l0 and (IDp, Pn, λ) to lpsk.

Create User Oracle

When TI requests a query on CU (IDp), if the public key Pkp = (Υ,Pn) already exists in lCU, ψ delivers it to TI. Otherwise, ψ does the following steps.

1.    If IDp=IDp∗, ψ selects α,β,z,υ∈ {1,2,…,(n−1)} and sets Pn = αD, H0 (IDp, S,Pn,η) = β, V = υ.D, and H1(IDp,V) = z. Now ψ sets Υ=Pn+h1 V = αD+z (υ.D) and adds (IDp, S,Pn, Ꞃ, β) to l0, (IDp,V,z) to l1, and (IDp,Υ,Pn,υ,⫝) to lCU. Finally, ψ delivers the public key Pkp= (Υ,Pn) to TI.

2.    If IDp≠IDp∗, ψ recovers (IDp, Pn, λ) from lpsk. ψ, sets V = υ.D, H1(IDp,V) = z (z,υ∈ {1,2,…,(n−1)} and Υ=Pn+z V = Pn+h1V. ψ produces Pkp= (Υ,Pn) as a public key and adds (IDp,V,z) to l1 and (IDp,Υ,Pn,υ,λ) to lCU.

Reveal Secret Value Oracle

When TI requests a query on RSK (IDp), ψ performs the following steps.

If  IDp=IDp∗, ψ aborts. Otherwise, ψ recovers (IDp,Υ,Pn,υ,λ) from lCU and sends υ to TI. If such tuple does not exist in lCU, ψ does a query on CU (IDp) to generate (υ,Υ) and add it to lCU. ψ, then delivers υ the secret value.

Reveal Public-Key Oracle:

If TI desires to replace the respective public key Pkp= (Υ,Pn) of IDp with Pkp∗= (Υ∗,Pn∗), then ψ finds (IDp,Υ,Pn,υ,λ) from lCU and updates Υ with Υ∗ and Pn withPn∗. Finally, ψ sets υ∗=⫝ and λ=⫝.

Hereafter, the replaced tuple looks like (IDp, Υ∗,Pn∗, ⫝,⫝).

Signing Oracle.

When TI requests a sign query on (IDp, c), ψ performs the following steps.

1.    If IDp≠IDp∗, te ψ recovers (IDp, Pn,S,η,h0),(IDp,V,h1), and (IDp,Υ,Pn,υ,λ) from l0 ,l1, and lCU respectively, and produces a valid signature using the following steps.

•   Select ϑ,h2,ε {1,2,…,(n−1)}, compute ω = ϑ + h2(λ+h1.υ) mod n, and compute δ = ϑ.D. ψ, then returns Ω = (δ, ω) to AV1 and inserts (IDp, c, Pkp, δ, h2) to l2.

•   2. If IDp=IDp∗, ψ recovers (IDp,Pn,S,η,h0) from l0 and (IDp,Υ,Pn,υ,λ) from lCU. Here, υ= ⫝ and λ=⫝. ψ chooses ϑ,h2∈ {1,2,…,(n−1)} and sets δ = ϑ.D−h2(Υ+h0.S), ω=ϑ. ψ, then returns Ω = (δ, ω) to TI and inserts (IDp, c, Pkp, δ, h2) to l2.

Forgery.

Here TI delivers a tuple of forged signature (IDp∗,c∗,Ω∗), as Ω∗ = (δ∗,ω∗).

If IDp≠IDp∗, ψ aborts the entire simulation. Otherwise, it recovers the given tuples (IDp∗,Pn∗,S,h2∗),(IDp∗,V∗,h1∗), (IDp∗,c∗,Pkp∗,δ∗,h2∗), (IDp∗,c∗,Pkp∗,δ∗,h2∗), and (IDp∗,Υ∗,Pn∗,υ∗,λ∗) from the given lists of l0, l1, l2, and lCU, respectively.

Since the Ω∗ is a valid signature, so ω∗.D = δ∗+h2∗(Υ∗+h0∗S), ⇒ω∗ = ϑ∗ + h2∗(n∗ + h0∗K) as ϑ∗, n∗ and K are unknown values to ψ. According to Forking Lemma, AV1 produces two other forged signatures Ω∗(t) = (δ∗,ω∗(t)) for t = 2, 3.

⇒ω∗(t) = ϑ∗ + h2∗(t)(n∗+h0∗K), for t = 1, 2, 3, as ϑ∗, n∗ and K are not known values to ψ. Hence by solving these linear independent equations, ψ obtains the value of K which is an HDLP.

Theorem II:

Under HDLP, the given scheme is existentially unforgeable against TII

Proof:

The proof is the same as that of Theorem I.

6  Comparative Analysis

This section is dedicated to the comparative analysis of cost complexity such as computational and communicational costs.

6.1 Computational Cost

Here, we analyzes and compare our new scheme with relevant recommended schemes [24–29] in terms of computational cost. However, to compute the operational computational cost of a scheme, we only consider the heavy mathematical operation that is used in any cryptographic solution.

For our computational cost analysis, we consider Bilinear Pairing (BP), Point Multiplication of Bilinear Pairing (PBM), exponentiation (E), Point Multiplication of ECC (ESPM), and Devisor Multiplication of HCC (HEDM). The software and hardware specifications [30,31] are presented in the following Tab. 2.

According to [30,31], the running time of BP is estimated to be 14.90 milliseconds, for PBM it is 4.31 milliseconds, for E it is 1.25 milliseconds, for ESPM it is estimated to be 0.97 milliseconds while the running time of HEDM is 0.48 milliseconds [32].

The results in Tabs. 3 and 4 and Fig. 2, shows that our scheme is more efficient in terms of computational time from previous recommended schemes.

Cost Reduction from Previous Recommended Schemes

The computational cost reduction can be obtained by using the following formula [32].

=(Computational cost of Previous scheme(x)−Computational cost of our scheme(y)Computational cost of Previous scheme(x))∗100

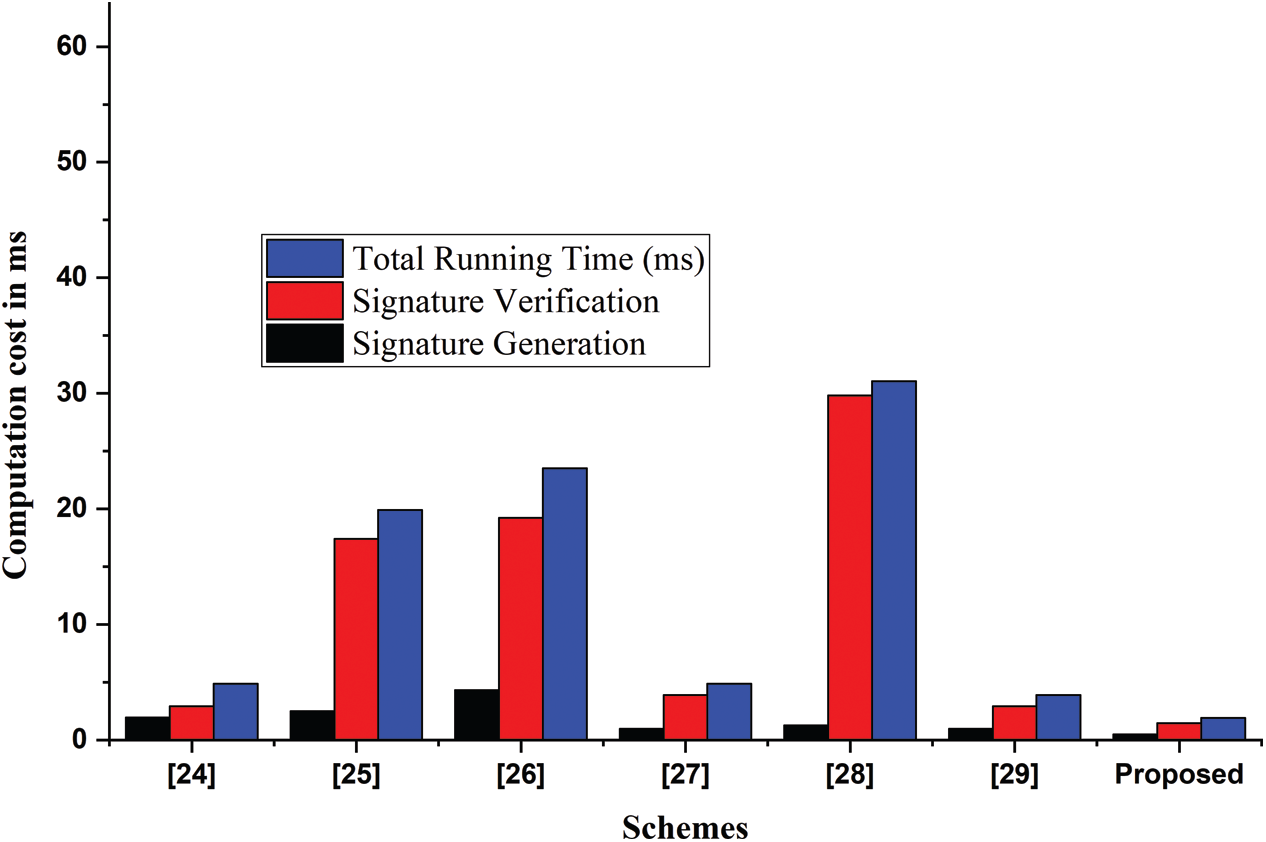
Figure 2: Computational cost complexity

6.2 Communication Overhead

The section is dedicated to the comparative analysis of the recommended schemes [24–29], with the proposed scheme in terms of communication complexity. Though, to compute the communication complexity of any cryptographic scheme, we consider the additional bits alone the original message. For our comparative analysis, we use the variables such as HCC (Q), ECC (N), message (M), and Bilinear pairing (G) as given in Tab. 5.

From the final outputs, as shown in Tabs. 6 and 7 and Fig. 3, it is obvious that the designed scheme outperforms the previously recommended schemes in terms of communicational complexity.

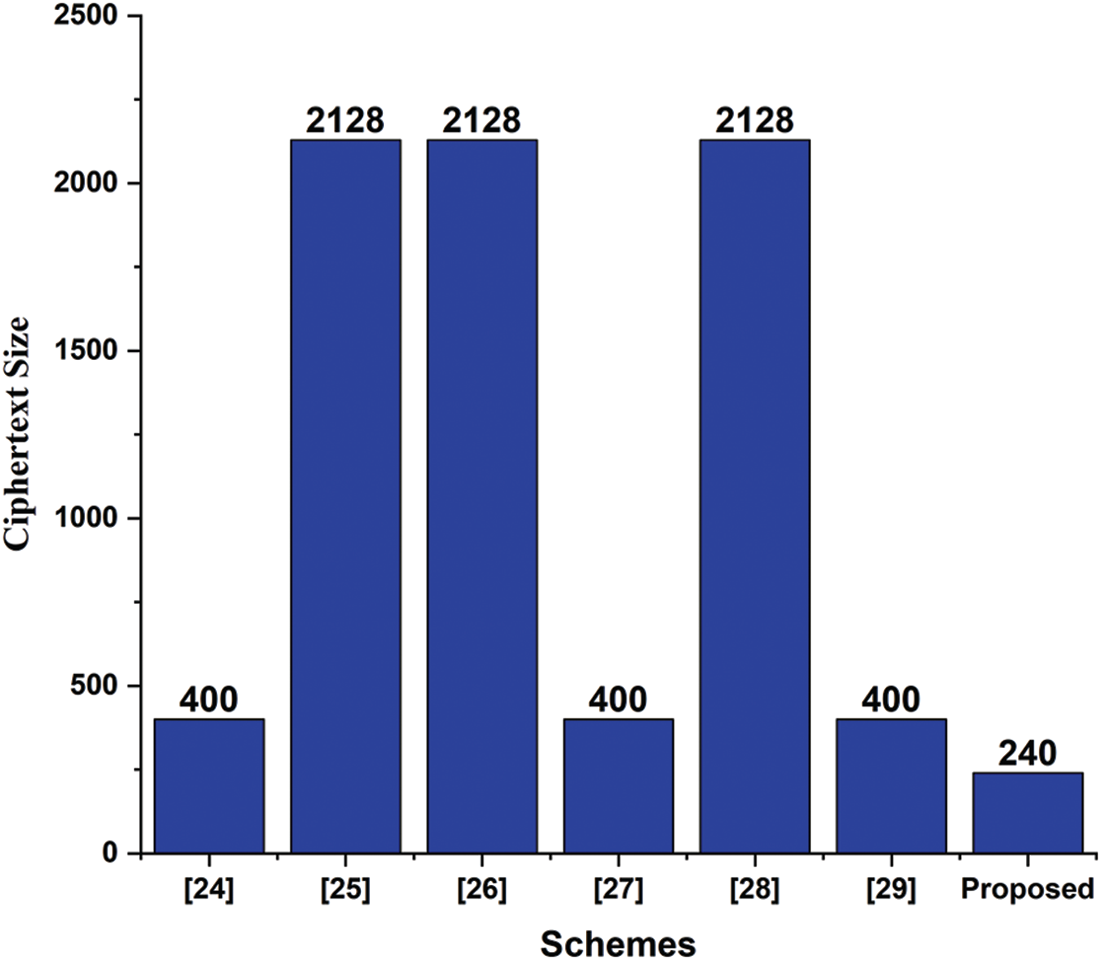
Figure 3: Communication cost complexity

6.3 Simulation Through AVISPA

Here we check the validity of the proposed approach through the backend checker of AVISPA known as OFMC and CL-AtSe [33,34].

Validation Results

Figs. 4 and 5 show the validation results of the proposed scheme under CL−AtSe and OFMC. The results indicate the safety of the proposed approach.

Figure 4: Validation result of OFMC

Figure 5: Validation result of CL-AtSe

7  Deployment on Internet of Medical Things

Here, we show the deployment of our new approach on IoMT-NDN. We assume several connected IoMT devices for the exchange of medical data. Also, the IoMT devices are connected based on the NDN standard policy. The comprehensive deployment scenario is labeled below.

7.1 Registration Phase

In this stage, both entities register themselves with the NM, and to do so, the NM picks l and D of the HEC of order n and secure hash functions (H1, H2, H3), choosesK∈{1,2,…,(n−1)} and computes S = K.D. Then the NM publishes the public parameters in the entire network Q = {n,H0,H1,H2,D,S}. After that, both participating entities assign their identities to the NM. After recaptioning IDP, the NM produces the PPK for the participants, and to do so, the KGC randomly picks a number Rn∈({1,2,…,(n−1)} and computes Pn = Rn.D, h0= H0 (IDp ,S,Pn), and λ= (Rn + Kh0) mod n. Finally, NM generates PPK O = (λ,Pn) for both entities.

After both participants set their secret υ∈{1,2,…,(n−1)} and compute their respective private key (Ptp) and public key (Pkp). The overall initialization and registration are shown in Fig. 6.

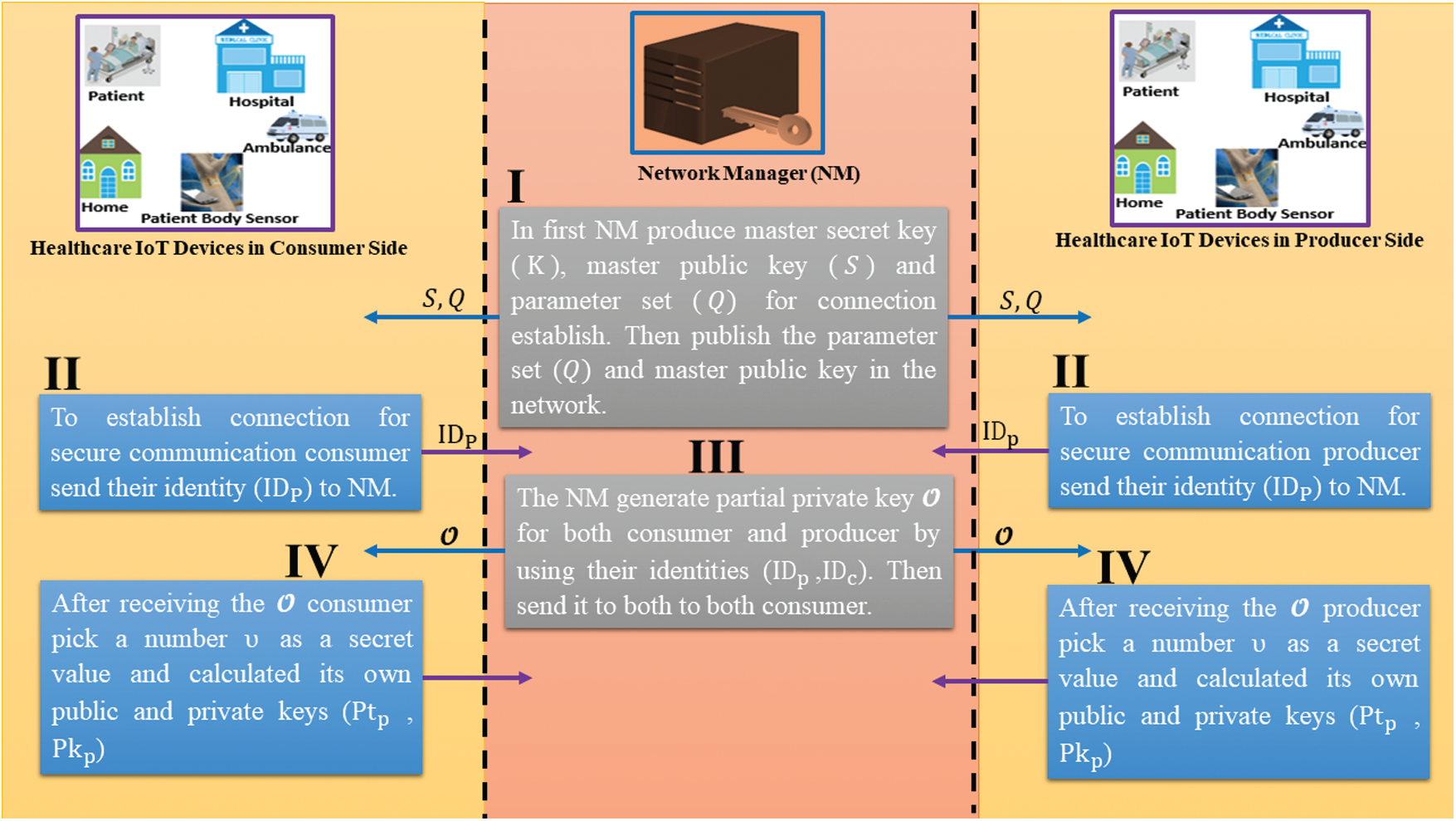
Figure 6: Initialization and registration phases

7.2 Sign Generation Phase

After registration, when a consumer requests content, the provider of the content generates a sign on the content. For this purpose, the legitimate provider takes the content c with a random number ϑ∈{1,2,…(n−1)}, and computes δ = ϑ.D, h1 = H1(IDp,V), h2 = H2 (c,IDp, Pkp, δ), and ω = ϑ + h2(λ+h1.υ) mod n. Lastly, the provider of the content generates a signed tuple Ω = (δ, ω) as shown in Fig. 6.

7.3 Verification Phase

After the reception, the consumer takes Q, Pkp, IDp, Ω = (δ, ω), and c to verify the signature (Ω) on the received content by computing h0 = H0 (IDp, S,Pn) and h2 = H2 (c, IDp, Pkp, δ). Finally, it verifies the equation ω.D = δ + h2(Υ+h0.S). If it holds, accept the content. Otherwise, reject the content as shown in Fig.7.

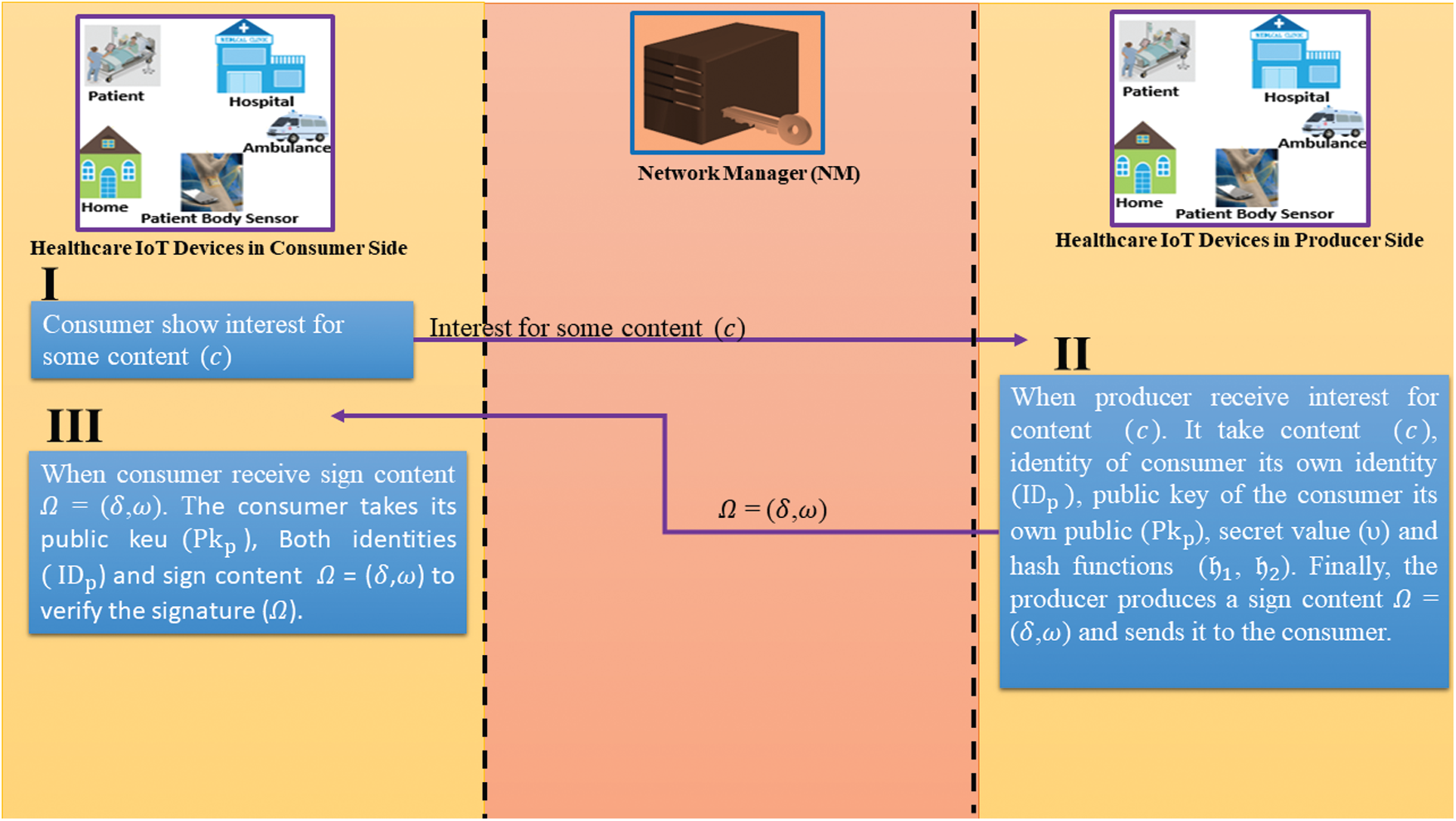
Figure 7: Signature generation and verification phases

8  Conclusions

In this article, we present a secure framework NDN-Based Internet of Medical Things (NDN-IoMT). In the proposed framework, we use a lightweight certificateless signature scheme. To reduce cost consumption, we utilized Hyperelliptic Curve Cryptosystem (HCC) which provides strong security using a smaller key size as compared to ECC. The designed approach is formally secured under ROM. Furthermore, we take the services of AVISPA to validate the security of the newly proposed scheme. For cost-efficiency, we compare our newly designed scheme with the recently proposed certificateless signature schemes. The final result shows that our scheme uses minimal computational and communicational resources. Finally, we deploy the given framework on NDN-IoMT.

Acknowledgement: The authors are grateful to the Deanship of Scientific Research, King Saud University for funding through Vice Deanship of Scientific Research Chairs.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  J. Khan, J. P. Li, B. Ahamad, S. Parveen, Haq AU et al., “SMSH: Secure surveillance mechanism on smart healthcare iot system With probabilistic image encryption,” IEEE Access, vol. 8, pp. 15747–15767, 2020. [Google Scholar]

 2.  X. Guo, H. Lin, Y. Wu and M. Peng, “A new data clustering strategy for enhancing mutual privacy in healthcare IoT systems,” Future Generation Computer Systems, vol. 113, pp. 407–417, 2020. [Google Scholar]

 3.  J. Gubbi, R. Buyya, S. Marusic and M. Palaniswami, “Internet of Things (IoTA vision, architectural elements, and future directions,” Future Generation Computer Systems, vol. 29, no. 7, pp. 1645–1660, 2013. [Google Scholar]

 4.  A. S. M. S. Arefin, K. M. T. Nahiyan and M. Rabbani, “The basics of healthcare IoT: Data acquisition, medical devices, instrumentations and measurements,” in A Handbook of Internet of Things in Biomedical and Cyber Physical System. Xerox Palo Alto Research Center-PARC 2010: Springer, pp. 1–37, 2020. [Google Scholar]

 5.  L. Zhang, D. Estrin, J. Burke, V. Jacobson, J. Thornton et al., “Named Data Networking (NDN) project, Relatório Técnico NDN-0001, Xerox Palo Alto Res,” Center-PARC, vol. 157, pp. 158, 2010. [Google Scholar]

 6.  K. Ahed, M. Benamar and R. E. Ouazzani, “Content delivery in named data networking-based Internet of Things,” in 2019 15th Int. Wireless Communications & Mobile Computing Conf., Tangier, Morocco, pp. 1397–1402, 2019. [Google Scholar]

 7.  B. Nour, H. Ibn-Khedher, H. Moungla, H. Afifi, F. Li et al., “Internet of Things mobility over information-centric/named-data networking,” IEEE Internet Computing, vol. 24, no. 1, pp. 14–24, 2019. [Google Scholar]

 8.  D. Saxena, V. Raychoudhury and N. SriMahathi, “SmartHealth-NDNoT: Named data network of things for healthcare services,” in MobileHealth@ MobiHoc, pp. 45–50, 2015. [Google Scholar]

 9.  D. Saxena and V. Raychoudhury, “Design and verification of an NDN-based safety-critical application: A case study with smart healthcare,” IEEE Transactions on Systems, Man, and Cybernetics: Systems, vol. 49, no. 5, pp. 991–1005, 2017. [Google Scholar]

10. X. Wang and S. Cai, “Secure healthcare monitoring framework integrating NDN-based IoT with edge cloud,” Future Generation Computer Systems, vol. 112, pp. 320–329, 2020. [Google Scholar]

11. A. Karati, S. H. Islam and G. P. Biswas, “A pairing-free and provably secure certificateless signature scheme,” Information Sciences, vol. 450, pp. 378–391, 2018. [Google Scholar]

12. A. Shamir, “Identity-based cryptosystems and signature schemes,” in Proc. of the CRYPTO 1984, Santa Barbara, CA, USA, 19–22, pp. 47–53, 1984. [Google Scholar]

13. S. S. Al-Riyami and K. G. Paterson, “Certificateless public key cryptography,” Advances in Cryptology-ASIACRYPT, vol. 2894, pp. 452–473, 2003. [Google Scholar]

14. S. Hussain, I. Ullah, H. Khattak, M. Adnan, S. Kumari et al., “A lightweight and formally secure certificate based signcryption with proxy re-encryption (CBSRE) for Internet of Things enabled smart grid,” IEEE Access, vol. 8, pp. 93230–93248, 2020. [Google Scholar]

15. S. Hussain, I. Ullah, H. Khattak, M. A. Khan, C. M. Chen et al., “A lightweight and provable secure identity-based generalized proxy signcryption (IBGPS) scheme for Industrial Internet of Things (IIoT),” Journal of Information Security and Applications, vol. 58, pp. 102625, 2021. [Google Scholar]

16. M. Rehman, H. Khattak, A. S. Alzahrani, I. Ullah, M. Adnanet al., “A lightweight nature heterogeneous generalized signcryption (hgsc) scheme for named data networking-enabled internet of things,” Wireless Communications and Mobile Computing, vol. 2020, pp. 1–20, 2020. [Google Scholar]

17. D. He, J. Chen and R. Zhang, “An efficient and provably secure certificateless signature scheme without bilinear pairings,” International Journal of Communication Systems, vol. 25, no. 11, pp. 1432–1442, 2011. [Google Scholar]

18. J. Tsai, N. Lo and T. Wu, “Weaknesses and improvements of an efficient certificateless signature scheme without using bilinear pairings,” International Journal of Communication Systems, vol. 27, no. 7, pp. 1083–1090, 2014. [Google Scholar]

19. M. Tian and L. Huang, “Cryptanalysis of a certificateless signature scheme without pairings,” International Journal of Communication Systems, vol. 26, pp. 1375–1381, 2013. [Google Scholar]

20. P. Gong and P. Li, “Further improvement of a certificateless signature scheme without pairing,” International Journal of Communication Systems, vol. 27, no. 10, pp. 2083–2091, 2015. [Google Scholar]

21. K. H. Yeh, K. Y. Tsai and C. Y. Fan, “An efficient certificateless signature scheme without bilinear pairings,” Multimedia Tools and Applications, vol. 74, pp. 1–12, 2014. [Google Scholar]

22. L. Wang, K. Chen, Y. Long, X. Mao and H. Wang, “A modified efficient certificateless signature scheme without bilinear pairings,” in Proc. of Int. Conf. on Intelligent Networking and Collaborative Systems, Taipei, Taiwan, pp. 82–85, 2015. [Google Scholar]

23. L. Wang, K. Chen, Y. Long and H. Wang, “An efficient pairing-free certificateless signature scheme for resource-limited systems,” Science China Information Sciences, vol. 60, no. 11, pp. 119102:1–119102:3, 2017. [Google Scholar]

24. K. H. Yeh, S. Chunhua, K. K. R. Choo and W. Chiu, “A novel certificateless signature scheme for smart objects in the Internet-of-Things,” Sensors, vol. 17, no. 5, pp. 1001, 2017. [Google Scholar]

25. A. Karati, S. H. Islam and M. Karuppiah, “Provably secure and lightweight certificateless signature scheme for IIoT environments,” IEEE Transactions on Industrial Informatics, vol. 14, no. 8, pp. 3701–3711, 2018. [Google Scholar]

26. Y. Zhang, R. H. Deng, D. Zheng and J. Li, “Efficient and robust certificateless signature for data crowdsensing in cloud-assisted industrial IoT,” IEEE Transactions on Industrial Informatics, vol. 15, pp. 5099–5108, 2019. [Google Scholar]

27. P. Nasrollah and B. A. Vanda, “Cryptanalysis and Improvement of a pairing-free certificateless signature scheme,” in 15th Int. ISC (Iranian Society of Cryptology) Conf. on Information Security and Cryptology, Tehran, Iran, pp. 1–5, 2018. [Google Scholar]

28. E. Rezaeibagha, Y. Mu, X. Huang, W. Yang and K. Huang, “Fully secure lightweight certificateless signature scheme for IIoT,” IEEE Access, vol. 7, pp. 144433–144443, 2019. [Google Scholar]

29. G. Thumbur, G. S. Rao, P. V. Reddy, N. B. Gayathri and D. V. R. K. Reddy, “Efficient pairing-free certificateless signature scheme for secure communication in resource-constrained devices,” IEEE Communications Letters, vol. 24, no. 8, pp. 1641–1645, 2020. [Google Scholar]

30. C. Zhou, Z. Zhao, W. Zhou and Y. Mei, “Certificateless key-insulated generalized signcryption scheme without bilinear pairings,” Security and Communication Networks, vol. 2017, pp. 1–17, 2017. [Google Scholar]

31. C. Zhou, “An improved lightweight certificateless generalized signcryption scheme for mobile-health system,” International Journal of Distributed Sensor Networks, vol. 15, no. 1, pp. 1–16, 2019. [Google Scholar]

32. S. S. U. H. Khattak, M. A. Khan, M. Adnan, S. Hussain, M. A. Khan et al., “A lightweight identity-based signature scheme for mitigation of content poisoning attack in named data networking with internet of things,” IEEE Access, vol. 8, pp. 98910–98928, 2020. [Google Scholar]

33. A. Armando, D. Basin, Y. Boichut, Y. Chevalier, L. Compagna et al., “The AVISPA tool for the automated validation of internet security protocols and applications,” in Int. Conf. on Computer Aided Verification, San Francisco, CA, USA, pp. 281–285, 2005. [Google Scholar]

34. S. Hussain, S. S. Ullah, A. Gumaei, M. Al-Rakhami, I. Ahmad et al., “A novel efficient certificateless signature scheme for the prevention of content poisoning attack in named data networking based internet of things,” IEEE Access, vol. 9, pp. 40198–40215, 2021. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.