DOI:10.32604/cmc.2022.017106

| Computers, Materials & Continua DOI:10.32604/cmc.2022.017106 |  |
| Article |
Scheduling Multi-Mode Resource-Constrained Projects Using Heuristic Rules Under Uncertainty Environment
1Faculty of Computers and Informatics, Zagazig University, Zagazig, 44519, Egypt
2Department of Computer Science and Engineering, Soonchunhyang University, Asan, 31538, Korea
3Department of Mathematics, Faculty of Science, Mansoura University, Mansoura, 35516, Egypt
4Department of Computational Mathematics, Science, and Engineering (CMSE), Michigan State University, East Lansing, 48824, MI, USA
*Corresponding Author: Yunyoung Nam. Email: ynam@sch.ac.kr
Received: 21 January 2021; Accepted: 06 May 2021
Abstract: Project scheduling is a key objective of many models and is the proposed method for project planning and management. Project scheduling problems depend on precedence relationships and resource constraints, in addition to some other limitations for achieving a subset of goals. Project scheduling problems are dependent on many limitations, including limitations of precedence relationships, resource constraints, and some other limitations for achieving a subset of goals. Deterministic project scheduling models consider all information about the scheduling problem such as activity durations and precedence relationships information resources available and required, which are known and stable during the implementation process. The concept of deterministic project scheduling conflicts with real situations, in which in many cases, some data on the activity' s durations of the project and the degree of availability of resources change or may have different modes and strategies during the process of project implementation for dealing with multi-mode conditions surrounded by projects and their activity durations. Scheduling the multi-mode resource-constrained project problem is an optimization problem whose minimum project duration subject to the availability of resources is of particular interest to us. We use the multi-mode resource allocation and scheduling model that takes into account the dynamicity features of all parameters, that is, the scheduling process must be flexible to dynamic environment features. In this paper, we propose five priority heuristic rules for scheduling multi-mode resource-constrained projects under dynamicity features for more realistic situations, in which we apply the proposed heuristic rules (PHR) for scheduling multi-mode resource-constrained projects. Five projects are considered test problems for the PHR. The obtained results rendered by these priority rules for the test problems are compared by the results obtained from 10 well-known heuristics rules rendered for the same test problems. The results in many cases of the proposed priority rules are very promising, where they achieve better scheduling dates in many test case problems and the same results for the others. The proposed model is based on the dynamic features for project topography.
Keywords: Constrained resource scheduling; multi-mode durations; dynamic scheduling; resource allocation; heuristic rules
Project management is the science of planning, organizing, and managing resources well to complete the project successfully and achieve the desired objectives of the project successfully [1]. A project is a group of activities arranged together by precedence relationships. Each activity needs specific time and resource requirements of various types for it to be carried out. The process of implementing activities and tasks to complete the implementation of the project in full is defined as the process of scheduling. Project scheduling is the task of allocating limited resources for activities to be implemented in a specific order depending on the relationships of precedence and subordination of the projects, and the availability of resources to achieve a specific goal or set of goals such as reducing the project implementation time as much as possible and reducing the cost of project implementation [2]. Scheduling is one of the most important topics of project management science.
Project scheduling in terms of availability and accuracy of activity data is divided into two types: deterministic project scheduling and construction schedules. Deterministic project scheduling considers all information such as activity durations and resource availability. Required, precedence relationships about the scheduling problem are very well known and stable during the implementation process. The concept of deterministic project scheduling conflicts with real situations, wherein in many cases, the activity durations of the project and the degree of availability of resources may change during the process of project implementation. The scheduling process must be flexible to dynamic environment features.
Construction schedules, as known, are can either be time- or resource-oriented, as shown in Fig. 1. The resource-oriented option has two aspects: resource leveling and resource allocation. Resource leveling deals with the distribution of resources within the fixed project duration, and resource allocation deals with the availability of resources under work constraint, as shown in Fig. 2. Resource leveling is the process of allocating resources between various activities such that the peak requirement of resources is reduced with a constraint on time, and the underlying assumptions in resource leveling are only one type of resource being considered throughout the project, and activities already underway should be completed first. Resource allocation has different and multiple meanings in different areas.
In project management, resource allocation or resource management is to schedule the activities and resources required by those activities, considering the availability of resources and the time of the project. Resource allocation under a constraint is performed when the availability of resources is constrained due to the limited availability of resources. Some activities may have to be necessarily delayed. The basic objective is to determine which of the activities can be delayed and finally arrive at the shortest possible time to complete the project satisfying resource constraints.
A heuristic method for allocating resources to projects often uses a decision rule called priority or dispatching rule. The priorities of the activities are determined using the priority rule during the exploratory search process while the structure of the network is preserved such that no activity can precede one of its dependencies. A priority rule contains information for activity, network, scheduling, and resources to construct the activity list for determining the priorities in which the activities are assigned to the project schedule. The heuristic determines which activity has the highest priority and receives resources for starting the scheduling process.
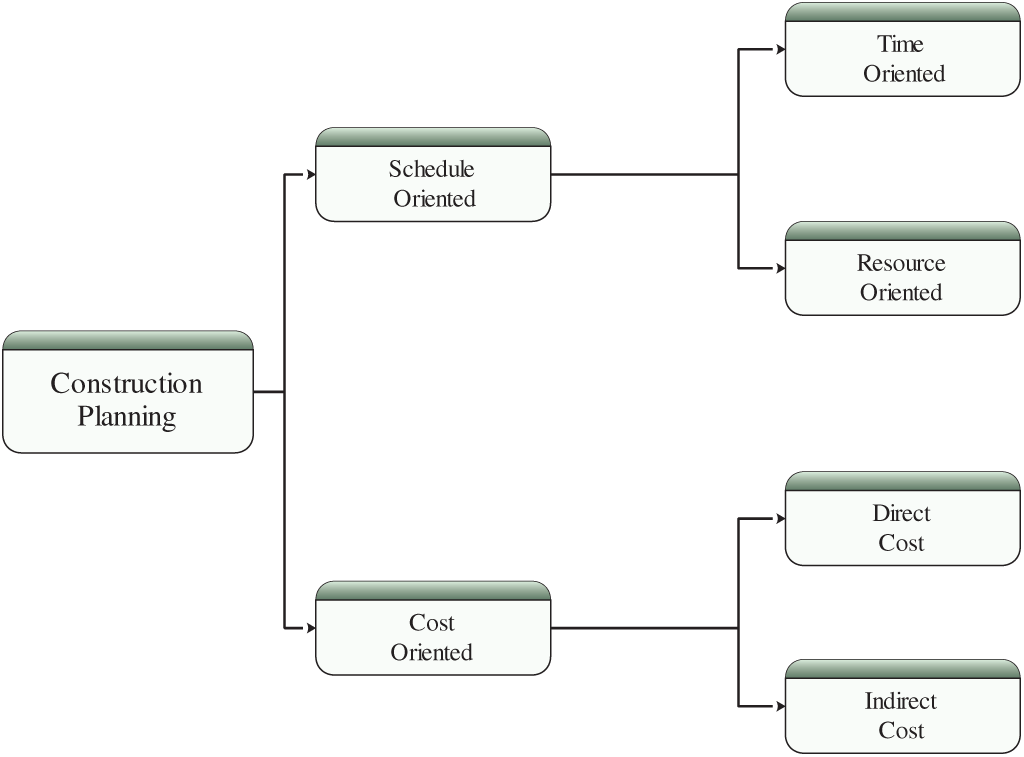
Figure 1: Construction planning and scheduling
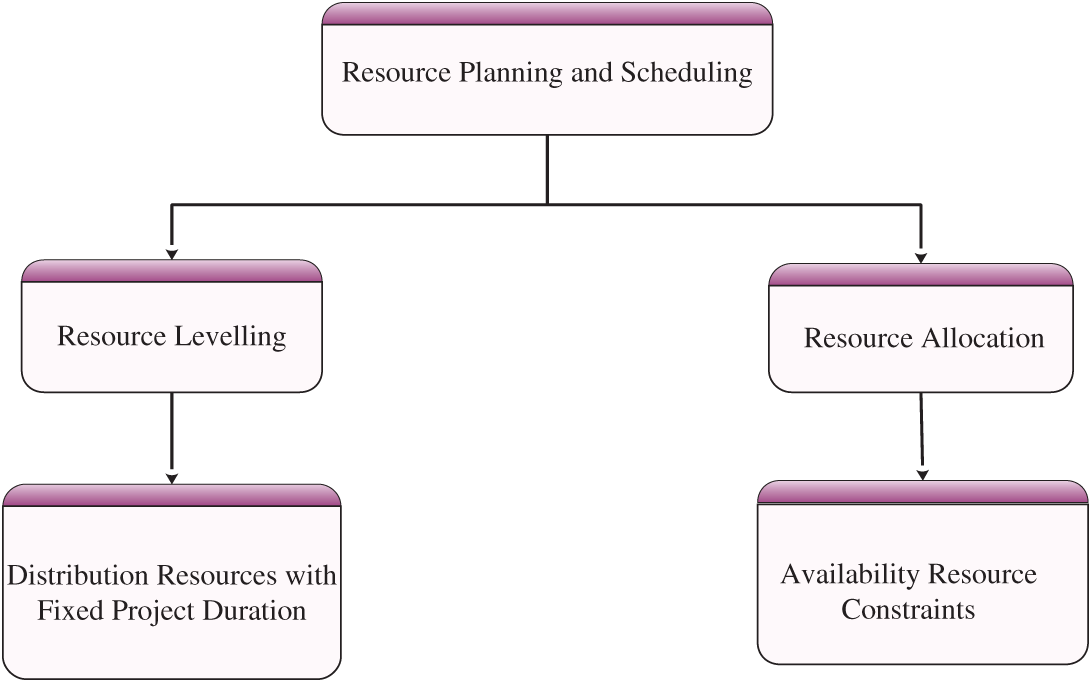
Figure 2: Resource leveling and resource allocation
Two broad categories of heuristic procedures are used, namely, serial, and parallel procedures. Serial procedures are procedures in which all activities of the project are ranked in order of priority as a single group and then scheduled one at a time. In serial procedures, we establish the priority of the job only once and we do not change it during the application of the algorithm. At the moment we pick up a project, we can identify the ranks of the activities, and these ranks stay with them as long as the activities are during the particular process. By contrast, parallel procedures request all activities starting in a given period are ranked as a group and the resources are allocated and at each successive period as a new rank ordering of all the eligible activities. These processes differ in terms of how the heuristic is used in a period. The limited resource allocation problem in projects is a combinatorial problem. Thus, many combinations of activity start times satisfy precedence and resource constraints. These combinations exist and because of these large combinations, we have a large number of possible heuristic procedures.
The two components of a priority rule-based scheduling approach are a priority rule for determining activities arrangements based on specific heuristic rules and a schedule generation scheme for constructing feasible scheduling [3], as shown in Fig. 3. The classification of the solution to the scheduling problem, as described in Shouman et al. [4,5] and Kolisch et al. [6], is classified in methods of scrolling according to X priority rules, classic meta-methods, and non-standard metadata inferred, as well as other deductions. In X-pass methods, a priority order is assigned to each specific activity listed in the project either in a sequential and/or parallel scheduling strategy.

Figure 3: Feasible project schedule using the priority rule-based scheduling approach
Lova et al. [7] provided some heuristics on the basis of the multiple-resource constrained project scheduling problems (MRCPSP) priority rule with the analysis of renewable resources. These methods are very important in building more sophisticated methods such as random sampling methods or meta-research methods. Thus, additional efforts are warranted to obtain better reasoning based on the priority rule. Three components of this type of inference are analyzed: schema creation schedule, priority rule, and status selection rule. On the basis of a well-known set of 240 randomly generated models, individual inference and multiple paths based on the priority rules developed in this work far outweigh those previously published. The sequential schedule creation system is significantly superior to the parallel scheme with most priority rules that have been tested to justify the high arithmetic effort previously required. Finally, the multi-lane method, which combines eight inferences based on the priority rule, has the least average deviation concerning critical path length (32.0%). This, the method is the best deterministic methodology for this problem.
Myszkowski et al. [8] presented some research methods for scheduling the problem of scheduling projects with multi-skilled resources and compared them with the state' s new priority rules on the basis of the duration of the task, resource salaries, and precedence relationships. New inference stands on a set of well-known methods but is promoted through the field of skills. The research aimed to investigate whether the methods evaluated can be used as tools to enhance durability in meta-processes, most of which are evolutionary algorithms. Experiments were performed using artificially created data set instances on the basis of instances in the real world. The results obtained demonstrate that these methods represent an important feature that can be included in more complex methods and their reliability.
Colak et al. [9] considered the problem of MRCPSP with renewable resources. In MRCPSP, an activity can be performed in one of several possible methods. Each mode has different resource requirements and according to different activity intervals. We assume that all resources are renewable from one period to another, such as employment and machinery. The solution to this problem mainly involves two decisions: (1) the start time for each activity and (2) the status of each activity. Owing to the nature of the NP-hard problem, heuristics and meta-reasoning are used to solve larger cases of this problem. A guide to this type of problem involves a combination of two priority rules, one for each of the two decisions. Inference generally tends to be greedy. In this study, we suggest two non-greedy inferences to choose a situation that performs better than does greed inference. Furthermore, we study the effect of double justification and front/frontal scheduling of MRCPS. We also study the effect of serial vs. parallel scheduling. We found that all these elements improved the quality of the solution. Finally, a meta-heuristic procedure is proposed on the basis of neural networks, improving the quality of the solution. The effectiveness of these proposed methods, compared with current approaches, is illustrated by pilot testing on two known sets of standard problems.
Chen et al. [10] provided a modified approach to the improvement of an ant colony (ACO) and its assessment of problems associated with project scheduling. A modified ACO system was proposed to solve limited resource scheduling problems.
A two-dimensional matrix was proposed in this study to schedule activities over time and has a parallel plan for solving project scheduling problems. Two types of course design were proposed. The dynamic rule was designed to modify the most recent start time of activities and thus the inference function. In exploring the solution space, this research suggests a rule for creating delay solutions to escape the optimal local solution. The simulation results demonstrate that the proposed modified colony algorithm provides an effective and effective way to solve project scheduling problems with resource constraints.
Andreica and Chira introduced a new recombination operator [11] for flipping-based encoding. This operator is suitable for the scheduling problem of resource-constrained projects and limits the problem of scheduling multi-resource projects because it preserves precedence in obtaining priority parental custody. The main feature of the proposed operator is the use of genetic information from the best individual alongside the parents who are considered for recombination. Experimental results performed on PROGEN project instances indicate the superior performance of the proposed operator, thereby emphasizing the role of the recombination process in accelerating research in an evolutionary process. A thorough study will be conducted of all recombination operators used in resource-constrained project scheduling problems (RCPSP) and MRCPSP. The trials will be expanded to include more cases with more activities.
Buddhakulsomsiri et al. [12] provided a rule-based guideline for the problem of scheduling multi-resource projects in a restricted situation with the division of activities around available non-available resources. All resources considered are renewable, and not every resource unit may be available at all times due to resource releases, which are known in advance. A new concept called mobile resource power has been developed to help identify project situations where activity splitting is likely to be useful during scheduling. The concept of mobile resource power is applied in priority-based reasoning to control the division of activity when scheduling. Multiple comparisons are provided to perform a combination of activity priority rules used in inference. The computational experiments show the effectiveness of the process in limiting the production of the project board and reducing the fragmentation of the activity.
Browning et al. [13] dealt with the RCMSPP with two delayed targets, namely, delayed project and portfolio lag. In this context, previous research reported conflicting results on the performance of the rule of priority and did not provide managers with clear guidance on which base to use in different situations. Using recently improved standards for RCMSPP features, they comprehensively analyzed 20 priority rules on 12, 320 test problems resulting from project, activity, and resource characteristics, including network complexity, resource allocation, and differences. They found many situations in which the widely-read priority rules performed poorly and emphasized that portfolio managers and project managers would prefer different priority rules depending on their local or global objectives, that is, the results in two decision tables. The practical use of managers requires only a rough and qualitative description of their projects in terms of complexity, degree of resource conflict, and resource allocation.
He et al. [14] proposed a forward-based guidance algorithm based on priority rules (FBHA). FBHA improves resource allocation by converting non-critical activities into its FFF, FFT, and BFF, respectively. The project is divided into several stages during each forward/backward scheduling unit. At each stage, the transformation sequence and the days of non-critical activities depend on a set of vital priority rules. FBHA is integrated into the Microsoft Project 2007 business software package to improve program performance and facilitate project planners.
Singh [15] attempted to integrate project priorities with the development of the project schedule. A hybrid algorithm was developed to accomplish this task. The algorithm provided is a new way to create a schedule for any scheduling problem constrained to multiple project resources where each project has a specific importance. The proposed method was validated with a case study under different scenarios. The experimental results were compared with the current priority transmission rules. The experimental results showed that the proposed method is superior to the current priority transmission rules under different operating conditions. In the real project management environment, a penalty is imposed if the project is completed after the due date. Some projects carry a higher penalty than do others.
In this context, the project manager can make a trade-off between project sanctions and can develop a cost-effective agenda that meets customer requirements. In this context, the proposed algorithm will be useful for the project manager to deal with these conditions. In the future, research can explore the possibility of integrating other knowledge areas including risk management and procurement management with the development of the project schedule. Meta-heuristics models were also proposed for scheduling multiple-resource constrained project scheduling problems [16–20]. Fuzzy models [21–23] also studied the problem of resource allocation under uncertain conditions.
In this paper, we will use a heuristic procedure for solving RCPSP and MRCPSP. We propose five priority heuristic rules for scheduling multi-mode resource-constrained projects under dynamicity features for real situations. Five projects are considered test problems for the PHR. The obtained results rendered by these priority rules for the test problems are compared by the results obtained from 10 well-known heuristics rules rendered for the same test problems. The results in many cases of the proposed priority rules are very promising, where the procedure achieves better scheduling dates in many test case problems and the same results for the others. The proposed model is based on the dynamic features for project topography.
Definition 1 Let X be a space of points and x∈ X. A neutrosophic set A in X is defined by a truth-membership function
Definition 2 Let X be a universe of discourse. A single-valued neutrosophic set A over X is an object taking the form A= {
Definition 3 Suppose
where
Scheduling multiple constrained resource project problems is an optimization problem whose minimum project duration subject to the availability of resources is of particular interest to us. Deterministic project scheduling models consider activities durations to be accurate and deterministic and this is not the real condition where the uncertainties conditions and dynamicity features that surround the projects and their activities duration. For this reason, we consider the dynamic features for scheduling multi-mode resource-constrained projects.
In this section, we will list the proposed five heuristic rules. Then, we present the proposed model for scheduling multi-mode resource-constrained projects using the PHR to minimize the project schedule time as much as possible in uncertain situations.
In this heuristic rule, all critical activities of the project receive the first preference and priority and weighted first and then the non-critical activities. The ordering for the critical and non-critical activities is given on the basis of the following steps of the proposed algorithm in this heuristic rule.
1-The first critical activity of the first starting point of the project is the first step, in which the maximum weight is given to the starting critical activity and equal to the number of activities. The weight of the next critical activity by is decreased by one unit and the remainder of all critical activities are weighted in the same way. If more than one critical activity is present at this point, the activity is selected on the basis of ascending (ASC) of the activities’ earliest times. In case of conflict, the activities are arranged on the basis of the max ratio between the time of immediate activity sons (the set of activities that follow this activity) to resources of immediate sons and activity resources to activity time for each critical activity. In case of conflict, the activities are arranged on the basis of DSC of their times. In case of conflict, the selection criteria will be random. The weight of this activity is set equal to the number of activities of the project.
2-The non-critical activities based on ASC of their earliest start times (ES) are arranged. In case of conflict, the selection will be on the basis of their max ratio between the time of immediate activity sons to resources of immediate sons and activity resources to activity time for each non-critical activity. In case of conflict, the selection criteria will be on the basis of descending (DSC) activity duration times. In case of conflict, the selection criteria will be random.
3-The weight of the first non-critical activity is decreased by one unit from the weight of the last critical activities.
4-Weights are set for the rest of all non-activities until the last activity weight equals one.
In this heuristic rule, only the first critical activity on the critical path is weighted first, and then all the remaining activities, either critical or non-critical, are weighted. The maximum weight is given to the starting critical activity of the project and equal to the number of project activities. The ordering for both the critical and non-critical activities is given on the basis of the following steps of the proposed algorithm in this heuristic rule.
1-The first critical activity of the first starting point of the project is the first step. If more than one critical activity is present at this point, the activity of maximum duration time is selected. The weight of this activity is set equal to the number of activities of the project.
2-The rest of all activities are arranged on the basis of ASC of their ES times. In case of conflict, the activities are arranged on the basis of the max ratio of the sum of activity resources and resources of all sons to the sum of activity time and time of all sons. In case of conflict, the selection criteria will be random.
3-The weight of the next activity is decreased by one unit and weights are set for the rest of the activities until the last activity weight equals one.
In this heuristic rule, all critical activities of the project receive the priority and weight first, followed by the non-critical activities. The ordering for the critical and non-critical activities is given on the basis of the following steps of the proposed algorithm in this heuristic rule.
1-The first critical activity of the first starting point of the project is the first step. The maximum weight is given to the starting critical activity and is equal to the number of activities. The weight of the next critical activity is decreased by one unit and the rest of all critical activities are weighted in the same way. If more than one critical activity is present at this point, the activity is selected on the basis of ASC of the activities’ earliest times. In case of conflict, the activities are arranged on the basis of the max ratio between resources of immediate activity sons to their times and activity resources to activity time for each critical activity. In case of conflict, the activities are arranged on the basis of DSC of their times. In case of conflict, the selection criteria will be random. The weight of this activity is set equal to the number of activities of the project.
2-The non-critical activities are arranged on the basis of ASC of their ES. In case of conflict, the selection will be on the basis of their max ratio between resources of immediate activity sons to their times and activity resources to activity time for each no activity. In case of conflict, the selection criteria will be on the basis of DSC activity duration times. In case of conflict, the selection criteria will be random.
3-The weight of the first non-critical activity is decreased by one unit from the weight of the last critical activities.
4-Weights are set for the rest of all non-activities until the last activity weight equals one.
In this heuristic rule, only the first critical activity on the critical path is weighted first, and then all the remaining activities, either critical or non-critical, are weighted. The maximum weight is given to the starting critical activity of the project and is equal to the number of project activities. The ordering for the critical and non-critical activities is given on the basis of the following steps of the proposed algorithm in this heuristic rule.
1-The first critical activity of the first starting point of the project is the first step. If more than one critical activity is present at this point, the activity of maximum duration time is selected. The weight of this activity is set equal to the number of activities of the project.
2-The rest of all activities are arranged on the basis of ASC of their ES times. In case of conflict, the activities are arranged on the basis of the max ratio of the sum of activity time and time of all sons to the sum of activity resources and resources of all sons for each activity. In case of conflict, the selection criteria will be random.
3-The weight of the next activity is decreased by one unit and weights are set for the rest of the activities until the weight of the last activity equal to one.
In this heuristic rule, all critical activities of the project receive priority and weight first, followed by the non-critical activities. The ordering for both the critical and non-critical activities is given on the basis of the following steps of the proposed algorithm in this heuristic rule.
1-The first critical activity of the first starting point of the project is the first step. The maximum weight is given to the starting critical activity and is equal to the number of activities. The weight of the next critical activity is decreased by one unit and the rest of all critical activities are weighted in the same way. If more than one critical activity is present at this point, the activity is selected on the basis of ASC of activities’ earliest times. In case of conflict, the activities are arranged on the basis of the max ratio between activity time to activity time and activity resources to time of all sons for each critical activity, In case of conflict, the activities are arranged on the basis of DSC of their times. In case of conflict, the selection criteria will be random. The weight of this activity is set equal to the number of activities of the project.
2-The non-critical activities are arranged on the basis of ASC of their earliest start times. In case of conflict, the selection will be on the basis of their max ratio between activity time to activity time and activity resources to time of all sons for each critical activity for each no activity. In case of conflict, the selection criteria will be on the basis of DSC activity duration times. In case of conflict, the selection criteria will be random.
3-The weight of the first non-critical activity is decreased by one unit from the weight of the last critical activities.
4-Weights are set for the rest of all non-activities until the last activity weight equals one.
3.2 Proposed Model for Scheduling Multi-Mode Resource-Constrained Projects Using the Proposed Heuristic Rules
Step 1. All the activity duration modes are considered on the basis of the dynamic features surrounded by the project execution.
Step 2. A crisp model of all different activities’ duration modes are obtained, then
Step 3. The PHR are applied to the five projects examples of multi-mode resource-constrained projects. Then, the priorities of all activities in the projects are listed. The durations (crisp values from different activities’ duration modes), resource(s) required, and limited resource(s) availability values for each activity for each project are added to this list.
Step 4. For each project, the scheduling process is started on the basis of the results of heuristic rules and the start and finish times are calculated for all activities until all activities of the project have been scheduled. Then, the scheduled time for this project is determined as the max number in the finish time row or the finish time of the last scheduled activity.
Step 5. Step 4 for all five projects is repeated using the proposed five heuristic rules.
Step 6. Final adjustments are made to the best (minimum) schedule time using the best PHR.
In this section, the five PHR are applied to the five multi-mode resource-constrained projects for the scheduling process. Five project data sets are listed first, followed by the results of scheduling these projects using the PHR, as shown below.
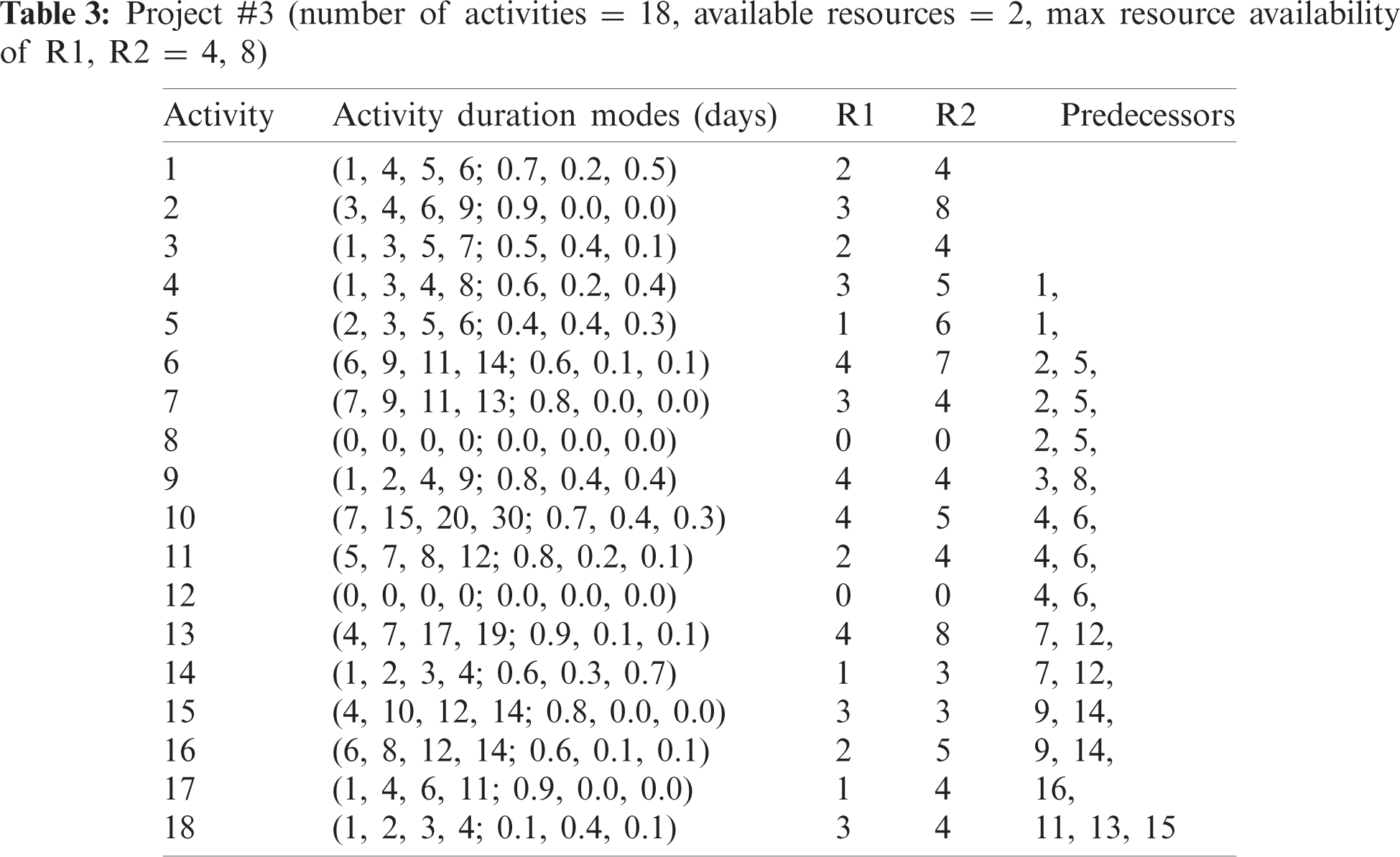
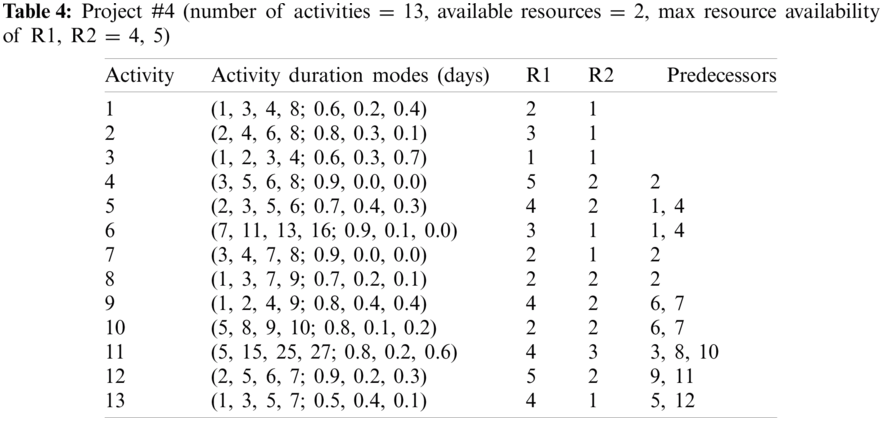
The activities duration modes of the five projects are listed in Tabs. 1–5 are considered as follows.
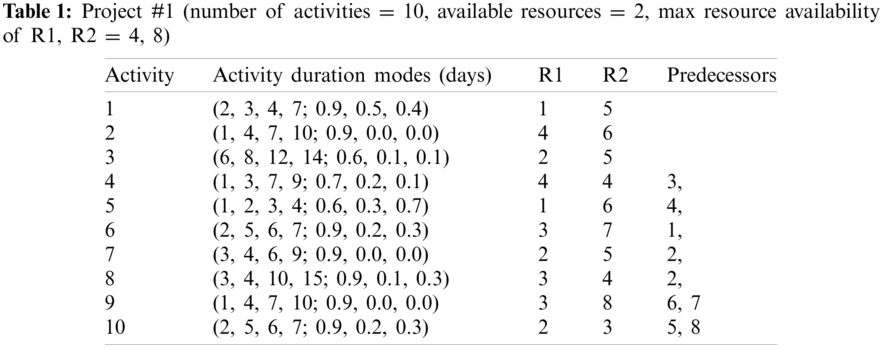
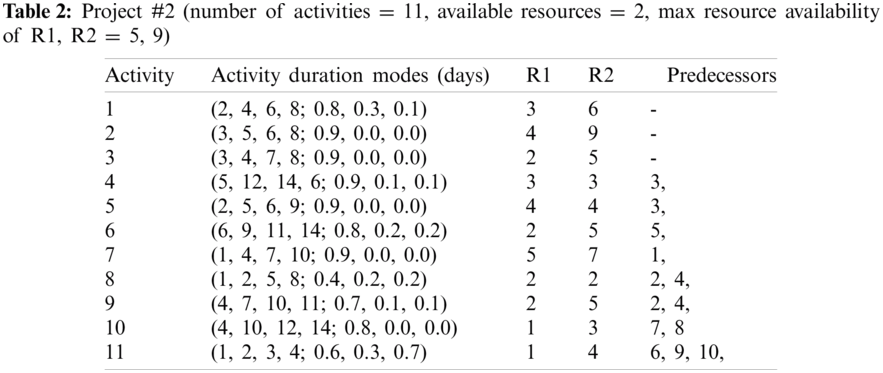

Projects differ in many aspects, such as the number of activities, precedence relationships between the activities, level of resource availability and resources required, different modes of activity durations, and project topography. Thus, no heuristic rule achieves the best scheduling results for all projects. In this section, the five PHR are applied to four multi-mode resource-constrained project datasets for scheduling them. The results of the PHR are very promising, as shown below, where each of the five PHR achieves the best scheduling results for each of the four multiple resources constrained project data sets.
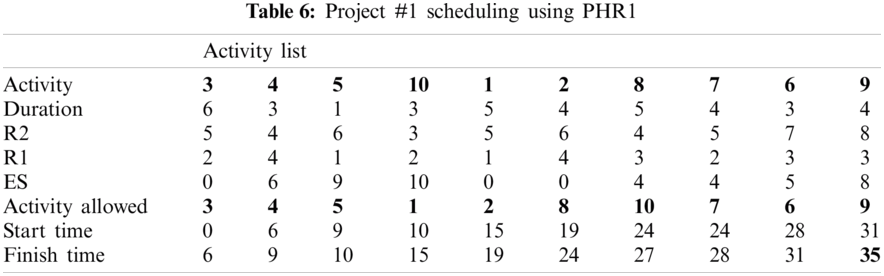
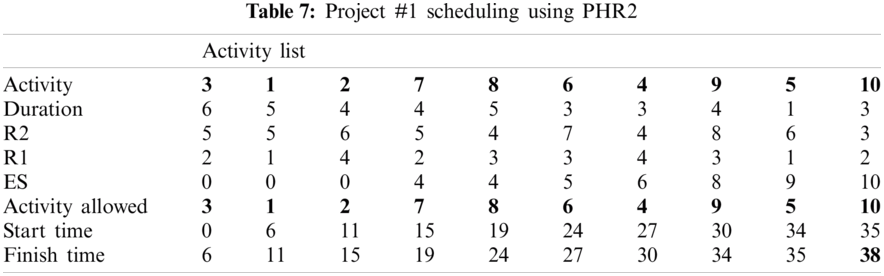
For example, PHR1 achieved the best scheduling results for Projects #1 and #2, PHR2 achieved the best scheduling result for Projects#3 and #4. PHR3 achieved the best scheduling result for Project #3. PHR4 achieved the best scheduling result for Project #4, and PHR5 achieved the best scheduling result for Project #1. All results for scheduling the five projects examples using the PHR under different multi-mode duration conditions are listed in Tabs. 6–27. Also, some detailed scheduling results using set of old heuristic rules are listed in Tabs. 28–33 as shown below:
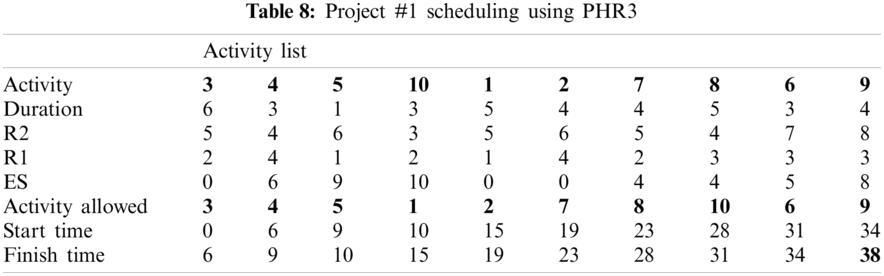
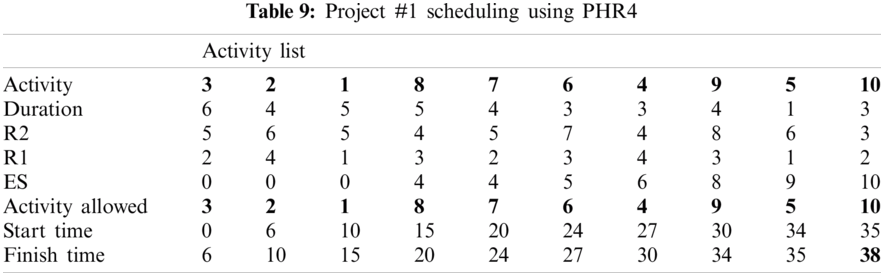
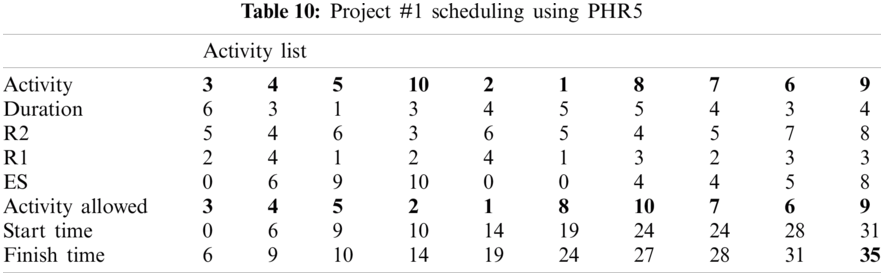
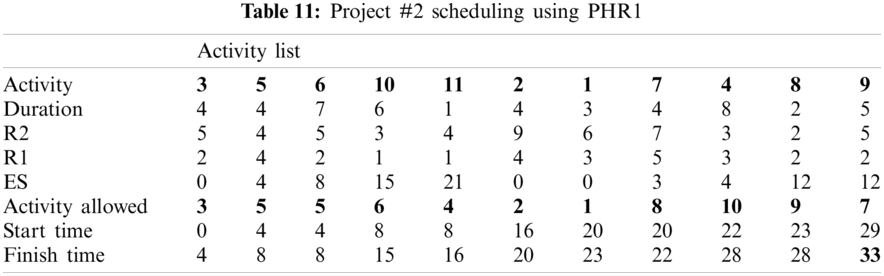

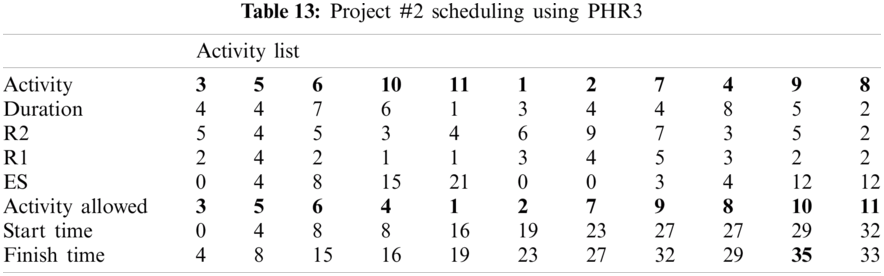
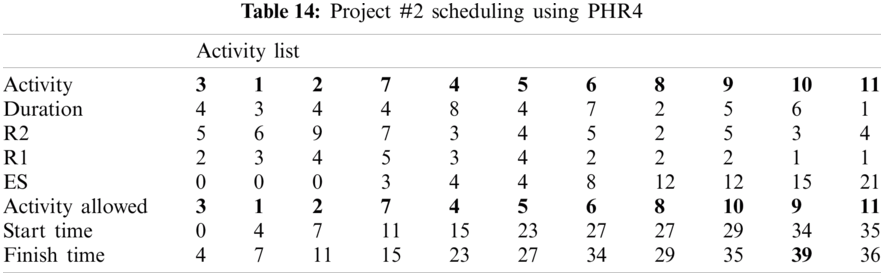
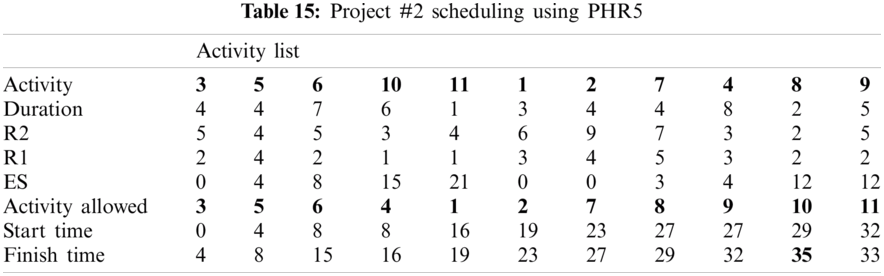
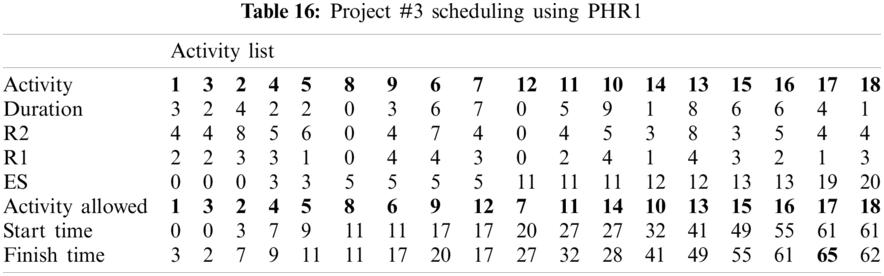
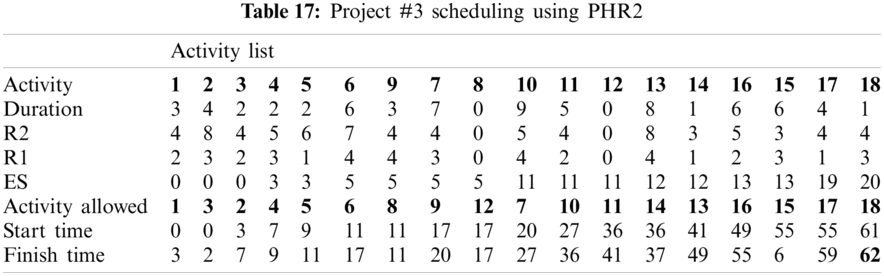
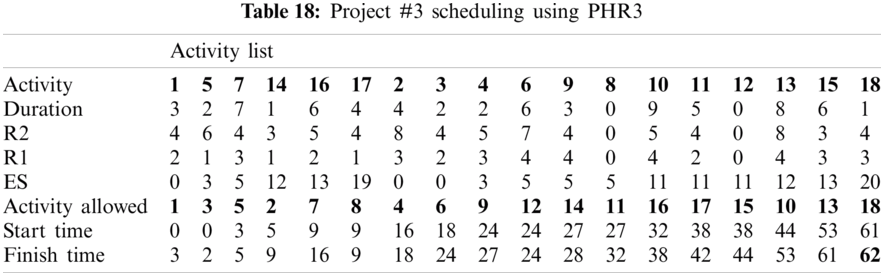
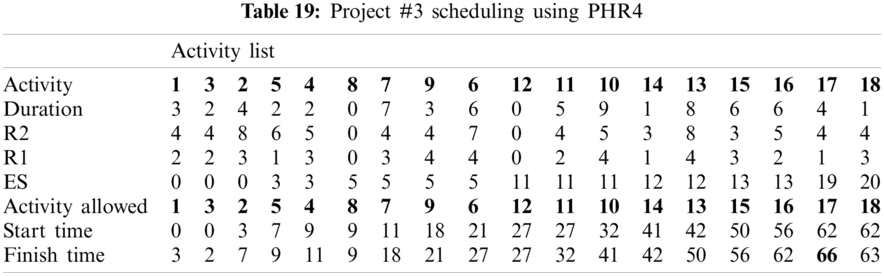
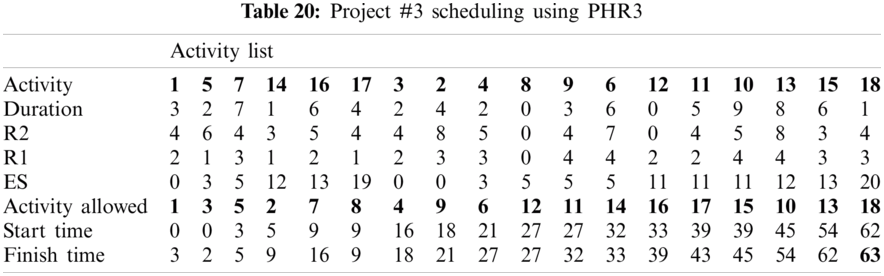
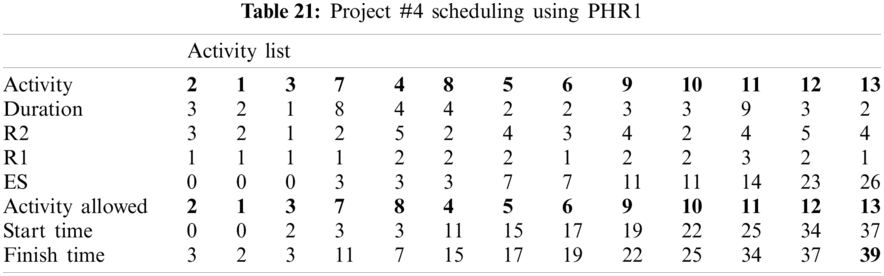
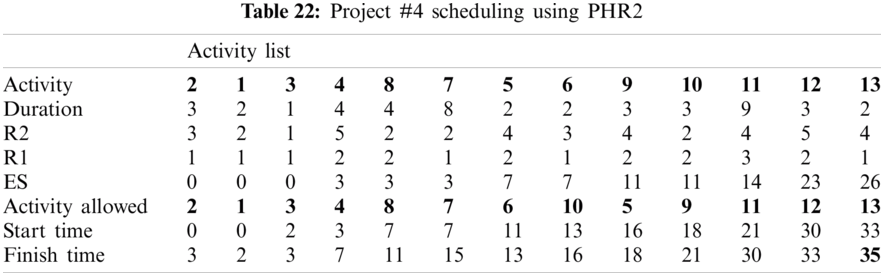
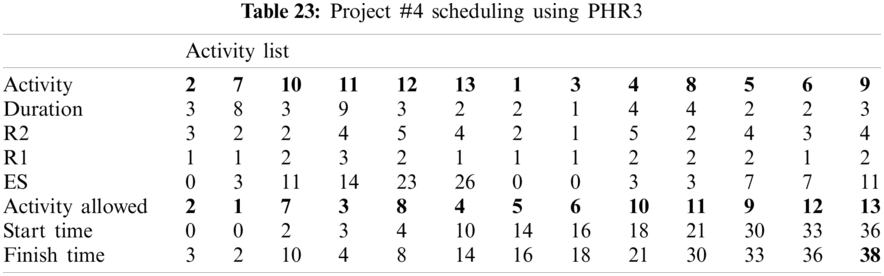
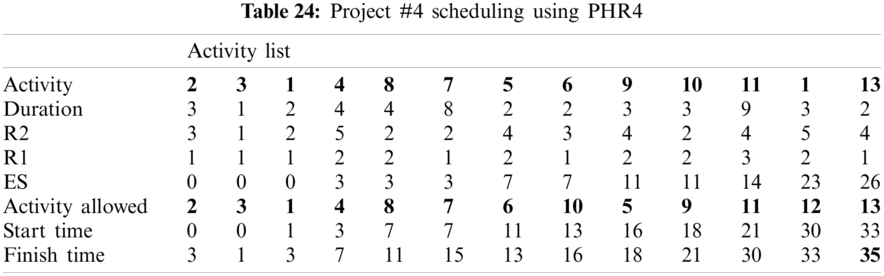
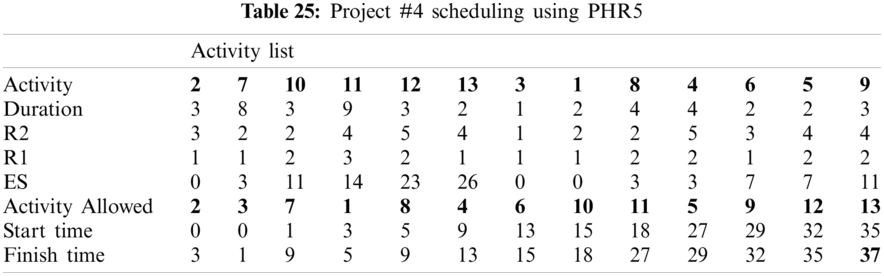
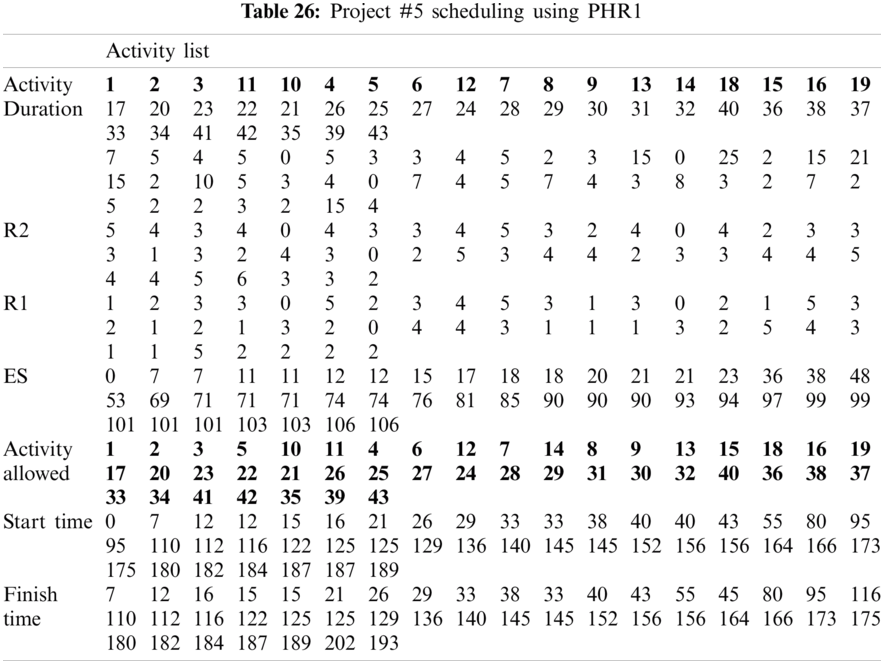
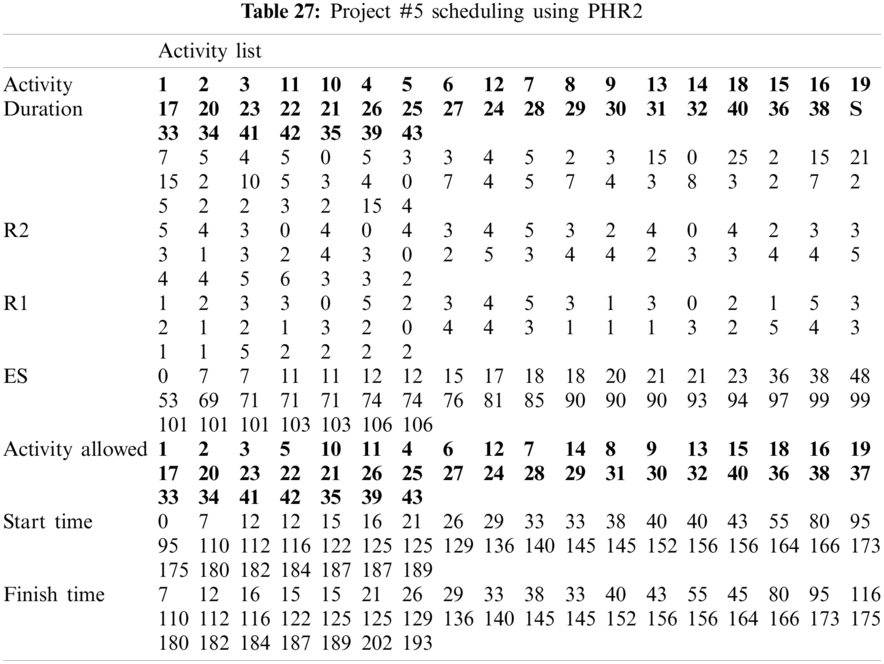
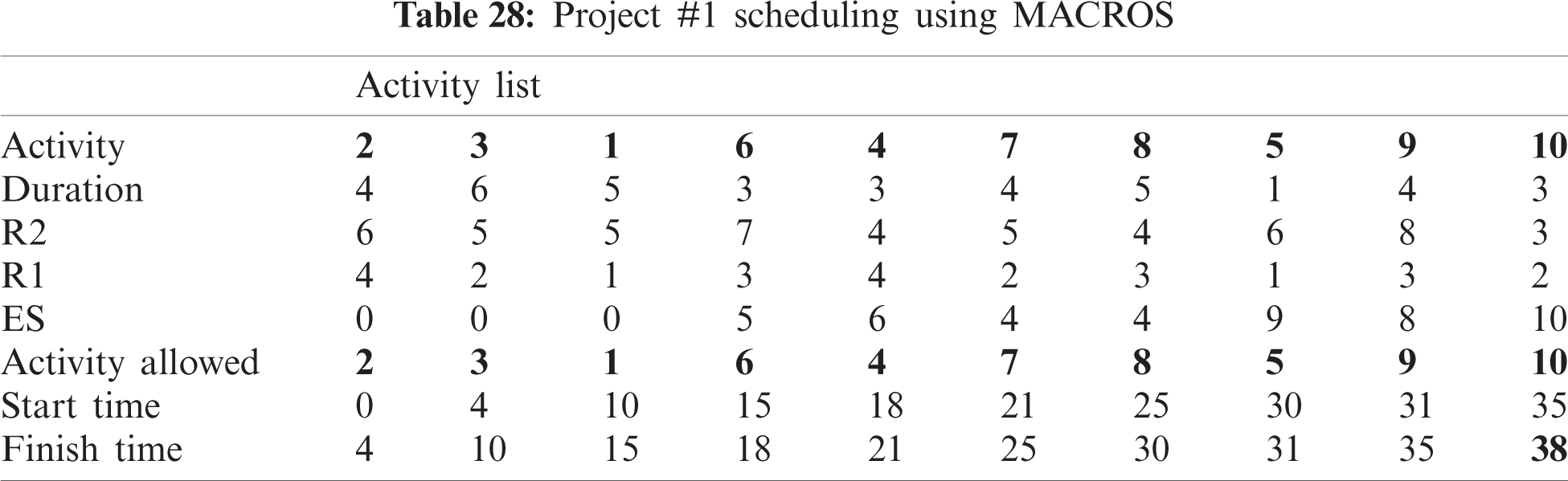
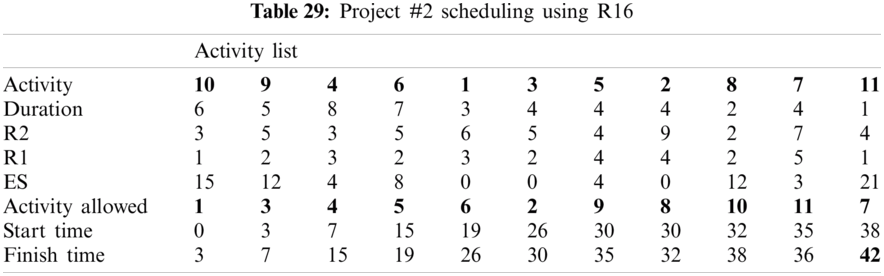
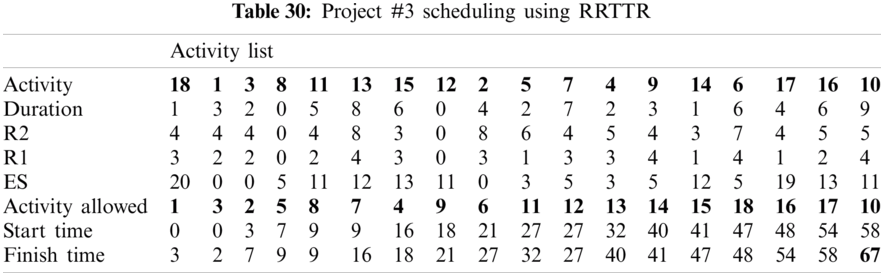
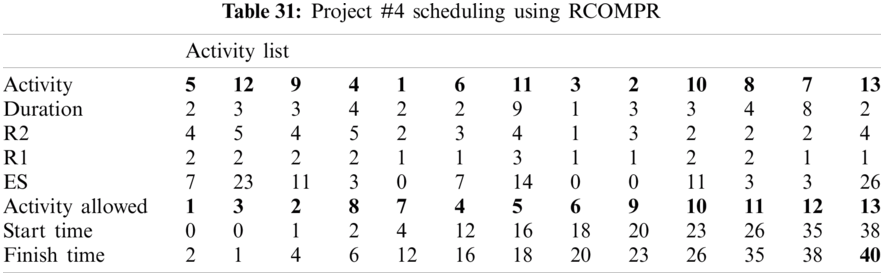
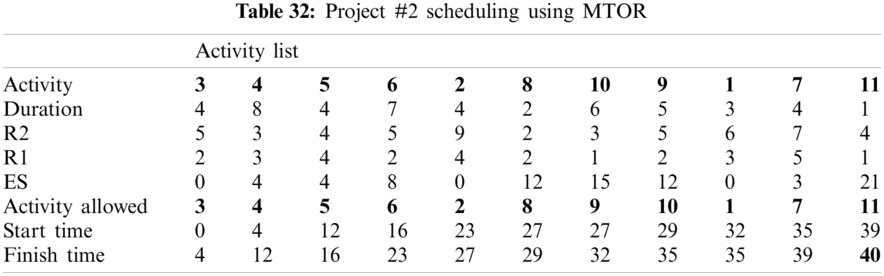
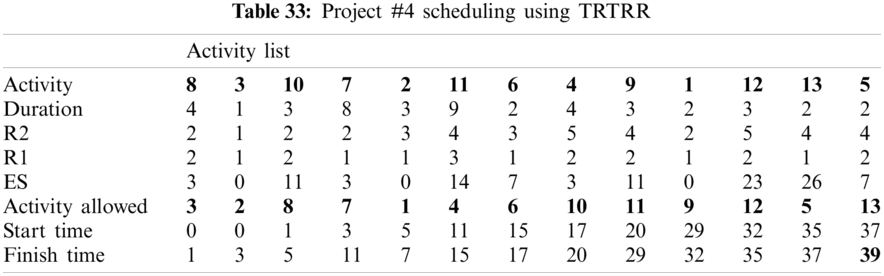
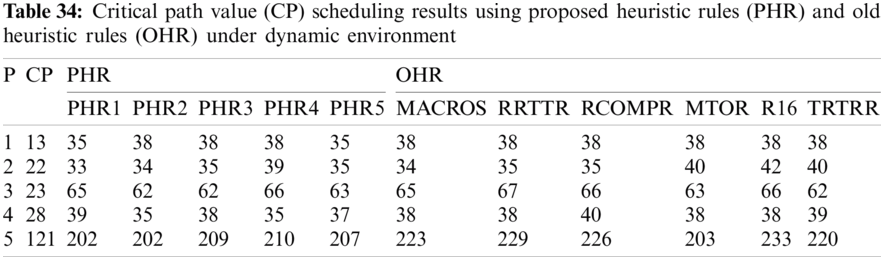
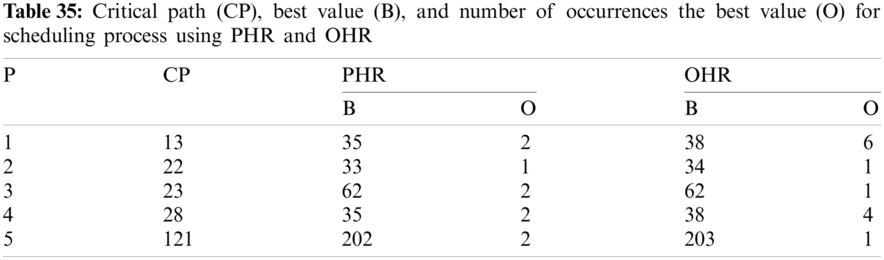
In this subsection, the obtained results rendered by the proposed priority rules under the dynamic environment for the four test problems (as shown in Subsection 4.2) are compared by the results obtained from six well-known heuristics rules rendered for the same test problems. This comparison is summed up in Tab. 34, which displays the results of the scheduling process for four multi-mode resource-constrained projects using both the proposed five heuristic priority rules and six well-known old rules (MACROS, RRTTR, RCOMPR, MTOR, R16, TRRTRR [2,4]). Tab. 35 lists the critical path value (CP), the best value (B) for scheduling results obtained by the PHR and the old heuristic rules (OHR), and the number of occurrences (O) for this best value when the required scheduling resources are two critical resources. Tabs. 34 and 35 show that the five PHR have achieved good results compared with the old rules and are among the most common rules used in scheduling resource-constrained projects.
The best results for scheduling the five previous projects are obtained from scheduling these projects using the PHR under the dynamic and multi-mode conditions, as shown in Figs. 4–7.
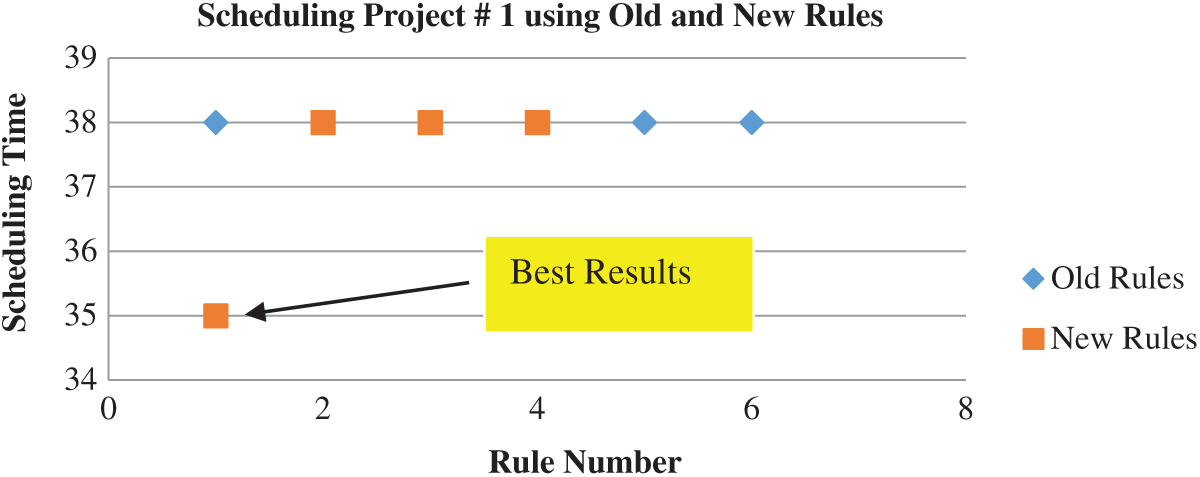
Figure 4: Scheduling results of project #1
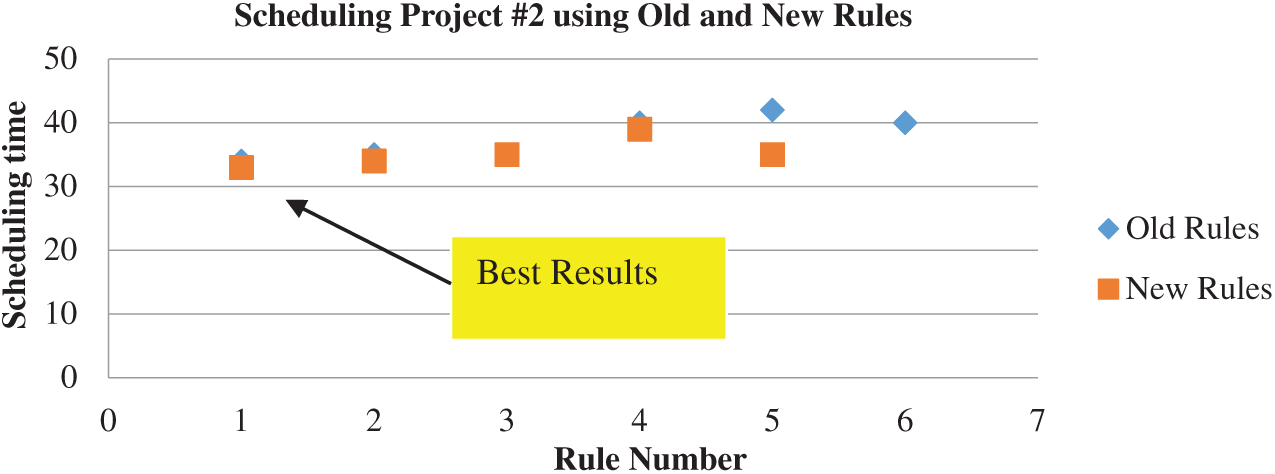
Figure 5: Scheduling results of project #2
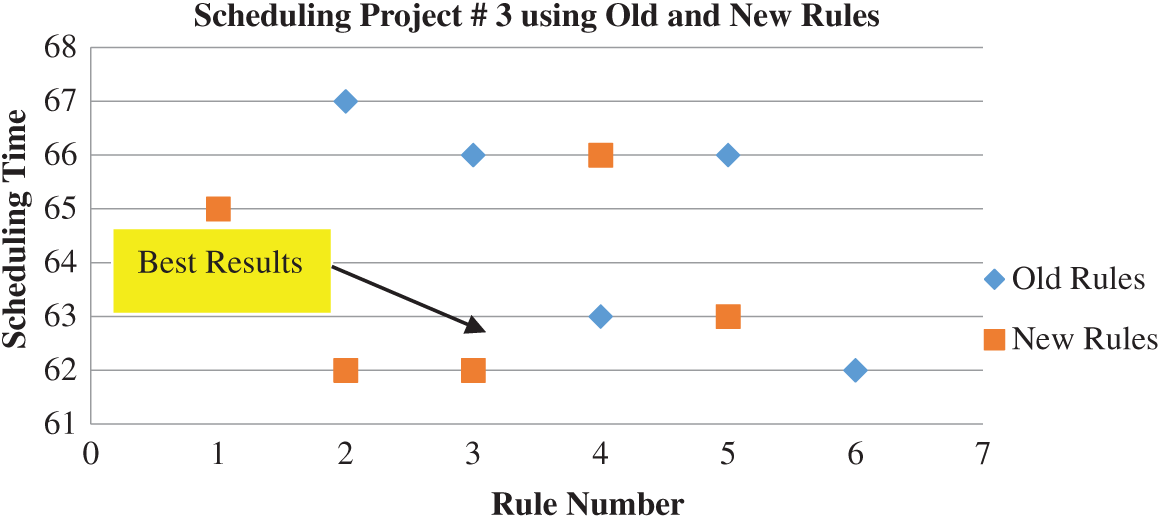
Figure 6: Scheduling results of project #3
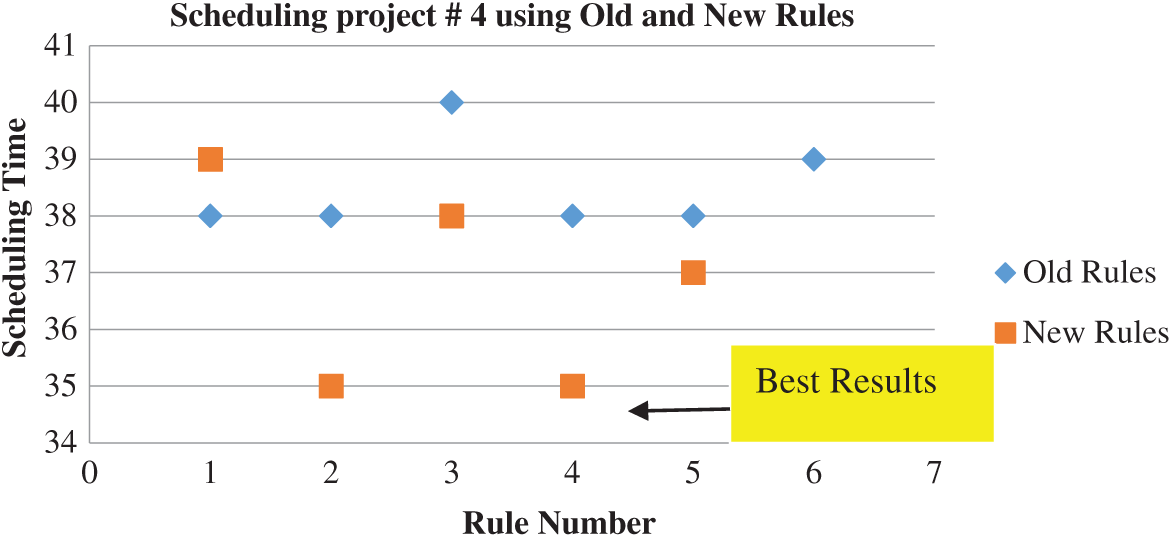
Figure 7: Scheduling results of project #4
Project scheduling is the process of best allocating limited resources to execute activities with specific order relative to the precedence relationship, level of resources available, and resources required by activities for achieving a set of objectives and multi-mode conditions. Heuristic procedures are one of the most commonly used procedures in solving the resource allocation problem and scheduling multi-mode resource-constrained project problems. Given that the estimation of the activity times in project management is always surrounded by a high degree of ambiguity and uncertainty, dynamic scheduling problems (multi-mode conditions) are needed for realistic situations.
In this paper, we proposed five composite priority rules for scheduling multi-mode resource-constrained projects under dynamicity features for more realistic situations. Five projects are considered test problems for these proposed heuristic rules. Results are very promising because the rules achieve better scheduling dates in many test case problems. The proposed model is based on dynamic features for project topography.
Funding Statement: This work was supported by the Soonchunhyang University Research Fund.
Ethical Approval: This article does not contain any studies with human participants or animals performed by any of the authors.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. A. Najafi and F. Azimi, “A priority rule-based heuristic for resource investment project scheduling problem with discounted cash flows and tardiness penalties,” Mathematical Problems in Engineering, vol. 2009, no. 2, pp. 1–11, 2009. [Google Scholar]
2. A. Atef, M. Abdel-Baset and I. El-henawy, “Composite heuristic priority rules-based on tie-breakers for scheduling multiple-constrained resource projects,” Advances in Information Sciences and Service Sciences, vol. 7, no. 3, pp. 43–52, 2015. [Google Scholar]
3. M. Vanhoucke, “Optimizing regular scheduling objectives: Schedule generation schemes,” Pm Knowledge Center, vol. 13, no. 2, pp. 12–25, 2012. [Google Scholar]
4. M. Shouman, M. Ibrahim and A. Elfrgany, “Some heuristic rules for scheduling single and multiple resources constrained projects,” AEJ Journal, vol. 20, no. 2, pp. 12–18, 2007. [Google Scholar]
5. M. Shtmman, A. Ghafagy, M. Zaghloul and A. BouShaala, “New heuristics for scheduling single constrained resource projects,” Alexandria Engineering Journal, vol. 38, no. 3, pp. 12–31, 1999. [Google Scholar]
6. R. Kolisch and S. Hartmann, “Experimental investigation of heuristics for resource-constrained project scheduling: An update,” European Journal of Operational Research, vol. 174, no. 1, pp. 23–37, 2006. [Google Scholar]
7. A. Lova, P. Tormos and F. Barber, “Multi-mode resource-constrained project scheduling: Scheduling schemes, priority rules and mode selection rules inteligencia artificial,” Revista Iberoamericana de Inteligencia Artificial, vol. 10, no. 30, pp. 69–86, 2006. [Google Scholar]
8. P. Myszkowski, M. Skowronski and L. Podlodowski, “Novel heuristic solutions for multi-skill resource-constrained project scheduling problem,” in Federated Conf. on Computer Science and Information Systems, IEEE, Krakow, Poland, pp. 159–166, 2013. [Google Scholar]
9. S. Colak, A. Agarwal and S. Erenguc, “Multi-mode resource-constrained project-scheduling problem with renewable resources: New solution approaches,” Journal of Business & Economics Research, vol. 11, no. 11, pp. 455–468, 2013. [Google Scholar]
10. R. M. Chen and S. Lo, “Using an enhanced ant colony system to solve resource-constrained project scheduling problem,” International Journal of Computer Science and Network Security, vol. 6, no. 1, pp. 75–84, 2006. [Google Scholar]
11. A. Andreica and C. Chira, “Best-order crossover in an evolutionary approach to multi-mode resource-constrained project scheduling,” International Journal of Computer Information System and Industrial Management Applications, vol. 6, no. 1, pp. 364–72, 2014. [Google Scholar]
12. J. Buddhakulsomsiri and D. Kim, “Priority rule-based heuristic for multi-mode resource-constrained project scheduling problems with resource vacations and activity splitting,” European Journal of Operational Research, vol. 178, no. 2, pp. 374–390, 2007. [Google Scholar]
13. T. Browning and A. Yassine, “Resource-constrained multi-project scheduling: Priority rule performance revisited,” International Journal of Production Economics, vol. 126, no. 2, pp. 212–228, 2010. [Google Scholar]
14. L. He and L. Zhang, “Dynamic priority rule-based forward-backward heuristic algorithm for resource levelling problem in construction project,” Journal of the Operational Research Society, vol. 64, no. 8, pp. 1106–1117, 2013. [Google Scholar]
15. A. Singh, “Resource-constrained multi-project scheduling with priority rules & analytic hierarchy process,” Procedia Engineering, vol. 69, no. 2, pp. 725–734, 2014. [Google Scholar]
16. A. Atef, M. Abdel-Baset and I. El-henawy, “Project scheduling: Survey and research potentials,” International Journal of Computer Applications Technology and Research, vol. 4, no. 4, pp. 12–18, 2015. [Google Scholar]
17. C. Kellenbrink and S. Helber, “Quality-and profit-oriented scheduling of resource-constrained projects with flexible project structure via a genetic algorithm,” European Journal of Industrial Engineering, vol. 10, no. 5, pp. 574–595, 2016. [Google Scholar]
18. V. Bilolikar, K. Jain and M. Sharma, “An adaptive crossover genetic algorithm with simulated annealing for multi mode resource constrained project scheduling with discounted cash flows,” International Journal of Operational Research, vol. 25, no. 1, pp. 28–46, 2016. [Google Scholar]
19. S. Nikoofal, M. Bagheri and M. Assadi, “Multi-objective model for solving resource levelling problem with discounted cash flows,” International Transactions in Operational Research, vol. 25, no. 6, pp. 2009–2030, 2018. [Google Scholar]
20. R. Zamani, “An effective mirror-based genetic algorithm for scheduling multi-mode resource constrained projects,” Computers & Industrial Engineering, vol. 127, no. 2, pp. 914–924, 2019. [Google Scholar]
21. K. Polat, S. Şahan, H. Kodaz and S. Güneş, “Breast cancer and liver disorders classification using artificial immune recognition system (AIRS) with performance evaluation by fuzzy resource allocation mechanism,” Expert Systems with Applications, vol. 32, no. 1, pp. 172–183, 2007. [Google Scholar]
22. S. Mojtaba, P. Azimi, A. Ghamginzadeh and A. Rahimzadeh, “A new fuzzy multi-objective multi-mode resource-constrained project scheduling model,” International Journal of Mathematics in Operational Research, vol. 11, no. 1, pp. 45–66, 2017. [Google Scholar]
23. V. Moradi, and L. Khanli, “A hybrid genetic algorithm and fuzzy set applied to multi-mode resource-constrained project scheduling problem,” Journal of Intelligent & Fuzzy Systems, vol. 26, no. 3, pp. 1103–1112, 2014. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |