Big Data Knowledge Pricing Schemes for Knowledge Recipient Firms

Chuanrong Wu; Haotian Cui; Zhi Lu; Xiaoming Yang; Mark McMurtrey

doi:10.32604/cmc.2021.019969

Processing math: 56%

[BACK]

Computers, Materials & Continua DOI:10.32604/cmc.2021.019969
Article

Big Data Knowledge Pricing Schemes for Knowledge Recipient Firms

Chuanrong Wu1,*, Haotian Cui1, Zhi Lu2, Xiaoming Yang3 and Mark E. McMurtrey4

1School of Economy and Management, Changsha University of Science & Technology, Changsha, China
2Peter B. Gustavson School of Business, University of Victoria, Canada
3College of Business Administration, University of Nebraska, Omaha, 68182, USA
4College of Business, University of Central Arkansas, 72035, USA
*Corresponding Author: Chuanrong Wu. Email: wuchuanrong01@126.com
Received: 02 May 2021; Accepted: 03 June 2021

Abstract: Big data knowledge, such as customer demands and consumer preferences, is among the crucial external knowledge that firms need for new product development in the big data environment. Prior research has focused on the profit of big data knowledge providers rather than the profit and pricing schemes of knowledge recipients. This research addresses this theoretical gap and uses theoretical and numerical analysis to compare the profitability of two pricing schemes commonly used by knowledge recipients: subscription pricing and pay-per-use pricing. We find that: (1) the subscription price of big data knowledge has no effect on the optimal time of knowledge transaction in the same pricing scheme, but the usage ratio of the big data knowledge affects the optimal time of knowledge transaction, and the smaller the usage ratio of big data knowledge the earlier the big data knowledge transaction conducts; (2) big data knowledge with a higher update rate can bring greater profits to the firm both in subscription pricing scheme and pay-per-use pricing scheme; (3) a knowledge recipient will choose the knowledge that can bring a higher market share growth rate regardless of what price scheme it adopts, and firms can choose more efficient knowledge in the pay-per-use pricing scheme by adjusting the usage ratio of knowledge usage according to their economic conditions. The model and findings in this paper can help knowledge recipient firms select optimal pricing method and enhance future new product development performance.

Keywords: Big data knowledge; knowledge transfer; subscription pricing; pay-per-use pricing; new product development performance

1 Introduction

The rapid development of information technology, Internet of Things, social networking, and cloud computing has ushered in a new era of big data. Against this unprecedentedly available data as a backdrop, the knowledge extracted from big data can help firms guide decision-making, cut costs and increase sales [1,2]. Big data knowledge, such as customer demands and user preferences, is among the important external knowledge that firms need for new product development in the hyper-competitive market. The general practice for firms to get big data knowledge is through knowledge transactions. In essence, the knowledge transaction is a process of knowledge transfer, in which knowledge sources own “exclusive” control of knowledge and then obtain economic benefits from the knowledge transaction [3]. The general agreement is that transaction of knowledge is different from that of ordinary commodities inasmuch as the value of knowledge can only be calculated after it is used, and the price of knowledge cannot be determined by the new product development cost [4].

Scholars have researched extensively from the perspective of pricing strategies for private knowledge such as private intellectual property licensing [4–6]. Nonetheless, the characteristics of big data knowledge including open-source, dynamic and multi-source heterogeneity, make its transaction and pricing methods different from that of the private knowledge [7,8]. Prior studies have also introduced an array of pricing schemes for big data knowledge (e.g., cloud services), such as value-based pricing, cost-based pricing, customer-based pricing, competition-based pricing, pay-for-resources pricing, subscription pricing, pay-as-you-go pricing and other dynamic pricing methods [4,9,10]. To date, the most popular pricing schemes for big data knowledge transactions are subscription pricing and pay-per-use pricing [11]. However, these pricing methods mainly focus on firms’ profitability from a big data knowledge provider’s standpoint rather than from that of a knowledge recipient. In the big data environment, firms need big data knowledge for new product development to survive in the marketplace, especially customer demands and consumer preferences knowledge garnered from a host of sources. To our knowledge, prior research has not examined the pricing schemes in big data knowledge transactions from the perspective of firms as knowledge recipients—a theoretical gap addressed by the present research and with practical implications for their knowledge transaction and new product development. More specifically, this study uses theoretical and numerical analysis to compare the profitability of two widely-employed pricing schemes among big data knowledge recipients: subscription pricing and pay-per-use pricing. The present research findings help knowledge recipient firms select the optimal time of knowledge transactions and consequently enhance their future new product performance.

The rest of the paper proceeds as follows. Section 2 discusses the conceptual model and hypotheses for pricing schemes of big data knowledge in new product development. A price-making model of big data knowledge is presented in Section 3. Simulation experiments and comparative analysis of the price schemes are described in Section 4. Section 5 concludes and discusses the limitations and future research directions.

2 Conceptual Model and Model Hypotheses

2.1 Conceptual Model for Pricing Schemes of Big Data Knowledge

Knowledge transaction is a process of knowledge transfer [3]. Therefore, we could employ the decision model of knowledge transfer for the price decision of the knowledge recipient. Suppose a firm needs to purchase one type of big data knowledge from a big data knowledge provider for its new product development. It would face two major decisions. One is which pricing scheme to choose, and the other is when to carry out new product development with the acquired big data knowledge. The selection of a pricing scheme requires a firm to take a comparative analysis of alternative pricing schemes. Meanwhile, the timing of new product development denotes the selection of optimal time of knowledge transactions.

To compare pricing scheme and select optimal time of knowledge transactions for new product development, a pricing decision model can be established based on the maximization of the discounted expected profit (DEP) of a knowledge recipient firm, which buys one type of big data knowledge from a big data knowledge provider for new product development. The total DEP includes the DEP before knowledge transfer, the DEP after knowledge transfer, and the transfer cost. The pricing scheme of modeling is shown in Fig. 1.

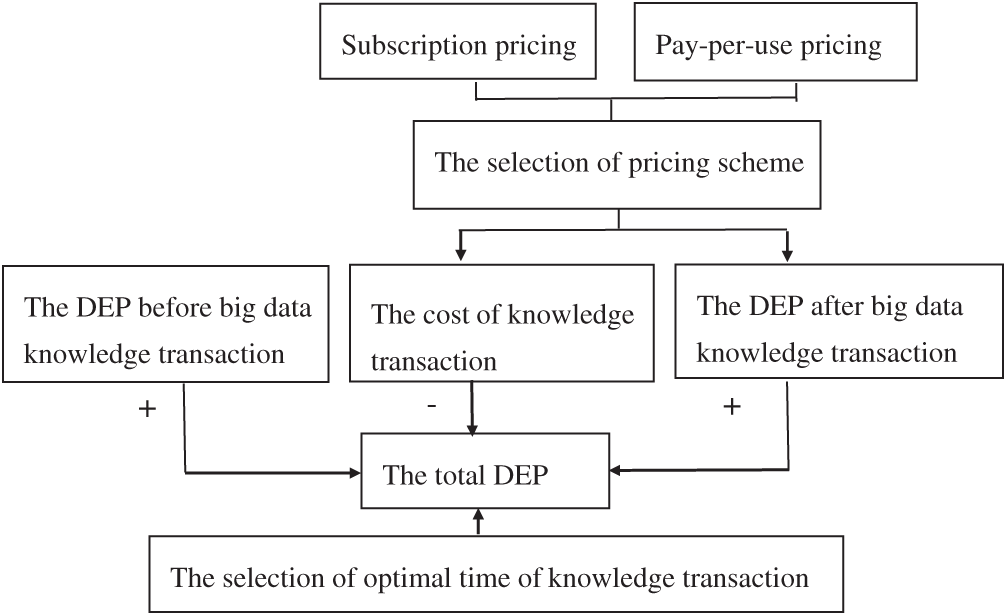
images

Figure 1: Conceptual model for pricing schemes of big data knowledge

2.2 Model Hypotheses

Hypothesis 1. $Vi$ is a firm that needs a type of big data knowledge for new product development, $BDk$ is a big data knowledge provider, and $Vi$ will buy a type of big data knowledge from $BDk$ . $Vi$ will take new product development immediately after big data knowledge transaction, and $Vi$ produces only one product.

Hypothesis 2. $k$ is the subscription price of the big data knowledge, and $k$ is a constant.

Hypothesis 3. $q(0≤q≤1)$ represents the usage ratio of the big data knowledge. When $q=1$ , it means the firm has purchased all the license rights of the big data knowledge.

Hypothesis 4. The cost of big data knowledge transaction $K$ consists of the fixed cost $kfix$ and the variable cost $kvar$ .

Hypothesis 5. The update rate of big data knowledge at the starting point is $β(0<β<1)$ .

Hypothesis 6. $ρ(0<θ1<ρ<1)$ is the growth rate of the market share of $Vi$ in the first $L2$ periods immediately after big data knowledge transaction and new product development when $Vi$ adopts subscription pricing in the big data knowledge transaction.

Hypothesis 7. $Vi$ conducts knowledge transaction at time period $T$ , and develops new product immediately after the knowledge transaction. $ζ(T)$ is the DEP of $Vi$ before knowledge transaction and new product development, $ξ(T)$ is the DEP of $Vi$ after the knowledge transaction and new product development, and $K(T)$ is the cost of knowledge transaction. The total DEP of $Vi$ is denoted as $ψ(T)$ and we shall have $ψ(T)=ζ(T)+ξ(T)−K(T)$ .

We keep the same assumptions and variables unchanged in order to verify the validity of the proposed model and compare it with the research results of previous models. Some other assumptions and variables are as follows: the total market volume of the new product is $Q$ ; the price of the new product is $p$ ; the marginal cost of the new product in the starting period is $MC$ ; the knowledge absorption capacity of $Vi$ is $α$ ( $0<α<1$ ); the market share of $Vi$ in the starting period is $ϕ$ ; the total market volume increases at a rate of $θ1(0<θ1<1)$ in the first $L1$ periods and decreases at a rate of $θ(0<θ<1)$ in other periods; the discount rate is $r$ ; the life cycle of the new product is $N$ , and $N$ is renumbered after the big data knowledge transaction and knowledge transfer. The detailed assumptions can be referred to Wu et al. [12].

3 Pricing Decision Model of Big Data Knowledge Transaction

3.1 DEP Before Big Data Knowledge Transaction and New Product Development

Given there is no knowledge transaction and new product development at this stage, $Vi$ produces a product using its prior knowledge. The DEP before knowledge transaction and new product development can be calculated by sales revenue minus production costs, which is as shown in Eq. (1). The detailed calculation method of expected profits can be referred to in the research of Wu et al. [12].

$ζ(T)={pQϕ∑n=1T(1+θ1)nrn−QϕMC∑n=1T(1+θ1)nαnrnT≤L1pQϕ∑n=1L1(1+θ1)nrn−QϕMC∑n=1L1(1+θ1)nαnrn+pQϕ(1+θ1)L1∑n=L1+1T(1−θ)n−L1rn−QϕMC(1+θ1)L1∑n=L1+1T(1−θ)n−L1αnrnT>L1$ (1)

3.2 Cost of Knowledge Transaction

From hypotheses 2–4, the cost of knowledge transaction $K$ is formed by the fixed cost $kfix$ and the variable cost $kvar$ . The fixed transfer cost $kfix$ can be calculated by the subscription price and the usage ratio of the big data knowledge. When $q=1$ , it means that $Vi$ adopts a subscription pricing scheme in the big data knowledge transaction. When $0<q<1$ , it means that $Vi$ adopts a pay-per-use pricing scheme in the big data knowledge transaction. Assume $k$ is the subscription price, so the fixed cost $kfix$ can be calculated by Eq. (2).

$kfix=qk(0≤q≤1)$ (2)

According to hypotheses 3 and 5, $q(0≤q≤1)$ represents the usage ratio of the big data knowledge, and $β(0<β<1)$ is the update rate of the big data knowledge at the starting point. Thus, the update rate of the big data knowledge at the starting point is $qβ$ when $Vi$ adopts pay-per-use pricing scheme in the big data knowledge transaction. The variable cost $kvar$ is related to the knowledge absorption capacity of $Vi$ and knowledge distance between original knowledge and the big data knowledge. Suppose $F$ is the coefficient of variable cost, and it is a constant. Then, the variable cost of big data knowledge transaction can be computed by Eq. (3).

$kvar=F[αT−(qβ)T](0≤q≤1)$ (3)

After discounting the fixed cost and the variable cost to the starting point, the total cost of big data knowledge transaction can be expressed as Eq. (4).

$K(T)=[qk+F[αT−(qβ)T]]rT(0≤q≤1)$ (4)

3.3 DEP After Big Data Knowledge Transaction and New Product Development

According to hypotheses 3 and 6, $q(0≤q≤1)$ represents the usage ratio of the big data knowledge, and $ρ(0<θ1<ρ<1)$ is the growth rate of the market share of $Vi$ in the first $L2$ periods immediately after big data knowledge transaction and new product development when $Vi$ adopts subscription pricing scheme in the big data knowledge transaction. Then, the growth rate of the market share of $Vi$ in the first $L2$ periods immediately after big data knowledge transaction and new product development is $qρ$ when $Vi$ adopts pay-per-use pricing scheme in the big data knowledge transaction.

If $Vi$ takes big data knowledge transaction and new product development at time period $T$ , when $T≤L1$ , the market share of $Vi$ in time period $T$ is $ϕ(1+θ1)T$ . When $T>L1$ , the market share of $Vi$ is $ϕ(1+θ1)L1(1−θ)T−L1$ . After the period of time $T$ , new big data knowledge begins to work on the market share of $Vi$ . From Hypotheses 3 and 6, the market share of $Vi$ will increase at a rate of $qρ$ in the $L2$ periods immediately after time period $T$ , and it will then decay at a rate of $θ$ . Hence, the market share of $Vi$ in period $n$ can be denoted as Eq. (5).

$λ(n,T)={ϕ(1+θ1)T(1+qρ)nn≤L2, T≤L1ϕ(1+θ1)L1(1−θ)T−L1(1+qρ)nn≤L2, T>L1ϕ(1+θ1)T(1+qρ)n(1−θ)n−L2n>L2, T≤L1ϕ(1+θ1)L1(1−θ)T−L1(1+qρ)L2(1−θ)n−L2n>L2, T>L1$ (5)

From hypothesis 5, the update rate of big data knowledge is $β(0<β<1)$ when $Vi$ adopts a subscription pricing scheme in the big data knowledge transaction. Then, the update rate of big data knowledge is $qβ(0<β<1)$ when $Vi$ adopts a pay-per-use pricing scheme in the big data knowledge transaction. The update rate of big data knowledge $β$ is set at the starting point. Considering the time cumulative effect, the big data knowledge at time period $T$ has been updated by $(qβ)T$ , which can reduce the marginal cost of $Vi$ at time period $T$ to $MC(qβ)T$ . The knowledge absorption capacity of $Vi$ is $α$ . Then, the marginal cost of $Vi$ at time period $T$ will become $MC(qβ)Tαn$ . The total production cost in time period $n$ after knowledge transaction and new product development is $Qλ(n,T)MC(qβ)Tαn$ . By subtracting the total production cost from the sales revenue $pQλ(n,T)$ and discounting the profits in time period $n$ to the starting point by multiplying $rTrn$ , the DEP after big data knowledge transaction and new product development is shown in Eq. (6).

$ξ(T)=∑n=1NpQλ(n,T)rTrn−∑n=1NQλ(n,T)MC(qβ)TαnrTrn$ (6)

Substitute $λ(n,T)$ in Eq. (6) by using Eq. (5); the DEP after the big data knowledge transaction and new product development can be expressed as Eq. (7).

$ξ(T)={pQϕ(1+θ1)TrT∑n=1L2(1+qρ)nrn−MCQϕ(1+θ1)TrT(qβ)T∑n=1L2(1+qβ)nαnrn+pQϕ(1+θ1)T(1+qρ)L2rT∑n=L2+1N(1−θ)n−L2rn−MCQϕ(1+θ1)TrT(qβ)T(1+qρ)L2∑n=L2+1N(1−θ)n−L2αnrnT≤L1pQϕ(1+θ1)L1(1−θ)T−L1rT∑n=1L2(1+qρ)nrn−MCQϕ(1+θ1)L1(1−θ)T−L1βTrT∑n=1L2(1+qρ)nαnrn+pQϕ(1+θ1)L1(1−θ)T−L1(1+qρ)L2rT∑n=L2+1N(1−θ)n−L2rn−MCQϕ(1+θ1)L1(1−θ)T−L1rT(qβ)T(1+qρ)L2∑n=L2+1N(1−θ)n−L2αnrnT>L1$ (7)

3.4 Total DEP

For a firm that buys a certain type of big data knowledge and utilizes that knowledge for its new product development, its goal oftentimes is to maximize the present value of the expected profit of the new product. Therefore, this given firm’s choice of pricing scheme and optimal time of knowledge transaction is to find the maximum of the total DEP $ψ(T)$ of $Vi$ for the given parameters. Taken together, the pricing decision model of $Vi$ can be expressed as Eq. (8).

$maxψ(T)=max(ζ(T)+ξ(T)−K(T))$ (8)

4 Simulation Experiments

4.1 Model Solution and Parameter Setting

$ψ(T)$ is a piecewise continuous differential function of $T$ . Therefore, we can find the maximum of $ψ(T)$ in a closed interval $0≤T≤N$ , which is the maximum profits in the life cycle of the new product. Accordingly, we obtain the optimal time of the big data knowledge transaction and new product development with the given pricing scheme.

Similar to a previous research model of knowledge transfer in a big data environment [13–15], we set some parameters in our model at the same values as follows. The total product sales $Q=1000$ ; the price of per unit product $p=60$ ; the marginal cost at the beginning period $MC=40$ ; the total market volume of $Vi$ increases in the first $L1=3$ period before the big data knowledge transaction and new product development; the natural attenuation rate of market volume $θ=3%$ ; the market share of $Vi$ in the starting period $ϕ=8%$ ; the knowledge absorption capacity $α=95%$ ; the discount rate is 10% and $r=0.9$ ; the variable cost coefficient of knowledge transaction $F=1000$ ; the subscription price of the big data knowledge $k=80$ ; and the update rate of big data knowledge $β=88%$ .

4.2 Simulation Experiment

4.2.1 Simulation with the Usage Ratio of the Big Data Knowledge $q=1$

According to prior assumptions and hypotheses, $q(0≤q≤1)$ represents the usage ratio of the big data knowledge. When $q=1$ , it means the firm has purchased all the license rights of the big data knowledge. The experimental results in Fig. 2 are the same as those in Wu et al. [7]. We show that the cost of the subscription pricing scheme in this paper is consistent, which aligns with the price of big data knowledge in the model of Wu et al. [7]. Thus, our model is valid. Meanwhile, as the experimental results in Fig. 2 show, the optimal time of big data knowledge transaction is $T=6$ .

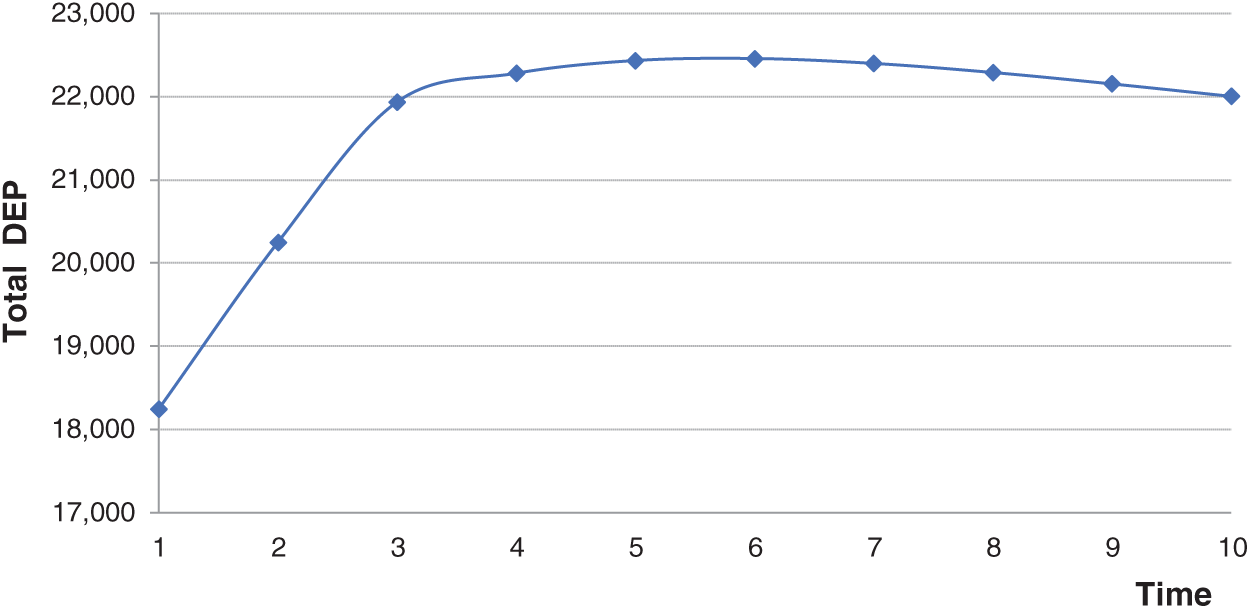
images

Figure 2: Changes of total DEP with $q=1$

4.2.2 Simulation with the Usage Ratio of the Big Data Knowledge $q(0<q<1)$

When $0<q<1$ , it means that $Vi$ adopts pay-per-use pricing scheme in the big data knowledge transaction. All the parameters except $q$ were set with the same values as in the previous section. Tab. 1 and Fig. 3 show the total DEP with $q$ varying from 0.2 to 0.8. The experimental results in Tab. 1 and Fig. 3 indicate that the smaller the usage ratio of the big data knowledge, the lower the cost and higher profit in the earlier time period, but the potential profitability brought by the big data knowledge is insufficient. These results suggest that big data knowledge transactions that adopted pay-per-use pricing scheme could bring higher economic benefits for the knowledge recipient firm in the short term.

From the experimental results in Tab. 1 and Fig. 3, we can also find that the optimal time of big data knowledge transaction change from $T=4$ to $T=3$ when the usage ratio of the big data knowledge $q$ decreases. It means that the optimal time of big data knowledge transaction will be earlier when the big data knowledge usage ratio is low. We reason that this is due to the fact that the cost that a firm spends on buying big data knowledge is lower when the usage ratio of the big data knowledge is low, and the lower cost consequently can bring higher revenue in a short time, hence firm will conduct knowledge transactions and new product development as soon as possible. Suppose the cost of the big data knowledge is low enough, the $Vi$ will take knowledge transaction and new product development immediately when it discovers the market share has the potential to decline. Meanwhile, we also find that the more the percentage of the big data knowledge purchased, the greater the potential growth of the new product development performance in the future. These simulation experiment results are in accordance with the actual economic situation, and therefore the model is valid.

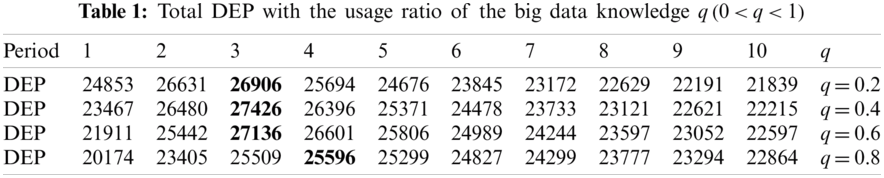
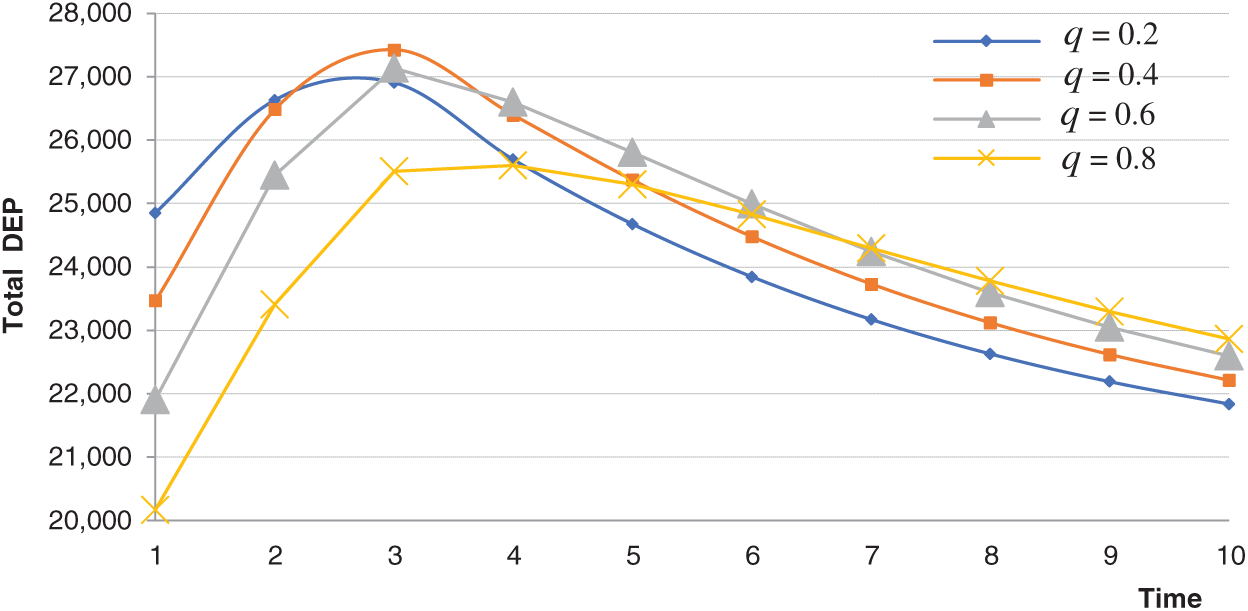
images

Figure 3: Changes of total DEP with $q(0<q<1)$

4.2.3 Simulation with $k$ and $q$

Let $q=1$ and adjust $k$ from 80 to 300, it means that the big data knowledge provider increases the price of its big data knowledge when $Vi$ adopts subscription pricing scheme in the big data knowledge transaction. From the experimental results in Fig. 4, the total DEPs decline, but the optimal time of knowledge transaction remains unchanged at $T=6$ . Let $q=0.8$ and adjust $k$ from 80 to 300, it means that the big data knowledge provider increases the subscription price of the big data knowledge when $Vi$ adopts pay-per-use pricing scheme in the big data knowledge transaction, and the usage ratio of the big data knowledge is 80%. From the experimental results in Fig. 4, the total DEPs drop slightly, but the optimal time of knowledge transaction remains unchanged at $T=4$ .

Comparing the two pricing schemes, it is suggested that the subscription price of the big data knowledge has no effect on the optimal time of knowledge transaction in the same pricing scheme, yet the usage ratio of the big data knowledge affects the optimal time of knowledge transaction. We infer that this is because the big data knowledge price holds the same for all firms in the same pricing scheme regardless of the subscription price increases or decreases. However, a caveat is that the increase in subscription price will reduce the total profit for the knowledge recipient firm.

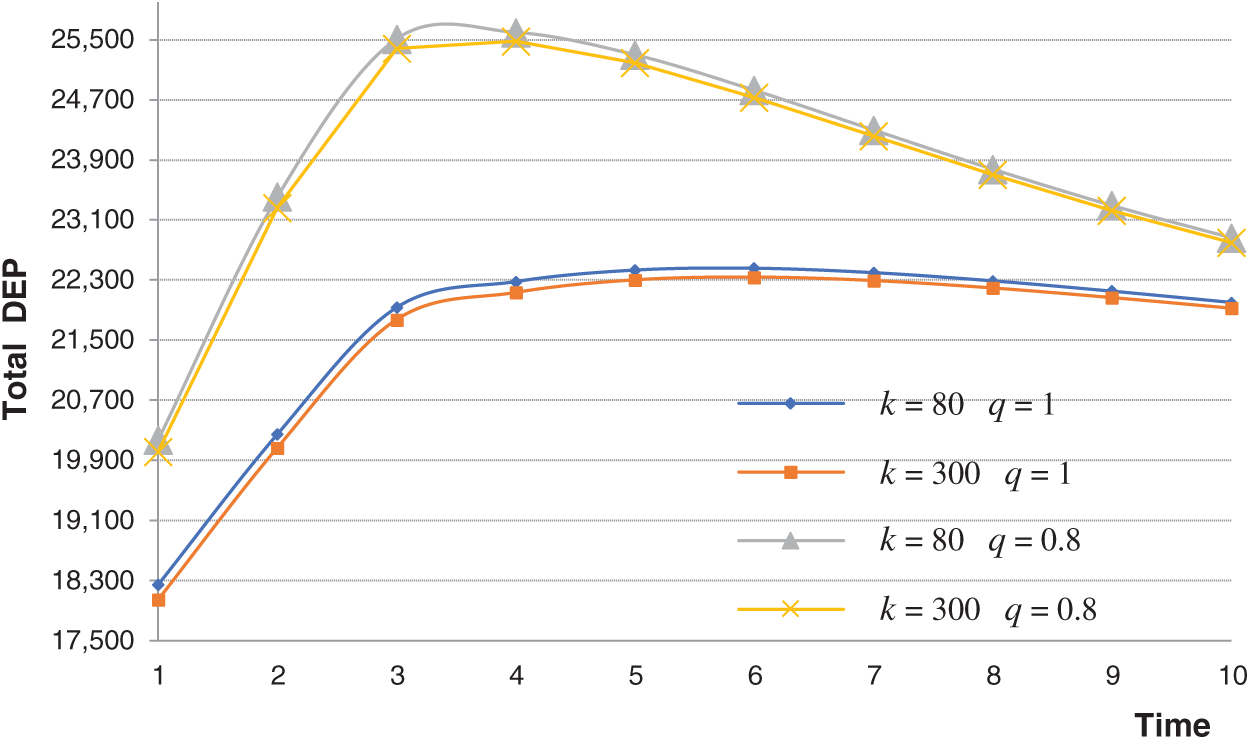
images

Figure 4: Changes of total DEP with k and q

4.2.4 Simulation with Big Data Knowledge Update Rate $β$

To explore the influence of update rate of big data knowledge $β$ on the profitability of $Vi$ with the two pricing schemes, we set all the parameters with the same values except $β$ and $q$ . Let $q=1$ and adjust $β$ from 88% to 80%, which means the big data knowledge’s update rate becomes bigger (Following previous assumptions, the big data knowledge at time period $T$ has been updated by $(qβ)T$ , which can reduce the marginal cost of $Vi$ at time period $T$ to $MC(qβ)T$ . Therefore, the smaller the value of knowledge update rate, the higher the knowledge update rate) when it adopts a subscription pricing scheme in the big data knowledge transaction. From the experimental results in Fig. 5, the total DEPs increase, and the optimal time of knowledge transaction changes from $T=6$ to $T=4$ . Then, let $q=0.8$ and adjust $β$ from 88% to 80%, it means that the update rate of big data knowledge increases when $Vi$ adopting pay-per-use pricing scheme in the big data knowledge transaction, and the usage ratio of the big data knowledge is 80%. The experimental results in Fig. 5 show, the total DEPs also increase, and the optimal time of knowledge transaction changes from $T=4$ to $T=3$ . The results show that no matter what price scheme a firm adopts in the big data knowledge transaction, a higher knowledge update rate will always bring greater profits to the firm, and the optimal time of knowledge transaction will be earlier. We conclude that firms usually choose highly efficient big data knowledge for new product development, and the higher the knowledge efficiency, the earlier the firm will conduct knowledge transactions.

Let $q=0.5$ , adjust $β$ from 95% to 88%, and then from 88% to 80%, which means that the update rate of big data knowledge becomes bigger and bigger when the usage ratio of the big data knowledge is 50%. Results in Fig. 6 show that the bigger the update rate of big data knowledge $β$ , the greater the total DEPs in the early time periods, but total DEPs in the late periods are roughly the same. Also, the optimal time of knowledge transaction remains unchanged at $T=3$ . Given we had supposed that total market share would decline at $L1=3$ , we thereby can conclude that the firm that takes lower knowledge usage ratio in the big data knowledge transaction will immediately conduct knowledge transactions and new product development as soon as it finds that the market share begins to decline. Moreover, due to the limited efficiency of knowledge at a lower usage ratio, firms must conduct knowledge transactions and update knowledge frequently.

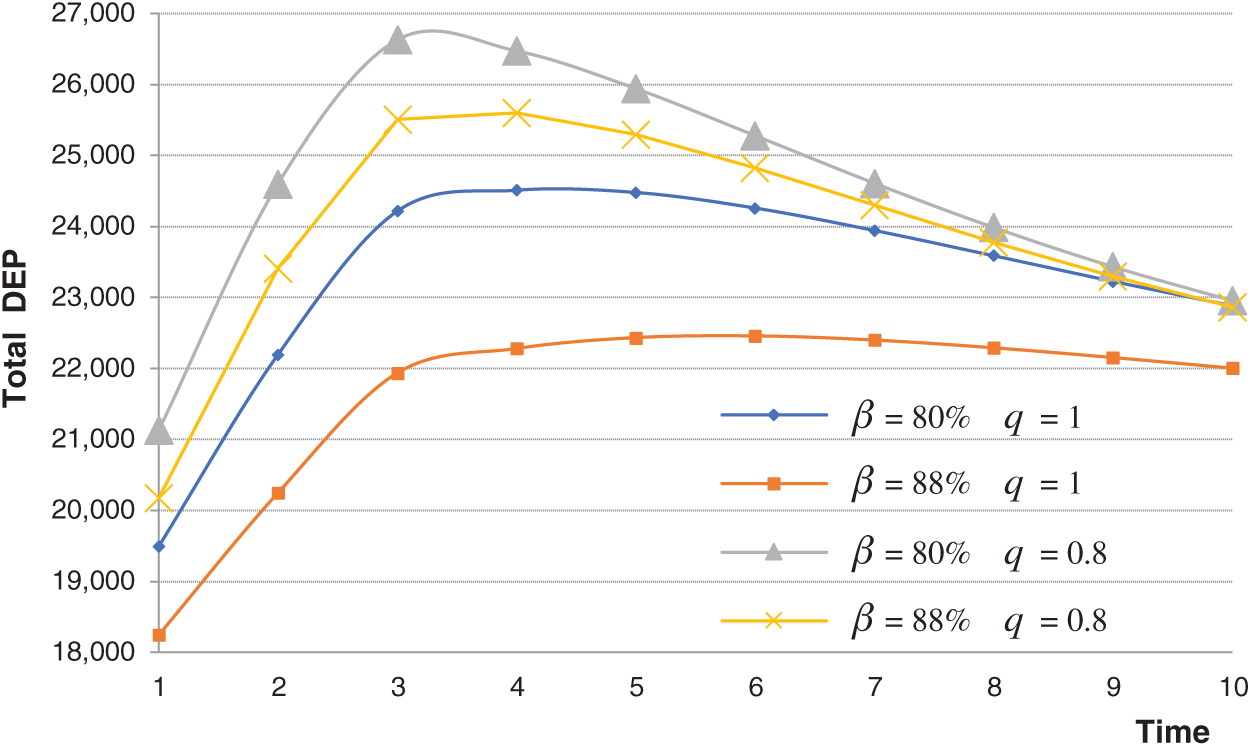
images

Figure 5: Changes of total DEP with $β$ and $q$

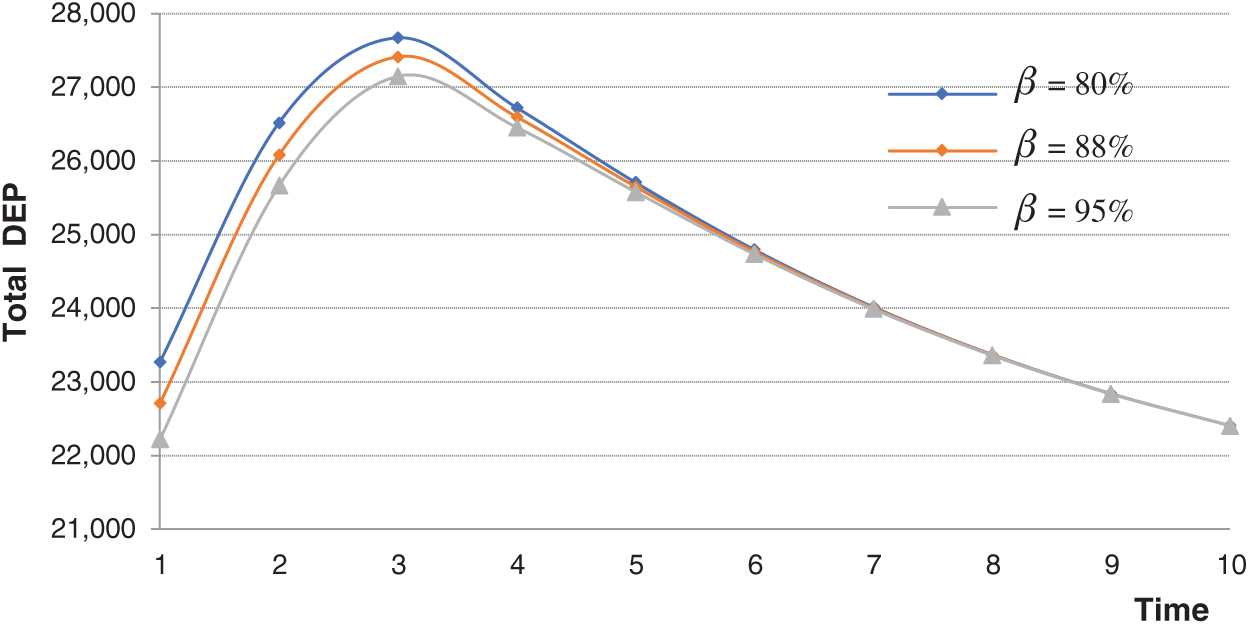
images

Figure 6: Changes of total DEP with $β$ and $q=0.5$

4.2.5 Simulation with the Market Share Growth Rate $ρ$

To compare the influence of the market share growth rate $ρ$ on the profitability of $Vi$ across the two pricing schemes, all the parameters are set with the same values except $ρ$ and $q$ . Let $q=1$ and adjust $ρ$ from 6% to 8%, which means that the new knowledge can bring bigger market share growth in the subscription pricing scheme. The experimental results in Fig. 7 indicate that the total DEPs increase consequently, and the optimal time of knowledge transaction changes from $T=6$ to $T=5$ . Then, let $q=0.8$ and adjust $ρ$ from 6% to 8%. Again, as the experiment results in Fig. 7 show, the total DEPs of $Vi$ also increase in the pay-per-use pricing scheme, and the optimal time of knowledge transaction changes from $T=4$ to $T=3$ . These results suggest that no matter what pricing scheme a firm adopts, the firm will choose the knowledge that can bring a higher market share growth rate, and the optimal time of knowledge transaction will be earlier.

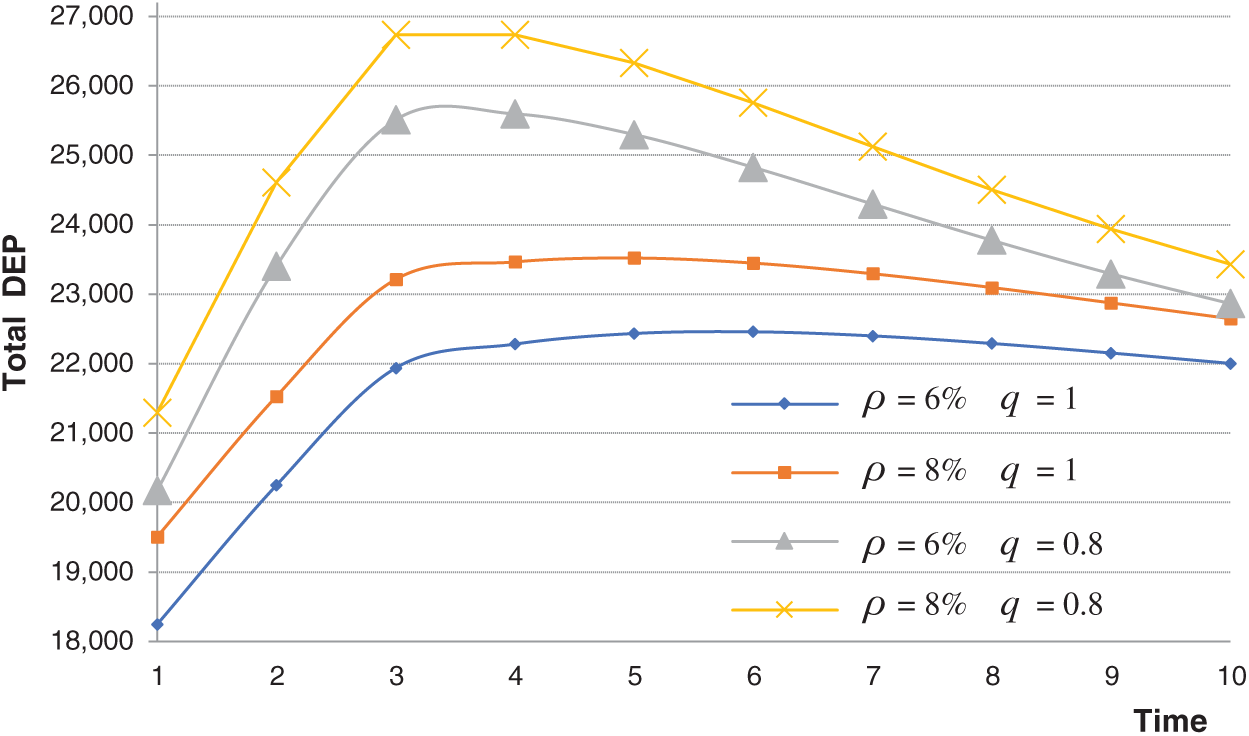
images

Figure 7: Changes of total DEP with $ρ$ and $q$

Let $q=0.5$ , adjust $ρ$ from 6% to 8%, and then from 8% to 15%, which means that there are three types of big data knowledge, and the growth rate of the market share they can bring increases sequentially. Fig. 8 shows that the highly efficient knowledge can also bring higher profits for each lower usage ratio of the big data knowledge. At the same time, the results show that the optimal time of knowledge transaction keeps unchanged at $T=3$ . Firms can choose more efficient knowledge in the pay-per-use pricing scheme by adjusting the usage ratio of knowledge usage according to their own economic conditions. Also, firms shall conduct knowledge transactions and new product development immediately when they find the market share begins to decline.

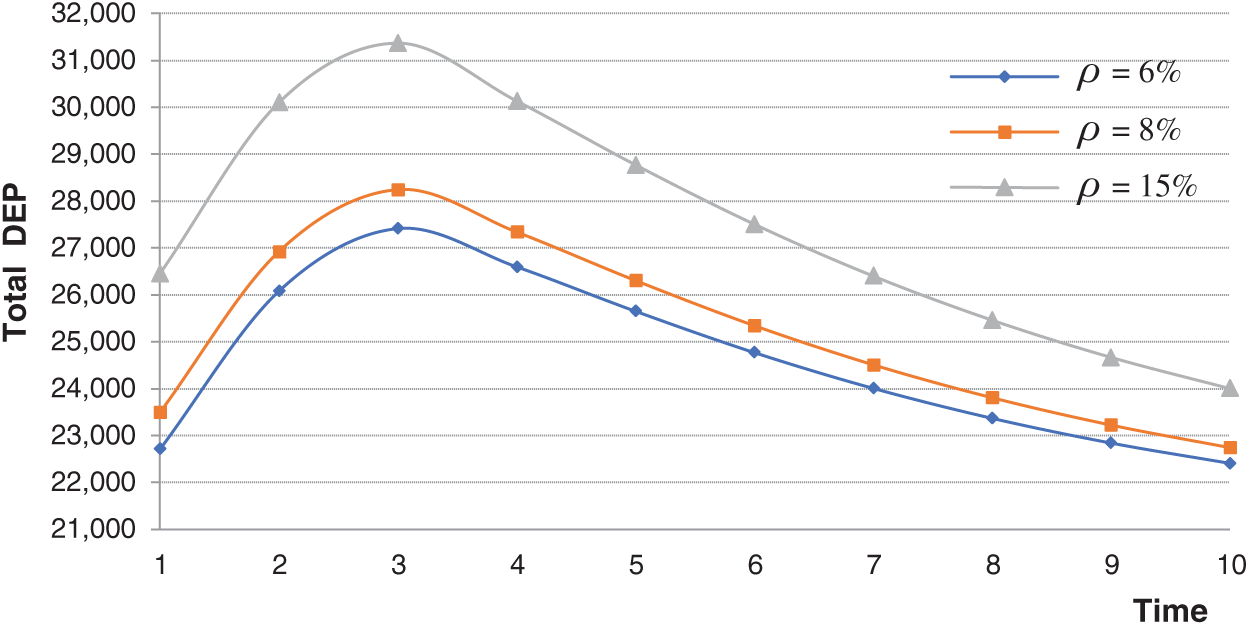
images

Figure 8: Changes of total DEP with $ρ$

5 Conclusions

Firms nowadays leverage external big data knowledge in their new product development. To facilitate more effective knowledge transactions from the perspective of firms as knowledge recipients, this present research developed a model that compares two pricing schemes commonly used by knowledge transactions recipients: subscription pricing and pay-per-use pricing. With solid theoretical and numerical analysis, we gauge and compare the two pricing schemes’ profitability in a novel and rigorous way. The theoretical model in this paper can help firms as knowledge recipients select a more suitable pricing method and forecast its effect on future new product performance.

Several important conclusions can be drawn from this research. First, the experimental result shows that the subscription price of the big data knowledge has no effect on the optimal time of knowledge transaction in the same pricing scheme, but the usage ratio of big data knowledge affects the optimal time of knowledge transaction. The smaller the usage ratio of big data knowledge the earlier the big data knowledge transaction conducts. Although the subscription price of big data knowledge has no effect on the optimal time of knowledge transaction in the same subscription pricing scheme, the increase in subscription price will make the cost of knowledge transaction increase and the firm’s total profit decrease. Second, knowledge with the higher update rate will bring greater profits to firms in these two pricing schemes. More specially, when a firm adopts the pay-per-use pricing scheme at a relatively low usage ratio, the profits brought by different update rates of knowledge are roughly the same in the later stages of the product life cycle. In addition, a firm that takes a lower knowledge usage ratio in a pay-per-use pricing scheme is suggested to conduct knowledge transactions and new product development as soon as it finds the market share begins to decline. Third, no matter what price scheme a firm adopts, the firm should choose the knowledge that can bring higher market share growth rate, so the optimal time of knowledge transaction will be earlier. Firms can choose more efficient knowledge in the pay-per-use pricing scheme by adjusting the usage ratio of knowledge usage according to their economic conditions.

However, due to the complexity of big data knowledge pricing methods, this paper’s model is subjected to a few limitations. First, we did not consider the two-part tariff pricing, albeit some scholars think it as the most profitable pricing scheme for firms [16]. Future research can take into account the two-part tariff pricing scheme. Second, the process of knowledge transactions always co-occurs with the transfer of free knowledge. Therefore, the influence of free knowledge on knowledge transactions and new product performance will be an important research avenue for further research. In addition, new product development usually requires not only big data knowledge but also private knowledge in the big data environment. Future research on pricing schemes of multiple knowledge sources is warranted.

Acknowledgement: This research was supported by the National Natural Science Foundation of China, Grant Number 71704016, the Key Scientific Research Fund of Hunan Provincial Education Department of China, Grant Number 19A006, and the Enterprise Strategic Management and Investment Decision Research Base of Hunan Province (19qyzd03).

Funding Statement: This research was funded by (the National Natural Science Foundation of China) Grant Number (71704016), (the Key Scientific Research Fund of Hunan Provincial Education Department of China) Grant Number (19A006), and (the Enterprise Strategic Management and Investment Decision Research Base of Hunan Province) Grant Number (19qyzd03).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. S. Lohr, “The age of big data,” The New York Times, 2012. [Online]. Available: http://www.nytimes.com/2012/02/12/sunday-review/big-datas-impact-in-the-world.html?_r=1&scp=1&sq=Big%20Data&st=cse. [Google Scholar]

2. F. Xhafa, “Advanced knowledge discovery techniques from big data and cloud computing,” Enterprise Information Systems, vol. 10, no. 9, pp. 945–946, 2016. [Google Scholar]

3. D. Teece, “Technology transfer by multinational firms: The resource cost of transferring technological know-how,” The Economic Journal, vol. 87, no. 346, pp. 242–261, 1977. [Google Scholar]

4. E. Chantrel, A. Grimaud and F. Tournemaine, “Pricing knowledge and funding research of new technology sectors in a growth model,” Journal of Public Economic Theory, vol. 14, no. 3, pp. 493–520, 2012. [Google Scholar]

5. E. Henry and C. J. Ponce, “Waiting to imitate: On the dynamic pricing of knowledge,” Journal of Political Economy, vol. 119, no. 5, pp. 959–981, 2011. [Google Scholar]

6. M. San Martín and A. I. Saracho, “Optimal two-part tariff licensing mechanisms,” The Manchester School, vol. 83, no. 3, pp. 288–306, 2015. [Google Scholar]

7. C. R. Wu, Y. W. Chen and F. Li, “Decision model of knowledge transfer in big data environment,” China Communications, vol. 13, no. 7, pp. 100–107, 2016. [Google Scholar]

8. C. R. Wu, V. Lee and M. E. Mcmurtrey, “Knowledge composition and its influence on new product development performance in the big data environment,” Computers, Materials & Continua, vol. 60, no. 1, pp. 365–378, 2019. [Google Scholar]

9. C. Weinhardt, A. Anandasivam, B. Blau and J. Stößer, “Business models in the service world,” IT Professional, vol. 11, no. 2, pp. 28–33, 2009. [Google Scholar]

10. A. K. Edinat, “Cloud computing pricing models: A survey,” International Journal of Scientific and Engineering Research, vol. 6, no. 9, pp. 22–26, 2019. [Google Scholar]

11. S. H. Chun and B. S. Choi, “Service models and pricing schemes for cloud computing,” Cluster Computing, vol. 17, no. 2, pp. 529–535, 2014. [Google Scholar]

12. C. R. Wu and D. M. Zeng, “Knowledge transfer optimization simulation for innovation networks,” Information Technology Journal, vol. 8, no. 4, pp. 548–594, 2009. [Google Scholar]

13. Y. H. Farzin, K. Huisman and P. Kort, “Optimal timing of technology adoption,” Journal of Economic Dynamics and Control, vol. 22, no. 5, pp. 779–799, 1998. [Google Scholar]

14. U. Doraszelski, “Innovations, improvements, and the optimal adoption of new technologies,” Journal of Economic Dynamics and Control, vol. 28, no. 7, pp. 1461–1480, 2004. [Google Scholar]

15. C. R. Wu, E. Zapevalova, Y. W. Chen and F. Li, “Time optimization of multiple knowledge transfers in the big data environment,” Computers, Materials & Continua, vol. 54, no. 3, pp. 269–285, 2018. [Google Scholar]

16. S. H. Chun, “Cloud services and pricing strategies for sustainable business models: Analytical and numerical approaches,” Sustainability, vol. 12, no. 49, pp. 1–15, 2020. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.